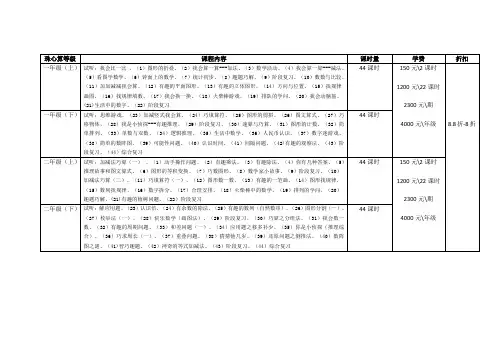
学而思奥数三年级学什么

三年级学而思奥数讲义学而思奥数作为一门培养孩子数学思维和解题能力的课程，为三年级的学生提供了更广阔的数学发展空间。

下面将对三年级学而思奥数课程的内容进行介绍，帮助孩子们更好地理解和应用数学。

一、思维培养学而思奥数注重培养孩子的数学思维能力，通过课程设计和题目训练，培养学生的逻辑思维、创造思维和问题解决能力。

在三年级的课程中，学生将接触到一些有趣的数学题目，例如数独、迷宫等，以此激发他们对数学问题的兴趣，同时提高他们的逻辑思维和推理能力。

二、数学知识点在三年级学而思奥数讲义中，包含了一系列的数学知识点。

例如，学生将学习整数的概念和运算规律，了解到整数的正负和绝对值。

同时，他们还会学习到分数的相关知识，包括分数的大小比较、分数的加减乘除等。

此外，几何图形的认识和计算也是三年级奥数的重点内容，学生将学习到平面几何和立体几何的基本概念，如长方形、正方形、圆等。

三、应用能力展示学而思奥数注重培养学生的应用能力，即将所学的数学知识应用到实际问题中。

三年级学而思奥数讲义会通过一些实际生活中的问题，如选购食材、算账等，让学生应用所学的数学知识和技巧解决问题。

这样的训练能够培养学生的数学思维和解决实际问题的能力，提高他们的数学应用水平。

四、趣味性培养学而思奥数注重培养学生对数学的兴趣和热爱。

在三年级学而思奥数讲义中，通过一些趣味的数学游戏和趣味题目，激发学生的求知欲和好奇心。

例如，谜题、魔方等，这些富有趣味性的内容能够让学生更加主动地投入到数学学习中，提高学习的积极性和主动性。

五、知识拓展除了三年级学而思奥数讲义中的基础知识之外，还有一些拓展内容供学生学习。

这些拓展内容包括数学奥赛题、高年级数学的预习等，帮助学生扩展数学知识面，提高数学素养和综合应用能力。

对于有特长或对数学感兴趣的学生而言，这些拓展内容能够提供更多的挑战和学习机会。

总结起来，在三年级学而思奥数课程中，学生将通过对数学思维的培养、数学知识点的学习、应用能力的展示、趣味性的培养以及知识的拓展等方面来提高自己的数学素养和解题能力。

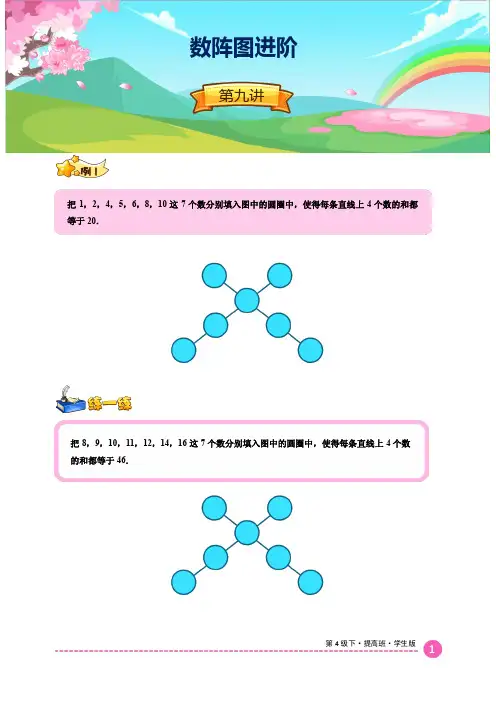
把8，9，10，11，12，14，16这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于46．把1，2，4，5，6，8，10这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于20．数阵图进阶第九讲第4级下·提高班·学生版第4级下·提高班·学生版把2，3，4，5，6，7，8这七个数分别填入图中的圆圈中，使两个正方形中四个数之和都等于19． 将5，9，13，14，17，21，25这7个数分别填入图中的圆圈中，使得每条直线上3个数的和都等于44．第4级下·提高班·学生版将5，6，9，11，14，15这6个数分别填入图中的圆圈里，使两个大圆上4个数的和都等于40．把1，5，9，10，16，21这6个数分别填入图中的○里，使每一个大圆上的四个数之和都等于36．第4级下·提高班·学生版1． 把5，6，7，8，9这5个数分别填在下图的内，使横行、竖列3个数的和都等于( )中的数．把1，3，4，5，6，8，11，15这8个数分别填入图中的圆圈里，使得每个大圆上5个数的和都等于33．第4级下·提高班·学生版2. 把3，5，7，9，11，13，15这7个数分别填入图中的圆圈内，使每条直线上的3个数的和都等于27．3. 把2，4，6，8，10，12，14，16，18这9个数分别填入下图的圆圈中，使得每条直线上的3个数的和都等于24．4.把2，3，4，5，6，7，8这七个数分别填入图中的圆圈内，使两个正方形中四个数之和都等于21．5.把1，2，4，5，6，11这6个数分别填入图中的○里，使每个圆圈上的四个数之和都等于22．第4级下·提高班·学生版第4级下·提高班·学生版6. 把2，5，6，8，10，12，14，22这8个数分别填入下图中，使得每个大圆上的5个数的和都等于49．思维跳板——剪指甲小华的爸爸1分钟可以剪好5个自己的指甲．那么，他在5分钟内可以剪好几个自己的指甲呢？。

学而思三年级奥数第十三讲巧算乘法一、乘11，101，1001的速算法一个数乘以11，101，1001时，因为11，101，1001分别比10，100，1000大1，利用乘法分配律可得a×11=a×(10＋1)=10a＋a，a×101=a×(101＋1)=100a＋a，a×1001=a×(1000＋1)=1000a＋a。

例如：38×101=38×100＋38=3838。

二、乘9，99，999的速算法一个数乘以9，99，999时，因为9，99，999分别比10，100，1000小1，利用乘法分配律可得a×9=a×(10-1)=10a-a，a×99=a×(100-1)=100a- a，a×999=a×(1000-1)=1000a-a。

例如：18×99=18×100-18=1782。

上面讲的两类速算法，实际就是乘法的凑整速算。

凑整速算是当乘数接近整十、整百、整千……的数时，将乘数表示成上述整十、整百、整千……与一个较小的自然数的和或差的形式，然后利用乘法分配律进行速算的方法。

例1 计算：(1) 356×1001 练习：38×102＝356×(1000＋1)＝356×1000＋356＝356000＋356＝356356；(2) 526×99 1234×9998＝526×(100-1)＝526×100-526＝52600-526＝52074；三、乘5，25，125的速算法一个数乘以5，25，125时，因为5×2＝10，25×4＝100，125×8＝1000，所以可以利用“乘一个数再除以同一个数，数值不变”及乘法结合律，得到例如，76×25＝7600÷4＝1900。

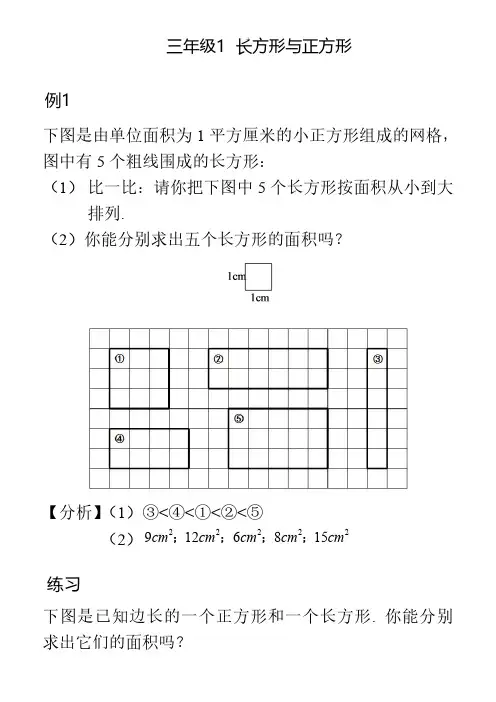
学而思三年级奥数第九讲长方形与正方形知识点：长方形的面积=长×宽正方形的面积=边长×边长不规则图形面积的计算方法与技巧合理平移、分析、转化等，即转化为标准的图形来进行面积计算。

例1 有一长方形草坪，长31米，宽26米，草坪中间留了1米的路，路把草坪分成4块（如图），求草坪的实有面积是多少？例2如下图，求出阴影部分的面积。

（四角是边长为10厘米的正方形）例3 如图，在一个正方形的水池周围，围绕着宽5米的小花园，小花园的面积为300平方米，水池的面积是多少平方米？例4 如图，求出阴影部分的面积。

（单位：厘米）例5 如图，图中大正方形比小正方形的边长多4厘米，大正方形的面积比小正方形的面积多96平方厘米，大正方形和小正方形的面积各是多少？例6如图，大正方形的面积比小正方形的面积大32平方厘米，求这两个正方形的面积。

（单位：厘米）例7 如图，正方形中套着一个长方形，正方形的边长是12分米，长方形的四个角的顶点恰好把正方形的四条边都分成两段，其中长的一段是短的一段的3倍，这个长方形的面积是多少？例8 用同样大小的长方形小纸片，摆成了如下图的形状，已知小纸片的宽度是12厘米，求阴影部分面积的和。

同步练习1、用长36厘米的一根铁丝围成一个正方形，它的面积是多少？用这根铁丝围成一个长12厘米的长方形，它的面积是多少？2、如图，有一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是花圃，花圃的面积是多少平方米？（单位：米）3、下图是由6个相等的三角形拼成的图形，求这个图形的面积？4、有两个相同的长方形，长13厘米，宽5厘米，如果把它们按如下图叠放在一起，这个图形的面积是多少？5、有一块菜地长16米，宽8米，如下图菜地中间留了2条宽2米的路，把菜地平均分成四块，每一块地的面积是多少？6、一个正方形，如果边长增加2厘米，它的面积增加16平方厘米，求原正方形面积？7、个周长为60分米的长方形，把它的长缩短6分米后，再把它的宽增加6分米，得到的新长方形面积比原来多24平方分米。

第八讲归一问题知识要点：1．概念：“归一问题”就是用除法求出单一量，现在我们所说的归一问题，一般是指已知两个相互关联的量，其中一种量在改变，而另一种量也随之按相同的变化规律而改变的问题。

2．归一问题的分类：．归一问题的分类：）正归一，也称为直进归一（1）正归一，也称为直进归一小时行驶多少千米？如：一辆汽车3小时行150千米，照这样，7小时行驶多少千米？）反归一（2）反归一千米需几小时？如：修路队6小时修路180千米，照这样，修路240千米需几小时？）常用关系公式（3）常用关系公式总数量正归一问题：单一量×份数=总数量份数反归一问题：总数量÷单一量=份数一星级题：1．一辆汽车3小时行150千米，照这样，7小时行驶多少千米？小时行驶多少千米？2．修路队6小时修路180千米，照这样，修路240千米需几小时？千米需几小时？3．学校买2套校服需要120元，照这样计算，买50套需要多少元？套需要多少元？4．一辆汽车4小时行驶240千米，照这样的速度，1分钟可行驶多少米？分钟可行驶多少米？5．一台幻灯机，6秒钟放映48张片子，照这样计算放72张片子需要多少时间？张片子需要多少时间？6．一只小蜗牛6分钟爬12分米，照这们速度1小时爬行多少米？小时爬行多少米？7．一列火车5小时行驶375公里，照这样计算，8小时行驶多少公里？小时行驶多少公里？8．妈妈买5双袜子需要15元，照这样计算，买15双袜子需要多少钱？双袜子需要多少钱？9．一艘船从甲地开往乙地，经过5小时行了250千米，照这样的速度，行驶8小时，可行多少千米？千米？10．一个粮食加工厂要磨面粉24吨，4小时磨了8吨，照这样计算，磨完剩下的面粉还要磨完剩下的面粉还要 小时？时？11．3台拖拉机耕地750平方米，照这样计算，增加12台拖拉机，一共可以耕地多少平方米？台拖拉机，一共可以耕地多少平方米？12．4台吊车7小时卸煤1414吨，照这样计算，增加5台同样的吊车，多工作8小时共卸煤多少吨？少吨？13．小明骑车3小时行60千米，照这样计算，6小时可以行多少千米？（用两种方法解）二星级题：1．豆腐加工厂磨1275千克豆腐，2小时磨150千克，照这样计算，磨完剩下的豆腐需要多少小时？小时？2．5辆拖拉机可耕地75亩，照这样计算，耕375亩地要增加几台拖拉机？亩地要增加几台拖拉机？3．一个车间要加工48个零件，4小时加工了24个，照这样计算，加工完剩下的零件还要多少小时？小时？4．4辆大卡车7次共运土140吨，照这样计算，一辆大卡车一次运土多少吨？5．修一条公路，路长48千米，前5天修10千米，照这样计算，还要修多少天才能完工？6．3台碾米机5小时可碾18750千克米，照这样计算，12台碾米机24小时可碾米多少千克？小时可碾米多少千克？7．粮食加工厂第一车间有5台磨粉机，3.2小时磨出面粉5600千克，第二车间有这样的8台磨粉机。

学而思三年级奥数第十三讲巧算乘法一、乘11，101，1001的速算法一个数乘以11，101，1001时，因为11，101，1001分别比10，100，1000大1，利用乘法分配律可得a×11=a×(10＋1)=10a＋a，a×101=a×(101＋1)=100a＋a，a×1001=a×(1000＋1)=1000a＋a。

例如：38×101=38×100＋38=3838。

二、乘9，99，999的速算法一个数乘以9，99，999时，因为9，99，999分别比10，100，1000小1，利用乘法分配律可得a×9=a×(10-1)=10a-a，a×99=a×(100-1)=100a- a，a×999=a×(1000-1)=1000a-a。

例如：18×99=18×100-18=1782。

上面讲的两类速算法，实际就是乘法的凑整速算。

凑整速算是当乘数接近整十、整百、整千……的数时，将乘数表示成上述整十、整百、整千……与一个较小的自然数的和或差的形式，然后利用乘法分配律进行速算的方法。

例1 计算：(1) 356×1001 练习：38×102＝356×(1000＋1)＝356×1000＋356＝356000＋356＝356356；(2) 526×99 1234×9998＝526×(100-1)＝526×100-526＝52600-526＝52074；三、乘5，25，125的速算法一个数乘以5，25，125时，因为5×2＝10，25×4＝100，125×8＝1000，所以可以利用“乘一个数再除以同一个数，数值不变”及乘法结合律，得到例如，76×25＝7600÷4＝1900。

三年级奥数课程简介一、课程概述三年级奥数课程旨在培养学生的数学思维能力和解决问题的能力，通过系统的讲解和丰富的练习，帮助学生掌握基础数学知识，并提高他们的逻辑思维和创新思维能力。

课程内容包括数的认识与计算、几何图形、逻辑推理、数学思维训练等方面。

二、课程目标1. 培养学生的数学兴趣和数学思维能力，提高他们的数学素养。

2. 培养学生的逻辑思维和创新思维，培养他们的问题解决能力和综合运用能力。

3. 培养学生的数学思维习惯，提高他们的思维敏锐性和逻辑推理能力。

4. 培养学生的数学语言表达能力，提高他们的沟通和合作能力。

三、课程内容1. 数的认识与计算：包括整数、小数、分数、百分数等数的认识和计算规则，通过各种实例和练习，帮助学生掌握数的概念和计算方法。

2. 几何图形：包括平面图形和立体图形的认识、性质和计算，通过绘图和实物展示，帮助学生理解各种几何图形的特点和应用。

3. 逻辑推理：通过解题和讲解，培养学生的逻辑思维和推理能力，让他们学会分析问题、找出规律和解决问题的方法。

4. 数学思维训练：通过各种练习和游戏，培养学生的数学思维能力，提高他们的数学思维水平和解决问题的能力。

四、教学方法1. 讲授法：通过系统的讲解，让学生掌握数学知识的基本概念、原理和计算方法。

2. 演示法：通过实例和练习，展示数学知识的应用和解决问题的方法，引导学生进行思考和分析。

3. 互动法：通过课堂讨论和小组合作，培养学生的合作意识和沟通能力，激发他们的学习兴趣和思维能力。

4. 实践法：通过实际操作和实物展示，让学生亲自参与，体验数学知识的应用和魅力。

五、教学效果经过三年级奥数课程的学习，学生将达到以下效果：1. 掌握数的基本概念和计算方法，能够灵活运用数学知识解决实际问题。

2. 培养良好的数学思维习惯，提高逻辑推理和问题解决能力。

3. 增强对数学的兴趣和自信心，培养数学学习的主动性和创造性。

4. 提高数学语言表达能力，培养良好的沟通和合作意识。

学而思三年级秋季课程大纲
学而思三年级秋季课程大纲包括以下内容：
1. 语文课程：
- 识字与拼音：学习更多的汉字和拼音，提高识字和拼音能力。

- 阅读理解：通过阅读课文，学习提取信息并理解课文的能力。

- 作文：培养写作能力，学习书写规范的句子和段落，提高表
达能力。

2. 数学课程：
- 数的认识：学习自然数的认识，认识数的大小关系。

- 加减法运算：掌握加减法的计算方法，并进行简单的口算练习。

- 时钟与日历：学习读时、写时、计算日期等基本技能。

3. 英语课程：
- 听力与口语：通过听力练习和口语训练，提高英语听说能力。

- 英语单词和句型：学习更多的英语单词和常用句型，扩大词
汇量。

- 阅读与写作：通过阅读故事和练习写作，培养阅读理解和写
作能力。

4. 社会课程：
- 地理：学习地理基础知识，如地球、大洲、国家等。

- 历史：了解中国的古代历史，如三皇五帝、夏商周等。

- 哲学与人文：培养思考和分析问题的能力，了解人文精神和
价值观。

5. 科学课程：
- 自然界：了解自然界的基本常识，如天气、地球等。

- 动植物：学习动植物的分类和特点，认识保护环境的重要性。

- 实验与观察：进行简单的实验和观察，培养科学实践能力。

这是一个概括性的学而思三年级秋季课程大纲，具体的课程安排和内容可能会有所变化，根据教材和教师的安排进行教学。

学而思三年级奥数第十三讲巧算乘法学而思三年级奥数第十三讲巧算乘法一、乘11，101，1001的速算法一个数乘以11，101，1001时，因为11，101，1001分别比10，100，1000大1，利用乘法分配律可得a×11=a×(10＋1)=10a＋a，a×101=a×(101＋1)=100a＋a，a×1001=a×(1000＋1)=1000a＋a。

例如：38×101=38×100＋38=3838。

二、乘9，99，999的速算法一个数乘以9，99，999时，因为9，99，999分别比10，100，1000小1，利用乘法分配律可得a×9=a×(10-1)=10a-a，a×99=a×(100-1)=100a- a，a×999=a×(1000-1)=1000a-a。

例如：18×99=18×100-18=1782。

上面讲的两类速算法，实际就是乘法的凑整速算。

凑整速算是当乘数接近整十、整百、整千……的数时，将乘数表示成上述整十、整百、整千……与一个较小的自然数的和或差的形式，然后利用乘法分配律进行速算的方法。

例1 计算：(1) 356×1001 练习：38×102＝356×(1000＋1)＝356×1000＋356＝356000＋356＝356356；(2) 526×99 1234×9998＝526×(100-1)＝ 526×100-526＝ 52600-526＝52074；三、乘5，25，125的速算法一个数乘以 5，25，125时，因为 5×2＝10，25×4＝100，125×8＝1000，所以可以利用“乘一个数再除以同一个数，数值不变”及乘法结合律，得到例如，76×25＝7600÷4＝1900。

第六讲 三年级奥数巧求周长1、 周长：围成一个图形的所有边长的总和就是这个图形的周长。

2、长方形周长 （长 宽） 2，如果 C 表示长方形的周长， a 表示长方形的长， b 表示 长方形的宽，则长方形的周长可以写成 C （a b ） 2 . 3、正方形的周长 =边长 4，如果用 C 表示正方形的周长， a 表示正方形的边长，则正方形的周长可以写成 C a 4.4、 正方形四条边都相等，长方形对边相等。

类型一：不规则图形——平移】2 厘米的正方形拼成的，你能算出这个图形的周长是多少变式 1：计算下面各图的周长。

（单位：厘米）9 厘米、 8 厘米和 7 厘米的 4 个正方形按从大到小的顺序排 成一行（如图） ，排成的图形周长是（ ）厘米。

变式 2：求下列图形的周长． （ 单位：米 ）3020801015134013例 2】把边长分别是 10 厘米、6 个边长都是 1008变式 1：下图是一座楼房的平面图 , 图中不同字母表示长度不同的各条边 . 已知 b 50 米,c 30米, g 10米, 这座楼房平面的周长是米。

变式 3：一个长为 12厘米， 宽为 10厘米的长方形， 挖去一个边长为 4 厘米的正方形补在另 边上（如图） 。

所得图形的周长为 _ 厘米。

【例 3】将 19张边长为 1分米的正方形纸片，按顺序一张一张地摆放在地板上，摆的时候， 要求后摆的纸片必须有一个顶点与前一张纸片的中心重合 （图中表示已经摆好的 5 张），地板 上摆好后图形的周长是多少？变式： 李明将 5 张扑克牌像下图那样摆放，已知扑克牌的长是 86 毫米，宽 56 毫米，那么这 个摆成后的图形的周长是多少？b 8 厘米，c 3 厘米，图形的周长为（ ）厘米。

a 10 厘米，类型二：等量代换】例1】8 个同样的小长方形拼成一个大长方形，大长方形的周长是84厘米，小长方形的周长是多少厘米？变式1：由9 个相等的小长方形拼成的大长方形，已知小长方形的宽是12厘米，求大长方形的周长是多少厘米？变式2：下图是由三个同样的长方形拼成的，求周长是多少？变式3：李明从A走到B再走到C再到 D ，走了38米，马力从B到C再到D再到A走了31 米，问此长方形的水池ABCD 的周长是多少米？【类型三：规则图形的变化】【例1】如图，一个正方形被分成 6 个大小、形状完全一样的长方形，每个长方形的周长都是14 厘米。

第4级下·提高班·学生版 1将两张同样长的纸粘成了一张长为80寸的长纸条，其中粘在一起的部分长10寸，这两张纸条各长多少寸？把两根长为20寸的短尺用绳子捆成一根长尺，中间捆在一起的重叠部分是3寸.捆成的长尺多少寸？重叠问题第八讲第4级下·提高班·学生版2 学校的学生人人参加比赛，有20人参加足球比赛，有26人参加毽子比赛．其中有4人两种比赛都参加．一共有学生多少人？有两根铁丝，一根长为30厘米，另一根长为50厘米，将这两根铁丝焊接成一根长为75厘米的长铁丝．那么，中间的焊接重叠部分长为多少厘米？3第4级下·提高班·学生版有蓝色和红色两种珠花，每人至少选一种，共有48人，有30人选了蓝色珠花，有13人两种都选了，那么选红色珠花的有多少人？20个学生参加琵琶表演和古筝表演，其中有16人参加了琵琶表演，12人参加了古筝表演．问两种表演都参加的有多少学生？第4级下·提高班·学生版4 1.有两块木板，一块长72厘米，另一块长56厘米，如果把两块木板重叠后钉成一块木板，重叠部分是20厘米.求钉成后的木板长多少厘米？有60人学习制作镜子，经过一段时间的训练后，有33人学会了制作星云镜，有25人学会了制作幻镜，其中既会制作星云镜又会制作幻镜的有10人．那么既不会制作星云镜又不会制作幻镜的有多少人？2.明明用胶水将两张同样长的纸粘成了一张长为195厘米的长纸条，其中粘在一起的部分长5厘米，这两张纸条各长多少厘米？3.三年级同学参加科技和美术两个课外兴趣小组，参加科技组的有36人，参加美术组的有28人，两个小组都参加的有8人，三年级一共有多少人参加课外兴趣小组？第4级下·提高班·学生版5第4级下·提高班·学生版6 4.三年级同学有50人参加科技和美术两个课外兴趣小组，其中参加科技组的有32人，参加美术组的有28人，两个小组都参加的有多少人？5.有101个同学带着水壶和水果去春游，其中带水壶的有78人，带水果的有71人，只带水壶和只带水果的各有多少人？6.某餐馆有27道招牌菜．小悦吃过其中的13道，冬冬吃过其中的7道，而且有2道菜是两人都吃过的．请问：有多少道招牌菜是两人都没有吃过的？思维跳板——水果一条街这里有一条街，整条街都是卖水果的店铺．其中卖苹果的有32家，卖香蕉的有46家，既卖苹果又卖香蕉的有20家，剩下的12家不卖苹果也不卖香蕉．那么，你知道这儿一共有多少家水果店吗?第4级下·提高班·学生版7。

小学奥数三年级知识点小学奥数是一种培养学生数学思维和解决问题能力的数学竞赛活动。

对于三年级的学生来说，奥数的学习不仅能够锻炼他们的逻辑思维，还能激发他们对数学的兴趣。

以下是一些适合三年级学生学习的关键奥数知识点：1. 四则运算三年级学生应该掌握基本的加减乘除运算，包括整数和小数的运算。

同时，他们还需要学会简单的分数运算，理解分数的基本性质。

2. 整数的性质学生需要了解整数的奇偶性、因数和倍数的概念。

同时，他们应该学会如何找到两个数的最小公倍数和最大公约数。

3. 简单的数列数列是数学中的一个重要概念，三年级学生可以从等差数列开始学习，理解数列的规律性，并能够根据数列的规律解决问题。

4. 简单的几何知识学生应该能够识别基本的几何图形，如三角形、正方形、长方形和圆形。

同时，他们需要了解这些图形的基本属性，如边长、周长和面积。

5. 图形的分割与组合学生需要学会如何将一个图形分割成更小的部分，或者将几个图形组合成一个新的图形。

这有助于他们理解图形的可变性和创造性。

6. 简单的逻辑推理逻辑推理是数学问题解决中不可或缺的一部分。

学生应该学会如何通过已知条件推导出未知条件，或者通过逻辑排除法解决问题。

7. 简单的代数概念虽然代数是稍高年级的课程内容，但三年级学生可以开始接触一些基础的代数概念，如变量、方程式和简单的代数表达式。

8. 问题解决策略学生需要学会如何分析问题，确定解决问题所需的步骤，并能够灵活运用不同的策略来解决问题。

9. 数学游戏和活动通过数学游戏和活动，学生可以在轻松愉快的氛围中学习数学，同时锻炼他们的数学思维和团队合作能力。

通过这些知识点的学习，三年级的学生不仅能够打下坚实的数学基础，还能够培养他们解决问题的兴趣和能力。

教师和家长应该鼓励学生积极参与数学活动，激发他们的学习热情。

同时，也要注意不要给学生过多的压力，让他们在享受学习的过程中自然地掌握这些知识。

三年级奥数知识点汇总三年级奥数知识点涵盖了数学基础和一些拓展思维的题目，以下是一些重要的知识点汇总：1. 基础运算：熟练掌握加减乘除的基本运算规则，包括多位数的加减法和乘法，以及简单的除法。

2. 数的认识：理解自然数、整数的概念，以及数的分类，如奇数、偶数、质数、合数等。

3. 数的分解：掌握数的分解方法，如将一个数分解成质因数的乘积。

4. 数列问题：初步了解等差数列和等比数列的概念，能够解决一些简单的数列问题。

5. 图形的计数：学会对图形进行计数，如点、线、面的数量统计。

6. 几何图形：认识基本的几何图形，如正方形、长方形、三角形、圆等，并理解其基本属性。

7. 图形的分割与组合：学会将复杂图形分割成简单图形，或将简单图形组合成复杂图形。

8. 逻辑推理：培养逻辑推理能力，解决一些简单的逻辑问题。

9. 时间与日期：理解时间的基本概念，如小时、分钟、秒，以及日期的计算。

10. 货币与交易：认识货币单位，理解基本的交易和找零问题。

11. 速度、路程与时间：理解速度、路程和时间之间的关系，能够解决相关问题。

12. 概率初步：了解概率的基本概念，能够解决一些简单的概率问题。

13. 问题解决策略：学会使用画图、列表、假设等方法来解决数学问题。

14. 数学游戏：参与一些数学游戏，如数独、24点游戏等，以培养数学兴趣和思维能力。

15. 数学思维训练：通过解决一些有趣的数学问题，训练逻辑思维和创造性思维。

结束语：三年级的奥数学习不仅能够巩固数学基础知识，还能激发孩子们的数学兴趣，培养他们的逻辑思维和解决问题的能力。

希望以上的知识点汇总能够帮助孩子们更好地理解和掌握奥数知识。

目录第一讲加减法的巧算（一） (2)第二讲加减法的巧算（二） (7)第三讲乘法的巧算 (12)第四讲配对求和 (16)第五讲找简单的数列规律 (17)第六讲图形的排列规律 (19)第七讲数图形 (23)第八讲分类枚举 (26)能力测试（一） (26)第九讲填符号组算式 (28)第十讲填数游戏 (31)第十一讲算式谜（一） (35)第十二讲算式谜（二） (37)第十三讲火柴棒游戏（一） (39)第十四讲火柴棒游戏（二） (40)第十五讲从数量的变化中找规律 (45)第十六讲数阵中的规律 (45)第17讲时间与日期……………第18讲推理……………能力测试（二） (63)第19讲循环………………第20讲最大和最小…………………………第21讲最短路线…………………………第22讲图形的分与合…………………第23讲格点与面积……………………第24讲一笔画………………………阶段测试（三）……………………第25讲移多补少与求平均数………………第26讲上楼梯与植树………………第27讲简单的倍数问题……………………第28讲年龄问题……………………………第29讲鸡兔同笼问题……………………第30讲盈亏问题…………………第32讲周长的计算……………………第33讲等量代换……………………第34讲一题多解……………………能力测试（四）………………………………第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。

选手们为争夺冠军，都在舞台上发挥着自己的最好水平。

台下的工作人员小熊和小白兔正在统计着最后的得分。

由于他们对每个选手分数的及时通报，台下的观众频频为选手取得的好成绩而热烈鼓掌，同时，观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。

观众的情绪也影响着两位分数统计者。

只见分数一到小白兔手中，就像变魔术般地得出了答案。

等小熊满头大汗地算出来时，小白兔已欣赏了一阵比赛，结果每次小熊算得结果和小白兔是一样的。

小熊不禁问：“白兔弟弟，你这么快就算出了答案，有什么决窍吗？”小白兔说：“比如2号选手是93、95、98、96、88、89、87、91、93、91，去掉最高分98，去掉最低分87，剩下的都接近90为基准数，超过90的表示成90+‘零头数’，不足90的表示成90－‘零头数’。

学而思三年级奥数鸡兔同笼进阶学而思第十五讲鸡兔同笼进阶我国古代数学名著《孙子算经》中有这样的一道应用题：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各有几何?意思是说:鸡和兔同关在一个笼子里，已知鸡与兔共有35只，鸡脚与兔脚共有94只，问鸡、兔各有多少只? 这就是著名的鸡兔同笼问题。

怎样解决这个问题呢?我们通常把题中相当于“鸡”和“兔”的两种量，全部假设看作“鸡”或“兔”，然后找出与实际数量的差，由此求出“鸡”或“兔”，这种解决问题的方法就是假设法。

鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置出来。

解鸡兔同笼问题的基本关系式是：解法1：鸡的只数=（每只兔脚数×兔总数－实际脚数）÷（每只兔子脚数－每只鸡的脚数）兔的只数=总只数－鸡的只数解法2：兔的只数=（总脚数－鸡的脚数×总只数）÷（兔的脚数－鸡的脚数）鸡的只数=总只数－兔的只数例1 、鸡兔同笼，头共46，足共128，鸡兔各几只？解：假设 46只都是兔。

共应有： 4×46=184（只）比128只脚多：184-128=56（只）如果用一只鸡来置换一只兔，就要减少：4-2=2（只）鸡的只数：56÷2=28（只）兔的只数：46－28=18（只）例2、小梅数她家的鸡与兔，数头有16个，数脚有44只。

问：小梅家的鸡与兔各有多少只？解：假设16只都是鸡。

共应有：2×16＝32（只）比44只脚少： 44-32＝12（只）如果用一只兔来置换一只鸡，就要增加：4-2=2（只）兔的只数：12÷2=6（只）鸡的只数：16－6=10（只）1、鸡兔同笼,共有头100个,足316只,那么鸡有多少只？兔有多少只？2、、鸡兔同笼，共有30个头，88只脚。

笼子中鸡、兔各有多少只？3、鸡与兔共40只，鸡的脚数与兔的脚数共有90只。

问鸡、兔各多少只？4、现在有大小油桶50个，每个大桶可装油4千克，每个小桶可装油2千克，大桶比小桶共多装油20千克，问大、小油桶各多少个?5、某人领得工资240元,有2元,5元,10元三种人民币共50张,其中2元和5元的张数一样多,那么10元的有多少张？6、四（6）班42个同学向2008年北京奥运会捐款。