下载文档原格式
![[课件]信息论课程讲义-第五章 纠错编码原理PPT](https://img.taocdn.com/s1/m/6d5e32f080eb6294dd886c6a.png)
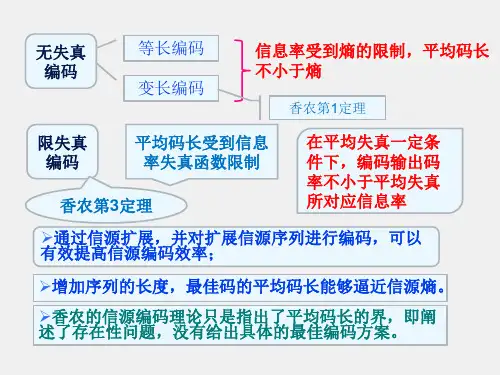
信息论与编码第5章第五章信源编码（第⼗讲）（2课时）主要内容：（1）编码的定义（2）⽆失真信源编码重点：定长编码定理、变长编码定理、最佳变长编码。
难点：定长编码定理、哈夫曼编码⽅法。
作业：5。
2，5。
4，5。
6；说明：本堂课推导内容较多，枯燥平淡，不易激发学⽣兴趣，要注意多讨论⽤途。
另外，注意，解题⽅法。
多加⼀些内容丰富知识和理解。
通信的实质是信息的传输。
⽽⾼速度、⾼质量地传送信息是信息传输的基本问题。
将信源信息通过信道传送给信宿，怎样才能做到尽可能不失真⽽⼜快速呢？这就需要解决两个问题：第⼀，在不失真或允许⼀定失真的条件下，如何⽤尽可能少的符号来传送信源信息；第⼆，在信道受⼲扰的情况下，如何增加信号的抗⼲扰能⼒，同时⼜使得信息传输率最⼤。
为了解决这两个问题，就要引⼊信源编码和信道编码。
⼀般来说，提⾼抗⼲扰能⼒（降低失真或错误概率）往往是以降低信息传输率为代价的；反之，要提⾼信息传输率常常⼜会使抗⼲扰能⼒减弱。
⼆者是有⽭盾的。
然⽽在信息论的编码定理中，已从理论上证明，⾄少存在某种最佳的编码或信息处理⽅法，能够解决上述⽭盾，做到既可靠⼜有效地传输信息。
这些结论对各种通信系统的设计和估价具有重⼤的理论指导意义。
§3.1 编码的定义编码实质上是对信源的原始符号按⼀定的数学规则进⾏的⼀种变换。
讨论⽆失真信源编码，可以不考虑⼲扰问题，所以它的数学描述⽐较简单。
图 3.1是⼀个信源编码器，它的输⼊是信源符号},,, {21q s s s S =，同时存在另⼀符号},,,{21r x x x X =，⼀般来说，元素xj 是适合信道传输的，称为码符号（或者码元）。
编码器的功能就是将信源符号集中的符号s i （或者长为N 的信源符号序列）变换成由x j (j=1,2,3,…r)组成的长度为l i 的⼀⼀对应的序列。
输出的码符号序列称为码字，长度l i 称为码字长度或简称码长。
可见，编码就是从信源符号到码符号的⼀种映射。
