立体几何证明简单例题
- 格式:doc
- 大小:282.00 KB
- 文档页数:4

2023年高考数学----两角相等(构造全等)的立体几何问题典型例题讲解【规律方法】 构造垂直的全等关系 【典型例题】例1.如图,已知三棱柱−111ABC A B C 的底面是正三角形,侧面11BB C C 是矩形,M ,N 分别为BC ,11B C 的中点,P 为AM 上一点.过11B C 和P 的平面交A B 于E ,交A C 于F . (1)证明:1//AA MN ,且平面⊥1A AMN 平面11EB C F ;(2)设O 为△111A B C 的中心.若//AO 平面11EB C F ,且=AO AB ,求直线1B E 与平面1A AMN 所成角的正弦值.【解析】(1)证明:M Q ,N 分别为BC ,11B C 的中点,底面为正三角形, ∴=1B N BM ,四边形1BB NM 为矩形,⊥111A N B C ,∴1//BB MN ,11//AA BB Q ,∴1//AA MN , ⊥11MN B C Q ,⊥111A N B C ,⋂=1MN A N N , ∴⊥11B C 平面1A AMN ,⊂11B C Q 平面11EB C F , ∴平面⊥1A AMN 平面11EB C F ,综上,1//AA MN ,且平面⊥1A AMN 平面11EB C F .(2)解:Q 三棱柱上下底面平行,平面11EB C F 与上下底面分别交于11B C ,EF ,∴11////EF B C BC ,//AO Q 面11EB C F ,⊂AO 面1A MNA ,面⋂1AMNA 面=11EB C F PN ,∴//AO PN ,四边形APNO 为平行四边形, O Q 是正三角形的中心,=AO AB ,∴=13A N ON ,=3AM AP ,===113PN BC B C EF ,由(1)知直线1B E 在平面1A AMN 内的投影为PN ,直线1B E 与平面1A AMN 所成角即为等腰梯形11EFC B 中1B E 与PN 所成角, 在等腰梯形11EFC B 中,令=1EF ,过E 作⊥11EH B C 于H , 则===113PN B C EH ,=11B H,=1B E∠==111sin B H B EH B E, ∴直线1B E 与平面1A AMN.例2.如图,在锥体−P ABCD 中,ABCD 是边长为1的菱形,且∠=︒60DAB,==PA PD =2PB ,E ,F 分别是BC ,PC 的中点(1)证明:⊥AD 平面DEF (2)求二面角−−P AD B 的余弦值.【解析】(1)取AD 的中点G ,连接PG ,BG ,在∆ABG 中,根据余弦定理可以算出==BG ,发现+=222AG BG AB ,可以得出⊥AD BG ,又//DE BG ∴⊥DE AD ,又=PA PD ,可以得出⊥AD PG ,而⋂=PG BG G , ∴⊥AD 平面PBG ,而⊂PB 平面PBG , ∴⊥AD PB ,又//PB EF , ∴⊥AD EF .又⋂=EF DE E , ∴⊥AD 平面DEF .(2)由(1)知,⊥AD 平面PBG ,所以∠PGB 为二面角−−P AD B 的平面角,在∆PBG 中,==PG ,=BG ,=2PB ,由余弦定理得+−∠==⋅222cos 2PG BG PB PGB PG BG ,因此二面角−−P AD B 的余弦值为.本课结束。

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点。
1)证明EFGH是平行四边形。
2)已知BD=23,AC=2,EG=2,求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图,已知空间四边形ABCD中,BC=AC,AD=BD,E 是AB的中点。
1)证明AB垂直于平面CDE。
2)证明平面CDE垂直于平面ABC。
3.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90,SA垂直于面ABC,AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点。
1)证明C1O平行于面AB1D1.2)证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1)证明AC垂直于平面B1D1D。
2)证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1)证明平面A1BD平行于平面B1DC。
2)已知E、F分别是AA1、CC1的中点,证明平面EB1D1平行于平面FBD。
8.四面体ABCD中,AC=BD,E、F分别为AD、BC的中点,且EF=AC/2,∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点,PA=PB,CB垂直于平面PAB,M是PC的中点,N是AB上的点,AN=3NB。
1)证明XXX垂直于AB。
2)当∠APB=90,AB=2BC=4时,求MN的长度。
10.如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
1)证明A1C平行于平面BDE。
2)证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD,PA垂直于平面ABCD,AB=2,PA=AD=4,E为BC的中点。

立体几何证明题精选1.在多面体中,矩形ABB1A1和ACC1A1,AC垂直于BC。
证明BC垂直于平面ACC1A1,同时在线XXX上存在一点M,使得DE与平面A1MC平行。
2.在三棱锥P-ABC中,D,E,F分别是棱PC,AC,AB 的中点。
已知PA垂直于AC,PA=6,BC=8,DF=5.证明PA 平行于平面DEF,同时平面BDE垂直于平面ABC。
3.在四棱锥P-ABCD中,AP垂直于平面PCD,AD平行于BC,AB和BC分别为线段AD和PC的中点。
证明AP平行于平面BEF,同时BE垂直于平面PAC。
4.在四棱锥P-ABCD中,底面ABCD是平行四边形,BA=BD=BC=1,AD=2,PA=PD=√5,E和F分别是棱AD和PC的中点。
证明EF平行于平面PAB,同时平面PBC垂直于平面ABCD。
5.在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB垂直于BC,AA1=AC=2,BC=1,E和F分别是A1C1和BC的中点。
证明平面ABE垂直于平面B1BCC1,C1F平行于平面ABE,同时求三棱锥E-ABC的体积。
6.在四棱锥P-ABCD中,底面ABCD为矩形,PA垂直于平面ABCD,E为PD的中点。
证明PB平行于平面AEC,同时若AP=1,AD=3,则三棱锥P-ABD的体积为2/3,求A到平面PBC的距离。
7.在四棱锥中,平面ACD和平面ABD的交线为直线L,平面ABC和平面ACD的交线为直线M,平面ABC和平面ABD的交线为直线N,P为直线L上一点,Q为直线M上一点,R为直线N上一点,且PQR平行于平面ABCD,证明PR 平行于直线BD,同时求四面体PQRD的体积。
8.在长方体ABCD-A1B1C1D1中,底面A1B1C1D1为正方形,O为BD的中点,E为棱AA1上任意一点。
证明BD垂直于EC1,同时若AB=2,AE=2,OE垂直于EC1,则AA1的长度为2√2.。

高中数学第八章立体几何初步知识总结例题单选题1、如图,点N为正方形ABCD的中心,ΔECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线答案:B解析:利用垂直关系,再结合勾股定理进而解决问题.如图所示,作EO⊥CD于O,连接ON,过M作MF⊥OD于F.连BF,∵平面平面ABCD.EO⊥CD,EO⊂平面CDE,∴EO⊥平面ABCD,MF⊥平面ABCD,∴ΔMFB与ΔEON均为直角三角形.设正方形边长为2,易知EO=√3,ON =EN=2,MF=√32,BF=52,∴BM=√7.∴BM≠EN,故选B.CDE小提示:本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.2、如图直角△O′A′B′是一个平面图形的直观图,斜边O′B′=4,则原平面图形的面积是()A.8√2B.4√2C.4D.√2答案:A解析:根据斜二测画法规则可求原平面图形三角形的两条直角边长度,利用三角形的面积公式即可求解. 由题意可知△O′A′B′为等腰直角三角形,O′B′=4,则OʹAʹ=2√2,所以原图形中,OB=4,OA=4√2,故原平面图形的面积为1×4×4√2=8√2.2故选:A3、如图,用斜二测画法作水平放置的正三角形A1B1C1的直观图,则正确的图形是()A.B.C.D.分析:由斜二侧画法的规则分析判断即可先作出一个正三角形A1B1C1,然后以B1C1所在直线为x轴,以B1C1边上的高所在的直线为y轴建立平面直角坐标系,画对应的x′,y′轴,使夹角为45°,画直观图时与x轴平行的直线的线段长度保持不变,与y轴平行的线段长度变为原来的一半,得到的图形如图,然后去掉辅助线即可得到正三角形的直观图如图,故选:A4、下列空间图形画法错误的是()A.B.C.D.分析:根据空间图形画法:看得见的线画实线,看不见的线画虚线.即可判断出答案.D选项:遮挡部分应画成虚线.故选:D.5、如图,已知正方体的棱长为a,沿图1中对角面将它分割成两个部分,拼成如图2的四棱柱,则该四棱柱的全面积为()A.(8+2√2)a2B.(2+4√2)a2C.(4+2√2)a2D.(6−4√2)a2答案:C分析:拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,据此变化,进行求解. 由题意,拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,由于截面为矩形,长为√2a,宽为a,所以面积为√2a2,所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选:C.6、已知三棱锥A−BCD的所有顶点都在球O的球面上,且AB⊥平面BCD,AB=2√3,AC=AD=4,CD= 2√2,则球O的表面积为()A.20πB.18πC.36πD.24π答案:A分析:根据AB⊥平面BCD,得到AB⊥BC,AB⊥BD,再由AB=2√3,AC=AD=4,CD=2√2,得到BC⊥BD,则三棱锥A−BCD截取于一个长方体,然后由长方体的外接球即为三棱锥的外接球求解.因为AB⊥平面BCD,所以AB⊥BC,AB⊥BD,∴BC=BD=√42−(2√3)2=2,在△BCD中,CD=2√2,∴CD2=BC2+BD2,∴BC⊥BD.如图所示:三棱锥A−BCD的外接球即为长方体AGFH-BCED的外接球,设球O的半径为R,则2R=√BA2+BC2+BD2=√(2√3)2+22+22=2√5,解得R=√5,所以球O的表面积为20π,故选:A.7、下列条件中,能得出直线m与平面α平行的是()A.直线m与平面α内的所有直线平行B.直线m与平面α内的无数条直线平行C.直线m与平面α没有公共点D.直线m与平面α内的一条直线平行答案:C分析:根据线面平行的判定,线面平行的性质逐个辨析即可.对A ,直线m 与平面α内的所有直线平行不可能,故A 错误;对B ,当直线m 在平面α内时,满足直线m 与平面α内的无数条直线平行,但m 与α不平行;对C ,能推出m 与α平行;对D ,当直线m 在平面α内时,m 与α不平行.故选:C.8、如图是长方体被一平面所截得到的几何体,四边形EFGH 为截面,长方形ABCD 为底面,则四边形EFGH 的形状为( )A .梯形B .平行四边形C .可能是梯形也可能是平行四边形D .矩形答案:B解析:利用面面平行的性质判断EF 与的平行、EH 与FG 平行.因为平面ABFE //平面CGHD ,且平面EFGH ∩平面ABFE =EF ,平面EFGH ∩平面CGHD =GH ,根据面面平行的性质可知EF //,同理可证明EH //FG .所以四边形EFGH 为平行四边形.故选:B.小提示:本题考查长方体截面形状判断,考查面面平行的性质应用,较简单.多选题9、(多选)一个几何体有6个顶点,则这个几何体可能是( )A .三棱柱B .三棱台C .五棱锥D .四面体答案:ABCGH GH分析:根据棱柱、棱台、棱锥及四面体的图形分析,即可得答案.对于A ,三棱柱是上下两个三角形,有6个顶点,满足题意;对于B ,三棱台是上下两个三角形,有6个顶点,满足题意;对于C ,五棱锥是底面为五边形及一个顶点,有6个顶点,满足题意;对于D ,四面体的顶点个数为4个,不满足题意.故选:ABC.10、我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知半球内有一个方锥,方锥的底面内接于半球的底面,方锥的顶点在半球的球面上,若方锥的体积为18,则半球的说法正确的是( )A .半径是3B .体积为18πC .表面积为27πD .表面积为18π答案:ABC分析:作出正四棱锥的对角面,为半球的半个大圆的内接三角形,由图形可用球的半径表示出棱锥底面边长,高,由棱锥体积求得半球半径.然后计算半球体积,表面积,判断各选项.如图,是正四棱锥的对角面,设球半径为r ,AC 是半圆的直径,则正四棱锥底面边长为√2r ,棱锥体积为V =13×(√2r)2×r =23r 3=18,r =3, 半球体积为V =23πr 3=23π×33=18π,表面积为S =2π×32+π×32=27π,故选:ABC .11、如图,正方体ABCD −A 1B 1C 1D 1的棱长为1,则下列四个命题正确的是( )PAC △PAC△A.两条异面直线D1C和BC1所成的角为π4B.直线BC与平面ABC1D1所成的角等于π4C.点D到面ACD1的距离为√33D.三棱柱AA1D1−BB1C1外接球半径为√32答案:BCD分析:对于A:根据异面直线的求法易得:异面直线D1C和BC1所成的角为∠AD1C;对于B:可证B1C⊥平面ABC1D1,则直线BC与平面ABC1D1所成的角为∠CBC1;对于C:根据等体积转换V D−ACD1=V D1−ACD,求点D到面ACD1的距离;对于D:三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球,直接求正方体外接球的半径即可.连接AC、AD1∵AB∥C1D1且AB=C1D1,则四边形ABC1D1为平行四边形,∴异面直线D1C和BC1所成的角为∠AD1C∵AC=AD1=D1C,则△ACD1为正三角形,即∠AD1C=π3A不正确;连接B1C在正方形BB1C1C中,BC1⊥B1C∵AB⊥平面BB1C1C,B1C⊂平面BB1C1C∴AB⊥B1CAB∩BC1=B,则B1C⊥平面ABC1D1∴直线BC与平面ABC1D1所成的角为∠CBC1=π4 B正确;根据等体积转换可知:V D−ACD1=V D1−ACD即13×ℎ×12×√2×√2×√32=13×1×12×1×1,则ℎ=√33C正确;三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球则外接球的半径即为正方体ABCD−A1B1C1D1体对角线的一半,即R=√32D正确;故选:BCD.12、如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E−ACD,F−ABC,F−ACE的体积分别为V1,V2,V3,则()A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1答案:CD分析:直接由体积公式计算V1,V2,连接BD交AC于点M,连接EM,FM,由V3=V A−EFM+V C−EFM计算出V3,依次判断选项即可.设AB=ED=2FB=2a,因为ED⊥平面ABCD,FB∥ED,则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3,V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3,连接BD交AC于点M,连接EM,FM,易得BD⊥AC,又ED⊥平面ABCD,AC⊂平面ABCD,则ED⊥AC,又ED∩BD=D,ED,BD⊂平面BDEF,则AC⊥平面BDEF,又BM=DM=12BD=√2a,过F作FG⊥DE于G,易得四边形BDGF为矩形,则FG=BD=2√2a,EG=a,则EM=√(2a)2+(√2a)2=√6a,FM=√a2+(√2a)2=√3a,EF=√a2+(2√2a)2=3a,EM2+FM2=EF2,则EM⊥FM,S△EFM=12EM⋅FM=3√22a2,AC=2√2a,则V3=V A−EFM+V C−EFM=13AC⋅S△EFM=2a3,则2V3=3V1,V3=3V2,V3=V1+V2,故A、B错误;C、D正确.故选:CD.13、正三棱锥底面边长为3,侧棱长为2√3,则下列叙述正确的是()A.正三棱锥高为3B.正三棱锥的斜高为√392C.正三棱锥的体积为27√34D.正三棱锥的侧面积为9√394答案:ABD分析:先求出正三棱锥的高和斜高,从而可判断AB的正误,再计算出体积和侧面积,从而可判断CD的正误.设E为等边三角形ADC的中心,F为CD的中点,连接PF,EF,PE,则PE为正三棱锥的高,PF为斜高,又PF=√12−94=√392,EF=32×√33=√32,故PE=√394−34=3,故AB正确.而正三棱锥的体积为13×3×√34×9=9√34,侧面积为3×12×3×√392=9√394,故C错误,D正确.故选:ABD.填空题14、如图,在棱长为2的正方体ABCD−A1B1C1D1中,P为线段A1B上的动点(不含端点),则下列结论正确的是____.①平面A 1D 1P ⊥平面BB 1P ;②DC 1⊥PC ;③∠APD 1的取值范围是[π2,π); ④三棱锥C 1−D 1PC 的体积为定值43.答案:①②④分析:由正方体的特征知A 1D 1⊥平面AA 1B 1B ,DC 1⊥对角面A 1BCD 1,由面面垂直的判定和线面垂直的性质可知①②正确;当点P 为线段A 1B 的一个四等分点且靠近点B 时,由长度关系可求得cos∠APD 1>0,知③错误;由体积桥和三棱锥体积公式可确定④正确.对于①,∵几何体是正方体,∴A 1D 1⊥平面AA 1B 1B ,又A 1D 1⊂平面A 1D 1P ,∴平面A 1D 1P ⊥平面BB 1P ,①正确;对于②,在正方体ABCD −A 1B 1C 1D 1中,DC 1⊥对角面A 1BCD 1,对角面A 1BCD 1,∴DC 1⊥PC ,②正确;对于③,当点P 为线段A 1B 的一个四等分点且靠近点B 时,可得:AP =√102,D 1P =√342,AD 1=2√2,由余弦定理得:cos∠APD 1=AP 2+D 1P 2−AD 122AP⋅D 1P =52+172−82×√102×√342=√85>0,此时∠APD 1<π2,③错误; 对于④,∵△D 1C 1C 的面积是定值S =12×2×2=2,点P 到面D 1C 1C 的距离为BC =2,∴三棱锥C 1−D 1PC的体积V =13×2×2=43,④正确. PC所以答案是:①②④.15、如图,在正方体中,A 、B 、C 、D 分别是顶点或所在棱的中点,则A 、B 、C 、D 四点共面的图形______(填上所有正确答案的序号).答案:①③④分析:四点共面主要通过证明两线平行说明,本题利用中位线、平行四边形的性质结合平行线的传递性进行说明,证明平行时绝不能凭直观感觉或无理论依据.图①:证明AB ∥EF ,CD ∥EF ,可得AB ∥CD ;图③:证明BD ∥EF ,AC ∥EF ,可得BD ∥AC ;图④:证明GH ∥EF ,AC ∥EF , BD ∥GH ,可得BD ∥AC .图①:取GD 的中点F ,连结BF 、EF ,∵B 、F 均为相应边的中点,则:BF ∥HG又∵HG ∥,则BF ∥即ABFE 为平行四边形∴AB ∥EF同理: CD ∥EF则AB ∥CD 即A 、B 、C 、D 四点共面,图①正确;图②:显然AB 与CD 异面,图②不正确;AEAE图③:连结AC,BD,EF,∵BE∥DF即BDFE为平行四边形∴BD∥EF又∵A、C分别为相应边的中点,则AC∥EF∴BD∥AC即A、B、C、D四点共面,图③正确;图④:连结AC,BD,EF,GH,∵GE∥HF即GEFH为平行四边形,则GH∥EF又∵A、C分别为相应边的中点,则AC∥EF同理:BD∥GH∴BD∥AC即A、B、C、D四点共面,图④正确.所以答案是:①③④.16、一个正四棱柱的底面边长为2,高为4,则该正四棱柱的体积为________.答案:16分析:根据棱柱的体积公式直接计算即可.由题可得该正四棱柱的体积为2×2×4=16.所以答案是:16.解答题17、在正方体ABCD—A1B1C1D1中,E是棱BB1的中点.(1)求证:B1D∥平面ACE.(2)若F是棱CC1的中点,求证:平面B1DF∥平面ACE.答案:(1)证明见解析(2)证明见解析分析:(1)连BD,使BD∩AC=G,连EG,由中位线定理以及线面平行判定定理证明即可;(2)证明B1F∥平面ACE,结合B1D∥平面ACE,利用面面平行判定定理证明即可.(1)连BD,使BD∩AC=G,连EG.∵ABCD是正方形,BD∩AC=G,∴DG=BG.又∵E是BB1中点,∴B1E=BE,∴DB1∥GE,又DB1⊄平面ACE,GE⊂平面ACE,∴B1D∥平面ACE.(2)∵E是棱BB1的中点,F是棱CC1的中点.∴B1E∥CF且B1E=CF,∴四边形B1ECF是平行四边形,∴B1F∥CE,又∴B1F⊄平面ACE,CE⊂平面ACE,∴B1F∥平面ACE,由(1)B1D∥平面ACE,又∵DB1∩B1F=B1,∴平面B1DF∥平面ACE.18、用符号表示下列语句,并画出图形.(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.答案:(1)α∩β=l,a∩α=A,a∩β=B;图象见解析;(2)A∈α,B∈α,a∩α=C,C∉AB;图象见解析分析:由题意将自然语言转化为符号语言,根据点线面的关系,借用集合符号,表示即可.(1)用符号表示:α∩β=l,a∩α=A,a∩β=B,如图.(2)用符号表示:A∈α,B∈α,a∩α=C,C∉AB,如图.小提示:本题主要考查点、线、面的关系的符号表达,属于基础题.。
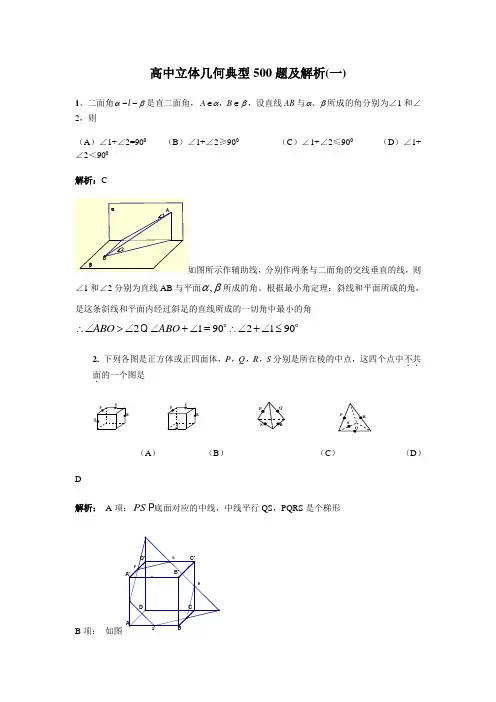
高中立体几何典型500题及解析(一)1、二面角βα--l 是直二面角,βα∈∈B A ,,设直线AB 与βα、所成的角分别为∠1和∠2,则(A )∠1+∠2=900 (B )∠1+∠2≥900 (C )∠1+∠2≤900 (D )∠1+∠2<900 解析:C分别作两条与二面角的交线垂直的线,则∠1和∠2分别为直线AB 与平面,αβ所成的角。
根据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤2. 下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共..面.的一个图是PPQQRSSPPPQQRR RSSSPP PQQQ R RS SS PP Q QR RRSS(A ) (B ) (C ) (D ) D解析: A 项:PS 底面对应的中线,中线平行QS ,PQRS 是个梯形B 项:如图C 项:是个平行四边形D 项:是异面直线。
3. 有三个平面α,β,γ,下列命题中正确的是(A )若α,β,γ两两相交,则有三条交线 (B )若α⊥β,α⊥γ,则β∥γ(C )若α⊥γ,β∩α=a ,β∩γ=b ,则a ⊥b (D )若α∥β,β∩γ=∅,则α∩γ=∅ D解析:A 项:如正方体的一个角,三个平面相交,只有一条交线。
B 项:如正方体的一个角,三个平面互相垂直,却两两相交。
C 项:如图4. 如图所示,在正方体ABCD -A 1B 1C 1D 1的侧面AB 1内有一动点P到直线AB 与直线B 1C 1的距离相等,则动点P 所在曲线的形状为1111C解析:11B C ⊥平面AB 111,B C PB ∴⊥,如图:点到定点B 的距离与到定直线AB 的距离相等,建立坐标系画图时可以以点B 1B 的中点为原点建立坐标系。
5. 在正方体ABCD -A 1B 1C 1D 1中与AD 1成600角的面对角线的条数是(A )4条 (B )6条 (C )8条 (D )10条C解析:如图这样的直线有4条,另外,这样的直线也有4条,共8条。
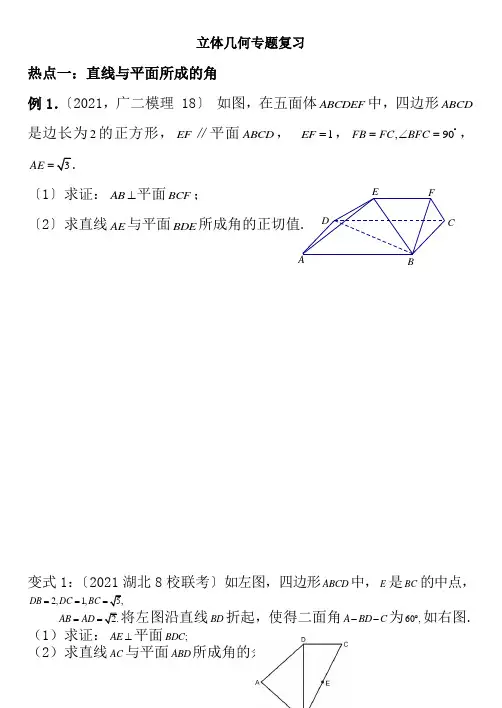
FEDCBA立体几何专题复习热点一:直线与平面所成的角例1.〔2021,广二模理 18〕 如图,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥平面ABCD , 1EF =,,90FB FC BFC ︒=∠=,3AE =.〔1〕求证:AB ⊥平面BCF ;〔2〕求直线AE 与平面BDE 所成角的正切值.变式1:〔2021湖北8校联考〕如左图,四边形ABCD 中,E 是BC 的中点,2,1,5,DB DC BC ===2.AB AD ==将左图沿直线BD 折起,使得二面角A BD C --为60,︒如右图. (1)求证:AE ⊥平面;BDC(2)求直线AC 与平面ABD 所成角的余弦值.变式2:[2021·福建卷] 在平面四边形中,===1,⊥,⊥.将△沿折起,使得平面⊥平面,如图15所示.(1)求证:⊥;(2)假设M为中点,求直线与平面所成角的正弦值.热点二:二面角例2.[2021·广东卷] 如图14,四边形为正方形,⊥平面,∠=30°,⊥于点F,∥,交于点E.(1)证明:⊥平面;(2)求二面角DE的余弦值.变式3: [2021·浙江卷] 如图15,在四棱锥A中,平面⊥平面,∠=∠=90°,==2,==1,=.(1)证明:⊥平面;(2)求二面角BE的大小.变式4:[2021·全国19] 如图11所示,三棱柱A1B1C1中,点A1在平面内的射影D在上,∠=90°,=1,=1=2.(1)证明:1⊥A1B; (2)设直线1与平面1B1的距离为,求二面角A1的大小.热点三:无棱二面角例3.如图三角形与三角形都是边长为2的正三角形,平面⊥平面,⊥平面,3AB〔1〕求点A到平面的距离;〔2〕求平面与平面所成二面角的正弦值.变式5:在正方体1111ABCD A B C D -中,1K BB ∈,1M CC ∈,且,. 求:平面与所成角的余弦值.变式6:如图1111ABCD A B C D -是长方体,=2,11AA AD ==,求二平面1AB C 与1111A B C D 所成二面角的正切值.高考试题精选1.[2021·四川,18] 三棱锥A及其侧视图、俯视图如图14所示.设M,N分别为线段,的中点,P为线段上的点,且⊥.(1)证明:P是线段的中点;(2)求二面角A M的余弦值.2.[2021·湖南卷] 如下图,四棱柱A1B1C1D1的所有棱长都相等,∩=O,A1C1∩B1D1=O1,四边形1A1和四边形1B1均为矩形.(1)证明:O1O⊥底面;(2)假设∠=60°,求二面角C11D的余弦值.3.[2021·江西19] 如图16,四棱锥P中,为矩形,平面⊥平面.(1)求证:⊥.(2)假设∠=90°,=,=2,问为何值时,四棱锥P的体积最大?并求此时平面与平面夹角的余弦值.立体几何专题复习 答案例1.〔2021,广二模〕〔1〕证明:取AB 的中点M ,连接EM ,那么1AM MB ==,∵EF ∥平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =, ∴EF ∥AB ,即EF ∥MB .……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形.……………2分 ∴EM ∥FB ,EM FB =. 在△BFC 中,2224FB FC BC +==,又FB FC =,得FB = ∴EM =……………3分在△AME 中,AE =1AM =,EM =∴2223AM EM AE +==,∴AM EM ⊥.……………4分 ∴AM FB ⊥,即AB FB ⊥. ∵四边形ABCD 是正方形, ∴AB BC ⊥.……………5分∵FB BC B =,FB ⊂平面BCF ,BC ⊂平面BCF , ∴AB ⊥平面BCF .……………6分〔2〕证法1:连接AC ,AC 与BD 相交于点O ,那么点O 是AC 的中点,M OHFEDCBA取BC 的中点H ,连接,OH EO ,FH , 那么OH ∥AB ,. 由〔1〕知EF ∥AB ,且, ∴EF ∥OH ,且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==.……………7分 由〔1〕知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥. ……………8分 ∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD , ∴EO ⊥AO .……………10分 ∵AO BD ⊥,,EOBD O EO =⊂平面EBD ,BD ⊂平面EBD ,∴AO ⊥平面EBD .……………11分∴AEO ∠是直线AE 与平面BDE 所成的角.……………12分 在△AOE 中,.……………13分 ∴直线AE 与平面BDE (14)分证法2:连接AC ,AC 与BD 相交于点 取BC 的中点H ,连接,OH EO , 那么OH ∥AB ,.由〔1〕知EF ∥AB ,且, ∴EF ∥OH ,且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==.……………7分 由〔1〕知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥. ∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD .∴EO ⊥平面ABCD .……………8分以H 为坐标原点,BC 所在直线为x 轴,OH 所在直线为y 轴,HF 所在直线为z 轴,建立空间直角坐标系H xyz -,那么()1,2,0A -,()1,0,0B ,()1,2,0D --,()0,1,1E -.∴()1,1,1AE =-,()2,2,0BD =--,()1,1,1BE =--.……………9分 设平面BDE 的法向量为=n (),,x y z ,由n 0BD ⋅=,n 0BE ⋅=, 得220x y --=,0x y z --+=,得0,z x y ==-.令1x =,那么平面BDE 的一个法向量为=n ()1,1,0-.……………10分设直线AE 与平面BDE 所成角为θ, 那么sin θ=cos ,n AE.……………11分∴cos θ==,.……………13分∴直线AE 与平面BDE .……………14分变式1:〔2021湖北8校联考〕〔1〕取BD 中点F ,连结,EF AF ,那么11,,60,2AF EF AFE ==∠=……………2分由余弦定理知222360,2AE AF EF AE AE EF==+=∴⊥………4分又BD ⊥平面AEF ,,BD AE AE ∴⊥⊥平面BDC ………6分 〔2〕以E 为原点建立如图示的空间直角坐标系,那么,11(1,,0),(1,,0)22B D ---………8分 设平面ABD 的法向量为n (,,)x y z =, 由得,取z ,那么3,(0,y =-∴=-n .13(1,,),cos ,224||||AC AC AC AC =--∴<>==-n n n 11分故直线AC 与平面ABD . …………12分变式2:〔2021福建卷〕解:(1)证明:∵平面⊥平面,平面∩平面=,⊂平面,⊥,∴⊥平面.…………3分 又⊂平面,∴⊥.…………4分 (2)过点B 在平面内作⊥.由(1)知⊥平面,⊂平面,⊂平面,∴⊥,⊥.……6分以B 为坐标原点,分别以,,的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如下图).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),.那么=(1,1,0),=,=(0,1,-1).…………7分 设平面的法向量n =(x 0,y 0,z 0),那么即取z 0=1,得平面的一个法向量n =(1,-1,1).…………9分 设直线与平面所成角为θ, 那么θ===.…………11分即直线与平面所成角的正弦值为.…………12分例2.〔2021,广东卷〕:(1):,,,,A ,,,,,,,,,,.(2):E EG//CF DF G,,,G GH AF H,EH,PD ABCD PD PCD PCD ABCD PCD ABCD CD D ABCD AD CD AD PCD CF PCD CF AD AF PC CF AF AD AF ADF ADAF A CF ADF CF DF EG DF ⊥⊂∴⊥=⊂⊥∴⊥⊂∴⊥⊥∴⊥⊂=∴⊥⊥∴⊥⊥∠解证明平面平面平面平面平面平面平面平面又平面平面解法一过作交于平面A 平面A 过作于连则00,CD 2,30,130,==1,21324,,,,,22333EG .,423EHG D AF E DPC CDF CF CDDE CF CP EF DC DEDF DP CP DE EF AE AF EF DF AE EF EH HG AF --=∠=∴∠==∴=∴⋅=====⋅∴====为二面角的平面角设从而∥还易求得EF=从而易得故cos GH EHG EH ∴∠===12:,,,,,2,1(0,0,2),C(0,2,0),,(23,22,0),,,431,0),ADF CP (3,1,0),22AEF (x DP DC DA x y z DC A CF CP F DFCF F E n n λλλλ==-⊥===-=解法二分别以为轴建立空间直角坐标系设则设则可得从而易得取面的一个法向量为设面的一个法向量为2212212,y,z),0,0,4||||2n AE n AF n n n n n ⋅=⋅=⋅==⋅⨯利用且得可以是从而所求二面角的余弦值为变式3:〔2021浙江卷〕解:(1)证明:在直角梯形中,由==1,=2,得==, 由=,=2, 得2=2+2,即⊥.…………2分 又平面⊥平面,从而⊥平面,所以⊥.又⊥,从而⊥平面.…………4分 (2)方法一:过B 作⊥,与交于点F ,过点F 作∥,与交于点G ,连接.由(1)知⊥,那么⊥.所以∠是二面角B E 的平面角.…………6分在直角梯形中,由2=2+2,得⊥.又平面⊥平面,得⊥平面,从而⊥.由⊥平面,得⊥. 在△中,由=2,=,得=.在△中,由=1,=,得=.…………7分 在△中,由=,=2,=,得=,=.从而==.…………9分在△,△中,利用余弦定理分别可得∠=,=.…………11分 在△中,∠==.…………13分所以,∠=,即二面角B E 的大小是.14分方法二:以D 为原点,分别以射线,为x ,y 轴的正半轴,建立空间直角坐标系D ,如下图.由题意知各点坐标如下:D(0,0,0),E(1,0,0),C(0,2,0),A(0,2,),B(1,1,0).设平面的法向量为m=(x1,y1,z1),平面的法向量为n=(x2,y2,z2).可算得=(0,-2,-),=(1,-2,-),=(1,1,0).…………7分由即可取m=(0,1,-).…………9分由即可取n=(1,-1,).…………11分于是〈m,n〉|===.…………13分由题意可知,所求二面角是锐角,故二面角BE的大小是.…………14分变式4:〔2021全国卷〕19.解:方法一:(1)证明:因为A1D⊥平面,A1D⊂平面C,故平面1C1C⊥平面.又⊥,所以⊥平面1C1C.1C1连接A1C,因为侧面1C1C为菱形,故1⊥A1C.由三垂线定理得1⊥A1B.……4分〔注意:这个定理我们不能用〕(2)⊥平面1C1C,⊂平面1B1,故平面1C1C⊥平面1B1.作A1E⊥1,E为垂足,那么A1E⊥平面1B1.…………6分又直线1∥平面1B1,因而A1E为直线1与平面1B1的距离,即A1E=.因为A1C为∠1的平分线,所以A1D=A1E=.…………8分作⊥,F为垂足,连接A1F.由三垂线定理得A1F⊥,故∠A1为二面角A1C的平面角.…………10分由=-A1D2)=1,得D为中点,=,∠A1==,……12分所以∠A1=.…………13分所以二面角A1C的大小为.…………14分方法二:以C为坐标原点,射线为x轴的正半轴,以的长为单位长,建立如下图的空间直角坐标系C.由题设知A1D与z轴平行,z轴在平面1C1C内.(1)证明:设A1(a,0,c).由题设有a≤2,A(2,0,0),B(0,1,0),那么=(-2,1,0),=(-2,0,0),=(a-2,0,c=+=(a-4,0,c),=(a,-1,c).由|=2,得=2a2-4a+c2=0.①又·=a2-4a+c2=0,所以1⊥A1B.…………4分(2)设平面1B1的法向量m=(x,y,z),那么m⊥,m⊥,即m·=0,m·=(0,1,0),==(a-2,0,c),所以y=0且(a-2)x+=0.令x=c,那么z=2-a,所以m=(c,0,2-a),故点A到平面1B1的距离为|·〈m,〉|===c.…………6分又依题设,A到平面1B1的距离为,所以c=,代入①,解得a=3(舍去)或a=1,于是=(-1,0,).…………8分设平面1的法向量n=(p,q,r),那么n⊥,n⊥,即n·=0,n·=0,-p+r=0,且-2p+q=0.令p =,那么q =2,r =1,所以n =(,2,1).…………10分 又p =(0,0,1)为平面的法向量,…………11分 故〈n ,p 〉==.…………13分所以二面角A 1C 的大小为.…………14分例3. 无棱二面角〔2021年江西卷〕 解法一:〔1〕取中点O ,连,,那么⊥,⊥.又平面MCD ⊥平面BCD ,那么⊥平面BCD ,所以∥,A 、B 、O 、M 共面.延长、相交于E ,那么∠就是与平面3∥,面,M 、O到平面的距离相等,作⊥于H ,连,那么⊥,求得: 60315,利用体积相等得:215A MBC M ABC V V d --=⇒=。

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1},E,F分别是AB,BC的中点,求证:EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中,因为E,F分别是AB,BC的中点,所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中:- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D,EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理,所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中,D是AB的中点,求证:AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1},交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中,E为BC_{1}的中点。
2. 因为D是AB的中点:- 所以在 ABC_{1}中,DE∥ AC_{1}。
- 又DE⊂平面CDB_{1},AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理,可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中,底面ABCD是正方形,PA = PB = PC = PD,求证:PA⊥平面ABCD。
解析1. 连接AC,BD交于点O,连接PO。
- 因为底面ABCD是正方形,所以O为AC,BD中点。
- 又PA = PC,PB = PD,根据等腰三角形三线合一的性质:- 可得PO⊥ AC,PO⊥ BD。
- 而AC∩ BD = O,AC⊂平面ABCD,BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理,所以PO⊥平面ABCD。
- 又PA = PB = PC = PD,AO = BO = CO = DO,所以 PAO≅ PBO≅ PCO ≅ PDO。

立体几何证明题简单全文共四篇示例,供读者参考第一篇示例:立体几何学是几何学的一个分支,主要研究三维空间的图形与性质。
在解决立体几何证明题时,我们需要运用一定的空间想象能力和逻辑推理能力。
下面我们将介绍一些简单的立体几何证明题,并给出详细的解答过程。
第一个题目:证明一个正方体的对角线可以长出来。
正方体是一个六个面都是正方形的立体图形,我们知道正方体的对角线是由相对的顶点连接而成的一条线段。
我们可以通过勾股定理来证明正方体的对角线可长出来。
解答:设正方体的边长为a,则正方体的对角线长度为√(a^2 + a^2) = √2a,而正方体的对角线长短并不相等,证明正方体的对角线可长出来。
第二个题目:证明一个棱台的棱台截面是一个梯形。
棱台是一个底面为多边形,顶面为一个平行于底面的多边形的立体图形,我们知道棱台截面是由截面平行于底面的直线与顶部多边形的边相交而成的。
解答:设底面为多边形ABCD,顶面为多边形EFGH,棱台的高为h,取一个截面平行于底面ABCD的平面,与顶部多边形的边EF相交于点I,与底面多边形的边BC相交于点J,则可以得到梯形ABFE。
通过勾股定理可以证明I到J的距离小于EF,即梯形ABFE的底边小于顶边,证明棱台的棱台截面是一个梯形。
通过以上两个例子,我们可以看到在解决立体几何证明题时,我们需要灵活运用几何相关知识,尤其是勾股定理、相似三角形等几何常识。
细心观察图形的结构和特点也是解决立体几何证明题的关键。
希望通过这些简单的例子,能够帮助读者更加深入地理解立体几何的相关知识。
第二篇示例:立体几何学是数学中的一个重要分支,主要研究空间内图形的性质、相互关系和计算方法。
在立体几何学中,经常需要进行证明题,通过证明来说明一些规律和性质。
本文将介绍一些关于立体几何证明题的简单例题,帮助读者更深入理解立体几何学的知识。
1.证明空间内一条直线与一个平面的交点不唯一证明:假设在空间内有一条直线l和一个平面P,直线l与平面P 有两个交点A和B。
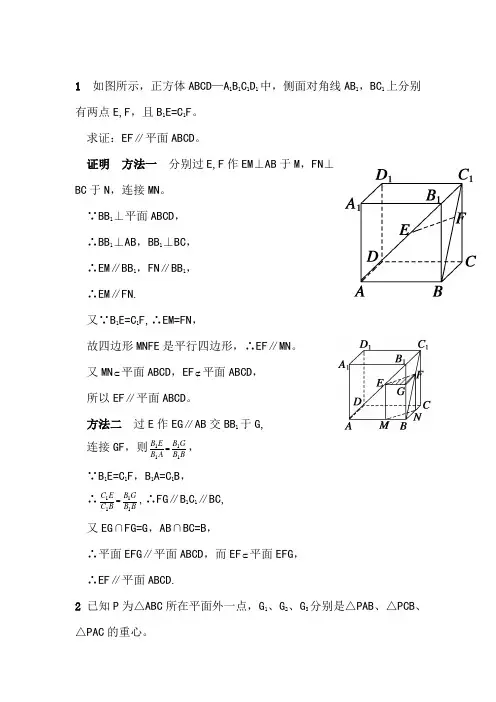
1 如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E =C 1F 。
求证:EF ∥平面ABCD 。
证明 方法一 分别过E ,F 作EM ⊥AB 于M ,FN ⊥BC 于N ,连接MN 。
∵BB 1⊥平面ABCD , ∴BB 1⊥AB ,BB 1⊥BC , ∴EM ∥BB 1,FN ∥BB 1, ∴EM ∥FN .又∵B 1E =C 1F ,∴EM =FN ,故四边形MNFE 是平行四边形,∴EF ∥MN 。
又MN ⊂平面ABCD ,EF ⊄平面ABCD , 所以EF ∥平面ABCD 。
方法二 过E 作EG ∥AB 交BB 1于G , 连接GF ,则BB G B AB E B 1111=,∵B 1E =C 1F ,B 1A =C 1B , ∴BB G B BC E C 1111=,∴FG ∥B 1C 1∥BC ,又EG ∩FG =G ,AB ∩BC =B ,∴平面EFG ∥平面ABCD ,而EF ⊂平面EFG , ∴EF ∥平面ABCD .2 已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC 的重心。
(1)求证:平面G 1G 2G 3∥平面ABC ; (2)求S △321G G G ∶S △ABC .(1)证明 如图所示,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F ,连接DE 、EF 、FD ,则有PG 1∶PD =2∶3, PG 2∶PE =2∶3,∴G 1G 2∥DE . 又G 1G 2不在平面ABC 内,∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC 。
又因为G 1G 2∩G 2G 3=G 2, ∴平面G 1G 2G 3∥平面ABC 。
(2)解 由(1)知PE PG PD PG 21 =32,∴G 1G 2=32DE 。

1.空间角与空间距离在高考的立体几何试题中,求角与距离是必考查的问题,其中最主要的是求线线角、线面角、面面角、点到面的距离,求角或距离的步骤是“一作、二证、三算”,即在添置必要的辅助线或辅助面后,通过推理论证某个角或线段就是所求空间角或空间距离的相关量,最后再计算。
2.立体几体的探索性问题立体几何的探索性问题在近年高考命题中经常出现,这种题型有利于考查学生归纳、判断等方面的能力,也有利于创新意识的培养。
近几年立体几何探索题考查的类型主要有:(1)探索条件,即探索能使结论成立的条件是什么?(2)探索结论,即在给定的条件下命题的结论是什么。
对命题条件的探索常采用以下三种方法:(1)先观察,尝试给出条件再证明;(2)先通过命题成立的必要条件探索出命题成立的条件,再证明充分性;(3)把几何问题转化为代数问题,探索出命题成立的条件。
对命题结论的探索,常从条件出发,再根据所学知识,探索出要求的结论是什么,另外还有探索结论是否存在,常假设结论存在,再寻找与条件相容还是矛盾。
(一)平行与垂直关系的论证由判定定理和性质定理构成一套完整的定理体系,在应用中:低一级位置关系判定高一级位置关系;高一级位置关系推出低一级位置关系,前者是判定定理,后者是性质定理。
1.线线、线面、面面平行关系的转化:面面平行性质α//βαI γ=a ,βI γ⎫⎬⇒a =b ⎭//baa //b⎫⎬ba ⊄α,b ⊂α⎭α⇒a //αa ⊂α,b ⊂αAb a I b =Aαaa //β,b //ββ⎫⎪⎬⎪⎭(a//b,b//c线线∥⇒a //c)公理4线面平行判定线面平行性质线面∥⇒α//β面面平行判定1面面∥面面平行性质面面平行性质1α//γ⎫β//γ⎭⎫⎪a ⊂β⎬αI β=b ⎪⎭a //α⇒a //bα//β⎫a ⊂α⎭⎬⎬⇒α//β⇒a //β2.线线、线面、面面垂直关系的转化:⎫⎪a Ib =O ⎬l ⊥a ,l ⊥b ⎪⎭a ,b ⊂α⇒l ⊥α⎫⎬⇒α⊥βa ⊂β⎭a ⊥α面面⊥三垂线定理、逆定理线线⊥PA ⊥α,AO 为PO 在α内射影a ⊂α则a ⊥OA ⇒a ⊥PO a ⊥PO ⇒a ⊥AOl ⊥α线面垂直判定1线面垂直定义线面⊥α⊥β面面垂直判定面面垂直性质,推论2⎫⎬a ⊂α⎭⇒l ⊥a⎫⎪αI β=b ⎬⇒a ⊥αa ⊂β,a ⊥b ⎪⎭α⊥γβ⊥γαI β⎫⎪⎬⇒a ⊥γ=a ⎪⎭面面垂直定义αI β=l ,且二面角α-l -β⎫成直二面角⎬⇒α⊥β⎭3.平行与垂直关系的转化:a //b ⎫a ⊥αa ⊥α⎫⇒b ⊥αa⎬⎭⎬⇒αa ⊥β⎭//β线线∥线面垂直判定2线面垂直性质2a ⊥α⎫线面⊥面面平行判定2面面平行性质3面面∥⎬⇒a //b b ⊥α⎭α//β⎫a ⊥α⎬a ⊥β⎭4.应用以上“转化”的基本思路——“由求证想判定,由已知想性质。
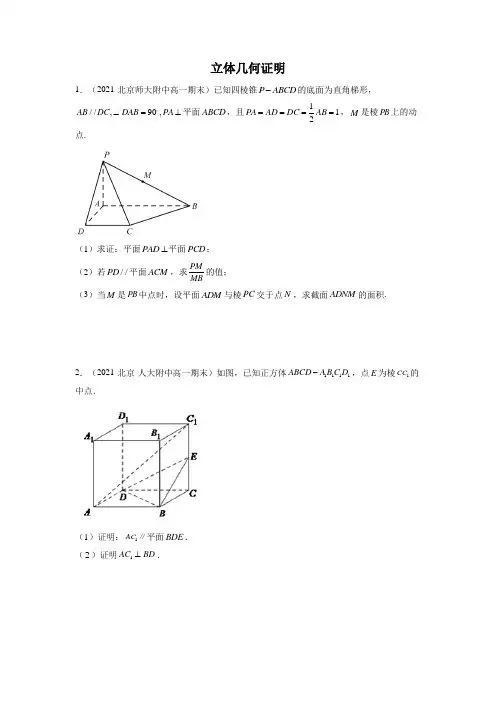
立体几何证明1.(2021·北京师大附中高一期末)已知四棱锥P ABCD -的底面为直角梯形,//,90,AB DC DAB PA ∠=⊥平面ABCD ,且112PA AD DC AB ====,M 是棱PB 上的动点.(1)求证:平面PAD ⊥平面PCD ;(2)若//PD 平面ACM ,求PM MB的值; (3)当M 是PB 中点时,设平面ADM 与棱PC 交于点N ,求截面ADNM 的面积.2.(2021·北京·人大附中高一期末)如图,已知正方体1111ABCD A B C D -,点E 为棱1CC 的中点.(1)证明:1AC ∥平面BDE .(2)证明1AC BD ⊥.3.(2021·北京·汇文中学高一期末)如图1,已知菱形AECD 的对角线AC ,DE 交于点F ,点E 为AB 的中点.将三角形ADE 沿线段DE 折起到PDE 的位置,如图2所示.(1)求证:DE PC ⊥;(2)试问平面PFC 与平面PBC 所成的二面角是否为90︒,如果是,请证明;如果不是,请说明理由;(3)在线段PD ,BC 上是否分别存在点M ,N ,使得平面//CFM 平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.4.(2021·北京·首都师范大学附属中学高一期末)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,O ,M 分别为BD ,PC 的中点.设平面PAD 与平面PBC 的交线为l .(1)求证://OM 平面PAD ;(2)求证://BC l ;(3)在棱PC 上是否存在点N (异于点C ),使得//BN 平面PAD ?若存在,求出PN PC的值;若不存在,说明理由.5.(2021·北京·101中学高一期末)已知正四棱柱1111ABCD A B C D -中,M 是1DD 的中点.(1)求证:1//BD 平面AMC ;(2)求证:1AC BD ⊥;(3)在线段1BB 上是否存在点P ,当1BP BB λ=时,平面11//A PC 面AMC ?若存在,求出λ的值并证明;若不存在,请说明理由.6.(2021·北京师大附中高一期末)在正方体1111ABCD A B C D -中,E 为1CC 中点.(1)求证:1//BC 平面1AD E ;(2)求证:1A D ⊥平面11ABC D .7.(2021·北京·汇文中学高一期末)如图所示,在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .(1)求证://MN 平面ABD ;(2)若MN CD ⊥,BD CD ⊥,求证:平面CBD ⊥平面ABD .8.(2019·北京师大附中高一期末)如图,在三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=,2AB AC ==,1AA ,M N 分别为1,BC CC 的中点,P 为侧棱1BB 上的动点(Ⅰ)求证:平面APM ⊥平面11BB C C ;(Ⅱ)若P 为线段1BB 的中点,求证:1//A N 平面APM ;(Ⅲ)试判断直线1BC 与平面APM 是否能够垂直.若能垂直,求PB 的值;若不能垂直,请说明理由9.(2019·北京师大附中高一期末)如图,已知四棱锥S ABCD-,底面ABCD是边长为2的菱形,60∠=,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,ABCE为线段AD的中点SD平面MAC;(Ⅰ)求证://⊥;(Ⅱ)求证:SE AC-的体积(Ⅲ)求三棱锥M ABC-中,PA⊥平面ABCD,底10.(2019·北京·101中学高一期末)如图,在四棱锥P ABCD部ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.11.(2019·北京·中央民族大学附属中学高一期末)在四面体ABCD 中,CB =CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点,求证:(I )直线EF ACD 面;(II )EFC BCD ⊥面面.12.(2020·北京师大附中高一期末)如图,四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点.(1)求证://CD 平面PAB ;(2)求证://PC 平面BDE ;(3)证明:BD CE ⊥.13.(2021·北京·人大附中高一期末)如图1,已知△ABD 和△BCD 是两个直角三角形,∠BAD =∠BDC =2π.现将△ABD 沿BD 边折起到1A BD 的位置,如图2所示,使平面1A BD ⊥平面BCD .(1)求证:平面1A BC ⊥平面1A CD ;(2)1A C 与BD 是否有可能垂直,做出判断并写明理由.14.(2020·北京·101中学高一期末)如图1,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB AC ==4BC =.将△ADE 沿DE 折起到△1A DE 的位置,使得平面1A DE ⊥平面BCED ,F 为1A C 的中点,如图2.(1)求证://EF 平面1A BD ;(2)求证:平面1A OB ⊥平面1A OC ;(3)线段OC 上是否存在点G ,使得OC ⊥平面EFG ?说明理由.15.(2020·北京师大附中高一期末)如图,在多面体ABCDEF 中,底面ABCD 为矩形,侧面ADEF 为梯形,//AF DE ,DE AD ⊥,DC DE =.⊥;(Ⅰ)求证:AD CEBF平面CDE;(Ⅱ)求证://(Ⅲ)判断线段BE上是否存在点Q,使得平面ADQ⊥平面BCE?并说明理由.-中,平面16.(2020·北京·中国人民大学附属中学朝阳学校高一期末)在三棱锥P ABC⊥.设D,E分别为PA,AC中点.PAC⊥平面ABC,PA AC⊥,AB BCDE平面PBC;(Ⅰ)求证://(Ⅱ)求证:BC⊥平面PAB;(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.答案:1.(1)证明见解析;(2)12;【分析】 (1) 要证平面PAD ⊥平面PCD ,只需证明DC ⊥平面PAD ,利用线面垂直的判定可证DC ⊥平面PAD .(2) 根据题意,作出点M ,再利用相似三角形求PM MB的值 (3) 从四点共面角度出发,利用平面向量基本定理确定点N 的位置,再求截面面积.【详解】(1)证明:因为90DAB ∠=,所以AB AD ⊥,又//AB DC ,所以DC AD ⊥.因为PA ⊥平面ABCD ,DC ⊂平面ABCD ,所以PA DC ⊥.又AD ,PA 在平面PAD 内,且相交于点A ,所以DC ⊥平面PAD . 又DC ⊂平面PCD ,所以平面PAD ⊥平面PCD .(2)如图,连接AC ,BD 相交于点E ,过点E 作//EM PD ,交PB 于点M . 因为//EM PD ,PD ⊄平面ACM ,EM ⊂平面ACM ,所以//PD 平面ACM . 故上述所作点M 为使得//PD 平面ACM 的点M .如图在梯形ABCD 中,有//AB DC ,112AD DC AB === 令()22DE DB DA DC DA DC λλλλ==+=+, 因为A ,E ,C 三点共线,所以21λλ+=,13λ=.即13DE DB =,所以23BE DB =,12DE BE =. 因为//EM PD ,所以BME BPD ,12DE P MB BE M ==. (3)设PN PC μ=, 因为,,,A D N M 四点共面,所以存在实数m ,n ,使得AN mAD nAM =+. 因为()12AN AP PN AP PC AD AB AP μμμμ=+=+=++-,22n n mAD nAM mAD AB AP +=++, 又AD ,AB ,AP 为一组基底, 所以,,2212m n n μμμ⎧⎪=⎪⎪=⎨⎪⎪-=⎪⎩解得23m n ==. 所以2233AN AD AM =+.因为PA ⊥平面ABCD ,AD ⊂平面ABCD ,所以PA AD ⊥. 又AD AB ⊥,PA ,AB 在平面PAB 内,且相交于点A , 所以AD ⊥平面PAB ,又AM ⊂平面PAB ,所以AD AM ⊥. 在四边形AMND 中,AD AM ⊥,1AD =,AM = 因为2233AN AD AM =+,点N 到AM 的距离为2233AD =,点N 到AD的距离为23AM . 所以截面ADNM的面积1121223ADN AMNS S S =+=⨯+2.(1)见解析;(2)见解析【详解】试题分析:(1)连结AC 交BD 于F ,连结EF ,通过正方形对角线的性质以及三角形中位线可得112EF AC ,根据线面平行判定定理可得结果;(2)通过证明BD ⊥平面1ACC 可得结论.试题解析:(1)证明:连结AC 交BD 于F ,连结EF ,正方形ABCD 中,AC 与BD 互相平分,∴F 为AC 中点,在1ACC 中,∵E ,F 分别为1CC 与AC 中点,∴112EF AC ,∵EF ⊂平面BDE ,1AC ⊄平面BDE ,∴EF 平面BDE .(2)证明:在正方形ABCD 中,AC BD ⊥,在正方体1111ABCD A B C D -中, 1CC ⊥平面ABCD ,∵BD ⊂平面ABCD ,∴1CC BD ⊥,∵1AC CC C ⋂=,∴BD ⊥平面1ACC ,∵1AC ⊂平面1ACC ,∴1AC BD ⊥.3.(1)证明见解析;(2)平面PFC 与平面PBC 所成的二面角为90︒,证明见解析;(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明见解析. 【分析】(1)根据线面垂直的判定可证得DE ⊥平面PCF ,由线面垂直性质可证得结论; (2)根据平行关系可证得BC ⊥平面PCF ,由面面垂直的判定可证得两平面垂直,由此得到所成角为90︒;(3)利用平行四边形和三角形中位线性质可证得线线平行关系,由此证得线面平行和面面平行,从而确定存在满足条件的,M N . 【详解】(1)四边形AECD 为菱形,AC DE ∴⊥,即DE PF ⊥,DE CF ⊥, 又,PF CF ⊂平面PCF ,PFCF F =,DE ∴⊥平面PCF ,PC ⊂平面PCF ,DE PC ∴⊥.(2)平面PFC 与平面PBC 所成的二面角为90︒,证明如下:E 为AB 中点且四边形AECD 为菱形,//BE CD ∴,∴四边形BCDE 为平行四边形,//BC DE ∴,由(1)知:DE ⊥平面PCF ,BC ∴⊥平面PCF ,又BC ⊂平面PBC ,∴平面PCF ⊥平面PBC ,即平面PFC 与平面PBC 所成的二面角为90︒.(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明如下:由(2)知:四边形BCDE 为平行四边形,又,F N 分别为,DE BC 中点,//EF CN ∴,∴四边形EFCN 为平行四边形,//CF EN ∴,又EN ⊂平面PEN ,CF ⊄平面PEN ,//CF ∴平面PEN ;,M F 分别为,PD DE 中点,MF ∴为PDE △中位线,//MF PE ∴,又PE ⊂平面PEN ,MF ⊄平面PEN ,//MF ∴平面PEN ,又MFCF F =,,MF CF ⊂平面FCM ,∴平面//CFM 平面PEN .【点睛】本题考查立体几何中线线垂直关系、面面垂直与平行关系的证明问题,涉及到线面垂直的判定与性质、面面垂直的判定、线面平行与面面平行的判定等定理的应用,属于常考题型.4.(1)证明见解析;(2)证明见解析;(3)不存在,理由见解析. 【分析】(1)连接AC , 易知O 为AC 的中点,进而得//AP OM ,再结合线面平行的判定定理即可证明;(2)由题知//BC 平面PAD ,进而根据线面平行的性质定理即可证明//BC l ;(3))假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD ,进而在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E ,故平面//BEN 平面PAD ,进而得//BE AD ,另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾,故不存在. 【详解】解:(1)证明:连接AC ,因为底面ABCD 为平行四边形,O 为BD 的中点, 所以O 为AC 的中点,因为M 为PC 的中点, 所以在APC △中,//AP OM ,因为OM ⊄平面PAD ,AP ⊂平面PAD , 所以//OM 平面PAD(2)因为底面ABCD 为平行四边形, 所以//AD BC ,因为AD ⊂平面PAD ,BC ⊄平面PAD , 所以//BC 平面PAD ,因为平面PAD 与平面PBC 的交线为l ,BC ⊂平面PBC , 所以//BC l(3)假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD , 在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E , 因为EN ⊄平面PAD ,PD ⊂平面PAD ,所以//EN 平面PAD , 因为EN BN N ⋂=,所以平面//BEN 平面PAD , 因为BE ⊂平面BEN ,所以//BE 平面PAD ,又因为BE ⊂平面ABCD ,平面ABCD 平面PAD AD =,所以//BE AD 另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾, 所以在棱PC 上不存在点N (异于点C ),使得//BN 平面PAD .5.(1)证明见解析;(2) 证明见解析;(3)在线段1BB 上存在点P ,当12λ=时,平面11//A PC 平面AMC . 【分析】(1) 利用线面平行的判定定理证明1//BD 平面AMC ;(2) 利用线面垂直的判定定理证明AC ⊥平面11BB D D ,则有1AC BD ⊥; (3) 先确定λ的值,再根据面面平行的判定定理证明两平面平行. 【详解】因为四棱柱1111ABCD A B C D -是正四棱柱,所以底面ABCD 为正方形,侧棱垂直底面,侧面均为矩形.(1)证明:记AC 和BD 相交于点N ,因为ABCD 为正方形,所以N 为BD 的中点.又M 是1DD 的中点, 所以1//MN BD .又1BD ⊄平面AMC ,MN ⊂平面AMC , 所以1//BD 平面AMC .(2)证明:因为ABCD 为正方形,所以AC BD ⊥.因为1D D ⊥平面ABCD ,AC ⊂平面ABCD ,所以1D D AC ⊥. 又BD ,1D D 在平面11BB D D 内,且相交于点D , 所以AC ⊥平面11BB D D .又1BD ⊂平面11BB D D , 所以1AC BD ⊥.(3) 在线段1BB 上存在点P ,当12λ=,即112BP BB =时,平面11//A PC 面AMC . 理由如下:当112BP BB =时,P 为1BB 的中点. 取1CC 的中点G ,连接1PC ,GB ,则有1//PC GB .连接MG ,因为四边形11CC D D 是矩形,M 是1DD 的中点,G 是1CC 的中点, 所以//MG CD ,MG CD =.在正方形ABCD 中,有,//CD AB ,CD AB =.所以//MG AB ,MG AB =,四边形ABGM 为平行四边形. 有//BG AM ,又1//PC GB ,所以1//PC AM ,又1PC ⊄平面AMC ,AM ⊂平面AMC ,所以1PC //平面AMC . 同理可证:1//PA 平面AMC .又1PC ,1PA 在平面11A PC 内,且相交于点P , 所以平面11//A PC 平面AMC . 6.(1)证明见解析;(2) 证明见解析. 【分析】(1)先证明四边形11ABC D 为平行四边形,得到11//BC AD ,再利用线面平行的判定定理证明1//BC 平面1AD E ;(2)先证明11A D AD ⊥,再由线面垂直的性质得到1AB A D ⊥,最后由线面垂直的判定定理证明1A D ⊥平面11ABC D.(1)证明:在正方体1111ABCD A B C D -中, 有//AB CD ,11//CD C D ,所以11//AB C D .又11AB C D =,所以四边形11ABC D 为平行四边形,有11//BC AD . 又1BC ⊄平面1AD E ,1AD ⊂平面1AD E , 所以1//BC 平面1AD E(2)证明:因为1A D ,1AD 为正方形的对角线,所以11A D AD ⊥. 因为AB ⊥平面11AA D D ,1A D ⊂平面11AA D D ,所以1AB A D ⊥. 又1AD ,AB 在平面11ABC D 内,且相交于点A , 所以1A D ⊥平面11ABC D .7.(1)证明见解析;(2)证明见解析. 【分析】(1)由//MN AB ,利用直线与平面平行的判断定理,证明//MN 平面ABD .(2)推导出BA DC ⊥,DC BD ⊥,从而CD ⊥平面ABD ,由此能证明平面ABD ⊥平面BCD . 【详解】(1)∵在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .MN ⊄平面ABD ,AB 平面ABD ,∴//MN 平面ABD(2)∵MN CD ⊥,//MN AB ,∴AB CD ⊥, ∵BD CD ⊥,ABBD B =∴CD ⊥平面ABD , ∵CD ⊂平面BCD ∴平面ABD ⊥平面BCD . 【点睛】本题考查的是空间中平行与垂直的证明,较简单.8.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)直线BC 1与平面APM 不能垂直,详见解析 【分析】(Ⅰ)由等腰三角形三线合一得AM BC ⊥;由线面垂直性质可得1AM BB ⊥;根据线面垂直的判定定理知AM ⊥平面11BB C C ;由面面垂直判定定理证得结论;(Ⅱ)取11C B 中点D ,可证得1//A D AM ,//DN MP ;利用线面平行判定定理和面面平行判定定理可证得平面1//A DN 平面APM ;根据面面平行性质可证得结论;(Ⅲ)假设1BC ⊥平面APM ,由线面垂直性质可知1BC PM ⊥,利用相似三角形得到111C B PB MB BB =,从而解得BP 长度,可知满足垂直关系时,P 不在棱1BB 上,则假设错误,可得到结论.(Ⅰ)AB AC =,M 为BC 中点 AM BC ∴⊥1AA ⊥平面ABC ,11//AA BB 1BB ∴⊥平面ABC又AM ⊂平面ABC 1AM BB ∴⊥ 1,BB BC ⊂平面11BB C C ,1BB BC B = AM ∴⊥平面11BB C C又AM ⊂平面APM ∴平面APM ⊥平面11BB C C (Ⅱ)取11C B 中点D ,连接11,,,A D DN DM B C,D M 分别为11,C B CB 的中点 1//DM AA ∴且1DM AA = ∴四边形1A AMD 为平行四边形 1//A D AM ∴又1A D ⊄平面APM ,AM ⊂平面APM 1//A D ∴平面APM,D N 分别为111,C B CC 的中点 1//DN B C ∴又,P M 分别为1,BB CB 的中点 1//MP B C ∴ //DN MP ∴ 又DN ⊄平面APM ,MP ⊂平面APM //DN ∴平面APM 1,A D DN ⊂平面1A DN ,1A DDN D = ∴平面1//A DN 平面APM又1A N ⊂平面1A DN 1//A N ∴平面APM(Ⅲ)假设1BC ⊥平面APM ,由PM ⊂平面APM 得:1BC PM ⊥设PB x =,x ⎡∈⎣当1BC PM ⊥时,11BPM B C B ∠=∠ Rt PBM ∴∆∽11Rt B C B ∆ 111C B PB MB BB =∴由已知得:MB11C B =1BB=,解得:x ⎡=⎣ ∴假设错误 ∴直线1BC 与平面APM 不能垂直【点睛】本题考查立体几何中面面垂直、线面平行关系的证明、存在性问题的求解;涉及到线面垂直的判定与性质、线面平行的判定、面面平行的判定与性质定理的应用;处理存在性问题时,常采用假设法,通过假设成立构造方程,判断是否满足已知要求,从而得到结论. 9.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)12【分析】(Ⅰ)连接BD ,交AC 于点O ;根据三角形中位线可证得//MO SD ;由线面平行判定定理可证得结论;(Ⅱ)由等腰三角形三线合一可知SE AD ⊥;由面面垂直的性质可知SE ⊥平面ABCD ;根据线面垂直性质可证得结论;(Ⅲ)利用体积桥的方式将所求三棱锥体积转化为14S ABCD V -;根据已知长度和角度关系分别求得四边形面积和高,代入得到结果. 【详解】(Ⅰ)证明:连接BD ,交AC 于点O四边形ABCD 为菱形 O ∴为BD 中点 又M 为SB 中点 //MO SD ∴MO ⊂平面MAC ,SD ⊄平面MAC //SD ∴平面MAC (Ⅱ)SAD ∆为正三角形,E 为AD 中点 SE AD ∴⊥平面SAD ⊥平面ABCD ,平面SAD ⋂平面ABCD AD =,SE ⊂平面SADSE ∴⊥平面ABCD ,又AC ⊂平面ABCD SE AC ∴⊥ (Ⅲ)M 为SB 中点 11112443M ABC M ABCD S ABCD ABCDV V V SSE ---∴===⨯⋅又2AB BC AD CD SA SD ======,60ABC ∠= 2AC ∴=,12222sin 60232ABCDABC SS ∆==⨯⨯⨯=由(Ⅱ)知,SE AD ⊥ SE ∴=11122M ABC V -=⨯∴ 【点睛】本题考查立体几何中线面平行、线线垂直关系的证明、三棱锥体积的求解问题;涉及到线面平行判定定理、面面垂直性质定理和判定定理的应用、体积桥的方式求解三棱锥体积等知识,属于常考题型. 10.(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)见解析. 【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论;(Ⅱ)由几何体的空间结构特征首先证得线面垂直,然后利用面面垂直的判断定理可得面面垂直;(Ⅲ)由题意,利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点. 【详解】(Ⅰ)证明:因为PA ⊥平面ABCD ,所以PA BD ⊥; 因为底面ABCD 是菱形,所以AC BD ⊥; 因为PAAC A =,,PA AC ⊂平面PAC ,所以BD ⊥平面PAC .(Ⅱ)证明:因为底面ABCD 是菱形且60ABC ∠=︒,所以ACD ∆为正三角形,所以AE CD ⊥, 因为//AB CD ,所以AE AB ⊥;因为PA ⊥平面ABCD ,AE ⊂平面ABCD , 所以AE PA ⊥; 因为PA AB A = 所以AE ⊥平面PAB ,AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .(Ⅲ)存在点F 为PB 中点时,满足//CF 平面PAE ;理由如下:分别取,PB PA 的中点,F G ,连接,,CF FG EG , 在三角形PAB 中,//FG AB 且12FG AB =;在菱形ABCD 中,E 为CD 中点,所以//CE AB 且12CE AB =,所以//CE FG 且CE FG =,即四边形CEGF 为平行四边形,所以//CF EG ; 又CF⊄平面PAE ,EG ⊂平面PAE ,所以//CF 平面PAE .【点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力. 11.(I )证明见解析. (II )证明见解析. 【详解】证明:(I )E ,F 分别为AB ,BD 的中点EF AD ⇒}EF ADAD ACD EF ACD EF ACD⇒⊂⇒⊄面面面. (II )}}}EF ADEF BDAD BD CD CB CF BD BD EFCF BD EF CF F⇒⊥⊥=⇒⊥⇒⊥⋂=面为的中点,又BD BCD ⊂面,所以EFC BCD ⊥面面.12.(1)证明见解析;(2)证明见解析;(3)证明见解析. 【分析】(1)根据底面是正方形,得到CDAB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥. 【详解】(1)∵四棱锥P ABCD -的底面是正方形, ∴CDAB ,∵CD CD ⊄平面PAB ,AB 平面PAB ,∴CD ∥平面PAB . (2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.13.(1)证明见解析;(2)1A C 与BD 不可能垂直,证明见解析.【分析】(1)证得1A B ⊥平面1A CD ,结合面面垂直的判定定理即可得出结论;(2)假设1A C 与BD 垂直,然后推出与已知条件11A B A D ⊥矛盾,即可得出1A C 与BD 不可能垂直.【详解】(1)因为平面1A BD ⊥平面BCD ,平面1A BD 平面BCD =BD ,CD ⊂平面BCD ,CD ⊥BD ,所以CD ⊥平面1A BD ,又因为1A B ⊂平面1A BD ,所以CD ⊥1A B ,又因为11A B A D ⊥,1A D CD D =,所以1A B ⊥平面1A CD ,且1A B ⊂平面1A BC ,所以平面1A BC ⊥平面1A CD ;(2)假设1A C 与BD 垂直,又因为CD ⊥BD ,且1AC CD C ⋂=,所以DB ⊥平面1A CD ,又因为1A D ⊂平面1A CD ,所以1DB A D ⊥,这与11A B A D ⊥矛盾,故假设不成立,即1A C 与BD 不可能垂直.23.(1)见解析;(2)见解析;(3)见解析【解析】试题分析:(1)取线段1A B 的中点H ,由三角形中位线性质以及平行四边形性质得四边形DEFH 为平行四边形,即得//EF HD .再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得1A O DE ⊥.再根据面面垂直性质定理得1A O ⊥平面BCED ,即得1CO A O ⊥,根据勾股定理得CO BO ⊥,所以由线面垂直判定定理得 CO ⊥平面1A OB ,最后根据面面垂直判定定理得结论,(3)假设线段OC 上存在点G ,使得OC ⊥平面EFG ,则EO EC =,与条件矛盾.试题解析:解:(1)取线段1A B 的中点H ,连接HD ,HF .因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 //DE BC ,12DE BC =. 因为 H ,F 分别为1A B ,1A C 的中点,所以 //HF BC ,12HF BC =, 所以 //HF DE ,HF DE =,所以 四边形DEFH 为平行四边形,所以 //EF HD . 因为 EF ⊄平面1A BD , HD ⊂平面1A BD ,所以 //EF 平面1A BD .(2)因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 AD AE =.所以11A D A E =,又O 为DE 的中点,所以 1A O DE ⊥.因为平面1A DE ⊥平面BCED ,且1AO ⊂平面1A DE , 所以 1A O ⊥平面BCED ,所以 1CO A O ⊥.在△OBC 中,4BC =,易知 OB OC ==所以 CO BO ⊥,所以 CO ⊥平面1A OB ,所以 平面1A OB ⊥平面1A OC .(3)线段OC 上不存在点G ,使得OC ⊥平面EFG .否则,假设线段OC 上存在点G ,使得OC ⊥平面EFG ,连接 GE ,GF ,则必有 OC GF ⊥,且OC GE ⊥.在Rt △1A OC 中,由F 为1A C 的中点,OC GF ⊥,得G 为OC 的中点.在△EOC 中,因为OC GE ⊥,所以EO EC =,这显然与1EO =,EC =所以线段OC 上不存在点G ,使得OC ⊥平面EFG .14.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析【分析】(I )由AD ⊥DE ,AD ⊥CD 可得AD ⊥平面CDE ,故而AD ⊥CE ;(II )证明平面ABF ∥平面CDE ,故而BF ∥平面CDE ;(III )取CE 的中点P ,BE 的中点Q ,证明CE ⊥平面ADPQ 即可得出平面ADQ ⊥平面BCE .【详解】(Ⅰ)由底面ABCD 为矩形,知AD CD ⊥.又因为DE AD ⊥,DE CD D ⋂=,所以AD ⊥平面CDE .又因为CE ⊂平面CDE ,所以AD CE ⊥.(Ⅱ)由底面ABCD 为矩形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE ,所以//AB 平面CDE .同理//AF 平面CDE ,又因为AB AF A ⋂=,所以平面//ABF 平面CDE .又因为BF ⊂平面ABF ,所以//BF 平面CDE .(Ⅲ)结论:线段BE 上存在点Q (即BE 的中点),使得平面ADQ ⊥平面BCE . 证明如下:取CE 的中点P ,BE 的中点Q ,连接,,AQ DP PQ ,则//PQ BC .由//AD BC ,得//PQ AD .所以,,,A D P Q 四点共面.由(Ⅰ),知AD ⊥平面CDE ,所以AD DP ⊥,故BC DP ⊥.在△CDE 中,由DC DE =,可得DP CE ⊥.又因为BC CE C ⋂=,所以DP ⊥平面BCE .又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE (即平面ADQ ⊥平面BCE ).即线段BE 上存在点Q (即BE 中点),使得平面ADQ ⊥平面BCE【点睛】本题考查了线面垂直、面面垂直的判定与性质定理的应用,线面平行的判定,熟练运用定理是解题的关键,属于中档题.15.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.【分析】(Ⅰ)证明以DE ∥平面PBC ,只需证明DE ∥PC ;(Ⅱ)证明BC ⊥平面PAB ,根据线面垂直的判定定理,只需证明PA ⊥BC ,AB ⊥BC ;(Ⅲ)当点F 是线段AB 中点时,证明平面DEF ∥平面PBC ,可得平面DEF 内的任一条直线都与平面PBC 平行.【详解】(Ⅰ)证明:因为点E 是AC 中点,点D 为PA 的中点,所以//DE PC .又因为DE ⊄面PBC ,PC ⊂面PBC ,所以DE ∥平面PBC .(Ⅱ)证明:因为平面PAC ⊥面ABC ,平面PAC ∩平面ABC =AC ,又PA ⊂平面PAC ,PA ⊥AC , 所以PA ⊥面ABC ,因为BC ⊂平面ABC ,所以PA ⊥BC .又因为AB ⊥BC ,且PA ∩AB =A ,所以BC ⊥面PAB .(Ⅲ)当点F 是线段AB 中点时,过点D ,E ,F 的平面内的任一条直线都与平面PBC 平行. 取AB 中点F ,连EF ,连DF .由(Ⅰ)可知DE ∥平面PBC .因为点E 是AC 中点,点F 为AB 的中点,所以EF ∥BC .又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以EF ∥平面PBC .又因为DE ∩EF =E ,所以平面DEF ∥平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.故当点F 是线段AB 中点时,过点D ,E ,F 所在平面内的任一条直线都与平面PBC 平行.【点睛】本题考查线面平行,考查线面垂直,考查面面平行,考查学生分析解决问题的能力,掌握线面平行、线面垂直、面面垂直的判定定理是关键.16.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)根据底面是正方形,得到CD AB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥.【详解】(1)∵四棱锥P ABCD -的底面是正方形,∴CD AB ,∵CD ⊄平面PAB ,AB平面PAB , ∴CD ∥平面PAB .(2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.。
1. 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比. 【解析】(Ⅰ)由题设知BC BC⊥⊥1CC ,BC ,BC⊥⊥AC AC,,1CC AC C Ç=,∴BC ^面11ACC A , , 又又∵1DC Ì面11ACC A ,∴1DC BC ^,由题设知01145A DC ADC Ð=Ð=,∴1CDC Ð=090,即1DC DC ^, 又∵DC BC C Ç=, , ∴∴1DC ⊥面BDC , , ∵∵1DC Ì面1BDC , ∴面BDC ⊥面1BDC ;(Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132+´´´=12,由三棱柱111ABC A B C -的体积V =1,∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2. 如图5所示,在四棱锥P ABCD -中,AB ^平面PAD ,//AB CD ,PD AD =,E 是PB 的中点,F 是CD 上的点且12DF AB =,PH 为△PAD 中AD 边上的高. (1)证明:PH ^平面ABCD ;(2)若1PH =,2AD =,1FC =,求三棱锥E BCF -的体积;的体积;(3)证明:EF ^平面PAB . B 1C B A D C 1A 1【解析】(1)证明:因为AB ^平面PAD ,所以PH AB ^。
因为PH 为△PAD 中AD 边上的高,边上的高, 所以PH AD ^。
因为AB AD A = ,所以PH ^平面ABCD 。
(2)连结BH ,取BH 中点G ,连结EG 。
立体几何第二讲:(平行与垂直问题)例1在四棱锥P-ABCD中,底面ABCD是平行四边形,M,N分别是AB,PC的中点,求证:MN∥平面P AD.例2在直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,求证:A1C⊥BC1.例3在三棱锥P-ABC中,平面P AB⊥平面ABC,AB⊥BC,AP⊥PB,求证:平面P AC⊥平面PBC.例4如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.(Ⅰ)求证:直线EF∥平面A1ACC1;(Ⅱ)在线段AB上确定一点G,使平面EFG⊥平面ABC,并给出证明.例题5.,在四面体ABC P -中,已知6==BC PA ,342,8,10====PB AC AB PC .F 是线段PB 上一点,341715=CF ,点E 在线段AB 上,且PB EF ⊥. (Ⅰ)证明:CEF PB 平面⊥;(Ⅱ)求二面角F CE B --的大小.例题6如图,在锥体P ﹣ABCD 中,ABCD 是边长为1的菱形,且∠DAB=60°,PA=PD=,PB=2, E ,F 分别是BC ,PC 的中点 ( 1)证明:AD ⊥平面DEF(2)求二面角P ﹣AD ﹣B 的余弦值.AC B PF E 图3例题解答:例题1【分析】要证明“线面平行”,可通过“线线平行”或“面面平行”进行转化;题目中出现了中点的条件,因此可考虑构造(添加)中位线辅助证明.证明:方法一,取PD 中点E ,连接AE ,NE .∵底面ABCD 是平行四边形,M ,N 分别是AB ,PC 的中点,∴MA ∥CD ,.21CD MA = ∵E 是PD 的中点, ∴NE ∥CD ,.21CD NE =∴MA ∥NE ,且MA =NE , ∴AENM 是平行四边形, ∴MN ∥AE .又AE ⊂平面P AD ,MN ⊄平面P AD , ∴MN ∥平面P AD .方法二取CD 中点F ,连接MF ,NF . ∵MF ∥AD ,NF ∥PD , ∴平面MNF ∥平面P AD , ∴MN ∥平面P AD .例2 【分析】要证明“线线垂直”,可通过“线面垂直”进行转化,因此设法证明A 1C 垂直于经过BC 1的平面即可.证明:连接AC 1.∵ABC -A 1B 1C 1是直三棱柱, ∴AA 1⊥平面ABC , ∴AB ⊥AA 1. 又AB ⊥AC ,∴AB ⊥平面A 1ACC 1, ∴A 1C ⊥A B .① 又AA 1=AC ,∴侧面A 1ACC 1是正方形, ∴A 1C ⊥AC 1.②由①,②得A 1C ⊥平面ABC 1, ∴A 1C ⊥BC 1.例3 【分析】要证明“面面垂直”,可通过“线面垂直”进行转化,而“线面垂直”又 可以通过“线线垂直”进行转化.证明:∵平面P AB ⊥平面ABC ,平面P AB ∩平面ABC =AB ,且AB ⊥BC , ∴BC ⊥平面P AB , ∴AP ⊥BC . 又AP ⊥PB ,∴AP ⊥平面PBC , 又AP ⊂平面P AC ,∴平面P AC ⊥平面PBC .例4 如图,在斜三棱柱ABC -A 1B 1C 1中,侧面A 1ABB 1是菱形,且垂直于底面ABC ,∠A 1AB =60°,E ,F 分别是AB 1,BC 的中点.(Ⅰ)求证:直线EF ∥平面A 1ACC 1;(Ⅱ)在线段AB 上确定一点G ,使平面EFG ⊥平面ABC ,并给出证明. 证明:(Ⅰ)连接A 1C ,A 1E .∵侧面A 1ABB 1是菱形, E 是AB 1的中点, ∴E 也是A 1B 的中点,又F 是BC 的中点,∴EF ∥A 1C .∵A 1C ⊂平面A 1ACC 1,EF ⊄平面A 1ACC 1, ∴直线EF ∥平面A 1ACC 1. (2)解:当31=GA BG 时,平面EFG ⊥平面ABC ,证明如下: 连接EG ,FG .∵侧面A 1ABB 1是菱形,且∠A 1AB =60°,∴△A 1AB 是等边三角形. ∵E 是A 1B 的中点,31=GA BG ,∴EG ⊥AB . ∵平面A 1ABB 1⊥平面ABC ,且平面A 1ABB 1∩平面ABC =AB , ∴EG ⊥平面ABC .又EG ⊂平面EFG ,∴平面EFG ⊥平面ABC . 例题5.,【答案】 (Ⅰ)证明:在ABC ∆中, ∵,6,10,8===BC AB AC∴,222AB BC AC =+∴△PAC 是以∠PAC 为直角的直角三角形, 同理可证,△PAB 是以∠PAB 为直角的直角三角形,△PCB 是以∠PCB 为直角的直角三角形. 在PCB Rt ∆中,∵,341715,342,6,10====CF PB BC PC ∴,CF PB BC PC ⋅=⋅ ∴,CF PB ⊥又∵,,F CF EF PB EF =⊥ ∴.CEF PB 平面⊥ (II )解法一:由(I )知PB ⊥CE ,PA ⊥平面ABC∴AB 是PB 在平面ABC 上的射影,故AB ⊥CE ∴CE ⊥平面PAB ,而EF ⊂平面PAB , ∴EF ⊥EC ,故∠FEB 是二面角B —CE —F 的平面角,∵EFB PAB ∆∆~∴35610cot tan ===∠=∠AP AB PBA FEB , ∴二面角B —CE —F 的大小为35arctan.例6如图,在锥体P ﹣ABCD 中,ABCD 是边长为1的菱形,且∠DAB=60°,PA=PD=,PB=2,E,F分别是BC,PC的中点(1)证明:AD⊥平面DEF(2)求二面角P﹣AD﹣B的余弦值.解:(1)取AD的中点G,连接PG,BG,在△ABG中,根据余弦定理可以算出BG=,发现AG2+BG2=AB2,可以得出AD⊥BG,又DE∥BG∴DE⊥AD,又PA=PD,可以得出AD⊥PG,而PG∩BG=G,∴AD⊥平面PBG,而PB⊂平面PBG,∴AD⊥PB,又PB∥EF,∴AD⊥EF.又EF∩DE=E,∴AD⊥平面DEF.(2)由(1)知,AD⊥平面PBG,所以∠PGB为二面角P﹣AD﹣B的平面角,在△PBG中,PG=,BG=,PB=2,由余弦定理得cos∠PGB=,因此二面角P﹣AD﹣B的余弦值为.点评:本题考查立体几何中基本的线面关系,考查线面垂直的判定方法,考查二面角的求法,训练了学生基本的空间想象能力,考查学生的转化与化归思想,解三角形的基本知识和学生的运算能力,属于基本的立体几何题.练习一、选择题:1.已知m ,n 是两条不同直线,α ,β ,γ 是三个不同平面,下列命题中正确的是( ) (A)若m ∥α ,n ∥α ,则m ∥n (B)若m ⊥α ,n ⊥α ,则m ∥n (C)若α ⊥γ ,β ⊥γ ,则α ∥β (D)若m ∥α ,m ∥β ,则α ∥β 2.已知直线m ,n 和平面α ,β ,且m ⊥n ,m ⊥α ,α ⊥β ,则( ) (A)n ⊥β (B)n ∥β ,或n ⊂β (C)n ⊥α (D)n ∥α ,或n ⊂α3.设a ,b 是两条直线,α 、β 是两个平面,则a ⊥b 的一个充分条件是( ) (A)a ⊥α ,b ∥β ,α ⊥β (B)a ⊥α ,b ⊥β ,α ∥β (C)a ⊂α ,b ⊥β ,α ∥β (D)a ⊂α ,b ∥β ,α ⊥β 4.设直线m 与平面α 相交但不垂直,则下列说法中正确的是( ) (A)在平面α 内有且只有一条直线与直线m 垂直 (B)过直线m 有且只有一个平面与平面α 垂直 (C)与直线m 垂直的直线不可能与平面α 平行 (D)与直线m 平行的平面不可能与平面α 垂直 二、填空题:5.在三棱锥P -ABC 中,6==PB PA ,平面P AB ⊥平面ABC ,P A ⊥PB ,AB ⊥BC ,∠BAC =30°,则PC =______.6.在直四棱柱ABCD -A 1B 1C 1D 1中,当底面ABCD 满足条件______时,有A 1C ⊥B 1D 1.(只要求写出一种条件即可)7.设α ,β 是两个不同的平面,m ,n 是平面α ,β 之外的两条不同直线,给出四个论断: ①m ⊥n ②α ⊥β ③n ⊥β ④m ⊥α以其中三个论断作为条件,余下的一个论断作为结论,写出正确的一个命题______.8.已知平面α ⊥平面β ,α ∩β =l ,点A ∈α ,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α ,m ∥β ,给出下列四种位置:①AB ∥m ;②AC ⊥m ;③AB ∥β ;④AC ⊥β , 上述四种位置关系中,不一定成立的结论的序号是______. 三、解答题:9.如图,三棱锥P -ABC 的三个侧面均为边长是1的等边三角形,M ,N 分别为P A ,BC 的中点.(Ⅰ)求MN 的长; (Ⅱ)求证:P A ⊥BC .10.如图,在四面体ABCD 中,CB =CD ,AD ⊥BD ,且E 、F 分别是AB 、BD 的中点.求证:(Ⅰ)直线EF ∥平面ACD ; (Ⅱ)平面EFC ⊥平面BCD .11.如图,平面ABEF ⊥平面ABCD ,四边形ABEF 与ABCD 都是直角梯形,∠BAD =∠F AB =90°,BC ∥AD ,AF BE AF BE AD BC 21,//,21==,G ,H 分别为F A ,FD 的中点.(Ⅰ)证明:四边形BCHG 是平行四边形;(Ⅱ)C ,D ,F ,E 四点是否共面?为什么?(Ⅲ)设AB =BE ,证明:平面ADE ⊥平面CDE .例2 如图,正三棱柱ABC -A 1B 1C 1中,E 是AC 的中点.(Ⅰ)求证:平面BEC 1⊥平面ACC 1A 1;(Ⅱ)求证:AB 1∥平面BEC 1.【分析】本题给出的三棱柱不是直立形式的直观图,这种情况下对空间想象能力提出了更高的要求,可以根据几何体自身的性质,适当添加辅助线帮助思考.证明:(Ⅰ)∵ABC -A 1B 1C 1是正三棱柱,∴AA 1⊥平面ABC , ∴BE ⊥AA 1.∵△ABC 是正三角形,E 是AC 的中点,∴BE ⊥AC ,∴BE ⊥平面ACC 1A 1,又BE ⊂平面BEC 1, ∴平面BEC 1⊥平面ACC 1A 1.(Ⅱ)证明:连接B 1C ,设BC 1∩B 1C =D .∵BCC 1B 1是矩形,D 是B 1C 的中点, ∴DE ∥AB 1. 又DE ⊂平面BEC 1,AB 1⊄平面BEC 1, ∴AB 1∥平面BEC 1.例3 【分析】本题中的数量关系较多,可考虑从“算”的角度入手分析,如从M 是PC 上的动点分析知,MB ,MD 随点M 的变动而运动,因此可考虑平面MBD 内“不动”的直线BD 是否垂直平面P AD .证明:(Ⅰ)在△ABD 中,由于AD =4,BD =8,54=AB ,所以AD 2+BD 2=AB 2. 故AD ⊥BD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,BD ⊂平面ABCD , 所以BD ⊥平面P AD ,又BD ⊂平面MBD ,故平面MBD ⊥平面P AD . (Ⅱ)解:过P 作PO ⊥AD 交AD 于O ,由于平面P AD ⊥平面ABCD ,所以PO ⊥平面ABCD . 因此PO 为四棱锥P -ABCD 的高,又△P AD 是边长为4的等边三角形.因此.32423=⨯=PO 在底面四边形ABCD 中,AB ∥DC ,AB =2DC ,所以四边形ABCD 是梯形,在Rt △ADB 中,斜边AB 边上的高为5585484=⨯,即为梯形ABCD 的高, 所以四边形ABCD 的面积为.2455825452=⨯+=S 故.316322431=⨯⨯=-ABCD P V立体几何参考答案练习7-1一、选择题:1.B 2.D 3.C 4.B 二、填空题:5.10 6.AC ⊥BD (或能得出此结论的其他条件)7.②、③、④⇒①;或①、③、④⇒② 8.④ 三、解答题:9.(Ⅰ)解:连接MB ,MC .∵三棱锥P -ABC 的三个侧面均为边长是1的等边三角形,∴23==MC MB ,且底面△ABC 也是边长为1的等边三角形. ∵N 为BC 的中点,∴MN ⊥BC . 在Rt △MNB 中,⋅=-=2222BN MB MN (Ⅱ)证明:∵M 是P A 的中点,∴P A ⊥MB ,同理P A ⊥MC .∵MB ∩MC =M ,∴P A ⊥平面MBC , 又BC ⊂平面MBC ,∴P A ⊥BC .10.证明:(Ⅰ)∵E 、F 分别是AB 、BD 的中点,∴EF 是△ABD 的中位线,∴EF ∥AD .又EF ⊄平面ACD ,AD ⊂平面ACD ,∴直线EF ∥平面ACD .(Ⅱ)∵EF ∥AD ,AD ⊥BD ,∴EF ⊥BD .∵CB =CD ,F 是BD 的中点,∴CF ⊥BD .∵CF ∩EF =F ,∴BD ⊥平面CEF .∵BD ⊂平面BCD ,∴平面EFC ⊥平面BCD .11.(Ⅰ)由题意知,FG =GA ,FH =HD ,∴GH ∥AD ,,21AD GH =又BC ∥AD ,AD BC 21=,∴GH ∥BC ,GH =BC , ∴四边形BCHG 是平行四边形. (Ⅱ)C ,D ,F ,E 四点共面.理由如下: 由BE ∥AF ,AF BF 21=,G 是F A 的中点, 得BE ∥FG ,且BE =FG .∴EF ∥BG .由(Ⅰ)知BG ∥CH ,∴EF ∥CH ,故EC ,FH 共面,又点D 在直线FH 上, 所以C ,D ,F ,E 四点共面. (Ⅲ)连结EG ,由AB =BE ,BE ∥AG ,BE =AG 及∠BAG =90°,知ABEG 是正方形,故BG ⊥EA .由题设知F A ,AD ,AB 两两垂直,故AD ⊥平面F ABE ,∴BG ⊥AD . ∴BG ⊥平面EAD ,∴BG ⊥ED . 又ED ∩EA =E ,∴BG ⊥平面ADF . 由(Ⅰ)知CH ∥BG ,∴CH ⊥平面ADE .由(Ⅱ)知F ∈平面CDE ,故CH ⊂平面CDE ,得平面ADE ⊥平面CDE .。
1、如图,已知空间四边形ABCD 中,,BCAC ADBD ,E 是AB 的中点。
求证:(1)AB平面CDE; (2)平面CDE 平面ABC 。
2、如图,在正方体1111ABCDA B C D 中,E 是1AA 的中点,求证:1//AC 平面BDE 。
3、已知ABC 中90ACB o,SA面ABC ,AD SC ,求证:AD面SBC .4、已知正方体1111ABCDA B C D ,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC 面11AB D .5、正方体''''ABCD A B C D 中,求证:(1)''AC B D DB 平面;(2)''BD ACB 平面.6、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ;(2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .AED BCAED 1CB 1DCBASDCBAD 1ODBAC 1B 1A 1CA 1B 1C 1C D 1DGEF7、四面体ABCD 中,,,ACBD E F 分别为,AD BC 的中点,且22EFAC ,90BDCo,求证:BD平面ACD8、如图,在正方体1111ABCDA B C D 中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .9、如图,在正方体1111ABCDA B C D 中,E 是1AA 的中点.(1)求证:1//A C 平面BDE ;(2)求证:平面1A AC 平面BDE .10、已知ABCD 是矩形,PA 平面ABCD ,2AB,4PA AD ,E 为BC 的中点.(1)求证:DE 平面PAE ;(2)求直线DP 与平面PAE 所成的角.11、如图,在四棱锥P ABCD 中,底面ABCD 是60DAB且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG 平面PAD ;(2)求证:AD PB .12、如图1,在正方体1111ABCDA B C D 中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO 平面MBD .13、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .14.(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.已知:如图,三棱锥S—ABC,SC∥截面EFGH,AB∥截面EFGH.求证:截面EFGH是平行四边形.15.(12分)已知正方体ABCD—A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=23a,如图.(1)求证:MN∥面BB1C1C;(2)求MN的长.16.(12分)(2009·浙江高考)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(1)证明:PQ∥平面ACD;(2)求AD与平面ABE所成角的正弦值.17.(12分)如图,在四面体ABCD中,CB=CD,AD⊥BD,点E、F分别是AB、BD的中点.求证:(1)直线EF∥面ACD.(2)平面EFC ⊥平面BCD.1、如图,已知空间四边形ABCD 中,,BC AC AD BD ,E 是AB 的中点。
高中数学必修二第八章立体几何初步典型例题单选题1、如图,△A′B′C′是水平放置的△ABC的直观图,其中B′C′=C′A′=2,A′B′,A′C′分别与x′轴,y′轴平行,则BC=()A.2B.2√2C.4D.2√6答案:D分析:先确定△A′B′C′是等腰直角三角形,求出A′B′,再确定原图△ABC的形状,进而求出BC.由题意可知△A′B′C′是等腰直角三角形,A′B′=2√2,其原图形是Rt△ABC,AB=A′B′=2√2,AC=2A′C′=4,∠BAC=90°,则BC=√8+16=2√6,故选:D.2、如图直角△O′A′B′是一个平面图形的直观图,斜边O′B′=4,则原平面图形的面积是()A.8√2B.4√2C.4D.√2答案:A解析:根据斜二测画法规则可求原平面图形三角形的两条直角边长度,利用三角形的面积公式即可求解.由题意可知△O′A′B′为等腰直角三角形,O′B′=4,则O′A′=2√2,所以原图形中,OB=4,OA=4√2,×4×4√2=8√2.故原平面图形的面积为12故选:A3、正方体中,点P,O,R,S是其所在棱的中点,则PQ与RS是异面直线的图形是()A.B.C.D.答案:C分析:对于A,B,D,利用两平行线确定一个平面可以证明直线PQ与RS共面,对于C,利用异面直线的定义推理判断作答.对于A,在正方体ABCD−A1B1C1D1中,连接AC,A1C1,则AC//A1C1,如图,因为点P,Q,R,S是其所在棱的中点,则有PQ//AC,RS//A1C1,因此PQ//RS,则直线PQ与RS共面,A错误;对于B,在正方体ABCD−A1B1C1D1中,连接AC,QS,PR,如图,因为点P,Q,R,S是其所在棱的中点,有AP//CR且AP=CR,则四边形APRC为平行四边形,即有AC//PR,又QS//AC,因此QS//PR,直线PQ与RS共面,B错误;对于C,在正方体ABCD−A1B1C1D1中,如图,因为点P,Q,R,S是其所在棱的中点,有RS//BB1,而BB1⊂平面ABB1A1,RS⊄平面ABB1A1,则RS//平面ABB1A1,PQ⊂平面ABB1A1,则直线PQ与RS无公共点,又直线PQ与直线BB1相交,于是得直线PQ与RS不平行,则直线PQ与RS是异面直线,C正确;对于D,在正方体ABCD−A1B1C1D1中,连接A1B,D1C,PS,QR,如图,因为A1D1//BC且A1D1=BC,则四边形A1D1CB为平行四边形,有A1B//D1C,因为点P,Q,R,S是其所在棱的中点,有PS//A1B,QR//D1C,则PS//QR,直线PQ与RS共面,D错误.故选:C4、下面四个选项中一定能得出平面α/⁄平面β的是()A.存在一条直线a,a//α,a//βB.存在一条直线a,a⊂α,a//βC.存在两条平行直线a,b,a⊂α,b⊂β,a//β,b//αD.存在两条异面直线a,b,a⊂α,b⊂β,a//β,b//α答案:D分析:对于A,B,C,举出符合条件的特例即可判断;对于D,过直线a作平面γ∩β=c,再证c//α即可. 如图,ABCD−A1B1C1D1是长方体,平面ABCD为平面α,平面ABB1A1为平面β,对于A,直线C1D1为直线a,显然a//α,a//β,而α与β相交,A不正确;对于B,直线CD为直线a,显然a⊂α,a//β,而α与β相交,B不正确;对于C,直线CD为直线a,直线A1B1为直线b,显然a⊂α,b⊂β,a//β,b//α,而α与β相交,C不正确;对于D,因a,b是异面直线,且a⊂α,b⊂β,过直线a作平面γ∩β=c,如图,则c//a,并且直线c与b必相交,而c⊄α,于是得c//α,又b//α,即β内有两条相交直线都平行于平面α,⁄平面β.因此,平面α/故选:D5、某正方体被截去部分后得到的空间几何体的三视图如图所示,则该空间几何体的体积为()A .132B .223C .152D .233答案:C分析:根据几何体的三视图,可知该几何体是棱长为2的正方体截去两个小三棱锥,根据三棱锥的体积公式即可求解.解:根据几何体的三视图,该空间几何体是棱长为2的正方体截去两个小三棱锥,由图示可知,该空间几何体体积为V =23−(13×12×12×1+13×12×12×2)=152,故选:C.6、已知圆锥的母线长为3,其侧面展开图是一个圆心角为2π3的扇形,则该圆锥的体积为( ) A .√23πB .2√23πC .πD .√2π 答案:B分析:根据弧长计算公式,求得底面圆半径以及圆锥的高,即可求得圆锥的体积.设圆锥的底面圆半径为r ,故可得2πr =2π3×3,解得r =1,设圆锥的高为ℎ,则ℎ=√32−12=2√2,则圆锥的体积V =13×πr 2×ℎ=13×π×2√2=2√23π. 故选:B.7、已知正四棱锥的底面边长为6,侧棱长为5,则此棱锥的侧面积为( )A .6B .12C .24D .48答案:D分析:首先由勾股定理求出斜高,即可求出侧面积;解:正四棱锥的底面边长为6,侧棱长为5,则其斜高ℎ′=√52−(62)2=4,所以正四棱锥的侧面积S =12×4×6×4=48故选:D8、已知三棱锥P −ABC ,其中PA ⊥平面ABC ,∠BAC =120°,PA =AB =AC =2,则该三棱锥外接球的表面积为( )A .12πB .16πC .20πD .24π答案:C分析:根据余弦定理、正弦定理,结合球的性质、球的表面积公式进行求解即可.根据题意设底面△ABC 的外心为G ,O 为球心,所以OG ⊥平面ABC ,因为PA ⊥平面ABC ,所以OG//PA ,设D 是PA 中点,因为OP =OA ,所以DO ⊥PA ,因为PA ⊥平面ABC ,AG ⊂平面ABC ,所以AG ⊥PA ,因此OD//AG ,因此四边形ODAG 是平行四边形,故OG =AD =12PA =1, 由余弦定理,得BC =√AB 2+AC 2−2AB ⋅AC ⋅cos120°=√4+4−2×2×2×(−12)=2√3,由正弦定理,得2AG =√3√32⇒AG =2,所以该外接球的半径R 满足R 2=(OG )2+(AG )2=5⇒S =4πR 2=20π,故选:C .小提示:关键点睛:运用正弦定理、余弦定理是解题的关键.多选题9、(多选)下列说法中正确的是()A.若直线l与平面α不平行,则l与α相交B.直线l在平面外是指直线和平面平行C.如果直线l经过平面α内一点P,又经过平面α外一点Q,那么直线l与平面α相交D.如果直线a∥b,且a与平面α相交于点P,那么直线b必与平面α相交答案:CD分析:由线面直线的位置关系逐一判断即可求解.若直线l与平面α不平行,则l与α相交或l⊂α,所以A不正确.若l⊄α,则l//α或l与α相交,所以B不正确.由线面直线的位置关系可知,C、D正确.故选:CD10、如图,长方体ABCD−A1B1C1D1中,AB=BC=1,AA1=2,M为AA1的中点,过B1M作长方体的截面α交棱CC1于N,则()A.截面α可能为六边形B .存在点N ,使得BN ⊥截面αC .若截面α为平行四边形,则1≤CN ≤2D .当N 与C 重合时,截面面积为3√64答案:CD分析:利用点N 的位置不同得到的截面α的形状判断选项A ,C ,利用线面垂直的判定定理分析选项B ,利用平面几何知识求相应的量结合梯形的面积公式求得截面的面积,从而可判断选项D .长方体ABCD −A 1B 1C 1D 1中,AB =BC =1,AA 1=2,M 为AA 1的中点,过B 1M 作长方体的截面α交棱CC 1于N , 设N 0为CC 1的中点,根据点N 的位置的变化分析可得:当1≤CN ≤2时,截面α为平行四边形,当0<CN <1时,截面α为五边形,当CN =0时,即点N 与点C 重合时,截面α为梯形,故A 不正确,C 正确;设BN ⊥截面α,因为B 1M ⊂面α,所以BN ⊥B 1M ,所以N 只能与C 重合才能使BN ⊥B 1M ,因为BN 不垂直平面B 1CQM ,故此时不成立,故B 不正确;因为当点N 与点C 重合时,截面α为梯形,如下图所示:过M 作MH 垂直于B 1C 于H ,设梯形的高为ℎ,MH =x ,则由平面几何知识得:ℎ2=(√2)2−x 2=(√52)2−(√52−x)2,解得x =2√55,ℎ=√305,所以截面α的面积为:12×(√5+√52)×ℎ=12×3√52×√305=3√64,故D 正确;故选:CD .小提示:关键点睛:本题考查长方体的截面的形状,关键在于分析动点在不同的位置时,截面的形状,运用线面平行的判定定理和平面几何知识求得截面的面积.11、在棱长为2的正方体ABCD−A1B1C1D1中,点P是正方体的棱上一点,|PB|+|PC1|=λ,则()A.λ=2时,满足条件的点P的个数为1B.λ=4时,满足条件的点P的个数为4C.λ=4√2时,满足条件的点P的个数为2D.若满足|PB|+|PC1|=λ的点P的个数为6,则λ的取值范围为(2√2,4)答案:BC分析:根据各棱上的点P到B,C1两点距离之和对选项进行逐一分析,由此确定正确选项.设E,F分别是C1D1,AB的中点,|BD1|=√22+(2√2)2=2√3,|BE|=|C1F|=√12+(2√2)2=3,|A1C1|=|A1B|=2√2.由于|BC1|=2√2,所以|PB|+|PC1|=λ≥2√2,所以A选项错误.λ=4,满足|PB|+|PC1|=4的点为B1,C,E,F共4个,所以B选项正确.λ=4√2,满足|PB|+|PC1|=4√2的点为A1,D共2个,所以C选项正确.当P在正方形ADD1A1(不包括A,D,D1,A1)上运动时,λ∈(2+2√3,4√2),此时棱A1B1与棱CD上,也存在点使λ∈(2+2√3,4√2).所以当λ∈(2+2√3,4√2)时,满足|PB|+|PC1|=λ的点P的个数为6,所以D选项错误.故选:BC填空题12、已知A、B、C、D四点不共面,且AB//平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG是______四边形.答案:平行分析:由题,平面ABD∩平面α=FH,结合AB//平面α可得AB//FH,同理可得四边形EFHG另外三边与AB,CD的位置关系,即可得到答案.由题,平面ABD∩平面α=FH,因为AB//平面α,所以AB//FH,又平面ABC∩平面α=EG,所以AB//EG,则FH//EG,同理GH//CD//EF,所以四边形EFHG是平行四边形,所以答案是:平行13、如图已知A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点,若异面直线AD与BC所成角的大小为π3,则AD与EF所成角的大小为___________.答案:π3或π6分析:取AC的中点G,连接EG,GF,则∠EGF=π3或∠EGF=2π3,分别分析这两种情况下∠GFE的大小即为AD与EF所成角.解:如图所示:取AC的中点G,连接EG,GF,则EG//BC,GF//AD,所以∠EGF为异面直线AD与BC所成角或其补角.因为AD=BC,所以EG=GF,当∠EGF=π3时,△EGF为等边三角形,∠GFE=π3,即AD与EF所成角的大小为π3;当∠EGF=2π3时,EG=GF,△EGF为等腰三角形,∠GFE=π6,即AD与EF所成角的大小为π6.所以答案是:π3或π6.14、已知三棱柱ABC −A 1B 1C 1中,棱长均为2,顶点A 1在底面ABC 上的射影恰为AB 的中点D ,E 为AC 的中点,则直线BE 与直线AB 1所成角的余弦值为________.答案:34分析:根据三棱柱性质与题中的中点条件,可将所求直线BE 与直线AB 1所成角的余弦值转化为求直线GB 1与直线AB 1所成角的余弦值,那么就要通过多次转化最终求得△AGB 1中三边长,然后直接在△AGB 1中运用余弦定理即可.如图,取A 1C 1中点G ,连接B 1G,AG,AE,DE,GE ,由三棱柱的性质易证得GE //BB 1,GE =BB 1,所以四边形GEBB 1为平行四边形,所以GB 1//BE ,所以下面即求直线GB 1与直线AB 1所成角的余弦值.由题意知,A 1D ⊥平面ABC ,因为AB,DE ⊂平面ABC ,所以A 1D ⊥AB,A 1D ⊥DE ,在Rt △AA 1D 中,AA 1=2,AD =12AB =1,∠A 1DA =90°,求得A 1D =√3,∠A 1AD =60°. 所以在菱形AA 1B 1B 中,AB 1=2ABcos30°=2√3.在Rt △A 1DE 中,∠A 1DE =90°,A 1D =√3,DE =12BC =1,求得A 1E =2. 所以在△A 1AE 中,根据余弦定理得cos∠A 1AE =AA 12+AE 2−A1E 22AE⋅AA 1=14,所以cos∠AA 1G =cos(π−∠A 1AE)=−14.在△A 1AG 中根据余弦定理得AG 2=AA 12+A 1G 2−2AA 1⋅A 1Gcos∠AA 1G,AG =√6.在△AGB 1中,AG =√6,AB 1=2√3,GB 1=√3,根据余弦定理得cos∠GB 1A =GB 12+AB12−AG 22GB 1⋅AB 1=34,所以直线GB 1与直线AB 1所成角的余弦值为34,即直线BE 与直线AB 1所成角的余弦值为34. 故答案为:34解答题15、在空间四边形ABCD中,AB=CD,点M、N分别为BD、AC的中点.(1)若直线AB与MN所成角为60°,求直线AB与CD所成角的大小;(2)若直线AB与CD所成角为θ,求直线AB与MN所成角的大小.答案:(1)60°(2)θ2或π−θ2分析:根据异面直线所成角的定义,借助平行关系作出平行直线,从而找到异面直线所成角(或补角)即可求解.(1)如图,取AD的中点为P,连接PM、PN.因为点M、N分别为BD、AC的中点,所以PM//AB,PN//CD,且PM=12AB,PN=12CD,所以,∠MPN为直线AB与CD所成的角(或补角),∠PMN为直线AB与MN所成的角(或补角). 又AB=CD,所以PM=PN,即△PMN为等腰三角形.直线AB与MN所成角为60°,即∠PMN=60°,则∠MPN=180°−2×60°=60°.所以,直线AB与CD所成的角为60°.(2)(2)若直线AB与CD所成的角为θ,则∠MPN=θ或∠MPN=π−θ.若∠MPN=θ,则∠PMN=π−∠MPN2=π−θ2,即直线AB与MN所成角为π−θ2;若∠MPN=π−θ,则∠PMN=π−∠MPN2=θ2,即直线AB与MN所成角为θ2.综上所述,直线AB与MN所成的角为θ2或π−θ2.。
立体几何问题
1、如图,一个瓶子里装着一些水,瓶子的下面部分是圆柱形,根据图中的数据可以计算出瓶子的容积是立方厘米。
(π取3.14)
2、阿呆买来一个模型,形状如图所示,上面的圆柱底面半径为3厘米,高为4厘米,下面的正方体棱长为6厘米,那么这个模型的表面积是平方厘米。
(π取3.14)
3、阿瓜买来一个模型,形状如下图所示,正方体棱长为12厘米,内部挖掉一个底面半径为6厘米,高为12厘米的圆柱,那么这个模型的表面积是平方厘米。
(π取3)
4、如图,一个底面周长为18.84厘米的圆柱,斜着截取一段后如图,那么部分的体积是立方厘米。
(π取3.14)
5、一个圆柱形的水池,底面半径为2米,池中有一些水,将一块石头完全浸没在水中,发现水面上升了0.5米,这块石头的体积是立方米。
(π取3.14)
6、一个底面长10分米,宽8分米,高10分米的长方形水池,存有二分之一的水,将一个高4分米,底面积为40平方分米的长方体竖直放入池中,水面会上升分米。
7、一个底面直径为10厘米,高为20厘米的圆柱形容器中装有6厘米的水,把一个土豆完全浸没在水中,水面高度现在是16厘米,那么这个土豆的体积是立方厘米。
8、一个底面半径为6厘米的圆柱形水池,里面装了一些水,水中淹没着一个底面半径为3厘米,高6厘米的圆锥体,当圆锥体取出后水面将降低厘米。
9、一个长方体容器内装着水,水面高3厘米,从里面量,容器的底面积是20平方厘米,将一个底面积为10平方厘米、高2厘米的铁块放入容器中,水面的高度会变成厘米。
10、一个高是5分米的圆柱形容器里装满了水,将一个底面积为6平方分米,高1.5分米的圆锥体放入容器中,有水溢出,溢出水的体积是立方分米。
立体几何证明基础题一.解答题(共28小题)1.如图,在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点(1)求证:PB∥平面EFG;(2)求证:BC⊥EG.2.如图,在三棱锥P﹣ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.(1)求证DE∥PA(2)求证:DE∥平面PAC;(3)求证:AB⊥PB.3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE且CE=AC=2BD,试在AE上确定一点M,使得DM∥平面ABC.4.如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且PA=AB=2.(Ⅰ)证明:BC⊥平面AMN;(Ⅱ)求三棱锥N﹣AMC的体积;(Ⅲ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.5.如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.(1)求四棱锥P﹣ABCD的体积;(2)如果E是PA的中点,求证:PC∥平面BDE;(3)是否不论点E在侧棱PA的任何位置,都有BD⊥CE?证明你的结论.6.已知四棱锥A ﹣BCDE ,其中AB=BC=AC=BE=1,CD=2,CD ⊥面ABC,BE ∥CD,F 为AD 的中点. (Ⅰ)求证:EF ∥面ABC ; (Ⅱ)求证:平面ADE ⊥平面ACD ; (Ⅲ)求四棱锥A ﹣BCDE 的体积.7.如图,四棱柱ABCD ﹣A 1B 1C 1D 1中,平面A 1ABB 1⊥平面ABCD ,且∠ABC=.(1)求证:BC ∥平面AB 1C 1;(2)求证:平面A 1ABB 1⊥平面AB 1C 1.8.如图,三角形ABC中,AC=BC=,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.(Ⅰ)求证:GF∥底面ABC;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.9.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(Ⅰ)证明:PA∥平面BMQ;(Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离.10.已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中,∠C=90°,BC=,BB 1=2,O 是AB 1的中点,D是AC 的中点,M 是CC 1的中点, (1)证明:OD ∥平面BB 1C 1C ; (2)试证:BM ⊥AB 1.11.如图,在四棱锥P ﹣ABCD 中,四边形ABCD 是平行四边形,E 、F 分别是AB 、PC 中点,求证:EF ∥面PAD .12.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是AA 1的中点,求证: (Ⅰ)A 1C ∥平面BDE ; (Ⅱ)平面A 1AC ⊥平面BDE .13.如图,四棱锥P ﹣ABCD 中,底面ABCD 为矩形,E 为PD 的中点. (1)求证:PB ∥平面AEC ;(2)若PA ⊥平面ABCD ,PA=AD ,求证:平面AEC ⊥平面PCD .14.如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,E 是PC 的中点. 求证: (1)PA ∥平面BDE ; (2)BD ⊥平面PAC .15.如图,正四棱柱ABCD ﹣A 1B 1C 1D 1,底面边长AB=1,侧棱长AA 1=2. (Ⅰ)求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积; (Ⅱ)证明:AC ⊥平面BDD 1B 1.16.已知正方体ABCD ﹣A 1B 1C 1D 1,O 是底ABCD 对角线的交点.求证: (1)C 1O ∥面AB 1D 1; (2)A 1C ⊥面AB 1D 1.17.如图所示,在正方体ABCD ﹣A 1B 1C 1D 1中,M ,E,F,N 分别为A 1B 1,B 1C 1,C 1D 1,D 1A 1的中点,求证: (1)E ,F ,D ,B 四点共面; (2)面AMN ∥平面EFDB .18.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 是DD 1的中点. 求证:(1)直线BD 1∥平面PAC(2)①求异面直线PC 与AA 1所成的角. ②平面PAC ⊥平面BDD 1.19.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.(Ⅰ)求证:AB1⊥平面A1CE;(Ⅱ)求直线A1C1与平面A1CE所成角的正弦值.20.如图,在正方体ABCD﹣A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点.求证:平面D1EF∥平面BDG.21.(文科)如图,正方体ABCD﹣A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.22.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点,求证:(1)EN∥平面PDC;(2)BC⊥平面PEB;(3)平面PBC⊥平面ADMN.23.如图,在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.(1)求证:DE∥平面PAC;(2)求证:AB⊥PC.24.如图所示,在四棱锥P﹣ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=.(1)求证:PD⊥平面ABCD;(2)求证:平面PAC⊥平面PBD.25.如图,在三棱柱ABC ﹣A 1B 1C 1中,侧棱AA 1⊥底面ABC ,AB ⊥BC,D 为AC 的中点,A 1A=AB=2. (1)求证:AB 1∥平面BC 1D ;(2)过点B 作BE ⊥AC 于点E,求证:直线BE ⊥平面AA 1C 1C (3)若四棱锥B ﹣AA 1C 1D 的体积为3,求BC 的长度.26.如图,已知四棱锥P ﹣ABCD 的底面ABCD 是菱形,PA ⊥平面ABCD ,点F 为PC 的中点. (1)求证:PA ∥平面BDF ; (2)求证:PC ⊥BD .27.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是CC 1的中点. (1)求证:AC 1⊥BD . (2)求证:AC 1∥平面BDE .28.已知空间四边形ABCD (如图所示),E 、F 分别是AB 、AD 的中点,G 、H 分别是BC 、CD 上的(完整)立体几何证明基础题点,且CG=BC,CH=DC.求证:①E、F、G、H四点共面;②三直线FH、EG、AC共点.立体几何证明基础题参考答案与试题解析一.解答题(共28小题)1.如图,在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点(1)求证:PB∥平面EFG;(2)求证:BC⊥EG.【分析】(1)推导出GF∥PB,由此能证明PB∥平面EFG.(2)推导出EF⊥BC,GF⊥BC,从而BC⊥平面EFG,由此能证明BC⊥EG.【解答】证明:(1)∵点F,G分别为BC,PC,的中点,∴GF∥PB,∵PB⊄平面EFG,FG⊂平面EFG,∴PB∥平面EFG.(2)∵在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点,∴EF∥AC,GF∥PB,∴EF⊥BC,GF⊥BC,∵EF∩FG=F,∴BC⊥平面EFG,∵EG⊂平面EFG,∴BC⊥EG.【点评】本题考查线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.2.如图,在三棱锥P﹣ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.(1)求证DE∥PA(2)求证:DE∥平面PAC;(3)求证:AB⊥PB.【分析】(1)由D,E分别是AB,PB的中点,能证明DE∥PA.(2)由PA⊂平面PAC,DE∥PA,且DE⊄平面PAC,能证明DE∥平面PAC.(3)推导出AB⊥PC,AB⊥BC,得AB⊥平面PBC,由此能证明AB⊥PB.【解答】证明:(1)因为D,E分别是AB,PB的中点,所以DE∥PA.(2)因为PA⊂平面PAC,DE∥PA,且DE⊄平面PAC,所以DE∥平面PAC.(3)因为PC⊥平面ABC,且AB⊂平面ABC,所以AB⊥PC.又因为AB⊥BC,且PC∩BC=C.所以AB⊥平面PBC.又因为PB⊂平面PBC,所以AB⊥PB.【点评】本题考查线线平行、线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE且CE=AC=2BD,试在AE上确定一点M,使得DM∥平面ABC.【分析】AE中点为M,取AC中点为N,通过证明四边形MNBD是平行四边形得出DM∥BN,从而可得DM∥平面ABC.【解答】解:取AE中点为M,取AC中点为N,连结MD,MN,NB,在△ABC中,∵M,N分别是边AC,AE的中点,∴CE=2MN且MN∥CE,又∵CE=2BD且BD∥CE,∴MN∥BD且MN=BD,∴四边形BDMN是平行四边形.∴DM∥BN,又∵BN⊂平面ABC,DM⊄平面ABC,∴DM∥平面ABC.故M为AE的中点时,DM∥平面ABC.【点评】本题考查了线面平行的判定,属于基础题.4.如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且PA=AB=2.(Ⅰ)证明:BC⊥平面AMN;(Ⅱ)求三棱锥N﹣AMC的体积;(Ⅲ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.【分析】(I)要证线与面垂直,只要证明线与面上的两条相交线垂直,找面上的两条线,根据四边形是一个菱形,从菱形出发找到一条,再从PA⊥平面ABCD,得到结论.(II)要求三棱锥的体积,首先根据所给的体积确定用哪一个面做底面,会使得计算简单一些,选择三角形AMC,做出底面面积,利用体积公式得到结果.(III)对于这种是否存在的问题,首先要观察出结论,再进行证明,根据线面平行的判定定理,利用中位线确定线与线平行,得到结论.【解答】解:(Ⅰ)证明:∵ABCD为菱形,∴AB=BC又∠ABC=60°,∴AB=BC=AC,又M为BC中点,∴BC⊥AM而PA⊥平面ABCD,BC⊂平面ABCD,∴PA⊥BC 又PA∩AM=A,∴BC⊥平面AMN(II)∵又PA⊥底面ABCD,PA=2,∴AN=1•AN∴三棱锥N﹣AMC的体积S△AMC=(III)存在点E,取PD中点E,连接NE,EC,AE,∵N,E分别为PA,PD中点,∴又在菱形ABCD中,∴,即MCEN是平行四边形∴NM∥EC,又EC⊂平面ACE,NM⊄平面ACE∴MN∥平面ACE,即在PD上存在一点E,使得NM∥平面ACE,此时.【点评】本题考查空间中直线与平面之间的位置关系,是一个非常适合作为高考题目出现的问题,题目包含的知识点比较全面,重点突出,是一个好题.5.如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.(1)求四棱锥P﹣ABCD的体积;(2)如果E是PA的中点,求证:PC∥平面BDE;(3)是否不论点E在侧棱PA的任何位置,都有BD⊥CE?证明你的结论.【分析】(1)利用四棱锥的体积计算公式即可;(2)利用三角形的中位线定理和线面平行的判定定理即可证明;(3)利用线面垂直的判定和性质即可证明.【解答】解:(1)∵PA⊥底面ABCD,∴PA为此四棱锥底面上的高.∴V==.四棱锥P﹣ABCD(2)连接AC交BD于O,连接OE.∵四边形ABCD是正方形,∴AO=OC,又∵AE=EP,∴OE∥PC.又∵PC⊄平面BDE,OE⊂平面BDE.∴PC∥平面BDE.(3)不论点E在侧棱PA的任何位置,都有BD⊥CE.证明:∵四边形ABCD是正方形,∴BD⊥AC.∵PA⊥底面ABCD,∴PA⊥BD.又∵PA∩AC=A,∴BD⊥平面PAC.∵CE⊂平面PAC.∴BD⊥CE.【点评】熟练掌握线面平行、垂直的判定和性质定理及四棱锥的体积计算公式是解题的关键.6.已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.(Ⅰ)求证:EF∥面ABC;(Ⅱ)求证:平面ADE⊥平面ACD;(Ⅲ)求四棱锥A﹣BCDE的体积.【分析】(Ⅰ)取AC中点G,连接FG、BG,根据三角形中位线定理,得到四边形FGBE为平行四边形,进而得到EF∥BG,再结合线面平行的判定定理得到EF∥面ABC;(Ⅱ)根据已知中△ABC为等边三角形,G为AC的中点,DC⊥面ABC得到BG⊥AC,DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC,则EF⊥面ADC,再由面面垂直的判定定理,可得面ADE⊥面ACD;(Ⅲ)方法一:四棱锥四棱锥A﹣BCDE分为两个三棱锥E﹣ABC和E﹣ADC,分别求出三棱锥E﹣ABC和E﹣ADC的体积,即可得到四棱锥A﹣BCDE的体积.的高,求出底面面积和方法二:取BC的中点为O,连接AO,可证AO⊥平面BCDE,即AO为VA﹣BCDE高代入棱锥体积公式即可求出四棱锥A﹣BCDE的体积.【解答】证明:(Ⅰ)取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点∴FG∥CD,且FG=DC=1.∵BE∥CD∴FG与BE平行且相等∴EF∥BG.EF⊄面ABC,BG⊂面ABC∴EF∥面ABC…(4分)(Ⅱ)∵△ABC为等边三角形∴BG⊥AC又∵DC ⊥面ABC ,BG ⊂面ABC ∴DC ⊥BG ∴BG 垂直于面ADC 的两条相交直线AC,DC ,∴BG ⊥面ADC . …(6分) ∵EF ∥BG ∴EF ⊥面ADC∵EF ⊂面ADE ,∴面ADE ⊥面ADC . …(8分) 解:(Ⅲ)方法一:连接EC ,该四棱锥分为两个三棱锥E ﹣ABC 和E ﹣ADC ..…(12分)方法二:取BC 的中点为O ,连接AO,则AO ⊥BC ,又CD ⊥平面ABC , ∴CD ⊥AO ,BC ∩CD=C ,∴AO ⊥平面BCDE , ∴AO 为V A ﹣BCDE 的高,,∴.【点评】本题考查的知识点是直线与平面平行的判定,平面与平面垂直的判定,棱锥的体积,其中熟练掌握空间线面平行或垂直的判定、性质、定义、几何特征是解答此类问题的关键.7.如图,四棱柱ABCD ﹣A 1B 1C 1D 1中,平面A 1ABB 1⊥平面ABCD,且∠ABC=.(1)求证:BC ∥平面AB 1C 1;(2)求证:平面A 1ABB 1⊥平面AB 1C 1.【分析】(1)根据BC ∥B 1C 1,且B 1C 1⊂平面AB 1C 1,BC ⊄平面AB 1C 1,依据线面平行的判定定理推断出BC ∥平面AB 1C 1.(2)平面A 1ABB 1⊥平面ABCD ,平面ABCD ∥平面A 1B 1C 1D 1,推断出平面A 1ABB 1⊥平面A 1B 1C 1D 1,又平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1,A 1B 1⊥C 1B 1,C 1B 1⊂平面AB 1C 1,根据面面垂直的性质推断出平面A 1ABB 1⊥平面AB 1C 1.【解答】证明:(1)∵BC ∥B 1C 1,且B 1C 1⊂平面AB 1C 1,BC ⊄平面AB 1C 1, ∴BC ∥平面AB 1C 1.(2)∵平面A 1ABB 1⊥平面ABCD ,平面ABCD ∥平面A 1B 1C 1D 1, ∴平面A 1ABB 1⊥平面A 1B 1C 1D 1,∵平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1,A 1B 1⊥C 1B 1, ∴C 1B 1⊂平面AB 1C 1,∴平面A 1ABB 1⊥平面AB 1C 1.【点评】本题主要考查了线面平行和面面垂直的判定定理.注重了对基础知识的考查.8.如图,三角形ABC 中,AC=BC=,ABED 是边长为1的正方形,平面ABED ⊥底面ABC ,若G 、F 分别是EC 、BD 的中点. (Ⅰ)求证:GF ∥底面ABC ;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.【分析】(1)证法一:证明一条直线与一个平面平行,除了可以根据直线与平面平行的判定定理以外,通常还可以通过平面与平面平行进行转化,比如取BE的中点H,连接HF、GH,根据中位线定理易证得:平面HGF∥平面ABC,进一步可得:GF∥平面ABC.证法二:根据直线与平面平行的判定定理可知:如果不在一个平面内的一条直线和平面内的一条直线平行,那么直线和这个平面平行.故只需在平面ABC中找到与GF平行的直线即可.因为G、F分别是EC、BD的中点,故平移是可以通过构造特殊的四边形、三角形来实现.证法三:根据直线与平面平行的判定定理可知:如果不在一个平面内的一条直线和平面内的一条直线平行,那么直线和这个平面平行.故只需在平面ABC中找到与GF平行的直线即可.因为G、F分别是EC、BD的中点,所以构造中位线是常用的找到平行直线的方法.(2)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直或者平面与平面垂直去转化一下.由第一问可知:GF∥平面ABC,而平面ABED⊥平面ABC,所以BE⊥平面ABC,所以BE⊥AC;又由勾股定理可以证明:AC⊥BC.(3)解决棱锥、棱柱求体积的问题,关键在于找到合适的高与对应的底面,切忌不审图形,盲目求解;根据平面与平面垂直的性质定理可知:CN⊥平面ABED,而ABED是边长为1的正方形,进一步即可以求得体积.【解答】解:(I)证法一:取BE的中点H,连接HF、GH,(如图)∵G、F分别是EC和BD的中点∴HG∥BC,HF∥DE,(2分)又∵ADEB为正方形∴DE∥AB,从而HF∥AB∴HF∥平面ABC,HG∥平面ABC,HF∩HG=H,∴平面HGF∥平面ABC∴GF∥平面ABC(5分)证法二:取BC的中点M,AB的中点N连接GM、FN、MN(如图)∵G、F分别是EC和BD的中点∴(2分)又∵ADEB为正方形∴BE∥AD,BE=AD∴GM∥NF且GM=NF∴MNFG为平行四边形∴GF∥MN,又MN⊂平面ABC,∴GF∥平面ABC(5分)证法三:连接AE,∵ADEB为正方形,∴AE∩BD=F,且F是AE中点,(2分)∴GF∥AC,又AC⊂平面ABC,∴GF∥平面ABC(5分)(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF∥平面ABC(5分)又∵平面ABED⊥平面ABC,∴BE⊥平面ABC(7分)∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC,∵BC∩BE=B,∴AC⊥平面BCE(9分)(Ⅲ)连接CN,因为AC=BC,∴CN⊥AB,(10分)又平面ABED⊥平面ABC,CN⊂平面ABC,∴CN⊥平面ABED.(11分)∵三角形ABC是等腰直角三角形,∴,(12分)∵C﹣ABED是四棱锥,==(14分)∴VC﹣ABED【点评】本小题主要考查空间线面关系、面面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.9.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(Ⅰ)证明:PA∥平面BMQ;(Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离.【分析】(1)连结AC交BQ于N,连结MN,只要证明MN∥PA,利用线面平行的判定定理可证;(2)由(1)可知,PA∥平面BMQ,所以点P到平面BMQ的距离等于点A到平面BMQ的距离.【解答】解:(1)连结AC交BQ于N,连结MN,因为∠ADC=90°,Q为AD的中点,所以N为AC的中点.…(2分)当M为PC的中点,即PM=MC时,MN为△PAC的中位线,故MN∥PA,又MN⊂平面BMQ,所以PA∥平面BMQ.…(5分)(2)由(1)可知,PA∥平面BMQ,所以点P到平面BMQ的距离等于点A到平面BMQ的距离,所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ,取CD的中点K,连结MK,所以MK∥PD,,…(7分)又PD⊥底面ABCD,所以MK⊥底面ABCD.又,PD=CD=2,所以AQ=1,BQ=2,,…(10分)所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ=.,…(11分)则点P到平面BMQ的距离d=…(12分)【点评】本题考查了线面平行的判定定理的运用以及利用三棱锥的体积求点到直线的距离.10.已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中,∠C=90°,BC=,BB 1=2,O 是AB 1的中点,D 是AC 的中点,M 是CC 1的中点, (1)证明:OD ∥平面BB 1C 1C ; (2)试证:BM ⊥AB 1.【分析】(1)连B 1C 利用中位线的性质推断出OD ∥B 1C ,进而根据线面平行的判定定理证明出OD ∥平面BB 1C 1C .(2)先利用线面垂直的性质判断出CC 1⊥AC ,进而根据线面垂直的判定定理证明出AC ⊥平面BB 1C 1C ,进而可知AC ⊥MB .利用证明△BCD ∽△B 1BC,推断出∠CBM=∠BB 1C ,推断出BM ⊥B 1C ,最后利用线面垂直的判定定理证明出BM ⊥平面AB 1C ,进而可知BM ⊥AB 1. 【解答】证明:(1)连B 1C ,∵O 为AB 1中点,D 为AC 中点, ∴OD ∥B 1C ,又B 1C ⊂平面BB 1C 1C,OD ⊄平面BB 1C 1C,∴OD ∥平面BB 1C 1C . (2)连接B 1C ,∵直三棱柱ABC ﹣A 1B 1C 1,∴CC 1⊥平面ABC AC ⊂平面ABC, ∴CC 1⊥AC,又AC ⊥BC ,CC 1,BC ⊂平面BB 1C 1C , ∴AC ⊥平面BB 1C 1C ,BM ⊂平面BB 1C 1C , ∴AC ⊥MB .在Rt △BCM 与Rt △B 1BC 中,==,∴△BMC ∽△B 1BC, ∴∠CBM=∠BB 1C,∴∠BB 1C+∠B 1BM=∠CBM+∠B 1BM=90°, ∴BM ⊥B 1C ,AC ,B 1C ⊂平面AB 1C , ∴BM ⊥AB 1C , ∵AB 1⊂平面AB 1C , ∴BM ⊥AB 1.【点评】本题主要考查了线面平行和线面垂直的判定定理的应用.证明线线平行和线线垂直是解题的关键.11.如图,在四棱锥P ﹣ABCD 中,四边形ABCD 是平行四边形,E 、F 分别是AB 、PC 中点,求证:EF ∥面PAD .【分析】取PD的中点G,连接FG、AG,由PF=CF,PG=DG,所以FG∥CD,且FG=CD.又因为四边形ABCD是平行四边形,且E是AB的中点.所以AE∥CD,且AE=CD.证得四边形EFGA是平行四边形,所以EF∥AG,由线面平行的判定定理即可得证.【解答】证明:取PD的中点G,连接FG、AG.因为PF=CF,PG=DG,所以FG∥CD,且FG=CD.又因为四边形ABCD是平行四边形,且E是AB的中点.所以AE∥CD,且AE=CD.所以FG∥AE,且FG=AE,所以四边形EFGA是平行四边形,所以EF∥AG.又因为EF⊄平面PAD,AG⊂平面PAD,所以EF∥平面PAD.【点评】本题考查直线与平面平行的证明,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.12.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是AA 1的中点,求证: (Ⅰ)A 1C ∥平面BDE ; (Ⅱ)平面A 1AC ⊥平面BDE .【分析】(Ⅰ)连接AC 交BD 于O,连接EO ,△A 1AC 中利用中位线,得EO ∥A 1C .再结合线面平行的判定定理,可得A 1C ∥平面BDE;(II )根据正方体的侧棱垂直于底面,结合线面垂直的定义,得到AA 1⊥BD .再结合正方形的对角线互相垂直,得到AC ⊥BD ,从而得到BD ⊥平面A 1AC,最后利用面面垂直的判定定理,可以证出平面A 1AC ⊥平面BDE .【解答】证明:(Ⅰ)连接AC 交BD 于O ,连接EO , ∵E 为AA 1的中点,O 为AC 的中点 ∴EO 为△A 1AC 的中位线 ∴EO ∥A 1C又∵EO ⊂平面BDE ,A 1C ⊄平面BDE ∴A 1C ∥平面BDE ;…(6分)(Ⅱ)∵AA 1⊥平面ABCD,BD ⊂平面ABCD ∴AA 1⊥BD又∵四边形ABCD 是正方形 ∴AC ⊥BD ,∵AA1∩AC=A,AA1、AC⊂平面A1AC∴BD⊥平面A1AC又∵BD⊂平面BDE∴平面A1AC⊥平面BDE.…(12分)【点评】本题以正方体为例,要求我们证明线面平行和面面垂直,着重考查了空间直线与平面的位置关系和平面与平面位置关系等知识点,属于基础题.13.如图,四棱锥P﹣ABCD中,底面ABCD为矩形,E为PD的中点.(1)求证:PB∥平面AEC;(2)若PA⊥平面ABCD,PA=AD,求证:平面AEC⊥平面PCD.【分析】(1)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(2)要证平面PDC⊥平面AEC,需要证明CD⊥AE,AE⊥PD,即垂直平面AEC内的两条相交直线.【解答】证明:(1)连接BD交AC于O点,连接EO,∵O为BD中点,E为PD中点,∴EO∥PB,又EO⊂平面AEC,PB⊄平面AEC,∴PB∥平面AEC.(2)∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD,又AD⊥CD,且AD∩PA=A,∴CD⊥平面PAD,又AE⊂平面PAD,∴CD⊥AE.∵PA=AD,E为PD中点,∴AE⊥PD.又CD∩PD=D,∴AE⊥平面PDC,又AE⊂平面PAD,∴平面PDC⊥平面AEC.【点评】本题考查了线面平行,面面垂直的判定定理,属于基础题.14.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(1)PA∥平面BDE;(2)BD⊥平面PAC.【分析】(1)连接OE,根据三角形中位线定理,可得PA∥EO,进而根据线面平行的判定定理,得到PA∥平面BDE.(2)根据线面垂直的定义,可由PO⊥底面ABCD得到BD⊥PO,结合四边形ABCD是正方形及线面垂直的判定定理可得BD⊥平面PAC【解答】证明(1)连接OE,在△CAP中,CO=OA,CE=EP,∴PA∥EO,又∵PA⊄平面BDE,EO⊂平面BDE,∴PA∥平面BDE.(2)∵PO⊥底面ABCD,BD⊂平面ABCD,∴BD⊥PO又∵四边形ABCD是正方形,∴BD⊥AC∵AC∩PO=O,AC,PO⊂平面PAC∴BD⊥平面PAC【点评】本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间线面关系的判定定理是解答的关键.15.如图,正四棱柱ABCD ﹣A 1B 1C 1D 1,底面边长AB=1,侧棱长AA 1=2. (Ⅰ)求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积; (Ⅱ)证明:AC ⊥平面BDD 1B 1.【分析】(I)求出各面的面积即可得出表面积;(II )根据BB 1⊥平面ABCD 可得AC ⊥BB 1,根据正方形ABCD 的性质可得AC ⊥BD ,从而有AC ⊥平面BDD 1B 1.【解答】解:(I)正四棱柱的表面积为1×1×2+1×2×4=10. (II )连接AC,BD,B 1D 1,∵BB 1⊥平面ABCD ,AC ⊂平面ABCD , ∴AC ⊥BB 1,∵四边形ABCD 是正方形, ∴AC ⊥BD,又BD ⊂平面BDD 1B 1,BB 1⊂平面BDD 1B 1,BD ∩BB 1=B , ∴AC ⊥平面BDD 1B 1.【点评】本题考查了直棱柱的结构特征,线面垂直的判定,属于基础题.16.已知正方体ABCD ﹣A 1B 1C 1D 1,O 是底ABCD 对角线的交点.求证: (1)C 1O ∥面AB 1D 1; (2)A 1C ⊥面AB 1D 1.【分析】(1)欲证C 1O ∥面AB 1D 1,根据直线与平面平行的判定定理可知只需证C 1O 与面AB 1D 1内一直线平行,连接A 1C 1,设A 1C 1∩B 1D 1=O 1,连接AO 1,易得C 1O ∥AO 1,AO 1⊂面AB 1D 1,C 1O ⊄面AB 1D 1,满足定理所需条件;(2)欲证A 1C ⊥面AB 1D 1,根据直线与平面垂直的判定定理可知只需证A 1C 与面AB 1D 1内两相交直线垂直根据线面垂直的性质可知A 1C ⊥B 1D 1,同理可证A 1C ⊥AB 1,又D 1B 1∩AB 1=B 1,满足定理所需条件.【解答】证明:(1)连接A 1C 1,设A 1C 1∩B 1D 1=O 1,连接AO 1, ∵ABCD ﹣A 1B 1C 1D 1是正方体, ∴A 1ACC 1是平行四边形,∴A1C1∥AC且A1C1=AC,又O1,O分别是A1C1,AC的中点,∴O1C1∥AO且O1C1=AO,∴AOC1O1是平行四边形,∴C1O∥AO1,AO1⊂面AB1D1,C1O⊄面AB1D1,∴C1O∥面AB1D1;(2)∵CC1⊥面A1B1C1D1∴CC1⊥B1D!,又∵A1C1⊥B1D1,∴B1D1⊥面A1C1C,即A1C⊥B1D1,∵A1B⊥AB1,BC⊥AB1,又A1B∩BC=B,AB1⊥平面A1BC,又A1C⊂平面A1BC,∴A1C⊥AB1,又D1B1∩AB1=B1,∴A1C⊥面AB1D1【点评】本题主要考查了线面平行、线面垂直的判定定理,考查对基础知识的综合应用能力和基本定理的掌握能力.17.如图所示,在正方体ABCD﹣A1B1C1D1中,M,E,F,N分别为A1B1,B1C1,C1D1,D1A1的中点,求证:(1)E,F,D,B四点共面;(2)面AMN∥平面EFDB.【分析】(1)由E,E分别是B1C1,C1D1的中点,知EF∥B1D1,从而得到EF∥BD,由此能证明E,F,B,D,四点共面.(2)由题设条件推导出MN∥EF,AN∥CF,由此能够证明面MAN∥面EFDB.【解答】证明:(1)∵E,E分别是B1C1,C1D1的中点,∴EF∥B1D1 ,∵B1D1∥BD,∴EF∥BD,∴E,F,B,D,四点共面.(2)∵M,N分别是A1B1,D1A1的中点,∴MN∥B1D1,∵EF∥B1D1,∴MN∥EF,∵F,N分别是D1C1、A1B1的中点,∴NF A1D1,∵,∴NF AC,∴四边形NFCA是平行四边形,∴AN∥CF,∵MN∩AN=N,EF∩DF=F,∴面MAN∥面EFDB.【点评】本题考查四点共面的证明,考查两个平面平行的证明.解题时要认真审题,注意中位线定理和平行公理的合理运用.18.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 是DD 1的中点. 求证:(1)直线BD 1∥平面PAC(2)①求异面直线PC 与AA 1所成的角. ②平面PAC ⊥平面BDD 1.【分析】(1)连接BD ,交AC 于O,连接PO ,由三角形的中位线定理和线面平行的判定定理,即可得证;(2)①连接PC 1,AA 1∥CC 1,∠C 1CP 即为异面直线PC 与AA 1所成的角,分别求出△C 1CP 的三边,由解三角形即可得到所求角;②运用正方形的对角线垂直和线面垂直的性质定理,可得AC ⊥平面BDD 1B 1,再由面面垂直的判定定理,即可得证.【解答】(1)证明:连接BD ,交AC 于O ,连接PO , 在△BDD1中,OP 为中位线,可得OP∥BD1,又OP⊂平面PAC,BD1⊄平面PAC,则直线BD1∥平面PAC;(2)①连接PC1,AA1∥CC1,∠C1CP即为异面直线PC与AA1所成的角,在△C1CP中,C1C=2,PC===,PC1===,由PC2+PC12=CC12,可得△C1CP为等腰直角三角形,则异面直线PC与AA1所成的角为45°;②证明:在底面ABCD中,AB=AD,即有四边形ABCD为正方形,可得AC⊥BD,D1D⊥平面ABCD,AC⊂平面ABCD,即有D1D⊥AC,D1D∩BD=D,可得AC⊥平面BDD1B1,AC⊂平面PAC,则平面PAC⊥平面BDD1.【点评】本题考查线面平行的判定,注意运用中位线定理和线面平行的判定定理,考查异面直线所成角的求法,注意运用平移法,考查面面垂直的判定,注意运用线面垂直的判定和性质,考查空间想象能力和推理能力,属于基础题.19.如图,在直三棱柱ABC ﹣A 1B 1C 1中,∠ACB=90°,AC=CB=CC 1=2,E 是AB 中点. (Ⅰ)求证:AB 1⊥平面A 1CE ;(Ⅱ)求直线A 1C 1与平面A 1CE 所成角的正弦值.【分析】(Ⅰ)由ABC ﹣A 1B 1C 1是直三棱柱,可知CC 1⊥AC ,CC 1⊥BC ,∠ACB=90°,AC⊥BC .建立空间直角坐标系C ﹣xyz .则A ,B 1,E ,A 1,可得,,,可知,根据,,推断出AB 1⊥CE ,AB 1⊥CA 1,根据线面垂直的判定定理可知AB 1⊥平面A 1CE . (Ⅱ)由(Ⅰ)知是平面A 1CE 的法向量,,进而利用向量数量积求得直线A 1C 1与平面A 1CE 所成角的正弦值【解答】(Ⅰ)证明:∵ABC ﹣A 1B 1C 1是直三棱柱, ∴CC 1⊥AC,CC 1⊥BC, 又∠ACB=90°, 即AC ⊥BC .如图所示,建立空间直角坐标系C ﹣xyz .A (2,0,0),B 1(0,2,2),E(1,1,0),A 1(2,0,2), ∴,,.又因为 ,,∴AB 1⊥CE ,AB 1⊥CA 1,AB 1⊥平面A 1CE . (Ⅱ)解:由(Ⅰ)知,是平面A 1CE 的法向量,,∴|cos <,>|==.设直线A 1C 1与平面A 1CE 所成的角为θ,则sinθ=|cos <,>|=.所以直线A 1C 1与平面A 1CE 所成角的正弦值为.【点评】本题主要考查了线面垂直的判定定理,向量的数量积的运用,法向量的运用.综合考查了学生所学知识的灵活运用.20.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 、F 、G 分别是AB 、AD 、C 1D 1的中点.求证:平面D 1EF ∥平面BDG .【分析】欲证平面D 1EF ∥平面BDG,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,EF ∥BD 又EF ⊄平面BDG ,BD ⊂平面BDG 根据线面平行的性质可知EF ∥平面BDG ,同理可证D 1E ∥平面BDG ,EF ∩D 1E=E ,满足定理条件. 【解答】证明:∵E 、F 分别是AB 、AD 的中点,∴EF ∥BD 又EF ⊄平面BDG ,BD ⊂平面BDG ∴EF ∥平面BDG ∵D 1G EB ∴四边形D 1GBE 为平行四边形,D 1E ∥GB 又D 1E ⊄平面BDG,GB ⊂平面BDG∴D 1E ∥平面BDG,EF ∩D 1E=E , ∴平面D 1EF ∥平面BDG【点评】本小题主要考查空间中的线面关系,考查线面平行的判定,考查识图能力和逻辑思维能力与推理论证能力,考查转化思想,属于基础题.21.(文科)如图,正方体ABCD ﹣A 1B 1C 1D 1中,M ,N,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点, 求证:平面AMN ∥平面EFDB .【分析】连接B 1D 1,NE ,分别在△A 1B 1D 1中和△B 1C 1D 1中利用中位线定理,得到MN ∥B 1D 1,EF ∥B 1D 1,从而MN ∥EF,然后用直线与平面平行的判定定理得到MN ∥面BDEF .接下来利用正方形的性质和平行线的传递性,得到四边形ABEN 是平行四边形,得到AN ∥BE ,直线与平面平行的判定定理得到AN ∥面BDEF,最后可用平面与平面平行的判定定理,得到平面AMN ∥平面EFDB ,问题得到解决.【解答】证明:如图所示,连接B 1D 1,NE∵M,N ,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点 ∴MN ∥B 1D 1,EF ∥B 1D 1 ∴MN ∥EF又∵MN ⊄面BDEF ,EF ⊂面BDEF ∴MN ∥面BDEF∵在正方形A 1B 1C 1D 1中,M ,E ,分别是棱 A 1B 1,B 1C 1的中点∴NE∥A1B1且NE=A1B1又∵A1B1∥AB且A1B1=AB∴NE∥AB且NE=AB∴四边形ABEN是平行四边形∴AN∥BE又∵AN⊄面BDEF,BE⊂面BDEF∴AN∥面BDEF∵AN⊂面AMN,MN⊂面AMN,且AN∩MN=N∴平面AMN∥平面EFDB【点评】本题借助于正方体模型中的一个面面平行位置关系的证明,着重考查了三角形的中位线定理、线面平行的判定定理和面面平行的判定定理等知识点,属于基础题.22.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点,求证:(1)EN∥平面PDC;(2)BC⊥平面PEB;(3)平面PBC⊥平面ADMN.【分析】(1)先证明AD∥MN由N是PB的中点,E为AD的中点,底面ABCD是边长为2的菱形得EN∥DM,DM⊂平面PDC,可得EN∥平面PDC;(2)由侧面PAD是正三角形,且与底面ABCD垂直,E为AD的中点,得PE⊥AD,PE⊥EB,PE⊥BC,由∠BAD=60°,AB=2,AE=1,由余弦定理可得BE=,由正弦定理可得:BE⊥AD,有由AD∥BC可得BE⊥BC,可得BC⊥平面PEB;(3)由(2)知BC⊥平面PEB,EN⊂平面PEB可得PB⊥MN,由AP=AB=2,N是PB的中点,得PB ⊥AN,有MN∩AN=N.PB⊥平面ADMN,可证平面PBC⊥平面ADMN.【解答】解:(1)∵AD∥BC,AD⊂平面ADMN,BC⊄平面ADMN,∴BC∥平面ADMN,∵MN=平面ADMN∩平面PBC,BC⊂平面PBC,∴BC∥MN.又∵AD∥BC,∴AD∥MN.∴ED∥MN∵N是PB的中点,E为AD的中点,底面ABCD是边长为2的菱形,∴ED=MN=1∴四边形ADMN是平行四边形.∴EN∥DM,DM⊂平面PDC,∴EN∥平面PDC;(2)∵侧面PAD是正三角形,且与底面ABCD垂直,E为AD的中点,∴PE⊥AD,PE⊥EB,PE⊥BC∵∠BAD=60°,AB=2,AE=1,由余弦定理可得BE=,由正弦定理可得:BE⊥AD∴由AD∥BC可得BE⊥BC,∵BE∩PE=E∴BC⊥平面PEB;(3)∵由(2)知BC⊥平面PEB,EN⊂平面PEB∴BC⊥EN∵PB⊥BC,PB⊥AD∴PB⊥MN∵AP=AB=2,N是PB的中点,∴PB⊥AN,∴MN∩AN=N.PB⊥平面ADMN,∵PB⊂平面PBC∴平面PBC⊥平面ADMN.【点评】本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定,属于基本知识的考查.23.如图,在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.(1)求证:DE∥平面PAC;(2)求证:AB⊥PC.【分析】(1)推导出DE∥AC,由此能证明DE∥平面PAC.(2)连结PD,CD,则PD⊥AB,CD⊥AB,从而AB⊥平面PDC,由此能证明AB⊥PC.【解答】证明:(1)∵在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.∴DE∥AC,∵DE⊄平面PAC,AC⊂平面PAC,∴DE∥平面PAC.(2)连结PD,CD,∵正三棱锥P﹣ABC中,D是AB的中点,∴PD⊥AB,CD⊥AB,∵PD∩CD=D,∴AB⊥平面PDC,∵PC⊂平面PDC,∴AB⊥PC.【点评】本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.24.如图所示,在四棱锥P﹣ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=.(1)求证:PD⊥平面ABCD;(2)求证:平面PAC⊥平面PBD.【分析】(1)由勾股定理逆定理可证明AD⊥PD,PD⊥CD即可得出PD⊥平面ABCD;(2)由(1)可得PD⊥AC,结合AC⊥BD,得出AC⊥平面PBD,从而平面PAC⊥平面PBD.。
考点:线面垂直,面面垂直的判定
2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;
(2)平面CDE ⊥平面ABC 。
考点:线面平行的判定
3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。
考点:线面垂直的判定
4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .
考点:线面平行的判定(利用平行四边形),线面垂直的判定 5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.
求证:(1) C 1O ∥面11AB D ;(2)1
AC ⊥面11AB D .
考点:线面垂直的判定
A
E
D 1
C
B 1
D
C
B
A
S
D
C
B
A
D 1O
D
B A
C 1
B 1
A 1
C
N
M
P
C
B
A
6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.
考点:线面平行的判定(利用平行四边形)
7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .
考点:线面垂直的判定,三角形中位线,构造直角三角形
8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且2
2
EF AC =
, 90BDC ∠=,求证:BD ⊥平面ACD
考点:三垂线定理
9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,
3AN NB = 求证:MN AB ⊥;(2)当90APB ∠=,24AB BC ==时,求MN 的长。
考点:线面平行的判定(利用三角形中位线)
10、如图,在正方体1111ABCD A B C D -中,E 、F 、G 分别是AB 、
AD
、
A 1
A
B 1
C 1
C D 1
D G E
F
11C D 的中点.求证:平面1D EF ∥平面BDG .
考点:线面平行的判定(利用三角形中位线),面面垂直的判定 11、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. (1)求证:1//A C 平面BDE ; (2)求证:平面1A AC ⊥平面BDE .
考点:线面垂直的判定,构造直角三角形
12、已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.
(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角.
考点:线面垂直的判定,运用勾股定理寻求线线垂直
14、在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,
求证:1
AO 平面MBD .
考点:线面垂直的判定
15、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H. 求证:AH ⊥平面BCD .
考点:线面垂直的判定,三垂线定理
16、证明:在正方体ABCD -A 1B 1C 1D 1中,A 1C ⊥平面BC 1D
考点:面面垂直的判定(证二面角是直二面角) 17、如图,过S 引三条长度相等但不共面的线段SA 、SB 、SC ,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC ⊥平面BSC .
D 1 C 1
A 1
B 1 D
C A B。