第六章循环控制概要
- 格式:doc
- 大小:145.00 KB
- 文档页数:12

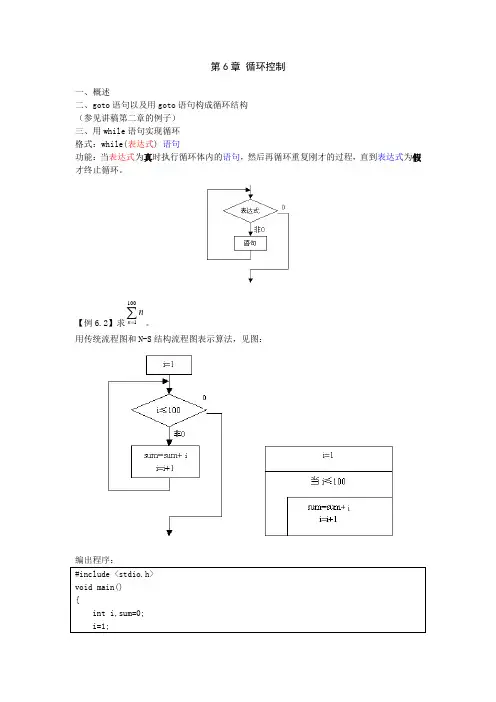
第6章 循环控制一、概述二、goto 语句以及用goto 语句构成循环结构 (参见讲稿第二章的例子) 三、用while 语句实现循环 格式:while(表达式) 语句功能:当表达式为真时执行循环体内的语句,然后再循环重复刚才的过程,直到表达式为假才终止循环。
【例6.2】求∑=1001n n。
用传统流程图和N-S 结构流程图表示算法,见图:四、用do…while 语句实现循环 格式:特别注意最后的分号不能省略。
先执行一遍循环体语句,再进行表达式的求值,如果表达式为真,则继续循环,否则终止循环。
【例6.3】用do-while 语句求∑=1001n n。
用传统流程图和N-S 结构流程图表示算法,见图:编出程序:五、用for 语句实现循环格式:for(表达式1;表达式2;表达式3)语句 执行过程如下:(1)先求解表达式1。
(2)求解表达式2,若其值为真,则执行语句。
若为假,则结束循环。
(3)求解表达式3。
(4)转回上面第(2)步继续执行。
换种理解的格式表示:for(循环变量赋初值;循环条件;循环变量增量)循环体语句 执行过程理解如下:(1)先对循环变量进行初始化。
(2)判断是否符合循环条件,若符合,则执行语句进行循环。
若不符合,则结束循环。
(3)每次循环结束后对循环变量进行增量改变。
(4)转回上面第(2)步继续循环。
例:用for 语句求∑=1001n n。
编出程序:(1)利用逗号表达式可以进行多个变量的初始化,如for(sum=0,i=1;i<=100;i++)循环增量表达式写到循环体的末尾。
(3)还可以写成:初始化表达式写在循环之前。
(4)括号中必须有两个分号。
比较三种循环求∑=1001nn:例:求5的阶乘。
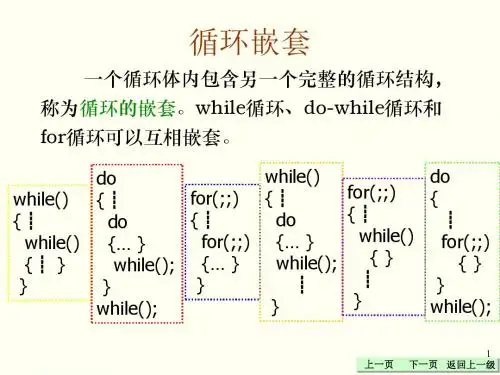
六、循环的嵌套循环内的循环体中也可以包含另一个完整的循环结构,称为循环的嵌套。
(参见书本121页)七、集中循环的比较(参见课本122页和本文档稍上部分的描述)八、break语句和continue语句含义:这两个语句都写在循环体中。





第六章循环控制通过本章实验作业应达目标1.熟悉while、for、do_while、break、continue语句的作用与使用规范。
2.学习并掌握利用while语句、for语句、do_while语句实现循环结构。
3.掌握循环结构和选择结构之间嵌套、多重循环间嵌套的设计方法。
4.进行算法设计训练,能综合所学控制结构语句解决一般问题。
本章必须上交作业程序6_1.c、6_2.c、6_5.c、6_6.c、6_8.c上传至211.64.135.121/casp。
本章开始,上机实验项目量加大,希望同学们多多自行上机。
本章实验项目有余力都可以做一下并上交。
循环程序设计计算机解决问题都是按指定的顺序执行一系列的动作。
按照特定的顺序执行相应的动作来求解问题的过程称为算法。
程序中的语句是算法的体现,而算法要解决的是“做什么”和“怎么做”的问题。
计算机程序中指定语句的执行顺序称为“程序控制”。
结构化的程序控制包含三种基本结构:顺序结构,选择结构和循环结构。
1. 循环设计循环是在循环条件为真时反复执行的一组计算机指令,是计算机解题的一个重要结构。
循环控制有两种基本方法:计数法和标志法。
1)计数器控制的循环事先准确地知道循环次数,因此设计一个循环控制变量,由变量值来控制循环次数。
每循环一次,循环变量的值会递增(增值通常为1或-1),当其值达到终值时结束循环。
教材例6.2、6.3、6.7都是典型的计数器控制的固定次数次数循环。
2)标志控制的循环事先不知道准确的循环次数,由某一目标值标记循环的结束。
如,教材例6.6中以|t|的值达到标记下限值1e-6作为循环的结束。
循环设计时要注意合理设计循环条件,使得循环不会成为死循环。
2. 算法程序设计的首要工作是算法设计,离开了算法也就没有了程序。
算法,是指完成某一项工作而采取的方法和步骤,具体到程序设计,是对解题过程的准确而完整的描述,并用一种程序设计语言的来实现。
循环主要用来解决程序设计中两类基本的算法:穷举和迭代。
1)穷举穷举的基本思想是对问题的所有可能状态一一测试,直到找到解或将全部可能状态都测试过为止。
穷举是一种重复型算法,其核心是设计循环,在循环体中依次测试。
例:输入两个正整数x和y,求其最大公约数。
main(){int x,y,i,flag;printf("Please input two numbers:");scanf("%d%d",&x,&y);for(i=x<y?x:y;i>=1;i--) /* 使用i进行穷举*/ if(x%i==0&&y%i==0) break; /* 条件满足,就结束循环*/ printf("greatest common divisor=%d\n",i);}两个数中的小者到2之间任何一个数都有可能是公约数,因此用变量i从大到小一一穷举,直到找到为止。
若两数互质,当i==1时也能使条件满足。
2)迭代按照特定规律和方法,不断用新值取代变量的旧值,或由旧值递推出变量新值,直至问题解决为止,这种解决问题的方法为迭代。
迭代的关键因素是:迭代初值、迭代公式和迭代次数(精度要求)。
例:使用辗转相除法求两数的最大公约数。
辗转相除法:如果x除以y的余数为0,则除数y就是最大公约数,或余数不为0,则被除数x被除数y取代,除数y被余数取代,再用新的x除以新的y,判断余数是否为0,如果不为0,则重复此迭代过程,直至余数为0,此时的除数y即为最大公约数。
main(){int x,y,temp;printf("Please input tw o numbers:");scanf("%d%d",&x,&y);temp=x%y;while(temp!=0) /* 辗转相除,直到temp为0 */{x=y; /*迭代*/y=temp; /*迭代*/temp=x%y;}printf("greatest common divisor=%d\n",y);}运行时输入:66 121输出:greatest common divisor=11 各值的变化如下:x y temp=x%y66 121 66121 66 1166 11 0实验一固定次数的循环设计【实验目的】学习设计固定次数的循环。
【实验内容】编写程序,计算x的y次方。
这里x为double型,y为int型。
x、y通过键盘输入,要考虑y为负数的情况。
例:当输入2.5 3时,输出15.625000;当输入2.5 -3时则输出0.064000。
程序以6_1.c命名并上交。
输入输出屏幕示例【指导】本实验中,假设y为正数时,可定义结果变量sum,想办法使sum*=x语句执行y次。
对固定次数的循环,通常方法是设计一个循环变量i,让其在初值与终值之间变化控制控制循环次数,循环条件通常是:i≤终值。
如:for(i=初值;i≤终值;i++)循环体语句;实验二整数按位折分求和【实验目的】学习设计与控制循环,并熟练%(求余)运算。
【实验内容】输入一个不大于2×109(用long型数据)的正整数x,求这个数每位数字之和。
例如,若输入33456781,输出37。
程序以6_2.c命名并上交。
【提示】设计循环,每次求出x的个位数(使用求余运算)并累加到和值变量中,再迭代操作,改变x的值,使原来的十位变个位。
【讨论与思考】long型数据的最大值是2147483647,受变量类型限制,本程序只能接收不大于2×109的正整数。
如果进行扩充,要求能接收并计算一个30位整数的各位之和,那么数据类型应如何设置,程序应该如何编写?实验三输出九九乘法表【实验目的】学习多重循环的嵌套。
【实验内容】下面程序输出九九乘法表如下图。
请完善程序并以6_3.c命名。
#include<stdio.h>void main(){int i,j;clrscr();for(_________________________){for(_________________________ )printf("%d*%d=%-2d ",i,j,i*j);_______________________;}}实验四打印数字塔图形【实验目的】学习使用循环语句构成的多重循环嵌套。
【实验内容】编写程序,使用循环输出如下图所示的数字塔图形。
程序以6_4.c命名。
【提示】此图形上下对称,可将程序分为上下两部分实现。
上半部输出9行,下半部输出8行。
每一行包含三部分内容:开始的空格、中间的数字及最后的换行符。
需要考虑的是字符个数与行号的关系。
下面程序用于输出如下*字符塔,供本题参考。
#include<stdio.h>void main(){int i,j;clrscr(); /* 清屏 */for(i=1;i<=9;i++) /* 行循环 */{for(j=1;j<=9-i;j++) /* 输出行左空格*/printf(" ");for(j=1;j<=2*i-1;j++) /* 输出若干* 字符 */printf("%c",'*');printf("\n"); /* 换行 */}}实验五寻找素数【实验目的】领会并牢固掌握素数算法,深入循环结构设计。
【实验内容】从键盘输入一个大于3的正整数,输出距离该数最近的素数。
根据输入的数不同,此问题可能有一个答案(或者比输入的数大或者比输入的数小),也可能需要输出两个值(一个比输入的数大,一个比输入的数小,两个距离输入的数一样近)。
程序以6_5.c命名并上交。
实验六不等式求解【实验目的】学习在循环中使用break控制语句。
【实验内容】键盘输入一个数给m,计算并返回满足表达式:1+(1+2)+(1+2+3)+(1+2+3+4)+……+(1+2+3+……+n)<=m最大的n。
例如,当m=10000时,程序输出:n=38。
程序以6_6.c 命名并上交。
【提示】参考解法:for(i=1;1;i++) /* 循环条件为恒真 */{计算(1+2+3+……+i) s;将计算结果s累加到变量sum中;判断sum的值是否大于m是,则终止循环否,则继续进入下一次循环}输出与对应结果,其值会与i相关。
实验七统计字数【实验目的】学习使用循环处理字符串相关问题。
【实验内容】完善以下程序6_7.C 。
程序任务:输入一串字符,以“#”作为输入结束标志,显示其中字母与数字字符的个数。
#include<stdio.h>void main(){int ch_num,dig_num;char ch;ch_num=dig_num=0;do{ch=getchar();/* 完善程序,统计52个英文字母与十个数字字符的个数 */ }while(__________); /* 给出循环条件*/printf("The number of chars is:%d\n",ch_num);printf("The number of digital is:%d\n",dig_num);}实验八礼炮响声统计【实验目的】学习循环中条件的设计与数据统计。
【实验内容】活动中有三门礼炮,各装有十枚炮弹。
第一门礼炮每隔3秒发一枚炮弹,第二门每隔5秒、第三门每隔7秒发一枚炮。
问观礼群众一共听到几声炮响。
同一时间发出炮声算一响。
程序以6_8.c命名并上交。
【实验提示】程序中可分别设置计时器变量与计数器变量。
计时器以秒为单位递增,测试此时有无炮发出。
只要有一枚炮发出,则计数器增1。
注意不要重复统计。
实验九验证哥德巴赫猜想【实验目的】综合运用多重循环结构、标志法、穷举法解决问题。
【问题描述】1742年6月,德国数学家哥德巴赫在给大数学家欧拉的信中提出一个问题:任何大于4的偶数均可以表示为两个素数之和吗?欧拉复信道:任何大于4的偶数均可以表示为两个素数之和,这一猜想我还不能证明,但我确信无疑地认为这是完全正确的定理。
哥德巴赫猜想是世界著名的数学难题,至今未能在理论上得到证明,自从计算机出现后,人们就开始用计算机去尝试解各种各样的数学难题,包括费马大定理、四色问题、哥德巴赫猜想等,虽然计算机无法从理论上严密地证明它们,只能在有限的范围内对其进行检验,但也不失其意义。
【实验内容】程序要求:输入一个int型数据范围内的偶数x(x>4),找到两个素数a、b,满足x=a+b。
最后输出此等式。
如输入98,输出98=19+79。