安全过河问题

过河智力题目1. 四个人过河问题：四个人在夜晚来到一条河边，只有一艘船，船最多只能承载两个人。

这四个人中有一个警察，一个小偷，一个父亲和一个儿子。

规则是如果父亲不在时，小偷会伤害儿子；如果母亲不在时，父亲会伤害女儿。

请问如何才能安全地将这四个人全部渡过河去？2. 狼、羊和白菜过河问题：一个人要带着一只狼、一只羊和一篮白菜过河。

但船只能载他自己和其中的一样东西。

如果狼单独留在羊身边，狼会吃掉羊；如果羊单独留在白菜身边，羊会吃掉白菜。

如何才能将它们都安全地运到河对岸？3. 三个快慢不一的人过桥问题：在一座桥上有一盏灯，只够三个人同时过桥，过桥的速度不同。

这三个人分别需要1 分钟、2 分钟和5 分钟过桥。

问题是：如何才能用最短的时间让这三个人都通过这座桥？4. 燃烧时间不同的绳子过桥问题：有一根可以在30 分钟内燃烧完全的绳子，一根可以在15 分钟内燃烧完全的绳子。

问题是：如何在45 分钟内，通过这两根绳子测量出30 分钟的时间？5. 神秘老人过河问题：一个神秘的老人要过河，他有一条小船，但船只能携带老人和一件物品。

老人有一只鸡、一只狐狸和一筐粮食。

规定是：如果老人不在场时，狐狸会吃掉鸡；如果鸡不在场时，鸡会吃掉粮食。

请问老人如何安全地将这三样物品都渡过河去？6. 火把过桥问题：四个人夜晚过桥，只有一支火把，过桥的速度不同。

他们需要1 分钟、2 分钟、5 分钟和10 分钟来通过这座桥。

问题是：如何才能在17 分钟内让所有人通过桥？7. 携带动物过河问题：有一条河，一只狼、一只羊和一株白菜需要被运到河对岸。

只有一个人可以划船，但船只能携带这个人和另外一样东西。

规定是：如果狼单独留在羊身边，狼会吃掉羊；如果羊单独留在白菜身边，羊会吃掉白菜。

如何才能将它们都安全地运到河对岸？8. 四个人过河问题2：有四个人需要过一条河。

他们需要在17 分钟内全部过河，而且只有一艘船。

他们分别需要1 分钟、2 分钟、5 分钟和10 分钟过河。

过河问题引言过河问题是一类经典的数学逻辑问题，涉及到河岸上有一群人/动物需要通过一条狭窄且危险的河流，但只有一艘小船。

这个问题涉及到一系列规则和条件，并要求找到一种最优的解决方案，使得所有人/动物都能够安全地通过河流。

这个问题可以被视为一种思维训练，有助于提高逻辑推理和问题解决能力。

问题描述在典型的过河问题中，通常会有一群人/动物（如农夫、狼、羊、菜）需要通过一条河流。

以下是一个典型的问题描述：- 河岸上有一个农夫、一只狼、一只羊和一颗菜。

- 这个小船只能够携带农夫以及一样其他物品。

- 如果农夫不在场，狼会吃掉羊，羊会吃掉菜。

- 目标是将所有的人/动物都安全地从一岸带到另一岸，而不违反上述条件。

解决方案为了解决这个过河问题，需要找到一个安全且合理的船运策略。

以下是一个可能的解决方案：1. 农夫将羊带到另一岸，然后返回原岸。

2. 农夫将菜带到另一岸，然后把羊带回原岸。

3. 农夫将狼带到另一岸，然后返回原岸。

4. 农夫将羊带到另一岸。

在这个解决方案中，农夫每次都会携带一只人/动物过河，并在返回时如果出现潜在的危险，则在另一岸留下该人/动物。

通过这种方式，可以确保没有任何一种组合会出现危险情况。

思考扩展过河问题可以被进一步扩展和改变，以增加难度和挑战性。

以下是一些可能的扩展：1. 添加更多的人物/动物：例如，增加一只狗和一个猫到过河问题中。

这样会增加更多的可能性和限制条件，使得解决方案更加复杂。

2. 调整规则和条件：可以根据需要调整问题的规则和条件，以提供更多的难度和挑战性。

例如，可以添加时间限制或改变特定物品之间的关系。

3. 使用不同的交通工具：除了小船之外，也可以考虑使用其他交通工具，如桥梁、绳索等。

这些不同的工具可能会改变问题的解决方案。

实际应用过河问题虽然是一个数学逻辑问题，但它可以反映现实生活中的许多情况。

例如，在项目管理中，团队需要合作解决一系列问题，每个问题都有特定的限制和条件。

通过训练逻辑思维和解决问题的能力，可以更好地应对实际挑战。

安全过河写一篇数学日记
案例一：
今天，我做了一道关于过河的数学题，可有趣了。

让我来告诉你们吧！
题目是这样的：一位老爷爷带着狼、羊和白菜要过河。

只有一条小船，一次只能运一个。

还要保证羊不被狼吃掉，白菜不被羊吃掉。

请问，需要运几趟？该怎么运？
我看到这个题，觉得很简单。

就随口答说：“先把白菜运过去，再运狼，最后运羊。

”在看书的妈妈听见了，笑着说：“你把白菜运过河了，那还没过河的狼和羊会怎么样呢？”
“啊！羊会被狼吃掉的。

”我说：“那我先运狼，不让它吃掉羊。

”我忽然想起来，不如做一做实验吧！看看会怎么样。

妈妈说这是个好办法！说做就做。

我把布娃娃喜羊羊当做“羊”，把沙皮狗当做“狼”，把我的绿皮球当做“白菜”……我做了一次次的实验，终于找到了正确答案。

案例二：
今天晚上，我看见一道会迷惑人的数学题，题目：37个同学要渡河，渡口有一只能乘上5人的空小船，他们要全部渡过河，至少
要使用这只小船多少次?
粗心的人往往会忽略“空小船”，就是忘了要有一个撑船，那么每次只能乘4人。

这样37人减去一位撑船的同学，剩36位同学，36除以4等于9，最后一次到对岸当船夫的同学也上岸4，所以至少要走9趟。

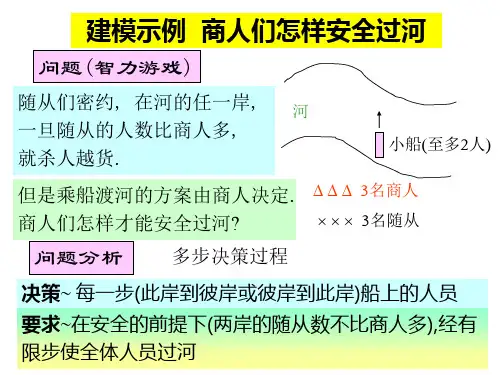
商人们怎样安全过河摘要：四名商人各带一名随从乘船渡河，一只小船至多容纳两人，由他们自己制定，随从约定，在河的任一岸，一旦随从的人数比商人多，就杀了越货。

但是如何乘船渡河的大权掌握在商人们手中，另外，当船的的容量增大为3，最多可以有几对商人安全过河。

商人们怎么才安全渡河，那将再此文中分析过河问题。

模型主要通图表法对过河的方案进行举例，然后根据小船的容量和商人们要安全过河为前提对各种方案进行层层筛选，最终得到商人安全过河方案。

关键词：多步决策图解法商人过河一、问题重述四名商人各带一名随从乘船渡河，一只小船至多容纳俩人，由他们自己划行，随从约，在河的任一岸，一旦随从的人数比商人多，就杀了越货。

另外，当船的的容量增大为3最多可以有几对商人安全过河但是如何乘船渡河的大权掌握在商人们手中。

现在需要解决的问题如下：1.四名商人在不被随从谋杀和小船最多能为2人的情况下，商人们将如何安全过河？2.如果有m名商人m名随从，小船的容量为3时，最多可以有多少商人各带一名随从过河。

二、模型的假设1.假设过河的过程中不会发生以外事故。

2.假设当随从人数多国商人时，不会改变杀人越货计划。

3.假设所有人最终都必须到达河对岸。

三、符号说明=0,1,2,3,4…;x k~第k次渡河前此岸的商人数x k,yk~第k次渡河前此岸的随从数k=1,2,…,) ~过程的状态S ~ 允许状态集合xS={(x , y)x=0, y=0,1,2,3,..; x=m, y=0,1,2,3,..; x=y=1,2,3..}=0, 1, 2..;~第k次渡船上的商人数~第k次渡船上的随从数k=1,2,…=( , ) ~过程的决策 D ~允许决策集合D={(u , v)u+v=1, 2, ….，u, v=0, 1, 2,…}状态因决策而改变~状态转移律四、模型分析针对商人们能否安全过河问题，需要选择一种合理的过河方案，对该问题可将看为一个多步决策模型，通过对每一次过河的方案的筛选优化，最终得到商人们全部安全过河。

4名商人带4名随从安全过河一．问题提出：4名商人带4名随从乘一条小船过河，小船每次自能承载至多两人。

随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货.乘船渡河的方案由商人决定，商人们如何才能安全渡河呢？二．模型假设：商人和随从都会划船。

三．问题分析：商随过河问题可以视为一个多步决策过程，通过多次优化，最后获取一个全局最优的决策方案。

对于每一步，即船由此岸驶向彼岸或由彼岸驶向此岸，都要对船上的人员作出决策，在保证两岸的商人数不少于随从数的前提下，在有限步内使全部人员过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员状况，可以找出状态随决策变化的规律，问题转化为在状态的允许变化范围内(即安全渡河条件)，确定每一步的决策，达到安全渡河的目标。

四．模型构成：xk~第k次渡河前此岸的商人数，yk~第k次渡河前此岸的随从数xk, yk=0,1,2,3,4; k=1,2,……Sk=(xk, yk)~过程的状态,S~允许状态集合，S={(x,y)| x=0, y=0,1,2,3,4; x=4 ,y=0,1,2,3,4; x=y=1,2,3} uk~第k次渡船上的商人数vk~第k次渡船上的随从数dk=(uk, vk)~决策，D={(u , v)| 1=<u+v=<2,uk, vk=0,1,2} ~允许决策集合 k=1,2,……因为k为奇数时船从此岸驶向彼岸，k为偶数时船从彼岸驶向此岸，所以状态Sk随决策dk的变化规律是Sk1=Sk+(-1)k dk~状态转移律求dk∈D(k=1,2, …n), 使Sk∈S, 并按转移律由S1=(4,4)到达状态Sn1=(0,0)。

五．模型求解：1.图解法：对于人数不多的情况，可以利用图解法来求解。

在xoy平面坐标系上画出如图所示的方格，方格点表示状态s=(x,y)，允许状态集合S是圆点标出的13个格子点，允许决策dk是沿方格线移动1格或2格，k为奇数时向左、下方移动，k为偶数时向右、上方移动。

人狼羊菜安全渡河问题1500字人狼羊菜安全渡河问题是一个著名的逻辑推理问题，常常用来考察人们在面对复杂情况时的思考能力和解决问题的能力。

问题描述如下：有一天，一个人带着一只狼、一只羊和一颗白菜来到了一条河边，他想把它们都安全地带到对岸去。

但是，他只有一条小船，而且这条小船只能承载他和另外一个物品（人、狼、羊、菜）。

问题是，如果他将狼与羊或羊与菜一起留在岸上，那么狼会吃掉羊，羊会吃掉菜。

请问，这个人应该如何才能够将所有物品都安全地带到对岸去？这个问题可以通过逐步分析来解决。

首先，我们可以将问题简化为只有三个物品的情况，即人、狼和羊。

这样，我们可以列出所有可能的情况如下：1. 人和狼一起过河，然后人回来，再把狼带过去。

这种情况下，狼会吃掉羊。

2. 人和羊一起过河，然后人回来，再把狼带过去。

这种情况下，羊会吃掉菜。

3. 人和羊一起过河，然后人回来，再把羊带过去。

这种情况下，狼会吃掉羊。

通过分析可以发现，前两种情况都是不可行的，因为狼或羊会被吃掉。

所以，我们只能选择第三种情况。

具体而言，我们可以按照以下步骤来解决问题：1. 人带着羊过河，然后人回来。

2. 人带着狼过河，然后把狼放在对岸，但是人自己回来。

3. 人带着菜过河，然后人放菜在对岸，再一起回去。

4. 人带着羊过河，完成。

通过这个方法，我们可以确保所有物品都能够安全地过河。

而且，我们也可以通过类似的方法解决更复杂的问题，比如加入更多的物品。

总结起来，人狼羊菜安全渡河问题是一个充满挑战和乐趣的逻辑推理问题。

通过逐步分析和合理安排，我们可以找到解决问题的方法，并将所有物品都安全地带到对岸。

这种问题可以提高人们的思维能力和解决问题的能力，同时也展示了逻辑推理的重要性。

小学生过河注意什么安全小学生过河时，要注意以下几个方面的安全问题：1.选择合适的过河地点。

小学生在过河时应选择水流平稳的地方，避免选择水流湍急、水面较宽的地方。

同时，要尽量选择水流不深的地方，以便小学生更容易掌握平衡和行走。

2.避免单独行动。

小学生在过河时最好不要单独行动，最好有成年人陪同。

如果没有成年人的陪同，可以与同伴一起过河，互相照应和帮助。

在途中要注意与同伴保持一定距离，避免相互影响和碰撞。

3.选择适合的过河方式和工具。

小学生可以通过多种方式过河，如步行、跳跃或利用其他的交通工具。

选择适合的过河方式和工具，要根据实际情况来决定。

在过河时，可以利用拐杖或长棍等工具来稳固身体，防止意外摔倒。

4.防止滑倒和摔倒。

小学生在过河时要注意脚下的地面情况，避免脚底滑倒或踩到尖锐的物体。

过河途中有可能会湿滑，所以要小心行走，保持身体重心稳定，并注意脚下的平衡。

5.注意穿着合适的衣物和鞋子。

小学生在过河时应选择合适的衣物和鞋子，避免穿着过长或过松的裤子和衣服。

鞋子要选择防滑的鞋底，以防止滑倒和摔倒。

6.留意河流的变化和周围环境。

小学生在过河时要时刻留意河流的变化，如水位是否上涨、水流是否加速等。

同时，要注意周围的环境，避免撞到岩石或其他危险物体。

7.遵守规则和指挥。

在过河时，小学生要遵守规则和指挥，听从成年人或老师的安排和指导。

不要随意改变行动计划，以免产生安全隐患。

8.保持冷静和沉着。

小学生在过河时要保持冷静和沉着，不要惊慌失措。

面对突发情况，要根据自己的实际情况，采取相应的应对措施，以保护自己的安全。

9.了解基本的救生知识。

小学生可以提前学习一些基本的救生知识，如人工呼吸、心脏按压等，以便在危险时能够采取正确的救援措施。

10.遵守家长和老师的安排。

最重要的是，小学生要严格遵守家长和老师的安排和要求，不要擅自行动，以保证自己的安全。

总结起来，小学生过河时要选择合适的地点，遵守规则和指挥，穿着合适的衣物和鞋子，留意河流的变化，保持冷静和沉着，了解基本的救生知识，并且要严格遵守家长和老师的安排和要求。

商人们怎样安全过河的数学模型示例文章篇一：话说啊，商人们遇到了一个棘手的问题：他们得带着随从们一起过河，但随从们可不是省油的灯，一有机会就想着害商人抢货。

这河又不宽不窄，一只小船每次只能载两个人，怎么过河才能确保安全呢？咱们来聊聊这个问题吧。

首先，商人们得明白，随从们人多势众，要是他们比商人多了，那可就危险了。

所以，商人们得想个法子，让随从们没法儿耍花招。

其实啊，这个问题可以变成一个数学模型。

想象一下，我们把每次过河的人都看成是一个状态，就像打游戏一样，每过一次河就是进入了一个新的关卡。

在这个关卡里，商人们得保证自己的人数不能少于随从们。

那具体怎么做呢？咱们得先设定一些规则。

比如说，每次过河的人数只能是两个，这是小船的容量决定的。

然后，商人们得选择让哪些人过河，这就得靠他们的智慧和策略了。

想象一下这个场景：商人们先让两个随从过河，然后一个商人再带一个随从回来。

这样，河对岸的随从人数虽然多了，但商人这边还有足够的人手可以应对。

接下来，两个商人再过河，这样河对岸的商人数就比随从数多了，安全就得到了保障。

然后，再让一个商人带一个随从回来，这样河这边也有足够的商人保护随从不敢造次。

最后，两个随从再过河，问题就解决了。

这个数学模型虽然简单，但却非常实用。

它告诉我们，在面对困难和挑战时，只要我们善于运用智慧和策略，就一定能够找到解决问题的方法。

所以，商人们要想安全过河，就得靠他们的智慧和勇气了。

示例文章篇二：话说啊，有这么一个古老的谜题，叫做“商人过河”。

话说有三名聪明的商人，他们各自带着一个狡猾的随从，准备乘船过河。

这船啊，一次只能载两个人，问题就在于，这些随从们心里都有个小九九，他们密谋着，只要到了河的对岸，随从人数多于商人人数，就立马动手抢货。

这商人们也不是吃素的，他们知道随从们的阴谋，但他们毕竟都是聪明人，于是就想出了一个绝妙的策略。

咱们来想想啊，这过河其实就是一个多步决策的过程。

每次渡河，船上的人员选择都至关重要。