第7章DSP定点数和浮点数(重要)
- 格式:pdf
- 大小:389.43 KB
- 文档页数:8


关于dsp中程序定点数和浮点数转换问题(Q15格式)看ti的逆变器程序,看到采集后的ADBUF数据全部都是《5,这就搞不明白了,为什么要左移5呀?然后看到上面说是兼容Q15,在QQ群里也问了高手,说是用于DSP小数运算,于是在网上找了下Q15的定义,下面把Q15整理下。
许多DSP都是定点DSP,处理定点数据会相当快,但是处理浮点数据就会非常慢。
可以利用Q格式进行浮点数据到定点的转化,节约CPU时间。
实际应用中,浮点运算大都时候都是既有整数部分,也有小数部分的。
所以要选择一个适当的定标格式才能更好的处理运算。
Q格式表示为:Qm.n,表示数据用m比特表示整数部分,n比特表示小数部分,共需要m+n+1位来表示这个数据,多余的一位用作符合位。
假设小数点在n位的左边(从右向左数),从而确定小数的精度例如Q15表示小数部分有15位,一个short型数据,占2个字节,最高位是符号位,后面15位是小数位,就假设小数点在第15位左边,表示的范围是:-1<X<0.9999695 。
浮点数据转化为Q15,将数据乘以2^15;Q15数据转化为浮点数据,将数据除以2^15。
例如:假设数据存储空间为2个字节,0.333×2^15=10911=0x2A9F,0.333的所有运算就可以用0x2A9F 表示,同理10911×2^(-15)=0.332977294921875,可以看出浮点数据通过Q格式转化后是有误差的。
例:两个小数相乘,0.333*0.414=0.1378620.333*2^15=10911=0x2A9F,0.414*2^15=13565=0x34FDshort a = 0x2A9F;short b = 0x34FD;short c = a * b >> 15; //两个Q15格式的数据相乘后为Q30格式数据,因此为了得到Q15的数据结果需要右移15位这样c的结果是0x11A4=0001000110100100,这个数据同样是Q15格式的,它的小数点假设在第15位左边,即为0.001000110100100=0.1378173828125...和实际结果0.137862差距不大。


Q格式有符号数的表示法,机器数(出现在电脑的二进位数值)有3个特点,无符号或符号转换成数值来表示,没有+10101这样的资料,而是以010101来表示,只表示单纯的整数或小数,小数点的位置预设在一定的位置而较少变动,它的长度受到电脑硬体的限制,而不能无限增长。
Q格式,就是将一个小数放大若干倍后,用整数来表示小数。
Q格式前提无符号数:当参与运算的数值没有负数且运算的结果也没有负数时,则所有字元都可以表示数值,这种没有符号的数,称为无符号数(如记忆体储存位址),有符号数:数值中有某位数值代表符号,通常最高位作为符号位,0代表正,1代表负。
真值:有符号数所代表的数值,例如:110所代表的值是-2 而非6,有符号数只要去除符号位就可以获得该数的大小,在运算时,它的符号位可参与运算。
但在加减运算时,必须将它分离出来,才能进行运算。
有时,还要确定哪个有符号数的真值比较大,才能确定结果的符号。
为了达到这些功能,电路的设计就相当复杂。
所以很多电脑系统不直接使用有符号数,而使用有符号数的1’s补数或2’s补数表示法作为编码系统正弦脉波宽度调变(SPWM)之控制方法经Q 格式乘法器转换成振幅与频率可变V/F 控制,当成其单相感应马达的输入信号,藉由控制责任周期的大小,以达到变电压相对改变频率的效果。
DSP1.实现数位系统的第一步在自然世界中,所有的物理量包括时间、电压、质量、位移等等,都是类比的、连续的。
可是在数位系统中,讯号是在不连续的时间点取样,物理量或讯号的大小也不再是连续,而是被量化(Quantized)。
在数位系统中,只能用有限字元长度的数字去表示数量的大小,而不能以无限精确的数值(实数)去表示。
为了实现数位系统;使用了定数数与浮点数的表示法。
a)定点数(Fixed Point Number):指一个数字的表示,其小数点是在固定的位置(位元)。
b)浮点数(Floating Point Number):使用假数以及指数两部分来表示数值。

DSP学习笔记(⼆)——DSP中浮点数与定点数格式与运算处理DSP学习笔记(⼆)——DSP中浮点数与定点数格式与处理1 DSP中的数据表述DSP中数据通常是有定点数与表⽰,其中可以对字长进⾏相关定义,可以选取字长为16位、24位、32位不同字长使⽤。
⽽格式与字长决定了数据的精度与动态范围,同时也⼀定程度上决定了DSP处理器的功耗、成本与编程难度。
定点数:⼩数点位置为确定的。
浮点数:⼩数点位置可以改变。
定点运算的硬件实现较为简单,功耗较⼩,主要注意的是数据的定标、溢出以及误差。
器减结构较为复杂,但是精度较⾼,⾼级语⾔容易⽀持。
2 定点数的格式与相关运算2.1 定点数格式定点数格式:Q n 格式,n为⼩数位数。
即Q15 ,⼩数点右边有15个⼩数位,如果我们定义了⼀个长度为32位的数字,那么⼩数位为15,1位符号位,16位为整数位。
整数⼩数点固定在最后,定点数⼩数位固定使⽤上⽂的Q n 格式表⽰,两者都使⽤⼆进制补码形式表⽰。
例: Q4格式:01010011b=1·22+1·20+1·2-3+1·2-4=83/24=5.1875对于负数(最⾼位MSB为1),要先把它转化为⽆符号⼆进制数,再进⾏计算,最后加上负号。
图2-1 ⼆进制Q格式表⽰定点数与浮点数转化时需要使⽤2n 的关系进⾏转化。
转化关系如下图:图2-2 定点数与浮点数转化关系浮点数转换为定点数时,由于⼩数点后的位数有限,会产⽣截断误差。
2.2 数值范围与精度Qn 格式,字长为N数值范围: -2N-12n~2N-1-12n精度:12n由于符号位占1位,所以数据位为N-1,n越⼤范围越⼩,但精度越⾼。
图2-3 数值范围与精度2.3 动态范围数据格式中最⼤值与最⼩值之⽐即为动态范围。
N位定点数动态范围:分贝表⽰:dsp⼤多采⽤16位定点数,动态范围为90.3db。
Dsp⼤多采⽤16为定点数,运算硬件实现较为简单,更⼤动态范围应⽤可以使⽤拓展字长⽅式。

定点DSP处理浮点数BG6RDFTMS320C5509A是16位定点数处理器,其累加器是32位/40位的。
在定点处理器中处理浮点数需要对定点数进行定标。
下面所说的定点数都是指有符号数。
通常采用的定标有Q15和Q31,分别表示小数点后有二进制15位和二进制16位。
因此16位Q15最大能表示的数是1 2 ,32位Q31最大能表示的数是1 2 。
定标不同的数可以直接相乘,例如Q13*Q15=Q28。
两个定标不同的数不能直接相加,比如Q13+Q15,通常要将Q15右移两位,转换为Q13后再相加,当然这样损失了两位的精度。
DSP进行的乘累加操作常常Q15的数,这样结果为Q30,存储在累加器中。
为了将累加器的结果转换为更为常用的Q31定标,55x系列DSP在状态寄存器ST1_55中设置了FRCT 控制位,FRCT=1时,乘积自动左移一位,这样乘积变成了Q31。
对于累加器中Q31定标的数,直接取累加器中高16位,就能获得结果的Q15定标数。
很多时候Q15不能解决问题,比如IIR滤波器num, den系数中通常有大于等于1的系数,超过了Q15的范围,只能用Q14,Q13等定标。
这时乘累加操作就需要进行修正了,比如IIR滤波器中系数用Qx定标,输入数据和输出数据用Qy定标,Q Q Q ,为获得Qy的输出数据必须将累加器中的乘积右移x位,另外在乘累加操作开始前必须将输入数据在累加器中左移y位,进行对齐后才能进行乘累加。
当然,这种修正都是在没有考虑FRCT 的情况下。
在C5500 DSPLIB中iircas51函数中,FRCT设置为1,输入输出数据采用Q15定标,如果系数也是Q15定标,则程序运行无误,如果系数采用Q14及以下定标则会产生严重的问题。
以下是其代码片段:MOV *AR0+ << #16, AC1 ; HI(AC1) = x(n)||RPTBLOCAL loop2‐1 ;inner loop: process a bi‐quadMPYM *AR1+, AC1, AC0 ; AC0 = b0*x(n)MACM *AR1+, *(AR3+T0), AC0 ; AC0 += b1*x(n‐1)MACM *AR1+, *AR3, AC0 ; AC0 += b2*x(n‐2)MOV HI(AC1), *AR3 ; x(n) replaces x(n‐2)||AADD T1, AR3 ; point to next x(n‐1)MASM *AR1+, *(AR4+T0), AC0 ; AC0 ‐= a0*y(n‐1)MASM *AR1+, *AR4, AC0 ; AC0 ‐= a1*y(n‐2)MOV rnd(HI(AC0)), *AR4 ; y(n) replaces y(n‐2)||AADD T1, AR4 ;point to next y(n‐1)MOV AC0, AC1 ;input to next biquad从代码片段可以看出,累加器AC0为Q31定标,输出数据是累加器高16位。



声明:本文章系转载并稍加整理标注,可能对于入门级的dsp开发者有所帮助。
本文关注定点dsp与浮点dsp的对比,感谢我所引用的资料的作者。
定点dsp与浮点dsp的比较(1)DSP数字信号处理器是一种特别适合于进行数字信号处理的微处理器,主要用于实时快速地实现各种数字信号处理算法定点运算DSP数字信号处理器在应用中已取得了极大的成功,而且仍然是DSP应用的主体。
然而,随着对DSP处理速度与精度、存储器容量、编程的灵活性和方便性要求的不断提高、自80年代中后期以来,各DSP生产厂家陆续推出了各自的32bit浮点运算DSP。
定点DSP指令集定点DSP指令集是按两个目标来设计的:·使处理器能够在每个指令周期内完成多个操作,从而提高每个指令周期的计算效率。
·将存贮DSP程序的存储器空间减到最小(由于存储器对整个系统的成本影响甚大,该问题在对成本敏感的DSP应用中尤为重要)。
和定点运算DSP相比,浮点运算DSP具有许多优越性:浮点运算DSP比定点运算DSP的动态范围要大很多。
定点DSP的字长每增加1bit,动态范围扩大6dB。
16bit字长的动态范围为96dB。
程序员必须时刻关注溢出的发生。
例如,在作图像处理时,图像作旋转、移动等,就很容易产生溢出。
这时,要么不断地移位定标,要么作截尾。
前者要耗费大量的程序空间和执行时间,后者则很快带来图像质量的劣化。
总之,是使整个系统的性能下降。
在处理低信噪比信号的场合,例如进行语音识别、雷达和声纳信号处理时,也会发生类似的问题。
而32bit浮点运算DSP的动态范围可以作到1536dB,这不仅大大扩大了动态范围,提高了运算精度,还大大节省了运算时间和存储空间,因为大大减少了定标,移位和溢出检查。
由于浮点DSP的浮点运算用硬件来实现,可以在单周期内完成,因而其处理速度大大高于定点DSP。
这一优点在实现高精度复杂算法时尤为突出,为复杂算法的实时处理提供了保证。

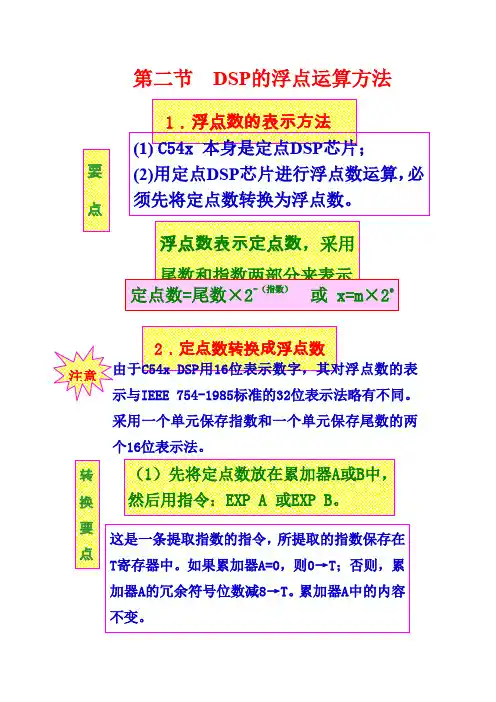
第3章 DSP 芯片的定点运算3.1 数 的 定 标在定点DSP 芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP 芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP 芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,1则表示数值为负。
其余15位表示数值的大小。
因此二进制数0010000000000011b =8195 二进制数1111111111111100b =-4对DSP 芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP 芯片是如何处理小数的呢?应该说,DSP 芯片本身无能为力。
那么是不是说DSP 芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q 表示法和S 表示法两种。
表3.1列出了一个16位数的16种Q 表示、S 表示及它们所能表示的十进制数值范围。
从表3.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如:16进制数2000H =8192,用Q0表示 16进制数2000H =0.25,用Q15表示但对于DSP 芯片来说,处理方法是完全相同的。
从表3.1还可以看出,不同的Q 所表示的数不仅范围不同,而且精度也不相同。
Q 越大,数值范围越小,但精度越高;相反,Q 越小,数值范围越大,但精度就越低。
例如,Q0的数值范围是-32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为 1/32768 = 0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想提高精度,则数的表示范围就相应地减小。
一DSP定点算数运算1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,l则表示数值为负。
其余15位表示数值的大小。
因此,二进制数0010000000000011b=8195二进制数1111111111111100b= -4对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表1.1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。
从表1.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如,16进制数2000H=8192,用Q0表示16进制数2000H=0.25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表1.1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0 的数值范围是一32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为1/32768=0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想精度提高,则数的表示范围就相应地减小。
定点DSP如何做浮点运算2008-10-16 08:46许多DSP芯片只支持整数运算,如果现在这些芯片上进行小数运算的话,定点小数运算应该是最佳选择了,此外即使芯片支持浮点数,定点小数运算也是最佳的速度选择。
在DSP 世界中,由于DSP芯片的限制,经常使用定点小数运算。
所谓定点小数,实际上就是用整数来进行小数运算。
下面先介绍定点小数的一些理论知识,然后以C 语言为例,介绍一下定点小数运算的方法。
在TI C5000 DSP系列中使用16比特为最小的储存单位,所以我们就用16比特的整数来进行定点小数运算。
先从整数开始,16比特的储存单位最多可以表示0x0000到0xffff,65536种状态,如果它表示C语言中的无符号整数的话,就是从0到 65535。
如果需要表示负数的话,那么最高位就是符号位,而剩下的15位可以表示32768种状态。
这里可以看出,对于计算机或者DSP芯片来说,符号并没有什么特殊的储存方式,其实是和数字一起储存的。
为了使得无论是无符号数还是符号数,都可以使用同样的加法减法规则,符号数中的负数用正数的补码表示。
我们都知道-1 + 1 =0,而0x0001表示1,那么-1用什么来表示才能使得-1 + 1 =0呢?答案很简单:0xffff。
现在就可以打开Windows的计算器,用16进制计算一下0xffff+0x0001,结果是0x10000。
那么 0x10000和0x0000等价麽,我们刚才说过用16比特来表达整数,最高位的1是第17位,这一位是溢出位,在运算寄存器中没有储存这一位,所以结果是低16位,也就是0x0000。
现在我们知道负数的表达方式了。
举个例子:-100。
首先我们需要知道100的16进制,用计算器转换一下,可以知道是0x0064,那么-100就是0x10000 - 0x0064,用计算器算一下得0xff9c。
还有一种简单的转换符号的方法,就是取反加一:把数x写成二进制格式,每位0变1,1变0,最后把结果加1就是-x了。
DSP中浮点转定点运算--浮点与定点概述⼀:浮点与定点概述1.1相关定义说明 定点数:通俗的说,⼩数点固定的数。
以⼈民币为例,我们⽇常经常说到的如123.45¥,789.34¥等等,默认的情况下,⼩数点后⾯有两位⼩数,即⾓,分。
如果⼩数点在最⾼有效位的前⾯,则这样的数称为纯⼩数的定点数,如0.12345,0.78934等。
如果⼩数点在最低有效位的后⾯,则这样的数称为纯整数的定点数,如12345,78934等。
浮点数:⼀般说来,⼩数点不固定的数。
⽐较容易的理解⽅式是,考虑以下我们⽇常见到的科学记数法,拿我们上⾯的数字举例,如123.45,可以写成以下⼏种形式:12.345x1011.2345 x1020.12345 x103……为了表⽰⼀个数,⼩数点的位置可以变化,即⼩数点不固定。
1.2定点数与浮点数的对⽐为了简单的把问题描述清楚,这⾥都是⼗进制数字举例,详细的分析,⼤家可以在后⾯的⽂章中看到。
(1)表⽰的精度与范围不同例如,我们⽤4个⼗进制数来表达⼀个数字。
对于定点数(这⾥以定点整数为例),我们表⽰区间[0000,9999]中的任何⼀个数字,但是如果我们要想表⽰类似1234.3的数值就⽆能为⼒了,因为此时的表⽰精度为1/100=1;如果采⽤浮点数来表⽰(以归整的科学记数法,即⼩数点前有⼀位有效位,为例),则可以表⽰[0.000,9.999]之间的任何⼀个数字,表⽰的精度为1/103=0.001,精度⽐上⼀种⽅式提⾼了很多,但是表⽰的范围却⼩了很多。
也就是说,⼀般的,定点数表⽰的精度较低,但表⽰的数值范围较⼤;⽽浮点数恰恰相反。
(2)计算机中运算的效率不同⼀般说来,定点数的运算在计算机中实现起来⽐较简单,效率较⾼;⽽浮点数的运算在计算机中实现起来⽐较复杂,效率相对较低。
(3)硬件依赖性⼀般说来,只要有硬件提供运算部件,就会提供定点数运算的⽀持(不知道说的确切否,没有听说过不⽀持定点数运算的硬件),但不⼀定⽀持浮点数运算,如有的很多嵌⼊式开发板就不提供浮点运算的⽀持。
一DSP定点算数运算1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,l则表示数值为负。
其余15位表示数值的大小。
因此,二进制数0010000000000011b=8195二进制数1111111111111100b= -4对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表1.1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。
从表1.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如,16进制数2000H=8192,用Q0表示16进制数2000H=0.25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表1.1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0 的数值范围是一32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为1/32768=0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想精度提高,则数的表示范围就相应地减小。
第7章D S P定点数和浮点数(重要)本期教程主要跟大家讲解一下定点数和浮点数的基础知识,了解这些基础知识对于后面学习ARM官方的DSP库大有裨益。
特别是初学的一定要理解这些基础知识。
7.1 定点数和浮点数概念7.2 IEEE浮点数7.3 定点数运算7.4总结7.1定点数和浮点数概念如果小数点的位置事先已有约定,不再改变,此类数称为“定点数”。
相比之下,如果小数点的位置可变,则称为“浮点数”(定点数的本质是小数,整数只是其表现形式)。
7.1.1定点数常用的定点数有两种表示形式:如果小数点位置约定在最低数值位的后面,则该数只能是定点整数;如果小数点位置约定在最高数值位的前面,则该数只能是定点小数。
7.1.2浮点数在计算机系统的发展过程中,曾经提出过多种方法表达实数。
典型的比如相对于浮点数的定点数(Fixed Point Number)。
在这种表达方式中,小数点固定的位于实数所有数字中间的某个位置。
货币的表达就可以使用这种方式,比如 99.00 或者 00.99 可以用于表达具有四位精度(Precision),小数点后有两位的货币值。
由于小数点位置固定,所以可以直接用四位数值来表达相应的数值。
SQL 中的 NUMBER 数据类型就是利用定点数来定义的。
还有一种提议的表达方式为有理数表达方式,即用两个整数的比值来表达实数。
定点数表达法的缺点在于其形式过于僵硬,固定的小数点位置决定了固定位数的整数部分和小数部分,不利于同时表达特别大的数或者特别小的数。
最终,绝大多数现代的计算机系统采纳了所谓的浮点数表达方式。
这种表达方式利用科学计数法来表达实数,即用一个尾数(Mantissa ),一个基数(Base),一个指数(Exponent)以及一个表示正负的符号来表达实数。
比如 123.45 用十进制科学计数法可以表达为 1.2345 × 102,其中 1.2345 为尾数,10 为基数,2 为指数。
浮点数利用指数达到了浮动小数点的效果,从而可以灵活地表达更大范围的实数。
提示: 尾数有时也称为有效数字(Significand)。
尾数实际上是有效数字的非正式说法。
同样的数值可以有多种浮点数表达方式,比如上面例子中的 123.45 可以表达为 12.345 × 101,0.12345 × 103 或者 1.2345 × 102。
因为这种多样性,有必要对其加以规范化以达到统一表达的目标。
规范的(Normalized)浮点数表达方式具有如下形式:±d.dd...d × βe, (0 ≤ d i < β)其中 d.dd...d 即尾数,β 为基数,e 为指数。
尾数中数字的个数称为精度,在本文中用 p 来表示。
每个数字 d 介于 0 和基数之间,包括 0。
小数点左侧的数字不为 0。
基于规范表达的浮点数对应的具体值可由下面的表达式计算而得:±(d0 + d 1β-1+ ... + d p-1β-(p-1))βe, (0 ≤ d i < β)对于十进制的浮点数,即基数 β 等于 10 的浮点数而言,上面的表达式非常容易理解,也很直白。
计算机内部的数值表达是基于二进制的。
从上面的表达式,我们可以知道,二进制数同样可以有小数点,也同样具有类似于十进制的表达方式。
只是此时 β 等于 2,而每个数字 d 只能在 0 和 1 之间取值。
比如二进制数 1001.101 相当于 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 + 1 × 2-1 + 0 × 2-2 + 1 × 2-3,对应于十进制的 9.625。
其规范浮点数表达为 1.001101 × 23。
7.2I E E E浮点数说明:Cortex-M4F中的FPU(浮点单元)就是用的这个IEEE 754标准,初学的要认真学习。
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。
这个标准定义了表示浮点数的格式(包括负零-0)与反常值(denormal number)),一些特殊数值(无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”;它也指明了四种数值舍入规则和五种例外状况(包括例外发生的时机与处理方式)。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80比特实做)。
只有32位模式有强制要求,其他都是选择性的。
大部分编程语言都有提供IEEE浮点数格式与算术,但有些将其列为非必需的。
例如,IEEE 754问世之前就有的C语言,现在有包括IEEE算术,但不算作强制要求(C语言的float通常是指IEEE单精确度,而double是指双精确度)。
该标准的全称为IEEE二进制浮点数算术标准(ANSI/IEEE Std 754-1985),又称IEC 60559:1989,微处理器系统的二进制浮点数算术(本来的编号是IEC 559:1989)。
后来还有“与基数无关的浮点数”的“IEEE 854-1987标准”,有规定基数为2跟10的状况。
现在最新标准是“IEEE 854-2008标准”。
在六、七十年代,各家计算机公司的各个型号的计算机,有着千差万别的浮点数表示,却没有一个业界通用的标准。
这给数据交换、计算机协同工作造成了极大不便。
IEEE的浮点数专业小组于七十年代末期开始酝酿浮点数的标准。
在1980年,英特尔公司就推出了单片的8087浮点数协处理器,其浮点数表示法及定义的运算具有足够的合理性、先进性,被IEEE采用作为浮点数的标准,于1985年发布。
而在此前,这一标准的内容已在八十年代初期被各计算机公司广泛采用,成了事实上的业界工业标准。
在 IEEE 标准中,浮点数是将特定长度的连续字节的所有二进制位分割为特定宽度的符号域,指数域和尾数域三个域,其中保存的值分别用于表示给定二进制浮点数中的符号,指数和尾数。
这样,通过尾数和可以调节的指数(所以称为"浮点")就可以表达给定的数值了。
具体的格式参见下面的图例:IEEE单精度浮点数1bit 8bit 38bitIEEE双精度浮点数1bit 11bit 52bit●在上面的图例中,第一个域为符号域。
其中 0 表示数值为正数,而 1 则表示负数。
●第二个域为指数域。
其中单精度数为 8 位,双精度数为 11 位。
以单精度数为例,8 位的指数为可以表达 0 到 255 之间的 255 个指数值。
但是,指数可以为正数,也可以为负数。
为了处理负指数的情况,实际的指数值按要求需要加上一个偏差(Bias)值作为保存在指数域中的值,单精度数的偏差值为 127,而双精度数的偏差值为 1023。
比如,单精度的实际指数值 0 在指数域中将保存为 127;而保存在指数域中的 64 则表示实际的指数值 -63。
偏差的引入使得对于单精度数,实际可以表达的指数值的范围就变成 -127 到 128 之间(包含两端)。
我们不久还将看到,实际的指数值 -127(保存为 全 0)以及 +128(保存为全 1)保留用作特殊值的处理。
这样,实际可以表达的有效指数范围就在 -127 和 127 之间。
在本文中,最小指数和最大指数分别用 emin 和 emax 来表达。
●图例中的第三个域为尾数域,其中单精度数为 23 位长,双精度数为 52 位长。
除了我们将要讲到的某些特殊值外,IEEE 标准要求浮点数必须是规范的。
这意味着尾数的小数点左侧必须为 1,因此我们在保存尾数的时候,可以省略小数点前面这个 1,从而腾出一个二进制位来保存更多的尾数。
这样我们实际上用 23 位长的尾数域表达了 24 位的尾数。
比如:对于单精度数而言,二进制的 1001.101(对应于十进制的 9.625)可以表达为 1.001101 × 23,所以实际保存在尾数域中的值为 0011 0100 0000 000 0000 0000,即去掉小数点左侧的 1,并用 0 在右侧补齐。
值得注意的是,对于单精度数,由于我们只有 24 位的指数(其中一位隐藏),所以可以表达的最大指数为 224 - 1 = 16,777,215。
特别的,16,777,216 是偶数,所以我们可以通过将它除以 2 并相应地调整指数来保存这个数,这样 16,777,216 同样可以被精确的保存。
相反,数值 16,777,217 则无法被精确的保存。
由此,我们可以看到单精度的浮点数可以表达的十进制数值中,真正有效的数字不高于 8 位。
事实上,对相对误差的数值分析结果显示有效的精度大约为 7.22 位。
参考下面的示 例:true value stored value--------------------------------------16,777,215 1.6777215E716,777,216 1.6777216E716,777,217 1.6777216E716,777,218 1.6777218E716,777,219 1.677722E716,777,220 1.677722E716,777,221 1.677722E716,777,222 1.6777222E716,777,223 1.6777224E716,777,224 1.6777224E716,777,225 1.6777224E7--------------------------------------根据标准要求,无法精确保存的值必须向最接近的可保存的值进行舍入。
这有点像我们熟悉的十进制的四舍五入,即不足一半则舍,一半以上(包括一半)则进。
不过对于二进制浮点数而言,还多一条规矩,就是当需要舍入的值刚好是一半时,不是简单地进,而是在前后两个等距接近的可保存的值中,取其中最后一位有效数字为零者。
从上面的示例中可以看出,奇数都被舍入为偶数,且有舍有进。
我们可以将这种舍入误差理解为"半位"的误差。
所以,为了避免 7.22 对很多人造成的困惑,有些文章经常以 7.5 位来说明单精度浮点数的精度问题。
提示: 这里采用的浮点数舍入规则有时被称为舍入到偶数(Round to Even)。
相比简单地逢一半则进的舍入规则,舍入到偶数有助于从某些角度减小计算中产生的舍入误差累积问题。
因此为 IEEE 标准所采用。
7.2.1规范化浮点数通过前面的介绍,大家应该已经了解的浮点数的基本知识,这些知识对于一个不接触浮点数应用的人应该足够了。