下载文档原格式
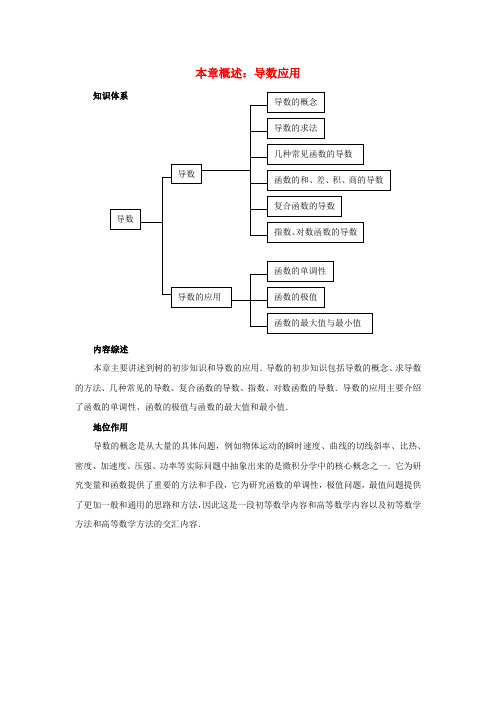
本章概述：导数应用
内容综述
本章主要讲述到树的初步知识和导数的应用．导数的初步知识包括导数的概念、求导数的方法、几种常见的导数、复合函数的导数、指数、对数函数的导数．导数的应用主要介绍了函数的单调性、函数的极值与函数的最大值和最小值．
地位作用
导数的概念是从大量的具体问题，例如物体运动的瞬时速度、曲线的切线斜率、比热、密度、加速度、压强、功率等实际问题中抽象出来的是微积分学中的核心概念之一．它为研究变量和函数提供了重要的方法和手段，它为研究函数的单调性，极值问题，最值问题提供了更加一般和通用的思路和方法，因此这是一段初等数学内容和高等数学内容以及初等数学方法和高等数学方法的交汇内容．。
2.1 导数的概念及其应用导数是数学中最重要的概念之一，是我们这一章内容的根本，只有准确把握好导数的概念才能用它指导相关知识的学习，才能用它来解决问题．一 细说导数的概念１． 函数()f x 在某一点0x 处的导数：它是用函数在这一点的函数值的改变量与自变量的改变量的比值，当自变量的改变量趋与零时的极限来度量的，即 ()'0000()()limx f x x f x f x x ∆→+∆-=∆，或者()0'000()()lim x x f x f x f x x x →-=-，或者()'0000()()lim x f x f x x f x x∆→--∆=∆，或者在k 为非零常数时()'0000()()lim x f x k x f x f x k x∆→+∆-=∆等．这几种形式是等价的，明确这点对解题很有帮助． 例１．已知函数()f x 中，()'12f =,求xf x f x ∆-∆-→∆)1()21(lim 0． 分析：当0x ∆→时，20x -∆→，只需将xf x f x ∆-∆-→∆)1()21(lim 0变形为(2)0[1(2)](1)2lim (2)x f x f x -∆→+-∆---∆，即可用导数的定义解决． 解：()'0(2)0(12)(1)[1(2)](1)lim 2lim 214(2)x x f x f f x f f x x ∆→-∆→-∆-+-∆-=-=-=-∆-∆． 点评：函数在某一点0x 处的导数，就是函数在这一点的函数值的增量与自变量的增量的比值在自变量的增量趋近于零时的极限，分子分母中的自变量的增量x ∆必须保持对应一致，它是非零的变量，它可以是2x -∆， 12x ∆等． ２． 函数()f x 在开区间(),a b 内的导数：如果函数()f x 在开区间(),a b 内可导，对于开区间(),a b 内的每一个0x ，都对应着一个导数 ()0f x ' ，这样'()f x 在开区间(),a b 内构成一个新的函数，这一新的函数叫做()f x 在开区间(),a b 内的导函数， 记作 ()()()00lim lim x x f x x f x y f x y x x∆→∆→+∆-∆'='==∆∆，导函数也简称为导数．例２．求()22f x x =的导数．分析：我们先认定x 为函数()f x 在定义域内的某一个固定的点，用导数的定义求其在这一点处的导数，而这个x 在定义域内又是任意的，故所求出的导数就是函数()22f x x =的导数．解：()()()()222'0002242lim lim lim 424x x x x x x x x x f x x x x x x ∆→∆→∆→+∆-⋅∆+∆===+⋅∆=∆∆． 点评：定义法是求函数导数的基本方法．二 导数在解决问题中的应用例３．求证：偶函数的导数是奇函数．分析：根据偶函数的定义和导数的定义进行变换．证明：设()f x 是偶函数，则()()()()()()()()'00'()0limlim ()lim ()x x x f x x f x f x xf x x f x xf x x f x f x x ∆→∆→-∆→+∆-=∆--∆--=∆-+-∆--=-=---∆， 即对函数()f x 的定义域内的任意x 有()''()f x f x -=-，即'()f x 是奇函数．点评：0030x x x ∆→⇔-∆→⇔∆→等是活用导数的定义的关键，变形时注意分子分母中自变量改变量的一致性．小结：从上面不难看出导数概念中的关键是＂自变量改变量的一致性和自变量的改变量趋于零的绝对任意性＂．。
2.1 导数的概念及其应用
导数是数学中最重要的概念之一，是我们这一章内容的根本，只有准确把握好导数的概念才能用它指导相关知识的学习，才能用它来解决问题．
一 细说导数的概念
１． 函数()f x 在某一点0x 处的导数：它是用函数在这一点的函数值的改变量与自变量的改变量的比值，当自变量的改变量趋与零时的极限来度量的，即 ()'0000()()lim
x f x x f x f x x ∆→+∆-=∆，或者()0'000()()lim x x f x f x f x x x →-=-，或者()'0000()()lim x f x f x x f x x
∆→--∆=∆，或者在k 为非零常数时()'0000()()lim x f x k x f x f x k x
∆→+∆-=∆等．这几种形式是等价的，明确这点对解题很有帮助． 例１．已知函数()f x 中，()'12f =,求x
f x f x ∆-∆-→∆)1()21(lim 0． 分析：当0x ∆→时，20x -∆→，只需将x
f x f x ∆-∆-→∆)1()21(lim 0变形为(2)0[1(2)](1)2lim (2)
x f x f x -∆→+-∆---∆，即可用导数的定义解决． 解：()'0
(2)0(12)(1)[1(2)](1)lim 2lim 214(2)x x f x f f x f f x x ∆→-∆→-∆-+-∆-=-=-=-∆-∆． 点评：函数在某一点0x 处的导数，就是函数在这一点的函数值的增量与自变量的增量的比值在自变量的增量趋近于零时的极限，分子分母中的自变量的增量x ∆必须保持对应一致，它是非零的变量，它可以是2x -∆， 12
x ∆等． ２． 函数()f x 在开区间(),a b 内的导数：如果函数()f x 在开区间(),a b 内可导，对于开区间(),a b 内的每一个0x ，都对应着一个导数 ()0f x ' ，这样'()f x 在开区间(),a b 内构成一个新的函数，这一新的函数叫做()f x 在开区间(),a b 内的导函数， 记作 ()()()00lim lim x x f x x f x y f x y x x
∆→∆→+∆-∆'='==∆∆，导函数也简称为导数．
例２．求()22f x x =的导数．
分析：我们先认定x 为函数()f x 在定义域内的某一个固定的点，用导数的定义求其在这一点处的导数，而这个x 在定义域内又是任意的，故所求出的导数就是函数()22f x x =的导数．
解：()()()()22
2'0002242lim lim lim 424x x x x x x x x x f x x x x x x ∆→∆→∆→+∆-⋅∆+∆===+⋅∆=∆∆． 点评：定义法是求函数导数的基本方法．
二 导数在解决问题中的应用
例３．求证：偶函数的导数是奇函数．
分析：根据偶函数的定义和导数的定义进行变换．
证明：设()f x 是偶函数，则
()()()()()()()()'
00'()0lim lim ()lim ()x x x f x x f x f x x
f x x f x x
f x x f x f x x ∆→∆→-∆→+∆-=∆--∆--=∆-+-∆--=-=---∆， 即对函数()f x 的定义域内的任意x 有()''()f x f x -=-，即'()f x 是奇函数．
点评：0030x x x ∆→⇔-∆→⇔∆→等是活用导数的定义的关键，变形时注意分子分母中自变量改变量的一致性．
小结：从上面不难看出导数概念中的关键是＂自变量改变量的一致性和自变量的改变量趋于零的绝对任意性＂．。
