中考试题江苏省连云港市灌云县小伊中学专题复习二__图表信息题

专题(二) 地理计算1.某中学地理兴趣小组拟绘制一幅校园平面图。

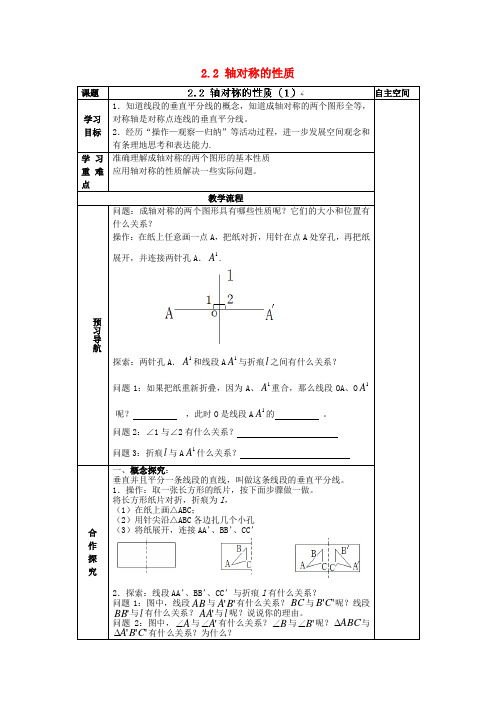
图书室与操场间的实地距离为400米，假如绘到图上的距离为20厘米，那么同学们采纳的比率尺应为()∶20000B.∶2000D.图上1厘米代表实地距离200米2.在一幅比率尺为1∶250000的地图上，量得某河流长度为50厘米，那么这条河的实地长度为( )250米千米千米千米以下列图是“某地等高线地形图〞，假定甲村到a处耕地的图上距离为2厘米，那么实地距离是( )图ZT2-5米米米米读图，达成4~7题。

图ZT2-64.假定此时乙村的气温是20℃，那么甲村的气温最可能是()℃℃℃℃5.图中等高线单位为米，那么①地与③地的相对高度是()米米米米6.几条等高线在A处重叠在一同，说明A处是()A.平川B.沟谷C.悬崖D.山脊7.测得A、B间的图上距离是厘米，那么两地实地距离是()千米千米千米千米8.以下列图为某气象站测得该市某日的气温数值，那么该日气温的日较差是()图ZT2-7℃℃℃℃9.某地7月的均匀气温是℃，1月的均匀气温是-℃，那么该地的气温年较差是()℃℃℃℃10.下边四幅图中，山顶可能有终年积雪的是(图中山麓气温为均匀气温)()图ZT2-8①B.②C.③D.④以下列图为“重庆与峨眉山顶七月均匀气温表示图〞。

依据图中信息，达成11~12题。

图ZT2-9计算此时该地域海拔每高升1000米，气温约降低()℃℃℃℃12.下边能表达这一地理现象的语句是()A.山下百花山上雪昨夜寒潮到临，气温骤降C.清明节气雨纷繁D.天有不测风云依据某地各月的均匀气温表，达成以下问题。

月份123456气温(℃)月份789101112气温(℃)绘制该地的月均匀气温变化曲线。

(3)图ZT2-10(4)(5)(2)该地的气温年较差是。

(6)(7)该地位于(南、北)半球，判断的依照是。

(8)该地位于地球上五带中的带。

14.阅读下边地形图，达成以下问题。

图ZT2-11(1)量算图中甲、乙两山顶的实地距离是。

二次函数y ＝ax2＋bx ＋c 的图象与性质一、阅读课本：第14页～第15页上方． 二、学习目标：1．配方法求二次函数一般式y ＝ax 2＋bx ＋c 的顶点坐标、对称轴；2．熟记二次函数y ＝ax 2＋bx ＋c 的顶点坐标公式；3．会画二次函数一般式y ＝ax 2＋bx ＋c 的图象． 三、探索新知：1．求二次函数y ＝12 x 2－6x ＋21的顶点坐标与对称轴．解：将函数等号右边配方：y ＝12 x 2－6x ＋212．画二次函数y ＝12x 2－6x ＋21的图象．解：y ＝12 x 2－6x ＋21配成顶点式为_______________________．列表：x… 3 4 5 6 7 8 9 … y ＝12 x 2－6x ＋21……3．用配方法求抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点与对称轴．y ＝ax 2y ＝ax 2＋k y ＝a(x －h)2y ＝a(x －h)2＋ky ＝ax 2＋bx ＋c开口方向顶点对称轴最值增减性 （对称轴左侧）五、课堂练习1．用配方法求二次函数y ＝－2x 2－4x ＋1的顶点坐标．2．用两种方法求二次函数y ＝3x 2＋2x 的顶点坐标．3．二次函数y ＝2x 2＋bx ＋c 的顶点坐标是（1，－2），则b ＝________，c ＝_________．4．已知二次函数y ＝－2x 2－8x －6，当___________时，y 随x 的增大而增大；当x ＝________时，y 有_________值是___________．六、目标检测1．用顶点坐标公式和配方法求二次函数y ＝12 x 2－2－1的顶点坐标．2．二次函数y ＝－x 2＋mx 中，当x ＝3时，函数值最大，求其最大值．。

6.2 二次函数的图像和性质（2）【自学课】1.复习上节课学习的画二次函数y=ax 2的方法，分为哪几个步骤？2．通过上述方法在同一个平面直角坐标系中画出函数y=21x 2；y= - 21x 2 ；y=2x 2 与y=-2x 2的图像，并观察你所画图像的特征。

【展示课】学习目标：1. 经历探索二次函数y=ax 2性质的过程，进一步体验数形结合的思想方法。

2合作探究 y【反馈课】 当堂检测完成等级： 必做题： 1.填空：（1） 函数y=（k+1） x 2（k+1≠0）的图像的顶点坐标是 ，对称轴是 ，当k 时，图像的开口向上，这时函数有最 值；当k 时，图像的开口向下，这时函数有最 值。

（2）已知抛物线y=ax 2与抛物线y=2x 2关于x 轴对称,则a= 。

（3）抛物线y=3x 2与直线y=kx ＋3的交点为（2，b ），则k= ，b= 。

（4）已知抛物线的顶点在原点，对称轴为y 轴，且经过点（－1，－2），则抛物线的表达式为 。

2．选择：（1）已知点A （-1，y 1）、点B(-2,y 2)、C （2，y 3）在函数y=41x 2的图像上，则 y 1 、y 2、 y 3的大小关系是（ ）A y 1＞y 2＞y 3B y 1＞ y 3＞ y 2C y 3＞y 2＞ y 1D y 2＞y 3＞y 1 （2）在同一坐标系中，图象与y=2x 2的图象关于x 轴对称的是（ ）｜越取何值A ．y=21x 2B ．y=－21x 2C ．y=－2x 2D ．y=－x 2（3）抛物线y=41x 2，y=4x 2，y=－2x 2的图象，开口最大的是（ ）A ．y=41x 2B ．y=4x 2C ．y=－2x 2D ．无法确定（4）对于抛物线y=31x 2和y=－31x 2在同一坐标系里的位置，下列说法错误的是（ ）A ．两条抛物线关于x 轴对称B ．两条抛物线关于原点对称C ．两条抛物线关于y 轴对称D ．两条抛物线的交点为原点（5）二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（ ）3．求符合下列条件的抛物线y=ax 2的表达式：（1）y=ax 2与y=21x 2的开口大小相等，开口方向相反； （2）y=ax 2与直线y=21x ＋3交于点（2，m ）。

二次函数的应用班级 姓名一、基础练习：1. 抛物线23(1)2y x =-+的对称轴是（ ）A ．直线1x =B ．直线1x =-C ．直线2x =D ．直线2x =- 2.要得到二次函数222y x x =-+-的图象，需将2y x =-的图象（ ）．A ．向左平移2个单位，再向下平移2个单位B ．向右平移2个单位，再向上平移2个单位C ．向左平移1个单位，再向上平移1个单位D ．向右平移1个单位，再向下平移1个单位3. 在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++（m 是常数，且0m ≠）的图象可．能．是（ ）4. 从地面垂直向上抛出一小球，小球的高度h （单位：米）与小球运动时间t （单位：秒）的函数关系式是29.8 4.9h t t =-，那么小球运动中的最大高度h =最大5． 如图所示，有一座抛物线形拱桥，桥下面在正常水位AB 时，宽20cm ，水位上升3m 就达到警戒线CD ，这时水面宽度为10cm.（1）在如图所示的坐标系中求抛物线的解析式；（2）若洪水到来时，水位以每小时0.2m 的速度上升，从警戒线开始，再持续多少小时才能到达拱桥桥顶？二、精讲点拨：例1．为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y （万件）与销售单价x （元）之间的函数关系如图所示．（1）求月销售量y （万件）与销售单价x （元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？例2. 正方形ABCD 边长为4，M 、N 分别是BC 、CD 上的两个动点，当M 点在BC 上运动时，保持AM 和MN 垂直，（1）证明：Rt Rt ABM MCN △∽△；（2）设BM x =，梯形ABCN 的面积为y ，求y 与x 之间的函数关系式；当M 点运动到什么位置时，四边形ABCN 面积最大，并求出最大面积；（3）当M 点运动到什么位置时Rt Rt ABM AMN △∽△，求x 的值．例3.已知关于x 的一元二次方程22410x x k ++-=有实数根，k 为正整数. （1）求k 的值；（2）当此方程有两个非零的整数根时，将关于x 的二次函数2241y x x k =++-的图象向下平移8个单位，求平移后的图象的解析式；（3）在（2）的条件下，将平移后的二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线()12y x b b k =+<与此图象有两个公共点时，b 的取值范围.例4. 如图，在矩形OABC 中，已知A 、C 两点的坐标分别为(40)(02)A C ，、，，D 为OA 的中点．设点P 是AOC ∠平分线上的一个动点（不与点O 重合）． （1）试证明：无论点P 运动到何处，PC 总与PD 相等； （2）当点P 运动到与点B 的距离最小时，试确定过O P D 、、三点的抛物线的解析式；（3）设点E 是（2）中所确定抛物线的顶点，当点P 运动到何处时，PDE △的周长最小？求出此时点P 的坐标和PDE △的周长；（4）设点N 是矩形O A B C 的对称中心，是否存在点P ，使90CPN ∠=°？若存在，请直接写出点P 的坐标．三、课堂练习：1.已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表：则下列判断中正确的是（ ）A ．抛物线开口向上B ．抛物线与y 轴交于负半轴C ．当x ＝4时，y ＞0D ．方程02=++c bx ax 的正根在3与4之间 2. 二次函数2(0)y ax bx c a =++≠称轴是直线1x =，则下列四个结论错误．．的是（ A ．0c > B ．20a b += C ．240b ac -> D ．0a b c -+>C3. 抛物线2y x bx c =-++的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论： ， ． （对称轴方程，图象与x 正半轴、y 轴交点坐标例外）4．一次函()()2322++++-=m x m x m y 的图象过点（0，5） ⑴ 求m 的值，并写出二次函数的关系式； ⑵ 求出二次函数图象的顶点坐标、对称轴．5．商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y （件）与销售单价x （元）符合一次函数y kx b =+，且65x =时，55y =；75x =时，45y =．（1）求一次函数y kx b =+的表达式；（2）若该商场获得利润为W 元，试写出利润W 与销售单价x 之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？。

第五章圆复习知识回顾(第五章复习题)一、圆1．圆是的点的集合．2．点与圆的位置关系：设⊙O的半径为r，点到圆心的距离为d，则（1）点A在⊙O上﹤＝﹥；（2）点A在⊙O内﹤＝﹥；（3）点A在⊙O外﹤＝﹥．3．圆的确定：（1）圆心确定圆的位置，半径确定圆的大小；（2）不在同一直线上的三点可以确定一个圆；（3）经过三角形的三个顶点可以确定一个圆，这个圆称为三角形的．外接圆的圆心就是的交点．4 ．圆的基本性质：（1）同圆或等圆的半径相等；（2）圆是轴对称图形，也是中心对称图形；对称轴是，对称中心是（3）在同圆或等圆中，如果、、或，这四组量中只要有一组量相等，那么它们所对应的其余三组量也分别相等；（4）如果圆的直径垂直于弦，那么这条直径，并且．（5）一条弧的度数是n°，它所对的圆周角是，它所对的圆心角是二、直线与圆1．直线与圆的位置关系：设⊙O的半径为r，圆心到直线的距离为d，则（1）直线与⊙O相切﹤＝﹥；（2）直线与⊙O相交﹤＝﹥；（3）直线与⊙O相离﹤＝﹥．2．圆的切线的判定：（1）直线与圆只有一个交点；（2）圆心到直线的距离等于半径；（3）直线过半径的外端，并且垂直于这条半径．3．圆的切线的性质：圆的切线半径；4．切线长定理：从圆外一点引圆的两条切线，它们相等，这点与圆心的连线平分．5.Rt△ABC，∠C=90°，三边为a、b、c它的外接圆半径等于它的内切圆的半径为或三、圆与圆1．圆与圆的位置关系：设两圆的半径为R 和r ，圆心距d ，则（1）两圆外离﹤＝﹥ ，此时公共点有 ； （2）两圆外切﹤＝﹥ ，此时公共点有 ； （3）两圆相交﹤＝﹥ ，此时公共点有 ； （4）两圆内切﹤＝﹥ ，此时公共点有 ； （5）两圆内含﹤＝﹥ ，此时公共点有 ． 2．两圆连心线的性质：（1）相交两圆的连心线 公共弦；（2）相切的两圆的连心线经过 ，并且垂直于过切点的切线． 四、有关圆的计算弧长的计算公式为： 扇形的面积公式为： 圆锥的侧面积公式为： 圆锥的全面积公式为： 圆锥的侧面展开图是 这个扇形的半径等于 弧长等于圆锥的 巩固练习 一、精心选一选1、如右图，AB 是⊙O 的直径，AC 是弦，∠BAC=30°，则AC 的度数是（ ） A. 30° B. 60° C. 90° D. 120°2、下列命题是真命题的是（ ）. A 、垂直于圆的半径的直线是圆的切线 B 、经过半径外端的直线是圆的切线C 、直线上一点到圆心的距离等于圆的半径的直线是圆的切线D 、到圆心的距离等于圆的半径的直线是圆的切线3、⊙O 的半径为R ，圆心到点A 的距离为d ，且R 、d 分别是方程x 2－6x ＋8＝0的两根，则点A 与⊙O 的位置关系是（ ）A ．点A 在⊙O 内部B ．点A 在⊙O 上C ．点A 在⊙O 外部D ．点A 不在⊙O 上 4、如右图，△ABC 的内切圆⊙O 与各边相切于D 、E 、F ，且∠FOD=∠EOD=120°，•则△ABC 是（ ） A ．等腰三角形 B ．等边三角形 C ．直角三角形 D ．等腰直角三角形5、⊙O 的直径为4，圆心O 到直线l 的距离为3，则直线l 与⊙O 的位置关系是（ ） A. 相离 B. 相切 C. 相交 D. 相切或相交6、⊙O 的半径为2，点P 在⊙O 外一点，OP 的长为3，那么以P 为圆心，且与⊙O•相切的圆的半径一定是（ ）A ．1或5B ．1C ．5D ．1或4⌒OACEAOF7、已知：Rt △ABC 的斜边AB=13cm ，一条直角边AC=5cm ，•以直线BC 为轴旋转一周得一个圆锥，则这个圆锥的表面积为（ ）A ．65πcm 2B ．90πcm 2C ．156πcm 2D ．300πcm28、一个底面半径为5c m ，母线长为16cm 的圆锥，它的侧面展开图的面积是 ( ) A ．80πcm 2B ． 40πcm 2C ． 80 cm 2D ． 40 cm 29、已知AB 、CD 是⊙O 两条直径，则四边形ACBD 为（ ）A 平行四边形；B 菱形；C 矩形；D 正方形。

一．选择题（共10小题，每小题3分，满分30分） 1.3--的相反数是（ ）A.3B.3-C.31-D.312.不等式组⎩⎨⎧<->-02032x x 的解集是（ ）A.223≤<x B.232<≤x C.223<<x D.223≤≤x 3.下列是最简二次根式的是（ ）A.3B.27C.122++a a D.324.下列计算正确的是（ ）A.532a a a =+B.222)2)((b ab a b a b a ++=-+ C.1)1)(1(2-=+-a a a D.22)1(1+=++m m m5.四边形ABCD 为平行四边形，若四边形的面积是BD AC ⋅21则下列说法正确的是（ ）A.四边形ABCD 是矩形B.四边形ABCD 是正方形C.四边形ABCD 是等腰梯形D.四边形ABCD 是菱形6.02)1(122=-+-+-c b a ，则c b a -+23的值是（ ）A.23B.0C.4D.3- 7.在ABC RT ∆中，斜边的高4=h ，三角形的面积24=S ,则ABC RT ∆的两直角边可能是（ ）A.73，9B.73，207C.5，304D.6，35 8.关于一元二次方程0)1(2=+++a x a x 说法正确的是（ ） A.一定有两个相等的实数根 B.一定有实数根C.一定有两个不相等的实数根D.一定没有实数根9.等腰梯形ABCD 的高为cm 3，底角是顶角的21，若较长的底BC 长为8，则梯形的中位线长是（ ）A.328-B.38-C.38+ 3216-10.（2012广州）如图3，正比例函数x k y 11=和反比例函数xk y 22=的图象交于)2,1(-A 、），（21-B 两点，若21y y <， 则x 的取值范围是 （ ）A ．1-<x 或1>xB ．1-<x 或10<<xC ．01<<-x 或10<<xD ．01<<-x 或1>x二．填空题（每小题3分，满分18分） 11.等边三角形的边长为cm 3，则等边三角形的高 =h .12.分式方程221=+-x x 的解是 .13.人民网广州2012年5月31日电.据悉，今年“新广州·新商机”首场推介会——天津推介会6月7日在天津拉开帷幕.广东省委常委、广州市委书记万庆良，广州市市长陈建华等都将亲赴天津参加推介活动.广州-天津两市将在推介会上签署战略合作框架协议，“请进来”37个项目，总投资额约33830000000元.将33830000000保留两位有效数字是 . 14.分解因式：=--16062x x . 15.反比例函数xy 1=与一次函数1+-=x y 的交点的个数是 个. 16.正方形ABCD 的对角线25=AC ，P 是对角线AC 上的一点，F E ,分别是边BC AB ,的中点，则当EFP ∆是直角三角形时，=PE .参考答案060一．选择题（共10小题，每小题3分，满分30分）1--5 ACACD 6--10 BABBD 部分题目解析：5.BD AC ,均为平行四边形的对角线.平行四边形的面积是BD AC ⋅21，所以ABD ∆的面积h BD AC BD S ⋅=⋅=21)21(21，易知BD AC ⊥，所以平行四边形ABCD 为菱形.选D 6.由已知02112=-=-=-c b a ，所以2,1,21===c b a ，代入可得B 项为正确选项.7.提示：设斜边为c ，两直角边分别为b a ,；则2421==ah S ，求出斜边的值，b a ,只要满足222c b a =+即可.答案：A 9.如右图所示，易得出3==CF BE ，所以上底328-=AD ，中位线38)]328(8[21-=-+ 答案：B二．填空题（共6小题，每小题3分，满分18分）11.cm 233 12.5-=x 13. 10104.3⨯ 14. )16)(10(-+x x 15. 0 16. 425或25或4105.部分题目解析：15.画出一次函数和反比例函数的图像，由图像可知无交点，即交点是0个.16.提示：EFP ∆是直角三角形有以下三种情况：090=∠EFP ，090=∠FEP ，090=∠EPF 结合已知条件当090=∠FEP 时，425=PE ； 当090=∠EFP 时，4105=PE ； 当090=∠EPF 时，25=PE3B E F CA D初中数学试卷鼎尚图文**整理制作。

一．选择题（共10小题，每小题3分，满分30分） 1.x -2有意义，则下列说法是正确的是（ ）A.2<xB.2>xC.2≤xD.2≥x2.某市第一中学抽取了6名同学参加体能测试，成绩如下：87，83，87，87，80，82.则中位数是（ ）A.87B.83C.85.D.82.53.二次函数322++=x ax y 与x 轴有2个交点，则a 的取值范围是（ ） A.41≤a B.41≥a C.41>a D.0≠a 且41≤a 4.下列各式中计算正确的是( ) A.222)(y x y x +=+ B.226)3(x x =C.623)(x x = D.422a a a =+ 5. 如图，△ABC 中，AB =AC =15，D 在BC 边上，DE ∥BA 于点E ，DF ∥CA 交AB 于点F ，那么四边形AFDE 的周长是( )A.30B.25C.20D.156.如图是一个由若干个棱长为1的正方体组成的几何体的主视图和左视图，则俯视图不可能是( )7.反比例函数xy 2=向左平移两个单位，然后再向下平移三个单位只有解析式变为（ ） A.22-+x x B.222+-x x C.222++-x x D.262++x x 8.圆锥的底面半径为3，母线长为5，则圆锥的体积是（ ）A.π9B.π12C.π24D.π36 9.直线2+=ax y 分别与y x ,轴交于两点A 、B ，且O A B ∆的面积是2，则2013211a a +-的值是（ ）A.1B.2C.2D. 3 10.已知一列数：1，32，73，134，215， .按照此规律，这列数的第十个数是（ ） A.91 B.9110 D.465 D.7310 二．填空题（共6小题，每小题3分，满分18分） 主视图 左视图11. 因整体上市和王老吉凉茶两大重磅题材，2012年广药集团及下属上市公司广州药业和白云山A 可谓赚尽眼球.近日，广药集团宣布得益于大南药大健康双轮驱动战略，全集团2012年实现工商销售收入42815000000元，同比增长29.58%，无论是营收还是增幅均创历史新高.其中42815000000用科学记数法表示为 .（保留2位有效数字） 12. 如图，将△OAB 绕点O 按逆时针方向旋转至△OA ′B ′，这时点B 在边A ′B ′上，已知AB =5cm ，BB ′= 2cm ，则A ′B 的长是 .13.分解因式：)]104(2[)2(--+-x x x .14.已知关于x 的一元二次方程02=--c bx x 有两个相等的实数根，则3)24(2)(422-+--++c b c b b 的值是 . 15.P 是直线3=y 上的一个动点，二次函数a x a x y 3)13(2++-=（a 是整数）与x 轴的交点是)0,(1x A ，)0,(2x B ，则PAB ∆的面积的最小值是 .16. 如图，已知正方形纸片ABCD 的边长为8，⊙O 的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA ′恰好与⊙O 相切于点A ′（△EFA ′与⊙0除切点外无重叠部分），延长FA ′交CD 边于点G ，则A ′G 的长是 .初中数学试卷灿若寒星 制作'B ' A '第16题图。

操作性问题是指通过动手测量、作图、取值、计算等试验，猜想获得数学结论的研究性问题。

最常见的两种类型:（1）折叠型问题（2）平移和旋转型问题解题关键：（1）抓住折叠过程中的全等（隐含条件）和勾股定理的运用（2）抓住平移旋转过程中的全等以及图形的变化分解成点的变化。

1、如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）.按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（ ）A ．都是等腰梯形B ．都是等边三角形C ．两个直角三角形，一个等腰三角形D ．两个直角三角形，一个等腰梯形2、用一把带有刻度尺的直角尺, ①可以画出两条平行的直线a 和b, 如图(1); ②可以画出∠AOB 的平分线OP, 如图(2); ③可以检验工件的凹面是否为半圆, 如图(3); ④可以量出一个圆的半径, 如图(4). 这四种说法正确的有（ ）A. 4个B. 3个C. 2个D. 1个3、如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长（ ）Ａ．2cm Ｂ．3cm Ｃ． 23cm Ｄ．25cm4、如图1所示，将长为20cm ，宽为2cm 的长方形白纸条，折成图2所示的图形并在其一面着色，则着色部分的面积为（ ）A ．234cmB ．236cmC ．238cmD ．240cm5、在同一平面内，用两个边长为a 的等边三角形纸片(纸片不能裁剪)可以拼成的四边形是（4）（3）沿虚线剪开对角顶点重合折叠（2）（1）上折6、如图，是用形状、大小完全相同的等腰提梯形密铺成的图案，则这个图案中的等腰梯形的底角（指锐角）是度.7、用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC＝度.8、如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA 至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1、B1C1、C1A1至点A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2、B2、C2，得到△A2B2C2，记其面积为S2；…；按此规律继续下去，可得到△A5B5C5，则其面积S5=_____________ .9、小华将一条直角边长为1的一个等腰直角三角形纸片（如图1），沿它的对称轴折叠1次后得到一个等腰直角三角形（如图2），再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形（如图3），则图3中的等腰直角三角形的一条腰长为_____________；同上操作，若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形（如图n+1）的一条腰长为_________．10、操作与探究：（1）图①是一块直角三角形纸片。

2024年江苏省连云港市灌云县中考数学二模试题一、单选题1．15−的相反数是（ ） A ．15 B ．15− C ．5− D ．52．中国古代数学著作《九章算术》中，将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放，则它的左视图为（ ）A ．B ．C ．D ．3．若a b <<，其中a 、b 为两个连续的整数，则ab 的值为（ ）．A ．2B ．5C ．6D ．124．下列计算正确的是（ ）A ．325m m m +=B ．623m m m ÷=C ．329()m m =D ．325m m m ⋅= 5．如图，正方形的边长为6,,C A 分别位于x 轴，y 轴上，点P 在AB 上，CP 交OB 于点Q ，函数k y x =的图像经过点Q ，若14BPQ OQC S S =，则k 的值为（ ）A ．12−B ．12C ．16D ．18 6．如图，点O 是ABC 外接圆的圆心，点I 是ABC 的内心，连接OB ，IA ．若35CAI ∠=︒，则OBC ∠的度数为（ ）A ．15︒B ．17.5︒C ．20︒D ．25︒7．如图，ABC 为等边三角形，点D ，E 分别在边BC ，AB 上，60ADE ∠=︒，若4BD DC =，2.4DE =，则AD 的长为（ ）A ．1.8B ．2.4C ．3D ．3.28．如图，在Rt ABC △中，90ACB ∠=︒，4,60AB A =∠=︒，将Rt ABC △绕点C 顺时针旋转90︒后得到Rt DEC △，点B 经过的路径为弧BE ，将线段AB 绕点A 顺时针旋转60︒后，点B 恰好落在CE 上的点F 处，点B 经过的路径为弧BF ，则图中阴影部分的面积是（ ）A ．14π+B ．23πC ．512πD ．13π+二、填空题9．在函数12y x =+中，自变量x 的取值范围是 . 10．因式分解：2a 2﹣8= ．11．如图，在ABC 中，点D 在边AB 上，过点D 作DE BC ∥，交AC 点E ．若2,3AD BD ==，则AE AC的值是 ．12．为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为x ，根据题意，请列出方程 ．13．若一个圆锥的底面圆的半径是5，侧面展开图的圆心角的度数是150︒，则该圆锥的母线长为 ．14．若关于x 的方程220x kx ++=没有实数根，则k 的值可以是 （只填一个即可）15．如图，在ABC 中，按以下步骤作图：①分别以点B 和C 圆心，以大于12BC 的长为半径作弧，两弧相交于点M 和N ；②作直线MN 交边AB 于点E ．若54，==AC BE ，45B ∠=︒，则AB 的长为 ．16．如图，在O 的内接五边形ABCDE 中，=31EBD ∠︒，则A C ∠+∠= °．17．如图，AB ＝3，BD ⊥AB ，AC ⊥AB ，且AC ＝1．点E 是线段AB 上一动点，过点E 作CE 的垂线，交射线BD 于点F ，则BF 的长的最大值是 ．18．正方形ABCD 的边长是6，点E 是DC 边延长线上一点，连接,EB EA ，过点A 作AF AC ⊥，交EB的延长线于点,F AE =，则AF 的长为 ．三、解答题19．（112cos30|32|2−++．（2）解不等式组：()312532x x x ⎧−<⎪⎨+>⎪⎩，并写出所有整数解． 20．先化简，再求值：2222(1)32111x x x x x x x x ++−÷−−+−−，其中1x =+． 21．为了了解某地居民的用电量情况，随机抽取了该地200户居民六月份的用电量（单位：kW h ⋅）进行调查，整理样本数据得到下面的频数分布表：根据抽样调查的结果，回答下列问题：（1）该地这200户居民六月份的用电量的中位数落在第组内．（2）估计该地1万户居民六月份的用电量低于178kW h⋅的大约有多少户．22．扬州是个好地方，有着丰富的旅游资源．某天小华、小丽两人来扬州旅游，两人分别从A、B、C三个景点中随机选择一个景点游览．(1)甲选择C景点的概率为；(2)请用画树状图或列表的方法，求小华、小丽两人中至少有一人选择B景点的概率．23．如图，点E是矩形ABCD对角线AC上的点（不与A，C重合），连接BE，过点E作EF BE⊥交CD于点F．连接BF交AC于点,G BE AD=．(1)求证：FEC FCE∠=∠；(2)试判断线段BF与AC的位置关系，并说明理由．24．中华优秀传统文化源远流长、是中华文明的智慧结晶．《孙子算经》、《周髀算经》是我国古代较为普及的算书、许多问题浅显有趣．某书店的《孙子算经》单价是《周髀算经》单价的34，用600元购买《孙子算经》比购买《周髀算经》多买5本．(1)求两种图书的单价分别为多少元？(2)为等备“3．14数学节”活动，某校计划到该书店购买这两种图书共80本，且购买的《周髀算经》数量不少于《孙子算经》数量的一半．由于购买量大，书店打折优惠，两种图书均按八折出售．求两种图书分别购买多少本时费用最少？25．如图，在电视背景墙上，银幕投影区域的下沿B 距离地面的高度BC 为72cm ，投影区域的上沿A 距离地面228厘米．小明为了获得最大的投影效果，将投影仪镜调整到影像达到银幕投影区域的上下沿．经测量，此时投影仪镜头D 到上沿A 的仰角为17.7︒，到下沿B的俯角为11.3︒，求此时镜头D 到地面的距离．（参考数据：tan11.30.2,tan17.70.32︒≈︒≈）26．如图，在Rt ABC △中，90,C AC BC ∠=︒=，点O 在AB 上，以O 为圆心，OA 为半径的半圆分别交,AC BC ，AB 于点,,D E F ，且点E 是弧DF 的中点．(1)求证：BC 是O 的切线；(2)若CE =π）．27．(1)【问题呈现】如图1，△ABC 和△ADE 都是等边三角形，连接BD ，CE ．求证：BD ＝CE ．(2)【类比探究】如图2，△ABC 和△ADE 都是等腰直角三角形，∠ABC ＝∠ADE ＝90°．连接BD ，CE ．请直接写出BD CE的值．(3)【拓展提升】如图3，△ABC 和△ADE 都是直角三角形，∠ABC ＝∠ADE ＝90°，且AB BC ＝AD DE ＝34．连接BD ，CE ． ①求BD CE的值； ②延长CE 交BD 于点F ，交AB 于点G ．求sin ∠BFC 的值．28．如图，在平面直角坐标系中，O 为坐标原点，抛物线2y x bx c =−++与x 轴交于点A ，B 两点，它的对称轴直线1x =交抛物线于点M ，过点M 作MC y ⊥轴于点C ，连接BC ，已知点A 的坐标为()1,0−．(1)求此抛物线的函数表达式；(2)动点P ，Q 在此抛物线上，其横坐标分别为,1m m +，其中11m −<<．①若POA QBO ∠=∠，请求此时点Q 的坐标；②在线段BC 上是否存在一点D ，使得以C ，P ，D ，Q 为顶点的四边形为平行四边形？若存在，请直接写出此时m 的值；若不存在，说明理由．。