高中--含绝对值的函数

高中数学绝对值函数的应用实例及解题方法绝对值函数是高中数学中常见的一种函数形式，它在数学建模和实际问题中具有广泛的应用。

本文将通过具体的实例，来介绍绝对值函数的应用和解题方法，帮助高中学生更好地理解和掌握这一知识点。

一、求解绝对值不等式绝对值不等式是绝对值函数应用的重要形式之一。

我们以一个简单的例子开始，假设有如下的不等式：|2x - 1| < 3要求解这个不等式，我们可以将其拆分为两个不等式，即：2x - 1 < 3 和 2x - 1 > -3解得：x < 2 和 x > -1所以，原始的不等式的解集为 -1 < x < 2。

这个例子展示了如何通过拆分不等式来求解绝对值不等式，这也是解决绝对值不等式常用的方法之一。

二、求解含有绝对值的方程除了不等式，绝对值函数还常常出现在方程的解中。

我们以一个实际问题为例，来说明如何求解含有绝对值的方程。

例题：某地的温度每天都在变化，已知温度的变化规律可以用函数T(t) = |t - 5| - 3来表示，其中t表示时间（单位：小时），T(t)表示温度（单位：摄氏度）。

现在要求解在什么时间温度为0度。

解答：根据题意，我们需要求解方程|t - 5| - 3 = 0。

将绝对值函数的定义展开，得到两个方程：t - 5 - 3 = 0 或者 -(t - 5) - 3 = 0解得：t = 8 或者 t = 2所以，温度为0度的时间有两个解，分别是t = 8和t = 2。

这个例子展示了如何通过将绝对值函数的定义展开，来求解含有绝对值的方程。

这是解决这类问题常用的方法之一。

三、绝对值函数在距离和模型中的应用绝对值函数在距离和模型中的应用也是高中数学中的重要内容。

我们以一个典型的例子来说明。

例题：甲、乙两地相距200公里，甲地有一辆车以每小时50公里的速度往乙地行驶，乙地有一辆车以每小时40公里的速度往甲地行驶。

问多少小时后，两车相遇？解答：设两车相遇的时间为t小时，则甲地车行驶的距离为50t公里，乙地车行驶的距离为40t公里。

1、ABS函数函数名称：ABS主要功能：求出相应数字的绝对值。

使用格式：ABS(number)参数说明：number代表需要求绝对值的数值或引用的单元格。

应用举例：如果在B2单元格中输入公式：=ABS(A2)，则在A2单元格中无论输入正数（如100）还是负数（如-100），B2中均显示出正数（如100）。

特别提醒：如果number参数不是数值，而是一些字符（如A等），则B2中返回错误值“#VALUE！”。

2、AND函数函数名称：AND主要功能：返回逻辑值：如果所有参数值均为逻辑“真（TRUE）”，则返回逻辑“真（TRUE）”，反之返回逻辑“假（FALSE）”。

使用格式：AND(logical1,logical2, ...)参数说明：Logical1,Logical2,Logical3……：表示待测试的条件值或表达式，最多这30个。

应用举例：在C5单元格输入公式：=AND(A5>=60,B5>=60)，确认。

如果C5中返回TRUE，说明A5和B5中的数值均大于等于60，如果返回FALSE，说明A5和B5中的数值至少有一个小于60。

特别提醒：如果指定的逻辑条件参数中包含非逻辑值时，则函数返回错误值“#VALUE!”或“#NAME”。

3、AVERAGE函数函数名称：AVERAGE主要功能：求出所有参数的算术平均值。

使用格式：AVERAGE(number1,number2,……)参数说明：number1,number2,……：需要求平均值的数值或引用单元格（区域），参数不超过30个。

应用举例：在B8单元格中输入公式：=AVERAGE(B7:D7,F7:H7,7,8)，确认后，即可求出B7至D7区域、F7至H7区域中的数值和7、8的平均值。

特别提醒：如果引用区域中包含“0”值单元格，则计算在内；如果引用区域中包含空白或字符单元格，则不计算在内。

含绝对值的函数知识定位灵活的掌握含有绝对值的函数，主要包括图像画法、函数解析式、与分段函数之间的联系。

本节我们通过一些实例的求解，旨在介绍数学竞赛中与二次函数相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用知识梳理1、用“三点定形法”画单绝对值函数)0()(≠+-=a k h x a x f 的图象：)0()(≠+-=a k h x a x f 与)0()()(2≠+-=a k h x a x g 的图象类似，它们的顶点都是（k h ,），开口方向相同，对称轴相同，单调区间相同。

所不同的是前者的图象是折线，在对称轴两侧是两条射线，而后者的图象是抛物线，在对称轴两侧是两条曲线。

所以可用三点定其型。

三点中，顶点（k h ,）必取，然后在其两侧任意各取一点，分别以顶点为端点，过另一点作出射线，即得)0()(≠+-=a k h x a x f 的图象。

2.用“两点定形法”作双绝对值差式函数b x a x x f ---=)(的图象（1）当a<b 时，⎪⎩⎪⎨⎧>-≤≤-+<-=---=)()(2)()(b x a b b x a ba x a x ba b x a x x f ，可见其图象是由两端为两条平行的射线，中间为连接两射线的端点构成的图形，而图象总是在两个绝对值代数式的零点处转折。

（2）当a>b 时同理。

据此，可以点))(,()),(,(b f b a f a 确定函数b x a x x f ---=)(的图象3.用“多点定形法”作多绝对值函数)()(212211i i i a a a a x m a x m a x m x f <<<-++-+-= 的图象因为⎪⎪⎩⎪⎪⎨⎧≥+++-++++<≤+++-+---+<++++----=)()()()()()()()()()(221121212211211221121i i i i i i i i i i a x a m a m a m x m m m a x a a m a m a m x m m m a x a m a m a m x m m m x f可知其图象是由i 个顶点i A A A 21、、、 决定的折线图，各顶点横坐标由各绝对值代数式的零点决定，中间由1-i 条顺次连接相邻两点的线段组成，两端为两条射线。

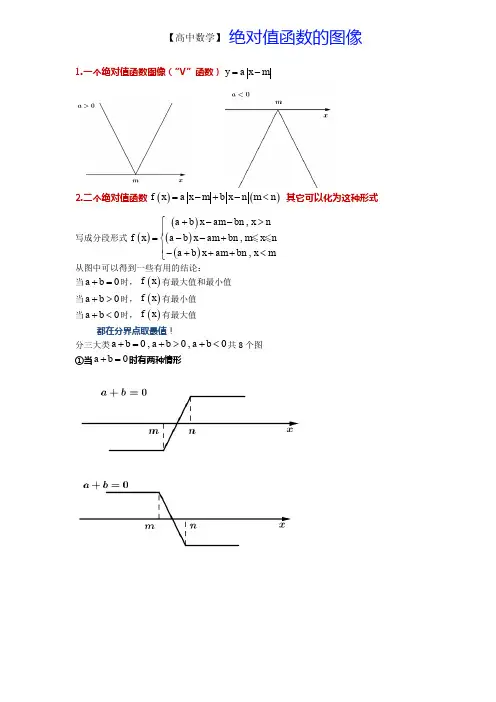
1.一个绝对值函数图像（“V ”函数）y m a x =-
2.二个绝对值函数()()f x a x m b x n m n =-+-< 其它可以化为这种形式 写成分段形式()()()(),,,a b x am bn x n f x a b x am bn m a b x am bn x x n m +-->⎧⎪=--+⎨⎪-+++<⎩
从图中可以得到一些有用的结论：
当0a b +=时，()f x 有最大值和最小值
当0a b +>时，()f x 有最小值
当0a b +<时，()f x 有最大值
都在分界点取最值！
分三大类0,0,0a b a b a b +=+>+<共8个图
①当0a b +=时有两种情形
【高中数学】绝对值函数的图像
a b+>时有三种情形
②当0
a b+<时有三种情形
③当0
注：对于三个以上的绝对值函数图像，用同样的方法可以得到。

（高考很难见到！）三个以上绝对值配合图像求最值：奇尖偶平，取中间。

含绝对值的二次函数含绝对值的二次函数其本质是分段函数，研究含绝对值的二次函数就是分段研究二次函数的局部性态．设定分类讨论的标准是问题解决的前提条件，数形结合则是问题能否正确解决的关键 所在．例1．解下列各题：（1）（2010全国）直线1=y 与曲线a x x y +-=2有4个交点，则实数a 的取值范围是 ．（2）（2008浙江）已知t 为常数，函数t x x y --=22在区间]3,0[上的最大值为2，则=t ．（3）设集合{}{}2,,022<=∈<++-=x x B R a a a x x x A ，若Φ≠A 且B A ⊆，则实数a 的取值范围是 ．例2．设函数R x a x x x f ∈+-+=,1)(2（1）判断函数)(x f 的奇偶性；（2）求函数)(x f 的最小值．例3．已知函数1)(,1)(2-=-=x a x g x x f ．（1）若关于x 的方程)()(x g x f =只有一个实数解，求实数a 的取值范围；（2）若R x ∈时，)()(x g x f ≥恒成立，求实数a 的取值范围；（3）求函数)()()(x g x f x h +=在区间]2,2[-上的最大值．例4．设a 为实数，函数2()2()f x x x a x a =+--．（1）若(0)1f ≥，求实数a 的取值范围；（2）求()f x 的最小值．5.含绝对值的二次函数班级 姓名一、综合练习1．设b a <<0，且xx x f ++=11)(，则下列大小关系式成立的是（ ） （A ）)()2()(ab f b a f a f <+< （B ）)()()2(ab f b f b a f <<+ （C ）)()2()(a f b a f ab f <+< （D ）)()2()(ab f b a f b f <+< 2．已知{}n a 为等差数列，n S 是{}n a 的前n 项和,若9843=++a a a ，则9S = ．3．直线750x y +-=截圆221x y +=所得的两段弧长之差的绝对值是 ．4．函数y k x a b =--+与y k x c d =-+的图象1(k 0k )3>≠且交于两点)3,8(),5,2(，则c a +的值是_______________. 5．任意满足305030x y x y x -+≤⎧⎪+-≥⎨⎪-≤⎩的实数,x y ，若不等式222()()a x y x y +<+恒成立，则实数a 的取值范围是 .6．已知双曲线22221(0,0)x y a b a b-=>>，N M ,是双曲线上关于原点对称的两点，P 是双曲线上的动点，且直线PN PM ,的斜率分别为12,k k ，021≠k k ，若21k k +的最小值为1,则双曲线的离心率为 ．二、本讲练习1．设函数c bx x x x f ++=)(给出下列四个命题：① 0=c 时，)(x f y =是奇函数； ② 0,0>=c b 时，方程0)(=x f 只有一个实根； ③ )(x f y =的图象关于),0(c 对称； ④ 方程0)(=x f 至多有两个实根．其中正确的命题是 （ ）（A ）①④ （B ）①③ （C ）①②③ （D ）①②④2．若不等式21x x a <-+的解集是区间()33-，的子集，则实数a 的范围为 . 3．设a 为实数，函数a x x x f -=)(，求函数)(x f 在]2,2[-上的最大值．4．己知2)(,0bx ax x f a -=>函数，（1）();2,10b a x f R x b ≤≤∈>证明：都有时，若对任意当（2）当 1>b 时，证明：对任意]1,0[∈x ，1|)(|≤x f 的充要条件是：b a b 21≤≤-．5．已知函数)1(52)(2>+-=a ax x x f ．（1）若函数)(x f 的定义域和值域均为],1[a ，求实数a 的值；（2）若)(x f 在区间]2,(-∞上是减函数，且对]1,1[,21+∈∀a x x ，总有4)()(21≤-x f x f ，求实数a 的取值范围．6．已知函数2()(1)||f x x x x a =+--．（1）若1a =-，解方程()1f x =；（2）若函数()f x 在R 上单调递增，求实数a 的取值范围；（3）若1a <且不等式()23f x x ≥-对一切实数x R ∈恒成立，求a 的取值范围．6．已知函数2()(1)||f x x x x a =+--．（1）若1a =-，解方程()1f x =；（2）若函数()f x 在R 上单调递增，求实数a 的取值范围；（3）若1a <且不等式()23f x x ≥-对一切实数x R ∈恒成立，求a 的取值范围．解：（1）当1-=a 时，有⎩⎨⎧-<-≥-=1,11,12)(2x x x x f ………2分 当1-≥x 时，1122=-x ，解得：1=x 或1-=x当1-<x 时，1)(=x f 恒成立 ………4分∴方程的解集为：1|{-≤x x 或}1=x ………5分（2）⎩⎨⎧<-+≥++-=a x a x a a x a x a x x f ,)1(,)1(2)(2 ………7分 若)(x f 在R 上单调递增，则有⎪⎩⎪⎨⎧>+≤+0141a a a ，解得：31≥a ………10分 （3）设)32()()(--=x x f x g ，则⎩⎨⎧<+--≥+++-=a x a x a a x a x a x x g 3)1(,3)3(2)(2 即不等式0)(≥x g 对一切实数R x ∈恒成立 ………11分∵1<a∴当a x <时，)(x g 单调递减，其值域为：),32(2∞++-a a∵22)1(3222≥+-=+-a a a ，∴0)(≥x g 恒成立 ………13分当a x ≥时，∵1<a ，∴43+<a a ， ∴08)3(3)43()(2min ≥+-+=+=a a a g x g ，得53≤≤-a∵1<a ，∴13<≤-a ………15分 综上：13<≤-a ………16分。

人教A版高中数学必修1知识点总结Chapter 1: Concepts of Sets and nsLesson 1: XXX1.Meaning of Sets: A set is the n of XXX are aware of。

and XXX.2.The general object of study is collectively called elements。

and a n of some elements is called a set。

abbreviated as set。

3.Three characteristics of XXX:1) Determinacy of elements: If a set is determined。

then it is certain whether an element belongs to this set or not: belongs or does not belong。

Example: the highest mountain in the world。

the four ancient beauties of China。

all the people in the classroom。

2) Uniqueness of elements: The elements in a given set are unique and cannot be repeated。

Example: the set composed of the letters of the word "HAPPY" {H。

A。

P。

Y}.3) Unorderedness of elements: The n of elements in a set can be changed。

and changing the n does not affect the set。

高一含绝对值的对数函数问题高一数学中，绝对值的对数函数是一个常见的题型。

这类题目通常涉及到对数函数的性质和图像，以及绝对值函数的性质和图像。

我将从不同角度来解答这类问题。

首先，我们来看绝对值的对数函数的定义。

绝对值的对数函数通常表示为f(x) = log |x|，其中log表示以10为底的对数。

这个函数的定义域是所有实数，而值域是负无穷到正无穷。

当x大于0时，f(x) = log x；当x小于0时，f(x) = log(-x)。

这意味着函数图像会在x轴的正半轴和负半轴分别有一条对称的分支。

其次，我们可以讨论绝对值的对数函数的性质。

由于对数函数的性质，绝对值的对数函数在x大于0时是单调递增的，在x小于0时是单调递减的。

另外，绝对值的对数函数的图像会经过点（1, 0），并且在x=1处有一个垂直渐近线。

接着，我们可以探讨绝对值的对数函数的图像特点。

由于绝对值的对数函数的特殊性质，它的图像会呈现出两条分支，分别位于x轴的正负半轴。

这两条分支会在（1, 0）这一点相交，并且在这一点有一个水平切线。

最后，我们可以考虑一些与绝对值的对数函数相关的典型问题。

比如，求函数的定义域、值域；求函数在某个区间上的增减性；求函数与坐标轴的交点等等。

这些问题需要运用对数函数和绝对值函数的性质，以及图像特点来进行分析和解答。

综上所述，高一含绝对值的对数函数问题涉及到对数函数和绝对值函数的性质、图像特点以及相关的典型问题。

在解答这类问题时，我们需要全面理解和掌握这两类函数的知识，从而能够准确地分析和解决问题。

第五节 含绝对值符号的函数26.7 含绝对值符号的函数1.形如)(x f y =的函数试一试 如何作出函数21+=x y 的图像？ 根据绝对值的定义，函数21+=x y 可以表示为⎪⎪⎩⎪⎪⎨⎧<+-≥+=021021x x x x y ，， （1）作当x ≥0时，21+=x y 的图像，即图26.7.1中的射线AC ； （2）作当x >0时，21+-=x y 的图像，即图26.7.1的射线AB ； （3）图26.7.1中的折线BAC 即为函数21+=x y 的图像。

由上面我们可以看出，对于函数)(x f y =，当自变量x 取值互为相反数时，所得到的函数值相等，即)()(x f x f -=，因此函数)(x f =图像就是函数)(x f y =（x ≥0）的图像与)0)((<-=x x f y 的图像的全部，并且函数)(x f 的图像关于y 轴对称。

例1 作函数3412--=x x y 的图像解 因为222x x x ==，所以3412--=x x y 是)(x f y =类型的函数 （1）作出当x ≥0时，3412--=x x y 的图像，这是一个开口向上的抛物线在y 轴右边的部分。

由03412=--x x 可以得知，抛物线与x 轴的交点为（2-，0）和（6，0），与y 轴的交点为（0，－3）.抛物线的顶点坐标为（2，－4），如图26.7.2所示，曲线ABC 就是当x ≥0时，3412--=x x y 的图像； （2）以y 轴为对称轴，作曲线ABC 的对称图形''C AB ；（3）图中的曲线ABC B C ''即为3412--=x x y 的图像由此，我们可以发现： 画函数)(x f y =的图像的一般步骤：①先作出)0)((>=x x f y 的图像；②将)0)((>=x x f y 的图像沿y 轴翻折到y 轴左侧，就得到了函数)(x f y =的图像例2 已知方程1+=ax x ，有一个负根且无一正根，求a 的取值范围分析 可以把等号两边的式子看作是函数，从函数图像入手比较直观地解决问题 解 原方程即ax x =-1，如图26.7.3，在同一坐标系作函数1-=x y 与ax y =的图像 1-=x y 是尖点（0，－1）的“V ”字形折线，而ax y =是过原点斜率为a 的直线，如图虚线OA 是ax y =的一个极根位置，y 轴是它的另一根限位置，易见当1≥a （即直线OA 的向上的方向与x 轴正方向的夹角不小于︒45）时，OA 与1-=x y 的图像交点位于第三 象限，即方程ax x =-1有一个负根且没有正根。

含绝对值函数图像处理之我见高中数学的函数作图中，常出现函数的自变量或因变量带有绝对值符号的函数，对于此类函数图像的作法不仅要从函数的角度来考虑，还得结合绝对值的意义来共同探讨，本文针对含绝对值函数的性质进行分析，然后利用对称性作出函数图象，并借助图象来展示绝对值对函数性质特征的影响。

一、含绝对值函数的六种类型：已知函数y=f（x），x∈R，x叫做函数的自变量；y叫做函数的应变量（函数值）。

①对自变量x取绝对值：y=f（x），x∈R；②对应变量y取绝对值：y=f（x），x∈R；③对x，y全都取绝对值：y=f（x），x∈R；④对整个函数取绝对值：y=f（x），x∈R；⑤对x，f（x）都取绝对值：y=f（x），x∈R；⑥部分自变量取绝对值：y=f（x，x），x∈R。

二、分析不同情况含绝对值函数的性质特点及图象作法：①对自变量x取绝对值y=f（x），x∈R；：【函数性质分析：】已知函数y=f（x），x∈R；，设（x，y）是函数图象上任意一点，则该点与点（-x，y）关于y轴对称。

因为点（x，y）与（-x，y）都在函数y=f（x）上，所以其函数图象关于y轴对称。

【作图步骤：】（1）作出函数y=f（x）的图象；（2）保留x>0时函数y=f（x）的图象；（3）当x0时函数y=f（x）的图象；（3）当y0，Y>0 （第一象限）时函数y=f（x）的图象；（3）利用对称性作出（2）中图象关于x轴、y轴及原点对称后的图象。

【作图展示：】作函数y=f（x）=2x -2的图像④对整个函数取绝对值：：y=f（x），x∈R；【函数性质分析：】已知函数：y=f（x），x∈R，当f（x）>0时y=f（x）=f（x）；当f（x）0时不变，在f（x）0的函数图象（x轴上方图象）不变；（3）当y=f（x）<0时，利用对称性作出x轴下方图象关于x轴对称后的图象。

【作图展示：】作函数y=f（x）=2x-2的图象⑤对x，f（x）都取绝对值y=f（x），x∈R：【函数性质分析：】已知函数y=f（x），x∈R，由于该函数既对自变量取了绝对值，又对应变量取了绝对值，因此可看做是前两种情况的逐步复合，若令u=f（x）（偶函数），则y=u 。

含绝对值的一次函数含绝对值的函数问题是近年来高考及县市级统考中的热点问题.由于绝对值本身的意义,解决此类问题一般是需要讨论的.当然,如果我们比较熟悉它,有时可以有比较简单的方法的.解决含绝对值的函数的问题,方法大致有:⑴分类讨论:通过讨论,去掉绝对值符号;⑵数形结合:通过画图,寻求问题的几何意义,从而是比较简单地求解.例1.画出()3|2|1f x x =+-的图像总结：此类绝对值函数的性质与图像特征（V 型或倒V ）；变式1.若函数()||2f x a x b =-+在区间(2,)+∞上为增函数，则实数a,b 的取值范围是________.变式 2.对,a b R ∈，记,max{,},a a b a b b a b≥⎧=≤⎨<⎩，则函数()max{|1|,|2|}()f x x x x R =+-∈的最小值是_________.变式3.已知函数|}||,1min(|)(a x x x f -+=的图像关于直线2=x 对称,则实数a = _______.变式4.y k x a b =--+的图象与y k x c d =-+的图象（0k >且13k ≠）交于两点（2,5），（8,3），则c a +的值是( )A ．7B ．8C ．10D ．13变式5.已知函数()|2|f x x =-，()|3|g x x m =-++，若函数()f x 的图像恒在函数()g x 图像的上方，求m 的取值范围.变式6(2017浙江高考). 17.已知∈a R ，函数()4=+-+f x x a a x 在区间[1,4]上的最大值是5，则a 的取值范围是例2⑴.画出函数|2||1|)(++-=x x x f 的图像. ⑵.画出函数|2||1|)(+--=x x x f 的图像.⑶.画出函数|2||12|)(++-=x x x f 的图像. ⑷.画出函数|2||12|)(+--=x x x f 的图像.总结：此类绝对值函数的性质与图像特征（U 型或倒U ）；变式1.若函数()|1|||f x x x a =++-的图像关于直线1x =对称，则a 的值为______.变式2设函数()3|4|||f x x x a =-+-，则()f x 的最小值为3，则a =________.变式3若关于x 的不等式|1||2|x x a ---<的解集为R ，求a 的取值范围；变式4.函数()()(2)f x x a x a x =+-+-的图象为中心对称图形，则实数a 的值为 .变式 5.将函数1112122y x x =-+-+的图像绕原点顺时针方向旋转角02πθθ≤≤（）得到曲线C .若对于每一个旋转角θ，曲线C 都是一个函数的图像，则θ的取值范围是 ．参考答案:例1.画出()3|2|1f x x =+-的图像总结：归纳此类绝对值函数的性质与图像特征（V 型或倒V ）；变式1.若函数()||2f x a x b =-+在区间(2,)+∞上为增函数，则实数a,b 的取值范围是________. 0,2a b >≤变式 2.对,a b R ∈，记,max{,},a a b a b b a b ≥⎧=≤⎨<⎩，则函数()max{|1|,|2|}()f x x x x R =+-∈的最小值是_________. 32变式3.已知函数|}||,1min(|)(a x x x f -+=的图像关于直线2=x 对称,则实数a = _________. 5变式4.y k x a b =--+的图象与y k x c d =-+的图象（0k >且13k ≠）交于两点（2,5），（8,3），则c a +的值是( )A ．7B ．8C ．10D ．13C变式5.已知函数()|2|f x x =-，()|3|g x x m =-++，若函数()f x 的图像恒在函数()g x 图像的上方，求m 的取值范围.m<5变式6(2017浙江高考). 17.已知∈a R ，函数()4=+-+f x x a a x在区间[1,4]上的最大值是5，则a 的取值范围是9-，2⎛⎤∞ ⎥⎝⎦ 例2⑴.画出函数|2||1|)(++-=x x x f 的图像. ⑵.画出函数|2||1|)(+--=x x x f 的图像. ⑶.画出函数|2||12|)(++-=x x x f 的图像. ⑷.画出函数|2||12|)(+--=x x x f 的图像.变式1.若函数()|1|||f x x x a =++-的图像关于直线1x =对称，则a 的值为______.3变式2设函数()3|4|||f x x x a =-+-，则()f x 的最小值为3，则a =________. 17或变式3若关于x 的不等式|1||2|x x a ---<的解集为R ，求a 的取值范围；1a >变式4.函数()()(2)f x x a x a x =+-+-的图象为中心对称图形，则实数a 的值为 . 32- 变式 5.将函数1112122y x x =-+-+的图像绕原点顺时针方向旋转角02πθθ≤≤（）得到曲线C .若对于每一个旋转角θ，曲线C 都是一个函数的图像，则θ的取值范围是 ．[0,)4π。

七类函数一．对号函数：形如()bf x ax x=+的函数称为对号函数。

（1）0,0a b >>时，示意图如下：可看成以直线y ax =与y 轴为渐近线的双曲线， 两个顶点A 、B 可由不等式中的均值定理确定， 此时()f x 的单调性、奇偶性、定义域与值域、 对称性可从图中看出结论。

（2）0a >且0b <时，示意图如下：此时()f x 为奇函数，分段递增，当0(0)x x ><或时，y R ∈1.已知函数f(x)=2x+x8（1）当x ∈(0,+∞) 时.求()x f 的值域。

（2）当x ∈[1，3 ] 时.求()x f 的值域。

（3）当x ∈[-2，0）时.求()x f 的值域。

2. 已知函数f(x)=2x —x8，研究该函数的性质。

3. 已知函数(x)=4522++x x ,求f(x)的最小值及此时x 的值.y ax=b aO x yB2ab1． 一次分函数的定义我们把形如(0,)cx dy a ad bc ax b+=≠≠+的函数称为一次分函数。

2． 一次分函数的图象和性质(0,)cx dy a ad bc ax b+=≠≠+2.1 图象：其图象如图所示.2.2定义域：⎭⎬⎫⎩⎨⎧-≠a b x x ；2.3 值域：⎭⎬⎫⎩⎨⎧≠a c y y ；2.4 对称中心：⎪⎭⎫⎝⎛-a c a b ,；2.5 渐近线方程：b x a =-和cy a=；2.6 单调性：当ad>bc 时，函数在区间(,)b a -∞-和(,)ba-+∞分别单调递减；当ad<bc 时，函数在区间(,)b a -∞-和(,)ba-+∞分别单调递增；1．函数21()3x f x x +=+的单调增区间是 ．2．函数21()3x f x x -=+的对称中心是 ．3. 函数21()3x f x x -=+（()5,2-∈x ），则()x f 的值域是________．4. 函数21()3x f x x -=+（())5,2(4,5⋃--∈x ），则()x f 的值域是________1.已知函数f(x)=112+++x x x ,求(1) f(x)的值域。

含有绝对值函数的性质及应用函数是高中阶段数学的核心内容,贯穿着整个高中数学的教学过程.含有绝对值的函数是一类常见的函数类型,这类函数看起来是由一次函数、二次函数等基本函数组成的,但又与它们有很大差异,并且通常与函数的值域(最值)、不等式、方程等知识联系在一起,综合性比较强,学生在处理这类问题时,往往由于考虑不严密而引起种种错误,如何解决这类问题呢？分段讨论是基本的策略, 逐段处理,将问题转化为基本函数后,再各个击破,最后归纳总结.这一过程包含着分类、转化、数形结合等多种数学思想的综合运用.下面就其常见类型及解题策略举例说明.一 与一次函数有关的绝对值函数 1 函数h k x a +-=||y 的性质及应用函数||y x =的图象是由第一、二象限的角平分线构成的V 字形(如图1),而函数h k x a +-=||y 是由函数||y x =的图象经过平移翻折等图形变换得到的,其中a 的符号决定V 字开口方向:当0>a 时,V 字开口向上;当0<a 时,沿着x 轴翻折后V 字开口向下.||a 的大小决定V 字开口大小:若1||=a ,则张口角度为直角;若1||>a ,则张口角度为锐角;则1||<a ,则张口角度为钝角.把函数||y x a =的图象沿着x 轴向左（0<k ）或向右（0>k ）平移||k 个单位,再沿着y 轴向上（0>h ）或向下（0<h ）平移||h 个单位后得到h k x a +-=||y 的图象,即顶点为),(h k 的V 字形(如图2).例1 （07安徽）图3中的图象所表示的函数的解析式为（ ） (A)|1|23-=x y(0≤x ≤2) (B) |1|2323--=x y (0≤x ≤2) (C) |1|23--=x y (0≤x ≤2) (D) |1|1--=x y (0≤x ≤2) 分析与解：由上述性质容易得到应选B.例2 已知不等式||22t x x --<有负数解,求t 的取值范围.xy 图1xykOh图2图3图4分析与解：原不等式等价于“||2x -2t x ->+”, ||y t x -=表示顶点在x 轴上的V 字, 如 图4.从图象上来看,要使该不等式有负数解,则在左半平面抛物线2-x y 2+=上至少有一点在V 字形的上方,所以当V 字顶点在线段AB 之间时,原不等式有负数解,对应t 的取值范围是:)2,49(-.2 形如∑=-=ni i ik x a1||y 的函数对于含有多个绝对值的形如∑=-=ni i i k x a 1||y 的函数,一般是先根据n 个分界点i k 将函数分成1+n 段,去掉绝对值符号写出分段函数形式,然后根据一次函数的性质或由图象(折线)解答问题..例3 (09 重庆) 设函数|1||3|)(--+=x x x f ,若不等式a a x f 3)(2-≤对任意实数x 恒成立，则实数a 的取值范围为（ ） A (,1][4,)-∞-+∞ B (,2][5,)-∞-+∞C [1,2]D (,1][2,)-∞+∞解:由图象（图5）可知,当1≥x 时,函数4)(max =x f .所以有: 432≥-a a ,解得1-≤a 或4≥a .故本题选:A例4 (08山东) 设函数|||1|)(a x x x f -++=的图象关于直线1=x 对称,则=a ___. 解: 因为分界点1-=x 和a x =是关于直线1=x 对称的,所以3=a . 例5 (08宁夏) 已知函数|4||12|)(---=x x x f . （1） 解不等式2)(>x f . （2） 求函数)(x f y =的最小值.解: (1) 原函数可化为:⎪⎩⎪⎨⎧+---=.5,335)(x x x x f ，，，.442121≥<<--≤x x x 作出函数)(x f y =的图象,图5它与直线的交点为: )2,7(- 和 )2,35(.所以2)(>x f 的解集是: ),35()7,(+∞⋃--∞. （2）由函数)(x f y =的图象可知,当21-=x 时,函数取得最小值29-. 二 与二次函数有关的含有绝对值函数1 形如)0(||y 2≠++=a c bx ax 的函数函数)0(||y 2≠++=a c bx ax 的图象是：函数 c bx ax ++=2y 位于x 轴下方的图象沿x 轴向上翻折后与其上方的部分组成.例6设1,0≠>a a ,函数||log )(2x ax x f a -=在]4,3[上是增函数,求实数a 的取值范围.解:令||)(2x ax x g -=(如图6).若1>a ,由),1(]4,3[+∞⊆a,则)(x g 在]4,3[上是增函数.所以,)(x f 在]4,3[上是增函数. 若1>a ,欲使)(x f 在]4,3[是增函数, )(x g 在]4,3[上应为减函数,则)1,21[]4,3[a a ⊆,所以aa 14,213<≥,即4161<≤a .故a 的取值范围是1>a 或4161<≤a . 例7（08浙江）已知t 为常数，函数|2|y 2t x x --=在区间]20[，上最大值为2，求t .解:因为函数|2|y 2t x x --=在]20[，上只有在2,1,0=x 处才有可能取得最大值.若在0=x 或2处取得最大值2, 解得2±=t ,其中2=t 不合题意舍去; 若在1=x 处取得最大值2,解得1=t 或3-,其中3-=t 不合题意舍去.所以2-=t 或1. 2 形如)(,0(||)()(y 21x f a b x b x a x f ≠+++=至多为二次函数）先由分界点2b -去掉绝对值符号,把函数写成分段形式后逐段讨论,最后再归纳总结. 例8 (09 江苏) 设a 为实数，函数||)(2)(2a x a x x x f --+=. (1) 若1)0(≥f ,求a 的取值范围; (2) 求)(x f 的最小值；(3) 设函数),(),()(+∞∈=a x x f x h ，直接写出(不需给出演算步骤)不等式1)(≥x h 的解集.解:（1）若1)0(≥f ,则1101||2-≤⇒⎩⎨⎧≥<⇒≥-a a a a a .(2) 当a x ≥时,,23)(22a ax x x f +-=⎪⎩⎪⎨⎧<≥=⎪⎩⎪⎨⎧<≥=0,320,20),3(0),()(22min a a a a a a f a a f x f 当a x ≤时,,2)(22a ax x x f -+=⎩⎨⎧<≥-=⎩⎨⎧<≥-=0,20,20),(0),()(22min a a a a a a f a a f x f 综上得 ⎪⎩⎪⎨⎧<≥-=0,320,2)(22min a a a a x f .(3)),(+∞∈a x 时,由1)(≥x h 得,012322≥-+-a ax x .812)1(124222a a a -=--=∆① 当26-≤a 或26≥a 时, .0≤∆此时不等式的解集为:);,(+∞∈a x ② 当2626<<-a 时, ,0>∆所以有⎪⎩⎪⎨⎧>≥-+----a x a a x a a x 0)323)(323(22 )26,22(∈a 时,原不等式的解集为:);,(+∞∈a x ]22,22[-∈a 时, 原不等式的解集为:);,323[2+∞-+∈a a x )22,26(--∈a 时, 原不等式的解集为:).,323[]323,(22+∞-+--∈a a a a a x 本题第(2)问也可以分0≥a 和0<a 两种情况分别画出函数的草图:在分界点a x =处由两支抛物线拼接而成的.再根据草图求出函数的最小值表达式.三 与其他基本函数有关的绝对值函数与指数、对数及三角函数有关的绝对值函数,一般利用数形结合的思想,通过图形解决问题. 例9 (08 江西)函数tan sin tan sin y x x x x =+--在区间3(,)22ππ内的图象是( ).解:因为函数⎩⎨⎧>≤=--+=)sin (tan sin 2)sin (tan tan 2|sin tan |sin tan x x x x x x x x x x y ,所以本题应选（D ）.例10 若函数|log |)(3x x f =,若)5.3()(f x f >,则x 的取值范围是___________. 解:画出函数|log |)(3x x f =的图象,由图象可知x 的取值范围是:720<<x 或27>x .ABCD-。

浅析含绝对值的二次函数问题
徐加生
【期刊名称】《数理化解题研究：高中版》
【年(卷),期】2004(000)008
【摘要】含绝对值的二次函数是二次函数与绝对值及不等式的一类综合性问题，是高考的重要命题类型。

本文归纳了几种常见类型及解题方略，供参考。

【总页数】2页(P1-2)
【作者】徐加生
【作者单位】江苏省金湖县教师进修学校211600
【正文语种】中文
【中图分类】G633.62
【相关文献】
1.教学夯实基础解题水到渠成——例谈含绝对值的二次函数综合题解题策略 [J], 顾红俏;
2.对一道含绝对值的二次函数的变式探究 [J], 耿道永
3.例谈含绝对值的二次函数相关题型再探讨 [J], 岳建卿
4.例谈含绝对值的二次函数的最值问题 [J], 高鹏
5.含参二次函数中绝对值问题的解题策略 [J], 叶兴炎
因版权原因，仅展示原文概要，查看原文内容请购买。

|bx-a|≤b-ax2成立,则
答案 [-1,
2+1
]
2

的取值范围是

.






解析 因为|bx-a|≤b-ax2,且 b>0,所以丨 x- 丨≤1- x2.令 t= ,则原不等
式为|x-t|≤1-tx2,即 tx2-1≤x-t≤1-tx2,
+1
1
且
t≥,
2 +1
+1
2+1
t∈[-1,
].
(ⅲ)当a>1时,因为x∈[-1,1],
1
2
1
4
所以 f(x)=|x2-a|+|a2-x|=a-x2+a2-x=-(x+ )2+a2+a+ ,
1
1
2
此时 M=f(- )=a +a+ ,
2
4
1
3
2 + + ≤ 4,
4
由
得 1<a≤ .
2
> 1,
3
2
综上所述,a 的取值范围为[-1, ].
5.(2020年1月浙江学考)设a,b∈R,函数f(x)=ax2+bx-3,g(x)=|x-a|,
.
答案 2+2 3
解析 因为函数f(x)=|x2+ax-2|-6在[2,b]上恰有两个零点,则必在x=2
与x=b时恰好取到零点的边界.
若x=2,f(x)的零点满足f(2)=|22+2a-2|-6=0,解得a=2或a=-4.
当a=2时,f(x)=|x2+2x-2|-6,满足f(x)在[2,b]上恰好有两个零点,则

高考数学函数专题训练《含绝对值的函数》含答案解析1.函数y=sinxcosxtanx的值域为（）+（）A．{1,3} B.{-1,3} C.{-1,-3} D.{1,-3}答案】B解析】当sinx>0,cosx>0时y=3，sinx>0,cosx0时y=-1，sinx<0,cosx<0时y=3，所以值域为{-1,3}。

2．函数f(x)=lnx-1/(1-x)的图像大致为()A． B． C． D．答案】D解析】由于f(3)>ln2/2，排除C选项，f(-1)>0，排除B选项，f(1/2)<0，不选A选项，所以选D。

3．设函数f(x),g(x)的定义域为R，且f(x)是奇函数，g(x)是偶函数，设h(x)=f(x-1)+g(x-1)，则下列结论中正确的是() A．h(x)关于(1,)对称 B．h(x)关于(-1,)对称 C．h(x)关于x=1对称 D．h(x)关于x=-1对称答案】C解析】因为函数f(x)是奇函数，所以f(x-1)是偶函数，即f(x-1)与g(x-1)均为偶函数，其图像均关于y轴对称，所以f(x-1)与g(x-1)的图像都关于直线x=1对称，即h(x)=f(x-1)+g(x-1)的图像关于直线x=1对称，故选C。

4.已知f(x)=ax+x-a(-1≤x≤1)且a≤1，则f(x)的最大值为()A．5/4 B．3/4 C．3 D．1答案】A解析】由题意得：f(x)=ax-1+x≤ax-1+x≤x-1+x/2，-1≤x≤1.所以当x=±1时，x-1+x=±2，f(x)max=5/4，即f(x)≤5/4，所以选A。

5．若函数f(x)=1(x≠1)，f(x+)=2x-1，则关于x的方程f(x)+bf(x)+c=0有3个不同的实数根，则（）A．b0 B．b-2且c>0 D．b>-2且c<0答案】C解析】因为f(x+)=2x-1，所以当x>1时，f(x)=2x-1；当x1时，f(x)max=2x-1；当x1时，f(x)≤2x-1；当x1时，f(x)≤2x-1，即b≥2；当x-2且c>0，所以选C。

绝对值不等式绝对值不等式||||||a b a b +≤+，||||||a b a b -≤+ 基本的绝对值不等式：||a|-|b||≤|a ±b|≤|a|+|b| ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝y=|x-3|+|x+2|≥|(x-3)-(x+2)|=|x-3-x-2|=|-5|=5 所以函数的最小值是5，没有最大值＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝|y|=||x-3|-|x+2||≤|(x-3)-(x+2)|=|x-3-x-2|=|-5|=5 由|y|≤5得-5≤y ≤5即函数的最小值是-5，最大值是5＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝也可以从几何意义上理解，|x-3|+|x+2|表示x 到3，-2这两点的距离之和，显然当-2≤x ≤3时，距离之和最小，最小值是5；而|x-3|-|x+2|表示x 到3，-2这两点的距离之差，当x ≤-2时，取最小值-5，当x ≥3时，取最大值5［变题1］解下列不等式：(1)|x +1|>2－x ；(2)|2x －2x －6|<3x［思路］利用｜f(x)｜<g(x) ⇔-g(x)<f(x)<g(x)和｜f(x)｜>g(x) ⇔f(x)>g(x)或f(x)<-g(x)去掉绝对值后转化为我们熟悉的一元一次、一元二次不等式组来处理。

解：(1)原不等式等价于x +1>2－x 或x +1<－(2－x )解得x >12或无解，所以原不等式的解集是{x |x >12} (2)原不等式等价于－3x <2x －2x －6<3x 即222226360(3)(2)032(1)(6)016263560x x x x x x x x x x x x x x x x x ⎧⎧-->-+->+-><->⎧⎧⎪⎪⇒⇒⇒⎨⎨⎨⎨+-<-<<--<--<⎪⎪⎩⎩⎩⎩或2<x <6所以原不等式的解集是{x |2<x <6}1．解不等式（1）｜x-x 2-2｜>x 2-3x-4；（2）234x x -≤1解：（1）分析一 可按解不等式的方法来解.原不等式等价于：x-x 2-2>x 2-3x-4 ①或x-x 2-2<-(x 2-3x-4) ②解①得：1-2<x<1+2解②得：x>-3故原不等式解集为｛x ｜x>-3｝分析二 ∵｜x-x 2-2｜＝｜x 2-x+2｜而x 2-x+2＝(x-14)2+74>0 所以｜x-x 2-2｜中的绝对值符号可直接去掉.故原不等式等价于x 2-x+2>x 2-3x-4解得：x>-3∴ 原不等式解集为｛x>-3｝（2）分析 不等式可转化为-1≤234x x -≤1求解，但过程较繁，由于不等式234x x -≤1两边均为正，所以可平方后求解. 原不等式等价于2234x x -≤1⇒9x 2≤(x 2-4)2 (x ≠±2) ⇒x 4-17x 2+16≥0⇒x 2≤1或x 2≥16⇒-1≤x ≤1或x ≥4或x ≤-4注意：在解绝对值不等式时，若｜f(x)｜中的f(x)的值的范围可确定(包括恒正或恒非负，恒负或恒非正)，就可直接去掉绝对值符号，从而简化解题过程. 第2变 含两个绝对值的不等式［变题2］解不等式（1）|x －1|<|x +a |；（2）｜x-2｜+｜x+3｜>5.［思路］（1）题由于两边均为非负数，因此可以利用｜f(x)｜〈｜g(x)｜⇒f 2(x)〈g 2(x)两边平方去掉绝对值符号。

第一章集合与函数概念课时一：集合有关概念1.集合的含义：集合为一些确定的、不同的东西的全体，人们能意识到这些东西，并且能判断一个给定的东西是否属于这个整体。

2.一般的研究对象统称为元素，一些元素组成的总体叫集合，简称为集。

3.集合的中元素的三个特性：（1）元素的确定性：集合确定，则一元素是否属于这个集合是确定的：属于或不属于。

例：世界上最高的山、中国古代四大美女、教室里面所有的人……（2）元素的互异性：一个给定集合中的元素是唯一的，不可重复的。

例：由HAPPY的字母组成的集合{H,A,P,Y}（3）元素的无序性:集合中元素的位置是可以改变的，并且改变位置不影响集合例：{a,b,c}和{a,c,b}是表示同一个集合3.集合的表示：{…} 如：{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}（1）用大写字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}（2）集合的表示方法：列举法与描述法。

1）列举法：将集合中的元素一一列举出来{a,b,c……}2）描述法：将集合中元素的公共属性描述出来，写在大括号内表示集合。

{x∈R| x-3>2} ,{x| x-3>2}①语言描述法：例：{不是直角三角形的三角形}②Venn图:画出一条封闭的曲线，曲线里面表示集合。

4、集合的分类：（1）有限集：含有有限个元素的集合（2）无限集：含有无限个元素的集合（3）空集：不含任何元素的集合 例：{x|x2=－5｝5、元素与集合的关系：（1）元素在集合里，则元素属于集合，即：a∈A（2）元素不在集合里，则元素不属于集合，即：a A注意：常用数集及其记法：非负整数集（即自然数集）记作：N正整数集N*或N+整数集Z有理数集Q实数集R课时二、集合间的基本关系1.“包含”关系—子集（1）定义：如果集合A的任何一个元素都是集合B的元素，我们说这两个集合有包含关系，称集合A是集合B的子集。

记作：（或BＡ）BA⊆⊇注意：有两种可能（1）A是B的一部分，；BA⊆（2）A与B是同一集合。