各种信号处理方法总结
- 格式:ppt
- 大小:402.50 KB
- 文档页数:19

电路信号处理与分析方法总结在电子设备和通信系统中,电路信号处理与分析是非常重要的技术,它涉及信号采集、处理、传输和分析等多个方面。
本文将对电路信号处理与分析的方法进行总结,帮助读者更好地理解和应用这些方法。
一、信号采集与处理方法1. 模拟信号采集与处理模拟信号指的是连续变化的信号,通常通过传感器等转换成电压或电流信号进行采集。
采集后的模拟信号需要进行处理,常见的处理方法包括滤波、放大、采样和保持等。
滤波可以去除杂散干扰,放大可以增加信号的强度,采样和保持可以将连续信号转换为离散信号。
2. 数字信号采集与处理数字信号是离散的信号,常见的数字信号采集设备是模数转换器(ADC)。
数字信号的处理方法包括数字滤波、数字放大、数字化、数据压缩和误差校正等。
数字滤波可以通过计算机算法实现,数字化可以将模拟信号转换为二进制数字,数据压缩可以减少存储和传输的需求,误差校正可以提高数字信号的精度和准确性。
二、信号传输与调制方法1. 信号传输方法信号传输是将采集或处理后的信号传送到其他设备或系统的过程。
常见的信号传输方法包括有线传输和无线传输两种。
有线传输主要通过电缆、光纤等介质进行信号传输,无线传输则利用无线电波或红外线等无线介质进行信号传输。
2. 信号调制方法信号调制是将原始信号按照一定规则转换为适合传输的信号的过程。
常见的信号调制方法有调幅(AM)、调频(FM)和调相(PM)等。
调幅是通过改变信号的振幅来实现信号调制,调频是通过改变信号的频率来实现信号调制,调相是通过改变信号的相位来实现信号调制。
三、信号分析与识别方法1. 时域与频域分析时域分析是将信号在时间轴上进行分析,常见的时域分析方法有时间序列分析和自相关函数分析等。
频域分析是将信号在频率域上进行分析,常见的频域分析方法有傅里叶变换和功率谱分析等。
时域和频域分析可以对信号的幅值、频率和相位等特性进行全面的分析和描述。
2. 数据挖掘与模式识别数据挖掘是通过对大量数据进行分析和挖掘来发现隐藏在数据中的有价值的信息。

绪论:本章介绍数字信号处理课程的基本概念。
0.1信号、系统与信号处理1.信号及其分类信号是信息的载体,以某种函数的形式传递信息.这个函数可以是时间域、频率域或其它域,但最基础的域是时域。
分类:周期信号/非周期信号确定信号/随机信号能量信号/功率信号连续时间信号/离散时间信号/数字信号按自变量与函数值的取值形式不同分类:2.系统系统定义为处理(或变换)信号的物理设备,或者说,凡是能将信号加以变换以达到人们要求的各种设备都称为系统。
3。
信号处理信号处理即是用系统对信号进行某种加工。
包括:滤波、分析、变换、综合、压缩、估计、识别等等。
所谓“数字信号处理”,就是用数值计算的方法,完成对信号的处理.0.2 数字信号处理系统的基本组成数字信号处理就是用数值计算的方法对信号进行变换和处理。
不仅应用于数字化信号的处理,而且也可应用于模拟信号的处理。
以下讨论模拟信号数字化处理系统框图。
(1)前置滤波器将输入信号x a(t)中高于某一频率(称折叠频率,等于抽样频率的一半)的分量加以滤除。
(2)A/D变换器在A/D变换器中每隔T秒(抽样周期)取出一次x a(t)的幅度,抽样后的信号称为离散信号。
在A/D 变换器中的保持电路中进一步变换为若干位码。
(3)数字信号处理器(DSP)(4)D/A变换器按照预定要求,在处理器中将信号序列x(n)进行加工处理得到输出信号y(n)。
由一个二进制码流产生一个阶梯波形,是形成模拟信号的第一步.(5)模拟滤波器把阶梯波形平滑成预期的模拟信号;以滤除掉不需要的高频分量,生成所需的模拟信号y a(t).0.3 数字信号处理的特点(1)灵活性.(2)高精度和高稳定性。
(3)便于大规模集成。
(4)对数字信号可以存储、运算、系统可以获得高性能指标。
0。
4 数字信号处理基本学科分支数字信号处理(DSP)一般有两层含义,一层是广义的理解,为数字信号处理技术-—DigitalSignalProcessing,另一层是狭义的理解,为数字信号处理器—-DigitalSignalProcessor.0。

数字信号处理第0章绪论1.数字信号处理是利用计算机或专用处理设备,以数字形式对信号进行采集、变换、滤波、估值、增强、压缩、识别等处理,以得到符合人们需要的信号形式。
2.DSP系统构成输入抗混叠滤波A/DDSP芯片D/A平滑滤波输出输入信号首先进行带限滤波和抽样,然后进行A/D(Analog to Digital)变换将信号变换成数字比特流。
根据奈奎斯特抽样定理,为保证信息不丢失,抽样频率至少必须是输入带限信号最高频率的2倍。
DSP芯片的输入是A/D变换后得到的以抽样形式表示的数字信号。
3.信号的形式(1)连续信号在连续的时间范围内有定义的信号。
连续--时间连续。
(2)离散信号在一些离散的瞬间才有定义的信号。
离散--时间离散。
4.数字信号处理主要包括如下几个部分(1)离散时间信号与系统的基本理论、信号的频谱分析(2)离散傅立叶变换、快速傅立叶变换(3)数字滤波器的设计第一章离散时间信号一、典型离散信号定义1.离散时间信号与数字信号时间为离散变量的信号称作离散时间信号;而时间和幅值都离散化的信号称作为数字信号。
2.序列离散时间信号-时间上不连续上的一个序列。
通常定义为一个序列值的集合{x(n)},n 为整型数,x(n)表示序列中第n 个样值,{·}表示全部样本值的集合。
离散时间信号可以是通过采样得到的采样序列x(n)=x a (nT),也可以不是采样信号得到。
二.常用离散信号1.单位抽样序列(也称单位冲激序列))(n δ⎩⎨⎧≠==0,00,1)(n n n δδ(n):在n=0时取值为12.单位阶跃序列)(n u ,⎩⎨⎧<≥=0,00,1)(n n n u 3.矩形序列,⎩⎨⎧=-≤≤=其它n N n n R N ,010,1)(4.实指数序列,)()(n u a n x n =,a 为实数5.正弦型序列)sin()(φω+=n A n x 式中,ω为数字域频率,单位为弧度。
15On 1-10()0sin nω()t 0sin Ω16.复指数序列nj e n x )(0)(ωσ+=7.周期序列如果对所有n 存在一个最小的正整数N ,使下面等式成立:)()(N n x n x +=,则称x(n)为周期序列,最小周期为N 。

信号的基本操作与处理实验总结1. 实验概述哎呀,信号处理这块儿,乍一听可能觉得有点高大上,但其实说白了就是把数据转来转去,做个大修,弄个小清新。
我们这次实验主要就是玩转那些信号的基本操作和处理技巧。
从最基础的信号处理,到如何用一些小工具去改造信号,整个过程就像是在做一盘大菜,不同的调料和步骤决定了最后的味道。
首先,我们接触了信号的采样和量化,就像是把一块大面团切成了小块儿。
接着,我们用一些数学方法来处理这些“小块儿”,使它们变得更有用。
真是个充满趣味的旅程!2. 实验步骤2.1 采样与量化首先,我们要搞清楚信号是怎么来的。
想象一下你在听音乐,音乐信号其实就是一个个小的声音波动。
为了在电脑里处理这些信号,我们需要把它们“取样”——简单来说,就是把连续的信号变成离散的点,就像用网筛把细沙分离出来一样。
这一步叫做采样。
而量化呢,就是给这些点上颜色,使它们能更好地被计算机识别。
量化过程就像是给这些点定个价,让它们的价值更明确。
就这么简单,我们的信号就被变成了可以处理的数字了!2.2 滤波与变换接下来,信号处理的工作就更有意思了。
比如说,噪声就像是搅拌在咖啡里的颗粒,虽然不是特别显眼,但如果不去掉的话,味道可是大打折扣的。
为了去掉这些不需要的噪声,我们用了滤波器。
滤波器就像是筛子,把那些不需要的“颗粒”给筛除。
滤波后,信号就变得干净了。
接着,我们还用了傅里叶变换,将信号从时域转到频域,轻松搞定了信号的频率成分。
傅里叶变换就像是用显微镜看信号的内部结构,发现了很多有趣的细节。
3. 实验结果与分析3.1 实验结果经过一番折腾,我们的信号处理结果令人满意。
采样后的信号能够清晰地展示出音频的各种细节,而滤波后的信号干净得像新剥的橙子,完全看不到噪声的踪影。
傅里叶变换后的频谱图,更是像是打开了信号的“藏宝图”,让我们一目了然地看到了各种频率成分的分布。
这些处理步骤让信号看起来焕然一新,仿佛为它穿上了新衣服。
3.2 实验分析从实验中我们学到了很多,不仅是技术上的细节,还有怎么处理信号中的各种“问题”。

第1章 离散时间信号与系统1、 傅里叶分析和Z 变换的区别、缺陷、特点关系:点数为N 的有限长序列x(n)的Z 变换为X(z),而其离散傅里叶变换为X(k),两者均表示了同一有限长序列x(n)的变换,它们之间的关系是:对z 变换在单位圆上取样可得DFT 。
而DFT 的内插就是变换。
傅里叶变换优缺点(1) 傅里叶变换缺乏时间和频率的定位功能 (2) 傅里叶变换对于非平稳信号的局限性(3) 傅里叶变换在时间和频率分辨率上的局限性傅立叶变换是最基本得变换,由傅里叶级数推导出。
傅立叶级数只适用于周期信号,把非周期信号看成周期T 趋于无穷的周期信号,就推导出傅里叶变换,能很好的处理非周期信号的频谱。
但是傅立叶变换的弱点是必须原信号必须绝对可积,因此适用范围不广。
Z 变换的本质是离散时间傅里叶变换(DTFT ),如果说拉普拉斯变换专门分析模拟信号,那Z 变换就是专门分析数字信号,Z 变换可以把离散卷积变成多项式乘法,对离散数字系统能发挥很好的作用。
Z 变换看系统频率响应,就是令Z 在复频域的单位圆上跑一圈,即Z=e^(j2πf),即可得到频率响应。
2、系统的记忆性、因果性、可逆性(1)记忆性如果系统在任意时刻n0的响应仅与该时刻的输入f(n0)有关,而与其它时刻的输入无关,则称该系统为非记忆系统(或系统无记忆性),否则称为记忆系统。
系统的记忆性有时也被称为动态特性。
该特性强调系统的响应是否仅与当前时刻的输入有关。
对于无记忆LTI 系统,其系统冲激响应为,其中()()h n K n δ=,K 为一常数。
由于系统频率响应是冲激响应的傅氏变换、系统函数为系统冲激响应的z 变换,因此,无记忆LTI 系统的系统频率响应和系统函数分别为H(ω)=K ,H(z)=K 。
(2) 因果性如果系统任意时刻的响应与以后的输入无关,则该系统称为因果系统(或系统具有因果性),否则为非因果系统。
该特性强调的是,系统的响应是否与未来的输入有关。

信号处理知识点总结 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】第一章信号1.信息是消息的内容,消息是信息的表现形式,信号是信息的载体2.信号的特性:时间特性,频率特性3.若信号可以用确定性图形、曲线或数学表达式来准确描述,则该信号为确定性信号若信号不遵循确定性规律,具有某种不确定性,则该信号为随机信号4.信号分类:能量信号,一个信号如果能量有限;功率信号,如果一个信号功率是有限的5.周期信号、阶跃信号、随机信号、直流信号等是功率信号,它们的能量为无限6.信号的频谱有两类:幅度谱,相位谱7.信号分析的基本方法:把频率作为信号的自变量,在频域里进行信号的频谱分析第二章连续信号的频域分析1.周期信号频谱分析的常用工具:傅里叶三角级数;傅里叶复指数2.利用傅里叶三角级数可以把周期信号分解成无穷多个正、余弦信号的加权和3频谱反映信号的频率结构,幅频特性表示谐波的幅值,相频特性反映谐波的相位4.周期信号频谱的特点:离散性,谐波性,收敛性5.周期信号由无穷多个余弦分量组成周期信号幅频谱线的大小表示谐波分量的幅值相频谱线大小表示谐波分量的相位6.周期信号的功率谱等于幅值谱平方和的一半,功率谱反映周期信号各次谐波的功率分配关系,周期信号在时域的平均功率等于其各次谐波功率之和7.非周期信号可看成周期趋于无穷大的周期信号8.周期T0增大对频谱的影响:谱线变密集,谱线的幅度减少9.非周期信号频谱的特点:非周期信号也可以进行正交变换;非周期信号完备正交函数集是一个无限密集的连续函数集;非周期信号的频谱是连续的;非周期信号可以用其自身的积分表示10.常见奇异信号:单位冲激信号,单位直流信号,符号函数信号,单位阶跃信号11.周期信号的傅里叶变换:周期信号:一个周期绝对可积à傅里叶级数à离散谱非周期信号:无限区间绝对可积à傅里叶变换à连续谱12.周期信号的傅立叶变换是无穷多个冲激函数的线性组合脉冲函数的位置:ω=nω0 , n=0,±1,±2, …..脉冲函数的强度:傅里叶复指数系数的2π倍周期信号的傅立叶变换也是离散的;谱线间隔与傅里叶级数谱线间隔相同13.信号的持续时间与信号占有频带成反比14.信号在时域的翻转,对应信号在频域的翻转15.频域频移,时域只有相移,幅频不变;时域相移,只导致频域频移,相位不变第三章 连续信号分析1.正弦信号的性质:两个同频正弦信号相加,仍得同频信号,且频率不变,幅值和相位改变;频率比为有理整数的正弦信号合成为非正弦周期信号,以低频(基频f0)为基频,叠加一个高频 (频nf0)分量2.函数f(t)与冲激函数或阶跃函数的卷积: f(t)与冲激函数卷积,结果是f(t)本身; f(t)与冲激偶的卷积,d(t)称为微分器f(t)与阶跃函数的卷积, u(t)称为积分器 3. 函数正交的充要条件是它们的内积为0第二章 离散傅里叶变换及其快速算法1.时域上周期序列的离散傅里叶级数在频域上仍是一个周期序列2.周期卷积特性:同周期序列的时域卷积等于频域的乘积同周期序列的时域乘积等于频域的卷积3.周期卷积与线性卷积的区别:线性卷积在无穷区间求和;周期卷积在一个主值周期内求和4.有限长序列隐含着周期性5.有限长序列的循环移位导致频谱线性相移而对频谱幅度无影响6.FFT 的计算工作量:FFT 算法对于N 点DFT,仅需(N/2)log2N次复数乘法运算和Nlog2N 次复数加法)()()(t f t t f '='*δ⎰∞-=*td f t u t f λλ)()()(第三章随机信号分析与处理1 随机信号是随时间变化的随机变量,用概率结构来描述。
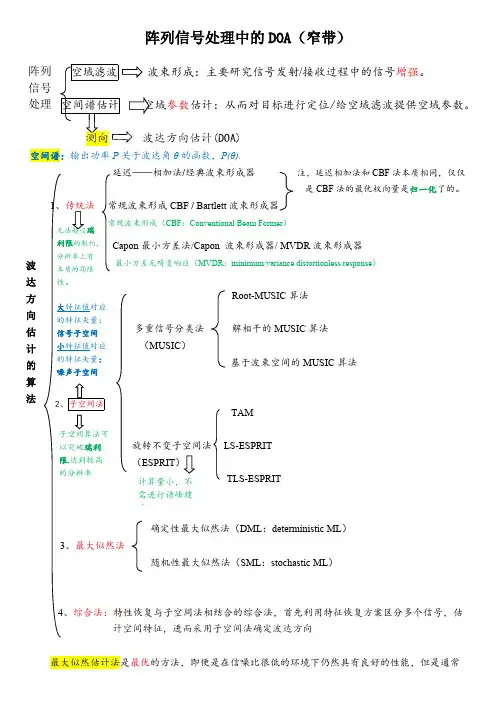
阵列信号处理中的DOA (窄带)/接收过程中的信号增强。
参数估计:从而对目标进行定位/给空域滤波提供空域参数。
(DOA)空间谱:输出功率P 关于波达角θ的函数,P(θ).——相加法/经典波束形成器注,延迟相加法和CBF 法本质相同,仅仅是CBF 法的最优权向量是归一化了的。
CBF / Bartlett 波束形成器CBF :Conventional Beam Former )最小方差法/Capon 波束形成器/ MVDR 波束形成器MVDR :minimum variance distortionless response )Root-MUSIC 算法多重信号分类法解相干的MUSIC 算法(MUSIC )基于波束空间的MUSIC 算法TAM旋转不变子空间法LS-ESPRIT TLS-ESPRIT 确定性最大似然法(DML :deterministic ML )随机性最大似然法(SML :stochastic ML )最大似然估计法是最优的方法,即便是在信噪比很低的环境下仍然具有良好的性能,但是通常计算量很大。
同子空间方法不同的是,最大似然法在原信号为相关信号的情况下也能保持良好的性能。
阵列流形矩阵(导向矢量矩阵)只要确定了阵列各阵元之间的延迟τ,就可以很容易地得出一个特定阵列天线的阵列流形矩阵A。
传统的波达方向估计方法是基于波束形成和零波导引概念的,并没有利用接收信号向量的模型(或信号和噪声的统计特性)。
知道阵列流形 A 以后,可以对阵列进行电子导引,利用电子导引可以把波束调整到任意方向上,从而寻找输出功率的峰值。
①常规波束形成(CBF)法CBF法,也称延迟—相加法/经典波束形成器法/傅里叶法/Bartlett波束形成法,是最简单的DOA 估计方法之一。
这种算法是使波束形成器的输出功率相对于某个信号为最大。
(参考自:阵列信号处理中DOA估计及DBF技术研究_赵娜)注意:理解信号模型注意:上式中,导向矩阵A的行向量表示第K个天线阵元对N个不同的信号s(i)的附加权值,列向量表示第i个信号s(i)在M个不同的天线上的附加权值。

生物医学信号处理中的常用方法和技术汇总引言:生物医学信号处理是一个广泛的领域,涵盖了从生物电信号到成像技术的众多方法和技术。
这些方法和技术对于理解和诊断疾病、监测生理功能、研究神经科学等方面至关重要。
本文将总结生物医学信号处理中的一些常用方法和技术,并对其原理和应用进行简要介绍。
一、滤波技术在处理生物医学信号时,由于信号受到各种噪声和干扰的影响,常常需要应用滤波技术进行去噪。
常见的滤波方法包括高通滤波、低通滤波、带通滤波和带阻滤波等。
高通滤波可以滤除低频信号,突出高频特征,适用于心电图(ECG)等信号的分析。
低通滤波可以滤除高频噪声,保留低频特征,常用于脑电图(EEG)等信号的处理。
带通滤波和带阻滤波可以选择性地滤除或保留特定频段的信号。
二、特征提取方法为了从生物医学信号中提取有用的信息或特征,常常需要采用特征提取方法。
常见的特征提取方法包括时间域特征、频域特征和时频域特征等。
时间域特征包括均值、方差、能量等,反映了信号的平均水平、波动性和能量分布等指标。
频域特征通过对信号进行傅立叶变换或小波变换,得到信号在频域上的能量分布,常常用于分析心电图、脑电图等周期性信号。
时频域特征结合了时域和频域特征的优点,能够有效地反映信号在时间和频率上的变化。
三、信号分类和识别方法在生物医学信号处理中,常常需要对信号进行分类和识别,以实现对疾病的诊断和监测。
常见的信号分类和识别方法包括决策树、支持向量机(SVM)、人工神经网络(ANN)等。
决策树是一种基于树结构的分类方法,通过逐步划分数据集,构建一颗能够对新数据进行分类的树。
SVM是一种二分类模型,通过在不同类别之间找到一个最优超平面,将数据点分隔开来。
ANN模型模拟人脑神经网络的结构和功能,能够对复杂的非线性关系进行建模和分类。
四、图像处理技术在生物医学成像中,图像处理技术起到了至关重要的作用。
常见的图像处理技术包括增强、去噪、分割和配准等。
增强技术通过调整图像的对比度、亮度等参数,使图像更清晰、更易于观察和分析。

数字信号处理的常见问题及解决方法总结数字信号处理在科学、工程领域中的应用越来越广泛。
在实际应用过程中,我们常常会遇到一些问题。
本文总结了一些常见的问题及其解决方法,以帮助读者更好地理解和应用数字信号处理技术。
问题一:信号滤波数字信号往往包含噪声和干扰,需要进行滤波处理以提取有效信息。
常见的信号滤波问题包括滞后滤波器、移动平均滤波器、低通滤波器等。
解决这些问题的方法通常包括设计合适的滤波器参数、选择适当的滤波器类型,并进行滤波器性能评估。
问题二:信号采样率选择在数字信号处理中,采样率的选择对信号重构和频谱分析等方面具有重要影响。
选择过低的采样率会导致信号失真,选择过高的采样率会浪费存储和计算资源。
解决这个问题的方法包括根据信号的带宽和特性选择合适的采样率,并根据需要进行抽取或插值处理。
问题三:频谱分析频谱分析是数字信号处理中的重要步骤,用于研究信号的频域特性。
常见的频谱分析问题包括功率谱密度估计、傅里叶变换等。
解决这些问题的方法包括选择合适的频谱分析方法(如快速傅里叶变换)、处理频谱分辨率问题,并进行频谱分析结果的解释和应用。
问题四:数字滤波器设计数字滤波器的设计是数字信号处理领域的关键问题之一。
常见的数字滤波器设计问题包括低通滤波器设计、高通滤波器设计、带通滤波器设计等。
解决这些问题需要根据滤波器的要求和性能指标,选择适当的设计方法(如窗函数法、频率抽样法),并进行滤波器参数调整和性能评估。
问题五:数字信号压缩数字信号压缩是在保证信号质量的前提下,减少信号数据量的一种技术。
常见的数字信号压缩问题包括有损压缩和无损压缩。
解决这些问题的方法通常包括选择适当的压缩算法(如哈夫曼编码、小波变换压缩),根据压缩效率和信号质量要求进行参数调整。
以上是数字信号处理中常见问题的一些总结及解决方法。
希望能够帮助读者更好地应用数字信号处理技术,解决实际应用中的问题。

信号的基本操作与处理实验总结1. 实验概述嘿,大家好!今天咱们聊聊信号的基本操作与处理实验,这可是个有趣的东西哦。
其实,这个实验就像是在玩“信号大作战”,把各种信号像积木一样拆开重组,让我们看见隐藏在数据背后的秘密。
咱们这次实验主要涉及了几个重要的方面,比如信号的采样、滤波、以及信号的变换。
这些操作就像是给信号穿衣服,有时候需要换成时尚的高档西装,有时候则要换成舒适的运动装,看你需要什么风格啦!2. 信号采样2.1 采样的基本概念首先,说到信号采样,那可是信号处理的基础了。
大家可以把信号采样想象成拍照。
我们用相机拍照,每次拍出的照片其实只是一个静止的快照。
信号采样也是类似的,我们把连续的信号用一定的频率“拍下来”,变成离散的数值序列。
这就像是把信号的流动美景定格在一个个“快照”中,让我们可以更清楚地看到信号的细节。
不过,记住了,采样频率一定要高,否则就像用马赛克处理图片,细节全都丢了,那就糟了。
2.2 采样定理的作用咱们还得提到采样定理,这就像是信号采样的“护身符”。
根据奈奎斯特定理,信号的采样频率必须是信号带宽的两倍以上,才能确保不丢失信息。
也就是说,我们得确保我们的“快照”足够密集,才能抓住信号的每一个细节。
想象一下,如果你拍照时只拍了几张照片,那肯定无法完整记录整个场景,对吧?3. 信号滤波3.1 滤波的基本操作接下来,我们要聊聊信号滤波。
滤波就像是在信号里搞清扫,去除那些“杂质”,让信号变得更加干净、清晰。
就好比是把一个脏兮兮的窗户擦干净,你会发现外面的风景更加明亮、清楚。
我们在实验中用到了低通滤波器和高通滤波器。
低通滤波器就像是一把“筛子”,只让低频信号通过,把高频的噪声“筛掉”;高通滤波器则相反,专门去掉低频成分,只保留高频信号。
3.2 滤波的实际应用滤波的实际应用可真不少,比如在音频处理上,我们经常需要用滤波器去掉背景噪音,提升声音的清晰度。
就像你听音乐时,偶尔会有杂音,滤波器的作用就是把这些干扰的噪音去掉,让你能够更专注地享受音乐。
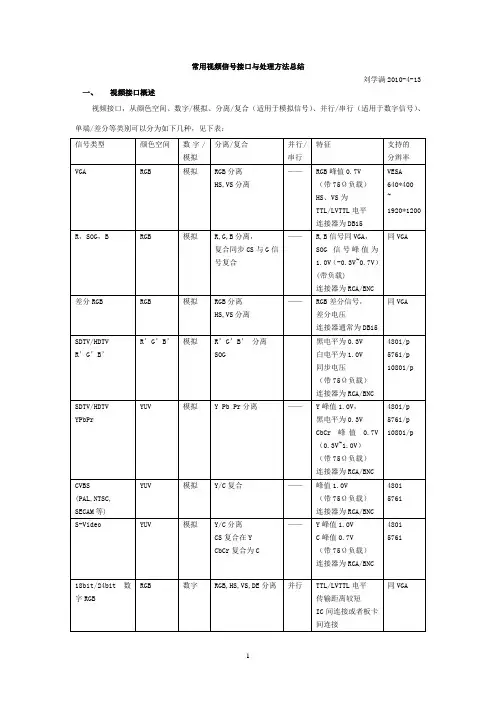
常用视频信号接口与处理方法总结刘学满2010-4-13 一、视频接口概述视频接口,从颜色空间、数字/模拟、分离/复合(适用于模拟信号)、并行/串行(适用于数字信号)、单端/差分等类别可以分为如下几种,见下表:二、模拟视频信号接口1.接口设计模拟信号由于其电压范围很小,如果接口电路设计不当,很可能造成最终的信号质量下降。
因此需要注意以下几个事项:1)阻抗匹配:通常为75Ω,包括发送端,接收端以及传输路径上的阻抗。
2)隔直电容:为了防止不同设备间地电压差对信号造成的影响,此电容不宜过大或者过小。
3)滤波网络:尽可能地消除低频和高频纹波。
4)地平面:根据理论,地平面分隔可以防止数字信号对模拟地干扰,但从实际经验来看,分隔成小的地平面后,实际上会造成环流(AD9883资料中有叙述)。
因此大部分情况下,还是用同一个地。
多层地平面,以及多打过孔,保持地电平的稳定是非常必要的。
5)PCB走线:等长是需要的,而且要确保三个器件经过不同的选择器/缓冲器之后的延时也相差不多,否则很难保证采样相位。
6)ESD保护:如果视频接口经常插拔,就需要加ESD保护二极管。
2.视频ADC完成模拟信号到数字信号的转换,在使用过程中需要注意的主要问题有:1)A/D是否支持交流耦合方式输入2)A/D内部是否有信号增益调整功能3)是否支持差分输入4)A/D内部是否有PLL等器件,采样相位是否可调整5)A/D输出的信号格式(24bit RGB,YCbCr)6)是否支持SOG或者SOY等同步信号输入模拟信号在A/D转换时,通常需要进行一些调整,以达到最佳显示效果:1)调整黑电平位置和最大辐值,通常可以配置A/D芯片有关offset和gain的寄存器,经过此番调整之后,实际上是校准了RGB三色,同时提高了灰度等级。
2)调整PLL锁相环,以达到合适的采样频率,并保证PLL在各种温度条件下均能稳定工作。
3)调整采样起始点和终止点,确保有效信号不丢失。
生理信号监测与处理技术评估方法总结概述生理信号监测与处理技术是现代医疗领域中一项关键的技术,可以通过监测人体的各种生理信号,如心电图、脑电图、血压等,来对人体的健康状况进行评估与监测。
然而,不同的监测与处理技术存在一定的差异,并且需要进行科学、准确的评估,以确保其可靠性和有效性。
本文将介绍一些常用的生理信号监测与处理技术评估方法,并总结其优势和局限性。
一、生理信号质量评估方法1. 信号清洗:在进行信号分析之前,需要对原始信号进行预处理,去除噪声和干扰。
常用的信号清洗方法包括滤波、降噪和去伪迹等。
评估方法主要可通过信噪比(SNR)和峰值信噪比(PSNR)来进行,值越高表示信号质量越好。
2. 信号特征提取:信号特征提取是对生理信号进行分析与识别的关键步骤。
评估方法包括频域分析、时域分析和小波分析等。
常用的评估指标包括熵、功率谱密度和相关系数等。
3. 信号分类与识别:通过对提取的特征进行分类与识别,可以实现对生理信号的自动化处理。
评估方法主要通过准确率、灵敏度和特异性进行评估。
二、生理信号传感器评估方法1. 精准度评估:传感器的精准度是评估其测量结果与实际值之间的差异程度。
评估方法主要包括附加误差、线性度和准确性等。
2. 稳定性评估:传感器的稳定性是评估其输出值在相同条件下的长期稳定性。
评估方法包括稳定性系数和漂移等。
3. 响应时间评估:传感器的响应时间是评估其检测值与输入信号变化之间的响应速度。
评估方法主要通过上升时间和下降时间来进行。
三、生理信号处理算法评估方法1. 效率评估:生理信号处理算法的效率主要是评估其运算复杂度和执行速度。
评估方法主要包括计算时间和计算资源消耗。
2. 准确性评估:生理信号处理算法的准确性是评估其处理结果与真实结果之间的差异程度。
评估方法主要通过均方根误差(RMSE)和相关系数来进行评估。
3. 适应性评估:生理信号处理算法的适应性是评估其在不同信号数据和应用场景下的适应能力。
医学信号处理的原理和方法医学信号处理是指将医学领域中获取到的生理信号(如心电图、脑电图、血压信号等)进行分析、提取有用信息的一种方法。
医学信号处理的主要目标是通过信号处理技术对生理信号进行滤波、特征提取、分类和识别等操作,以从中获取有价值的信息,用于诊断、监测和治疗疾病。
1.信号的获取:医学信号是通过生物传感器、监护仪器等设备获取到的,这些设备会将生理变化转换为电信号,并通过模数转换将其转换为数字信号。
通常,医学信号的采样频率较高,以保证时间和频率的精度。
2.信号的预处理:医学信号在采集过程中可能受到各种噪声的干扰,如电源干扰、肌电干扰等。
因此,需要对信号进行预处理,包括去除基线漂移、去噪和滤波等操作。
预处理可以提高后续信号处理算法的准确性。
3.特征提取:特征提取是医学信号处理的核心步骤,它通过运用数学算法和信号处理技术,从信号中抽取出能够表征生理变化的特征。
常用的特征包括时域特征(如均值、方差)、频域特征(如功率谱密度)、时频域特征(如小波变换)等。
特征提取能够减小信号的维度并保留重要信息,为后续的分类和识别提供基础。
4.分类和识别:在经过特征提取后,医学信号可以通过分类和识别算法进行进一步分析。
分类是将信号分成几个类别,可以通过监督学习算法(如支持向量机、人工神经网络)来实现。
而识别则是将信号与预定义的模型进行匹配,确定信号所属的类别,可以通过模式识别算法(如隐马尔可夫模型、贝叶斯分类器)来实现。
1.滤波:使用数字滤波器对信号进行滤波,去除噪声和干扰。
常见的滤波器包括低通滤波器和带通滤波器。
2.小波变换:将信号分解为不同尺度的频带,对不同频带的信号进行分析,提取特征。
3.自相关和互相关分析:用于分析信号的周期性和相关性,常用于心电图的QRS检测和波形分析等。
4.谱分析:通过将信号映射到频域,分析信号的频率分布和功率谱密度,常用于脑电图和血压信号的研究。
5.图像处理:对医学图像进行处理,如模糊处理、边缘检测、图像增强等。
信号处理方法信号处理是指对信号进行采集、处理、分析和解释的过程。
在现代科技发展中,信号处理方法被广泛应用于通信、图像处理、生物医学工程、雷达、声音处理等领域。
本文将介绍几种常见的信号处理方法,包括滤波、傅里叶变换、小波变换和自适应信号处理。
首先,滤波是一种常见的信号处理方法。
滤波器可以通过增强或者抑制信号的某些频率成分来改变信号的特性。
在通信系统中,滤波器可以用来去除噪声,提高信号的质量;在图像处理中,滤波器可以用来平滑图像、增强图像的边缘等。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
其次,傅里叶变换是一种重要的信号处理方法。
傅里叶变换可以将一个时域信号转换为频域信号,从而可以分析信号的频率成分。
傅里叶变换在音频处理、图像处理和通信系统中都有着广泛的应用。
通过傅里叶变换,我们可以得到信号的频谱信息,从而可以进行频域滤波、频域分析等操作。
另外,小波变换是一种近年来备受关注的信号处理方法。
小波变换可以将信号分解为不同尺度的小波函数,从而可以同时获得信号的时域和频域信息。
小波变换在信号压缩、信号去噪、图像处理等领域有着广泛的应用。
与传统的傅里叶变换相比,小波变换可以更好地适应非平稳信号的分析和处理。
最后,自适应信号处理是一种针对信号动态特性的处理方法。
自适应滤波器可以根据信号的实时特性自动调整滤波器的参数,从而可以更好地适应信号的变化。
自适应信号处理在通信系统、雷达系统和生物医学工程中有着重要的应用,可以有效地提高系统的性能和稳定性。
综上所述,滤波、傅里叶变换、小波变换和自适应信号处理是几种常见的信号处理方法。
它们在不同领域有着广泛的应用,可以帮助我们分析和处理各种类型的信号。
随着科技的不断发展,信号处理方法也在不断创新和完善,为我们提供了更多更强大的工具来处理信号,从而推动了科技的进步和应用的拓展。
信号工工作总结共6篇信号工作总结(一)自去年进入信号工作岗位以来,我始终坚持学习与实践相结合的原则,不断提高自己的技能和能力。
通过不断钻研信号处理的相关知识,我逐渐掌握了信号工作的重要基础知识和实践操作技巧。
在工作中,我始终保持积极的工作态度,不怕遇到困难和挑战。
无论是解决复杂的信号处理问题还是运用算法优化工作流程,我总是尽力做到最好。
我注重与团队成员的合作,分享我的经验和知识,也乐于倾听并学习他们的意见和建议。
在信号工作中,我对数据处理和分析有着丰富的经验。
我熟练使用MATLAB等工具进行信号处理、特征提取和算法实现。
通过对大量的数据进行分析和处理,我能够准确地捕捉到信号中的特征和模式,并能够根据需要进行相应的处理和优化。
在团队合作方面,我参与了几个信号处理项目的开发和实施。
与团队成员合作,在项目中我担任了主要的信号处理人员。
我设计了有效的信号处理算法,解决了一些关键性的技术难题,并组织了一些讨论会和培训班,以确保团队成员在项目中有足够的理解和掌握。
总的来说,我在信号工作中取得了一定的成绩。
通过不断地学习和实践,我提高了自己的技术水平,并且在团队中发挥了积极的作用。
希望在今后的工作中能够继续努力,不断提升自己的能力,为团队的发展做出更大的贡献。
信号工作总结(二)在信号工作岗位上,我认真负责地完成了各项任务,并且不断学习和提升自己的技术能力。
通过不断地实践和思考,我积累了一定的经验和技巧,能够更好地处理各种信号。
在工作中,我关注信号的特征和变化趋势,通过合适的算法和方法对信号进行分析和处理。
我熟练使用MATLAB等工具进行信号处理、特征提取和算法实现,能够准确地捕捉到信号中的关键信息。
在项目中,我充分发挥了团队合作的精神,与其他成员密切配合,共同完成了各项任务。
我们相互学习和交流,在项目中遇到问题时能够迅速解决,并提出合理的解决方案。
我也积极参与项目讨论会和培训班,与其他成员分享我的经验和知识。
电子电路中常见的信号处理问题解决方法在电子电路设计与应用过程中,我们经常会遇到各种信号处理问题。
这些问题多种多样,例如信号滤波、信号增益、信号放大失真、信号采样等等。
本文将针对这些常见的信号处理问题,提供一些解决方法和技巧。
一、信号滤波信号滤波是电子电路中常见的信号处理问题之一。
滤波的目的是为了去除或减弱信号中的噪声成分,使得信号更加清晰和稳定。
信号滤波的方法多种多样,下面列举几种常用的方法:1. 低通滤波器:适用于滤除高频噪声。
常见的低通滤波器包括RC滤波器和巴特沃斯滤波器。
RC滤波器由电阻和电容构成,巴特沃斯滤波器是一种更复杂的设计。
选择适当的滤波器可以根据具体的应用需求和性能指标进行。
2. 高通滤波器:适用于滤除低频噪声。
与低通滤波器相反,高通滤波器可以通过设置截止频率来滤除低频信号。
常见的高通滤波器有RC滤波器和巴特沃斯滤波器等。
3. 带通滤波器:适用于滤除特定频段外的信号。
带通滤波器可以通过设置上下截止频率来滤除指定范围外的信号。
二、信号增益信号增益是指在电子电路中放大信号的幅度。
在某些应用中,信号可能由于传输距离远或其它原因而衰减,需要进行增益处理。
以下是几种常用的信号增益方法:1. 放大器:放大器是对信号进行放大处理的电路。
常见的放大器有运放放大器、差分放大器等。
通过选择合适的放大器类型和参数,可以实现对信号的增益效果。
2. 变压器:变压器是一种通过磁耦合实现信号变压的装置。
通过变压器可以改变信号的电压值,实现信号的增益效果。
3. 可调增益电路:可调增益电路可以根据需要调节信号的增益大小。
例如,通过调节电阻或电容值,可以实现对信号增益的调节。
三、信号放大失真在信号处理过程中,信号的放大可能会引起一定程度的失真。
能否有效地处理信号失真是衡量信号处理质量的重要指标。
下面介绍几种常见的信号放大失真处理方法:1. 负反馈:负反馈是通过引入反向信号来减小放大器的放大程度,从而减小失真。
通过负反馈可以提高放大器的线性度,降低失真程度。