第三章习题答案及作业分析_1

第三章练习题一、判断正误并解释1.所谓商品的效用，就是指商品的功能。

分析：这种说法是错误的。

商品的效用指商品满足人的欲望的能力，指消费者在消费商品时所感受到的满足程度2.不同的消费者对同一件商品的效用的大小可以进行比较。

分析：这种说法是错误的。

同一个消费者对不同商品的效用大小可以比较。

但由于效用是主观价值判断，所以同一商品对不同的消费者来说，其效用的大小是不可比的。

3.效用的大小，即使是对同一件商品来说，也会因人、因时、因地而异。

分析：这种说法是正确的。

同一商品给消费者的主观心理感受会随环境的改变而改变。

4.边际效用递减规律是指消费者消费某种消费品时，随着消费量的增加，其最后一单位消费品的效用递减。

分析：这种说法是错误的。

必须在某一特定的时间里，连续性增加。

5.预算线的移动表示消费者的货币收入发生变化。

分析：这种说法是错误的。

只有在收入变动，商品价格不变，预算线发生平移时，预算线的移动才表示消费者的收入发生了变化。

6.效应可以分解为替代效应和收入效应，并且替代效应与收入效应总是反向变化。

分析：这种说法是错误的。

正常物品的替代效应和收入效应是同向变化的。

二、选择1.当总效用增加时，边际效用应该：（A ）A.为正值，但不断减少；B.为正值，且不断增加；C.为负值，且不断减少；D.以上都不对２.当某消费者对商品Ｘ的消费达到饱合点时，则边际效用ＭＵχ为：（C ）Ａ.正值Ｂ.负值Ｃ.零Ｄ.不确定３.正常物品价格上升导致需求量减少的原因在于：（C ）Ａ.替代效应使需求量增加，收入效应使需求量减少；Ｂ.替代效应使需求量增加，收入效应使需求量增加；Ｃ.替代效应使需求量减少，收入效应使需求量减少；Ｄ.替代效应使需求量减少，收入效应使需求量增加。

4.无差异曲线的形状取决于（C ）A.消费者收入；B.所购商品的价格；Ｃ.消费者偏好；Ｄ.商品效用水平的大小。

5.无差异曲线为斜率不变的直线时，表示相组合的两种商品是（B ）Ａ.可以替代的；Ｂ.完全替代的；Ｃ.互补的；Ｄ.互不相关的。

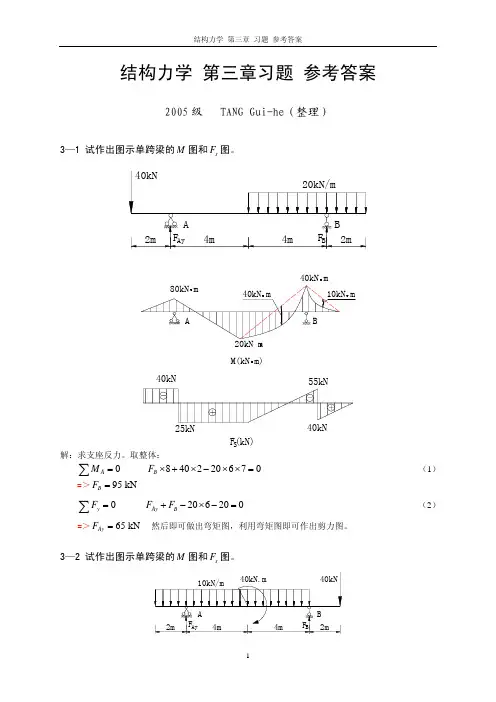
《编译原理》课后习题答案第三章第3 章文法和语言第1 题文法G＝({A,B,S},{a,b,c},P,S)其中P 为：S→Ac|aBA→abB→bc写出L(G[S])的全部元素。

答案：L(G[S])={abc}第2 题文法G[N]为：N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么？答案:G[N]的语言是V+。

V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D或者：允许0 开头的非负整数？第３题为只包含数字、加号和减号的表达式，例如9-2＋5，3-1，７等构造一个文法。

答案：G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4 题已知文法G[Z]：Z→aZb|ab写出L(G[Z])的全部元素。

盛威网（）专业的计算机学习网站 1《编译原理》课后习题答案第三章答案：Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={anbn|n>=1}第5 题写一文法，使其语言是偶正整数的集合。

要求：(1) 允许0 打头；(2)不允许0 打头。

答案：(1)允许0 开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0 开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6 题已知文法G：<表达式>::=<项>｜<表达式>＋<项><项>::=<因子>｜<项>*<因子><因子>::=（<表达式>）｜i试给出下述表达式的推导及语法树。

（５）i+(i+i)（６）i+i*i盛威网（）专业的计算机学习网站 2 《编译原理》课后习题答案第三章答案：<表达式><表达式> + <项><因子><表达式><表达式> + <项><因子>i<项><因子>i<项><因子>i（ )(5) <表达式>=><表达式>＋<项>=><表达式>＋<因子>=><表达式>＋（<表达式>）=><表达式>＋（<表达式>＋<项>）=><表达式>＋（<表达式>＋<因子>）=><表达式>＋（<表达式>＋i）=><表达式>＋（<项>＋i）=><表达式>＋（<因子>＋i）=><表达式>＋（i＋i）=><项>＋（i＋i）=><因子>＋（i＋i）=>i＋（i＋i）<表达式><表达式> + <项><项> * <因子><因子> i<项><因子>ii(6) <表达式>=><表达式>＋<项>=><表达式>＋<项>*<因子>=><表达式>＋<项>*i=><表达式>＋<因子>*i=><表达式>＋i*i=><项>＋i*i=><因子>＋i*i=>i＋i*i盛威网（）专业的计算机学习网站 3《编译原理》课后习题答案第三章第7 题证明下述文法G[〈表达式〉]是二义的。

第三章语法分析3.1 完成下列选择题：(1) 文法G：S→xSx|y所识别的语言是。

a. xyxb. (xyx)*c. xnyxn(n≥0)d. x*yx*(2) 如果文法G是无二义的，则它的任何句子α。

　a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导，但它们对应的语法树相同(3) 采用自上而下分析，必须。

a. 消除左递 a. 必有ac归b. 消除右递归c. 消除回溯d. 提取公共左因子(4) 设a、b、c是文法的终结符，且满足优先关系ab和bc，则。

b. 必有cac. 必有bad. a～c都不一定成立(5) 在规范归约中，用来刻画可归约串。

a. 直接短语b. 句柄c. 最左素短语d. 素短语(6) 若a为终结符，则A→α·aβ为项目。

a. 归约b. 移进c. 接受d. 待约(7) 若项目集Ik含有A→α· ，则在状态k时，仅当面临的输入符号a∈FOLLOW(A)时，才采取“A→α· ”动作的一定是。

a. LALR文法b. LR(0)文法c. LR(1)文法d. SLR(1)文法(8) 同心集合并有可能产生新的冲突。

a. 归约b. “移进”/“移进”c.“移进”/“归约”d. “归约”/“归约”【解答】(1) c (2) a (3) c (4) d (5) b (6) b (7) d (8) d3.2 令文法G[N]为G[N]: N→D|NDD→0|1|2|3|4|5|6|7|8|9(1) G[N]的语言L(G[N])是什么?(2) 给出句子0127、34和568的最左推导和最右推导。

【解答】(1) G[N]的语言L(G[N])是非负整数。

(2) 最左推导：NNDNDDNDDDDDDD0DDD01DD012D0127NNDDD3D34NNDNDDDDD5DD56D568最右推导：NNDN7ND7N27ND27N127D1270127NNDN4D434NNDN8ND8N68D685683.3 已知文法G[S]为S→aSb|Sb|b，试证明文法G[S]为二义文法。

第3章 力学基本定律与守恒律 习题及答案1．作用在质量为10 kg 的物体上的力为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化．(2)为了使这力的冲量为200 N ·s ，该力应在这物体上作用多久，试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静止，则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向，ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速，则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理， 12v v ∆=∆,12I I=这说明，只要力函数不变，作用时间相同，则不管物体有无初动量，也不管初动量有多大，那么物体获得的动量的增量(亦即冲量)就一定相同，这就是动量定理． (2)同上理，两种情况中的作用时间相同，即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2．一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为 F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量． 解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3．如图所示，一质量为m 的球，在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。

概率论与数理统计03-第三章作业及答案习题3-1⽽且12{0}1P X X ==. 求1和2的联合分布律.解由12{0}1P X X ==知12{0}0P X X ≠=. 因此X 1和X 2的联合分布于是根据边缘概率密度和联合概率分布的关系有X 1和X 2的联合分布律(2) 注意到12{0,0}0P X X ===, ⽽121{0}{0}04P X P X =?==≠, 所以X 1和X 2不独⽴.2. 设随机变量(X ,Y )的概率密度为(,)(6),02,24,0,.f x y k x y x y =--<<<其它求: (1) 常数k ; (2) {1,3}P X Y <<; (3) { 1.5}P X <; (4) {4}P X Y +≤.解 (1) 由(,)d d 1f x y x y +∞+∞-∞, 得2424222204211d (6)d (6)d (10)82y k x y x k y x x y k y y k =--=--=-= , 所以 18k =. (2) 31201,31{1,3}d (6)d 8(,)d d x y P X Y y x y x f x y x y <<<<==--??1322011(6)d 82y x x y =--321113()d 828y y =-=?. (3) 1.51.5 { 1.5}d (,)d ()d X P X x f x y y f x x +∞-∞-∞-∞<==??4 1.521d (6)d 8y x y x --=22011(6)d 82y x x y =--?421633()d 882y y =-? 2732=. (4) 作直线4x y +=, 并记此直线下⽅区域与(,)0f x y ≠的矩形区域(0,2)(0,4)?的交集为G . 即:02,0G x y <<<≤4x -.见图3-8. 因此{P X Y +≤4}{(,)}P X Y G =∈(,)d d Gf x y x y =??44201d (6)d 8x y x y x -=--??4422011(6)d 82xy x x y -=--?42211[(6)(4)(4)]d 82y y y y =----? 42211[2(4)(4)]d 82y y y =-+-? 423211(4)(4)86y y =----?23=. 图3-8 第4题积分区域3. ⼆维随机变量(,)X Y 的概率密度为2(,),1,01,0,f x y kxy x y x =≤≤≤≤其它.试确定k , 并求2{(,)},:,01P X Y G G x y x x ∈≤≤≤≤. 解由2111401(,)d d d (1)d 26xk k f x y xdy x kxy y x x x +∞+∞-∞-∞====-??,解得6=k .因⽽ 2112401{(,)}d 6d 3()d 4x xP X Y G x xy y x x x x ∈==-=. 4. 设⼆维随机变量(X , Y )概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -=??≤≤≤≤其它求关于X 和Y 边缘概率密度.解 (,)X Y 的概率密度(,)f x y 在区域:0G ≤x ≤1,0≤y ≤x 外取零值.因⽽, 有24.8(2)d ,01,()(,)d 0,2.4(2),01,0,x X y x y x f x f x y y x x x +∞-∞-<<==-<<=其它.其它. 124.8(2)d ,01,()(,)d 0,2.4(34),01,0,yY y x x y f y f x y x y y y y +∞-∞-<<==-+<<=其它.其它.5. 假设随机变量U 在区间[-2, 2]上服从均匀分布, 随机变量 1,1,1,1,U X U --=>-??若≤若 1,1,1, 1.U Y U -=>??若≤若试求：(1) X 和Y 的联合概率分布；(2){P X Y +≤1}.解 (1) 见本章第三节三(4).(2){P X Y +≤1}1{1}P X Y =-+>1{1,1}P X Y =-==13144=-=. 习题3-21. 设(X , Y )的分布律为求: (1) 在条件X =2下Y 的条件分布律;(2) {22}P X Y ≥≤.解 (1) 由于6.02.01.003.0}2{=+++==X P ,所以在条件X =2下Y 的条件分布律为216.03.0}2{}1,2{}2|1{========X P Y X P X Y P ,06.00}2{}2,2{}2|2{========X P Y X P X Y P ,616.01.0}2{}3,2{}2|3{========X P Y X P X Y P ,316.02.0}2{}4,2{}2|4{========X P Y X P X Y P ,{P Y ≤2}{1}{2}P Y P Y ==+==0.10.3000.20.6++++=. ⽽{2,2}{2,1}{2,2}{3,1}{3,2}P X Y P X Y P X Y P X Y P X Y ===+==+==+==≥≤0.3000.20.5=+++=.因此{2,2}{22}{2}P X Y P X Y P Y =≥≤≤≥≤0.550.66==. 2. 设⼆维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<其它求：(1) (X , Y )的边缘概率密度(),()X Y f x f y ；(2)11{}.22P Y X ≤≤ 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===?;当x ≤0时或x ≥1时, ()0X f x =.故 2,01,()0,其它.X x x f x <<=??当02()(,)d d 12y Y y f y f x y x x +∞-∞===-;当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=其它 (2) 当z ≤0时,()0Z F z =; 当z ≥2时,1)(=z F Z ;当0z f x y x y -=≤2x12202-2d 1d d 1d zxz x zx y x y =?+24z z =-.故 1,02,()20,.()其它Z zzz f z F z -<<'== (3) {}{}11311322161122442≤，≤≤≤≤P X Y P Y X P X ===. 3. 设G 是由直线y =x , y =3,x =1所围成的三⾓形区域, ⼆维随机变量(,)X Y 在G 上服从⼆维均匀分布.求: (1) (X , Y )的联合概率密度；(2) {1}P Y X -≤；(3) 关于X 的边缘概率密度.解 (1)由于三⾓形区域G 的⾯积等于2, 所以(,)X Y 的概率密度为∈=.),(,0,),(,21),(G y x G y x y x f (2)记区域x y y x D -=|),{(≤}1与G 的交集为0G ,则{1}P Y X -≤0011113d d (2)22224G G x y S ===-=??. 其中0G S 为G 0的⾯积.(3) X 的边缘概率密度()(,)d X f x f x y y +∞-∞=?. 所以,当]3,1[∈x 时, 311()d (3)22X xf x y x ==-?. 当1x 时, 0)(=x f X .因此∈-=.,0],3,1[),1(21)(其它x x x f X习题3-31. 设X 与Y 相互独⽴, 且分布律分别为下表:求⼆维随机变量(,)X Y 的分布律.解由于X 与Y 相互独⽴, 所以有}{}{},{j i j i y Y P x X P y Y x X P =?====,6,5,2,0;0,21,1=--=j i .因此可得⼆维随机变量(,)X Y 的联合分布律2. 设(X , Y )的分布律如下表:问,αβ为何值时X 与Y 相互独⽴? 解由于边缘分布满⾜23111,1i j i j p p ??====∑∑, ⼜X , Y 相互独⽴的等价条件为p ij = p i . p .j (i =1,2; j =1,2,3).故可得⽅程组 21,3111().939αβα++==?+解得29α=,19β=.经检验, 当29α=,19β=时, 对于所有的i =1,2; j =1,2,3均有p ij = p i .p .j 成⽴. 因此当29α=,19β=时, X 与Y 相互独⽴..3. 设随机变量X 与Y 的概率密度为()e (,)0,.,01,0,x y b f x y x y -+=?<<>?其它 (1) 试确定常数b .(2) 求边缘概率密度()X f x , ()Y f y . (3) 问X 与Y 是否相互独⽴？解 (1) 由11()101(,)d d e d d e d e d (1e )x y y x f x y x y b y x b y x b +∞+∞+∞+∞-+----∞-∞====-?,得 111e b -=-.(2) ()(,)d X f x f x y y ∞-∞=?1e ,01,1e 0,xx --<<=-??其它.()(,)d Y f y f x y x ∞-∞=?e ,0,0,y y ->=其它.(3) 由于(,)()()X Y f x y f x f y =?，所以X 与Y 相互独⽴.4. 设X 和Y 是两个相互独⽴的随机变量, X 在(0, 1)上服从均匀分布, Y 的概率密度为21e ,0,()20Y yy f y y ->=，≤0.(1) 求X 和Y 的联合概率密度.(2) 设关于a 的⼆次⽅程为220a Xa Y ++=, 试求a 有实根的概率.解 (1) 由题设知X 和Y 的概率密度分别为1,01,()0,X x f x <<=??其它， 21e ,0,()20,.yY y f y ->=其它因X 和Y 相互独⽴, 故(X , Y )的联合概率密度为21e ,01,(,)()()20,.yX Y x y f x y f x f y -<<>==其它 (2) ⽅程有实根的充要条件是判别式⼤于等于零. 即244X Y ?=-≥20X ?≥Y .因此事件{⽅程有实根}2{X =≥}Y .下⾯计算2211221(,)d d e d (1e)d 2yxx Df x y xdy x y x --===-2121ed 12[(1)(0)]0.1445xx πΦΦ-=-=--≈?.图3-3 第6题积分区域习题3-41. 设⼆维随机变量(X ,Y )的概率分布为YX 0 10 0.4 a 1 b 0.1若随机事件{X =0}与{X +Y =1}相互独⽴, 求常数a , b .解⾸先, 由题设知0.40.11a b +++=. 由此得0.5a b +=. 此外,{0}0.4P X a ==+,{1}{0,1}{1,0}0.5P X Y P X Y P X Y a b +====+===+=, {0,1}{0,1}P X X Y P X Y a =+=====. 根据题意有{0,1}{0}{1}P X X Y P X P X Y =+===+=,即(0.4)0.5a a =+?. 解得0.4,0.1a b ==.2. 设两个相互独⽴的随机变量X ,Y 的分布律分别为求随机变量Z = X + Y 的分布律.解随机变量Z = X + Y 的可能取值为7,5,3.Z 的分布律为18.06.0.03}2,1{}3{=?=====Y X P Z P , {5}{1,4}{3,2}0.30.4070.60.54P Z P X Y P X Y ====+===?+?=,28.04.07.0}4,3{}7{=?=====Y X P Z P ,或写为3. 设X 和Y 是两个相互独⽴的随机变量, 且X 服从正态分布N (µ, σ2 ), Y 服从均匀分布U (-a , a )( a >0), 试求随机变量和Z =X +Y 的概率密度.解已知X 和Y 的概率密度分别为22()2()x X f x µσ--=,),(+∞-∞∈x ;-?-∈=).,(,0),,(,21)(a a y a a y ay f Y .由于X 和Y 相互独⽴, 所以22()21()()()d d 2z y a Z X Y f z f z y f y y y a µσ---+∞=1[()()]2z µa z µa ΦΦa σσ-+---. 4. 设随机变量X 和Y 的联合分布是正⽅形G={(x,y )|1≤x ≤3, 1≤y ≤3}上的均匀分布, 试求随机变量U=|X -Y|的概率密度f (u ).解由题设知, X 和Y 的联合概率密度为111,3,3,(,)40,.x y f x y =≤≤≤≤其它记()F u 为U 的分布函数, 参见图3-7, 则有当u ≤0时,(){||F u P X Y =-≤u }=0; 当u ≥2时,()1F u =;当0< u <2时, 图3-7 第8题积分区域||(){}(,)d d x y uF u P U u f x y x y -==≤≤21[42(2)]412u =-?- 211(2)4u =--.故随机变量||U X Y =-的概率密度为1(2),02,()20,u u p u -<<=其它..总习题三1. 设随机变量(X , Y )的概率密度为<<<=.,0,10,||,1),(其它x x y y x f 求条件概率密度)|()|(||y x f x y f Y X X Y 和.解⾸先(,)其它X x x f x f x y dy +∞-∞<<==??1,01,()1,10,0,(,)≤其它.Y y y f y y y f x y dx +∞-∞-<<==+-图3-9第1题积分区域当01y <<时, |1,1,1(|)0,X Y y x y f x y x <<-=??取其它值.当1y -<≤0时, |1,1,1(|)0,X Y y x y f x y x -<<+=??取其它值.当10<,||,(|)20,Y X y x f y x x y <=取其它值.2. 设随机变量X 与Y 相互独⽴, 下表列出⼆维随机变量(,)X Y 的分布律及关于X 和关于Y 的边缘分布律中部分数值, 试将其余数值填⼊表中空⽩处 .解⾸先, 由于11121{}{,}{,}P Y y P X x Y y P X x Y y ====+==, 所以有24P X x Y y P Y y P X x Y y ====-===-=.在此基础上利⽤X 和Y 的独⽴性, 有11111{,}124{}1{}46P X x Y y P X x P Y y =======.于是 2113{}1{}144P X x P X x ==-==-=.再次, 利⽤X 和Y 的独⽴性, 有12211{,}18{}1{}24P X x Y y P Y y P X x =======. 于是 312111{}1{}{}1623P Y y P Y y P Y y ==-=-==--=.最后, 利⽤X 和Y 的独⽴性, 有2222313{,}{}{}428P X x Y y P X x P Y y ======?=; 2323311{,}{}{}434P X x Y y P X x P Y y ======?=; 1313111{,}{}{}43123.(34)e (,)0,.,0,0,x y k f x y x y -+=?>>??其它(1) 求常数k ；(2) 求(X ,Y )的分布函数；(3) 计算{01,02}P X Y <<≤≤; (4) 计算(),x f x ()y f y ；(5) 问随机变量X 与Y 是否相互独⽴?解 (1)由3401(,)d d e d e d 12xy kf x y x y k x y +∞+∞+∞+∞---∞-∞===,可得12=k .(2) (X ,Y )的分布函数(,)(,)d d x y F x y f u v x y -∞-∞=??.当x ≤0或y ≤0时,有 0),(=y x F ;当,0>>y x 时,34340(,)12e d e d (1e )(1e )x即 34(1e )(1e ),0,0,(,)0,.其它x y x y F x y --?-->>=??(3) {01,02}P X Y <<≤≤38(1,2)(0,0)(1e )(1e )F F --=-=--.(4) (34)012ed ,0,()(,)d 0,其它.x y X y x f x f x y y +∞-++∞-∞>==所以 33e ,0,()0,其它.x X x f x -?>=??类似地, 有44e ,0,()0,其它.y Y y f y -?>=?显然2),(),()(),(R y x y f x f y x f Y X ∈??=, 故X 与Y 相互独⽴. 4.解已知),(Y X 的分布律为注意到41260}1{}1{=++====Y P X P , ⽽0}1,1{===Y X P ,可见P{X=1, Y=1}≠P{X=1}P{Y=1}. 因此X与Y不相互独⽴.(2) Z X Y =+的可能取值为3, 4, 5, 6, 且316161}1,2{}2,1{}3{=+===+====Y X P Y X P Z P , }1,3{}2,2{}3,1{}4{==+==+====Y X P Y X P Y X P Z P 3 112161121=++=, 3(3) V =21}2,2{}1,2{}2,1{}2{===+==+====Y X P Y X P Y X P V P , 2 1}2{1}3{==-==V P V P . 即max(,)V X Y =的分布律为(4) min{U =}3,1{}2,1{}1{==+====Y X P Y X P U P}1,2{}1,3{==+==+Y X P Y X P 21=, 21}1{1}2{==-==U P U P .即min{,}U X Y =的分布律为(5) W U =+31}1,2{}2,1{}2,1{}3{===+=======Y X P Y X P V U P W P ,。

第三章知识的建构第一节习题作业1、名词解释1．陈述性知识2．程序性知识3．知识的表征4．命题5．命题网络6．产生式7．产生式系统2、填空1．根据认知心理学家安德森（J.Anderson）的观点，通过信息加工，人类获得两类知识，即________________和________________。

2．所有命题都是由____________和______________两个成分构成。

3．知识有不同类型，相应的表征方式也不同。

一般认为陈述性知识是以__________和____ ___________的方式表征，而程序性知识是以_______________和_______________的方式表征。

4．美国心理学家梅耶（R.E.Mayer）提出了一种_______________，即关于如何学习、如何感知、如何记忆、如何思维等方面是知识，现在看来这种有关学习策略或认知策略等方面的知识也应属于程序性知识中的一部分。

3、判断1．“菱形的两条对角线互相垂直”是程序性知识。

（ ）2．“小明爱吃苹果”是陈述性知识。

（ ）3．陈述性知识是以命题和产生式表征的。

（ ）4、简答题1．根据安德森的信息加工的观点，知识是如何分类的？2．陈述性知识的表征和程序性知识分别以何种方式表征？五、论述题试论述陈述性知识和程序性知识的异同。

参考答案：1、名词解释1．陈述性知识：陈述性知识是关于“是什么”的知识，是事物及其关系的知识。

包括各种事实、概念、原则和理论。

如，课本中的知识。

2．程序性知识：程序性知识是关于“怎么做”的知识，关于完成某项任务的行为或操作步骤的知识，它包括一切为了进行信息转换活动而采取的具体操作程序和从事这种活动的技能。

如，骑自行车。

3．知识的表征：知识或信息在人脑中记载和贮存的方式叫知识的表征。

4．命题：命题是知识的基本单元，一个命题相当于一个观念。

如，“维生素C能预防感冒”。

5．命题网络：命题网络是由命题之间的相互联系而形成的，也就是说两个或多个具有相同成分的命题构成命题网络。

第三章处理机调度与死锁1，高级调度与低级调度的主要任务是什么？为什么要引入中级调度？【解】（1）高级调度主要任务是用于决定把外存上处于后备队列中的那些作业调入内存，并为它们创建进程，分配必要的资源，然后再将新创建的进程排在就绪队列上，准备执行。

（2）低级调度主要任务是决定就绪队列中的哪个进程将获得处理机，然后由分派程序执行把处理机分配给该进程的操作。

（3）引入中级调度的主要目的是为了提高内存的利用率和系统吞吐量。

为此，应使那些暂时不能运行的进程不再占用宝贵的内存空间，而将它们调至外存上去等待，称此时的进程状态为就绪驻外存状态或挂起状态。

当这些进程重又具备运行条件，且内存又稍有空闲时，由中级调度决定，将外存上的那些重又具备运行条件的就绪进程重新调入内存，并修改其状态为就绪状态，挂在就绪队列上，等待进程调度。

3、何谓作业、作业步和作业流？【解】作业包含通常的程序和数据，还配有作业说明书。

系统根据该说明书对程序的运行进行控制。

批处理系统中是以作业为基本单位从外存调入内存。

作业步是指每个作业运行期间都必须经过若干个相对独立相互关联的顺序加工的步骤。

作业流是指若干个作业进入系统后依次存放在外存上形成的输入作业流；在操作系统的控制下，逐个作业进程处理，于是形成了处理作业流。

4、在什么情冴下需要使用作业控制块JCB？其中包含了哪些内容？【解】每当作业进入系统时，系统便为每个作业建立一个作业控制块JCB，根据作业类型将它插入到相应的后备队列中。

JCB 包含的内容通常有：1) 作业标识2)用户名称3)用户账户4)作业类型（CPU 繁忙型、I/O芳名型、批量型、终端型）5)作业状态6)调度信息（优先级、作业已运行）7)资源要求8)进入系统时间9) 开始处理时间10) 作业完成时间11) 作业退出时间12) 资源使用情况等5．在作业调度中应如何确定接纳多少个作业和接纳哪些作业？【解】作业调度每次接纳进入内存的作业数，取决于多道程序度。

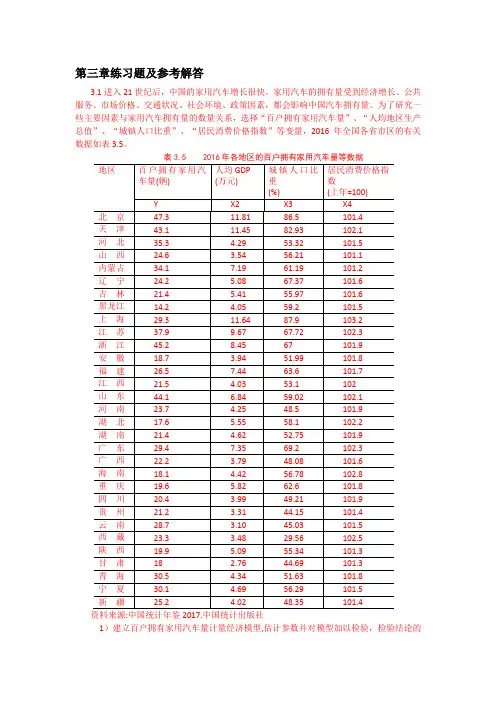
第三章练习题及参考解答3.1进入21世纪后，中国的家用汽车增长很快。

家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素，都会影响中国汽车拥有量。

为了研究一些主要因素与家用汽车拥有量的数量关系，选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量，2016年全国各省市区的有关数据如表3.5。

表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1）建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验，检验结论的依据是什么?。

2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】：1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007，可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。

解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=，表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。

2）X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。

由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。

汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。

中级财管第三章习题一、计算题1. 你正在分析一项价值250万元，残值为50万元的资产购入后从其折旧中可以得到的税收收益。

该资产折旧期为5年。

a. 假设所得税率为40%，估计每年从该资产折旧中可得到的税收收益。

b. 假设资本成本为10%，估计这些税收收益的现值。

参考答案：（1）年折旧额=（250-5）=40（万元）获得的从折旧税收收益=40*40%=16万元（2）P=16*(P/A,10%,5)=60.56万元2．华尔公司考虑购买一台新型交织字母机。

该机器的使用年限为4年，初始支出为100 000元。

在这4年中，字母机将以直线法进行折旧直到帐面价值为零，所以每年的折旧额为25 000元。

按照不变购买力水平估算，这台机器每年可以为公司带来营业收入80 000元，公司为此每年的付现成本30 000元。

假定公司的所得税率为40%，项目的实际资金成本为10%，如果通货膨胀率预期为每年8%，那么应否购买该设备？参考答案：NCF0=-100 000NCF1-4=（80 000-30 000-25 000）*（1-40%）+25 000NPV=NCF1-4/(P/A,18%,4)+NCF0若NPV>0，应该购买，否则不应该购买该项设备。

3.甲公司进行一项投资，正常投资期为3年，每年投资200万元，3年共需投资600万元。

第4年~第13年每年现金净流量为210万元。

如果把投资期缩短为2年，每年需投资320万元，2年共投资640万元，竣工投产后的项目寿命和每年现金净流量不变。

资本成本为20%，假设寿命终结时无残值，不用垫支营运资金。

试分析判断是否应缩短投资期。

参考答案：1、用差量的方法进行分析（1）计算不同投资期的现金流量的差量（单位：万元）（2）计算净现值的差量2、分别计算两种方案的净现值进行比较 （1）计算原定投资期的净现值（2）计算缩短投资期后的净现值（3）比较两种方案的净现值并得出结论：因为缩短投资期会比按照原投资期投资增加净现值20.27（24.38-4.11）万元，所以应该采用缩短投资的方案。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载马原,第三章习题及答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第三章人类社会及其发展规律（课后练习题）一、单项选择题1 ．人类社会历史发展的决定力量是（)A ．生产方式B ．地理条件C ．社会意识 D ．人口因素2 ．社会意识相对独立性的最突出表现是它（)A ．同社会存在发展的不同步性B ．具有历史的继承性C ．对社会存在具有能动的反作用D ．同社会经济的发展具有不平衡性3 ．在生产关系中起决定作用的是（)A ．生产资料所有制B ．产品的分配和交换C ．在生产中人与人的关系D ．管理者和生产者的不同地位4 . “手推磨产生的是封建主的社会，蒸汽磨产生的是工业资本家的社会” , 这句话揭示了（)A ．生产工具是衡量生产力水平的重要尺度B ．科学技术是第一生产力C ．社会形态的更替有其一定的顺序性D ．物质生产的发展需要建立相应的生产关系5 ．十一届三中全会以来，我党制定的一系列正确的路线、方针、政策促进了我国经济的迅猛发展，这说明（)A ．经济基础发展的道路是由上层建筑决定的B ．上层建筑的发展决定经济基础的发展方向C ．上层建筑对经济基础具有积极的能动作用D ．社会主义社会的发展不受经济基础决定上层建筑规律的制约6 ．一定社会形态的经济基础是（ )A ．生产力B ．该社会的各种生产关系C ．政治制度和法律制度D ．与一定生产力发展阶段相适应的生产关系的总和7 ．上层建筑是指（)A ．社会的经济制度B ．科学技术C ．社会生产关系D .建立在一定社会经济基础之上的意识形态及相应的制度和设施8 ．社会形态是（)A ．生产力和生产关系的统一B ．同生产力发展一定阶段相适应的经济基础和上层建筑的统一体C ．社会存在和社会意识的统一D ．物质世界和精神世界的统一9 ．人类社会发展的一般规律是（)A ．生产方式内部的矛盾规律B ．生产力和生产关系、经济基础和上层建筑之间的矛盾运动规律C ．社会存在和社会意识的矛盾规律D ．物质生产和精神生产的矛盾规律10 ．阶级斗争对阶级社会发展的推动作用突出表现在（)A ．生产力的发展B ．生产关系的变革C ．社会形态的更替 D ．科技的进步11 ．社会革命根源于（)A ．人口太多B ．少数英雄人物组织暴动C ．先进思想和革命理论的传播D ．社会基本矛盾的尖锐化12 ．社会主义改革的根本目的在于（)A ．改变社会主义制度B ．完善社会主义制度C ．解放和发展生产力D ．实现社会公平13 . “蒸汽、电力和自动纺织机甚至是比巴尔贝斯、拉斯拜尔和布朗基诸位公民更危险万分的革命家。

第三章处理机调度与死锁1，高级调度与低级调度的主要任务是什么？为什么要引入中级调度？【解】（1）高级调度主要任务是用于决定把外存上处于后备队列中的那些作业调入内存，并为它们创建进程，分配必要的资源，然后再将新创建的进程排在就绪队列上，准备执行。

（2）低级调度主要任务是决定就绪队列中的哪个进程将获得处理机，然后由分派程序执行把处理机分配给该进程的操作。

（3）引入中级调度的主要目的是为了提高内存的利用率和系统吞吐量。

为此，应使那些暂时不能运行的进程不再占用宝贵的内存空间，而将它们调至外存上去等待，称此时的进程状态为就绪驻外存状态或挂起状态。

当这些进程重又具备运行条件，且内存又稍有空闲时，由中级调度决定，将外存上的那些重又具备运行条件的就绪进程重新调入内存，并修改其状态为就绪状态，挂在就绪队列上，等待进程调度。

3、何谓作业、作业步和作业流？【解】作业包含通常的程序和数据，还配有作业说明书。

系统根据该说明书对程序的运行进行控制。

批处理系统中是以作业为基本单位从外存调入内存。

作业步是指每个作业运行期间都必须经过若干个相对独立相互关联的顺序加工的步骤。

作业流是指若干个作业进入系统后依次存放在外存上形成的输入作业流；在操作系统的控制下，逐个作业进程处理，于是形成了处理作业流。

4、在什么情冴下需要使用作业控制块JCB？其中包含了哪些内容？【解】每当作业进入系统时，系统便为每个作业建立一个作业控制块JCB，根据作业类型将它插入到相应的后备队列中。

JCB 包含的内容通常有：1) 作业标识2)用户名称3)用户账户4)作业类型（CPU 繁忙型、I/O芳名型、批量型、终端型）5)作业状态6)调度信息（优先级、作业已运行）7)资源要求8)进入系统时间9) 开始处理时间10) 作业完成时间11) 作业退出时间12) 资源使用情况等5．在作业调度中应如何确定接纳多少个作业和接纳哪些作业？【解】作业调度每次接纳进入内存的作业数，取决于多道程序度。

完美WORD 格式格式专业整理专业整理 知识分享知识分享3-1（1） )(2)(2.0t r t c =（2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==F 单位脉冲响应：s s C /10)(= 010)(³=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(³=t tt c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s f单位脉冲响应：124.004.01)(2++=s s s C t et g t4sin 325)(3-=单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t et et c tt4sin 434cos 1)(33----=3-2温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=F Ts s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Ts s s s G 1)(1)()(=F -F =îíì==11vT K用静态误差系数法，当t t r ×=10)( 时，C T Ke ss°===5.21010。

第三章习题与参考答案3.1 已知 (DS) = 1000H，(ES) = 2000H，(SS) = 3000H，(SI) = 0050H，(BX) =0100H，(BP) =0200H，数据变量DISP的偏移地址为1000。

指出下列指令的寻址方式和物理地址。

(1) MOV AX,0ABH 立即寻址无(2) MOV AX,BX 寄存器寻址无(3) MOV AX,[l000H] 直接寻址 10000H(4) MOV AX,DATA 直接寻址 (DS*16+DATA )(5) MOV AX,[BX] 寄存器间接寻址 10100H(6) MOV AX,ES:[BX] 寄存器间接寻址 20100H(7) MOV AX,[BP] 寄存器间接寻址 30200H(8) MOV AX,[SI] 寄存器间接寻址 10050H(9) MOV Ax,[BX+l0] 寄存器相对寻址 1010AH(10) MOV AX,DISP[BX] 寄存器相对寻址 11100H(1l) MOV AX,[BX+SI] 基址变址寻址 10150H(12) MOV AX,DISP[BX][SI] 相对基址变址寻址 11150H3.2 分别说明下例指令采用的寻址方式和完成的操作功能。

(1) MOV CX,2000H 立即寻址将立即数2000H送CX寄存器(2) MOV DS,AX 寄存器寻址将AX寄存器内容送DS段寄存器(3) AND CH,[1000H] 直接寻址将[DS*16+1000H]单元的内容送CH寄存器(4) ADD [DI],BX 寄存器间接寻址将CL寄存器的内容送[DS*16+DI]单元(5) MOV SS:[3000H],CL 直接寻址将CL寄存器的内容送[SS*16+3000H]单元(6) SUB [BX][SI],1000H 直接寻址将立即数1000H送[DS*16+BX+SI+50H]单元(7) ADD AX,50H[BX][SI] 相对基址变址寻址将[DS*16+BX+SI+50H]单元的内容送AX寄存器(8) PUSH DS 寄存器寻址将DS寄存器的内容送[SS*16+SP]单元(9) CMP [BP][DI],AL 寄存器寻址将AL寄存器的内容送[SS*16+DI+BP]单元3.3 判断下列指令正误，如果错误请指出原因。

第三章 作业与习题的解答一、作业：2、纯铁的空位形成能为105 kJ/mol 。

将纯铁加热到850℃后激冷至室温（20℃），假设高温下的空位能全部保留，试求过饱和空位浓度与室温平衡空位浓度的比值。

(e 31.8=6.8X1013）6、如图2-56，某晶体的滑移面上有一柏氏矢量为b 的位错环，并受到一均匀切应力τ。

（1）分析该位错环各段位错的结构类型。

（2）求各段位错线所受的力的大小及方向。

（3）在τ的作用下，该位错环将如何运动？（4）在τ的作用下，若使此位错环在晶体中稳定不动，其最小半径应为多大？解：（2）位错线受力方向如图，位于位错线所在平面，且于位错垂直。

（3）右手法则（P95）：（注意：大拇指向下，P90图3.8中位错环ABCD 的箭头应是向内，即是位错环压缩）向外扩展（环扩大）。

如果上下分切应力方向转动180度，则位错环压缩。

A B CDττ(4) P103-104： 2sin 2d ϑτdT s b =θRd s =d ； 2/sin 2θϑd d= ∴ τττkGb b kGb b T R ===2 注：k 取0.5时，为P104中式3.19得出的结果。

7、在面心立方晶体中，把两个平行且同号的单位螺型位错从相距100nm 推进到3nm 时需要用多少功（已知晶体点阵常数a=0.3nm,G=7﹡1010Pa ）？ (3100210032ln 22ππGb dr w r Gb ==⎰； 1.8X10-9J ）8、在简单立方晶体的（100）面上有一个b=a[001]的螺位错。

如果它(a)被（001）面上b=a[010]的刃位错交割。

(b)被（001）面上b=a[100]的螺位错交割，试问在这两种情形下每个位错上会形成割阶还是弯折？（（a ）：见P98图3.21， NN ′在（100）面内，为扭折，刃型位错；(b)图3.22，NN ′垂直（100）面，为割阶，刃型位错）9、一个]101[2-=a b 的螺位错在（111）面上运动。

第三章作业3-1 计算习题 3-1 中各散热器所在环路的作用压力 t g =95℃， t g1=85℃， t g2=80℃，t n =70℃。

解:如图示可知，第一个为并联环路双管管网，第二个为串联环路单管管网 系统供回水温度，t g =95℃， t n =70℃，t g1=85℃， t g2=80℃， 对应的密度为，3g kg/m 92.961=ρ，3n kg/m 81.977=ρ，3g1kg/m 65.968=ρ，3g2kg/m 83.971=ρ 并联：【双管路各层散热器的进出水温度是相同的，但是循环作用动力相差很大；】第一楼散热器作用压力：()()Pa 6.46792.96181.977381.9gh P g h 11=-⨯⨯==∆-ρρ第二楼散热器作用压力：()()Pa 3.93592.96181.977681.9gh P g h 22=-⨯⨯==∆-ρρ第三楼散热器作用压力：()()Pa 132592.96181.977681.9gh P g h 33=-⨯⨯==∆-ρρ 串联：【单管路各层散热器的循环作用动力是同一个数，但进出水温度越到下层越低】()()()()()()Pa3.92492.96165.9685.881.965.96883.971681.983.97181.977381.9gH gH gH P g 1g 3g1g22g2n 1h =-⨯⨯+-⨯⨯+-⨯⨯=-+-+=∆-ρρρρρρ3-2 通过水力计算确定习题图 3-2 所示重力循环热水采暖管网的管径。

图中立管Ⅲ、Ⅳ、Ⅴ各散热器的热负荷与Ⅱ立管相同。

只算 I 、II 立管，其余立管只 讲计算方法，不作具体计算，散热器进出水管管长 1.5m ，进出水支管均有截止 阀和乙字弯，每根立管和热源进出口设有闸阀。

解:（1）选择最不利环路。

有图3-2可知，最不利环路是通过立管I 的最底层散热器I 1（1800w ）的环路，这个环路从散热器I 1顺序经过○1、○2、○3、○4、○5、○6、进入锅炉，再经管段○7、○8、○9、○10、○11、○12进入散热器I 1。

第三章 作业与习题的解答一、作业：2、纯铁的空位形成能为105 kJ/mol 。

将纯铁加热到850℃后激冷至室温（20℃），假设高温下的空位能全部保留，试求过饱和空位浓度与室温平衡空位浓度的比值。

(e 31.8=6.8X1013）6、如图2-56，某晶体的滑移面上有一柏氏矢量为b 的位错环，并受到一均匀切应力τ。

（1）分析该位错环各段位错的结构类型。

（2）求各段位错线所受的力的大小及方向。

（3）在τ的作用下，该位错环将如何运动？（4）在τ的作用下，若使此位错环在晶体中稳定不动，其最小半径应为多大？解：（2）位错线受力方向如图，位于位错线所在平面，且于位错垂直。

（3）右手法则（P95）：（注意：大拇指向下，P90图3.8中位错环ABCD 的箭头应是向内，即是位错环压缩）向外扩展（环扩大）。

如果上下分切应力方向转动180度，则位错环压缩。

(4) P103-104： 2sin 2d ϑτdT s b =θRd s =d ； 2/sin 2θϑd d= ∴ τττkGb b kGb b T R ===2 注：k 取0.5时，为P104中式3.19得出的结果。

7、在面心立方晶体中，把两个平行且同号的单位螺型位错从相距100nm 推进到3nm 时需要用多少功（已知晶体点阵常数a=0.3nm,G=7﹡1010Pa ）？ (3100210032ln 22ππGb dr w r Gb ==⎰； 1.8X10-9J ）8、在简单立方晶体的（100）面上有一个b=a[001]的螺位错。

如果它(a)被（001）面上b=a[010]的刃位错交割。

(b)被（001）面上b=a[100]的螺位错交割，试问在这两种情形下每个位错上会形成割阶还是弯折？（（a ）：见P98图3.21， NN ′在（100）面内，为扭折，刃型位错；(b)图3.22，NN ′垂直（100）面，为割阶，刃型位错）9、一个]101[2-=a b 的螺位错在（111）面上运动。