梅森公式例子

梅森公式经典例题摘要：一、梅森公式简介二、梅森公式经典例题解析1.基本形式2.乘积形式3.复合形式4.应用场景三、梅森公式在实际问题中的应用四、总结与拓展正文：一、梅森公式简介梅森公式（Mason"s formula）是一种在概率论和统计学中广泛应用的公式，用于计算离散随机变量概率密度函数的积分。

梅森公式以数学家梅森（Mason）的名字命名，其一般形式如下：若离散随机变量X有n个可能的结果，对应的概率分别为p1, p2, ..., pn，则X的概率密度函数F(x)可以通过梅森公式计算：F(x) = Σ[pi * (1 - p1^(n-i))]二、梅森公式经典例题解析1.基本形式例题1：已知离散随机变量X有3个可能的结果，分别对应的概率为1/3，1/4，1/5。

求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/3) * (1 - 1/3^2) + (1/4) * (1 - 1/4^2) + (1/5) * (1 - 1/5^2)2.乘积形式例题2：已知离散随机变量X有2个可能的结果，分别为A和B，对应的概率分别为1/2和1/3。

若事件A和事件B互斥，求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/2) * (1 - 1/2^2) * (1 - 1/3^2)3.复合形式例题3：已知离散随机变量X有两个可能的结果A和B，对应的概率分别为1/2和1/3。

若随机变量Y = X + 1，求Y的概率密度函数。

解：根据梅森公式，计算得到：F(y) = (1/2) * (1 - 1/2^2) * (1 - 1/(y-1)^2)4.应用场景梅森公式在概率论和统计学中有广泛的应用，例如计算离散随机变量的累积分布函数、概率密度函数等。

此外，梅森公式还可以用于求解马尔可夫链、泊松分布等问题。

三、梅森公式在实际问题中的应用在实际问题中，梅森公式可以用于解决各种概率论和统计学问题。

梅森增益公式三个互不接触的回
路例题
梅森公式是梅森在创建流图时提出的一种计算传递函数的方法。

因为信号流程和框图没有本质区别，所以完全适用于框图。

它使传递函数的计算变得简单，过程完全格式化。

梅森增益公式三个互不接触的回路例题 1
如果两个回路之间没有共同点，则简称为两个非接触回路，否则称为接触，两个非接触回路的每个回路的增益的乘积称为两个非接触回路的增益。

同样，三个回路之间没有共同点，称为三个非接触回路，每个回路的增益的乘积称为三个非接触回路的增益。

如此类推，共计有n个回路的系统最多存在一个n个互不接触回路。

如果不存在b个互不接触回路，则一定不存在大于b的互不接触回路。

方框图是一种很有用的图示法，但对于复杂的控制系统，方框图的简化过程仍较复杂，且易出错.mason提出的倍号流图，既能及示系统的特点，而且还能直接应用梅森公式方便地写出系统的传递函数。

因此，信号流图在控制工程中也被广泛地应用。

信号流图是一种衣示线性化代数方程组变量间关系的图示方法，信号流图由节点和支路组成，每一个节点用符号“〇”表示系统的一个变量，而每两个节点间的支路用符号“一>” 连接，表示这两个变量之间信号的传输关系，信号流向由支路
上的箭头表示，而传输关系（增益、传递函数）则标注在支路上。

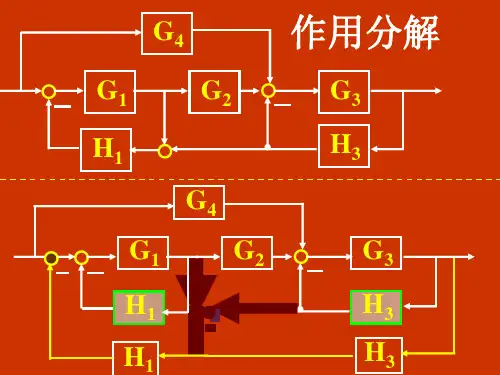
用梅森公式求传递函数例题
传递函数是描述系统输入和输出之间关系的数学表达式。

梅森公式是一种求解传递函数的方法，可以通过已知系统的差分方程来推导出传递函数表达式。

下面是一个例题：
考虑一个二阶离散系统，其差分方程为：
y[n] + 0.5y[n-1] - 0.25y[n-2] = x[n] + 0.2x[n-1]
我们要求解该系统的传递函数。

首先，将差分方程中的所有变量的z变换代替，其中z是复变量，表示单位延迟。

将y[n]表示为Y(z)，x[n]表示为X(z)，则有：Y(z) + 0.5z^(-1)Y(z) - 0.25z^(-2)Y(z) = X(z) + 0.2z^(-1)X(z)
整理得到传递函数表达式：
H(z) = Y(z)/X(z) = (1 + 0.5z^(-1) - 0.25z^(-2))/(1 + 0.2z^(-1))
这就是所求的该二阶离散系统的传递函数。

需要注意的是，梅森公式只适用于线性、时不变、时域因果的离散系统。

在实际应用中，我们可以通过求解差分方程或直接对系统的零极点进行分析来得到传递函数。

6-5 系统的信号流图与梅森公式一、信号流图的定义由节点与有向支路构成的能表征系统功能与信号流动方向的图，称为系统的信号流图，简称信号流图或流图。

例如，图6-29(a)所示的系统框图，可用图6-29(b)来表示，图(b)即为图(a)的信号流图。

图(b)中的小圆圈“o”代表变量，有向支路代表一个子系统及信号传输(或流动)方向，支路上标注的H(s)代表支路(子系统)的传输函数。

这样，根据图6-29(b)，同样可写出系统各变量之间的关系，即图6-29二、三种运算器的信号流图表示三种运算器：加法器、数乘器、积分器的信号流图表示如表6-3中所列。

由该表中看出：在信号流图中，节点“o”除代表变量外，它还对流入节点的信号具有相加(求和)的作用，如表中第一行中的节点Y(s)即是。

三、模拟图与信号流图的相互转换规则模拟图与信号流图都可用来表示系统，它们两者之间可以相互转换，其规则是：(1) 在转换中，信号流动的方向(即支路方向)及正、负号不能改变。

(2) 模拟图(或框图)中先是“和点”后是“分点”的地方，在信号流图中应画成一个“混合”节点，如图6-30所示。

根据此两图写出的各变量之间的关系式是相同的，即。

(3) 模拟图(或框图)中先是“分点”后是“和点”的地方，在信号流图中应在“分点”与“和点”之间，增加一条传输函数为1的支路，如图6-31所示。

(4) 模拟图(或框图)中的两个“和点”之间，在信号流图中有时要增加一条传输函数为1的支路(若不增加，就会出现环路的接触，此时就必须增加)，但有时则不需增加(若不增加，也不会出现环路的接触，此时即可以不增加。

见例6-17)。

(5) 在模拟图(或框图)中，若激励节点上有反馈信号与输入信号叠加时，在信号流图中，应在激励节点与此“和点”之间增加一条传输函数为1的支路(见例6-17)。

(6) 在模拟图(或框图)中，若响应节点上有反馈信号流出时，在信号流图中，可从响应节点上增加引出一条传输函数为1的支路(也可以不增加，见例6-17)。

梅森公式简介梅森公式是用来判断一个自然数是否为梅森数的公式。

梅森数是指形如2^p - 1的素数，其中p是一个自然数。

梅森公式可以用来生成梅森数，并且能够高效地验证一个给定的梅森数是否为素数。

梅森数的生成梅森数的生成基于梅森公式。

根据梅森公式，如果一个数p是素数，那么2^p - 1也是一个梅森数。

这个公式由法国数学家梅森（Marin Mersenne）在17世纪提出。

下面给出一个例子来说明梅森数的生成过程。

假设我们要生成第n个梅森数。

首先，我们需要找到第n个素数p。

我们可以使用素数生成算法来生成素数序列，并取第n个素数作为p的值。

接下来，我们使用梅森公式计算得到梅森数M，即M =2^p - 1。

这个过程可以简化为对2进行p次幂运算，然后减去1得到最终的梅森数。

验证梅森数的素性验证一个给定的梅森数是否为素数是一个关键的问题。

传统的素数测试算法在验证大数是否为素数时效率较低，而梅森公式给出了一种高效的验证方法。

根据梅森公式，如果一个梅森数M是素数，那么对于所有小于M的素数q，满足以下条件：2^q ≡ 1 (mod M)。

这个条件可以用来验证一个梅森数的素性。

具体的验证过程如下：1.首先，选择一个小于M的素数q（通常选择q为M的因子）。

2.计算2^q (mod M)的值。

3.如果计算得到的值等于1，那么继续选择下一个小于M的素数q进行计算。

若计算得到的值不等于1，说明M不是素数。

4.如果所有小于M的素数都满足2^q ≡ 1 (mod M)，那么M就是一个素数。

由于梅森数是形如2^p - 1的数，所以可以利用快速幂算法来高效地计算2^q (mod M)的值。

这样，通过选择合适的q和运用快速幂算法，可以在较短的时间内验证一个梅森数的素性。

应用和发展梅森数及其相关的梅森公式在数论和密码学中具有重要的应用和研究价值。

梅森数作为一类特殊的素数，具有较大的数值和特殊的性质，因此在数论研究中具有重要的地位。

梅森数也广泛应用于密码学领域，例如在RSA公钥加密算法中，使用了素数p和q的梅森数形式来增强算法的安全性。

是包含于，你理解的有点偏差，举个例子如果有三个互不接触的回路，取两个不接触的回路应有三项，取三个互不接触回路就一项。

具体的应该是这样：
梅森公式G(s)=Σ(Ρκ*△κ)╱△G(s)= ——系统总传递函数；n——是前向通道数；Ρκ——第k条前向通路的传递函数，由输入端单向传递至输出端的信号通道称为前向通道；△——流图的特征式△=1-ΣLi+ΣLjLk-ΣLiLjLk+······
L A
bc为每两个不接触回路增益乘积之和
a为所有回路增益之和；L a L b
Li——所有单独回路的增益之和；
LjLk——所有互不接触的单独回路中，取其中两个不接触的回路增益乘积之和；LiLjLk——所有互不接触的单独回路中，取三个互不接触回路增益之和；
△κ——第k条前向通路特征式的余因子，即对于流图的特征式△，将与第k 条前向通路相接触的回路
增益代以零值，余下的即为△κ。

对于复杂的结构，理论上有很多项，但实际上△就取到前两三项。

梅森增益公式推导梅森增益公式（Mason's Gain Formula）在控制工程和信号处理领域可是个相当重要的家伙！它能帮助咱们轻松搞定复杂系统的增益计算，可省了不少事儿。

先来说说啥是梅森增益公式。

简单来讲，它就是一个能让咱不费劲地求出系统传递函数（也就是增益）的神奇公式。

这公式长这样：\[G = \frac{1}{\Delta} \sum_{k} P_k \Delta_k\]这里的\(G\)就是系统的总增益啦，\(\Delta\)是特征式，\(P_k\)是第\(k\)条前向通路的增益，\(\Delta_k\)是第\(k\)条前向通路的余子式。

要推导这个公式，咱们得先从系统的信号流图入手。

信号流图就像是系统的“路线图”，能清晰地展示各个信号之间的关系。

比如说，咱们假设有个简单的系统，就像一个小工厂的生产线。

这个生产线有几个环节，每个环节对产品的处理就像是对信号的加工。

有的环节会让产品变得更好（增益为正），有的环节可能会让产品有点小瑕疵（增益为负）。

咱们先看看前向通路。

前向通路就像是生产线上的一条“直达通道”，从输入直接到输出，中间没有任何回头路或者岔路口。

计算每条前向通路的增益\(P_k\)相对来说还算简单，就是把这条路上各个环节的增益乘起来就行。

接下来是特征式\(\Delta\)。

这玩意儿可有点复杂，它得考虑到系统中的所有回路。

回路就像是生产线上绕了一圈又回到原点的小段，会对信号产生反复的影响。

计算特征式的时候，咱们得把每个回路的增益加起来，再减去两两回路乘积之和，再加上三个回路乘积之和，以此类推。

这听起来有点晕乎，但其实就是个规律，多算几次就熟悉了。

再说说余子式\(\Delta_k\)。

它是在去掉与第\(k\)条前向通路有关的节点和支路后，剩下部分的特征式。

咱们通过一个具体的例子来瞅瞅。

假设咱们有个系统，信号流图长成这样：有两个输入节点，三个中间处理节点，一个输出节点。

其中有两条前向通路，还有几个回路。

梅森公式的适用条件梅森公式在控制工程领域可是个相当重要的工具，它能帮助咱们在复杂的系统中快速求出传递函数。

但您知道吗，它可不是随便就能用的，得满足一些特定的条件才行。

咱先来说说梅森公式适用的系统得是线性的。

这就好比搭积木，每一块积木都得按照一定的规则来放，要是有哪块不守规矩，整个结构就可能不稳定。

比如说，一个电路系统里，电阻、电容、电感这些元件的关系得是线性的，电流和电压的变化得遵循线性规律，不能突然来个“大反转”，要不然梅森公式可就抓瞎啦。

还有呢，系统得是确定的。

啥叫确定？就是系统的结构和参数都得明明白白，不能一会儿变一个样。

我之前碰到过一个学生做的电路实验，他自己都没搞清楚到底用的是多大阻值的电阻，一会儿说是这个，一会儿又说是那个，这样的情况，梅森公式可没法帮忙。

再有就是系统得是单输入单输出的。

这就好像是从一个门进去，又从一个门出来，不能这边进几个，那边出几个，乱了套。

举个例子，咱们家里的电灯开关，按一下灯亮，再按一下灯灭，这就是单输入单输出，梅森公式就能派上用场。

另外，系统中的回路之间不能有接触。

这就好比是几条路，它们得各自独立，不能有交叉或者重叠的部分。

我记得有一次给学生讲这个知识点的时候，有个调皮的学生说：“老师，这就像是不能让几条小路手牵手嘛！”把大家都逗乐了。

总之，梅森公式虽好，但得在对的条件下使用，不然就会得出错误的结果。

就像我们做事一样，得找准方法，用对工具，才能事半功倍。

希望大家在学习和应用梅森公式的时候，都能牢记这些适用条件，让它真正成为我们解决问题的得力助手！。

梅森公式经典例题摘要：一、梅森公式简介1.梅森公式的定义2.梅森公式在数学中的重要性二、经典例题解析1.例题一：利用梅森公式求解2.例题二：利用梅森公式求解3.例题三：利用梅森公式求解三、例题解答与总结1.例题一解答2.例题二解答3.例题三解答4.总结：梅森公式在解题中的应用与技巧正文：一、梅森公式简介梅森公式，又称伯努利公式，是数学领域中一个非常重要的公式。

它是由瑞士数学家雅各布·伯努利（Jacob Bernoulli）提出的，用于描述调和级数的性质。

梅森公式在数学中具有很高的地位，被广泛应用于组合数学、概率论、数论等多个领域。

二、经典例题解析接下来，我们将通过三个经典例题来解析梅森公式在实际问题中的应用。

例题一：利用梅森公式求解题目：已知等差数列的前n 项和为S_n，求S_n^2 与n^3 之间的关系。

解答：根据梅森公式，我们可以得到S_n = n*(2a + (n-1)*d)/2，其中a 为数列的首项，d 为公差。

将S_n 代入S_n^2 中，我们可以得到S_n^2 = n^2*(4a^2 + 4a*d + d^2 + 2a*(n-1)*d)/4。

通过化简，我们可以发现S_n^2 与n^3 之间的关系为S_n^2 = n^2*(2a^2 + 2a*d + d^2)/4 +n^3*(a*d - a^2)/4。

例题二：利用梅森公式求解题目：求解组合数C(n, k) 的梅森公式表示。

解答：根据梅森公式，我们可以得到C(n, k) = n! / (k! * (n-k)!)。

将C(n, k) 的定义代入梅森公式中，我们可以得到C(n, k) = (n*(n-1)*...*(n-k+1)) / (k*(k-1)*...*1)。

进一步化简，我们可以得到C(n, k) = n*(n-1)*...*(n-k+1) / k!。

例题三：利用梅森公式求解题目：已知正整数n，求解1^2 + 2^2 + ...+ n^2 的值。

梅森公式经典例题
梅森公式（Mersenne prime）是指形如2^p-1的素数，其中p
是大于1的素数。

梅森公式称为公式是因为这种形式的素数是由法国数学家梅森首先研究并发现的。

经典的梅森公式例题如下所示：
1. 验证2^3-1是否是梅森素数。

解答：根据梅森公式，首先要验证指数p是素数。

3是素数，然后计算2^3-1=7，7也是素数。

所以2^3-1是梅森素数。

2. 计算2^5-1。

解答：首先验证指数5是素数，然后计算2^5-1=31。

因为
31是素数，所以2^5-1是梅森素数。

3. 试证明如果p是一个奇素数，那么2^p-1也是一个梅森素数。

解答：假设p是一个奇素数，我们需要证明2^p-1是一个梅
森素数。

根据梅森公式，指数p是素数，我们已知p是素数，然后计算2^p-1。

因为p是奇素数，所以2^p-1是一个整数。

接下来需要证明2^p-1是一个素数。

这个证明可以通过利用数
学归纳法来进行。

以上是一些经典的梅森公式例题，希望对你有帮助！。

、 梅森公式(Mason ’s Formula)从系统的信号流图直接求系统函数()()()s F s Y s H =的计算公式，称为梅森公式。

该公式如下：()()()∑∆∆==k kk P 1s F s Y s H (6-34)此公式的证明甚繁，此处略去。

现从应用角度对此公式予以说明。

式中+-+-=∆∑∑∑r,q .p r q p n,m n m iI L L L L L L 1 (6-35)Δ称为信号流图的特征行列式。

式中：i L 为第i 个环路的传输函数， i i L 为所有环路传输函数之和；n m L L 为两个互不接触环路传输函数的乘积，n m L mL 为所有两个互不接触环路传输函数乘积之和；r q p L L L 为三个互不接触环路传输函数的乘积， ∑rq,p,rq p L L L 为所有三个互不接触环路传输函数乘积之和；k P 为由激励节点至所求响应节点的第k 条前向开通路所有支路传输函数的乘积；k ∆为除去第k 条前向通路中所包含的支路和节点后所剩子流图的特征行列式。

求k ∆的公式仍然是式(6-35)。

例6-19 图6-34(a)所示系统。

求系统函数()()()s F s Y s H =。

解：1 求Δ(1) 求∑iiL：该图共有5个环路，其传输函数分别为2L 1=，8,42L 2=⨯=()-11-1L 3=⨯= 2L 4=，()421-2L 5=⨯⨯-=故 ∑iiL15L L L L L 54321=++++=)s ()a ()b图6-34(2) 求 ∑nm,nmL L:该图中两两互不接触的环路共有3组：()1628L L 422L L 212L L 424131=⨯==⨯=-=-⨯=故 18L L L L L L L L424131nm,n m=++=∑该图中没有3个和3个以上互不接触的环路，故有 0LL L rrq,p,qp=∑；…。

故得418151L L L L L L -1r rq,p,q p n,m n m ii =+-=+-+=∆∑∑∑2 求∑∆kkk P(1) 求k P ：该图共有3个前向通路，其传输函数分别为1111P 1=⨯⨯=()-41141-1P 2=⨯⨯⨯⨯= ()()2121-1P 3=⨯-⨯⨯=(2) 求k ∆:除去1P 前向通路中所包含的支路和节点后，所剩子图如图6-34(b)所示。