第八章 RLC电路与常微分方程的
- 格式:ppt
- 大小:302.00 KB
- 文档页数:48

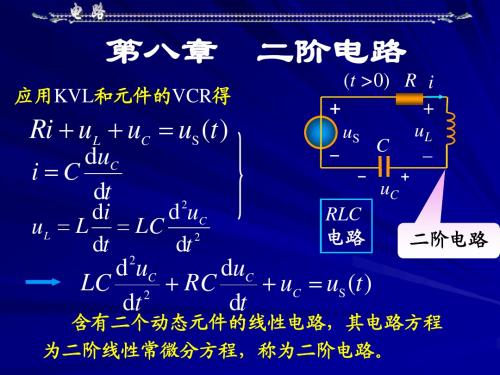
关于RLC二阶电路的分析方法——电路的微分方程与初始条件RLC二阶电路是由电感(L)、电阻(R)和电容(C)三个元件组成的电路。
在分析RLC二阶电路时,通常需要建立电路的微分方程,并考虑初始条件。
下面将详细介绍关于RLC二阶电路的分析方法。
首先,我们需要建立RLC二阶电路的微分方程。
对于串联的RLC电路,电感、电阻和电容的电压可以分别表示为VL、VR和VC。
根据基尔霍夫电压定律,我们可以得到以下微分方程:VL+VR+VC=0(1)根据电感和电容的特性,我们有以下关系式:VL = L(diL/dt) (2)VC = (1/C) ∫idt (3)将式(2)和式(3)代入式(1)中,我们可以得到电路的微分方程:L(diL/dt) + R(dL/dt) + (1/C) ∫i dt = 0 (4)其中i是电流。
对于并联的RLC电路,电感、电阻和电容的电流可以分别表示为IL、IR和IC。
类似地,根据基尔霍夫电流定律,我们可以得到以下微分方程:IL+IR+IC=0(5)根据电感和电容的特性,我们有以下关系式:IL = (1/L) ∫V dt (6)IC = C(dVc/dt) (7)将式(6)和式(7)代入式(5)中,我们可以得到电路的微分方程:(1/L) ∫V dt + R(dV/dt) + C(d^2V/dt^2) = 0 (8)其中V是电压。
以上就是建立RLC二阶电路微分方程的方法。
接下来,我们需要考虑电路的初始条件。
电路的初始条件指的是在t=0时刻的电流和电压值。
对于串联电路,初始条件为i(0)和v(0);对于并联电路,初始条件为v(0)和i(0)。
当我们知道初始条件后,可以将其代入微分方程中,求解得到电路的解析解或数值解,从而得到电路的电流和电压随时间的变化规律。
总结起来,RLC二阶电路的分析方法包括以下步骤:1.建立电路的微分方程,根据电路的连接方式选择合适的微分方程。
2.考虑电路的初始条件,确定t=0时刻的电流和电压值。



rlc电路微分方程例题
好的,让我们来看一个简单的RLC电路。
假设我们有一个由电
阻(R)、电感(L)和电容(C)组成的串联RLC电路。
我们可以通
过基尔霍夫电压定律和基尔霍夫电流定律来建立微分方程。
首先,我们可以使用基尔霍夫电压定律来建立电路的微分方程。
假设电感两端的电压为v_L(t),电容两端的电压为v_C(t),电阻两
端的电压为v_R(t),电源电压为v_s(t)。
根据基尔霍夫电压定律,我们有:
L(di/dt) + v_R + v_C = v_s.
其中,di/dt是电感电流的变化率。
电阻两端的电压v_R等于
电阻R与电感电流i的乘积,即v_R = Ri。
电容两端的电压v_C等
于电容C与电压v_C的变化率的乘积,即v_C = (1/C)∫i dt。
代
入这些关系,我们可以得到RLC电路的微分方程。
另一种方法是使用基尔霍夫电流定律来建立微分方程。
根据基
尔霍夫电流定律,电路中的总电流等于电感电流i加上电容电流
i_C,即i = i_L + i_C。
根据电感和电容元件的特性,我们可以得
到i_L = L(di/dt)和i_C = C(dv_C/dt)。
将这些关系代入基尔霍夫电流定律,我们同样可以得到RLC电路的微分方程。
综上所述,建立RLC电路的微分方程可以通过基尔霍夫电压定律或者基尔霍夫电流定律来实现。
这些微分方程可以用来描述电路中电流和电压随时间变化的规律。
希望这个例子能帮助你理解RLC 电路微分方程的建立过程。

数学与微分方程解析微分方程在科学与工程领域中的应用案例在科学与工程领域中,微分方程是一种重要的数学工具,用于描述物理、化学、生物等领域中的各种现象和问题。
微分方程解析的应用案例有很多,下面将介绍其中一些典型的案例。
案例一:电路中的RLC电路在电路中,RLC电路是一种常见的电路类型,由电阻(R)、电感(L)和电容(C)组成。
我们可以利用微分方程来描述电路中电压和电流的变化情况。
设电容的电压为Vc(t),电感的电流为I(t),电阻上的电压为VR(t)。
根据基尔霍夫电压定律和欧姆定律,可以得到如下微分方程:L(dI/dt) + RI + 1/C∫I(t)dt = V(t)通过解这个微分方程,我们可以得到电路中电流和电压随时间的变化规律,从而对电路的稳定性和响应进行分析和预测。
案例二:化学反应动力学在化学反应中,微分方程可以用来描述反应物的浓度随时间的变化规律。
例如,一级反应的速率可以用下面的微分方程来表示:d[A]/dt = -k[A]其中,[A]表示反应物A的浓度,k为反应速率常数。
通过求解这个微分方程,我们可以得到反应物浓度随时间的变化曲线,从而研究反应的速率和影响因素。
案例三:机械振动系统在工程领域中,微分方程可以用来描述机械振动系统的运动规律。
例如,单自由度弹簧振子的运动可以由下面的微分方程表示:m(d2x/dt2) + kx = 0其中,m为质量,k为弹簧的弹性系数,x为位移。
通过求解这个微分方程,我们可以得到振子的运动规律,包括振幅、频率和相位等信息。
案例四:人口增长模型微分方程还可以用来描述人口增长模型。
例如,常见的Logistic增长模型可以用下面的微分方程表示:dP/dt = rP(1-P/K)其中,P表示人口数量,r为人口增长率,K为环境容量。
通过解这个微分方程,我们可以研究人口的增长趋势和极限状态。
总结:微分方程在科学与工程领域中有着广泛的应用,上述案例只是其中的一部分。
数学与微分方程解析的应用可以帮助科学家和工程师更好地理解和预测自然和人工系统的行为,优化设计和控制方案。
rlc电路微分方程例题全文共四篇示例,供读者参考第一篇示例:RLC电路是一种常见的电路类型,由电阻(R)、电感(L)、电容(C)三种元件组成。
在电路中,产生电压和电流的关系可以用微分方程表示。
本文将为大家介绍关于RLC电路的微分方程例题,希望能帮助大家加深对此知识的理解。
假设我们有一个串联RLC电路,电阻的阻值为R欧姆,电感的电感值为L亨利,电容的电容值为C法拉。
当电路中的电压源为E(t)伏特时,可以通过基尔霍夫定律建立电路的微分方程。
根据基尔霍夫定律,在电路中,电压源E(t)等于电阻、电感和电容元件上的电压之和。
电阻上的电压可以表示为IR,电感上的电压可以表示为L(di/dt),电容上的电压可以表示为Q/C,其中Q为电容器上的电荷。
根据电压和电流的关系可以得到以下方程:E(t) = IR + L(di/dt) + Q/CI为电流强度,di/dt为电流的变化率,Q为电容器上的电荷。
我们知道电流等于电荷的导数,即I = dQ/dt,根据此关系可以对方程进行求导整理得到:对上式做微分运算,可以得到RLC电路的微分方程:这个微分方程描述了RLC电路中电荷Q随时间的变化情况。
通过解这个微分方程,我们可以得到电荷Q随时间的具体变化规律,从而了解电路中电流的行为。
下面我们通过一个具体的例题来演示如何解决RLC电路的微分方程。
假设一个串联RLC电路中,电阻R = 2欧姆,电感L = 1亨利,电容C = 0.5法拉,电压源为E(t) = 6sin(2t)伏特。
我们需要求解电路中电荷Q随时间的变化情况。
根据上述微分方程,我们有:带入已知的数值,得到:这是一个二阶常系数非齐次线性微分方程。
我们可以通过常数变易法或者拉普拉斯变换等方法进行求解。
在这里,我们选择通过试解法来求解该微分方程。
假设Q(t) = A cos(2t) + B sin(2t)是微分方程的一个特解,代入原方程,整理后可得到:Q(t) = -2.4sin(2t) + 0.224cos(2t) + (6/5)sin(2t)电路中电荷Q随时间的变化规律可表示为:通过上述例题的求解过程,我们可以看到如何使用微分方程求解RLC电路中电荷的变化情况。