五年级下册数学试题-五升六讲义第3讲找规律(奥数版块)北师大版(1)

书之屋教育
找规律补充篇
例1、将1到200的自然数，分别分成A、B、C三组。

A组：1,6,7,12,13,18,…
B组：2,5,8,11,14,17,…
C组 3,4,9,10,15,16,…
根据3组的规律，请回答：
(1)B组中一共有（）个自然数。

(2)A组中第24个数是（）。

(3)178是（）组里的第（）个数。

例2、2004年1月1日是星期四，这年的国庆节是星期几？
知识巩固
1、一条小虫，由幼虫长到成虫，每天长大1倍，10天长到10厘米，长到2.5厘米需要（）天。

2、有一列数，第一个数是6，第二个数是3，从第二个数起，每个数都比它前面那个数与后面那个数的和小5。

那么这列数从第一个数起到第2004个数为止的2004个数之和是_______。

3、如右图，每个小方格的边长为1厘米，
从A点开始画折线，并依次给每条线
段编号，那么编号为2004的线段长
是几厘米？
4、在下列数列中1, 2, 3, 2，3，4, 3，4, 5，4, 5，6 ,5 ,6 ，7…从左向右数第100个数是____。

5、80朵花，按2红，3黄，4白顺序排列，最后一朵是（）颜色，红花有（）朵，黄花（）朵，白花（）朵。

6、如图所示是一个堆放铅笔的V型架，它的最下面
一层放1支铅笔，往上每一层都比它下面一层多
放一支铅笔，最上面放了100支，问这个V型
架上共放了( )支铅笔。

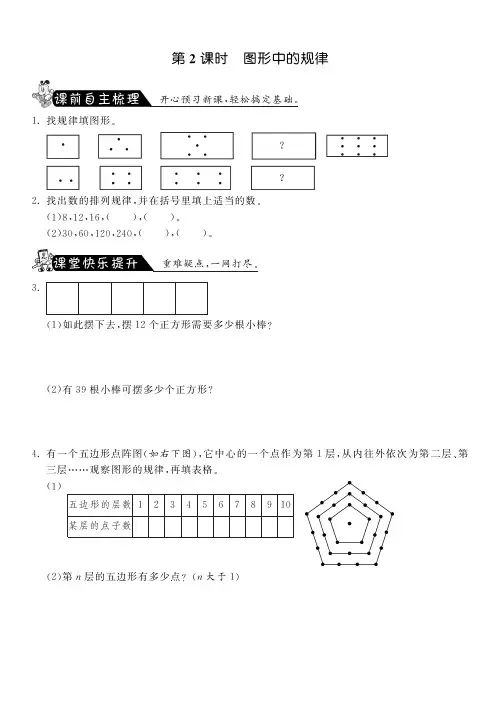
第2课时图形中的规律
开心预习新课,轻松搞定基础㊂
1.找规律填图形㊂
2.找出数的排列规律,并在括号里填上适当的数㊂
(1)8,12,16,(),()㊂
(2)30,60,120,240,(),()㊂
重难疑点,一网打尽㊂
3.
(1)如此摆下去,摆12个正方形需要多少根小棒?
(2)有39根小棒可摆多少个正方形?
4.有一个五边形点阵图(如右下图),它中心的一个点作为第1层,从内往外依次为第二层㊁第
三层 观察图形的规律,再填表格㊂
(1)
五边形的层数12345678910
某层的点子数
(2)第n层的五边形有多少点?(n大于1)
源于教材,宽于教材,拓展探究显身手㊂
5.一个正方形,每个面上分别写着1,2,3,4,5,6,有三个人从不同的角度观看,结果如下图:
这个正方体上每个数字的对面是什么数?
6.在括号里填上合适的数㊂
(1)1,4,7,10,(),()㊂
(2)2,3,5,8,12,(),()㊂
(3)1,3,9,27,(),()㊂
7.按顺序观察下图的变化规律,想一想在 ? 处应选择哪一个图形?
?
8.如下图,在正三角形内画小正三角形㊂
图形编号123456 100
正三角形的个数
第2课时
1.
2.(1)2024(2)480960
3.(1)37根(2)12个
4.(1)1 5 10 15 20 25 30 35 40 45 (2)5(n-1)
5.1对面是52对面是43对面是6
6.(1)1316(2)1723(3)81243
7.② 8.159131721397。

北师大版最新小学五年级下册数学奥数题带答案图文百度文库一、拓展提优试题1．观察下表中的数的规律，可知第8行中，从左向右第5个数是．2．（7分）对于a、b，定义运算“@”为：a@b＝（a+5）×b，若x@1.3＝11.05，则x＝．3．如图，在梯形ABCD中，若AB＝8，DC＝10，S△AMD＝10，S△BCM＝15，则梯形ABCD的面积是．4．某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B 两人各自答题，得分之和是58分，A比B多得14分，则A答对道题．5．如图，若长方形S长方形ABCD＝60平方米，S长方形XYZR＝4平方米，则四边形S四边＝平方米．形EFGH6．解放军战士在洪水不断冲毁大坝的过程中要修好大坝，若10人需45分钟，20人需要20分钟，则14人修好大坝需分钟．7．四位数的所有因数中，有3个是质数，其它39个不是质数．那么，四位数有个因数．8．对于自然数N，如果1﹣9这九个自然数中至少有六个数可以整除N，则称N是一个“六合数”，则在大于2000的自然数中，最小的“六合数”是．9．将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）10．（8分）如果两个质数的差恰好是2，称这两个质数为一对孪生质数．例如3和5是一对孪生质数，29和31也是一对孪生质数．在数论研究中，孪生质数是最热门的研究课题之一．华裔数学家张益唐在该课题的研究中取得了令人瞩目的成就，他的事迹激励着更多的青年学子投身数学研究．在不超过100的整数中，一共可以找到对孪生质数．11．小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后在道队尾继续排队领，直到鱼干发完．若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是．12．（15分）甲、乙两船顺流每小时行8千米，逆流每小时行4千米，若甲船顺流而下，然后返回；乙船逆流而上，然后返回，两船同时出发，经过3小时同时回到各自的出发点，在这3小时中有多长时间甲、乙两船同向航行？13．（8分）一个大于1的正整数加1能被2整除，加2能被3整除，加3能被4整除，加4能被5整除，这个正整数最小是．14．（8分）在如图每个方框中填入一个数字，使得乘法竖式成立．那么，两个乘数的和是．15．定义新运算：θa＝，则（θ3）+（θ5）+（θ7）（+θ9）+（θ11）的计算结果化成最简真分数后，分子与分母的和是．16．（8分）小胖把这个月的工资都用来买了一支股票．第一天该股票价格上涨，第二天下跌，第三天上涨，第四天下跌，此时他的股票价值刚好5000元，那么小胖这个月的工资是元．17．观察下面数表中的规律，可知x＝．18．同学们去春游，带水壶的有80人，带水果的有70人，两样都没带的有6人．若既带水壶又带水果的人数是所有参加春游人数的一半，则参加春游的同学共有人．19．如图，在△ABC中，D、E分别是AB、AC的中点，且图中两个阴影部分＝．（甲和乙）的面积差是5.04，则S△ABC20．如图，魔术师在一个转盘上的16个位置写下来了1﹣16共16个数，四名观众甲、乙、丙、丁参与魔术表演．魔术师闭上眼，然后甲从转盘中选一个数，乙、丙、丁按照顺时针方向依次选取下一个数，图示是一种可能的选取方式，魔术师睁开眼，说：“选到偶数的观众请举手．”，这时候，只有甲和丁举手，这时候魔术师就大喝一声：“我知道你们选的数了！”．你认为甲和丁选的数的乘积是．21．商店对某饮料推出“第二杯半价”的促销办法．那么，若购买两杯这种饮料，相当于在原价的基础上打折．22．（12分）甲、乙两人从A地步行去B地．乙早上6：00出发，匀速步行前往；甲早上8：00才出发，也是匀速步行．甲的速度是乙的速度的2.5倍，但甲每行进半小时都需要休息半小时．甲出发后经过分钟才能追上乙．23．（15分）如图，正六边形ABCDEF的面积为1222，K、M、N分别AB，CD，EF的中点，那么三角形PQR的边长是．24．甲乙两人分别从AB两地同时出发相向而行，当甲走到一半时，乙将速度提高一倍，结果两人在距离B地1200米处相遇，并且最后同时到达，那么两地相距米25．由120个棱长为1的正方体，拼成一个长方体，表面全部涂色，只有一面染色的小正方体，最多有块26．先将从1开始的自然数排成一列：123456789101112131415…然后按一定规律分组：1，23，456，7891，01112，131415，…在分组后的数中，有一个十位数，这个十位数是．27．如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”，那么，1000以内最大的“希望数”是．28．星期天早晨，哥哥和弟弟去练习跑步，哥哥每分钟跑110米，弟弟每分钟跑80米，弟弟比哥哥多跑了半小时，结果比哥哥多跑了900米，那么，哥哥跑了米．29．如图，若每个小正方形的边长是2，则图中阴影部分的面积是．30．小松鼠储藏了一些松果过冬．小松鼠原计划每天吃6个松果，实际每天比原计划多吃2个，结果提前5天吃完了松果．小松鼠一共储藏了个松果．31．如图，在等腰直角三角形ABC中，斜边AB上有一点D，已知CD＝5，BD比AD长2，那么三角形ABC的面积是．32．（8分）小张有200支铅笔，小李有20支钢笔．每次小张给小李6支铅笔，小李还给小张1支钢笔．经过次这样的交换后，小张手中铅笔的数量是小李手中钢笔数量的11倍．33．甲、乙两车从A城市出发驶向距离300千米远的B城市．已知甲车比乙车晚出发1小时，但提前1小时到达B城市．那么，甲车在距离B城市千米处追上乙车．34．已知一个五位回文数等于45与一个四位回文数的乘积（即＝45×），那么这个五位回文数最大的可能值是59895．35．如图，正方形的边长是6厘米，AE＝8厘米，求OB＝厘米．36．甲、乙两人进行射击比赛，约定每中一发得20分，脱靶一发扣12分，两人各打10分，共得208分，最后甲比乙多得64分，乙打中发．37．小明从家到学校去上课，如果每分钟走60米，可提前10分钟到校；如果每分钟走50米，要迟到4分钟到校．小明家到学校相距米．38．（8分）有四个人甲、乙、丙、丁，乙欠甲1元，丙欠乙2元，丁欠丙3元，甲欠丁4元．要想把他们之间的欠款结清，只因要甲拿出元．39．如图中，A、B、C、D为正六边形四边的中点，六边形的面积是16，阴影部分的面积是．40．小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元，那么，笔记本每个元，笔每支元．【参考答案】一、拓展提优试题1．解：由图可知，第1行的数为1，第2行的最后一个数为2×2＝4，第3行的最后一个数为3×3＝9，…所以第7行最后一个数为7×7＝49，则第8行第1个数为49+1＝50，第5个数为50+4＝54，故答案为：54．2．解：由定义可知：x @1.3＝11.05，（x +5）1.3＝11.05，x +5＝8.5，x ＝8.5﹣5＝3.5故答案为：3.53．解：△ADM 、△BCM 、△ABM 都等高，所以S △ABM ：（S △ADM +S △BCM ）＝8：10＝4：5，已知S △AMD ＝10，S △BCM ＝15，所以S △ABM 的面积是：（10+15）×＝20，梯形ABCD 的面积是：10+15+20＝45；答：梯形ABCD 的面积是45．故答案为：45．4．解：（58+14）÷2＝72÷2＝36（分）答错：（5×10﹣36）÷（2+5）＝14÷7＝2（道）答对：10﹣2＝8道．故答案为：8．5．解：根据分析，如下图所示：长方形S 长方形ABCD ＝S 长方形XYZR +△AEF +△EFR +△FBG +△FGX +△HCG +△HGY +△DHE +△HEZ＝S 长方形XYZR +2×（a +b +c +d ）⇒60＝4+2×（a +b +c +d ）⇒a +b +c +d ＝28四边形S 四边形EFGH ＝△EFR +△FGX +△HGY +△HEZ +S 长方形XYZR＝a +b +c +d +S 长方形XYZR＝28+4＝32（平方米）．故答案是：32．6．解：假设每人每分钟修大坝1份洪水冲毁大坝速度：（10×45﹣20×20）÷（45﹣20）＝（450﹣400）÷25＝50÷25＝2（份）大坝原有的份数45×10﹣2×45＝450﹣90＝360（份）14人修好大坝需要的时间360÷（14﹣2）＝360÷12＝30（分钟）答：14人修好大坝需30分钟．故答案为：30．7．解：首先根据奇偶位数和相等一定是11的倍数．因数一共的个数是3+39＝42（个），将42分解成3个数字相乘42＝2×3×7．＝a ×b 2×c 6．如果是11×52×26＝17600（不是四位数不满足条件）．再看一下如果这个数字最小是＝11×32×26＝6336．＝3663＝11×37×32．因数的个数共2×2×3＝12（个）．故答案为：12个．8．解：依题意可知：要满足是六合数．分为是3的倍数和不是3的倍数．如果不是3的倍数那么一定是1，2，4，8，5，7的倍数，那么他们的最小公倍数为：8×5×7＝280．那么280的倍数大于2000的最小的数字是2240．如果是3的倍数．同时满足是1，2，3，6的倍数．再满足2个数字即可．大于2000的最小是2004（1，2，3，4，6倍数）不符合题意；2010是（1，2，3，5，6倍数）不符合题意；2016是（1，2，3，4，6，7，8，9倍数）满足题意．2016＜2240；故答案为：20169．解：每一个计算周期运算3步，增加：15﹣12+3＝6，则26÷3＝8…2，所以，100+6×8+15﹣12＝100+48+3＝151答：得到的结果是 151．故答案为：151．10．解：在不超过100的整数中，以下8组：3，5；5，7；11，13；17，19；29，31；41，43；59，61；71，73是孪生质数．故答案为8．11．解：共有6只小猫咪，每发6条鱼重复出现，而278÷6＝46…2，余数是2，则最后一个领到鱼干的小猫咪是B．故答案为：B．12．解：设3小时顺流行驶单趟用时间为x小时，则逆流行驶单趟用的时间为（3﹣x）小时，故：x：（3﹣x）＝4：88x＝4×（3﹣x）8x＝12﹣4x12x＝12x＝1逆流行驶单趟用的时间：3﹣1＝2（小时），两船航行方向相同的时间为：2﹣1＝1（小时），答：在3个小时中，有1小时两船同向都在逆向航行．13．解：根据分析：这个数除以2，3，4，5均余1，那么这个数减去1后就能同时被2，3，4，5整除；2，3，4，5的最小公倍数是60，则这个数为60的倍数加1．又因为这个数大于1，所以这个数最小是61．故答案为：61．14．解：依题意可知：结果的首位是2，那么在第二个结果中的首位还是2．再根据第一个结果中有一个1，那么就是有和数字5相乘以后数字1的进位同时十位数字是偶数才能满足条件，第一个乘数的个位数字只能是2或者3才能满足进位是1．当第一个乘数尾数是2时，首位数字无论是哪一个偶数都不能得到200多的结果．不满足题意．当第一个乘数尾数是3时，来看看偶数的情况．23×9＝207.43，63，83无论乘以数字几都不能构成百位十位是20的结果．故是23×95＝2185，那么23+95＝118．故答案为：11815．解：原式＝++++＝++++＝×（﹣+﹣+…+﹣）＝×（）＝5+24＝29故答案为：2916．解：5000÷（1﹣）÷（1+）÷（1﹣）÷（1+）＝5000××××＝5000（元）答：小胖这个月的工资是5000元．故答案为：5000．17．解：根据分析可得，81＝92，所以，x＝9×5＝45；故答案为：45．18．解：设既带水壶又带水果的为x人，则参加春游的同学共有2x人，由题意可得：80+70﹣x+6＝2x156﹣x＝2x3x＝156x＝52则2x＝2×52＝104答：则参加春游的同学共有104人．故答案为：104．19．解：根据分析，S△BDC＝S△EBC⇒S△DOB＝S△EOC，∴S甲﹣S乙＝（S甲+S△DOB）﹣（S乙+S△EOC）＝5.04，又∵S△BDC ：S△DEC＝BC：DE＝2：1即：S△BDC＝2S△DEC∴S四边形DECB ＝3S△DEC；S△ADE＝S△DEC∴S△ABC ＝S四边形DECB+S△ADE＝4S△DEC，设S△DEC ＝X，则S△BDC＝2X，故有2X﹣X＝5.04，∴X＝5.04，S△ABC ＝4S△DEC＝4X＝4×5.04＝20.16故答案是：20.1620．解：依题意可知：2个偶数中间间隔是2个奇数．发现只有数字10，11，9，12是符合条件的数字．乘积为10×12＝120．故答案为：12021．解：设这种饮料每杯10，两杯售价是20元，实际用了：10+10×，＝10+5，＝15（元），15÷20＝0.75＝75%，所以是打七五折；故答案为：七五．22．解：法一：假设甲一小时走5米，乙一小时走2米，列表如下：时间甲（米）乙（米）时间甲（米）乙（米）0小时043小时7.5100.5小时 2.55 3.5小时10111小时 2.564小时10121.5小时57 4.5小时12.5132小时585小时12.5142.5小时7.59 5.5小时1515观察得5.5小时恰好追上（如果这时间超过了乙，就要用具体追及公式计算追及时间）法二：也可以设甲的速度为每小时10a（甲要休息，实际每小时走5a），乙的速度为每小时4a，因此要追8a．半小时内最多追3a，可以先从要追的8a中扣除3a，因为在此之前不可能追上（之前的距离差不止3a）．之后再开始按每半小时列出，若不够半小时的话，用追及公式算．前面追的5a，相当于每小时追a，可以用5a÷（5a﹣4a）＝5（小时）计算．之后，甲半小时再走2a，乙再走5a，加上还差的3a，正好追上．因此，要追5.5小时，即330分钟．故答案为：330．23．解：如图延长BA和EF交于点O，并连接AE，由正六边形的性质，我们可知S ABCM＝S CDEN＝S EF AK＝六边形面积，根据容斥原理，重叠部分三个三角形面积和等于阴影部分面积，且因为对称，△AKP，△CMQ，△ENR三个三角形是一样的，有KP＝RN，AP＝ER，RP＝PQ，＝，则＝，＝，由鸟头定理可知道3×KP×AP＝RP×PQ，综上可得：PR＝2KP＝RE，那么由三角形AEK是六边形面积的，且S△APK＝S △AKE ，S △APK ＝S ABCDEF ＝47，所以阴影面积为47×3＝141故答案为141．24．2800[解答] 设两地之间距离为S 。

北师大版最新小学五年级下册数学奥数题带答案图文百度文库一、拓展提优试题1．有一行数：1，1，2，3，5，8，13，21，…，从第三个数开始，每个数都是前两个数的和，问在前2007个数中，有是偶数．2．用1，2，3，4，5，6，7，8这八个数字组成两个不同的四位数（每个数字只用一次）使他们的差最小，那么这个差是．3．数一数，图中有多少个正方形？4．如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”，那么，1000以内最大的“希望数”是．5．如图，甲、乙两人按箭头方向从A点同时出发，沿正方形ABCD的边行走，正方形ABCD的边长是100米，甲的速度是乙的速度的1.5倍，两人在E 点第一次相遇，则三角形ADE的面积比三角形BCE的面积大1000平方米．6．已知一个五位回文数等于45与一个四位回文数的乘积（即＝45×），那么这个五位回文数最大的可能值是59895．7．（8分）有四个人甲、乙、丙、丁，乙欠甲1元，丙欠乙2元，丁欠丙3元，甲欠丁4元．要想把他们之间的欠款结清，只因要甲拿出元．8．将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）9．用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数（每个数字只能使用一次，且必须使用）．10．（8分）彤彤和林林分别有若干张卡片：如果彤彤拿6张给林林，林林变为彤彤的3倍；如果林林给彤彤2张，则林林变为彤彤的2倍．那么，林林原有张．11．如图六角星的6个顶点恰好是一个正六边形的6个顶点，那么阴影部分面积是空白部分面积的倍．12．观察下面数表中的规律，可知x＝．13．同学们去春游，带水壶的有80人，带水果的有70人，两样都没带的有6人．若既带水壶又带水果的人数是所有参加春游人数的一半，则参加春游的同学共有人．14．某场考试共有7道题，每道题问的问题都只与这7道题的答案有关，且答案只能是1、2、3、4中的一个．已知题目如下：①有几道题的答案是4？②有几道题的答案不是2也不是3？③第⑤题和第⑥题的答案的平均数是多少？④第①题和第②题的答案的差是多少？⑤第①题和第⑦题的答案的和是多少？⑥第几题是第一个答案为2的？⑦有几种答案只是一道题的答案？那么，7道题的答案的总和是．15．若2副网球拍和7个网球一共220元，且1副网球拍比1个网球贵83元．求网球的单价．【参考答案】一、拓展提优试题1．【分析】因为前两个数相加得偶数，即奇数+奇数＝偶数；同理，第四个数是：奇数+偶数＝奇数，以此类推，总是奇数、奇数、偶数、奇数、奇数、偶数…；每三个数一个循环周期，然后确定2007个数里面有几个循环周期，再结合余数，即可得出偶数的个数．解：2007÷3＝669，又因为，每一个循环周期中有2个奇数，1个偶数，所以前2007个数中偶数的个数是：1×669＝669；答：前2007个数中，有699是偶数．故答案为：699．2．【分析】设这两个数为a，b．，且a＜b．千位最小差只能是1．为了让差尽量小，只能使a其它位数最大，b的其它位数最小．所以要尽量使a的百位大于b的百位，a的十位大于b的十位，a的个位大于b的个位．因此分别是8和1，7和2，6和3，剩下的4，5分给千位．据此解答．解：设这两个数为a，b．，且a＜b．千位最小差只能是1．根据以上分析，应为：5123﹣4876＝247故答案为：247．3．解：通过有规律的数，得出：（1）边长为1的正方形有4×3＝12（个）；（2）边长为2的正方形有6个；（3）边长为3的正方形有2个．（4）以小正方形的对角线为边的正方形有8个；（5）以对角线的一半为边长的正方形是17个；（6）以3个对角线的一半为边长的正方形有1个．所以图中共有正方形：12+6+2+8+17+1＝46（个）．答：图中有46个正方形．4．解：根据分析可得：1000以内最大的“希望数”就是1000以内最大的完全平方数，而已知1000以内最大的完全平方数是312＝961，根据约数和定理可知，961的约数个数为：2+1＝3（个），符合题意，答：1000以内的最大希望数是961．故答案为：961．5．解：由于甲的速度是乙的速度的1.5倍所以两人速度比为：1.5：1＝3：2，所以两人在E点相遇时，甲行了：（100×4）×＝240（米）；乙行了：400﹣240＝160（米）；则EC＝240﹣100×2＝40（米），DE＝160﹣100＝60（米）；三角形ADE的面积比三角形BCE的面积大：60×100÷2﹣40×100÷2＝3000﹣2000，＝1000（平方米）．故答案为：1000．6．解：根据分析，得知，＝45＝5×9既能被5整除，又能被9整除，故a的最大值为5，b＝9，45被59□95整除，则□＝8，五位数最大为59895故答案为：598957．解：根据分析，从甲开始，乙欠甲1元，故甲应得1元，甲欠丁4元，故甲应还4元；清算时，甲还应拿出4﹣1＝3元，此时甲的账就结清了；再看看丁的账，丁得到甲的4元后，还给丙3元，即可结清；再看看丙的账，丙得到丁的3元后，还给乙2元，丙的账也清了；再看看乙的账，乙得到丙的2元后，还给甲1元，乙的账也结清；综上，甲只须先拿出4元还给丁，后得到乙的1元，故而甲总共只须拿出3元．故答案是：3．8．解：每一个计算周期运算3步，增加：15﹣12+3＝6，则26÷3＝8…2，所以，100+6×8+15﹣12＝100+48+3＝151答：得到的结果是 151．故答案为：151．9．解：可以组成下列质数：2、3、5、7、61、89，一共有6个．答：用1、2、3、5、6、7、8、9这8个数字最多可以组成 6个质数．故答案为：6．10．解：彤彤给林林6张，林林有总数的；林林给彤彤2张，林林有总数的；所以总数：（6+2）÷（﹣）＝96，林林原有：96×﹣6＝66，故答案为：66．11．解：根据分析，如图所示，将图进行分割成面积相等的三角形，阴影部分由18个小三角形组成，而空白部分有6个小三角形，故阴影部分面积是空白部分面积的18÷6＝3倍．故答案是：3．12．解：根据分析可得，81＝92，所以，x＝9×5＝45；故答案为：45．13．解：设既带水壶又带水果的为x人，则参加春游的同学共有2x人，由题意可得：80+70﹣x+6＝2x156﹣x＝2x3x＝156x＝52则2x＝2×52＝104答：则参加春游的同学共有104人．故答案为：104．14．解：因为每道题的答案都是1、2、3、4的一个，所以①的答案不宜太大，不妨取1，此时②的答案其实就是7个答案中1和4的个数，显然只能取2、3、4中的一个，若取2，则意味着剩余的题目只能有一道题答案为1，这是④填1，⑦填2，⑤填3，⑥填2，而③无法填整数，与题意矛盾；所以②的答案取3，则剩余的题目答案为1和4各有1道，此时④填2，显然⑦只能填1，那么⑤填2，则4应该是⑥的答案，从而③填3，此时7道题的答案如表；它们的和是1+3+3+2+2+4+1＝16．15．解：220﹣83×2＝220﹣166＝54（元）54÷（2+7）＝54÷9＝6（元）答：网球每个6元．。

五升六试题3一、 选择题(10分)1、在下面的说法中，正确的个数有（ ）A 、1B 、2C 、3D 、4○1甲数的数位比乙数的数位多，所以甲数一定比乙数大；○2最简分数的分子与分母没有公约数；○31立方米比1平方分米要大；○4两个等底等高的三角形不一定能拼成平行四边形；○5两个数的所有公因数都是它们最大公因数的因数。

2、右面是一个正方体的展开图，与C 相对的是 _________ 。

○1 A ○2B ○3E ○4F3、分数单位是81的所有真分数的和是（ ）A 、2B 、3C 、3.5D 、44、两个（不为零）不同自然数相乘，积是（ ）A 、质数B 、合数C 、奇数D 、质数或合数5、把5克盐放入120克水中，盐占盐水的( )A 、231B 、241C 、251D 、261二、填空题（1-13题每空2分，14-23题每题3分，共70分）1、直接写得数：0.4－31＝ ________ 141313 ÷13＝ __________7.15×2.5×18－1.25×28×7.15＝ （353－362 ）×35×36＝ ____ 3＋6＋9＋12＋……＋96＋99＝ __________（21＋31＋41＋51＋61）＋（32＋42＋52＋62）＋（43＋53＋63）＋（54 ＋64）＋65＝2、方程：7X －16＝66＋2X 的解是X ＝_______ 0.8小时＝_______分 75千克＝________吨1、 学校体育组买了28个足球，每个a 元，又买了b 个篮球，每个65元。

则“28a ＋65b ”表示_______。

2、 某校排球队18人合影留念，照6寸照片洗3张照片，需要13元5角。

要另外加洗，每张3角，如果每人各得一张，平均每人需交 _________ 元钱。

3、 买5张桌子和10把椅子共400元，买1张桌子和2把椅子的价钱正好相等。

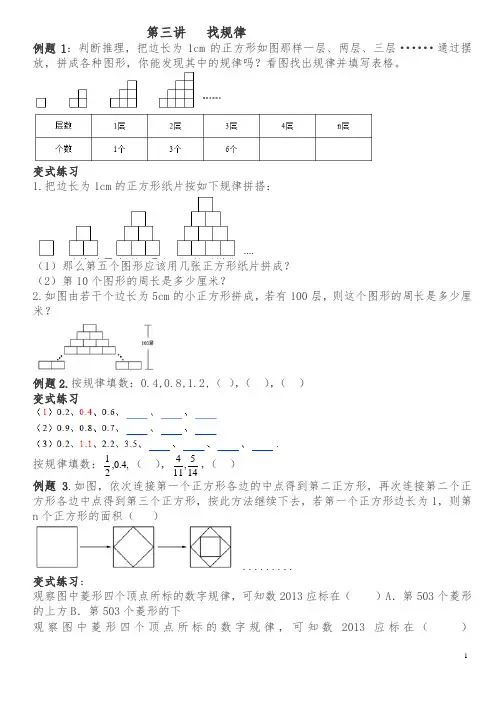
第三讲 找规律例题1：判断推理，把边长为1cm 的正方形如图那样一层、两层、三层······通过摆放，拼成各种图形，你能发现其中的规律吗？看图找出规律并填写表格。

变式练习1.把边长为1cm 的正方形纸片按如下规律拼搭：（1）那么第五个图形应该用几张正方形纸片拼成？（2）第10个图形的周长是多少厘米？2.如图由若干个边长为5cm 的小正方形拼成，若有100层，则这个图形的周长是多少厘米？例题2.按规律填数：0.4,0.8,1.2,（ ），（ ），（ ）变式练习按规律填数：,4.0,21（ ），145,114，（ ） 例题3.如图，依次连接第一个正方形各边的中点得到第二正方形，再次连接第二个正方形各边中点得到第三个正方形，按此方法继续下去，若第一个正方形边长为1，则第n 个正方形的面积（ ）.........变式练习：观察图中菱形四个顶点所标的数字规律，可知数2013应标在（ ）A ．第503个菱形的上方B ．第503个菱形的下观察图中菱形四个顶点所标的数字规律，可知数2013应标在（ ）A．第503个菱形的上方B．第503个菱形的下方C．第504个菱形的左方D．第504个菱形的右方例题4.有一个数学运算符号“□”，使下列算式成立：4□8=24, 10□6=46, 6□10=34，那么：5□2=（）。

变式练习：1.有一个数学运算符号“*”，使下列算式成立：2*4=8，4*6=14,5*3=13,8*7=23,按此规定，9*3=（）2.有一个数学运算符号“@”，使下列算式成立：6@2=12,4@3=13,3@4=15,5@1=8，求8@4=（）课后作业1..把边长为1cm的正方形如图那样一层、两层、三层······一直拼下去。

那么拼成的图形的周长恰为2016厘米时，这个图形共有（）层。

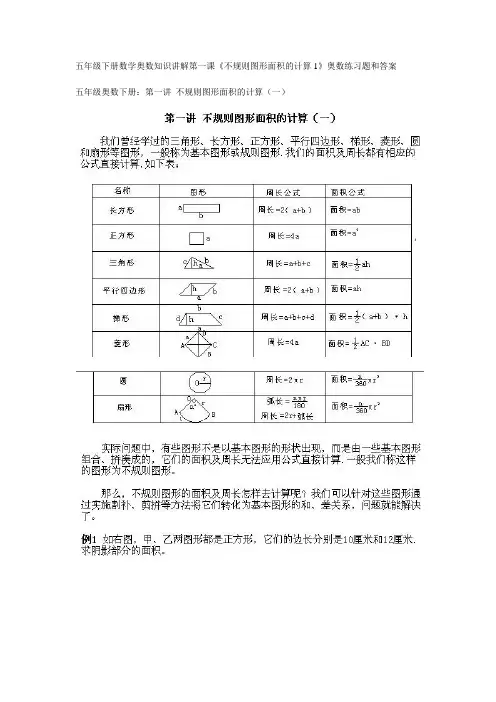
五年级下册数学奥数知识讲解第一课《不规则图形面积的计算1》奥数练习题和答案五年级奥数下册：第一讲不规则图形面积的计算（一）
五年级奥数下册：第一讲不规则图形面积的计算习题
五年级奥数下册：第一讲不规则图形面积的计算习题解答
学生每日提醒
励志名言：
1、播下一个信念，收获一种行动；播下一个行动，收获一种习惯；播下一个习惯，收获一种性格；播下一个性格，收获一种命运。

2、人生的绚丽多彩和卑微只因是平台不同，而决定平台的恰恰是自己平时的行为和习惯。

3、如果把学习看作投资的话，它应该是一本万利的，应该是世界回报最多的投资。

4、伟人所达到并保持着的高处，并不是一飞就到的，而是他们在同伴们都睡着的时候，一步步艰辛地向上攀爬的。

5、学习只是一种状态和一种习惯而已。

书之屋教育
找规律填数
图形规律周期规律数字规律培养学生通过观察、实验、猜测、推理等活动发现图形和数字简单的排列规律，加强对于一般性的数列规律的熟悉，虽然它有很多解，但主要是培养你寻找数列一般规律和猜测数列通项的能力（即运用不完全归纳法的能力），为以后学好数列打下基础。

找规律的类型简直数不清。

有的是所给数字间有规律，有的是隔一个数字间有规律；还有的是相邻两个数字之间的差呈某种规律；规律可能有同加同减同乘一个数或一个数列，或者平方。

找规律题型介绍：
数列规律
对于数列中的规律，我们一般情况下观察前后两个数的变化情况，也可以联系第几个数的“几”去观察规律。

数组规律
对于数组中的规律，我们往往是寻找这一组中几个数之间的变化规律。

图形变化规律
图形的变化规律往往比较复杂，同学们要从大小、方向、位置等几个方面去观察图形计算规律
结合等差数列和基础的组合排列概念。

例题全解
例1 找出下面数列的规律，并根据规律在括号里填上合适的数。

（1）1，5，9，13，17，（），（）， ??
（2）18，19，21，24，28，（），??
解：（1）先计算相邻的两个数的差，5-1=4，9-5=4，13-9=4，17-13=4。

由此可得相邻的两个数后一个都比前一个大4。

类型总结：等差数列型
（2）在这一组数列中每相邻两个数的差依次是1，2，3，4??，由此可以推算出28和括号里的数相差5。

类型总结：差为等差数列型
例2 先找出下面数列中的规律，并根据规律在括号内填上合适的数。

1。

小学五年级奥数全册讲义第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性（一）第8讲奇偶性（二）第9讲奇偶性（三）第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数（一）第13讲最大公约数与最小公倍数（二）第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题（一）第25讲行程问题（二）第26讲行程问题（三）第27讲逻辑问题（一）第28讲逻辑问题（二）第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜（一）数字谜的内容在三年级和四年级都讲过，同学们已经掌握了不少方法。

例如用猜想、拼凑、排除、枚举等方法解题。

数字谜涉及的知识多，思考性强，所以很能锻炼我们的思维。

这两讲除了复习巩固学过的知识外，还要讲述数字谜的代数解法及小数的除法竖式问题。

例1 把+，-，×，÷四个运算符号，分别填入下面等式的○内，使等式成立（每个运算符号只准使用一次）：（5○13○7）○（17○9）=12。

分析与解：因为运算结果是整数，在四则运算中只有除法运算可能出现分数，所以应首先确定“÷”的位置。

当“÷”在第一个○内时，因为除数是13，要想得到整数，只有第二个括号内是13的倍数，此时只有下面一种填法，不合题意。

（5÷13-7）×（17+9）。

当“÷”在第二或第四个○内时，运算结果不可能是整数。

当“÷”在第三个○内时，可得下面的填法：（5+13×7）÷（17-9）=12。

例2 将1～9这九个数字分别填入下式中的□中，使等式成立：□□□×□□=□□×□□=5568。

五升六综合试题（一）一、 填空题（10分）1、如果m ÷ n ＝ 10 ,那么 （ ）A 、m 一定能被n 整除B 、m 一定不能被n 整除C 、m 不一定能被n 整除D 、m 一定是n 的倍数2、去掉小数点后面的“0” ，小数的大小（ ）A 、不变B 、可能变大C 、可能变小D 、无法确定3、两个面积相等的三角形，（ ）拼成一个平行四边形。

A 、一定能B 、一定不能C 、不一定能D 、都不对4、一个真分数的分子、分母都加上同一个自然数（不为0），分数的大小（ ）A 、不变B 、变小C 、变大D 、无法确定5、大于131，小于111的分数有（ ）个A 、1个B 、2个C 、3个D 、无数个二、填空题（70分）1、 3.86×〔1÷（2.1－2.09）〕+ 0.6＝ 0.75×2.5＋0.085×75－7.5×0.1＝4.625＋6.25＋433＋83＝ ________ 7777×9＋1111×37＝ ________21－31＋41－51＋61＝ __________ 1＋2－3＋4＋5－6＋7＋8－9＋10＋……＋28＋29－30＝ __________2、服装厂计划生产1311套校服，已经做了5天，平均每天做75套，剩下的要求每天做78套，还要 ________天才能完成。

3、七名裁判员给一名歌手打分，平均分为9.6分。

去掉一个最高分，平均分为9.55分；去掉一个最低分，平均分为9.7分。

如果最高分和最低分都去掉，这位歌手的平均分为__________ 。

4、83的分子加上24 ，要使分数的大小不变，分母要加上 ______ 。

5、一个农场用拖拉机耕地，3台拖拉机4小时耕6公顷，照这样计算，5台拖拉机6小时可以耕地_____________ 公顷 。

6、一个四位数□72□，有约数3，又是5的倍数，这样的四位数一共有 _______ 。

五年下册奥数试题-尾数和余数姓名 得分【名师解析】自然数末尾的数字称为自然数的尾数；除法中，被除数减去商与除数积的差。

尾数与余数在运算时是有规律可循的，利用这种规律能解决一些看起来无从下手的问题。

【例题精讲】例1、写出除333后余3的全部两位数。

练习、317除以一个两位数后余数是2，符合条件的两位数有哪些？例2、 9519...999个⨯⨯⨯⨯积的个位数字是几？练习、 61201161...616161个⨯⨯⨯⨯积的尾数是几？例3、 64...4444100÷ 个，当商是整数时，余数是多少？练习、1355 (5555)2001÷个，当商是整数时，余数是多少？例4、有一列数，前两个数是3与4，从第三个数开始，每一个数都是前两个数的和。

这一列数中第2001个数除以4，余数是多少？练习、有一串数排成一行，其中第一个数是3，第二个数是10，从第三个数起，每个数恰好是前两个数的和。

在这一串数字中，第1991个数被3除，所得的余数是几？例5、已知，甲数除以9余7，乙数除以9余5，甲数比乙数大。

（1）甲、乙两数的和除以9余数是几？（2）甲、乙两数的差除以9余数是几？（3）甲、乙两数的积除以9余数是几？练习、甲数除以5余3，乙数除以5余2，甲数比乙数大，那么甲、乙两数的和除以5余数是几？甲、乙两数的差除以5余数是几？甲、乙两数的积除以5余数是几？例6、有一个自然数，用它分别去除70，98，143，都有余数（余数不为0），三个余数的和是25。

这个数是。

练习、有一个自然数，用它分别去除63，80，32都有余数，得到的三个余数的和是10,这个数是。

【选讲】有一个（大于1）数，除122，148，187得到相同的余数，这个数是。

练习、某个大于1的自然数分别去除442，297，210得到相同的余数，则该自然数是。

【综合精练】1、写出除349后余4的全部两位数。

2、写出除1095后余3的全部三位数。

3、 )3631(50)3631(...)3631()3631(⨯⨯⨯⨯⨯⨯⨯个积的尾数是几？4、 9919...999个⨯⨯⨯⨯积的个位数是多少？5、下列各小题中，当商是整数时，余数各是多少？（1）46...666650÷ 个 （2）78 (8888)80÷ 个（3）744...44441000÷ 个 （4）51 (1111)1000÷ 个6、把71化成小数，那么小数点后面第100位上的数字是多少？7、一列数1,2,4,7,11,16,22,29，...。

第1篇一、选择题（每题3分，共30分）1. 下列各数中，不是小数的是（）。

A. 0.25B. 0.4C. 2.5D. 0.1252. 下列各图中，面积最大的是（）。

A. 正方形B. 长方形C. 矩形D. 平行四边形3. 一个长方形的长是6厘米，宽是4厘米，它的周长是（）厘米。

A. 20B. 24C. 28D. 304. 下列各数中，是两位小数的是（）。

A. 0.003B. 0.3C. 3.00D. 0.305. 一个正方形的边长扩大2倍，它的面积扩大（）倍。

A. 2B. 4C. 8D. 166. 下列各数中，能被3整除的是（）。

A. 17B. 24C. 29D. 317. 一个长方体的长、宽、高分别是4厘米、3厘米、2厘米，它的体积是（）立方厘米。

A. 24B. 12C. 8D. 68. 下列各数中，是质数的是（）。

A. 15B. 17C. 19D. 219. 一个圆的半径是5厘米，它的直径是（）厘米。

A. 5B. 10C. 15D. 2010. 下列各数中，是偶数的是（）。

A. 3B. 5C. 7D. 8二、填空题（每题3分，共30分）11. 0.25乘以4等于（）。

12. 2.5除以0.5等于（）。

13. 一个长方形的长是8厘米，宽是4厘米，它的周长是（）厘米。

14. 一个正方形的边长是3厘米，它的面积是（）平方厘米。

15. 下列各数中，是三位数的是（）。

A. 100B. 1000C. 10000D. 10000016. 下列各数中，是奇数的是（）。

A. 2B. 3C. 4D. 517. 一个长方体的长、宽、高分别是6厘米、4厘米、3厘米，它的表面积是（）平方厘米。

18. 下列各数中，是偶数的是（）。

A. 17B. 18C. 19D. 2019. 一个圆的半径是7厘米，它的面积是（）平方厘米。

20. 下列各数中，是两位小数的是（）。

A. 0.25B. 0.3C. 3.00D. 0.30三、解答题（每题10分，共40分）21. 小明买了一本书，原价是24元，打八折后，小明需要支付多少元？22. 一个长方形的长是10厘米，宽是6厘米，求它的面积。

小学数学五年级下册单元专项巩固复习 6.确定位置五升六专用一、选择题（满分8分）1．以学校为观测点，广场在西偏北30的方向上，下图中正确的是（）。

A．B．C．D．2．看图判断位置，错误的是（）。

A．A点在红色圆点的西偏北30°方向B．B点在红色圆点的西偏南60°方向C．C点在红色圆点的北偏东30°方向D．D点在红色圆点的东偏南70°方向3．关于玲玲的位置（如图）描述错误的是（）。

A．玲玲在王琦东偏北19°的方向上B．玲玲在王琦北偏东71°的方向上C．玲玲（6，2）D．玲玲在王琦北偏东19°的方向上4．南偏东20°，还可以说成（）．A．北偏东20°B．东偏南20°C．东偏南70°D．北偏西80°二、填空题（满分35分）5．(8分)看图填空。

（1）少年宫位于学校的（________）面，商场在明明家的（________）面。

（2）从少年宫到商场，要向（________）方向走（________）米。

（3）小红放学回家，先向（______）方向走（______）米，再向（______）方向走（______）米就回到家了。

6．(4分)观察线路图填空。

小东从家到公园，他先向________方向走________米到电影院，再向________方向走________米就到公园了。

7．(8分)填一填．（1）B点在A点________偏________ ________方向上，距离是________．（2）A点在B点________偏________ ________方向上，距离是________．8．(15分)以广场为观测点。

（1）图书大厦在广场（______）偏（______）的方向上，距离广场（______）km。

（2）商场在广场（______）偏（______）的方向上，距离广场（______）km。

找规律一、课前热身1、找出下面各组数排列的规律，在括号里填上适当的数。

(1) 1, 2, 4, 8,( ), ( )(2) 1, 2, 2, 3, 3, 4, 5, 5,( ),( )(3) 1, 2, 4, 7, 11,( ),( ),29(4) 0, 1, 3, 12, 45, 171,( ),2457(5) 100, 102, 106, 112, 120, ( ),142, 156(6) 10, 30, 90, 270,( ), 2430, 7290(7) 3, 6, 4, 7, 5, 8,( ), 9, 7(8) 999, 994, 989, 984, ( ),974, 9692、(1, 5, 10} , (2, 10, 20), (3,15,30} , { ), { };(1)1, 11, 22, 34, 47,( ).(2)1, 3, 9, 27, 81,( ).(3)81, 64, 49, 36, ( ), 16, 9.二、典型例题类型1:对于几列数组成的一组数变化规律的分析，需要我们灵活地思考，没有一成不变的方法，有时需要综合运用其他知识，一种方法不行，就要及时调整思路，换一种方法在分析。

例1根据下表中的排列规律，在空格里填上适当的数。

练习：找规律填空(1) (2)(3) (4)（5）如图在七色球下面，按照图示的规律，依次逐个写自然数。

问：2008在什么颜色的球下面？赤橙菌痛1 2 3 4 5 671312 11 10 9 81415 16 17 18192524 23 2221202627• • • • • •• • • • • •类型2：对于那些分布在某些图中的数，它们之间的变化规律往往与这些数在图形中的特殊 位置有关，这是我们解这类题的突破口。

例2根据前面两个圈里三个数的关系，在第三个圈里的（【分析】经认真观察、分析可以发现前面两个圈中三个数之间有着样的关系:5X12=60, 604-10=6 ； 4X20=80, 804-10=8.练习：根据前面两个圈里三个数的关系，在第三个圈里的（(1)498 17 5 10119 121613 35 22 17258 18164 32 8 7 426981）里填上适当的数。

五年级奥数找规律题一、找规律的基本方法1. 数字规律（1）等差数列定义：相邻两项的差相等的数列。

例如：1，3，5，7，9，…，相邻两项的差都是2。

通项公式：公式，其中公式是第公式项的数，公式是首项，公式是项数，公式是公差。

题目：求等差数列3，7，11，15，…的第10项。

解析：首先确定公式，公式。

根据通项公式公式，当公式时，公式。

（2）等比数列定义：相邻两项的比值相等的数列。

例如：1，2，4，8，16，…，相邻两项的比值都是2。

通项公式：公式，其中公式是第公式项的数，公式是首项，公式是项数，公式是公比。

题目：等比数列2，6，18，54，…的第6项是多少？解析：这里公式，公式。

根据通项公式公式，当公式时，公式。

（3）混合规律有些数列是由多种规律组合而成的。

例如：1，2，3，5，8，13，…，这个数列从第三项起，每一项都是前两项的和。

题目：数列1，1，2，3，5，8，13，21，…，求第10项。

解析：这是斐波那契数列，规律是从第三项起公式。

依次计算可得：第7项公式，第8项公式，第9项公式，第10项公式。

2. 图形规律（1）图形数量规律题目：观察下列图形，找出规律并回答问题。

△□□△△□□□△△△□□□□…第20个图形是什么？解析：可以分组来看，第一组是1个△和2个□，第二组是2个△和3个□，第三组是3个△和4个□，以此类推。

设第公式组，前面公式组图形的总数为公式。

当公式时，公式，说明第20个图形是第5组的最后一个图形，是□。

（2）图形位置规律题目：下面是一组正方形按规律摆放。

第一个正方形：左上角有一个点；第二个正方形：左上角和右上角各有一个点；第三个正方形：左上角、右上角和右下角各有一个点；第四个正方形：四个角都有一个点。

问第10个正方形有几个点？解析：观察可得，第公式个正方形的点数是公式个角中从左上角开始按顺时针方向连续的角的个数之和。

第10个正方形的点数为公式。

3. 数表规律题目：观察下面的数表：12 34 5 67 8 9 1011 12 13 14 15…问第10行第5个数是多少？解析：先求前9行的数字个数，根据等差数列求和公式公式，当公式时，公式。

第1篇一、选择题（每题3分，共30分）1. 下列各数中，是整数的有（）A. √9B. -√16C. √-9D. √252. 一个长方形的长是8cm，宽是4cm，它的周长是（）A. 12cmB. 16cmC. 24cmD. 32cm3. 小明有5个苹果，小红比小明多3个苹果，小红有多少个苹果？（）A. 2个B. 3个C. 8个D. 10个4. 下列各数中，能被3整除的是（）A. 25B. 27C. 30D. 355. 一个正方形的面积是64平方厘米，它的边长是（）A. 8cmB. 16cmC. 32cmD. 64cm6. 小华用1.5小时走完5千米，他每小时的速度是（）A. 2千米/小时B. 3千米/小时C. 4千米/小时D. 5千米/小时7. 下列各数中，是负数的是（）A. -5B. 0C. 5D. -108. 一个梯形的上底是4cm，下底是6cm，高是2cm，它的面积是（）A. 10cm²B. 12cm²C. 14cm²D. 16cm²9. 下列各图形中，是轴对称图形的是（）A. 圆B. 正方形C. 等腰三角形D. 长方形10. 下列各数中，是最简分数的是（）A. 3/6B. 4/8C. 5/10D. 7/14二、填空题（每题3分，共30分）1. 0.25的小数点向右移动两位后，得到的数是______。

2. 下列各数中，是质数的是______。

3. 5个3相乘的积是______。

4. 一个长方形的长是12cm，宽是8cm，它的周长是______。

5. 下列各数中，是偶数的是______。

6. 下列各图形中，是长方体的是______。

7. 0.5乘以0.3等于______。

8. 下列各数中，是负数的是______。

9. 下列各数中，是互质数的是______。

10. 下列各图形中，是正方体的是______。

三、解答题（每题10分，共50分）1. 小明有苹果、香蕉、橙子共35个，其中苹果比香蕉多10个，香蕉比橙子多5个，请分别算出小明有多少个苹果、香蕉、橙子。

精选全文完整版（可编辑修改）第1讲 分数基本计算(一）一、知识点1. 分数的定义把一个整体分成若干等份，取其中的一份或几份所表示的数叫做分数.2. 分数的分类及转化所有分数分成三类：真分数、假分数、带分数. 分母比分子大的分数叫真分数，例如：；，，， 24179421 分子比分母大或者相等的分数叫假分数，例如：；，，， 13237745 包含整数部分的分数叫带分数，例如：.4310731219 ，，， 注 假分数化带分数：分母不变，分子除以分母所得整数为带分数左边整数部分，余数为分子.带分数化假分数：分母不变，用整数部分与分母的乘积再加上原分子的和作为分子.3. 分数的基本性质及约分、通分分数的基本性质：分数的分子和分母都乘或除以相同的数（0除外），分数的大小不变. 把分数的分子、分母同时除以某个数，使得分数的大小不变，这个过程叫约分； 把几个分母不同的分数分别化成与原分数相等的同分母分数，这个过程叫通分.4. 分数的加减运算分数加减：先把分数通分，化成同分母，再把分子相加减，计算结果要约分成最简分数.二、典型例题例1 将下面的假分数转化成带分数或整数..1272891564214735，，，，例2 将下面的带分数转化成假分数..1251011111211732313，，，，例3 将下列分数约分成最简分数..8491573824353628，，，例4 将下面几组分数进行通分.① ；，8361 ②；，，1254332 ③.127614397，，，例5 计算下列各式：（1）3175+ （2）41207-（3）2451127248273-+ （4）209515461274+-三、水平测试1. 将下面的假分数转化成带分数或整数..__________936_________,1325________,47===2. 将下面的带分数转化成假分数..__________859,__________723________,514===3. 计算下列各式：（1）8743+ （2）103125- （3）8311252433-+ 在这一学年中，不仅在业务能力上，还是在教育教学上都有了一定的提高。

找出数列的排列规律（一）小学数学五年级下册奥数试题及答案人教课标版找规律是我们在生活、学习、工作中经常使用的一种思想方法，在解数学题时人们也常常使用它，下面我们利用找规律的方法来解一些简单的数列问题。

（一）思路指导例1.在下面数列的（）中填上适当的数。

1，2，5，10，17，（），（），50分析与解：这个数列的排列规律是什么？我们逐项分析：第一项是：1第二项是：2，第三项是：5，第四项是：10，……可以看出，这个数列从第二项起，每一项都等于它的前一项依次分别加上单数1，3，5，7，9……，这样我们就可以由第五项算出括号内的数了，即：第一个括号里应填；第2个括号里应填。

例2.自1开始，每隔两个整数写出一个整数，这样得到一个数列：1，4，7，10……问：第100个数是多少？分析与解：这个题由于数太多，很难像例1那样递推，我们可以换一种思路：数列中每相邻两个数的差都是3，我们把这样的数列叫做等差数列。

我们把“3”叫做这个等差数列的公差。

观察下面的数列是等差数列吗？如果是，它们的公差是几？（1）2，3，4，5，6，7……（2）5，10，15，20，25，30……（3）1，2，4，8，16……（4）12，14，16，18，20……现在我们结合例2找一找每一项与第一项，公差有什么关系？第1项是1，第二项比第一项多3，第三项比第一项多2个3，第四项比第一项多3个3，……依次类推，第100项就比第一项多99个3，所以第100个数是。

由此我们可以得出这样的规律：等差数列的任一项都等于：第一项＋（这项的项数－1）×公差我们把这个公式叫做等差数列的通项公式。

利用通项公式可以求出等差数列的任一项。

试试看：你能求出数列3，5，7，9……中的第92个数是多少吗？例 3.已知一列数：2，5，8，11，14，……，44，……，问：44是这列数中的第几个数？分析与解：显然这是一个等差数列，首项（第一项）是2，公差是3。