Ch1 (1.3 信号的运算)
- 格式：pdf
- 大小：790.61 KB
- 文档页数：3
下载文档原格式
合集下载
信号与系统-CH1
2
3 4
t
抽样信号
可以看出，（1）
Sa (t ) 为偶函数；
（2）当 （3）
t
时， S
a
(t )的振幅衰减趋近于0；
f (k ) 0 ，（k为整数，且k≠0）；
Sa (t ) 信号满足：
0
S (t )dt 2
积分）具有不连续点。 四、单位阶跃信号
1V
uc (t )
ic (t ) C 1F
1V
uc (t )
ic (t ) C 1F
_
_
_
图2
_
图1
例：RC电路如图（1）所示，C=1F，R可调，开关K在t＝0时闭合，求uc（t）， ic（t）。当R→0时， uc（t），ic（t）有何变化？
解：一阶动态电路瞬态分析可采用三要素法，有
不具有周期性的信号称为非周期信号。
例1 判断下列信号是否为周期信号，若是，确定其周期。 （1）f1(t) = sin2t + cos3t （2）f2(t) = cos2t + sinπt 解：两个周期信号x(t)，y(t)的周期分别为T1和T2，若其周期之比 T1/T2为有理数，则其和信号x(t)+y(t)仍然是周期信号，其周期为T1和 T2的最小公倍数。
同理有
f (t ) (t t0 )dt f (t0 )
δ(t) 是广义函数，不用函数“是什么”，而用函数能“干什么”来定义。
(2)乘积(加权)性质: 设f(t)为一连续函数，且在t＝0时刻有值，则有
f (t ) (t ) f (0) (t )
f (t ) (t t 0 ) f (t 0 ) (t t 0 )
CH1 信号及其表述
n1
得
x(t)
a0
n1
[
1 2
(an
jbn )e jn0t
1 2
Random Signal）
析试限工
1
第1章 信号及其描述
1.0 序（Introduction）
信号（signal）：随时间或空间变化的物理量。 信号是信息的载体，信息是信号的内容。 依靠信号实现电、光、声、力、温度、压力、流量等的传输 电信号易于变换、处理和传输，非电信号 电信号。
信号分析与处理（signal analysis and processing） 不考虑信号的具体物理性质，将其抽象为变量之间的函数关 系，从数学上加以分析研究，从中得出具有普遍意义的结论。
信号的描述（9/53）
目录 上页 下页 返退回出 29
第1章 信号及其描述 课堂习题
信号的描述（10/53）
• 求题图1-1周期三角波的频谱，并作频谱图。
x(t)
T 0T
2
2
x(t) AA2T2AAt t T
t
T t0 2
0tT 2
目录 上页 下页 返退回出 30
第1章 信号及其描述 答案
目录 上页 下页 返退回出 15
第1章 信号及其描述 思 考？
信号的分类（9/13）
某钢厂减速机上测得的振动信号波形(测点3)如图所示， 其基本波形属于何种信号？
近似的看作为周期信号
目录 上页 下页 返退回出 16
第1章 信号及其描述 (2)非确定性信号（随机信号）
信号的分类（10/13）
• 无法用明确的数学关系式表达 。其幅值、相位变化是不 可预知的，所描述的物理现象是一种随机过程。如分子热 运动，环境的噪声等，分为平稳随机信号和非平稳随机信 号。
1.3信号基本运算
f (t) = fe(t) + fo(t)
可推得： 可推得：
f (t) + f (−t) fe(t) = 2 f (t) − f (−t) fo(t) = 2
• 对离散序列： 对离散序列：
f [n] = fe[n]+ fo[n]
1 fe[n] = ( f [n]+ f [−n]) 2
1 fo[n] = ( f [n]− f [−n]) 2
f1[n]+f2[n]=
(−1 +n )
n
2 + 2n
-n
乘法： 2 乘法：
两个信号对应时刻的函数值相乘。 两个信号对应时刻的函数值相乘。例
0
t
σ >0
0
t
σ<0
0
t
σ=0
ω≠ 0
3 时移： 时移：
将原信号沿时间轴左移或右移。 将原信号沿时间轴左移或右移。 其物理意义为：表示信号的接入时间不同。 其物理意义为：表示信号的接入时间不同。
f1(t) 1 t -1
3 1
f2(t) 1 0 1 -1 2 t
0 1
f1 ( t ) + f2 ( t )
解：
-1
-1
0 1
2
3
t
例3 f1[n]=
2 n
n , n<-3 < , n≥-3 ≥
f2[n]= ；
(-1) -n 2 + n
n
, ,
n<0 n ≥0
解：
Hale Waihona Puke (−1 +2 )n
n
n<-3 < n= -3,-2,-1 n ≥0
数字信号处理课后习题Ch1
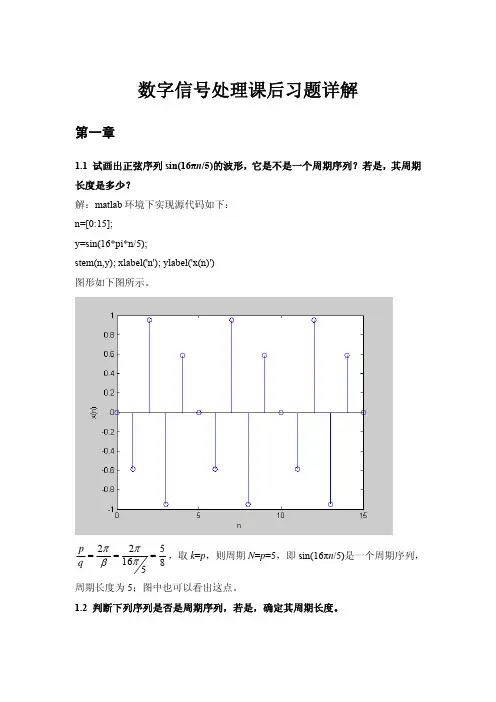
数字信号处理课后习题详解第一章1.1 试画出正弦序列sin(16πn /5)的波形，它是不是一个周期序列？若是，其周期长度是多少？解：matlab 环境下实现源代码如下： n=[0:15]; y=sin(16*pi*n/5);stem(n,y); xlabel('n'); ylabel('x(n)') 图形如下图所示。
2251685p q πππβ===，取k =p ，则周期N =p =5，即sin(16πn /5)是一个周期序列，周期长度为5；图中也可以看出这点。
1.2 判断下列序列是否是周期序列，若是，确定其周期长度。
(1) 3()cos(74x n n ππ=−解：2214337p q πππβ===∵ p ，q 是互为质数的整数，取k =q 则周期N =p =14∴周期长度为14 (2) 7cos()4sin()(nnn x ππ−=解：1284N ππ== 22147N ππ==∵N 1，N 2最小公倍数为56 ∴其周期长度为561.3 试画出如下序列的波形(1) x(n)=3δ(n+3)+2δ(n+1)-4δ(n-1)+2δ(n-2) (2)x(n)= 0.5n R 5(n)解：(1)(2)1.4 今对三个正弦信号)2cos()(1t t x a π=、)6cos()(2t t x a π−=、)10cos()(3t t x a π=进行理想采样，采样频率为π8=Ωs ，求这三个采样输出序列，比较其结果。
画出x a 1(t )、x a 2(t )、x a 3(t )的波形及采样点位置并解释频谱混叠现象。
解：matlab 环境下实现源代码如下：t=-1:0.01:1; x1=cos(2*pi*t); x2=-cos(6*pi*t); x3=cos(10*pi*t); t2=-1:0.25:1; y1=cos(2*pi* t2);y2=-cos(6*pi* t2);y3=cos(10*pi* t2);subplot(311)plot(t,x1);xlabel('t');ylabel('Xa1(t)') holdstem(t2, y1)subplot(312)plot(t,x2);xlabel('t');ylabel('Xa2(t)') holdstem(t2, y2)subplot(313)holdstem(t2, y3)plot(t,x3);xlabel('t');ylabel('Xa3(t)') 三个信号波形已知πω8=，则4182,42===πππωs T 。
1.3信号的基本运算
信号与线性系统
1.3 信号的基本运算
信号的＋、－、 ＋、－、× 一、信号的＋、－、×运算 两信号f1(·) 和f2 (·)的相+、－、×指 ) )的相+、－、× 同一时刻两信号之值对应相加减乘 两信号之值对应相加减乘。 同一时刻两信号之值对应相加减乘。
信号与线性系统
两信号相加和相乘
• 同一瞬时两信号对应值相加（相乘）。 同一瞬时两信号对应值相加（相乘）。
• 将f (t) → f (at) ，称为对信号f (t)的尺度变 换。 则波形沿横坐标压缩； • 若a >1 ，则波形沿横坐标压缩；若0< a < 1 ， 则展开。 则展开。如
信号与线性系统
• 对于离散信号，由于f (ak) 仅在ak为整数 对于离散信号， 时才有意义， 时才有意义， 进行尺度变换时可能会使部 分信号丢失。 分信号丢失。因此一般不作波形的尺度变 换。
信号与线性系统
平移、反转、 平移、反转、尺度变换相结合
三种运算的次序可任意。 进行。 三种运算的次序可任意。但一定要注意始终对时间t 进行。 例：已知f (t)，画出f (– 4 – 2t)。
信号与线性系统 已知f ，画出f 已知 (t)，画出 (– 4 – 2t)。 。
也可以先压缩、再平移、最后反转。 也可以先压缩、再平移、最后反转。
信号与线性系统
2. 平移
• 将 f ( t ) → f ( t – t 0) ， f ( k ) → f (t – k0)称为对信号f (·)的平移或移位。 ) 平移或移位。 >0， 若t0 (或k0) >0，则将f (·)右移；否则左 )右移； 移。
信号与线性系统
平移与反转相结合
• 已知f(t)如下图所示，请画出f(2-t)
1.3 信号的基本运算
信号的＋、－、 ＋、－、× 一、信号的＋、－、×运算 两信号f1(·) 和f2 (·)的相+、－、×指 ) )的相+、－、× 同一时刻两信号之值对应相加减乘 两信号之值对应相加减乘。 同一时刻两信号之值对应相加减乘。
信号与线性系统
两信号相加和相乘
• 同一瞬时两信号对应值相加（相乘）。 同一瞬时两信号对应值相加（相乘）。
• 将f (t) → f (at) ，称为对信号f (t)的尺度变 换。 则波形沿横坐标压缩； • 若a >1 ，则波形沿横坐标压缩；若0< a < 1 ， 则展开。 则展开。如
信号与线性系统
• 对于离散信号，由于f (ak) 仅在ak为整数 对于离散信号， 时才有意义， 时才有意义， 进行尺度变换时可能会使部 分信号丢失。 分信号丢失。因此一般不作波形的尺度变 换。
信号与线性系统
平移、反转、 平移、反转、尺度变换相结合
三种运算的次序可任意。 进行。 三种运算的次序可任意。但一定要注意始终对时间t 进行。 例：已知f (t)，画出f (– 4 – 2t)。
信号与线性系统 已知f ，画出f 已知 (t)，画出 (– 4 – 2t)。 。
也可以先压缩、再平移、最后反转。 也可以先压缩、再平移、最后反转。
信号与线性系统
2. 平移
• 将 f ( t ) → f ( t – t 0) ， f ( k ) → f (t – k0)称为对信号f (·)的平移或移位。 ) 平移或移位。 >0， 若t0 (或k0) >0，则将f (·)右移；否则左 )右移； 移。
信号与线性系统
平移与反转相结合
• 已知f(t)如下图所示，请画出f(2-t)
信号与系统-ch1
差分方程求解, z 变换
• 新工具：Matlab软件
1 信号与系统的基本概念（6课时） 2 连续系统的时域分析（4课时） 3 离散系统的时域分析（4课时） 4 连续系统的频域分析（12课时） 5 6 7
连续系统的S域分析（12课时） 离散系统的Z域分析（8课时）
系统函数（4课时）
8 系统的状态变量分析（4课时）
0, 0 直流 0, 0 升指数信号 0, 0 衰减指数信号
0, 0 等幅 0, 0 增幅振荡 0, 0 衰减
在实际中不能产生复信号，引入复信号能简化运算
复指数信号的实部与虚部
离散周期信号f (n)满足:f (n) = f(n + mN)，m = 0,±1,±2,…
满足上述关系的最小T(或整数N)称为该信号的周期
连续周期信号：
f (t )
1 -3 -2 -1 0 1 -1 2 3 4 t
T=4s
离散周期信号：
2 1 ... -4 -3 -2 -1 0 1
f (n)
2 1 1 1
• 抽样信号（Sa(t) 信号）
sin t Sa(t ) t
抽样信号特点
1. 偶函数， Sa t Sa t 2. 在t 的正负两端衰减 tlim Sa(t ) 0 3. 4.
0
Sa(t )dt Sa(t ) dt
0
2
Sa(t )dt
业技术工作的重要理论基础，是后续专业课（通 信原理、数字信号处理）的基础，也是上述各类 专业硕士研究生入学考试课程。
• 课程特点：
应用数学知识较多，与电路分析关系密切，用数学 工具分析物理概念。
信号的运算和处理 (2)
详细描述
卷积运算是信号处理中非常重要的概念，它表示两个信号的结合方 式。具体来说，如果两个信号`f(t)`和`g(t)`，则它们的卷积可以表示 为`h(t) = f(t) * g(t)`。在时域中，卷积运算相当于将一个信号通过另 一个信号进行滤波。在实际应用中，卷积运算广泛应用于图像处理、 音频处理等领域。
将一个信号逐点对应地除以另一个信号。
详细描述
信号的除法运算在数学上表示为`h(t) = f(t) / g(t)`，其中`f(t)`和`g(t)`是两个信号。在信号处理中，除法运 算常用于归一化、放大等操作。同样地，除法运算也可能会引入非线性失真，因此在实际应用中需要特别 小心。
卷积
总结词
将一个信号与另一个信号进行逐点对应相乘后再求和的操作。
信号的运算和处理 (2)
目
CONTENCT
录
• 信号的数学运算 • 信号的滤波处理 • 信号的调制与解调 • 信号的变换域处理 • 信号的采样与量化
01
信号的数学运算
加法
总结词
将两个信号在时间上逐点对应相加。
详细描述
信号的加法运算是最基本的数学运算之一，它逐点对应地相加两个信号。在时域中， 如果两个信号`f(t)`和`g(t)`，则它们的和可以表示为`h(t) = f(t) + g(t)`。这种运算在 信号处理中非常常见，特别是在处理噪声和其他干扰信号时。
详细描述
在通信中，带通滤波器用于提取特定频带的信号 ，实现信号的传输和接收；在雷达中，带通滤波 器用于提取目标回波的特定频带信号；在生物医 学信号处理中，带通滤波器用于提取心电图、脑 电图等生物电信号的特定频带成分。
带阻滤波器
总结词
详细描述
总结词
卷积运算是信号处理中非常重要的概念，它表示两个信号的结合方 式。具体来说，如果两个信号`f(t)`和`g(t)`，则它们的卷积可以表示 为`h(t) = f(t) * g(t)`。在时域中，卷积运算相当于将一个信号通过另 一个信号进行滤波。在实际应用中，卷积运算广泛应用于图像处理、 音频处理等领域。
将一个信号逐点对应地除以另一个信号。
详细描述
信号的除法运算在数学上表示为`h(t) = f(t) / g(t)`，其中`f(t)`和`g(t)`是两个信号。在信号处理中，除法运 算常用于归一化、放大等操作。同样地，除法运算也可能会引入非线性失真，因此在实际应用中需要特别 小心。
卷积
总结词
将一个信号与另一个信号进行逐点对应相乘后再求和的操作。
信号的运算和处理 (2)
目
CONTENCT
录
• 信号的数学运算 • 信号的滤波处理 • 信号的调制与解调 • 信号的变换域处理 • 信号的采样与量化
01
信号的数学运算
加法
总结词
将两个信号在时间上逐点对应相加。
详细描述
信号的加法运算是最基本的数学运算之一，它逐点对应地相加两个信号。在时域中， 如果两个信号`f(t)`和`g(t)`，则它们的和可以表示为`h(t) = f(t) + g(t)`。这种运算在 信号处理中非常常见，特别是在处理噪声和其他干扰信号时。
详细描述
在通信中，带通滤波器用于提取特定频带的信号 ，实现信号的传输和接收；在雷达中，带通滤波 器用于提取目标回波的特定频带信号；在生物医 学信号处理中，带通滤波器用于提取心电图、脑 电图等生物电信号的特定频带成分。
带阻滤波器
总结词
详细描述
总结词
数字信号处理ch1_3 DTFT
j( W π )
)} / 2
例：已知x[k]的频谱如图所示，试求y[k]=x[k]cos(pk)的频谱。
X(ejW )
1
2π
π
π 2
π 2
π
2π
W
解：
2π
1
π
X(ej(W p)
π 2
π
π
2π
W
1
2π
X(e
j(W p
2
)
π
π 2
π 2 1 Y(ejW )
π 2
π
2π
3
|X (ejW )|
2 1 0
3p
2p
p
0
p
2p
3p
W
DTFT的收敛性
定义X(ejW)的部分和 X N (e jW )
若
k
k N
N
x[k ]e jW k
x[k ]
绝对可和 一致收敛
则 lim X (e jW ) X N (e jW ) 0
若
k
序列DTFT的性质
2. 对称特性
x [ k ] X ( e
DTFT
jW
)
x [ k ] X ( e jW )
DTFT
当x [k]为实奇对称序列时，由于x[k]= x*[k] ，所以
X ( e jW ) X ( e jW )
X(ejW)是W 纯虚函数, XI(ejW)为奇对称
DTFT
序列DTFT的性质
2. 对称特性
DTFT x [ k ] X ( e jW ) DTFT x [ k ] X ( e jW )
ch1 数字信号
i =− m
∑
13 13
第一章
★ 二进制
绪
论
目前在数字电路中应用最广的是二进制。在二进制数中， 目前在数字电路中应用最广的是二进制。在二进制数中， 一个二进制数按位权展开式为： 一个二进制数按位权展开式为： 仅有0 两种数码，基数为2 仅有0和1两种数码，基数为2。低位和高位之间的进位关系是 n −1 逢二进一” “逢二进一”。 a (N ) = a ⋅⋅⋅ a a a a ⋅⋅⋅ a = a × 2i
15 15
i =− m
∑
第一章
绪
论
数制之间的转换
（一）将二、八、十六进制数转换为十进制数 将二、 转换时只要将待转换的二、 转换时只要将待转换的二、八、十六进制数按位权展 再按十进制运算规则运算，即可得到对应的十进制数。 开，再按十进制运算规则运算，即可得到对应的十进制数。 1-2：将十六进制数(12AF.B4)转换成十进制数。。 1-1：将八进制数 将二进制数(11010.011)2转换成十进制数。 转换成十进制数。 转换成十进制数。 例1-3：将十六进制数 ：将八进制数(137.504)8转换成十进制数。 将二进制数 16转换成十进制数 解： (12AF.B4)＝＝1×163××+16××2×16×215×1620 × 2× + 10× 1+ × (137.504)8 162＝ 1×+4+×81 237×80 2+ 1× 1+×× 0 (11010.011) 1××2 3+1× +20× ×82 0× 11× +×2 -2× 4× + 5×816-10××164×2-3 0×2-1+ 1×8-2+ 1×8 × × (4783.703125) (26.375)10 ＝(95.6328125)1010
∑
13 13
第一章
★ 二进制
绪
论
目前在数字电路中应用最广的是二进制。在二进制数中， 目前在数字电路中应用最广的是二进制。在二进制数中， 一个二进制数按位权展开式为： 一个二进制数按位权展开式为： 仅有0 两种数码，基数为2 仅有0和1两种数码，基数为2。低位和高位之间的进位关系是 n −1 逢二进一” “逢二进一”。 a (N ) = a ⋅⋅⋅ a a a a ⋅⋅⋅ a = a × 2i
15 15
i =− m
∑
第一章
绪
论
数制之间的转换
（一）将二、八、十六进制数转换为十进制数 将二、 转换时只要将待转换的二、 转换时只要将待转换的二、八、十六进制数按位权展 再按十进制运算规则运算，即可得到对应的十进制数。 开，再按十进制运算规则运算，即可得到对应的十进制数。 1-2：将十六进制数(12AF.B4)转换成十进制数。。 1-1：将八进制数 将二进制数(11010.011)2转换成十进制数。 转换成十进制数。 转换成十进制数。 例1-3：将十六进制数 ：将八进制数(137.504)8转换成十进制数。 将二进制数 16转换成十进制数 解： (12AF.B4)＝＝1×163××+16××2×16×215×1620 × 2× + 10× 1+ × (137.504)8 162＝ 1×+4+×81 237×80 2+ 1× 1+×× 0 (11010.011) 1××2 3+1× +20× ×82 0× 11× +×2 -2× 4× + 5×816-10××164×2-3 0×2-1+ 1×8-2+ 1×8 × × (4783.703125) (26.375)10 ＝(95.6328125)1010
数字信号处理 ch1
第1章 信号的抽样和重构 章 (Sampling and Reconstruction)
1
信号按连续性进行分类
• 模拟信号 (Analog Signals) ：独立时间变量连续有定 义，且信号幅值连续有定义。 • 连续时间信号 (Continuous-Time Signals) ：独立时间 变量连续有定义 (如x(t) )。 • 离散时间信号 (Discrete-Time Signals ) ：独立时间变 量在离散时间点有定义{ x(nT)}。 • 数字信号 (Digital Signals) ：独立时间变量在离散时间 点有定义、信号幅值仅取离散值，且通常用二进制编 码表示。 信号 模拟信号 连续时间信号 离散时间信号 数字信号
X ( jΩ) = 2πδ (Ω − Ω 0 )
或者
X ( f ) = δ ( f − f0 )
复指信号 e j 2π f 0t的频谱：
X(f )
(1)
0
f0
f
16
一般周期信号的傅立叶变换 • x(t ) =
k =−∞
∑ X ( kΩ ) e
0
∞
jk Ω0 t
X ( jΩ ) = 2π
k =−∞
∑ X ( kΩ )δ (Ω − kΩ )
2
因为
Ex = ∫
∞
−∞
x(t ) dt ≤ [ ∫
2
∞
−∞
x(t ) dt ]
2
所以，如果 x(t ) 是绝对可积的，那么它一定 是平方可积的，但是反之不一定成立。例如，
sin 2π t x(t ) = πt
是平方可积的，但不是绝对可积的。所以，取
x(t ) ∈ L2 更稳妥（即更严格）。
1
信号按连续性进行分类
• 模拟信号 (Analog Signals) ：独立时间变量连续有定 义，且信号幅值连续有定义。 • 连续时间信号 (Continuous-Time Signals) ：独立时间 变量连续有定义 (如x(t) )。 • 离散时间信号 (Discrete-Time Signals ) ：独立时间变 量在离散时间点有定义{ x(nT)}。 • 数字信号 (Digital Signals) ：独立时间变量在离散时间 点有定义、信号幅值仅取离散值，且通常用二进制编 码表示。 信号 模拟信号 连续时间信号 离散时间信号 数字信号
X ( jΩ) = 2πδ (Ω − Ω 0 )
或者
X ( f ) = δ ( f − f0 )
复指信号 e j 2π f 0t的频谱：
X(f )
(1)
0
f0
f
16
一般周期信号的傅立叶变换 • x(t ) =
k =−∞
∑ X ( kΩ ) e
0
∞
jk Ω0 t
X ( jΩ ) = 2π
k =−∞
∑ X ( kΩ )δ (Ω − kΩ )
2
因为
Ex = ∫
∞
−∞
x(t ) dt ≤ [ ∫
2
∞
−∞
x(t ) dt ]
2
所以，如果 x(t ) 是绝对可积的，那么它一定 是平方可积的，但是反之不一定成立。例如，
sin 2π t x(t ) = πt
是平方可积的，但不是绝对可积的。所以，取
x(t ) ∈ L2 更稳妥（即更严格）。
§1-3 信号的基本运算
x(n)
1 1
x(n 2)
1
x(n 2)
2 1
0 1 2 3 4 5
n
2 1
0 1 2 3 4 5 6 7
n
4 3 2 1
0 1 2 3
n
2、反褶：a=-1，b=0: x(t ) x(t ) , x(n) x(n)
x(t )
1 1
x ( t )
1
x(n)
x(t )
1 1
x(t 1)
1
x (2t )
1
0
1
2
t
2 1
0
1
2
t
1
0
1
2
t
x(1 t )
1 1
x(2t )
1
0
1
2
t
1
0
1
2
t
x(1 2t )
1 1
x(1 2t )
1
0
1
2
t
1
0
1
2
t
二、信号的加减与相乘：
两信号相加减或相乘，是两信号在同一时刻的函数值 相加减或相乘，形成新的时间信号。例如：
1
a 1
1 2
2 1
0
3
4
t
离散时间信号没有与连续时间信号一样意义的 展缩运算，但当a为一整数时，也相当于时域压缩:
x(n) x(an)
a 1
2 1
x(2n) y(n)
3
x(n)
3
2 1
3 2 1
称作减采样
0 1 2 3 4 5
n
3 2 1
0 1 2 3 4 5
1 1
x(n 2)
1
x(n 2)
2 1
0 1 2 3 4 5
n
2 1
0 1 2 3 4 5 6 7
n
4 3 2 1
0 1 2 3
n
2、反褶：a=-1，b=0: x(t ) x(t ) , x(n) x(n)
x(t )
1 1
x ( t )
1
x(n)
x(t )
1 1
x(t 1)
1
x (2t )
1
0
1
2
t
2 1
0
1
2
t
1
0
1
2
t
x(1 t )
1 1
x(2t )
1
0
1
2
t
1
0
1
2
t
x(1 2t )
1 1
x(1 2t )
1
0
1
2
t
1
0
1
2
t
二、信号的加减与相乘：
两信号相加减或相乘，是两信号在同一时刻的函数值 相加减或相乘，形成新的时间信号。例如：
1
a 1
1 2
2 1
0
3
4
t
离散时间信号没有与连续时间信号一样意义的 展缩运算，但当a为一整数时，也相当于时域压缩:
x(n) x(an)
a 1
2 1
x(2n) y(n)
3
x(n)
3
2 1
3 2 1
称作减采样
0 1 2 3 4 5
n
3 2 1
0 1 2 3 4 5
CH1-3指数信号与正弦信号
st
Cert cos0t jCert sin0t
e rt sin0t
r0
e rt sin0 t
r0
t
t
4
一般的复指数信号:
s r j 0
st
Ce
Ce e
rt
Ce
j
j( 0 t )
Ce
rt
实指数信号
实部： C cos( 0t ) 虚指数信号 虚部： C sin ( 0t )
k 0, 1, 2, (1.60)
在（1.60）所给的一组信号中，仅有N个互不相同 的周期复指数信号！ 【证明】k N [n] e j ( k N )(2 N )n e jk (2 N )n e j 2 n k [n]
(1.61)
(1.62)
0 [n] 1 , 1[n] e
非周期
15
e j0 n 的振荡性：
e
j 0 n
可由e
j0 t
抽样得到
e
j 0 n
e
j0 t
t nT
, 0 0T
j 0 n j0 t e 和 e 两者的区别:
e j 0n 的振荡频率不随角频率ω0的增加而增加。
e
j(0 k 2 π ) n
e
j0n j2 πkn
j (2 N )n
, 2 [n] e
j (4 N )n
, , N 1[n] e
j ( N 1)(2 N ) n
只有N 个不同的信号
即： N [n] 0[n], N 1[n] 1[n], N 1[n] 1[n],
22
3．一般复指数序列
x[n] Ae
Cert cos0t jCert sin0t
e rt sin0t
r0
e rt sin0 t
r0
t
t
4
一般的复指数信号:
s r j 0
st
Ce
Ce e
rt
Ce
j
j( 0 t )
Ce
rt
实指数信号
实部： C cos( 0t ) 虚指数信号 虚部： C sin ( 0t )
k 0, 1, 2, (1.60)
在（1.60）所给的一组信号中，仅有N个互不相同 的周期复指数信号！ 【证明】k N [n] e j ( k N )(2 N )n e jk (2 N )n e j 2 n k [n]
(1.61)
(1.62)
0 [n] 1 , 1[n] e
非周期
15
e j0 n 的振荡性：
e
j 0 n
可由e
j0 t
抽样得到
e
j 0 n
e
j0 t
t nT
, 0 0T
j 0 n j0 t e 和 e 两者的区别:
e j 0n 的振荡频率不随角频率ω0的增加而增加。
e
j(0 k 2 π ) n
e
j0n j2 πkn
j (2 N )n
, 2 [n] e
j (4 N )n
, , N 1[n] e
j ( N 1)(2 N ) n
只有N 个不同的信号
即： N [n] 0[n], N 1[n] 1[n], N 1[n] 1[n],
22
3．一般复指数序列
x[n] Ae
ch1离散信号与系统分析基础
例：x[k] 非零范围为 N1 k N2 ， h[k] 的非零范围为
N3 k N4 求： y[k]=x[k]* h[k]的非零范围。 结论：N1+ N3 k N4+ N2 例：用 MATLAB 函数 conv 计算两个序列的离散卷积。
x=[-0.5,0,0.5,1]; kx=-1:2;
h=[1,1,1];kh=-2:0;
k N
M j 2 km
eN
kM
当 m=0, N, 2N, 时有 X[m] 2M 1
对 m 的其它取值，利用等比级数的求和公式有
j 2 mM
j 2 m(M 1)
e N e N
X[m]
j 2 m
1e N
sin m 2M 1
y = conv(x, h);
k=kx(1)+kh(1):kx(end)+kh(end);
stem(k,y);
xlabel('k');ylabel('y');
1.2 离散时间系统
x[k ] 输入序列
离散时 间系统
y[k ]
输出序列
y[k] = T{x[k]} 1.2.1 系统分类 1. 线性(Linearity)
x[k]x[-k] x[k] x[k-N] x[k] x[Mk]
5)卷积
x[k / M ] k是M的整数倍
xI[k] 0
其他
y[k] x[n]h[k n] n
例：已知 x1[k] * x2[k]= y[k]，试求 y1[k]= x1[k-n] * x2[k-m]。
结论：
y1[k]= y[k-(m+n)]
0 1
N k 是 N 的整数倍 k 不是 N 的整数倍
ch1-信号描述及分析
1.2
正弦分量的幅值
信号的频域描述
T0 / 2 T0 / 2
2 bn T0
x(t ) sin n0tdt 0
该周期性三角波信号的傅里叶级数展开式为
x(t ) A 4A 1 1 2 cos0t 2 cos30 2 cos50t ... 2 3 5
例如：噪声信号可以表示为一个时间函数；机械零件的表面粗糙度
，可以表示为一个二元空间变量的高度函数。
测试工作是按一定的目的和要求，获取感兴趣的、有限的某些特定信 息，而信号是信息的载体，信息则是信号所载的内容。
第1章
1.1.1 信号的分类
信号描述及分析
从信号描述上：确定性信号与非确定性信号；
从信号幅值和能量：能量信号与功率信号；
t
0
1
fx
t
第1章
信号描述及分析
信息：可理解为消息、情报或知识，信息是事物运动的状态和方式。信息
本身不是物质，不具有能量，但信息的传输依靠物质和能量。例如：人类
的语言文字是社会信息；商品报道是经济信息；遗传密码是生物信息。 信号：传输信息的载体称为信号，信息蕴含于信号之中。信号具有能量， 它描述了物理量的变化过程，在数学上可以表示为一个或几个独立变量的 函数，可以取为随时间或空间变化的图形。
2
2
0
2
2A A (A t )dt T0 2
余弦分量的幅值
2 an T0
4 x ( t ) cos n tdt 0 T0 / 2 T0
T0 / 2
T0 / 2
0
x(t ) cos n0tdt
4A 4A n 2 2 sin 2 n 2 2 n 2 0
1.2信号的基本运算
f (t) 2 1 －3 －2 －1 0 1 2 3 4 (a) t f (2t) 2 1 －4 －3 －2 －1 0 1 2 3 4 (b) t
t f( ) 2
2 1 －4 －3 －2 －1 0 1 2 3 4 t (c)
f(t)、f(2t)、f(t/2)的波形
尺度变换：将信号横坐标的尺寸压缩或展宽。
a 1 尺度缩小
f (t ) f (at )
a 1 尺度放大
f(t) 2 1
当 a < 0 时还包括反转
f(2t) 2 1
t
-4 O 2
t
-2 O 1 f(-2t)
2 1
1 f ( t) 2
t
2 1
t
-1 O 2
-8
O
4
f (k ) f (ak )
4 2 1 k -4 -3 -2-1 O 1 2 3 4 3 f(k) 4 2 2
f (t) 1
d f (t ) dt
1
－2
－1 0
1
2
t
－2
－1 0 －1
1
2
t
(a)
(b)
信号的微分
f (t) 1 0 1 t 1 0 1 t
y(t ) f ( ) d
t
信号的积分
1
t
-3
O
2
f(k-1) 1
1 0
1
2
t
k -2 O 3
三. 展缩(尺度变换) ★
以变量at代替f(t)中的独立变量t可得f(at)，它是 f(t)沿时间轴展缩(尺度变换)而成的一个新的信号函数 或波形。 信号f(at)中，a为常数,|a|>1时表示f(t)沿时间轴压 缩成原来的1/|a|倍；|a|<1时表示f(t)沿时间轴扩展为原 来的1/|a|倍。 图中(a)、(b)、(c)分别表示f(t)、f(2t)、f(t/2)的波 形。
t f( ) 2
2 1 －4 －3 －2 －1 0 1 2 3 4 t (c)
f(t)、f(2t)、f(t/2)的波形
尺度变换：将信号横坐标的尺寸压缩或展宽。
a 1 尺度缩小
f (t ) f (at )
a 1 尺度放大
f(t) 2 1
当 a < 0 时还包括反转
f(2t) 2 1
t
-4 O 2
t
-2 O 1 f(-2t)
2 1
1 f ( t) 2
t
2 1
t
-1 O 2
-8
O
4
f (k ) f (ak )
4 2 1 k -4 -3 -2-1 O 1 2 3 4 3 f(k) 4 2 2
f (t) 1
d f (t ) dt
1
－2
－1 0
1
2
t
－2
－1 0 －1
1
2
t
(a)
(b)
信号的微分
f (t) 1 0 1 t 1 0 1 t
y(t ) f ( ) d
t
信号的积分
1
t
-3
O
2
f(k-1) 1
1 0
1
2
t
k -2 O 3
三. 展缩(尺度变换) ★
以变量at代替f(t)中的独立变量t可得f(at)，它是 f(t)沿时间轴展缩(尺度变换)而成的一个新的信号函数 或波形。 信号f(at)中，a为常数,|a|>1时表示f(t)沿时间轴压 缩成原来的1/|a|倍；|a|<1时表示f(t)沿时间轴扩展为原 来的1/|a|倍。 图中(a)、(b)、(c)分别表示f(t)、f(2t)、f(t/2)的波 形。
CH1-3指数信号与正弦信号
e
e
j0 n
15
若为周期序列 如何确定序列的周期？？？
0 m 如果 （N和m均 为 正 整 数 ） ， 2 N
则最小的 N 就 是e
j( 0 k )
的 周 期。
m 0 3 / 4 3 sin( 3k / 4) N 8 N 2 2 8
sin( 5k / 2)
N 1 N n
12
MATLAB函数cos(或sin)可用来产生正、余弦序列。
2．虚指数序列 和 正弦序列 j 0 n x[n] A cos( 0 n ) x[n] e
利用Euler 公式可以将正弦序列和虚指数序列联系起来，即
e j0n cos0n jsin0n
1 j 0 n cos 0 n (e e j 0 n ) 2
e
j0t
cos0t j sin0t (1.26)
数 信 号 ； k 0, 1, 2,
2
虚指数信号的实部和虚部都是周期为2π/ω0的正弦型信号。
e jk0t : 一组成谐 波关系的虚指
2. 正弦信号
x(t ) A cos( 0 t )
cos( 0 t )
a >1
a 1时,收敛
0< a <1
n
a<1
1< a <0
n
n
n
11
形如 { a n , n 0 }的单边指数序列称为‘ 几何级数’ 。
1 对 a 1, 该 级 数 收 敛 。a 。 1 a n0
n
1 a 该级数的有限项之和 ： a , a 1 a n0
N
18
N 12
1.3信号的运算
§1.3 信号的运算
要求：掌握信号的基本运算方法。 内容： 信号的移位、反褶与尺度 微分与积分 两信号相加与相乘
1 信号的代数运算 1）信号的加减运算 f (t ) = f1 (t ) ± f 2 (t ) 注意要在对应的时间上进行加减运算。
1 t1 1 0 -1 0 t2 t1 2 1 0 -1 t2
反褶 0 2 -2 0
-1
1
没有可实现此功能的实际器件。数字信号处理中可 以实现此概念，例如堆栈中的“后进先出”。
3. 信号的时移
y (t ) = f (t + t0 )
其中 t0 为实常数，即将原信号沿横轴（时间轴）向左 或向右做整体移动。
2 1
2 1
2 1
-1
0
2
-1
0
2
-2 -1
t0 < 0 向右移位
相加
2）信号的相乘运算：f (t ) = f1 (t ) f 2 (t ) 注意要在对应的时间上进行相乘运算。
1 t1 1 0 -1 0 t2 相乘 t1 1 0 -1 t2
3）信号的微分与积分
d f (t ) 微分： f 微分： ′(t ) = ， dt
1
（1）
积分： 积分： f (τ ) dτ ∫
0 1 t0 > 0 向左移位
4 信号的尺度变换
y (t ) = f (at )
其中 a 为实常数，即将原信号在时间轴 上进行压缩或扩展。
2 1 2 -1 0 2 4 |a|>1 原信号被压缩 0<|a|<1 原信号被扩展
-1
0
1
2
5 .综合变换 以变量 at + b 代替 f (t )中的独立变量 t ，可 得一新的信号函数 f (at + b) 。当 a > 0 时，它 是 f (t )沿时间轴展缩、平移后的信号波形；当 a < 0 时，它是f(t)沿时间轴展缩平移和反转后 的信号波形，下面举例说明其变换过程。
要求：掌握信号的基本运算方法。 内容： 信号的移位、反褶与尺度 微分与积分 两信号相加与相乘
1 信号的代数运算 1）信号的加减运算 f (t ) = f1 (t ) ± f 2 (t ) 注意要在对应的时间上进行加减运算。
1 t1 1 0 -1 0 t2 t1 2 1 0 -1 t2
反褶 0 2 -2 0
-1
1
没有可实现此功能的实际器件。数字信号处理中可 以实现此概念，例如堆栈中的“后进先出”。
3. 信号的时移
y (t ) = f (t + t0 )
其中 t0 为实常数，即将原信号沿横轴（时间轴）向左 或向右做整体移动。
2 1
2 1
2 1
-1
0
2
-1
0
2
-2 -1
t0 < 0 向右移位
相加
2）信号的相乘运算：f (t ) = f1 (t ) f 2 (t ) 注意要在对应的时间上进行相乘运算。
1 t1 1 0 -1 0 t2 相乘 t1 1 0 -1 t2
3）信号的微分与积分
d f (t ) 微分： f 微分： ′(t ) = ， dt
1
（1）
积分： 积分： f (τ ) dτ ∫
0 1 t0 > 0 向左移位
4 信号的尺度变换
y (t ) = f (at )
其中 a 为实常数，即将原信号在时间轴 上进行压缩或扩展。
2 1 2 -1 0 2 4 |a|>1 原信号被压缩 0<|a|<1 原信号被扩展
-1
0
1
2
5 .综合变换 以变量 at + b 代替 f (t )中的独立变量 t ，可 得一新的信号函数 f (at + b) 。当 a > 0 时，它 是 f (t )沿时间轴展缩、平移后的信号波形；当 a < 0 时，它是f(t)沿时间轴展缩平移和反转后 的信号波形，下面举例说明其变换过程。
matlab_ch1.1.3变量与函数
§1.3 变量与函数
1
MATLAB的数据类型主要包括数字、字符串、矩阵、单元 型数据及结构型数据等 下面重点介绍几个常用类型：
常量 变量 永久变量 符号变量
常量
2
MATLAB中的数据有常量与变量之分，常量也称为数值 数值量包括实数与复数，具体形式上包括标量、向量、数 组和矩阵等一切可以用数字表示的量
1 1 1 ˆ M Q1 M Q3 73.4 4 2 4
14
prctile 使用Matlab函数 p
1.1.2 表示分散性的数字特征
例1.3（续例1.2 ）求例1.2血清蛋白含量数据的方差、标准差 、变异系数、极差、四分位差，并分析是否有异常值.
74.3 79.5 75.0 73.5 75.8 70.4 73.5 67.2 75 8 75.8 73.5 78.8 75.6 73.5 75.0 75.8 72.0 79.5 76.5 73 5 73.5 79.5 68.8 75.0 78.8 72.0 68.8 76.5 73.5 72.7 75 0 75.0 70.4 78.0 78.8 74.3 64.3 76.5 74.3 74.7 70.4 72 7 72.7 76.5 70.4 72.0 75.8 75.8 70.4 76.5 65.0 77.2 73 5 73.5 72.7 80.5 72.0 65.0 80.3 71.2 77.6 76.5 68.8 73 5 73.5 77.2 80.5 72.0 74.3 69.7 81.2 67.3 81.6 67.3 72 7 72.7 84.3 69.7 74.3 71.2 74.3 75.0 72.0 75.4 67.3 81 6 81.6 75.0 71.2 71.2 69.7 73.5 70.4 75.0 72.7 67.3 70 3 70.3 76.5 73.5 72.0 68.0 73.5 68.0 74.3 72.7 72.7 74 3 74.3 70.4
1
MATLAB的数据类型主要包括数字、字符串、矩阵、单元 型数据及结构型数据等 下面重点介绍几个常用类型：
常量 变量 永久变量 符号变量
常量
2
MATLAB中的数据有常量与变量之分，常量也称为数值 数值量包括实数与复数，具体形式上包括标量、向量、数 组和矩阵等一切可以用数字表示的量
1 1 1 ˆ M Q1 M Q3 73.4 4 2 4
14
prctile 使用Matlab函数 p
1.1.2 表示分散性的数字特征
例1.3（续例1.2 ）求例1.2血清蛋白含量数据的方差、标准差 、变异系数、极差、四分位差，并分析是否有异常值.
74.3 79.5 75.0 73.5 75.8 70.4 73.5 67.2 75 8 75.8 73.5 78.8 75.6 73.5 75.0 75.8 72.0 79.5 76.5 73 5 73.5 79.5 68.8 75.0 78.8 72.0 68.8 76.5 73.5 72.7 75 0 75.0 70.4 78.0 78.8 74.3 64.3 76.5 74.3 74.7 70.4 72 7 72.7 76.5 70.4 72.0 75.8 75.8 70.4 76.5 65.0 77.2 73 5 73.5 72.7 80.5 72.0 65.0 80.3 71.2 77.6 76.5 68.8 73 5 73.5 77.2 80.5 72.0 74.3 69.7 81.2 67.3 81.6 67.3 72 7 72.7 84.3 69.7 74.3 71.2 74.3 75.0 72.0 75.4 67.3 81 6 81.6 75.0 71.2 71.2 69.7 73.5 70.4 75.0 72.7 67.3 70 3 70.3 76.5 73.5 72.0 68.0 73.5 68.0 74.3 72.7 72.7 74 3 74.3 70.4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11
LOGO
2
2012/9/1
1.3 信号的运算
3. 尺度变换（横坐标展缩）
1.3 信号的运算
平移、翻转和尺度变换相结合： 已知f(t)如图所示，求 y(t)=f(-3t+6)的波形。
方法1
尺度 反转
尺度——反转——平移
平移
|a|>1表示f(t)波形在时间轴上压缩1/|a|倍 |a|<1表示f(t)波形在时间轴上扩展|a|倍
4
1.3 信号的基本运算
1.3 信号的基本运算
2、离散信号的相加和相乘
LOGO
LOGO
2012/9/1
6
1
2012/9/1
1.3 信号的运算
p22 1.移位(平移):
1.3 信号的运算
移位(平移):
t t0 f (t ) t f (t t0 )
t0 0，f(t) 右移t0， t0 0，f(t) 左移|t 0|
LOGO
7
LOGO
1.3 信号的运算
2. 反转
1.3 信号的基本运算
练习
注意：是对 t 的变换！ 思考：f[-(t+1)]与f(t+1)关于纵轴对称吗？ f(-t+1)与f(t+1)关于纵轴对称吗？
LOGO
9
LOGO
2012/9/1
10
1.3 信号的基本运算
1.3 信号的运算
LOGO
2012/9/1
17
LOGO
LOGO
3
2012/9/1
第一章
信号与系统
绪论：信号和系统的概念 信号的描述和分类
第一章 导论 主讲：赵琳娜
信号的基本运算 阶跃函数和冲激函数 系统的描述、性质和分类； LTI 系统
LOGOLOGO来自1.3 信号的基本运算
1.3 信号的基本运算
1、连续信号的相加和相乘
LOGO
2012/9/1
3
LOGO
2012/9/1
LOGO
13 14
LOGO
1.3 信号的运算
已知f(t)如图所示，求 y(t)=f(-3t+6)的波形。
方法2：
1.3 信号的运算
二、微分和积分
1、微分 1 0 1 1
df (t ) dt
平移——尺度——反转
平 移
y(t )
f (t )
df (t ) f ' (t ) f (1) (t ) dt
展 缩
3 4
t
反折
4 0 -1 1 3
t
LOGO
LOGO
16
1.3 信号的运算
2、积分 f(t)
y (t )
1
0
f ( )d f
t
t
( 1)
(t )
1 0 t 1
1
f(t)=
0
t 1
0
1
t
t
t
(0 t 1) 1d t f ( )d 0 t 1 t 1 d 1 d 0 d 1 0 1 ( 1 t ) 0 1 0