第19章参考答案
- 格式:doc
- 大小:52.50 KB
- 文档页数:6

第19章爬行纲复习题一、填空题1、爬行动物的脊柱分化为(颈椎)、(胸椎)、(腰椎)、(荐椎)、(尾椎)5个部分。
2、爬行动物具有多枚颈椎,其中第一枚称为(环椎),第二枚称为(枢椎),具(2)枚荐椎。
3、爬行动物的牙齿按着生方式可分为(槽生齿)、(侧生齿)、(端生齿),鳄鱼牙齿的着生方式为(槽生)。
4、爬行动物的呼吸方式除具有吞咽呼吸外,又发展了(胸腹式呼吸)。
5、爬行动物心脏由(静脉窦)、(心房)、(心室)组成,其中(静脉窦)趋于退化,(心室)具有不完全的分隔,循环方式为(不完全的双)循环。
6、爬行类适应陆生的最主要特征是皮肤(干燥),缺乏(腺体),(角质层)层较厚,产大型(羊膜卵),(体内)受精。
7、从爬行动物开始,肌肉系统出现了陆生脊椎动物特有的(皮肤肌)和(肋间肌)。
8、五趾型附肢从(两栖)动物开始出现。
盲肠从(爬行)动物开始出现。
9、爬行动物的内耳司听觉感受的(瓶状囊)显著加长。
蜥蜴的听觉器官发达,出现了雏形的(外耳道);蛇类因穴居生活,声波沿地面通过头骨的(方骨)传递给(耳柱骨),从而使内耳产生听觉。
10、爬行动物的的代谢废物以(尿酸)形式排出。
11、胸廓是由(胸椎)、(胸骨)、(肋骨)三部分组成,最早出现胸廓的动物类群是(爬行类)。
二、选择题1、次生腭最完整的爬行动物是(A)。
A、鳄类B、龟类C、蜥蜴D、蛇类2、爬行类从外形上显著区别于两栖类的特征是(D)。
A、具有五趾型附肢B、有尾C、皮肤富有腺体D、皮肤干燥,有角质鳞片或盾片3、次生腭的作用是(D)。
A、使眼球不能下陷B、使头骨更加坚固C、使内鼻孔前移D、使内鼻孔后移,口腔和鼻腔分开4、具有1个枕骨髁的动物是(B)。
A、两栖类和爬行类B、鸟类和爬行类C、鸟类和哺乳类D、两栖类和哺乳类5、在下列动物中,具有颊窝的是(A)。
A、蝮蛇B、眼镜蛇C、蟒蛇D、乌梢蛇6、最早出现枢椎的动物是(B)。
A、两栖类B、爬行类C、鸟类D、哺乳类7、爬行动物的“盐腺”是(B)。

第19章生存分析思考与练习参考答案一、最佳选择题1. 下列有关生存时间的定义中正确的是( E )。
A.流行病学研究中,从开始接触某危险因素至某病发病所经历的时间B.乳腺增生症妇女治疗后阳性体征消失至首次复发的时间C.肺癌患者从手术治疗开始到死亡的时间D.急性白血病患者从治疗开始到缓解的时间E.以上均正确2. 教材表19-18表是急性白血病患者药物诱导后缓解至首次复发的随访记录。
教材表19-18 急性白血病患者药物诱导后缓解至首次复发的随访记录编号缓解日期终止观察日期结局生存时间/天1 2000.04.01 2000.09.06 复发1582 2001.11.05 2002.02.05 死亡913 2000.07.15 2000.12.10 复发1474 2001.05.20 2001.08.25 失访965 2002.09.03 2002.12.31 缓解119……………生存时间属删失数据的有(C)。
A.1号和3号B.1号和2号C.2号、4号和5号D.2号、3号和4号E.1号、2号和3号3. 下列有关log-rank检验的描述中正确的是(A)。
A.log-rank检验是各组生存率的整体比较B.log-rank检验是各组生存率某时间点的比较C.log-rank检验属生存曲线比较的参数法D.log-rank检验中,各组实际死亡数必等于理论死亡数E.log-rank检验的自由度为14. Log-rank检验与Breslow检验相比,( B )。
A.log-rank检验对组间死亡近期差异敏感B.log-rank检验对组间死亡远期差异敏感C.Breslow检验对组间死亡远期差异敏感D.两者对组间死亡远期差异同样敏感E.两者对组间死亡近期差异同样敏感5. Cox回归模型要求两个不同个体在不同时刻t的风险函数之比(D)。
A.随时间增加而增加B.随时间增加而减小C.开始随时间增加而增加,后来随时间增加而减小D.不随时间改变E.视具体情况而定二、思考题1. 生存分析的主要用途及其统计学方法有哪些?答:生存分析在生物医学领域主要解决如下问题。


综上可知,命题成立.评注如果两个互质的正整数之积是一个完全平方数,则这两个正整数都是完全平方数.这一命题是我们证明此题的出发点.19.4.27★★★如果正整数a 、b 、c 满足222c a b =+.证明:数2c ab +和2c ab -都可以表示为两个正整数的平方和.解析 巧妙运用下述命题:如果正整数x 可表示为两个正整数的平方和,则2x 也可表示为两个整数的平方和.事实上,设22x u v =+,这里x 、u 、v 都是正整数.则()()2222222x u v u v u v =+=++-.于是,2x 可表示为两个整数u v +和u v -的平方和,命题获证.注意到,由条件有 ()()22222222c ab c a ab b c a b ±=+±+=+±. 利用已证命题,可知()()()2224c ab c a b c a b ±=+±+- . 记c a b x +±=,c a b y -= ,由222c a b =+可知x 、y 都是正整数,并且()2224c ab x y ±=+.若x 、y 不同为偶数,则由平方数0≡或()1mod 4,可知221x y +≡或()2mod 4,这是一个矛盾.所以,x 、y 都是偶数,从而22222x y c ab ⎛⎫⎛⎫±=+ ⎪ ⎪⎝⎭⎝⎭,这就是 要证的结论.评注 这里本质上只是恒等式()()()22222u v u v u v +=++-的应用,在处理竞赛问题时,代数式变形能力显得十分重要.19.4.28是否存在正整数m 、n 使得331m n a =++是完全平方数?解析 分如下三种情形讨论:(1)若m m 、n 都是偶数,则()31mod 4m ≡,()31mod4n ≡,所以()3313mod4m n a =++≡, 故此时a 不是完全平方数.(2)若m 、n 都是奇数,则()33mod4m ≡,()33mod 4n =,所以()3313mod4m n a =++≡, 故此时a 不是完全平方数.(3)若m 、n 是一奇一偶,不妨设m 是奇数,n 是偶数,则()33mod8m ≡,()31mod8n ≡,所以()3315mod8m n a =++≡,故此时a 不是完全平方数.综上所述,对于任意正整数m 、n ,正整数331m n a =++都不是完全平方数.评注 判断一个数不是完全平方数,我们也可以用“模”的方法,例如,我们知道,偶数的平方是4的倍数,奇数的平方除以4余1,所以,若一个整数同余2或者3模4,则它一定不是完全平方数;类似地,若一个整数同余2模3,则它一定不是完全平方数;一个整数同余2、3模5,则它一定不是完全平方数等等.其实,考虑末位数也是用“模”的方法,即模10.19.4.29★★★已知n 是正整数,且21n +和31n +都是完全平方数,求证:40|n . 解析 因为34025=⨯,所以,只需证明:32|n ,且5|n 即可.设221n a +=,231n b +=,其中a 、b 都是正整数.由于a 是奇数,所以,()21mod8a ≡,从而4|n ,于是,31n +是奇数,所以,()21mod8b ≡,即()311mod8n +≡,从而()0mod8n ≡. 又对于任意整数x ,有()0 , 1 , 2mod5x ≡±±,所以,()20 , 1 , 4mod5x ≡,于是()22522mod5a b n +=+≡,故只能是()221mod5a b ≡≡,所以,()211mod5n +≡,从而()0mod5n ≡.因为(8,5)=1,所以,40|n19.4.30★★★—个正整数若能表示为两个正整数的平方差,称为“智慧数”,比如221653=-,16就是一个“智慧数”,从1开始数起,第2008个“智慧数”是哪个数? 解析 1不是“智慧数”,大于1的奇正整数()()22211 1 , 2 , 3 , k k k k +=+-= ,都是“智慧数”.被4整除的偶数4k ,有()()()22411 2 , 3 , k k k k =+--= ,都是“智慧数”,而4不能表示为两个正整数的平方差,4不是“智慧数”.被4除余2的数()42 1 , 2 , k k += ,设()()2242k x y x y x y +=-=+-,其中x 、y 为正整数,当x 、y 奇偶性相同时,x y +,x y -均为偶数,()()x y x y +⋅-被4整除,而42k +不被4整除,所以x 、y 奇偶性相同的假设不可能成立;当x 、y 奇偶性不同时,x y +,x y -均为奇数,()()x y x y +-为奇数,而42k +为偶数,故x 、y 奇偶性不同的假设也不可能成立.即不存在正整数x 、y ,使2242k x y +=-,即形如42k +的数均不是“智慧数”. 综述,在正整数列中,前四个正整数中只有3为“智慧数”,之后每连续四个数中有三个“智慧数”,其中第二个数,即形如42k +的数不是智慧数.200813669=+⨯,()466912680⨯+=.因此,第2008个“智慧数”是2680. 19.4.31★★★把能表示成两个正整数平方差的这种正整数,从小到大排成一列:12 , , , , n a a a ,例如:22222222123421 3 , 32 5 , 437 , 318 , a a a a =-==-==-==-= ,求122007a a a +++ 的值.解析 当9m ≥时,若21m k =+是奇数,则()221m k k =+-,即m 能表示成两个正整数的平方差;若4m k =,则()()211m k k =+--,即m 也能表示成两个正整数的平方差;若4m k =,则()()2211m k k =+--,即m 也能表示成两个正整数的平方差;若42m k =+,则m 不能表示成两个正整数的平方差.所以,59a =,611a =,712a =,…,一般地,343k a k =+,3144k a k +=+,3245k a k +=+, 1 , 2 , k =故3132334445471216k k k a a a k k k k +++++=+++++=+,而20073669=⨯,所以()12200712312116122161266816a a a a a a +++=+++⨯++⨯+++⨯+()166866815126681626920052+=++⨯=. 19.4.32★★在二个连续的平方数之间能不能有二个完全立方数?换言之,是否存在正整数a 、b 、n 使得()22331n a b n <<<+?解析 假设存在正整数a 、b 、n ,使得()22331n a b n <<<+.因33a b <,可得()()323311a a b n <+<+≤.又因为23n a <,可得24n a <,即2n a <.故()()323221331311a a a a n n n +=+++>++>+,矛盾. 故假设不成立,即二个连续的平方数之间不能有二个完全立方数.19.4.33★★★设n 为正整数,如果存在一个完全平方数,使得在十进制表示下此完全平方数的各位数字之和为n ,那么称n 为好数(例如13是一个好数,因为2749=的各位数字之和等于13).问:在1,2,…,2007中有多少个好数?解析 首先,对()0 , 1 , 2 , 3 , 4mod9x ≡±±±±分别计算,可得()20 , 1 , 4 , 0 , 7mod9x ≡,利用十进制下一个数与它的数码和模9同余,可知满足条件的()0 , 1 , 4 , 7mod7n ≡,即()0mod9n ≡或()1mod3n ≡.其次,注意到 23333512121225m m = 个个12,因此,若存在非负整数m ,使得37n m =+,则n 为好数,又由211=,224=可知1n =,4是好数,因此,若()1mod3n ≡,则n 为好数.最后,由()2211010110210199980001m m m m m ---=-⨯+= 个9个,可知若()0mod9n ≡,则n 是好数.综上可知,n 为好数的充要条件是()0mod9n ≡或()1mod3n ≡.依此可求得1,2,…,2007中好数的个数为669223892+-个.19.4.34★★★在黑板上依如下规则写下了若干个数:第一个数为1,以后的每一个数都等于已写数的个数加上这些已写数的平方和.证明:黑板上不可能出现除1以外的完全平方数.解析 利用相邻两个完全平方数之间的正整数都不是完全平方数这一结论.设第n 次所写的数为n ,则11a =,22a =,并且222112n n a n a a a +=++++ ,1n ≥. ①利用递推式①,可知()22111n n a n a a -=-+++ ,2n ≥,② 由①-②,可知211n n na a a +-=+,2n ≥, 即211n n n a a a +=++,2n ≥.注意到,()22211n n n n a a a a <++<+,故2n ≥时,1n a +不是完全平方数,又2a 不是完全平方数,故命题成立.评注 用递推式表示题中的条件后,问题得以数学化,从而获得解决.用恰当的方式将问题表示,这一过程是一个数学化的过程,是处理实际问题时必要的第一步.19.4.35★★★如果对x 的一切整数值,x 的二次三项式2ax bx c ++都是平方数(即整数的平方).证明:(1)2a 、2b 、c 都是整数;(2)a 、b 、c 都是整数,并且c 是平方数.反过来,如果(2)成立,是否对一切x 的整数值,2ax bx c ++的值都是平方数? 解析 (1)令0x =得c =平方数2l .令1x =±得2a b c m ++=,2a b c n -+=,其中m 、n 都是整数,所以2222a m n c =+-,222b m n =-都是整数.(2)如果2b 是奇数21k +(k 是整数),那么令4x =得22164a b l h ++=,其中h 是整数.由于2a 是整数,所以16a 被4整除,1641642a b a k +=++除以4余2.而()()22h l h l h l -=+-,在h 、l 的奇偶性不同时,()()h l h l +-是奇数;在h 、l 的奇偶性相同时,()()h l h l +-被4整除.因此22164a b h l +≠-,从而2b 是偶数,b 是整数.2a m c b =--也是整数. 在(2)成立时,2ax bx c ++不一定对x 的整数值都是平方数.例如,2a =,2b =,4c =,1x =时,28ax bx c ++=不是平方数. 19.4.36★★★设n 为任意正整数,p 为正整数. 试确定正整数p ,使123p p p p n ++++ 都是某个正整数的平方. 解析 令 , 123p p p p n p S n =++++ .首先我们知道:(1)() , 112n n n S +=,()() , 2126n n n n S ++=. 因此 2 , 13S =, 2 , 25S =均不为完全平方数. 所以1p =,2不满足所要求的条件.(2)()()222 , 31142n n n n n S ++⎛⎫== ⎪⎝⎭,对任意正整数而言,()12n n +必为整数,所以 , 3n S 必为完全平方数.(3)对任意4p ≥而言, 2 , 1221p p p p S =+=+必为奇数,但任一奇数m ,设21m k =+(k 为整数),则()()2221411m k k k =+=++. 显然2m 不可能是21p +型的数.(因为()1k k +必为一奇一偶,除1k =之外,()412p k k +≠,又4p ≥时,216p ≥,而1k =时,()418k k +=也不为2p 的数). 由(1)、(2)、(3)的讨论得知3p =是唯一使123p p p p n ++++ 恒为完全平方数的正整数.。

第十九章控制与控制过程一、教学要点1、控制的必要性。
2、控制的基本原理.3、种种类型控制的概念。
4、预先控制、现场控制和成果控制的内涵,及其各自的优缺点.5、有效控制有的基本特征。
6、控制过程的基本内容。
7、如何选择控制的重点?8、制定控制标准的方法。
9、纠偏措施应满足的要求.10、关键名词:控制、程序控制、跟踪控制、自适应控制、最佳控制、预先控制、现场控制、成果控制、适时控制、适度控制、客观控制、弹性控制、统计性标准、工程标准、评估性标准、二、习题(一)填充题1、控制是为了保证_________与_________适应的管理职能.2、控制工作的主要内容包括_________、_________和_________。
3、预先控制的内容包括_________和_________两个方面.4、成果控制的主要作用,是通过总结过去的经验和教训,为_________提供借鉴。
5、成果控制主要包括_________、_________、_________以及_________等内容。
6、企业应根据_________和_________来确定控制的范围和频度,建立有效的控制系统.7、适度控制是指控制的_________、_________和_________要恰到好处。
8、控制的过程都包括三个基本环节的工作:_________、_________和_________。
9、一般来说,企业可以使用的建立标准的方法有三种:_________、_________、_________ .10、工程标准也是一种用统计方法制定的控制标准,不过它不是对历史性统计资料的分析,而是通过对_________ .11、在采取任何纠正措施以前,必须首先对_________。
12、一般地说,弹性控制要求企业制定_________和_________。
(二)选择题1、1、有效的控制要求_________A. 选择关键的经营环节B。
确定恰当的控制频度C. 收集及时的信息D. 合理运用预算或非预算的控制手段2、根据确定控制标准Z值的方法,控制过程可以分为_________。
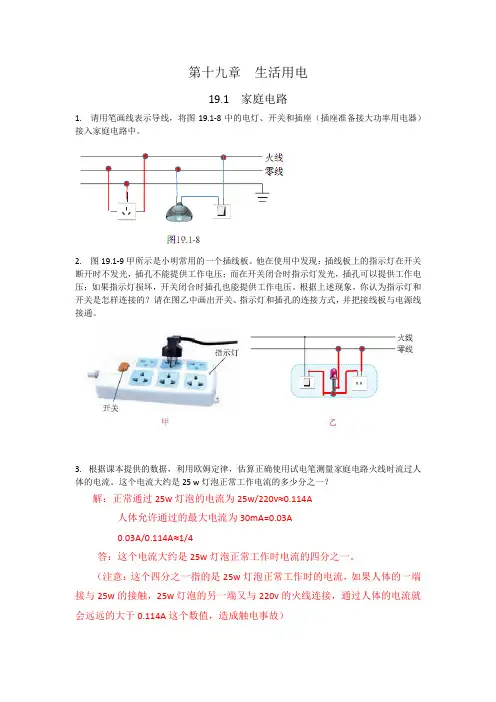
第十九章生活用电19.1 家庭电路1. 请用笔画线表示导线,将图19.1-8中的电灯、开关和插座(插座准备接大功率用电器)接入家庭电路中。
2. 图19.1-9甲所示是小明常用的一个插线板。
他在使用中发现:插线板上的指示灯在开关断开时不发光,插孔不能提供工作电压;而在开关闭合时指示灯发光,插孔可以提供工作电压;如果指示灯损坏,开关闭合时插孔也能提供工作电压。
根据上述现象,你认为指示灯和开关是怎样连接的?请在图乙中画出开关、指示灯和插孔的连接方式,并把接线板与电源线接通。
3.根据课本提供的数据,利用欧姆定律,估算正确使用试电笔测量家庭电路火线时流过人体的电流。
这个电流大约是25 w灯泡正常工作电流的多少分之一?解:正常通过25w灯泡的电流为25w/220v≈0.114A人体允许通过的最大电流为30mA=0.03A0.03A/0.114A≈1/4答:这个电流大约是25w灯泡正常工作时电流的四分之一。
(注意:这个四分之一指的是25w灯泡正常工作时的电流,如果人体的一端接与25w的接触,25w灯泡的另一端又与220v的火线连接,通过人体的电流就会远远的大于0.114A这个数值,造成触电事故)4. 你家里的空气开关是安装在家庭电路中哪个部位的?为什么要这样安装?答:安装在家庭电路的干路上,这样安装的好处是无论家庭电路中任何一个地方发生短路现象或者电流过大,都会自动切断整个电路。
19.2 家庭电路中电流过大的原因1. 如图19-2-6所示的甲、乙两个电路中,开关闭合后,输电线因电流过大而燃烧起来,甲、乙两图产生电流过大的原因是不同的。
其原因各是什么?答:甲图中电流过大的原因是:电路中用电总功率过大;乙图中电流过大的原因是发生了短路。
2. 电焊利用电流的热效应将焊条熔化,从而使金属部件连接在一起。
某电焊机输出电压40 V、输出功率2 000 w。
各种橡胶绝缘铜芯导线在常温下安全载流量(长时间通电时的最大安全电流)如下表。

暑期创业实践项目(一)已完成分数:100.01按照孕妇手机项目的调研,孕妇手机将具有多少元的市场价值A、70万B、70亿C、140万D、140亿正确答案:D 我的答案:D2孕妇手机项目目前并没有掌握“无辐射”技术正确答案:√我的答案:√3孕妇手机项目第二年不再有客户服务正确答案:×我的答案:×暑期创业实践项目(二)已完成分数:100.01特“色”吧的服务时间是A、周一至周五B、周一至周六C、周一至周日D、周六至周日正确答案:C 我的答案:C2hello tart蛋挞店需要融资多少A、1万B、1.5万C、2万D、2.5万正确答案:D 我的答案:D3特色吧里的服务员是以cosplay的形式出现正确答案:√我的答案:√4“青春纪念册”项目的目标客户不包括哪个A、初中生B、高中生C、大学生D、青年情侣正确答案:D 我的答案:D暑期创业实践项目(三)已完成分数:100.0 1上海理工大学旅游俱乐部打算每年开发几条路线A、3.0B、5.0C、7.0D、11.0正确答案:B 我的答案:B2上海理工大学旅游俱乐部项目前期流动资金预测为多少元A、5000.0B、10000.0C、15000.0D、20000.0正确答案:A 我的答案:A3校园二手自行车回收项目的业务只有出租,没有出售正确答案:×我的答案:×暑期创业实践项目(四)已完成分数:100.0 1carture的经营方式是B2C正确答案:×我的答案:×2carture启动资金最高不超过多少A、500万B、1000万C、1500万D、2000万正确答案:C 我的答案:C3carture是指汽车文化正确答案:√我的答案:√4校园全自动洗鞋机消费一次花费为几元钱A、3元B、5元C、6元D、7元正确答案:A 我的答案:A5DC town的定位是()A、抵挡汽车B、中档汽车C、高端汽车D、低中高档汽车正确答案:C 我的答案:C暑期创业实践项目(五)已完成分数:100.0 1移动酒吧车共有几个座位A、8个B、10个C、12个D、14个正确答案:D 我的答案:D2杨浦自行车租赁的客户是没有限制的正确答案:√我的答案:√3“杨浦自行车租赁”项目团队目前一共有几个人A、1.0B、2.0C、3.0D、4.0正确答案:B 我的答案:B暑期创业实践项目(六)已完成分数:100.0 1摩尔定律是指每隔多少月硬件就要升级一次A、6个月B、12个月C、18个月D、24个月正确答案:C 我的答案:C2校园互助网项目要求必须实名注册正确答案:√我的答案:√3全球移动互联网用户目前还没有达到10亿正确答案:×我的答案:×暑期创业实践项目(七)已完成分数:100.0 1世界牛奶日是哪天?()A、6月1日B、3月12日C、8月1日D、2月12日正确答案:A 我的答案:A2新新公司的做法比伊诺工作的做法更正确正确答案:×我的答案:×。

第19章爬行纲练习答案一、名词1. 羊膜卵amniotic egg:包括卵壳、卵膜、卵黄和胚胎等结构,在发育期间,发生羊膜、绒毛膜、尿囊膜等一系列胚膜结构的一种卵,它使羊膜动物获得了在陆地繁殖的能力。
2. 爬行动物reptile:是真正陆生脊椎动物的开始,是体被角质鳞片或盾片,完全用肺呼吸,以腹部贴地爬行,产大型羊膜卵,在陆地上繁殖的变温脊椎动物。
包括蜥蜴、蛇、龟、鳖、鳄等。
3. 颞窝(孔)与颊窝temporal fossa and facial pit:爬行动物头骨两侧眼眶后颞部的膜性硬骨的穿洞称为颞窝。
如蛇为双颞窝类。
蝮蛇的鼻孔与眼之间的颊部又一个陷窝,窝内有一个薄膜把腔分为内外二个室,为红外线感受器,被称为颞窝。
4. 红外线感受器infrared receptor:爬行类的蟒科蛇类和腹科蛇类在头部具有的特殊感受器,它具有对环境温度微小变化而发生反应的功能,这种热能感受器被称为红外线感受器。
如蟒蛇的唇窝和蝮蛇的颊窝。
5. 胸廓thorax(thoracic cage):脊椎动物从爬行类开始,胸椎、肋骨和胸骨借关节和韧带相互连接形成囊状结构的胸廓。
它保护内脏,加强呼吸。
6. 胸腹式呼吸thoracoabdominal breathing(respiration):爬行动物靠肋间肌和腹壁肌肉运动来扩大和缩小胸廓,从而完成呼吸动作,这种呼吸方式被称为胸腹式呼吸。
7. 次生腭secondary palate:脊椎动物从爬行动物开始,它的硬腭由前颌骨、上颌骨、腭骨的腭突和翼骨愈合组成,它位于脑颅底的口腔顶壁。
8. 闭锁式骨盆closed pelvis:爬行动物髂骨与荐椎的横突相连接,左右坐骨和耻骨在腹中线联合,构成的骨盆为闭锁式骨盆。
9. 同型齿与端生齿pleurodont and acrodont:绝大多数爬行动物的牙齿没有分化,都为同型的圆锥齿,这属于同型齿。
爬行动物低等种类如喙头蜥,其牙齿着生在颌骨的顶面,为端生齿。

华师大版八年级下册数学第19章矩形、菱形与正方形含答案一、单选题(共15题,共计45分)1、如图,在矩形ABCD中,M是BC边上一点,连接AM,过点D作,垂足为若,,则BM的长为A.1B.C.D.2、如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是()A.①②B.①③④C.①②④D.①②③④3、下列说法正确的是()A.有两个角为直角的四边形是矩形B.矩形的对角线相等C.平行四边形的对角线相等D.对角线互相垂直的四边形是菱形4、如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为()A.9B.9C.27D.275、如图,是北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13B.19C.25D.1696、如图,已知平行四边形ABCD的对角线的交点是0,直线EF过O点,且平行于AD,直线GH过0点且平行于AB,则图中平行四边形共有()A.15个B.16个C.17个D.18个7、如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A﹣D﹣E﹣F的路线爬行,乙虫沿着A﹣C﹣B﹣F的路线爬行,若它们的爬行速度相同,则()A.甲虫先到B.乙虫先到C.两虫同时到D.无法确定8、如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为()A. B. C. D.39、下列判断错误的是()A.两组对边分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.两条对角线垂直且平分的四边形是正方形D.四条边都相等的四边形是菱形10、如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AG,EG,AE,将△ABG和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE=3,CG=4,则DE的长度为()A. B. C.3 D.11、如图,平行四边形ABCD对角线AC、BD交于点O,∠ADB=20°,∠ACB=50°,过点O的直线交AD于点E,交BC于点F当点E从点A向点D移动过程中(点E与点A、点D不重合),四边形AFCE的形状变化依次是()A.平行四边形→矩形→平行四边形→菱形→平行四边形B.平行四边形→矩形→平行四边形→正方形→平行四边形C.平行四边形→菱形→平行四边形→矩形→平行四边形D.平行四边形→矩形→菱形→正方形→平行四边形12、如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )A.四边形AEDF是平行四边形B.若∠BAC=90°,则四边形AEDF是矩形 C.若AD⊥BC且AB=AC,则四边形AEDF是菱形 D.若AD平分∠BAC,则四边形AEDF是矩形13、如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是()A.3 :4B.5 :8C.9 :16D.1 :214、如图,在△ABC中,∠A=∠B=45 ,AB=4,以AC为边的阴影部分图形是一个正方形,则这个正方形的面积为()A.2B.4C.8D.1615、如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠,折叠后顶点D 恰好落在边OC上的点F处.若点D的坐标为,则点E的坐标为()A. B. C. D.二、填空题(共10题,共计30分)16、工人师傅在做矩形零件时,常用测量平行四边形的两条对角线是否相等来检查直角的精确度,这是根据________.17、阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.小明发现,过点E作E F∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).请回答:BC+DE的值为________参考小明思考问题的方法,解决问题:如图3,已知▱ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________18、如图,O是边长为4的正方形ABCD的中心,将一块足够大,圆心角为直角的扇形纸板的圆心放在点O处,并将纸板的圆心绕点O旋转,则正方形ABCD被纸板覆盖部分的面积为 ________。

第十九章习题 解答19-1:维恩位移定律:3( 2.89810)mT b b λ-==⨯ 331612.89810 5.3100.5510m bT K K λ--⨯===⨯⨯ 331612.898108.3100.3510m bT K K λ--⨯===⨯⨯ 341612.898101100.2910m bT K K λ--⨯===⨯⨯19-2: 斯特藩-波耳茨曼定律:4824( 5.6710/())M T w m k σσ-==⨯114443822.810 1.42105.6710M T K σ-⎛⎫⨯⎛⎫∴===⨯ ⎪⎪⨯⎝⎭⎝⎭19-3:(1) 最大动能:max 34819719()6.6310310 4.2 1.6102103.225102k cE h A hAJ eVνλ----=-=-⨯⨯⨯=-⨯⨯⨯=⨯≈(2) max19max 19()() 3.2251021.610k k eU E E U V E --=⨯∴===⨯ (3)34870196.6310310 2.96104.2 1.610hc m m A λ---⨯⨯⨯===⨯⨯⨯19-4:(1) 视网膜接收到光的能量为:834197183105 6.6310105101.9910cW n nh nhJ Jενλ----===⨯=⨯⨯⨯⨯⨯=⨯(2)功率为:181.9910E P w t-==⨯19-5: (1)每秒落到地面上单位面积的光子数量是:12834719128113106.63105102.0110n s m s m ------⨯⨯=⨯⨯⨯⨯=⨯(2)每秒钟进入人眼的光子数是:2318347141381 3.141023106.63105101.4210N S S -----⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=⨯⨯⨯⨯=⨯19-6: (1) 光子的频率为:()2020231820349.1103101.236106.6310h m c m c h HZ HZνν--=∴=⨯⨯⨯==⨯⨯(2) 光子的波长:()343180 6.63100.29.110310h m A m c ολ--⨯===⨯⨯⨯(3)光子的动量:()318102219.1103102.7310hP m c kg ms kg msλ----===⨯⨯⨯⋅=⨯⋅19-7: 光电效应和康普顿效应都通过光和物质的相互作用过程揭示了光具有粒子性的一面。

《海底两万里》阅读第二部分
一、第19章:
至此,阿龙纳斯等三人被迫留在艇上已经七个月,随艇航行了一万七千里,尼德·兰越来越暴躁阴郁,所以阿龙纳斯教授向尼摩船长提出离开潜艇恢复自由身,但尼摩船长拒绝了。
三、第20章:
尼摩船长在航行到靠近英吉利海峡的海域,吊唁沉船“复仇者号”,悼念的原因是:因为该战舰上的水兵很勇敢,奋战到生命最后一刻,宁愿葬身海底也不投降。
四、第21章:
吊唁完沉船后,诺第留斯号遭到了战舰的袭击,尼德·兰看到了逃跑的希望,先是摇手帕呼救,但是被尼摩船长制止了。
后面又想在离战舰近些的时候,跳海逃跑,但计划将要实施的时候,潜艇的舱盖关上了,计划泡汤。
尼摩船长驾驶诺第留斯号从水下冲撞战舰,直至击沉,阿龙纳斯目睹了沉落的全过程,触目惊心,简直是场大屠杀。
尼摩船长复仇的原因是:压迫者毁灭了他的祖国和家庭,他所喜欢和热爱的一切。
五、第22章:
在潜艇行驶到挪威海域,阿龙纳斯终于决定不顾一切逃跑,他们三人夺取附在诺第留斯号的小艇逃跑,但立即卷入了“迈尔大旋流”,他们三人最终被岛民救下,诺第留斯号则不知所踪。
19-1 19-2 19-3 19-5 19-4、19-8 19-1019-1 绘制图示各杆的扭矩图。
参考答案略19-2 直径为D =5cm 的圆轴,受到扭矩n M =2.15kN ·m 的作用,试求在距离轴心1cm 处的剪应力,并求轴截面上的最大剪应力。
参考答案:由圆轴扭转横截面上任意一点剪应力计算公式可知,距轴心1cm 处的剪应力为MPa I M pn 353250101015.246=⨯⨯⨯==πρτρ截面上的最大剪应力:MPa W M tn 6.8716501015.236max =⨯⨯==πτ 19-3 已知作用在变截面钢轴上的外力偶矩1m =1.8kN ·m ,2m =1.2kN ·m 。
试求最大剪应力和最大相对转角。
材料的G =80GPa 。
参考答案:直径为75mm 段的扭矩为m KN m m T .3)(211-=+-=; 直径为50mm 段的扭矩为KNm m T 2.122-=-=。
最大剪应力计算:MPa W T t 2.3616751033611max 1=⨯⨯==πτ;MPa W T t 9.481650102.13622max 2=⨯⨯==πτ则最大剪应力MPa 9.48max =τ最大相对转角计算:22.10212773.0102231.121005416.932501080500102.13275108075010333436436222111max 2max 1max ==⨯+⨯=⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=+=+=--rad rad rad GI lT GI l T P P ππϕϕϕ 19-4 已知圆轴的转速n =300r /min ,传递功率330.75kW ,材料的][τ=60MPa ,G =82GPa 。
要求在2m 长度内的相对扭转角不超过1º,试求该轴的直径。
参考答案:计算外力偶矩(即扭矩):m N n N Me T ⋅=⨯===875.1052830075.33095509550按强度条件设计轴的直径:[]MPa d W T t601610875.1052833max =≤⨯==τπτ mm d 32.966010875.105281633=⨯⨯≥π按刚度条件设计轴的直径:118032108210210875.105281804333max ≤⨯⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=⨯=πππϕd GI Tl p 得 mm d 64.110108232180********.1052842333=⨯⨯⨯⨯⨯⨯⨯≥π故该轴的直径mm d 64.110≥19-5 图示一圆截面直径为80cm 的传动轴,上面作用的外力偶矩为1m =1000N ·m ,2m =600N ·m ,3m =200N ·m ,4m =200N ·m ,(1)试作出此轴的扭矩图,(2)试计算各段轴内的最大剪应力及此轴的总扭转角(已知材料的剪切弹性模量G =79GPa );(3)若将外力偶矩1m 和2m 的作用位置互换一下,问圆轴的直径是否可以减少?注意:此题传动轴直径应为80mm 。
第十九章矩形,菱形与正方形章末测试(二)总分120分120分钟农安县合隆中学徐亚惠一.选择题(共8小题,每题3分)1.对角线相等且互相平分的四边形是()A.一般四边形B.平行四边形C.矩形 D.菱形2.下列说法中不能判定四边形是矩形的是()A.四个角都相等的四边形 B.有一个角为90°的平行四边形C.对角线相等的平行四边形D.对角线互相平分的四边形3.已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是()A.任意四边形B.矩形 C.菱形 D.正方形4.在平行四边形ABCD中,增加一个条件能使它成为矩形,则增加的条件是()A.对角线互相平分B.AB=BC C.AB=AC D.∠A+∠C=180°5.如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是()A.2 B.C.1 D.6.下列条件中,不能判定四边形ABCD为菱形的是()A.AC⊥BD,AC与BD互相平分B.AB=BC=CD=DAC.AB=BC,AD=CD,AC⊥BD D.AB=CD,AD=BC,AC⊥BD7.已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是()A.AC⊥BD B.AC=BD C.AC=BD且AC⊥BD D.AC平分∠BAD8.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为()A.2cm,2cm,2cm B.3cm,3cm,3cm C.4cm,4cm,4cm D.2cm,3cm,5cm二.填空题(共6小题,每题3分)9.如图,在四边形ABCD中,AD∥BC,且AD=BC,若再补充一个条件,如∠A= _________ 度时,就能推出四边形ABCD是矩形.10.如图,已知MN∥PQ,EF与MN,PQ分别交于A、C两点,过A、C两点作两组内错角的平分线,分别交于点B、D,则四边形ABCD是_________ .11.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是_________ .12.在四边形ABCD中,∠A=∠B=∠C=∠D,则四边形ABCD是_________ .13.一组邻边相等的_________ 是正方形,有一个角是_________ 角的菱形是正方形.14.如图,在△ABC中,点D是边BC上一动点,DE∥AC,DF∥AB,对△ABC及线段AD添加条件_________ 使得四边形AEFD是正方形.三.解答题(共11小题)15.(6分)如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.(1)求证:AC=FG.(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?16.(6分)如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形:△ABD,△BCE,△ACF,请解答下列问题:(1)求证:四边形AFED是平行四边形;(2)当△ABC满足什么条件时,四边形AFED是矩形?(3)当△ABC满足什么条件时,四边形AFED是菱形?(4)对于任意△ABC,▱AFED是否总存在?17.(6分)如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.18.(6分)如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.(1)求证:AC=BE;(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.19.(6分)已知:如图,在△ABC中,AB=AC,M是BC的中点,MD⊥AB,ME⊥AC,DF⊥AC,EG⊥AB,垂足分别为点D、E、F、G,DF、EG相交于点P.判断四边形MDPE的形状,并说明理由.20.(8分)如图:在平行四边形ABCD中,AC的垂直平分线分别交CD、AB于E、F两点,交AC于O点,试判断四边形AECF的形状,并说明理由.21.(8分)如图所示,▱ABCD的对角线AC的垂直平分线EF与AD、BC、AC分别交于点E、F、O,连接AF,EC,则四边形AFCE是菱形吗?为什么?22.(8分)在△ABC中,点O是AC边上一动点,点P在BC延长线上,过点O的直线DE∥BC交∠ACB与∠ACP的平分线于点D、E.(1)点O在什么位置时,四边形ADCE是矩形?说明理由.(2)在(1)的条件下,当AC与BC满足什么条件时,四边形ADCE是正方形?为什么?23.(8分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.(3)当点O在边AC上运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?24.(8分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)判断OE与OF的大小关系?并说明理由;(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF会是正方形.25.(8分)(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由。
第19章 习题参考答案19.1 习题1..欲使滴定时消耗0.10 mol·L -1 HC1溶液20~25 mL ,问应称取基准试剂Na 2CO 3多少克?此时称量误差能否小于0.1%?解:Na 2CO 3 + 2HC1 = 2NaCl + H 2O +CO 2↑依 H C l n :1:232=CO Na n所以 32)(21CO Na HCl M CV m ⋅= V=20mL 时,g m 11.099.105102010.0213=⨯⨯⨯⨯=-称量误差 E r =%18.011.00002.0=±V=25mL 时,g m 13.099.105102510.0213=⨯⨯⨯⨯=- 称量误差E r =%15.013.00002.0=±可见,称量误差不能小于0.1%。
2.确称取0.5877 g 基准试剂Na 2CO 3,溶解后在100 mL 容量瓶中配制成溶液,其浓度为多少?移取该标准溶液20.00 mL 标定某HC1溶液,滴定中用去HC1溶液21.96 mL ,计算该HCl 溶液的浓度。
解:C=105545.01000.099.105/5877.0/-⋅==L mol V M m Na 2CO 3 + 2HCl = 2NaCl + H 2O + CO 2↑依 H C l n :1:232=CO Na nC HCl ×0.02196:(0.02000×0.05545)=2:1解得:C HCl =0.1010mol•L -13.称取分析纯试剂K 2Cr 2O 7 14.709 g ,配成500.0 mL 溶液,计算K 2Cr 2O 7溶液的物质的量浓度。
解:1000.05000.018.294/709.14/===V M m C mol•L -14.称取分析纯试剂MgCO 3 1.850 g 溶解于过量的HC1溶液48.48 mL 中,待两者反应完全后,过量的HC1需3.83 mL NaOH 溶液返滴定。
2021学年人教版七年级数学下册《第19章一次函数》常考热点培优训练(附答案)1.如果P(2,m),A(1,1),B(4,0)三点在同一直线上,则m的值为()A.2B.﹣C.D.12.八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为()A.y=x+B.y=x+C.y=x+D.y=x+3.如图,已知直线y1=ax+b与y2=mx+n相交于点A(2,﹣1),若y1>y2,则x的取值范围是()A.x<2B.x>2C.x<﹣1D.x>﹣14.对于函数y=﹣3x+1,下列结论正确的是()A.它的图象必经过点(1,3)B.它的图象经过第一、二、四象限C.当x>0时,y<0D.y的值随x值的增大而增大5.一次函数y=kx+b,当k<0,b<0时,它的图象大致为()A.B.C.D.6.已知直线y=2x+b与坐标轴围成的三角形的面积是4,则b的值是()A.4B.2C.±4D.±27.把直线y=﹣2x向上平移后得到直线AB,若直线AB经过点(m,n),且2m+n=8,则直线AB的表达式为()A.y=﹣2x+4B.y=﹣2x+8C.y=﹣2x﹣4D.y=﹣2x﹣8 8.如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程kx+b=0的解为x=2;②关于x的方程kx+b=3的解为x=0;③当x>2时,y<0;④当x<0时,y<3.其中正确的是()A.①②③B.①③④C.②③④D.①②④9.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x>3时,y1<y2中.则正确的序号有.10.如图,在平面直角坐标系中,函数y=﹣2x与y=kx+b的图象交于点P(m,2),则不等式kx+b>﹣2x的解集为.11.将函数y=3x+1的图象平移,使它经过点(1,1),则平移后的函数表达式是.12.已知点A(2,﹣4),直线y=﹣x﹣2与y轴交于点B,在x轴上存在一点P,使得P A+PB 的值最小,则点P的坐标为.13.如图,O是坐标原点,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,则∠AOC的角平分线所在直线的函数关系式为.14.已知点P是直线y=﹣2x+4上的一个动点,若点P到两坐标轴的距离相等,则点P的坐标是.15.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为.16.已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则A2020的坐标是.17.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是.18.一次函数y=﹣x+3的图象与坐标轴围成三角形的面积是.19.九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为y1千米,骑自行车学生骑行的路程为y2千米,y1、y2关于x的函数图象如图所示.(1)求y2关于x的函数解析式;(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?20.资中某学校为了改善办学条件,计划购置一批电子白板和台式电脑.经招投标,购买一台电子白板比购买2台台式电脑多3000元,购买2台电子白板和3台台式电脑共需2.7万元.(1)求购买一台电子白板和一台台式电脑各需多少元?(2)根据该校实际情况,购买电子白板和台式电脑的总台数为24,并且台式电脑的台数不超过电子白板台数的3倍.问怎样购买最省钱?21.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;(2)当x=280(千米)时,求剩余油量Q的值;(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.22.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.(1)求该一次函数的解析式;(2)判定点C(4,﹣2)是否在该函数图象上?说明理由;(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.23.小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为ym.图中折线段OBA表示小亮在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).(1)点B所表示的实际意义是;(2)求出AB所在直线的函数关系式;(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?24.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.(1)求直线AB的解析式.(2)求△OAC的面积.(3)当△OMC的面积是△OAC的面积的时,求出这时点M的坐标.25.某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.(1)求一件A,B型商品的进价分别为多少元?(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?26.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数y=k1x+b1和y=kx+b的图象,分别与x轴交于点A、B,两直线交于点C.已知点A(﹣1,0),B(2,0),观察图象并回答下列问题:(1)关于x的方程k1x+b1=0的解是;关于x的不等式kx+b<0的解集是;(2)直接写出关于x的不等式组的解集;(3)若点C(1,3),求关于x的不等式k1x+b1>kx+b的解集和△ABC的面积.参考答案1.解:设直线的解析式为y=kx+b(k≠0),∵A(1,1),B(4,0),∴,解得,∴直线AB的解析式为y=﹣x+,∵P(2,m)在直线上,∴m=(﹣)×2+=.故选:C.2.解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,∵正方形的边长为1,∴OB=3,∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,∴三角形ABP面积是8÷2+1=5,∴BP•AB=5,∴AB=2.5,∴OA=3﹣2.5=0.5,由此可知直线l经过(0,0.5),(4,3)设直线方程为y=kx+b,则,解得.∴直线l解析式为y=x+.故选:A.3.解:根据题意当x>2时,若y1>y2.故选:B.4.解:A、当x=1时,y=﹣3x+1=﹣2,则点(1,3)不在函数y=﹣3x+1的图象上,所以A选项错误;B、k=﹣3<0,b=1>0,函数图象经过第一、二、四象限,所以B选项正确;C、当x>0时,y<1,所以C选项错误;D、y随x的增大而减小,所以D选项错误.故选:B.5.解:∵k<0,b<0,∴一次函数图象在二、三、四象限.故选:B.6.解:直线y=2x+b中,当x=0时,y=b;当y=0时,x=﹣;∴直线与坐标轴交于(0,b),(﹣,0)两点,∵直线y=2x+b与坐标轴围成的三角形的面积是4,∴×|b|×|﹣|=4,即b2=4,解得b=±4.故选:C.7.解:∵直线AB是直线y=﹣2x平移后得到的,∴直线AB的k是﹣2(直线平移后,其K不变)∴设直线AB的方程为y﹣y0=﹣2(x﹣x0)①把点(m,n)代入①并整理,得y=﹣2x+(2m+n)②∵2m+n=8 ③把③代入②,解得y=﹣2x+8,即直线AB的解析式为y=﹣2x+8.故选:B.8.解:由图象得:①关于x的方程kx+b=0的解为x=2,正确;②关于x的方程kx+b=3的解为x=0,正确;③当x>2时,y<0,正确;④当x<0时,y>3,错误;故选:A.9.解:根据图示及数据可知:①k<0正确;②a<0,原来的说法错误;③方程kx+b=x+a的解是x=3,正确;④当x>3时,y1<y2正确.故答案为:①③④10.解:当y=2时,﹣2x=2,x=﹣1,由图象得:不等式kx+b>﹣2x的解集为:x>﹣1,故答案为:x>﹣1.11.解:新直线是由一次函数y=3x+1的图象平移得到的,∴新直线的k=3,可设新直线的解析式为:y=3x+b.∵经过点(1,1),则1×3+b=1,解得b=﹣2,∴平移后图象函数的解析式为y=3x﹣2;故答案为:y=3x﹣2.12.解:作点B关于x轴的对称点B′,连接AB′,交x轴于P,连接PB,此时P A+PB的值最小.设直线AB′的解析式为y=kx+b,把A(2,﹣4),B′(0,2)代入得到,解得,∴直线AB′的解析式为y=﹣3x+2,令y=0,得到x=,∴P(,0),故答案为(,0).13.解:如图所示,延长BA交y轴于D,则BD⊥y轴,∵点A的坐标为(3,4),∴AD=3,OD=4,∴AO=AB=5,∴BD=3+5=8,∴B(8,4),设∠AOC的角平分线所在直线的函数关系式为y=kx,∵菱形OABC中,∠AOC的角平分线所在直线经过点B,∴4=8k,即k=,∴∠AOC的角平分线所在直线的函数关系式为y=x,故答案为:y=x.14.解:设点P(a,﹣2a+4)∵若点P到两坐标轴的距离相等,∴a=﹣2a+4 或a+(﹣2a+4)=0∴a=或a=4∴点P(,)或(4,﹣4)故答案为:(,)或(4,﹣4)15.解:根据题意得:CD的长为:8﹣x,则y=×6×(8﹣x)=24﹣3x,即y与x之间的函数表达式为:y=24﹣3x(0≤x<8),故答案为:y=24﹣3x(0≤x<8).16.解:∵直线y=x+1与y轴交于点A1,∴A1的坐标为(0,1),则OA1=1,∵四边形A1B1C1O是正方形,∴OC1=OA1=1,把x=1代入y=x+1得:y=2,∴A2的坐标为(1,2),同理A3的坐标为(3,4),…∴A n的坐标是(2n﹣1﹣1,2n﹣1),∴A2020的坐标是(22019﹣1,22019).故答案为:(22019﹣1,22019).17.解:令150t=240(t﹣12),解得,t=32,则150t=150×32=4800,∴点P的坐标为(32,4800),故答案为:(32,4800).18.解:由函数的解析式可知,函数图象与x轴的交点坐标为(6,0),与y轴的交点坐标为(0,3),直线y=﹣x+3与两坐标轴围成的三角形面积=×6×3=9.故答案为:9.=19.解:(1)设y2关于x的函数解析式是y2=kx+b,,得,即y2关于x的函数解析式是y2=0.2x﹣4;(2)由图象可知,步行的学生的速度为:4÷40=0.1千米/分钟,∴步行同学到达百花公园的时间为:6÷0.1=60(分钟),当y2=6时,6=0.2x﹣4,得x=50,60﹣50=10,答:骑自行车的学生先到达百花公园,先到了10分钟.20.解:(1)设购买一台电子白板需x元,一台台式电脑需y元,根据题意得:,解得:.答:购买一台电子白板需9000元,一台台式电脑需3000元;(2)设需购买电子白板a台,则购买台式电脑(24﹣a)台,根据题意得:24﹣a≤3a,解得:a≥6,设总费用为w元,则w=9000a+3000(24﹣a)=6000a+72000,∵6000>0,∴w随x的增大而增大,∴a=6时,w有最小值.答:购买电子白板6台,台式电脑18台最省钱.21.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;(2)当x=280时,Q=45﹣0.1×280=17(L).答:当x=280(千米)时,剩余油量Q的值为17L.(3)(45﹣3)÷0.1=420(千米),∵420>400,∴他们能在汽车报警前回到家.22.解:(1)在y=2x中,令x=1,解得y=2,则B的坐标是(1,2),设一次函数的解析式是y=kx+b,则,则一次函数的解析式是y=﹣x+3;(2)当x=4时,y=﹣1,则C(4,﹣2)不在函数的图象上;(3)一次函数的解析式y=﹣x+3中令y=0,解得:x=3,则D的坐标是(3,0).则S△BOD=OD×2=×3×2=3.23.解:(1)点B所表示的实际意义是:2min时,小亮到达距离出发点480m的坡顶开始下坡返回;=(2)小亮上坡速度:480÷2=240m/min,下坡速度:240×1.5=360m/min,所以,下坡时间为480÷360=min,2+=min,所以,点A的坐标为(,0),设直线AB的解析式为y=kx+b,则,解得.所以,y=﹣360x+1200;=(3)设两人出发后xmin相遇,∵小刚上坡平均速度是小亮上坡平均速度的一半,∴小刚的速度是240÷2=120m/min,第一次相遇时,小刚上坡,小亮下坡,由题意得,120x+360(x﹣2)=480,解得x=2.5.答:两人出发2.5min后第一次相遇.24.解:(1)设直线AB的解析式是y=kx+b,根据题意得:,则直线的解析式是:y=﹣x+6;(2)在y=﹣x+6中,令x=0,解得:y=6,S△OAC=×6×4=12;(3)设OA的解析式是y=mx,则4m=2,解得:m=,则直线的解析式是:y=x,∵当△OMC的面积是△OAC的面积的时,∴M的横坐标是×4=1,在y=x中,当x=1时,y=,则M的坐标是(1,);在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).则M的坐标是:M1(1,)或M2(1,5).25.解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+30)元.由题意:=×2,解得x=120,经检验x=120是分式方程的解,答:一件B型商品的进价为120元,则一件A型商品的进价为150元.=(2)因为客商购进A型商品m件,销售利润为w元.m≤100﹣m,m≤50,由题意:w=m(200﹣150)+(100﹣m)(180﹣120)=﹣10m+6000,∵﹣10<0,∴m=50时,w有最小值=5500(元)26.解:(1)∵一次函数y=k1x+b1和y=kx+b的图象,分别与x轴交于点A(﹣1,0)、B (2,0),∴关于x的方程k1x+b1=0的解是x=﹣1,关于x的不等式kx+b<0的解集,为x>2,故答案为x=﹣1,x>2;(2)根据图象可以得到关于x的不等式组的解集﹣1<x<2;(3)∵点C(1,3),∴由图象可知,不等式k1x+b1>kx+b的解集是x>1,∵AB=3,∴S△ABC=•y C==.。
人教版数学八年级下册第19章《一次函数》单元综合练习含答案解析一.选择题(共10小题)1.一本笔记本3元,买x本需要y元,在这一问题中,自变量是()A.笔记本B.3C.x D.y2.下列变量之间的关系不是函数关系的是()A.一天的气温和时间B.y2=x中的y与x的关系C.在银行中利息与时间D.正方形的周长与面积3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是()A.y=0.5x+5000B.y=0.5x+2500C.y=﹣0.5x+5000D.y=﹣0.5x+25004.函数中自变量x的取值范围是()A.x≥3B.x≤7C.3≤x≤7D.x≤3或x≥7 5.当x=3时,函数y=x﹣2的值是()A.﹣2B.﹣1C.0D.16.下列函数中y是x的一次函数的是()A.B.y=3x+1C.D.y=3x2+17.下列变量之间关系中,一个变量是另一个变量的正比例函数的是()A.正方形的面积S随着边长x的变化而变化B.正方形的周长C随着边长x的变化而变化C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t (min)的变化而变化D.面积为20的三角形的一边a随着这边上的高h的变化而变化8.两条直接y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的()A.B.C.D.9.下列图象中,可以表示一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)的图象的是()A.B.C.D.10.下列有关一次函数y=﹣3x+2的说法中,错误的是()A.y的值随着x增大而减小B.当x>0时,y>2C.函数图象与y轴的交点坐标为(0,2)D.函数图象经过第一、二、四象限二.填空题(共8小题)11.快餐每盒5元,买n盒需付m元,则其中常量是.12.当m=时,函数y=(m﹣1)x+m是常值函数.13.佛山移动公司有一种手机资费套餐,月租费16元,免费市话通话时间40分钟,超出部分每分钟0.25元,设该套餐每月市话话费为y元,月市话通话时间为x(x>40)分钟,则y与x的函数关系式为.14.已知函数,则自变量x的取值范围.15.函数y=(m﹣2)x|m|﹣1+5是y关于x的一次函数,则m=.16.若函数y=(m﹣2)是正比例函数,则m的值是.17.在平面直角坐标系中,函数y=kx+b的图象如图所示,则kb0(填“>”、“=”或“<”).18.(1)点P的坐标为(x,y),若x=y,则点P在坐标平面内的位置是;若x+y =0,则点P在坐标平面内的位置是;(2)已知点Q的坐标为(2﹣2a,a+8),且点Q到两坐标轴的距离相等,求点Q的坐标.三.解答题(共7小题)19.“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).(1)求该车平均每干米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;(2)当x=60(千米)时,求剩余油量Q的值;(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.20.已知等式y﹣ax2+2a﹣1=0(1)若等式中,已知a是非零常量,请写出因变量y与自变量x的函数解析式;当﹣1≤x≤3时,求y的最大值和最小值及对应的x的取值;(2)若等式中,x是非零常量,请写出因变量y与自变量a的函数解析式,并判断x在什么范围内取值时,y随a的增大而增大.21.已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.x…﹣3﹣2﹣1﹣﹣123…y…﹣﹣﹣m…小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)从表格中读出,当自变量是﹣2时,函数值是;(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(3)在画出的函数图象上标出x=2时所对应的点,并写出m=.(4)结合函数的图象,写出该函数的一条性质:.22.如图1,A是上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是y1cm,线段AD的长是y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:(1)对于点A在上的不同位置,画图、测量,得到了y1,y2的长度与x的几组值:位置1位置2位置3位置4位置5位置6位置7位置8 x/cm0.000.99 2.01 3.46 4.98 5.847.078.00y1/cm8.007.46 6.81 5.69 4.26 3.29 1.620.00y2/cm 2.50 2.08 1.88 2.15 2.99 3.61 4.62m 请直接写出上表中的m值是;(2)在同一平面直角坐标系xOy中,描出补全后表中各组数据所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为cm;当AC=2AD时,AB的长度约为cm.23.已知函数y=(m﹣1)x+n,(1)m为何值时,该函数是一次函数(2)m、n为何值时,该函数是正比例函数24.已知一次函数y=﹣2x+4,完成下列问题:(1)在所给直角坐标系中画出此函数的图象;(2)根据图象回答:当x时,y>2.25.在同一平面直角坐标系中,画出函数y=2x,y=﹣x+6,y=x+2,y=4x﹣4的图象.(1)观察这四个图象,说出它们共同特点;(2)若函数y=kx+5的图象也有该特点,求k的值.参考答案与试题解析一.选择题(共10小题)1.一本笔记本3元,买x本需要y元,在这一问题中,自变量是()A.笔记本B.3C.x D.y【分析】根据函数的定义进行解答即可.【解答】解:在这个问题中,x和y都是变量,且x是自变量.故选:C.2.下列变量之间的关系不是函数关系的是()A.一天的气温和时间B.y2=x中的y与x的关系C.在银行中利息与时间D.正方形的周长与面积【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.【解答】解:A、一天的气温和时间的关系是函数关系,故本选项不合题意;B、y2=x中的y与x的关系不是函数关系,故本选项符合题意;C、在银行中利息与时间是函数关系,故本选项不合题意;D、正方形的周长与面积是函数关系,故本选项不合题意;故选:B.3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是()A.y=0.5x+5000B.y=0.5x+2500C.y=﹣0.5x+5000D.y=﹣0.5x+2500【分析】根据题意可以写出题目中的函数解关系式,从而可以解答本题.【解答】解:由题意可得,y=0.5x+(5000﹣x)×1=﹣0.5x+5000,故选:C.4.函数中自变量x的取值范围是()A.x≥3B.x≤7C.3≤x≤7D.x≤3或x≥7【分析】根据被开方数大于等于0列式计算即可得解.【解答】解:由题意得x﹣3≥0且7﹣x≥0,解得x≥3且x≤7,所以3≤x≤7.故选:C.5.当x=3时,函数y=x﹣2的值是()A.﹣2B.﹣1C.0D.1【分析】把x的值代入函数关系式计算,得到答案.【解答】解:当x=3时,函数y=x﹣2=3﹣2=1,故选:D.6.下列函数中y是x的一次函数的是()A.B.y=3x+1C.D.y=3x2+1【分析】一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数.根据一次函数的定义条件进行逐一分析即可.【解答】解:A、y=不是一次函数,是反比例函数,不合题意;B、y=3x+1是一次函数,符合题意;C、y=不是一次函数,不合题意;D、y=3x2+1不是一次函数,是二次函数,不合题意.故选:B.7.下列变量之间关系中,一个变量是另一个变量的正比例函数的是()A.正方形的面积S随着边长x的变化而变化B.正方形的周长C随着边长x的变化而变化C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t (min)的变化而变化D.面积为20的三角形的一边a随着这边上的高h的变化而变化【分析】先依据题意列出函数关系式,然后依据函数关系式进行判断即可.【解答】解:A、S=x2是二次函数,故A错误;B、C=4x是正比例函数,故B正确;C、V=10﹣0.5t,是一次函数,故C错误;D、a=,是反比例函数,故D错误.故选:B.8.两条直接y1=ax﹣b与y2=bx﹣a在同一坐标系中的图象可能是图中的()A.B.C.D.【分析】根据一次函数图象的性质加以分析即可,一次项系数决定直线的走向,常数项决定直线与y轴的交点位置.【解答】解:根据一次函数的图象与性质分析如下:A.y1=ax﹣b:a>0,b<0;y2=bx﹣a:a<0,b<0.A错误;B.y1=ax﹣b:a>0,b<0;y2=bx﹣a:a>0,b<0.B正确;C.y1=ax﹣b:a>0,b>0;y2=bx﹣a:a<0,b<0.C错误;D.y1=ax﹣b:a>0,b>0;y2=bx﹣a:a>0,b<0.D错误;故选:B.9.下列图象中,可以表示一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)的图象的是()A.B.C.D.【分析】根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得k•b的符号,从而判断y=kbx的图象是否正确,进而比较可得答案.【解答】解:根据一次函数的图象分析可得:A、由一次函数y=kx+b图象可知k<0,b>0,kb<0;正比例函数y=kbx的图象可知kb<0,故此选项正确;B、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项错误;C、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与正比例函数y=kbx的图象可知kb>0,矛盾,故此选项错误;D、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb>0,矛盾,故此选项错误;故选:A.10.下列有关一次函数y=﹣3x+2的说法中,错误的是()A.y的值随着x增大而减小B.当x>0时,y>2C.函数图象与y轴的交点坐标为(0,2)D.函数图象经过第一、二、四象限【分析】利用一次函数的性质逐一判断后即可确定正确的选项.【解答】解:A、∵k=﹣3<0,∴当x值增大时,y的值随着x增大而减小,选项A不符合题意;B、当x=0时,y=﹣3x+2=2,∵y的值随着x增大而减小,∴当x>0时,y<2,∴选项B符合题意;C、当x=0时,y=﹣3x+2=2,∴函数图象与y轴的交点坐标为(0,2),选项C不符合题意;D、∵k=﹣3<0,b=2>0,∴一次函数y=﹣3x+2的图象经过第一、二、四象限,选项D不符合题意;当x=1时,y=﹣3x+2=﹣1,∴一次函数y=﹣3x+2的图象不经过点(1,5),选项D符合题意.故选:B.二.填空题(共8小题)11.快餐每盒5元,买n盒需付m元,则其中常量是5.【分析】根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.【解答】解:单价5元固定,是常量.故答案为:5.12.当m=1时,函数y=(m﹣1)x+m是常值函数.【分析】直接利用常值函数的定义分析得出答案.【解答】解:当m﹣1=0时,函数y=(m﹣1)x+m是常值函数,故m=1时,y=1.故答案为:1.13.佛山移动公司有一种手机资费套餐,月租费16元,免费市话通话时间40分钟,超出部分每分钟0.25元,设该套餐每月市话话费为y元,月市话通话时间为x(x>40)分钟,则y与x的函数关系式为y=0.25x+6.【分析】根据题意可得等量关系:话费=月租费16元+超出40分钟部分话费,根据等量关系列出函数解析式即可.【解答】解:由题意得:y=16+(x﹣40)×0.25=16+0.25x﹣10=0.25x+6,故答案为:y=0.25x+6.14.已知函数,则自变量x的取值范围x>.【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【解答】解:根据题意得,2x﹣3>0,解得x>.故答案为:x>.15.函数y=(m﹣2)x|m|﹣1+5是y关于x的一次函数,则m=﹣2.【分析】根据一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1,即可得出m的值.【解答】解:根据一次函数的定义可得:m﹣2≠0,|m|﹣1=1,由|m|﹣1=1,解得:m=﹣2或2,又m﹣2≠0,m≠2,则m=﹣2.故答案为:﹣2.16.若函数y=(m﹣2)是正比例函数,则m的值是﹣2.【分析】直接利用正比例函数的定义直接得出答案.【解答】解:∵函数y=(m﹣2)是正比例函数,∴m2﹣3=1,m﹣2≠0,解得:m=±2,m≠2,故m=﹣2.故答案为:﹣2.17.在平面直角坐标系中,函数y=kx+b的图象如图所示,则kb<0(填“>”、“=”或“<”).【分析】根据一次函数的图象与系数的关系进行解答即可.【解答】解:∵一次函数y=kx+b的图象经过一、二、四象限,∴k<0,b>0,∴kb<0.故答案为:<18.(1)点P的坐标为(x,y),若x=y,则点P在坐标平面内的位置是在一、三象限的角平分线上;若x+y=0,则点P在坐标平面内的位置是在二、四象限的角平分线上;(2)已知点Q的坐标为(2﹣2a,a+8),且点Q到两坐标轴的距离相等,求点Q的坐标.【分析】(1)根据互为相反数的两个数的和等于0判断出x、y互为相反数,然后解答.(2)根据点Q到两坐标轴的距离相等列出方程,然后求解得到a的值,再求解即可.【解答】解:(1)∵点P的坐标为(x,y),若x=y,∴点P在一、三象限内两坐标轴夹角的平分线上.∵x+y=0,∴x、y互为相反数,∴P点在二、四象限内两坐标轴夹角的平分线上.故答案为:在一、三象限的角平分线上.在二、四象限的角平分线上.(2)∵点Q到两坐标轴的距离相等,∴|2﹣2a|=|8+a|,∴2﹣2a=8+a或2﹣2a=﹣8﹣a,解得a=﹣2或a=10,当a=﹣2时,2﹣2a=2﹣2×(﹣2)=6,8+a=8﹣2=6,当a=10时,2﹣2a=2﹣20=﹣18,8+a=8+10=18,所以,点Q的坐标为(6,6)或(﹣18,18).三.解答题(共7小题)19.“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).(1)求该车平均每干米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;(2)当x=60(千米)时,求剩余油量Q的值;(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.【分析】(1)单位耗油量=耗油量÷行驶里程,剩余油量=油箱内油的升数﹣行驶路程的耗油量;(2)把x=60千米代入剩余油量公式,计算即可;(3)计算出35﹣3=32升油能行驶的距离,与200千米比较大小即可得.【解答】解:(1)该汽车平均每千米的耗油量为(35﹣25)÷80=0.125(升/千米),∴行驶路程x(千米)与剩余油量Q(升)的关系式为Q=35﹣0.125x;(2)当x=60时,Q=35﹣0.125×60=27.5(升),答:当x=60(千米)时,剩余油量Q的值为27.5升;(3)他们能在汽车报警前回到家,(35﹣3)÷0.125=256(千米),由256>200知他们能在汽车报警前回到家.20.已知等式y﹣ax2+2a﹣1=0(1)若等式中,已知a是非零常量,请写出因变量y与自变量x的函数解析式;当﹣1≤x≤3时,求y的最大值和最小值及对应的x的取值;(2)若等式中,x是非零常量,请写出因变量y与自变量a的函数解析式,并判断x在什么范围内取值时,y随a的增大而增大.【分析】(1)解方程得到y=ax2﹣4a+2,当x=﹣1时,y=5a+2,当x=3时,y=﹣3a+2,当a>0时当a<0时,根据题意求出结论即可;(2)解方程得到y=(x2﹣4)a+2,根据一次函数的性质解答即可..【解答】解:(1)∵y﹣ax2+2a﹣1=0,∴y=ax2﹣4a+2,当x=﹣1时,y=5a+2,当x=3时,y=﹣3a+2,当a>0时,﹣3a+2≤y≤5a+2,∴y的最大值是5a+2,对应的x的取值﹣1,最小值是﹣3a+2,对应的x的取值是3,当a<0时,5a+2≤y≤﹣3a+2,∴y的最大值是﹣3a+2,对应的x的取值3,最小值是5a+2,对应的x的取值是﹣1;(2)∵y﹣ax2+2a﹣1=0,∴y=(x2﹣4)a+2,当x2﹣4>0时,y随a的增大而增大,即x<﹣2或x>2时,y随a的增大而增大.21.已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.x…﹣3﹣2﹣1﹣﹣123…y…﹣﹣﹣m…小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)从表格中读出,当自变量是﹣2时,函数值是;(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(3)在画出的函数图象上标出x=2时所对应的点,并写出m=.(4)结合函数的图象,写出该函数的一条性质:当0<x<1时,y随x的增大而减小.【分析】(1)根据表中x,y的对应值即可得到结论;(2)按照自变量由小到大,利用平滑的曲线连结各点即可;(2)①在所画的函数图象上找出自变量为7所对应的函数值即可;②利用函数图象的图象求解.【解答】解:(1)当自变量是﹣2时,函数值是;故答案为:(2)该函数的图象如图所示;(3)当x=2时所对应的点如图所示,且m=;故答案为:;(4)函数的性质:当0<x<1时,y随x的增大而减小.故答案为:当0<x<1时,y随x的增大而减小.22.如图1,A是上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是y1cm,线段AD的长是y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:(1)对于点A在上的不同位置,画图、测量,得到了y1,y2的长度与x的几组值:位置1位置2位置3位置4位置5位置6位置7位置8 x/cm0.000.99 2.01 3.46 4.98 5.847.078.00y1/cm8.007.46 6.81 5.69 4.26 3.29 1.620.00y2/cm 2.50 2.08 1.88 2.15 2.99 3.61 4.62m 请直接写出上表中的m值是 5.5;(2)在同一平面直角坐标系xOy中,描出补全后表中各组数据所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为 5.7cm;当AC=2AD时,AB的长度约为 4.2cm.【分析】(1)由位置可知,AB=0时,即AB两点重合,此时AC=BC=8,AD=BD=2.5,再根据当y1=AC时,即A与重合即可求出表格中m=CD.(2)根据表中数据描点连线即可.(3)根据函数图象分别找出y1=y2和y1=2y2时对应的x即可.【解答】解:(1)∵当x=0时,y1=8,y2=2.5,∴BC=8cm,BD=2.5,∴当x=8.0时,即A点与C点重合,∴y2=AB=CD=BC﹣BD=8﹣2.5=5.5(cm),故答案为:5.5(2)(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为5.7cm;当AC=2AD时,AB的长度约为4.2cm.故答案为:5.7;4.2.23.已知函数y=(m﹣1)x+n,(1)m为何值时,该函数是一次函数(2)m、n为何值时,该函数是正比例函数【分析】(1)直接利用一次函数的定义得出答案;(2)直接利用正比例函数的定义得出答案.【解答】解:(1)∵函数y=(m﹣1)x+n,∴当m﹣1≠0时,该函数是一次函数,即m≠1;(2)当m≠1,且n=0时,该函数是正比例函数.24.已知一次函数y=﹣2x+4,完成下列问题:(1)在所给直角坐标系中画出此函数的图象;(2)根据图象回答:当x<1时,y>2.【分析】(1)分别求出直线与x轴、y轴的交点,画出函数图象即可;(2)根据函数图象可直接得出结论.【解答】解:(1)∵当x=0时y=4,∴函数y=﹣2x+4的图象与y轴的交点坐标为(0,4);∵当y=0时,﹣2x+4=0,解得:x=2,∴函数y=﹣2x+4的图象与x轴的交点坐标(2,0).函数图象如图所示.(2)由图象可得,当x<1时,y>2.故答案为:<1.25.在同一平面直角坐标系中,画出函数y=2x,y=﹣x+6,y=x+2,y=4x﹣4的图象.(1)观察这四个图象,说出它们共同特点;(2)若函数y=kx+5的图象也有该特点,求k的值.【分析】(1)根据一次函数的图象是直线,画出图象即可;(2)根据图象过定点,代入得出k的值即可.【解答】(1)解:如图:共同特点是:此组直线均经过(2,4),∵解方程组得,,∴直线y=2x,y=﹣x+6过(2,4)点.对于直线y=x+2,当x=2时,y=4;对于直线y=4x﹣4,当x=2时,y=4;∴验证发现此组直线均经过(2,4);(2)把(2,4)代入y=kx+5得4=2k+5,得k=﹣.。
第十九章社会主义条件下的经济增长与经济发展产业结构产业是按社会分工而从事物质产品生产或提供劳务的一切经济活动群体的总称。
产业结构一般是指国民经济中各产业之间的比例关系和结合状况,它是国民经济结构的一个基本方面。
一般来说,产业结构的变动可以从两个方面衡量:一是产值的部门构成,二是劳动力的部门构成。
区域结构指一国范围内各个地区之间的经济发展状况与相互关系,它涉及经济增长要素的空间分布。
经济发展的地区差异,客观上反映出生产要素空间分布的状况。
我国区域结构不合理,将会对我国国民经济的持续稳定协调发展产生不利影响。
为此,采取得力措施,促进地区协调发展,应是我国经济结构调整的重要内容。
二元经济指发展中国家在工业化初期阶段形成的现代部门和传统部门同时并存的经济。
发展中国家的工业化是在资本积累不足、劳动力素质普遍不高、科学技术极为落后、具有创新精神的企业家严重缺乏等基础上进行的,因此,国民经济各产业部门的现代化需要经历一个相当长的过程。
在这期间,发展中国家一般都会同时存在两种性质不同的结构和部门:一种是以传统方法进行生产、劳动生产率极为低下,收入只能维持劳动者最低生活水平的乡村农业部门;另一种是以现代方式进行生产、劳动生产率较高、劳动者工资水平也相应较高的城市工业部门。
这就是发展中国家工业化过程中必然出现的二元经济。
可持续发展其实质就是将当前经济发展与长远经济发展相结合,既要满足当前的需要和利益,又要重视后代人的需要和利益,正确处理经济发展与人口、资源、环境的相互关系,使人口增长与社会生产力的发展相适应,经济建设与资源、环境相协调,实现良性循环,促进社会的全面进步。
可持续发展包括三方面内容:经济可持续发展、生态可持续发展和社会可持续发展。
可持续发展的这三个方面互相联系、不可分割。
小康社会小康社会是一个经济发展与社会发展相结合、物质文明与精神文明协调发展、当前发展与可持续发展统一、精神文明建设与民主法制建设都取得明显进展的社会。
我国将全面建设小康社会确定为21世纪前20年经济社会全面发展的奋斗目标。
其内容是:1、在优化结构和提高效益的基础上,国内生产总值到二〇二〇年力争比二〇〇〇年翻两番,综合国力和国际竞争力明显增强。
基本实现工业化,建成完善的社会主义市场经济体制和更具活力、更加开放的经济体系。
城镇人口的比重较大幅度提高,工农差别、城乡差别和地区差别扩大的趋势逐步扭转。
社会保障体系比较健全,社会就业比较充分,家庭财产普遍增加,人民过上更加富足的生活。
2、社会主义民主更加完善,社会主义法制更加完备,依法治国基本方略得到全面落实,人民的政治、经济和文化权益得到切实尊重和保障。
基层民主更加健全,社会秩序良好,人民安居乐业。
3、全民族的思想道德素质、科学文化素质和健康素质明显提高,形成比较完善的现代国民教育体系、科技和文化创新体系、全民健身和医疗卫生体系。
人民享有接受良好教育的机会,基本普及高中阶段教育,消除文盲。
形成全民学习、终身学习的学习型社会,促进人的全面发展。
4、可持续发展能力不断增强,生态环境得到改善,资源利用效率显著提高,促进人与自然的和谐,推动整个社会走上生产发展、生活富裕、生态良好的文明发展道路。
这一奋斗目标,是中国特色社会主义经济、政治、文化全面发展的目标,是与加快推进现代化相统一的目标,符合我国国情和现代化建设的实际,符合人民的愿望,意义十分重大。
新型工业化道路新型工业化是与工业化相联系的新概念。
所谓工业化,一般是指传统的农业社会向现代化工业社会转变的过程。
工业化与现代化密切相联,工业化是现代化的基础和前提,高度发达的工业社会是现代化的重要标志。
新型工业化道路是指“坚持以信息化带动工业化,以工业化促进信息化,走出一条科技含量高、经济效益好、资源消耗低、环境污染少、人力资源优势得到充分发挥的新型工业化路子。
”新型工业化道路与传统的工业化道路相比,有如下特点:第一,新的要求和新的目标。
新型工业化道路所追求的工业化,不是只讲工业增加值,而是要做到“科技含量高、经济效益好、资源消耗低、环境污染少、人力资源优势得到充分发挥”,并实现这几方面的兼顾和统一。
这是新型工业化道路的基本标志和落脚点。
第二,新的物质技术基础。
新型工业化必须建立在更先进的技术基础上。
坚持以信息化带动工业化,以工业化促进信息化,要把信息产业摆在优先发展的地位,将高新技术渗透到各个产业中去。
这是新型工业化道路的技术手段和重要标志。
第三,新的处理各种关系的思路。
要从生产力和科技发展水平不平衡、城乡简单劳动力大量富余、虚拟资本市场发育不完善且风险较大的国情出发,正确处理发展高新技术产业和传统产业、资金技术密集型产业和劳动密集型产业、虚拟经济和实体经济的关系。
这是我国走新型工业化道路的重要特点和必须注意的问题。
第四,新的工业化战略。
新的要求和新的技术基础,要求大力实施科教兴国战略和可持续发展战略。
必须发挥科学技术是第一生产力的作用,依靠教育培育人才,使经济发展具有可持续性。
这是新型工业化道路的可靠根基和支撑力。
1、试分析决定经济增长的因素经济增长是指一个国家或地区在一定时期内因就业人数增加、资本积累和技术进步等原因,经济规模(包括物质产品和劳务)在数量上的扩大和增加,它反映了一国国民经济总量的变化状况。
在社会化大生产和市场经济的条件下,决定经济增长的因素很多,主要有:劳动力供给的数量与质量、自然资源及其开发利用程度、科学技术水平及其转化为现实生产力的状况、现有技术装备的水平、企业经营管理的水平、市场机制的完善程度、资本积累的最大可能性、社会有效需求总量与结构以及社会经济制度、经济体制等等。
如果将这些因素归类,决定经济增长的因素可以分为生产要素投入的增加和要素生产率的提高。
首先,分析生产要素投入特别是劳动就业量对经济增长的决定作用。
如果以一定时期(如一年)的国内生产总值作为衡量经济活动总量的综合指标,以国内生产总值增长率作为经济增长的指标,那么,在其他条件一定的情况下,国内生产总值就是这一时期所有部门的劳动就业量与社会平均劳动生产率的乘积,而国内生产总值增长率就等于劳动就业量增长率加上社会劳动生产率增长率。
其次,再分析社会劳动生产率的增长率对经济增长的决定作用。
劳动生产率的增长,就微观而言取决于劳动者的积极性、企业的经营管理水平和技术水平;从宏观来看,取决于产业结构和生产力地区布局的合理化。
由于影响社会劳动生产率增长率的因素较为复杂,例如投资增长也会伴随着新技术的应用,因而难以简单地量化为若干经济变量。
但是随着经济发展和“知识经济”的兴起,社会劳动生产率增长率对经济增长的贡献将越来越大。
综上所述,经济增长的一般公式可以表述为:经济增长率=(积累率×社会平均劳动生产率/资本-劳动比率)+社会劳动生产率增长率。
除了以上两个重要因素以外,经济增长还会受到另外一些因素的制约。
这些因素主要有:第一,投资增长率和投资效率。
在其他条件不变的情况下,经济增长率与投资增长率和投资效率成正比。
第二,科技进步程度及其应用。
一个国家能否实现持续的经济增长,归根结底取决于技术进步的程度和科技、教育的发展水平。
第三,自然资源的数量与开发利用程度。
自然资源是指存在于自然界中能够为人类利用的自然物和自然力的总称,包括土地、森林植被、矿藏、空气、水,等等。
一国的自然资源禀赋会影响该国经济结构,进而影响经济增长。
第四,制度或体制,包括产权制度、市场制度、分配制度等。
制度或体制是影响经济增长的重要因素。
制度或体制安排不仅会改变收入的分配,而且会改变经济中资源使用效率及其潜力。
第五,在对外开放的条件下,经济增长还要受到该国参与国际经济活动状况的制约。
一国经济发展可以突破国内资源和国内市场的限制,实行对外开放,参与国际分工,利用国内国际两个市场,开发国内国际两种资源,促进国内经济增长。
上述各个因素相互联系,共同对经济增长发挥作用,因此,应当通过实现各个因素的相互协调、彼此配合来促进经济增长。
2、为什么要实现和如何实现经济增长方式的转变?(1)经济增长方式有两种不同的类型:一种是粗放型增长方式,一种是集约型增长方式。
两种增长方式相比,粗放型增长方式实质就是单纯以数量的增长为中心,即单纯数量扩张型的外延式增长方式,效益相对低下;而集约型增长方式实质是以提高经济增长质量和经济效益为中心,即质量效益型的内涵式增长方式,效益相对较高。
就我国的实际而言,建国初期,我国工业基础比较落后,科技、教育水平较低,西方国家对我国进行经济、技术封锁。
在这种条件下,要合理安排生产力布局,摆脱短缺经济的状况,吸收更多的劳动力就业,只能实行粗放型的增长方式。
但随着我国社会主义建设的不断深入,这种粗放型的增长方式在我国生产、建设和流通等领域的弊端也逐渐显现,主要是:产品质量差,品种单一,技术含量低,附加值低,缺乏市场竞争力;资源消耗量大,浪费严重;单纯热衷于上新项目,铺新摊子等。
这些问题极大地损害了经济增长质量和经济效益,因此在这样的情况下,加快增长方式转变,具有十分重要的意义。
(2)要实现经济增长和经济增长方式的转变,首先要大力发展科技教育。
科技进步对于经济增长具有十分突出的作用,因为它是经济增长与实现集约型经济增长方式的基础。
科学技术获得了在较短时间内转化为现实生产力的能力,科学技术成为生产力要素体系中的主导因素,经济增长速度主要由科学技术转化为现实生产力的速度决定。
在过去长时期内,我国对科技进步促进经济增长的作用重视不够,科技的落后、科技与经济的脱节严重束缚了我国的经济增长。
目前,虽然我国科学研究水平并不低,许多领域已进入世界先进行列,但科技成果向产业的转化并不理想,不少研究成果没有进入现实的生产过程,不能转变为现实的生产力。
因此,目前我国的首要任务就是解放科学技术这个第一生产力,加快科技成果转化为现实生产力的速度,解决科技发展的结构性矛盾。
同时,实现科技进步要依靠对科技投入的增加,包括对科学研究的投入的增加,对科研成果转化为新产品的投入的增加和对生产单位采用新技术投入的增加。
但从根本上说,必须大力发展教育。
新中国成立以后,我国政府采取各种措施,大力发展全民教育事业,切实保障公民的受教育权利,特别是实行了九年制义务教育,教育事业有了很大发展。
但是,我国的教育投资明显不足,甚至还落后于发展中国家的平均水平。
教育投入不足,造成了劳动者人力资本的缺口,难以适应不同层次技术进步的要求,致使我国劳动力数量虽多,但劳动力质量不高,掌握较高知识和技术的熟练劳动力更是严重缺乏。
人力资本同物质资本存量不成比例,致使机器设备的利用率低,引进先进设备的消化吸收率低,造成物质资本的浪费严重。
面对人力资本缺乏这一资源供给的缺口,我国应进一步加大人力资本投资,通过教育提高劳动者素质,增加劳动者知识和技术的存量来促进经济增长。