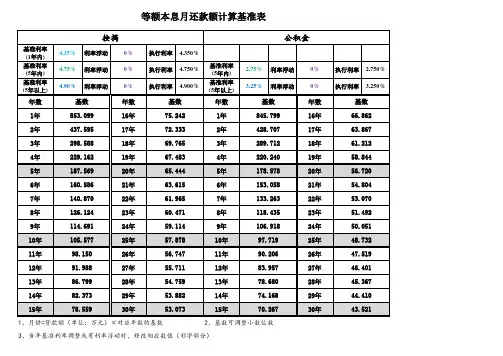
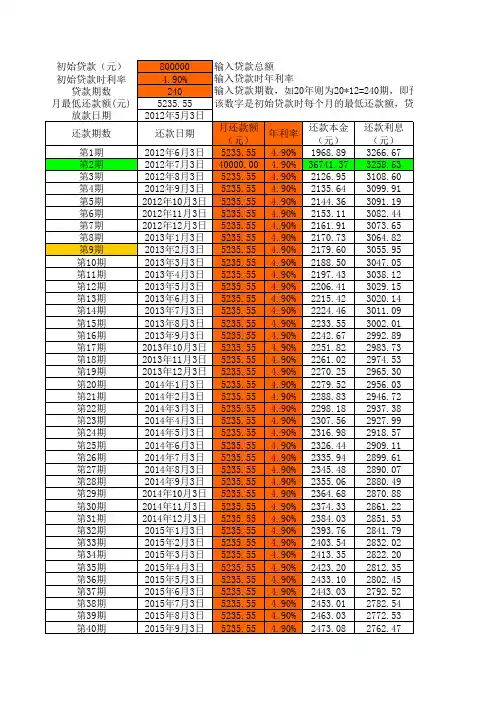
等额本息计算表

1 / 2
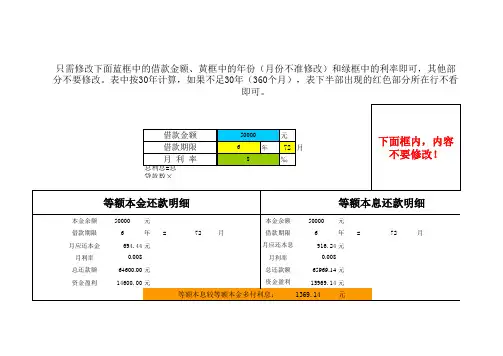
等额本息和等额本金
①等额本息还款法： 总还款额=每期还款额*
还款月数。

举例：贷款50万， 时间20年，利率按照利率5.9%计算：
每月应还款额＝5.9%/12×（1＋5.9%/12）^240/[（1＋5.9%/12）^240－1]×50
0000=3553.37元
总还款额=3553.37*240= 852808.79 元
②等额本金还款法：
每月还款额=每月还款本金+每月还款利息；
每月还款本金=贷款总额÷贷款月数 ；
每月还款利息=贷款本金余额×贷款月利率（ 贷款月利率=年利率÷12）；
贷款本金余额=贷款总额-已还款月数×每月还款本金。

例子：贷款50万；贷款20年；利率5.9%计算：
每月还款本金=500000/240=2083.33元；
第一个月还利息=500000*5.9%/12=2458.33元；
第一个月还款总额=2083.33+2458.33=4541.67元
第二个月还利息减少：2083.33*5.9%/12=10 .24元
第二个月还款总额=4541.67-10 .24=4531.43元；
以后每月递减10.24元。

总还款额为796229.17元
-----精心整理，希望对您有所帮助!。

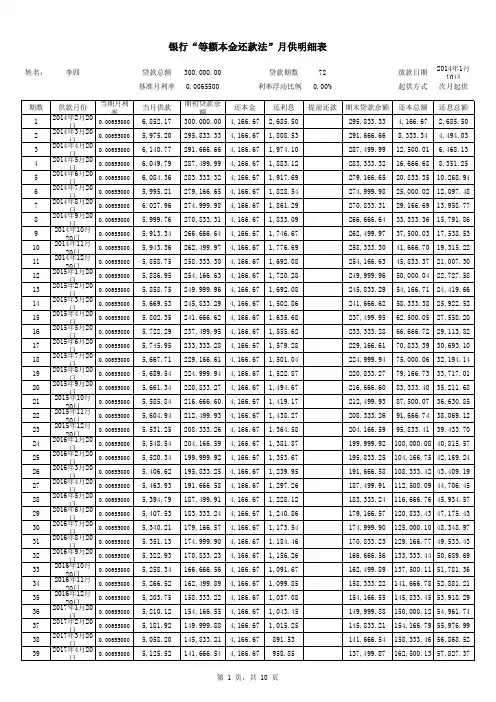
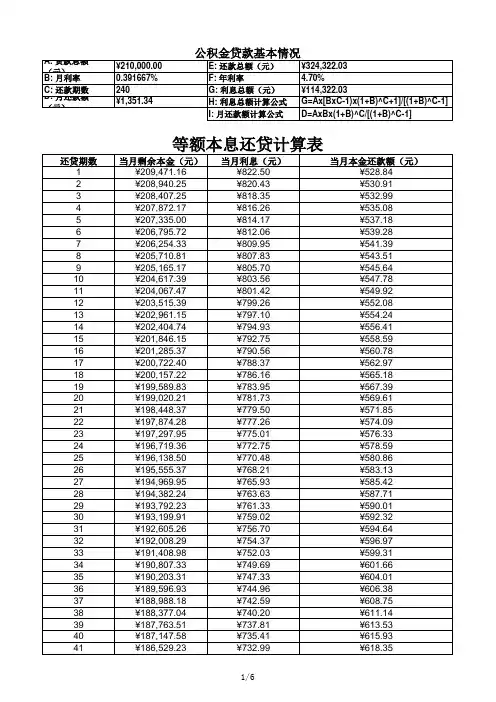
等额本息计算公式表一、等额本息计算公式。

1. 基本公式。

- 在等额本息还款方式中，每月还款额的计算公式为：M = P×(r(1 + r)^n)/((1 + r)^n-1)- 其中：- M为每月还款额；- P为贷款本金；- r为月利率（固定年利率除以12，即r=(年利率)/(12)）；- n为还款总月数。

2. 推导过程（供理解，可不作为重点记忆内容）- 设贷款本金为P，年利率为R，还款期数为n个月。

- 月利率r=(R)/(12)。

- 假设每月还款额为M。

- 第一个月还款后，剩余本金为P_1 = P(1 + r)-M；- 第二个月还款后，剩余本金为P_2=P_1(1 + r)-M=P(1 + r)^2 - M(1 + r)-M；- 以此类推，第n个月还款后，剩余本金为0，即P(1 + r)^n-M[(1 + r)^n - 1+(1 + r)^n - 2+·s+1]=0。

- 根据等比数列求和公式S = (a(1 - q^n))/(1 - q)（这里a = 1，q=(1 + r)），可得M=(P× r(1 + r)^n)/((1 + r)^n-1)。

3. 计算总利息公式。

- 总利息I = M× n - P- 因为每月还款额M乘以还款总月数n得到的是还款总额，减去贷款本金P 就是支付的总利息。

二、示例。

1. 题目。

- 假设小明贷款20万元，年利率为5%，贷款期限为20年（240个月），求每月还款额和总利息。

2. 解答。

- 首先计算月利率r=(5%)/(12)=(0.05)/(12)。

- 根据公式计算每月还款额M：- P = 200000，n = 240，r=(0.05)/(12)。

- 代入公式M = P×(r(1 + r)^n)/((1 + r)^n-1)- 先计算(1 + r)^n=(1+(0.05)/(12))^240- 通过计算器可得(1+(0.05)/(12))^240≈2.7126- 再计算M = 200000×(frac{0.05)/(12)×2.7126}{2.7126 - 1}- M=(200000×frac{0.05)/(12)×2.7126}{1.7126}- M=(200000×0.05×2.7126)/(12×1.7126)- 计算可得M≈1319.91（元）。