平面直角坐标系下图形面积的计算

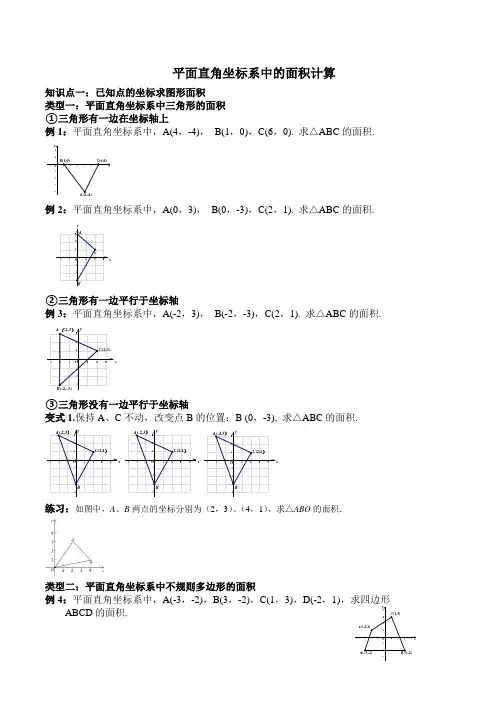
平面直角坐标系中的面积计算知识点一：已知点的坐标求图形面积类型一：平面直角坐标系中三角形的面积①三角形有一边在坐标轴上例1：平面直角坐标系中，A(4，-4)， B(1，0)，C(6，0). 求△ABC 的面积. x yO A (4,-4)B (1,0)C (6,0)例2：平面直角坐标系中，A(0，3)， B(0，-3)，C(2，1). 求△ABC 的面积. x y123–1–2123–1–2–3OCB A②三角形有一边平行于坐标轴例3：平面直角坐标系中，A(-2，3)， B(-2，-3)，C(2，1). 求△ABC 的面积.xy –1–2–3123–1–2–3123OA （-2,3）B (-2,-3)C (2,1)③三角形没有一边平行于坐标轴变式1.保持A 、C 不动，改变点B 的位置：B (0，-3), 求△ABC 的面积. x y –1–2–3–4123–1–2–31234OA (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B练习：如图中，A 、B 两点的坐标分别为（2，3）、（4，1），求△ABO 的面积．类型二：平面直角坐标系中不规则多边形的面积例4：平面直角坐标系中，A(-3，-2)，B(3，-2)，C(1，3)，D(-2，1)，求四边形ABCD 的面积. xyO A (-3,-2)B (3,-2)C (1,3)D (-2,1)练习：如图，已知四边形ABCD 四个顶点的坐标分别是A （-5，2），B （1，5），C （5，-2），D （-4，-5）.求四边形ABCD 的面积.知识点二：已知图形面积求点的坐标例5：（1）▲ABC 的两个顶点分别为A （2，3），B （-2，0），且▲ABC 的面积为9，若点C 在x 轴上，求点C 的坐标.（2）已知A （1，0），B （0，3），点P 在x 轴上，且▲PAB 的面积为6，求点P 的坐标.（3）已知O （0，0），B （3，2），点A 在坐标轴上，且6=∆OAB S ，求A 点的坐标.练习1.如图A （﹣4，0），B （6，0），C （2，4），D （﹣3，2）．（1）求四边形ABCD 的面积；（2）在y 轴上找一点P ，使△APB 的面积等于四边形的一半．求P 点坐标．练习2.如图，已知A （﹣2，0），B （4，0），C （2，4），D （0，2）（1）求三角形ABC 的面积；（2）设P 为坐标轴上一点，若S △APC ＝S △ABC ，求P 点的坐标．练习3.如图，已知三点A （0，1），B （2，0），C （4，3）（1）求三角形ABC 的面积；（2）设点P 在坐标轴上，且三角形ABP 与三角形ABC 的面积相等，求点P 的坐标．。

在直角坐标系中求图形的面积图形的面积可以利用相应的面积公式求得，但是在平面直角坐标系内的求面积问题，往往不直接给出边或高之类的条件，而是给出一些点的坐标。

我们常常会遇到在平面直角坐标系中求三角形面积和一些不规则图形面积的问题，解题时我们要注意其中的解题方法和解题技巧。

现对这类题目的解法举例说明如下：一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y 轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C （-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD ×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.。

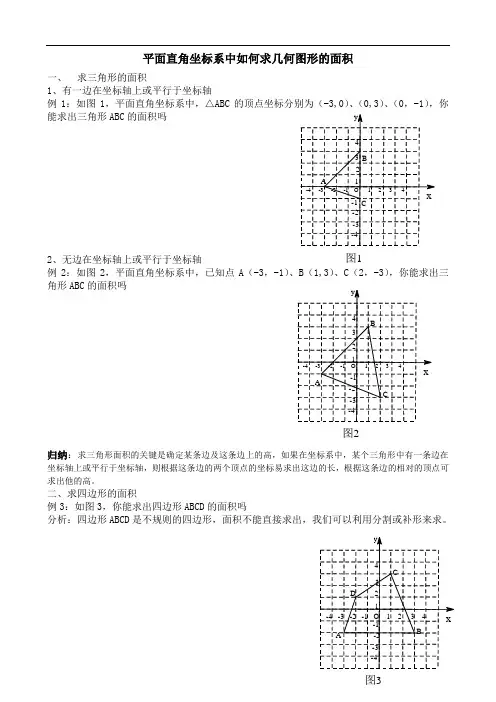
图1图2图3平面直角坐标系中如何求几何图形的面积一、 求三角形的面积1、有一边在坐标轴上或平行于坐标轴例1：如图1，平面直角坐标系中，△ABC 的顶点坐标分别为（-3,0）、（0,3）、（0，-1），你能求出三角形ABC 的面积吗2、无边在坐标轴上或平行于坐标轴例2：如图2，平面直角坐标系中，已知点A （-3，-1）、B （1,3）、C （2，-3），你能求出三角形ABC 的面积吗归纳：求三角形面积的关键是确定某条边及这条边上的高，如果在坐标系中，某个三角形中有一条边在坐标轴上或平行于坐标轴，则根据这条边的两个顶点的坐标易求出这边的长，根据这条边的相对的顶点可求出他的高。

二、求四边形的面积例3：如图3，你能求出四边形ABCD 的面积吗分析：四边形ABCD 是不规则的四边形，面积不能直接求出，我们可以利用分割或补形来求。

归纳：会将图形转化为有边与坐标轴平行的图形进行计算。

怎样确定点的坐标一、 象限点解决有关象限点问题的关键是熟记各象限的符号特征，由第一到底四象限点的符号特征分别为（+，+）、 （-，+）、（-，-）、（+，-）。

例1：已知点M （a 3-9,1-a ）在第三象限，且它的坐标都是整数，则a =（ ）A 、1B 、2C 、3D 、0二、轴上的点解决有关轴上点问题的关键是把握“0”的特征，x 轴上点的纵坐标为0，可记为（x ，0）；y 轴上点的横坐标为0，可记为（0，y ）；原点可记为（0,0）。

例2：点P （m+3,m+1）在直角坐标系的x 轴上，则P 点的坐标为（ ）A 、（0，-2）B 、（2,0）C 、（4,0）D 、（0，-4）三、象限角平分线上的点 所谓象限角平分线上的点，就是各象限坐标轴夹角平分线上的点。

解决这类问题的关键是掌握“y x =”的特征，一、三象限角平分线上点的横、纵坐标相等，可记为（x ，x ）；二、四象限角平分线上的点横、纵坐标互为相反数，可记为（x ，-x ）。

.；.例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

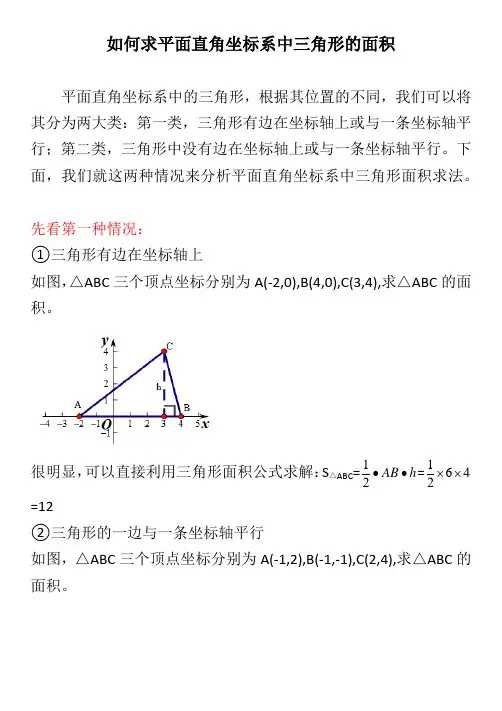
如何求平面直角坐标系中三角形的面积平面直角坐标系中的三角形，根据其位置的不同，我们可以将其分为两大类：第一类，三角形有边在坐标轴上或与一条坐标轴平行；第二类，三角形中没有边在坐标轴上或与一条坐标轴平行。

下面，我们就这两种情况来分析平面直角坐标系中三角形面积求法。

先看第一种情况：①三角形有边在坐标轴上如图，△ABC 三个顶点坐标分别为A(-2,0),B(4,0),C(3,4),求△ABC 的面积。

很明显，可以直接利用三角形面积公式求解：S △ABC =h AB ••21=4621⨯⨯=12②三角形的一边与一条坐标轴平行如图，△ABC 三个顶点坐标分别为A(-1,2),B(-1,-1),C(2,4),求△ABC 的面积。

这种情形，与①相比，只需利用顶点坐标求出底边AB 长及AB 边上的高h 的值，再代入三角形面积公式求解即可：S △ABC =h AB ••21=293321=⨯⨯以上①与②是坐标系中求三角形面积问题的基础。

位置无此特殊性的三角形可转化为该情况后再求解。

再看第二种情况：三角形中没有边在坐标轴上或与一条坐标轴平行。

例1：已知△ABC 三个顶点的坐标分别为：A(1,2)，B(4,6)，C(2,21)，求这个三角形的面积。

分析：如果用三角形面积公式进行求解，知道点的坐标，容易求得线段的长度，底的问题解决了，但底边上的高呢？有点麻烦。

我们不妨试试下面的方法。

分别过点A 、B 、C 作x 轴、y 轴的平行线，则所求三角形的面积S △ABC =S 矩形BDEF -S △ADB -S △AEC -S △BCF =4172112212312143212113=⨯⨯-⨯⨯-⨯⨯-⨯过点C 作y 轴的平行线交AB 边于点M ，将原三角形化作有边与一条坐标轴平行的问题来解决。

易知所求三角形面积S △ABC =S △AMC +S △BMC =)(2121212121h h MC h MC h MC +••=••+••=PQ MC ••21 其中，线段PQ 的长度可由A 、B 两点的横坐标求得，线段MC 的长度需知道点M 与点C 的纵坐标，所以，接下来主要是求得点M 的坐标的问题。

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为〔－3，0〕，〔0，3〕，〔0，－1〕，你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC ＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-〔-1〕=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A〔4，1〕，B〔4，5〕，C〔-1，2〕，求三角形ABC的面积.分析：由A〔4，1〕，B〔4，5〕两点的横坐标一样，可知边AB与y轴平行，因而AB 的长度易求.作AB边上的高CD，那么D点的横坐标与A点的横坐标一样，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标一样，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，那么D点的横坐标为4，所以CD=4-〔-1〕=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，点A〔-3，-1〕，B〔1，3〕，C〔2，-3〕，你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想方法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形〔长方形〕的上下底〔长〕与其中一坐标轴平行，高〔宽〕与另一坐标轴平行.这样，梯形〔长方形〕的面积容易求出，再减去围在梯形〔长方形〕边缘局部的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，那么四边形ADEC为梯形.因为A〔-3，-1〕，B〔1，3〕，C〔2，-3〕，所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=〔AD+CE〕×DE-AD×DB-CE×BE=×〔4+6〕×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题〔提高篇〕“割补法〞的应用一、点的坐标，求图形的面积。

坐标系中如何求三角形的面积
问题描述
在平面直角坐标系中，给定三角形的三个顶点坐标 A(x1, y1), B(x2, y2), C(x3,
y3)，如何通过坐标计算出这个三角形的面积呢？
基本原理
要计算三角形的面积，我们可以利用向量的知识来求解。

设向量AB为向量a，向量AC为向量b。

则向量a的坐标为 (x2 - x1, y2 - y1)，向量b的坐标为 (x3 - x1,
y3 - y1)。

具体步骤
1.计算向量a和向量b的叉乘，即 a × b = x1y2 + x2y3 + x3y1 - x1y3 -
x2y1 - x3y2。

2.三角形的面积等于叉乘结果的绝对值的一半，即 area = |a × b| / 2。

3.最终得出的结果即为这个三角形的面积。

例子
例子：
假设三角形ABC的三个顶点坐标为A(1, 2), B(4, 5), C(3, 7)。

计算过程如下：
向量a = AB = (4 - 1, 5 - 2) = (3, 3)
向量b = AC = (3 - 1, 7 - 2) = (2, 5)
叉乘结果为 a × b = 15 + 42 + 33 - 17 - 45 - 32 = 5 + 8 + 9 - 7 - 20 - 6 = -1
三角形的面积为 area = |-1| / 2 = 0.5
所以，三角形ABC的面积为0.5。

结论
通过向量的方法，我们可以方便地在坐标系中计算三角形的面积。

这种方法简
单直观，可以很好地应用于实际问题中。

1.面积公式：（1）三角形的面积：S三角形＝1/2×底×高（2）梯形的面积：S梯形＝1/2×（上底+下底）×高2.两点间的距离：（1）当两点横坐标相同时，两点间的距离为这两点纵坐标差的绝对值（2）当两点纵坐标相同时，两点间的距离为这两点横坐标差的绝对值基础篇——三角形面积的求法题型1 三角形有一边在坐标轴上【例1】如图，平面直角坐标系中，已知三角形ABC的三个顶点的坐标分别是A（2，3），B（-4，0），C（4，0），求三角形ABC的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边有一边在坐标轴上时，将此边作为底边，那么高便垂直于坐标轴，底和高就能通过两点间的距离很快求出.题型2 三角形有一边与坐标轴平行【例2】如图，平面直角坐标系中，已知三角形ABC的三个顶点的坐标分别是A（-1，-4），B（2，0），C（-4，-4），求三角形ABC 的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边有一边与坐标轴平行时，将此边作为底边，那么高便垂直于坐标轴，底和高就能通过两点间的距离很快求出.根据图形特殊，我们通常把平行于坐标轴的一边作为底边.题型3 三角形三边均不与坐标轴平行【例3】在如图所示的正方形网格中，每个小正方形的单位长度均为1，三角形ABC的三个顶点恰好是正方形网格的格点.（1）写出图中所示各顶点的坐标；（2）求三角形ABC的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边的三边均不与坐标轴平行时：（1）将原三角形围在一个梯形或长方形中，用长方形或梯形的面积，减去长方形或梯形边缘的直角三角形的面积，即可求得原三角形的面积，这种方法叫做补形法；（2）若三角形内一割线长度已知，并且它平行于坐标轴，那么可将其作为底边，把原三角形拆分为两个三角形，则两高的长度可得，面积即可求得，这种方法叫做分割法.以上两种方法就是数学几何图形运算中常用的割补法.例题讲授视频三角形面积的求法同学们，例题看明白了吗？方法掌握了吧！快来试试下面的变式训练吧！变式训练【变式训练1】如图，在平面直角坐标系中，三角形ABC的顶点坐标分别为A(－3，0)，B(0，3)，C(0，－1)，则三角形ABC的面积为．。

计算平面直角坐标系内图形的面积在平面直角坐标系中，求一个三角形的面积，则需要根据三角形的各顶点的坐标，确定边长或高，进而求出三角形的面积．而对于四边形，五边形等图形面积的计算，则往往需要转化为三角形解决．一、计算三角形的面积例1 如图1，△ABC 的三个顶点的坐标分别是A (2，3)，B (4，0)，C (-2，0)．求△ABC 的面积．分析:观察图形可知，BC 在x 轴上，BC 的长为4-(-2)=6．要求三角形的面积，还应确定BC 边上的高．点A 到x 轴的距离恰好点BC 边上的高．解：因为BC =4-(-2)=6，BC 边上的高就点A 到横轴的距离，因为点A 的坐标是(2，3)，所以BC 边上的高是3，所以S △ABC =21×6×3=9． 【评注】当三角形有一边在横轴上时，则以坐标轴上的边为底边，其长等于坐标轴上的两个顶点的横坐标差的绝对值;则这边上的高，等于另一顶点纵坐标的绝对值;当三角形的一边在纵轴上时，则以坐标轴上的边为底边，其长等于坐标轴上的两个顶点纵坐标差的绝对值，这边上的高，等于另一顶点的横最最坐标的绝对值．图1 图2例2 如图2，平面直角坐标系中，已知点A (-3，-2)，B (0，3)，C (-3，2)．求△ABC 的面积． 分析:在△ABC 中只有边AC 的长度是比较求得的，所以找到AC 边上的高，而点A 到纵坐标的距离恰好是AC 边上的高．解:AC =|2-(-2)|=4，作AC 边上的高BD ，而BD 就等于点A 到纵轴的距离，因为点A 的坐标是(-3，-2)，所以BD =|-3|=3，所以S △ABC =21×4×3=6． 【评注】当三角形的一边和坐标轴平行时，这条边的长等于两个顶点横坐标(平行横轴)或纵坐标(平行纵轴)的差的绝对值;这边上的高等于平行坐标轴的边与坐标轴的距离．例3 如图3，平面直角坐标系中，已知△ABC 三个顶点的坐标分别是A (-3，-1)，B (1，3)，C (2，-3)．求△ABC 的面积．分析:三角形的三边都不和坐标轴平行，根据平面直角坐标系的特点，可以将三角形面积转化为梯形或长方形的面积减去多余的直角三角形的面积，即可求到此三角形的面积．解:过点A ，C 分别作平行于y 轴的直线，与过B 点作平行于x 轴的直线交于点D 、E ．则四边形ACED 为梯形．根据点A (-3，-1)，B (1，3)，C (2，-3)， 可求得AD =4，CE =6， DB =4，BE =1，DE =5，所以△ABC 的面积为：S △ABC =21(AD +CE )·DE -21AD ·DB -21CE ·BE =21(4+6)×5-21×4×4-21×6×1=14． 【评注】当三角形的三边都不和坐标轴平行时，可将通过过三角形的顶点作坐标轴的平行线，将三角形的面积转化为梯形或长方形的面积与直角三角形的面积差求解．图3 图4例4 如图4，四边形ABCD 的四个顶点的坐标分别是A (4，2)，B (4，-2)，C (0，-4)，D (0，1)．求四边形ABCD 的面积．分析:因为点A 、B 的横坐标相同，点CD 在纵轴上，所以AB //CD ，则四边形ABCD 为梯形，可以过A 作CD 上的高AE ，则AE 的长就是点A 到y 轴的距离．解：因为CD =1-(-4)=5，AB =2-(-2)=4，AE =4，S ABCD =21(AB +CD )·AE =21(5+4)×4=18． 【评注】一般四边形的面积的计算，可将四边形的面积转化为特殊的四边形(如梯形)与特殊的三角形(如直角三角形)的面积和或差的形式计算．。

平面直角坐标系中三角形面积的求法嘿，伙计们！今天我们来聊聊一个非常有趣的话题——如何在平面直角坐标系中求三角形的面积。

我知道你们可能会觉得这个话题有点儿枯燥，但是别担心，我会用一种轻松幽默的方式来讲解这个问题，让你们在轻松愉快的氛围中学到知识。

我们要明确什么是三角形。

三角形就是由三条线段相互连接的图形，这三条线段叫做三角形的边，而它们相互连接的地方叫做三角形的顶点。

好了，现在我们知道了三角形的基本概念，接下来我们就要开始求三角形的面积了。

那么，三角形的面积到底是怎么求出来的呢？其实，这个问题还有一个更简单的方法，那就是：如果一个三角形的底边长是a,高是h,那么它的面积就是ah/2。

这个公式是不是很简单呢？而且还很好记，因为它的名字叫做“海伦公式”。

那么，我们如何应用这个公式来求解具体的三角形面积呢？其实，只要知道三角形的底边长和高，就可以直接将这两个数值代入公式进行计算了。

比如说，我们有一个三角形，它的底边长是10,高是8,那么它的面积就是10 * 8/2=40。

有时候我们并不知道三角形的具体尺寸，只知道其中两个顶点的坐标。

这时候，我们就需要运用一些几何知识来求解了。

具体来说，我们可以先求出三角形的另外两个顶点的坐标，然后再将这些坐标代入海伦公式进行计算。

这个过程可能会比较复杂一点儿，但是只要你掌握了方法，就一定能够成功求解。

那么，我们如何求出三角形的另外两个顶点的坐标呢？这里就要用到一些基本的几何知识了。

我们要知道三角形的三个顶点是共线的，也就是说它们在同一条直线上。

我们要知道三角形的内角和是180度。

有了这两个条件，我们就可以根据已知的两个顶点的坐标来求出第三个顶点的坐标了。

具体的求法有很多种，这里我就不一一介绍了，你们可以去网上找一些相关的教程学习一下。

求解三角形的面积并不是一件难事儿。

只要你掌握了海伦公式和一些基本的几何知识，就可以轻松地解决这个问题了。

如果你觉得这个问题还是有点儿难度的话，也不要灰心丧气。

图1图2图3平面直角坐标系中如何求几何图形的面积一、 求三角形的面积1、 有一边在坐标轴上或平行于坐标轴例1：如图1，平面直角坐标系中，△ABC 求出三角形ABC 的面积吗2、无边在坐标轴上或平行于坐标轴例2：如图2，平面直角坐标系中，已知点A （-3，-1）、B （1,3）、C （2，-3），你能求出三角形ABC 的面积吗归纳：求三角形面积的关键是确定某条边及这条边上的高，如果在坐标系中，某个三角形中有一条边在坐标轴上或平行于坐标轴，则根据这条边的两个顶点的坐标易求出这边的长，根据这条边的相对的顶点可求出他的高。

二、求四边形的面积例3：如图3，你能求出四边形ABCD 的面积吗分析：四边形ABCD 是不规则的四边形，面积不能直接求出，我们可以利用分割或补形来求。

归纳：会将图形转化为有边与坐标轴平行的图形进行计算。

怎样确定点的坐标一、 象限点解决有关象限点问题的关键是熟记各象限的符号特征，由第一到底四象限点的符号特征分别为（+，+）、 （-，+）、（-，-）、（+，-）。

例1：已知点M （a 3-9,1-a ）在第三象限，且它的坐标都是整数，则a =（ ） A 、1 B 、2 C 、3 D 、0二、轴上的点解决有关轴上点问题的关键是把握“0”的特征，x 轴上点的纵坐标为0，可记为（x ，0）；y 轴上点的横坐标为0，可记为（0，y ）；原点可记为（0,0）。

例2：点P （m+3,m+1）在直角坐标系的x 轴上，则P 点的坐标为（ ） A 、（0，-2） B 、（2,0） C 、（4,0） D 、（0，-4）三、象限角平分线上的点所谓象限角平分线上的点，就是各象限坐标轴夹角平分线上的点。

解决这类问题的关键是掌握“y x =”的特征，一、三象限角平分线上点的横、纵坐标相等，可记为（x ，x ）；二、四象限角平分线上的点横、纵坐标互为相反数，可记为（x ，-x ）。

例3：已知点Q （8,4m 222++++m m m ）在第一象限的角平分线上，则m=_________.四、对称点对称点的横、纵坐标之间有很密切的关系，点P （a ，b ）关于x 轴对称的点的坐标上（a ，-b ）；关于y 轴对称的点的坐标是（-a ，b ）；关于原点对称的点的坐标是（-a ，-b ）；关于一、三象限角平分线对称的点的坐标是（b ，a ）；关于二、四象限角平分线对称的点的坐标是（-b,-a ）. 例4：点（-1,4）关于原点对称的点的坐标是（ ）A、（-1，-4）B、（1，-4）C、（1,4）D、（4，-1）五、平行于坐标轴的直线上的点平行于x轴的直线上点的纵坐标相同，平行于y轴的直线上点的横坐标相同。

专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图，在平面直角坐标系中，点()0,4A b 为y 轴正半轴上一点，点()3,0B b 是x 轴正半轴上一点，其中b 满足()316b +=．（1）求点A ，B 的坐标．（2）点C 为x 轴上一点，且ABC 的面积为12，求C 点的坐标．【答案】（1）()0,4A ，()3,0B ；（2）点C 的坐标为()3,0-或()9,0【解析】（1）由()316b +=得1b =，∴()04A ，，()30B ，．（2）设点C 的坐标为()0x ，，则3BC x =-，由1（）可知4OA =，∴1432ABC S x =⨯⨯-= 12，解得：9x =或3-．∴点C 的坐标为()30-，或()90，．【变式训练1】在平面直角坐标系中，已知点(),0A a ，(),0B b ，a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩，（1）求A 、B 两点的坐标；（2）C 为y 轴正半轴上一点，且6ABC S = ，请求出C 的坐标．【答案】（1）A （-3，0），B （1，0）；（2）C （0，3）【解析】（1）解方程组24a b a b +=-⎧⎨-=-⎩，解得：31a b =-⎧⎨=⎩，∴A （-3，0），B （1，0）；（2）由（1）可知：AB =4，∵S △ABC =12AB •OC =6，∴12×4×OC =6，解得OC =3，∴C （0，3）．故答案为：（1）A （-3，0），B （1，0）；（2）C （0，3）类型二、割补法求面积例1.如图，三角形ABC 的面积等于（）A ．12B ．1122C ．13D ．1132【答案】D【解析】过点A 作AD x ⊥轴于D ，如图所示：由题意可得，3BO =，3OC =，6AD =，3CD =，∴6OD =，∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=，即272ABC S ∆=，故选：D ．【变式训练1】如图，连接AB 、BC 、AC ，则△ABC 的面积是（）A ．312B ．3C ．212D ．2【答案】C【解析】长方形AGDE 的面积为：3×2=6，AGC 的面积：3×1÷2=1.5，CDB △的面积：2×1÷2=1，ABE △的面积：2×1÷2=1，故ABC 的面积为：6-1.5-1-1=2.5，故答案为：C ；【变式训练2】如图，三角形ABO 中，()2,3A --，()2,1B -，A B O ''' 是ABO 平移之后得到的图形，并且O 的对应点O '的坐标为()5,4．（1）作出ABO 平移之后的图形A B O ''' ，并写出A '、B '两点的坐标分别为A '______，B '_____；（2）()00,P x y 为ABO 中任意一点，则平移后对应点P 的坐标为______．（3）求ABO 的面积；【解析】（1）如图，△A 'B 'O '即为所求，A '、B '两点的坐标分别（3，1），（7，3）．故答案为：（3，1），（7，3）．（2）点P '的坐标为（x 0+5，y 0+4）．故答案为：（x 0+5，y 0+4）．（3）S △ABO =3×4-12×2×3-12×1×2-12×4×2=4．【变式训练3】在平面直角坐标系xoy 中，△ABC 的位置如图所示，点A ，B ，C 都在格点上．（1）分别写出下列顶点的坐标：A ________；B ________；（2）请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′；（3）计算出△ABC 的面积．【答案】（1）(-1,6)，(-2,0)；（2）见解析；（3）152【解析】（1）由图知，点A 的坐标为(-1,6)，点B 的坐标为(-2,0)，故答案为：(-1,6)，(-2,0)（2）由图得，点C 的坐标为(-4,3)，则点A 、B 、C 关于y 轴的对称点A ′，B ′，C ′坐标分别为(1,6)，(2,0)，(4,3)，依次连接A ′，B ′，C ′，即得△A ′B ′C ′，所得图形如图所示（3）过A 、C 作x 轴的垂线，垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图，在平面直角坐标系中，点B ，C 的坐标分别为(),2a a -、()3,2a a ，其中0a >，点A 为BC 的中点，若4BC =，解决下列问题：（1）BC 所在直线与x 轴的位置关系是；（2）求出a 的值，并写出点A ，C 的坐标；（3）在y 轴上是否存在一点P ，使得三角形PAC 的面积等于5？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）平行；（2）()1,2A ，()3,2C ；（3）存在，P 点坐标为()0,3-或()0,7【解析】（1）∵点B ，C 的坐标分别为(),2a a -、()3,2a a ，∴BC 所在直线与x 轴的位置关系是平行．故答案为：平行．（2）∵4BC =，∴()34a a --=，∴1a =，∴B （-1，2），C （3，2），∵A 为BC 的中点，∴()1,2A ．（3）存在点P ．设()0,P m ，∵2AC =，∴12252m ⨯⨯-=，∴3m =-或7.∴P 为()0,3-或()0,7．【变式训练1】如图，在直角坐标系中，已知()0,2A ，()3,0B ，()3,4C 三点．（1）求四边形AOBC 的面积；（2）是否存在点()0.5P x x ,，使2ABC AOBC S S = 四边形？若存在，求出点P 的坐标．若不存在，请说明理由．【答案】（1）9；（2）存在，()189P --,或(18,9)【解析】如图，∵34C （，），∴33CD ==．∵()34C ，，30B （，），∴404CB =-=，∴4312DCBO S =⨯=四边形．∵()04D ，，()02A ，，∴422DA =-=，∴11236322DCA S =⨯⨯=⨯= ．∵DCA AOBC DCBO S S S =- 四边形四边形，∴1239AOBC S =-=四边形．（2）由（1）得1239AOBC S =-=四边形设存在点()0.5P x x ，，使△AOP 的面积为四边形AOBC 的面积的两倍．∵△AOP 的面积=122x x ⨯⨯=，∴29x =⨯，∴18x =±∴存在点P （18，9）或（-18，-9），使△AOP 的面积为四边形AOBC 的面积的两倍．【变式训练2】如图，A （0，3）是直角坐标系y 轴上一点，动点P 从原点O 出发，沿x 轴正半轴运动，速度为每秒2个单位长度，以P 为直角顶点在第一象限内作等腰Rt △APB ．设P 点的运动时间为t 秒．（1）若AB ∥x 轴，求t 的值；（2）如图2，当t ＝2时，坐标平面内有一点M （不与A 重合）使得以M 、P 、B 为顶点的三角形和△ABP 全等，请直接写出点M 的坐标．【答案】（1）t 的值为1.5；（2）点M 的坐标为（3，7），（8，﹣3），（11，1）．【解析】（1）过点B 作BC ⊥x 轴于点C ，如图所示．∵AO⊥x轴，BC⊥x轴，且AB∥x轴，∴四边形ABCO为矩形，∴AO=BC=3，∵△APB为等腰直角三角形，∴AP=BP，∠PAB=∠PBA=45°，∴∠OAP=90°-∠PAB=45°，∴△AOP为等腰直角三角形，∴OA=OP=3，∴t=3÷2=1.5（秒），故t的值为1.5；（2）当t=2时，OP=4，①如图3，若△ABP≌△MBP，则AP=PM，过点M作MD⊥OP于点D，∵∠AOP=∠PDM，∠APO=∠DPM，∴△AOP≌△MDP（AAS），∴OA=DM=3，OP=PD=4，∴M（8，-3）；②如图，若△ABP≌△MPB，连接AM，则AP=PB=BM，∠APB=∠MBP=90︒，∴AP∥MB，且AP=MB，∴四边形APBM是平行四边形，y轴于点E，又∠APB=∠MBP=90︒，∴四边形APBM是正方形，∴AP=AM，过点M作ME⊥同理可证△AOP≌△MEA（AAS），∴OA=EM=3，OP=AE=4，∴M（3，7）；③如图，若△ABP≌△MPB，则AP=BP=BM，过点M 、B 分别作x 轴的垂线，垂足分别为点F 、G ，过点M 作MH ⊥BF 于点H ，∴四边形FGMH 是矩形，∴MH =FG ，MG =HF ，同理可证△AOP ≌△PFB ≌△BHM （AAS ），∴OA =PF =BH =3，OP =BF =MH =4，∴MG =HF =BF -BH =1，OG =OP +PF +FG =11，∴M （11，1）；综合以上可得点M 的坐标为（3，7），（8，-3），（11，1）．【变式训练3】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为()1,0，点D 的坐标为()0,2．延长CB 交x 轴于点1A ，作第1个正方形111A B C C ；延长11C B 交x 轴于点2A ，作第2个正方形2221A B C C ，…，按这样的规律进行下去，第2021个正方形的面积是______．【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ，1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C，1113222A B A C ∴====⨯同理可得：22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为：404235.2⎛⎫⨯ ⎪⎝⎭。

小专题——平面直角坐标系中图形面积的求法
方法1 直接利用点的坐标求图形的面积
当图形有边在坐标轴上或与坐标轴平行时，可考虑直接将点的坐标转化为线段长，进而计算图
形面积．
1．如图1，在平面直角坐标系中，三角形ABC的顶点坐标分别为A(－3，0)，B(0，3)，C(0，－1)，则三角形ABC的面积为_______
图1 图2
2．如图2，三角形ABC三个顶点的坐标分别为A(4，2)，B(4，6)，C(－1，3)，三角形ABC的面积为______．
方法2 利用补形法求图形的面积
3．如图，在平面直角坐标系中，已知点A(－3，－1)，B(1，
3)，C(2，－3)，你能求出三角形ABC的面积吗？
方法3 利用分割法求图形的面积
4．在如图所示的平面直角坐标系中，四边形OABC各顶点的坐标分别是O(0，0)，A(－4，10)，B(－12，8)，C(－14，0)，求四边形OABC的面积．
方法4 根据已知图形的面积利用逆向思维求点的坐标
已知坐标系中图形的面积，求点的坐标时，可将点的横(纵)坐标转化为到坐标轴的距离，利用面积来解决线段数量关系，从而求出点的坐标．
5．如图，A(－1，0)，C(1，4)，点B在x轴上，且AB＝3.
(1)点B的坐标为______________；
(2)三角形ABC的面积为__________；
(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．。