下载文档原格式
数学课题会议记录范文第一章：引言在当前高速发展的信息时代，数学经济学作为一门交叉学科，在解决实际经济问题中发挥着重要的作用。
为了促进数学与经济学的深度融合，提升数学经济学在实际应用中的能力，我们召开了一场数学课题会议。
本次会议旨在研讨数学经济学的最新研究成果和发展趋势，加深学者之间的交流与合作，推动数学经济学在实践中的应用。
第二章：数学经济学的理论研究在本次会议上，与会专家学者们围绕数学经济学的理论研究进行了深入的讨论和交流。
其中，对于微分方程在经济学中的应用进行了探讨，特别是在宏观经济模型中的运用。
与会人员一致认为，微分方程在经济学中的应用可以更好地描述经济系统的动态变化，为经济的制定提供科学依据。
同时，多重复合函数理论也成为本次讨论的热点话题，与会人员讨论了其在经济增长模型、消费理论等方面的应用。
第三章：数学经济学的计量分析本章节主要介绍了数学经济学的计量分析方法及其在实践中的应用。
经济数据的分析与建模是数学经济学的重要组成部分，也是实际应用中最为关键的环节。
与会学者分享了自己在计量经济学方面的研究成果，包括时间序列分析、回归分析以及面板数据分析等。
与会人员一致认为，计量经济学的方法在解决实际经济问题中起到了重要的作用，为经济的制定提供了可靠的依据。
第四章：数学经济学的应用研究在这一章节中，与会人员分享了数学经济学在实际经济中的应用研究成果。
其中，对于金融领域的应用进行了重点探讨。
与会专家学者们通过数学模型的构建和计算方法的研究，为金融市场的风险管理、资产定价和金融衍生品的定价提供了有效的工具和方法。
另外，与会人员还就能源经济学、环境经济学以及决策分析等方面展开了讨论，为相关领域的研究和实践提供了有益的启示。
第五章：数学经济学的发展趋势在本章节中，与会学者们对数学经济学的未来发展进行了展望。
他们认为，数学经济学将更加深入地融入实际经济中，成为经济学研究和实践的重要工具。
与会人员还强调，数学与经济学的紧密结合将进一步推动学科的发展，为解决实际问题提供更加准确和可行的方法。
席位分配问题是一个常见的实际问题，涉及到资源的分配和管理。
为了解决这个问题，我们可以使用数学建模的方法，通过建立数学模型来分析和优化席位的分配方案。
一、问题描述假设有一个大型会议，需要分配给不同的参与者席位。
每个参与者可能有不同的资格和需求，我们需要根据一定的规则来分配席位。
具体问题包括：1. 参与者数量和席位数量2. 参与者的资格和需求3. 席位分配的规则和标准二、数学建模为了解决席位分配问题，我们可以使用以下数学模型：1. 参与者集合P：表示所有的参与者。
2. 席位集合S：表示所有的席位。
3. 资格矩阵A：表示每个参与者的资格情况，每一行表示一个参与者，每一列表示一个资格类型（例如，专业、身份等）。
4. 需求矩阵D：表示每个参与者对席位的需求情况，每一行表示一个参与者，每一列表示一个席位类型（例如，地点、时间等）。
5. 分配规则R：表示席位的分配规则和标准，如按照资格优先、按照需求优先、按照公平分配等。
根据以上描述，我们可以建立如下的数学模型：目标函数：最小化席位浪费（即席位数与参与者需求之差）约束条件：1. 资格约束：每个参与者的资格必须满足分配规则的要求。
2. 需求约束：每个参与者所需席位类型必须得到满足。
3. 数量约束：总的席位数必须不超过总席位数量。
4. 可行性约束：分配的席位必须是有效的，即不存在冲突和重复的情况。
三、求解方法根据上述数学模型，我们可以使用以下方法进行求解：1. 枚举法：逐个尝试所有可能的席位分配方案，找到满足约束条件的方案。
这种方法需要大量的计算时间和空间，但在某些情况下可能找到最优解。
2. 优化算法：使用优化算法如遗传算法、粒子群算法等，通过不断迭代找到最优解。
这种方法需要一定的编程知识和技能，但通常能够快速找到满意的解。
3. 启发式算法：使用启发式算法如模拟退火、蚁群算法等，通过不断尝试找到满意解。
这种方法相对简单易行，但可能无法找到最优解。
4. 数学软件求解：使用专门的数学软件如Matlab、Python等，通过编程求解上述数学模型。
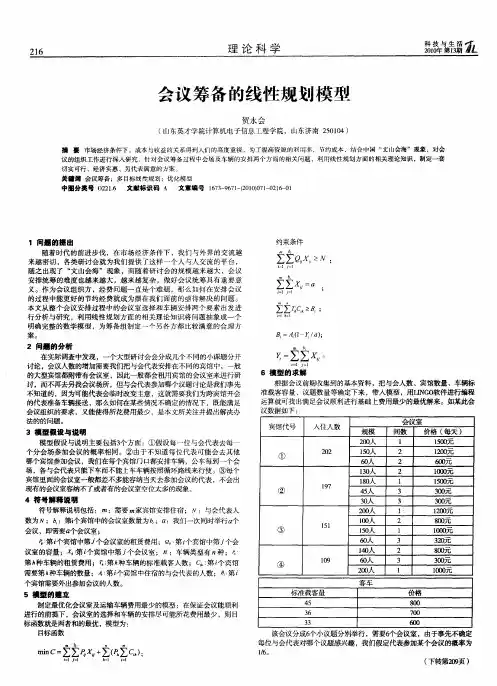
案例2.1 经理会议建议的分析解：依题意可以设：计划生产A1,A2,A3的数量分别为x1,x2,x3.则可建立线性规划数学模型：max=30*x1+20*x2+50*x3;约束条件：x1+2*x2+x3<=430;3*x1+2*x3<=460;x1+4*x2<=420;x1+x2+x3<=300;x2>=70;x3<=240;所以在LINGO中输入程序：max=30*x1+20*x2+50*x3;x1+2*x2+x3<=430;3*x1+2*x3<=460;x1+4*x2<=420;x1+x2+x3<=300;x2>=70;x3<=240;SOLVE：Global optimal solution found at iteration: 4Objective value: 12900.00Variable Value Reduced CostX1 0.000000 35.00000X2 70.00000 0.000000X3 230.0000 0.000000Row Slack or Surplus Dual Price1 12900.00 1.0000002 60.00000 0.0000003 0.000000 15.000004 140.0000 0.0000005 0.000000 20.000006 0.000000 0.0000007 10.00000 0.000000进行灵敏度分析有：Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase DecreaseX1 30.00000 0.0 0.0X2 20.00000 0.00.0X3 50.00000 0.00.0C 1.000000 0.00.0Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 430.0000 0.0 0.03 460.0000 0.0 0.04 420.0000 0.0 0.05 300.0000 0.0 0.06 70.00000 0.0 0.07 240.0000 0.0 0.0所以有最优解：x1=0 , x2=70 , x3=230 , max=12900 ;(a)max=30*x1+20*x2+60*x3;x1+2*x2+x3<=430;3*x1+2*x3<=460;x1+4*x2<=420;x1+x2+x3<=300;x2>=70;x3<=210;在LINGO中运行得：Global optimal solution found at iteration: 5Objective value: 14533.33Variable Value Reduced CostX1 13.33333 0.000000X2 76.66667 0.000000X3 210.0000 0.000000Row Slack or Surplus Dual Price1 14533.33 1.0000002 53.33333 0.0000003 0.000000 3.3333334 100.0000 0.0000005 0.000000 20.000006 6.666667 0.0000007 0.000000 33.33333灵敏度分析：Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient IncreaseDecreaseX1 30.00000 50.0000010.00000X2 20.00000 10.0000020.00000X3 60.00000 INFINITY33.33333Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 430.0000 INFINITY53.333333 460.0000 20.0000040.000004 420.0000 INFINITY100.00005 300.0000 25.000006.6666676 70.00000 6.666667 INFINITY7 210.0000 20.0000050.00000所以有最优解：x1=13.33333 , x2=76.66667 , x3=210 , max=14533.33>12900 ;所以这个建议可行。
会议筹划模型摘要：在会议服务公司承办专业领域全国性会议中，会议筹备组要为与会代表预定宾馆客房、租借会议室、并租用客车接送与会代表。
为了便于管理和满足代表在价位上的要求，本文采用线性规划建立会议筹划模型。
依据以往四届的回执与与会情况，通过二次拟合估计出本届与会人员数目为636人。
再根据附表2回执信息中要求合住与独住所占比例，得到与会人员对各种类型客房的需求间数。
在以上基础上，用0-1整数线性规划的方法以宾馆数最少为目标函数建立最优化模型，用lingo编程求解，得到需要预定的宾馆代号分别为1、2、5、7，而且得到入住该4个宾馆的总人数为636，与通过推算得到本届预测与会总人数636相符合。
其次，以客房总花费最少为原则，考虑到房间数不超过可供给的客房间数，以及与会人员对各种类型房间的要求，用同样的方法建模求解，得到最少花费为7978.00元，同时给出了客房安排的方案，经检验，四个宾馆的房间种类满足附表2提供的代表回执中有关住房的要求。
然后在得到的宾馆之中租借会议室，考虑到半天开6场会议需6间会议室，以租借各种类型会议室的总费用最小为目标函数。
由附表1提供的会议室的价格、间数、规模建立线性规划模型，用lingo求解得到需要租借的6间会议室都在7号宾馆。
最后由于所有会议室都在7号宾馆，故1、2、5号宾馆只需向7号宾馆接送代表。
在与会代表都能准时到达7号宾馆开会并且所有与会人员都有座位的前提下，对车辆进行合理安排。
在此基础上，以客车租借花费的最小值为目标函数，用线性规划，得到共需租借13辆客车，总花费为19400元。
依此该会议筹备组可安排入住1、2、5、7号宾馆,与会人员需要自付的住房总花费为79780元/天；会议室安排12个，上、下午都在7号宾馆，花费7000元/天；每天租借客车13辆，总费用19400元/天。
于是该公司的总花费为26400元/天。
关键词：0-1规划最优化费用 lingo一问题重述某市的一家会议筹备组负责承办某专业领域的一届全国性会议，会议筹备组要为与会代表预订宾馆客房，租借会议室，并租用客车接送代表。
会议分组问题摘要本文解决会议分组问题，即在会议次数以及参会人数确定的情况下求取不同地区之间最大的见面概率的会议安排方式，通过设置相应参数，逐步建立数学模型，并采用Lingo编程进行计算，并最终确定会议人员参加会议的分组方案。
下面将分别对三个问题进行阐述：问题1是已知有名代表参加会议，要分个场次，每场会议中有个小组，先对数据进行了矩阵化处理，其中引入常值元素来区分不同地区的代表，以L×N的矩阵表示每个人在某一场的出席情况，以此建立非线性整数变量规划模型。
为了达到尽可能使来自不同地区的代表能有见面交流机会的目的，本文以每组代表人数基本均衡、每个会议每个代表有且只能在一个小组内为约束条件，根据M个矩阵的加和等一系列运算的结果，得到M场会议之后与会人员的见面情况，从而进行优化，最终确立出最优的分组方案。
针对问题2，本文通过建立分组矩阵、开会矩阵，制定约束条件，构造相遇矩阵以及构造异地代表是否见面函数，逐步建立最终的数学模型。
但是用lingo 计算大量数据的非线性模型运行时间太长，无法获得运算结果（超过5个小时），因此采用分部计算的形式来求解此模型，也就是一共有次会议，须经过多次迭代，每次迭代只计算一次会议的会面情况，每次迭代时更新目标函数的系数，上一次已经会面的代表假设为同一地区，则这次计算常值系数，只计算未见面的代表会见面次数的最大值，迭代完毕之后将次结果综合考虑，并最后得到模型的最优方案。
针对问题3，将问题1中的N、M、L分别取做8、5、5，采用问题（1）所建立的模型以及问题2设计的算法，运行程序，得到的分配结果如下：表2 会议的分组方案第一组第二组第三组第四组第五组第一次2、874、513、6第二次514、63、82、7第三次3、741、82、65第四次74、82、631、5第五次41、673、82关键词：会议分组；矩阵分析；迭代运算；整数规划；约束条件一、问题的重述会议分组是一个很实际的问题，目前国内外许多重要会议都是以分组形式进行研讨，以便充分交流、沟通。
