三维目标表示方法之八叉树1

3dtile 八叉树原理
Windows 写时复制（Write Copy on Write，COW）是一种文件系
统技术，它通过在打开文件的副本中进行写操作，而不是直接在原始
数据上进行写操作，从而提高了文件系统的效率和可靠性。

当打开一个文件并对其进行修改时，Windows 会在内存中创建一
个该文件的副本。

然后，在进行写操作时，Windows 会将修改的数据
写入副本中，而不是原始文件。

这样，原来的文件保持不变，而打开
的副本中进行的所有写操作都是只读的。

这种方式可以有效地减少磁
盘 I/O 操作，提高文件系统的性能。

当文件被关闭时，系统会将副本中的更改写回原始文件中。

因为
在写操作期间创建了副本，原始文件和副本之间存在显式的版本控制，所以此过程被称作“写时复制”。

总的来说，写时复制技术在文件系统中起到了至关重要的作用。

它避免了对原始数据的意外修改，提高了文件系统的可靠性和数据完
整性，并降低了磁盘 I/O 操作的次数，从而提高了系统的性能。

八叉树原理
八叉树是一种重要的数据结构，被广泛应用于计算机科学领域。

它的名称源自每个节点最多有八个子节点的特性。

八叉树通常用于解决多维空间中的问题，比如图形图像处理、计算机视觉、数据压缩等领域。

八叉树的基本原理是将空间划分为八个相等大小的子空间，每个子空间对应树中的一个子节点。

这种划分方式可以递归地进行下去，直到满足某种条件为止。

通过这种方式，我们可以高效地组织和管理大量的空间数据。

在图形图像处理中，八叉树被用来表示和处理图像数据。

通过将图像空间划分为多个小区域，可以快速地定位和处理图像中的特定区域。

这种方法在图像压缩和搜索引擎中得到了广泛应用，极大地提高了处理效率和准确性。

在计算机视觉中，八叉树可以用来表示物体的三维模型。

通过在三维空间中建立八叉树，可以实现对物体的快速检索和碰撞检测。

这对于虚拟现实、游戏开发等领域具有重要意义，可以提高程序的性能和交互体验。

除了图形图像处理和计算机视觉，八叉树还被广泛应用于地理信息系统、数据库管理、物理模拟等领域。

在地理信息系统中，八叉树可以用来管理地图数据和实现空间查询。

在数据库管理中，八叉树
可以用来加速数据的检索和查询。

在物理模拟中，八叉树可以用来表示复杂的物体结构和实现碰撞检测。

总的来说，八叉树是一种非常强大和灵活的数据结构，可以应用于多个领域，提高程序的效率和性能。

通过充分利用八叉树的特性，我们可以更好地处理和管理大规模的空间数据，实现更加复杂和高效的算法和应用程序。

希望未来能够进一步深入研究和应用八叉树，为计算机科学领域的发展做出更大的贡献。

八叉树表示法
八叉树表示法是一种用于描述三维空间的数据结构，它将空间分割成多个八面体（或称为超立方体）的集合，每个八面体由八个相等的边组成。

每个八面体的中心节点表示该空间区域，而其子节点则代表该区域内更小的空间区域。

八叉树表示法的应用广泛，主要用于三维计算机图形、物理模拟、碰撞检测、空间索引和数据压缩等领域。

通过八叉树表示法，可以快速地查询和检索三维空间中的数据，并对物体进行精确的定位和渲染。

总结来说，八叉树表示法是一种用于描述三维空间的数据结构，通过将空间分割成多个八面体，实现快速查询和检索三维空间中的数据，适用于各种三维应用。

鬃塑篓凰基于八叉树的三维形体表示的探讨程敏(常州广播电视大学信息工程系；江苏常州213000)[}商要】八又树表示法是一种层次结构的占有空间计数法，由图象处理中的四又树法扩展而来。

占有空间计数法将实体所在空间进行分割。

分割成由立方体组成的网格。

于是。

一个实体可以可以由它所占有的立方体序列来表示。

当分割后的立方体越来越小时，就逐步接近用空问点的集合来表示实体。

饫薯萄硝实体；八爻树；立方体；几何随着计算机动画、三维空间数据场显示等的迅速发展，以及计算杌技术的不断发展，数据获取能力越来越强，所处理模型的数据量也越来越大。

要在计算棚屏幕上构造出三维物体的一幅图象，首先必须在计算机中构造出该物体的模型，这—模型是由一批几何数据及数据之间的拓扑关系来表示的。

这就是造型技术。

有了三维物体的模型，在给定了观察点和观察方向以后，就可以通过一系列的几何变换和投影变换在屏幕上显示出该三维体的二维图象。

在早期的计算机图形生成技术中，三维物体大多是用线框模型来表示的，线框模型由定义—个物体边界的直线和曲线组成，每一条直线和曲线都是单独构造出来的，并不存在面的信息。

采用这种造型技术表示的三维物体常常具有二义性，也易于构造出无效形体，更不能正确表示曲面信息。

要想在计算机内表示、构造一个实体，首先必须明确什么是实体。

V oe l c ker及R equi c ha等基于点集拓扑的理论，认为三维空间中的物体是空间中点的集合。

并且从点集拓扑的领域概念出发，通过定义点集的闭包给出正则集的定义。

—个开集的闭包指的是该开集与其所有边界点的集合的并集，其本身是—个闭集。

组成—个三维物体的点的集合可以分为内部点和边界点两部分。

由内部点构成的点集的闭包就是正则集。

三维空间中点集的正则集就是三维正则形体，也就是有效的实体。

在实体造型系统中，八叉树表示法是一种层次结构的占有空间计数法，由图象处理中的四叉树法扩展而来。

占有空间计数法将实体所在空间进行分割，—般是分割成由立方体组成的网格。

用多杈树法分解目标旋舞职场，不管你职业规划中的终极目标有多大多遥远，一定要耐心地将它细细切割、分解，直到你知道现在该去做什么。

（1）美丽的“多杈树”有人曾这样描述分解目标的重要作用：“通过分解目标，你可以给自己更宽广的视觉空间，更细腻生动的使用体验，更便捷的操作方式。

”关于分解目标有一个非常形象而美丽的方法多杈树分解法。

读着这个名字，你可以这样想象一下：一棵枝繁叶茂的大树图1 1多杈树法分解目标示意图，从树干开始，它就有一个分支，若干个树枝。

每一个树枝，又有更小的树枝，而每一个更小的树枝，又有再小的树枝，直到摇曳在风中的叶子。

若将这棵树联系到分解目标，你可以抽象地将树干比喻成大目标，而每一个树枝则代表一个小目标，直到最后的叶子。

你会发现，这些叶子其实就是你现在的目标，或者说是你现在要做的每一件事情所应该达到的结果。

如图1 1所示。

通过多杈树示意图，分解目标这一理念被演绎得可谓淋漓尽致。

而纵观示意图，不难发现，在“多杈树”中，大目标与小目标之间存在着这样一种逻辑关系：小目标是大目标的条件。

大目标是小目标的结果。

小目标的实现之“和”，一定是大目标的实现。

实践证明，将大目标分解成若干个小目标，再将每个小目标分解成若干个更小的目标，如此一直分解下去，到最后，那个最小的目标将会明确地告诉你：现在该去做什么。

因此，不管你所制定的终极目标有多大多遥远，一定要耐心地将它细细切割、分解，直到你知道现在该去做什么。

说白了，一棵完整的目标多杈树，其实也就是一套完整的达成该目标的行动计划。

因此又有人将目标多杈树称之为计划多杈树。

而任何一个目标最后都可以被描绘成一棵枝繁叶茂的大树。

（2）一个长跑运动员的启示山田本一在1984年出人意料地夺得了东京国际马拉松邀请赛的冠军。

记者问他凭什么取得了如此惊人的成绩，他说：“我是凭目标获胜的。

”两年后，他又在意大利国际马拉松邀请赛上获得冠军，当记者采访他时，他仍说：“我是凭目标获胜的。

八叉树数据模型在三维地质建模中的应用摘要介绍三维地质建模中的八叉树数据模型,并设计一个三维地质建模的实验系统,对这个实验系统实行的算法进行分析,实验分析结果表明实验系统和同类系统比具有很大的优越性。

关键词八叉树;三维地质建模;三维地质体1八叉树数据模型八叉树是一种能很好的表示三维地质体的数据结构,他能做到在压缩数据的同时很好地表达地质体的几何特征,它表现为以分支关系定义的层次结构或树形结构,对地质体的空间分析具有别的存储结构达不到的优势。

一般把三维地质体放在一个2n×2n×2n的立方体内,2n为立方体的边长,立方体与八叉树的根结点相对应;若整个立方体被地质体完全充满,那么这个八叉树就只有一个节点——根结点;否则这个立方体要继续分解成8个相等的子立方体,称为八分体(Octant)。

每个八分体与树根的一个子结点相对应,八分体的边长为根立方体边长的1/2。

对每个八分体,如果为空或为实节点,则该八分体不再分解;若八分体为部分满,则该八分体进一步分解为八个子八分体;如此递归地分解,直到每个子八分体已达到分解的精度,或子八分体均为全满或全空为止。

通过递归分解,最终形成一棵度为8的树,即八叉树(Octree)。

若经过n次分解,n 为八叉树的分辨精度或分辨率,立方体的边长为2n。

整个立方体空间用八叉树的根结点表示;部分满的八分体对应于八叉树的分支结点,称为灰结点(Grey Node);全满或全空的八分体对应于八叉树的叶结点,分别称为黑结点(Black Node)或白结点(White Node)。

结点的层次(Level)从根结点开始定义,根结点为第0层,根结点的所有孩子结点为第1层,第1层结点的所有孩子结点为第2层,依此类推。

八叉树的每个结点由1个编码(code)和8个指向结点的指针(指针号为0-7)组成。

如果code=black,则该结点所表示的空间部分全部为实心,且指针0-7为0,亦即该结点为叶结点。

八叉树是一种用于空间划分和快速搜索的数据结构。

在3D图形学中，八叉树被广泛应用于碰撞检测和场景管理等方面，而在three.js中，八叉树也扮演着重要的角色。

本文将从基本原理到实际应用，深入探讨three.js中八叉树的碰撞检测原理。

一、八叉树的基本原理八叉树是一种四叉树的扩展，用于将三维空间递归地划分为八个相等的子立方体。

这种分割方式使得空间能够被高效地表示和搜索，同时也适用于各种不规则的形状。

在碰撞检测中，八叉树能够快速地确定哪些物体可能相交，从而减少了不必要的计算。

二、three.js中八叉树的应用在three.js中，八叉树通常用于加速碰撞检测。

通过将场景中的物体进行空间划分，可以快速地确定哪些物体可能发生碰撞。

这对于实时渲染和交互式应用非常重要，能够显著提高性能和用户体验。

三、八叉树的构建和更新在使用八叉树进行碰撞检测时，需要首先构建整个场景的八叉树。

一般来说，这是一个耗时的过程，但在three.js中，可以通过一些优化的算法和数据结构来加快构建速度。

由于场景中的物体可能在运动或变形，因此需要及时更新八叉树以保持准确性。

四、个人观点和理解在我看来，八叉树作为一种高效的空间数据结构，对于碰撞检测等计算密集型任务有着重要的作用。

在使用three.js进行3D图形开发时，八叉树的应用可以大大提高性能，使得复杂的场景和交互更加流畅和真实。

总结回顾通过本文的介绍和讨论，我对three.js中八叉树的碰撞检测原理有了更深入的理解。

八叉树作为一种空间数据结构，在三维图形学和游戏开发中扮演着重要的角色。

在实际开发中，深入理解八叉树的原理和应用，对于提高性能和用户体验至关重要。

以上是我对three.js八叉树碰撞检测原理的思考和总结，希望对您有所帮助。

八叉树是一种用于空间划分和快速搜索的数据结构，通常用于加速碰撞检测和场景管理。

在3D图形学和游戏开发中，八叉树被广泛应用，而在现代的Web开发中，利用three.js库实现八叉树的碰撞检测也变得越来越普遍。

八叉树颜色量化原理一、引言八叉树是一种用于表示三维空间的数据结构，而颜色量化是一种将真彩色图像转换为索引颜色图像的技术。

本文将介绍八叉树在颜色量化中的应用原理，并深入探讨其实现方法和优缺点。

二、八叉树的定义与原理八叉树是一种二叉树的扩展，它用于表示三维空间中的体积数据。

八叉树的每个节点可以有最多八个子节点，分别代表空间中的八个方向。

通过不断细分空间，八叉树可以表示出越来越详细的空间信息。

三、颜色量化的定义与应用场景颜色量化是将真彩色图像中的每个像素点的RGB值转换为索引颜色的过程。

索引颜色图像只使用有限数量的颜色进行表示，从而减小图像的存储空间。

颜色量化广泛应用于图像压缩、图像处理等领域。

3.1 颜色量化的原理颜色量化的核心思想是通过聚类算法将真彩色图像中的颜色进行分组，然后用每个簇的代表颜色来替代所有该簇中的颜色。

常用的颜色量化算法有K-Means算法、Octree算法等。

3.2 颜色量化的应用场景颜色量化广泛应用于图像压缩、图片转换、图像处理等领域。

在图像压缩中，颜色量化可以大幅减小图像文件的大小，提高图像传输的效率。

在图像处理中，颜色量化可以用于调整图像的色彩效果、提取图像中的主要颜色等。

四、八叉树在颜色量化中的应用八叉树在颜色量化中的应用是利用其可以有效地表示三维空间的特点，在颜色空间中进行量化。

4.1 八叉树的构建•将真彩色图像中所有像素点的颜色值作为八叉树的输入数据。

•通过对颜色空间的划分，构建八叉树的根节点。

•递归地将颜色值插入到八叉树中的合适位置，直到所有颜色值都被插入到树中。

4.2 八叉树的剪枝•遍历八叉树的所有叶子节点，统计每个叶子节点所包含的颜色值数量。

•根据设定的量化色彩数量，选取叶子节点中包含颜色数量最多的一些节点。

•将这些叶子节点的颜色值修改为叶子节点所包含颜色的平均值。

4.3 八叉树的压缩•将八叉树的每个节点按照预先设定的顺序转换为索引值。

•将转换后的索引值按照顺序组合成一个索引颜色表（Palette）。

2009年2月5日读书2009-02-05 13:35:46 阅读68 评论2 字号：大中小订阅§2.5 三维数据结构目前GIS主要还停留在处理地球表面的数据，若数据是地表以下或以上，则先将它投影到地表，再进行处理，其实质是以二维的形式来模拟、处理任何数据，在有些领域可行，但涉及到三维问题的处理时，往往力不从心。

三维GIS的要求与二维GIS相似，但在数据采集，系统维护和界面设计等方面比二维GIS复杂得多，如三维数据的组织与重建，三维变换、查询、运算、分析、维护等方面。

下面主要介绍三维数据结构，三维数据结构表示有多种方法，其中运用最普遍的是具有拓扑关系的三维边界表示法和八叉树表示法。

一、八叉树三维数据结构主要阐述八叉树三维数据结构的原理和常见的几种存贮结构。

（一）基本原理用八叉树来表示三维形体，并研究在这种表示下的各种操作及应用是在进入80年代后才比较全面地开展起来的。

这种方法，既可以看成是四叉树方法在三维空间的推广，也可以认为是用三维体素阵列表示形体方法的一种改进。

八叉树的逻辑结构如下：假设要表示的形体V可以放在一个充分大的正方体C内，C的边长为2 n，形体V C，它的八叉树可以用以下的递归方法来定义：八叉树的每个节点与C的一个子立方体对应，树根与C本身相对应，如果V＝C，那么V的八叉树仅有树根，如果V≠C，则将C等分为八个子立方体，每个子立方体与树根的一个子节点相对应。

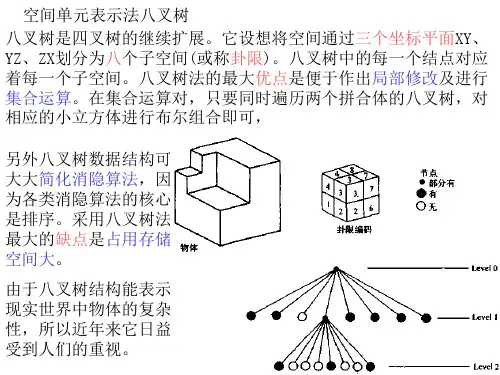
只要某个子立方体不是完全空白或完全为V所占据，就要被八等分（图2-5-1），从而对应的节点也就有了八个子节点。

这样的递归判断、分割一直要进行到节点所对应的立方体或是完全空白，或是完全为V占据，或是其大小已是预先定义的体素大小，并且对它与V之交作一定的“舍入”，使体素或认为是空白的，或认为是V占据的。

如此所生成的八叉树上的节点可分为三类：灰节点，它对应的立方体部分地为V所占据；白节点，它所对应的立方体中无V的内容；黑节点，它所对应的立方体全为V所占据。