(完整word版)高数辅导之专题十：高阶导数

专题十基础知识关于高阶导数，有：（1）几个常见的高阶导数公式，2sin()(sin )(π⋅+=n x x n )2cos()(cos )(π⋅+=n x x n ，1)(!)1()1(+-=n n n x n x 1)1(!)1()(ln ++-=n n n xn x ，)1()!(!)()(n k x k n n x k n k n ≤≤-=-)(0)()(n k x k n >=（2）分段函数在分段点处的二阶导数（3）莱布尼兹公式：设函数，皆阶可导，则u v n )()1(1)()()1(1)()()(n n n n k k n k n n n n n uv v u C v u C v u C v u uv +'++++'+=----)()(0k k n nk k n vu C -=∑=（实际上就是二项式定理）（4）隐函数及由参数方程确定的函数的二阶导数（不在本专题中涉及）例题1. 设，求。

⎪⎩⎪⎨⎧=≠=0,10,sin )(x x x xx f )0(f ''解：xf x f f x )0()(lim)0(0-='→ x x xx 1sin lim 0-=→ 20sin lim x x x x -=→xx x 21cos lim 0-=→xx x 221lim 20-=→=故⎪⎩⎪⎨⎧=≠-='0,00,sin cos )(2x x x xx x x f 于是xf x f f x )0()(lim)0(0'-'=''→ x x xx x x 0sin cos lim20--=→ 30sin cos lim x x x x x -=→ 203cos sin cos lim x x x x x x --=→ 203sin lim x x x x -=→31-=2. 已知，求。

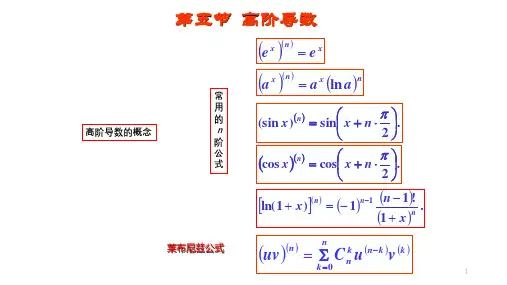
x x f 2cos )(=)0()2(n f 解：由知)22cos(2)()(π⋅+=n x x fn n nn n n n f 4)1(220cos(2)0(2)2(⋅-=⋅+=π3. 已知，求。

高阶导数的公式高阶导数的公式是在微积分中用于求解函数的导数的一种工具，它可以帮助我们了解一个函数在某一点上的变化趋势。

设函数 f(x) 在点 x=a 处可导，那么函数 f(x) 在点 x=a 处的导数 f'(a) 表示函数在该点的变化率，它描述了函数曲线在该点的切线的斜率。

而高阶导数则是指对函数进行多次求导得到的导数。

举例来说，二阶导数表示对函数求导一次后再求导一次的结果，三阶导数表示对函数求导三次的结果，以此类推。

设函数 f(x) 所有阶数的导数存在，那么高阶导数的公式如下：一阶导数（一阶导数即为函数的导函数）：f'(x) = lim(h→0) [f(x+h) - f(x)] / h二阶导数（二阶导数即为函数的二阶导函数）：f''(x) = d/dx [f'(x)]三阶导数（三阶导数即为函数的三阶导函数）：f'''(x) = d/dx [f''(x)]更一般地，n 阶导数（n 阶导数即为函数的 n 阶导函数）：f^(n)(x) = d^n/dx^n [f(x)]其中，lim 表示极限，d/dx 表示对变量 x 求导，d^n/dx^n 表示对变量 x 进行 n 次求导。

高阶导数的公式可以通过迭代求导的方式得到，每次对前一阶导数再次求导。

这种方法可以帮助我们研究函数的更深层次的性质和特征。

需要注意的是，高阶导数的计算可能存在复杂性和困难性，特别是当函数包含复杂的表达式或多重变量时。

在实际应用中，我们可以使用符号计算软件或数值计算方法来求解高阶导数。

总结起来，高阶导数的公式是一种用于求解函数的导数的数学工具，通过对函数进行多次求导，可以得到相应阶数的导函数。

高阶导数可以帮助我们更深入地了解函数在某一点上的变化特征，以及函数的曲线在该点的切线的斜率。

当我们计算高阶导数时，我们可以采用递归的方法进行求解。

递归是一种通过将问题分解为更小的子问题来解决整体问题的方法。

常用高阶导数公式1. 常数函数的高阶导数：任何常数函数的高阶导数都是0。

例如，f(x) = c（c为常数），则 f'(x) = f''(x) = f'''(x) = = 0。

2. 幂函数的高阶导数：对于幂函数 f(x) = x^n，其n阶导数为f^n(x) = n! / (n k)! x^(n k)，其中k为导数的阶数，n!表示n的阶乘。

3. 指数函数的高阶导数：对于指数函数 f(x) = a^x，其中a为常数，其n阶导数为 f^n(x) = a^x ln(a)^n。

4. 对数函数的高阶导数：对于对数函数 f(x) = ln(x)，其n阶导数为 f^n(x) = (1)^(n1) (n1)! / x^n。

5. 三角函数的高阶导数：对于三角函数 f(x) = sin(x) 或 f(x) = cos(x)，其n阶导数可以表示为 f^n(x) = (1)^(n/2) sin(x +nπ/2) 或f^n(x) = (1)^(n/2) cos(x + nπ/2)。

这些常用的高阶导数公式可以帮助我们在求解函数的高阶导数时更加简便和快速。

在实际应用中，这些公式经常被用于求解物理、工程、经济等领域中的问题。

掌握这些高阶导数公式对于深入理解和应用微积分知识至关重要。

常用高阶导数公式6. 反三角函数的高阶导数：对于反三角函数 f(x) = arcsin(x)或 f(x) = arccos(x)，其n阶导数可以表示为 f^n(x) = (1)^(n1) (n1)! / (1 x^2)^(n/2)。

7. 指数函数的复合函数的高阶导数：对于指数函数的复合函数f(x) = a^(g(x))，其中a为常数，g(x)为可导函数，其n阶导数可以表示为 f^n(x) = a^(g(x)) (ln(a))^n g'(x) g''(x) g^n(x)。

8. 对数函数的复合函数的高阶导数：对于对数函数的复合函数f(x) = ln(g(x))，其中g(x)为可导函数，其n阶导数可以表示为f^n(x) = (1)^(n1) (n1)! / g(x)^n g'(x) g''(x) g^n(x)。

,cos )(sin x x ='例,sin )(cos x x -='. sin 连续求两次导数的结果是x , sin 记为的二阶导数称为函数x x x x x sin )(cos ))((sin )(sin -='=''='' )( )( ,仍然的导函数如果函数一般说来x f x f '的二的导数为原来函数则称可导 )( )( ,x f x f '.))(()( ,''=''x f x f 记为阶导数一. 高阶导数的概念一个函数的导函数不一定再可导, 也不一定连续. 如果函数f ( x) 在区间 I 上有直到n 阶的导数f (n)(x) , 且f (n)( x) 仍是连续的 (此时低于n 阶的导数均连续 ), 则称f (x) 在区间 I 上n 阶连续可导, 记为如果f (x) 在区间 I 上的任意阶的高阶导数均存在且连续, 则称函数f (x) 是无穷次连续可导的, 记为1)(-='='n nxn x y 21)1()()(---='=''=''n n xn n xn y y 3)2()1()(---='''='''n xn n n y y …………………………kn k k xk n n n n yy--+---='=)1()2()1()()1()( ., 的高阶导数求幂函数+∈=Z n x y n )1(n k ≤≤解例1注意, 当 k = n 时!123)2()1()()(n n n n x n n =⋅⋅--= 综上所述：.0)( , 1 ,)(=+≥k n x n k 时当从而kn k n xk n n n x -+--=)1()1()()( )1(n k ≤≤0)()(=k n x )1(+≥n k)()())((k n k b ax y+=,1 时当n k ≤≤kkn ab ax k n n n ⋅++--=-))(1()1(, 1 时当+≥n k 0)(=k y解例2.)( 的高阶导数求nb ax y +=多项式的高阶导数.nn n n n a x a x a x a x P ++++=--1110)( 231202)2)(1()1(''---++--+-=n n n a x n n a x n n a y ………………!0)(n a yn ⋅=解12110)1('---++-+=n n n a xn a nxa y 例3)2()1(===++ n n yy对多项式而言,每求一次导数 , 多项式的次数降低一次 ; n 次多项式的n 阶导数为一常数 ;大于多项式次数的任何阶数的导数均为 0 .求 y = e x 的各阶导数.解xey =' y = e x 的任何阶导数仍为 e xxn x ee =)()()(N n ∈xxee y y ='=''='')()(xn ey=)(例4求 y = a x 的各阶导数.解aa y xln '=运用数学归纳法可得)( )(ln )()(+∈=Z n a a a n x n x 2)(ln )ln ()(''a a a a y y x x ='=''=kx k a a y)(ln )(=例511)1()()!1()1(---+---=k k k xk k y)1(1)1(!]1)1[()1(+--+-+-=k k xk )( )!1()1()(ln 1)(N n x n x y nn n n ∈--==--类似地, 有)( )()!1()1())(ln(1)(N n b ax a n b ax nn n n ∈+--=+--则故由数学归纳法得.1的高阶导数求xy =解)(ln 1'==x xy )1()()()(ln ))((ln +='=∴n n n x x y)1(1)1(!]1)1[()1(+--+-+-=n n xn )1(!)1(+--=n n xn 注意这里的方法例7解x y cos ='x y sin -=''x y cos -='''x ysin )4(=.cos , sin 的各阶导数求x y x y ==xy sin = 看出结论没有)24sin(π⋅+=x )23sin(π⋅+=x )22sin(π⋅+=x )21sin(π⋅+=x 例8运用数学归纳法可以证得)( )2sin()(sin )(+∈⋅+=Z n n x x n π类似地 , 可求得)( )2cos()cos ()(+∈⋅+=Z n n x x n π)sin (cos sin 2sin x ex ey xx-+='')sin (cos 2sin x x ex-=. ,sin y e y x''=求解xey xcos sin ='二阶导数经常遇到, 一定要掌握.例10。