SPC-计数型数据
- 格式：pptx
- 大小：419.85 KB
- 文档页数：3
下载文档原格式
合集下载
什么是SPC？怎么用SPC？
什么是SPC？怎么⽤SPC？1- What：什么是SPCSPC：统计过程控制SPC说到底，就是⼀个图表，把⽣产过程中的数据，收集起来⽤图表的形式展现出来。
它的作⽤可以⼤致总结为：⽅便⼤家从图表中，找出有异常的数据。
跟进数据趋势，预见异常发⽣的可能。
数据异常后，做出相应的改善对策SPC中有8种图表，根据不同的场景，使⽤不同的图表。
但是需要说明的是，这些图⽚都长的⼀样：是的，都长成上⾯这个样⼦。
当我花了两个星期，跟吃屎⼀样，把SPC⼿册啃完，画出那8个图之后，也发出了同样的感叹：卧草，都TM⼀样的，不就是个趋势图嘛！当然，趋势图也是数据统计，所以也可以看做是SPC的⼀种实现⽅法。
SPC本质上就是⼀种特殊的趋势图，不过SPC给他们起来⼀个更有⽓质的名字：控制图。
当然了，控制图还要和普通的趋势图有差异的，具体表现为以下⼏点：1. 控制图都有上下控制线和中⼼线，UCL和LCL（具体会在6-How⾥⾯说明）2. 控制图的数据收集规则、数据分析的规则，更加的繁琐，更加的严格3. 控制图⼀定要有相应的改善输出恩，SPC就是这么⼀个玩意⼉。
需要说明的是，SPC和标准值没有关系，没有标准值也是可以做SPC控制图的。
2- Why：为什么要⽤SPC说实话：都TM是客户要求的，是⽼板要求。
（当我们是⼯程师的时候，都是这么想的）说假话：为了及时发现⽣产过程中，由特殊原因导致的异常，及时改善。
为了深⼊分析系统中的普通原因，进⼀步提⾼产品品质，为客户提供更好的产品。
（当成为⼀个⼯⼚的品质副总时，如何将⼀线数据浮上来，你会⾃然⽽然的想到SPC）在思考为什么要⽤SPC时，我们的观点和认知，是随着职位不断成长的。
不要硬逼着⾃⼰去理解SPC⼿册⾥，那⼗⼏页鸡汤式的SPC概述。
格局到了，⾃然就理解了。
但是SPC的作⽤是不会发⽣变化的，做就对了。
3- When：在什么时候⽤SPCSPC⼿册⾥⾯说，SPC只有在过程受控状态下，才能使⽤。
但是实际上，SPC就是⼀个图表，任何情况，任何产品，只要有数据就可以⽤SPC控制图。
五大技术工具之SPC
（一）统计过程控制的基本概念1.什么是统计过程控制？使用诸如控制图等统计技术来分析过程或其输出，以便采取适当的措施来达到并保持统计控制状态从而提高过程能力，称之为统计过程控制。
2.什么是控制图：使用统计方法，将收集数据计算出一条中心线和两条控制界限，也就是我们所能做到制程能力水准。
随时将样本数据计算并点入控制图内，以提醒作业人员注意，如发现超出控制界限外或异常现象时，立即进行改善工作，以防止不合格发生。
3.什么是计量型数据？计量型数据就是定量的等级,可用测量值分析,如尺寸10.04,圆轴直径6.0mm。
4.什么是计数型数据？计数型数据就是可以用来记录和分析的定性数据，如一批产品不合格个数。
5.什么是变差过程的单个输出之间不可避免的差别，过程中由于受到人、机、物、法、环、测量等因素影响，输出的零件、半成品或成品个体之间必然会存在差异，这种差异就称之为变差，产生变差原因为普通原因和特殊原因。
6.什么是变差的普通原因和特殊原因？普通原因：（机遇原因）指的是造成随着时间的推移具有稳定的且可重复的分布过程中的许多变差原因。
普通原因的识别：①如用同一量具，由同一人测量某人身高数次，所得测量值有差异存在。
②在生产工作中，虽然定有操作标准，但在操作条件容许之范围内必有变化。
③原材料之品质在其规格范围内的变异，如材料重量、密度、厚薄等。
特殊原因：（非机遇原因）是指造成不是始终作用于过程的变差原因，即当它们出现时将造成整个过程的分布改变。
如果系统内存在变差的特殊原因，随着时间推移，过程的输出将不稳定。
特殊原因的识别：①如由于机器智步彤、材料之差异、人为之因素或操作原因，影响品质之变异，这些原因都是可以避免的；②未遵照操作标准而操作，所发生的变异；③机器设备之故障发生的变异；④操作人员之变动造成的变异。
普通原因与特殊原因的区别：普通原因的变异特殊原因的变异1.大量之微小原因引起。
2.不管发生何种之普通原因，其个别之变异极为微小。
SPC统计-计数型数据
SPC统计-计数型数据1. 简介SPC〔统计过程控制〕是一种统计方法，用于监测和控制过程的变异性。
计数型数据是SPC中常见的一种类型，它是指对一个过程中发生的事件进行计数或计量的数据。
在生产过程中，计数型数据常用于统计质量缺陷、产品故障等信息。
2. SPC统计-计数型数据的目的SPC统计-计数型数据的目的在于通过对计数型数据进行统计分析，了解和控制过程的变异性，从而实现生产过程的质量控制和改良。
3. SPC统计-计数型数据的方法SPC统计-计数型数据常用的方法有以下几种：3.1 控制图控制图是SPC统计-计数型数据中最常用的图表之一，通过绘制计数型数据的变化趋势以及控制限，可以及时发现过程的异常变异，并进行相应的调整和改良。
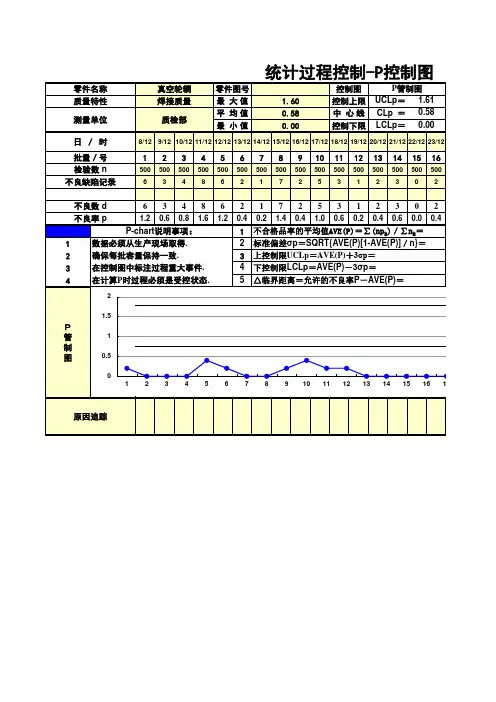
常见的控制图包括：•P图：用于统计不良事件的比例的控制图。
P图将观察时间分为假设干子组，然后统计每个子组内不良事件发生的比例，并计算上下控制限，以判断过程是否处于控制状态。
•C图：用于统计不良事件的数量的控制图。
C图将观察时间分为假设干子组，然后统计每个子组内不良事件的数量，并计算上下控制限，以判断过程是否处于控制状态。
•U图：用于统计不良事件的单位数的控制图。
U图将观察时间分为假设干子组，然后统计每个子组内不良事件的单位数〔如每个产品的不良事件数量〕，并计算上下控制限，以判断过程是否处于控制状态。
3.2 过程能力指数过程能力指数用于衡量过程的稳定性和一致性，是SPC统计-计数型数据评估过程能力的重要工具。
常见的过程能力指数有：•Cp指数：Cp指数用于评估过程的一致性，它比拟过程的控制限与规格限的距离。
Cp指数越大，说明过程越稳定，一致性越好。
•Cpk指数：Cpk指数用于评估过程的稳定性和一致性，考虑了过程的中心位置。
Cpk指数越大，说明过程的稳定性和一致性越好。
•Pp指数：Pp指数用于评估过程的一致性，考虑了样本大小的影响。
Pp指数越大，说明过程越稳定，一致性越好。
•Ppk指数：Ppk指数用于评估过程的稳定性和一致性，考虑了过程的中心位置和样本大小的影响。
SPC(精要版)
过程控制和QS
[质量体系]所有活动都是过程。 [质量策划]要求采用APQP的过程控制策划 [过程控制]要求质量策划的实施包括以下内容: —过程控制计划 —过程监控和操作者作业指导书 —预防性维护 —监视过程能力、效率、有效性。
统计过程控制
使用诸如控制图等统计技术来分析过程或 其输出，以便采取适当的措施来达到并保 持统计控制状态，并从而提高过程能力。 SPC：使过程持续、稳定地具备所需要的 能力！
பைடு நூலகம்
过程控制
过程控制：是为了确保满足顾客的要求， 而对过程所执行的一套程序，和经过计划 的措施。这些程序和措施包括： 经过计划的用以搜集有关输入和输出的信 息的信息性经验 基于已搜集的信息而对过程进行的调整。
过程控制
过程控制系统的目标：是对影响过程的措施作 出经济合理的决定。平衡不需控制时采取了措 施(过度控制或擅自改变)和需要控制时未采取措 施(控制不足)的后果。必须在变差的两种原因— —特殊原因和普通原因的关系下处理好这些风 险。 过程在统计控制下运行：指的是仅存在造成变 差的普通原因。这样，过程控制系统的一个作 用是当出现变差的特殊原因时提供统计信号， 并且当不存在特殊原因对避免提供错误信息。
区分计量型数据和计数型数据
计量型数据（ Variables Data）：定量的数据，可用测 量值来分析。例如：用毫米表示的轴承轴颈直径，用牛 顿表示关门的力，用百分数表示电解液的浓度，用牛 顿．米表示紧固件的力矩。 计数型数据 （Attributes Data ）：为可数的定性数据。 例如所要求的标签是否存在，紧固件是否全部安装，一 个报告中的差错数，由通止规检验出的轴的直径的可接 受率等特性。 －计数型数据即可以是通止型的，也可以表示为计量型 数据的个数。
SPC计数型(P图)
零件名称 质量特性
测量单位
日／时 批量／号 检验数 n 不良缺陷记录
真空轮辋 焊接质量
质检部
零件图号 最 大值 平 均值 最 小值
统计过程控制-P控制图
1.60 0.58 0.00
控制图 控制上限 中 心线 控制下限
P管制图 UCLp＝ 1.61 CLp ＝ 0.58 LCLp＝ 0.00
8/12 9/12 10/12 11/12 12/12 13/12 14/12 15/12 16/12 17/12 18/12 19/12 20/12 21/12 22/12 23/12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 6348621725312302
不良数 d
6348621725312302
不良率 p
1.2 0.6 0.8 1.6 1.2 0.4 0.2 1.4 0.4 1.0 0.6 0.2 0.4 0.6 0.0 0.4
6241301
73
1.2 0.4 0.8 0.2 0.6 0.0 0.2 0.58%
过程能力CPK
请设定参数
＝
△临界距离／3σp
允许的P= 样本量n=
2.00% 500
＝
1.3851
子组数k= 25
结论
满足
过程能力 ≥1.33
UCLp 说明栏 A分检 M反馈 R维修 S调整
CL p W工装 X换人
17 18 19 20 21 22 23 24 25
制定者
张明君
24/12 25/12 26/12 27/12 28/12 29/12 30/12 31/12 1/01
测量单位
日／时 批量／号 检验数 n 不良缺陷记录
真空轮辋 焊接质量
质检部
零件图号 最 大值 平 均值 最 小值
统计过程控制-P控制图
1.60 0.58 0.00
控制图 控制上限 中 心线 控制下限
P管制图 UCLp＝ 1.61 CLp ＝ 0.58 LCLp＝ 0.00
8/12 9/12 10/12 11/12 12/12 13/12 14/12 15/12 16/12 17/12 18/12 19/12 20/12 21/12 22/12 23/12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 6348621725312302
不良数 d
6348621725312302
不良率 p
1.2 0.6 0.8 1.6 1.2 0.4 0.2 1.4 0.4 1.0 0.6 0.2 0.4 0.6 0.0 0.4
6241301
73
1.2 0.4 0.8 0.2 0.6 0.0 0.2 0.58%
过程能力CPK
请设定参数
＝
△临界距离／3σp
允许的P= 样本量n=
2.00% 500
＝
1.3851
子组数k= 25
结论
满足
过程能力 ≥1.33
UCLp 说明栏 A分检 M反馈 R维修 S调整
CL p W工装 X换人
17 18 19 20 21 22 23 24 25
制定者
张明君
24/12 25/12 26/12 27/12 28/12 29/12 30/12 31/12 1/01
SPC常用术语
SPC常用术语1、高级统计方法（AdvancedStatisticalMethods）-比基本的统计方法更复杂的统计过程分析及控制技术，包括更高级的控制图技术、回归分析、试验设计、先进的解决问题的技术等。
2、计数型数据（AttributesData）可以用来记录和分析的定性数据，例如：要求的标签出现，所有要求的紧固件安装，经费报告中不出现错误等特性量即为计数型数据的例子。
其他的例子如一些本来就可测量（即可以作为计量型数据处理）只是其结果用简单的“是/否”的形式来记录，例如：用通过/不通过量规来检验一根轴的直径的可接受性，或一张图样上任何设计更改的出现。
计数型数据通常以不合格品或不合格的形式收集，它们通过p、np、c和u控制图来分析（参见计量型数据）。
3、均值（Average）（参见平均值Mean）数值的总和被其个数（样本容量）除，在被平均的值的符号上加一横线表示。
例如，在一个子组内的x值的平均值记为X，X（X两横）为子组平均值的平均值，X（X上加一波浪线）为子组中位数的平均值。
R为子组极差的平均值。
4、认知（AwarenesS个人对质量和生产率相互关系的理解，把注意力引导到管理义务的要求和达到持续改进的统计思想上。
5、基本的统计方法（BasicStatisticalMethods）通过使用基本的解决问题的技术和统计过程控制来应用变差理论，包括控制图的绘制和解释（适用于计量型数据和计数型数据）和能力分析。
6、二项分布（BinomialDistribution）应用于合格和不合格的计数型数据的离散型概率分布。
是p和np控制图的基础。
7、因果图（Cause-EffectDiagram）一种用于解决单个或成组问题的简单工具，它对各种过程要素采用图形描述来分析过程可能的变差源。
也被称作鱼刺图（以其形状命名）或石川图（以其发明者命名）。
8、中心线（CentralLine）控制图上的一条线，代表所给数据平均值。
SPC - 计数型数据
不合格品的数量时。 ❖ 当各子组样本容量均相等时。
np 图
❖ 计算np 图的方法
确定子组 的容量，通常为>50 个零件。 确定检验的频率。 收集数据。 确定该子组 中不合格品的数量。 在 np 图上记录有缺陷的零件数量。 在 np 图上描绘该数据。
np 图
❖ 计算 np 图控制线的示例
确定不合格品的平均数
。 在P图上描绘该值。
p图
❖ 计算P图控确定不制合格品线的平均的比 示例 率 - p
p = n1p1 + n2p2 + + nkpk n1+ n2 + nk
UCLp p 3 p (1 p ) n
LCLp p 3 p (1 p ) n
注：如果 LCL 的计算结果为负值，则 LCL 应为默认值 0 。
围的情况。
不合格数的
c图
❖ 何时使用 c 图
❖ 当数据为计数型数据时（一种可以计数的属性）。
❖ 当不合格是分布于整个产品时，如油漆部件上的缺 陷数，装配工序上的缺陷数等。
❖ 当不合格现 象可从多个来源发现，或由多种原因造 成时。
❖ 计算 c 图的方法 c 图
确保检验样本的容量都相等，如零件的数量，规定 的面积或体积。
况。
单位产品不合格数的 u图
❖ 何时使用 u 图
❖ 当数据为计数型数据时( 一种可以计数的属性 )。 ❖ 在样本容量不等的情况下，当不合格数的情况分布于整个
产品时（如油漆零件的缺陷数，装配工序的缺陷数）
❖ 当不合格现象可从多个来源发现，或由于多种原因造成时 。
单位产品不合格数的 u图
❖ 计算 图的方法
SPC - 计数型数据
课程目标
❖ 到本课程结束时，学员应能识别： 1. 计数型SPC数据控制图
np 图
❖ 计算np 图的方法
确定子组 的容量，通常为>50 个零件。 确定检验的频率。 收集数据。 确定该子组 中不合格品的数量。 在 np 图上记录有缺陷的零件数量。 在 np 图上描绘该数据。
np 图
❖ 计算 np 图控制线的示例
确定不合格品的平均数
。 在P图上描绘该值。
p图
❖ 计算P图控确定不制合格品线的平均的比 示例 率 - p
p = n1p1 + n2p2 + + nkpk n1+ n2 + nk
UCLp p 3 p (1 p ) n
LCLp p 3 p (1 p ) n
注：如果 LCL 的计算结果为负值，则 LCL 应为默认值 0 。
围的情况。
不合格数的
c图
❖ 何时使用 c 图
❖ 当数据为计数型数据时（一种可以计数的属性）。
❖ 当不合格是分布于整个产品时，如油漆部件上的缺 陷数，装配工序上的缺陷数等。
❖ 当不合格现 象可从多个来源发现，或由多种原因造 成时。
❖ 计算 c 图的方法 c 图
确保检验样本的容量都相等，如零件的数量，规定 的面积或体积。
况。
单位产品不合格数的 u图
❖ 何时使用 u 图
❖ 当数据为计数型数据时( 一种可以计数的属性 )。 ❖ 在样本容量不等的情况下，当不合格数的情况分布于整个
产品时（如油漆零件的缺陷数，装配工序的缺陷数）
❖ 当不合格现象可从多个来源发现，或由于多种原因造成时 。
单位产品不合格数的 u图
❖ 计算 图的方法
SPC - 计数型数据
课程目标
❖ 到本课程结束时，学员应能识别： 1. 计数型SPC数据控制图
SPC统计-计数型数据
• 课堂练习
– 用附录7中的数据计算np 图的 UCL 和 LCL。
– 把数据标在图上并确定是否有任何超为 出控制范围的情况。
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 当不合格是分布于整个产品时，如油漆部件 上的缺陷数，装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现，或由多 种原因造成时。
SPC统计-计数型数据
课程目标
• 到本课程结束时，学员应能识别： 1. 计数型SPC数据控制图
2. 何时使用这些图最合适
如何选择正确的SPC图
计数型 数据
P图
计算零件数 N = 固定值或变 值
Np 图
计算零件数 N = 固定值
U图
计算发生次数 N = 变值
C图
计算发生次数 N = 固定值
不合格品率 p图
• 更重要的是，当您必须了解正在检验的一组 产品中不合格品的数量时。
• 当各子组样本容量均相等时。
np 图
• 计算np 图的方法
– 确定子组 的容量，通常为>50 个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 在 np 图上记录有缺陷的零件数量。 – 在 np 图上描绘该数据。
• 在样本容量不等的情况下，当不合格数的情况分 布于整个产品时（如油漆零件的缺陷数，装配工 序的缺陷数）
• 当不合格现象可从多个来源发现，或由于多种原 因造成时。
单位产品不合格数的 u图
• 计算 u 图的方法
– 定义检验内容。 – 确定检验频率。 – 确定在该样本上发现的不合格数。 – 以样本容量除以所发现的不合格数。 – 在 u 图上记录不合格的比率。 – 在 u 图上描绘此数据。
– 用附录7中的数据计算np 图的 UCL 和 LCL。
– 把数据标在图上并确定是否有任何超为 出控制范围的情况。
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 当不合格是分布于整个产品时，如油漆部件 上的缺陷数，装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现，或由多 种原因造成时。
SPC统计-计数型数据
课程目标
• 到本课程结束时，学员应能识别： 1. 计数型SPC数据控制图
2. 何时使用这些图最合适
如何选择正确的SPC图
计数型 数据
P图
计算零件数 N = 固定值或变 值
Np 图
计算零件数 N = 固定值
U图
计算发生次数 N = 变值
C图
计算发生次数 N = 固定值
不合格品率 p图
• 更重要的是，当您必须了解正在检验的一组 产品中不合格品的数量时。
• 当各子组样本容量均相等时。
np 图
• 计算np 图的方法
– 确定子组 的容量，通常为>50 个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 在 np 图上记录有缺陷的零件数量。 – 在 np 图上描绘该数据。
• 在样本容量不等的情况下，当不合格数的情况分 布于整个产品时（如油漆零件的缺陷数，装配工 序的缺陷数）
• 当不合格现象可从多个来源发现，或由于多种原 因造成时。
单位产品不合格数的 u图
• 计算 u 图的方法
– 定义检验内容。 – 确定检验频率。 – 确定在该样本上发现的不合格数。 – 以样本容量除以所发现的不合格数。 – 在 u 图上记录不合格的比率。 – 在 u 图上描绘此数据。
如何用SPC进行统计分析
• 计算上、下控制线
• 计算R图的刻度
– 方法一：上控制界限为图总高度的2/3 – 方法二：上控制线除以2再加上上控制线
21 Process Improvement
计量型数据控制图
均值-级差控制图（x-R图）制作步骤
➢ 计算x图控制线
• 计算中心线值X：即将所有样本均值加总除以 样本数。
• 计算上、下控制线
什么是计量型数据
➢ 计量型数据来源于度量。如：长度、深度、 温度、时间等。
➢ 它可以是整数也可以是分数。不仅能告诉我 们读数是太大还是太小，更能告诉我们读数 的多少。
19 Process Improvement
计量型数据控制图
均值-级差控制图（x-R图）制作步骤
➢ 收集和记录数据
• 制作数据模板供记录数据时使用
计量型数据控制图
x-s图制作步骤
➢ 计算样本标准差 ➢ 计算样本标准差的均值s，其值为中心线
➢ 计算s图的上下控制线
➢ 计算x图的上下控制线
➢ 注：在大样本的情况下，用x-s图代替x-R图
24 Process Improvement
过程能力研究
机械容忍度与自然容忍度
➢ 机械容忍度
• 已确定的规格以容忍范围的方式来确定客户的要求， 它所度量的是机械容忍度。
采取局部措施，稳定过程。
39 Process Improvement
控制图分析
聚束分析
➢ 聚束变现为当一组样本中的一些数据点很接近时， 它们的读数也很接近。
➢ 这样的图案模式往往代表着引起变异的原因有了突 然的变化。
➢ 行动：找到引起变异的原因，分析对过程稳定性的 影响，找到特殊原因和局部解决办法，使过程稳定。
• 计算R图的刻度
– 方法一：上控制界限为图总高度的2/3 – 方法二：上控制线除以2再加上上控制线
21 Process Improvement
计量型数据控制图
均值-级差控制图（x-R图）制作步骤
➢ 计算x图控制线
• 计算中心线值X：即将所有样本均值加总除以 样本数。
• 计算上、下控制线
什么是计量型数据
➢ 计量型数据来源于度量。如：长度、深度、 温度、时间等。
➢ 它可以是整数也可以是分数。不仅能告诉我 们读数是太大还是太小，更能告诉我们读数 的多少。
19 Process Improvement
计量型数据控制图
均值-级差控制图（x-R图）制作步骤
➢ 收集和记录数据
• 制作数据模板供记录数据时使用
计量型数据控制图
x-s图制作步骤
➢ 计算样本标准差 ➢ 计算样本标准差的均值s，其值为中心线
➢ 计算s图的上下控制线
➢ 计算x图的上下控制线
➢ 注：在大样本的情况下，用x-s图代替x-R图
24 Process Improvement
过程能力研究
机械容忍度与自然容忍度
➢ 机械容忍度
• 已确定的规格以容忍范围的方式来确定客户的要求， 它所度量的是机械容忍度。
采取局部措施，稳定过程。
39 Process Improvement
控制图分析
聚束分析
➢ 聚束变现为当一组样本中的一些数据点很接近时， 它们的读数也很接近。
➢ 这样的图案模式往往代表着引起变异的原因有了突 然的变化。
➢ 行动：找到引起变异的原因，分析对过程稳定性的 影响，找到特殊原因和局部解决办法，使过程稳定。
计数型SPC
由题意知: n1=n2=n3…nk=50 p= 0.2729
第十八页，共39页。
创建
(chuàngjiàn)P
图
第十九页，共39页。
08-10
P图练习(liànxí)1
打开(dǎ kāi):P1.mtw
第二十页，共39页。
选项及结果(jiē
guǒ)
第二十一页，共39页。
08-11
P图练习
(liànxí)2
。通过在一个计数型控制图上展示缺陷模式,它可以用来(yònɡ lái)确定
模式 中的变化是由普便原因引起
或是由特殊原因引起.
＊在技术和服务领域皆可应用. 。技术: 使用p图和np图
。服务: 使用c图和u图
最大的困难是决定不良品
第七页，共39页。
08-4
计量型控制图的优点 (yōudiǎn)&缺点
＊优点 。收集数据不用花费太多的时间和成本 。当对某一过程的关键输入变量不了解,但已确定客户要求及建立检验系
＊计数或离散型数据 。数据由记数或分类产生(好/不好(bù hǎo),合格/不合格/通过/通过)
＊数据的取值为有限个数
第三页，共39页。
08-2
计数(jìshù)型 术语
＊ 缺陷: 。不满足规格要求的质量特性 。一个产品会具有一个或多个缺陷 。 它可能(kěnéng)会也可能(kěnéng)不会影响产品性能或对客户规格的
例题(lìtí)1: Minitab创建P图
打开文件ATC.mtw
1.选择图表类型: p-chart 2.选择变量(biànliàng):不良 品数
第十五页，共39页。
08-8
例题(lìtí)1: Minitab创建P图
Proportion
第十八页，共39页。
创建
(chuàngjiàn)P
图
第十九页，共39页。
08-10
P图练习(liànxí)1
打开(dǎ kāi):P1.mtw
第二十页，共39页。
选项及结果(jiē
guǒ)
第二十一页，共39页。
08-11
P图练习
(liànxí)2
。通过在一个计数型控制图上展示缺陷模式,它可以用来(yònɡ lái)确定
模式 中的变化是由普便原因引起
或是由特殊原因引起.
＊在技术和服务领域皆可应用. 。技术: 使用p图和np图
。服务: 使用c图和u图
最大的困难是决定不良品
第七页，共39页。
08-4
计量型控制图的优点 (yōudiǎn)&缺点
＊优点 。收集数据不用花费太多的时间和成本 。当对某一过程的关键输入变量不了解,但已确定客户要求及建立检验系
＊计数或离散型数据 。数据由记数或分类产生(好/不好(bù hǎo),合格/不合格/通过/通过)
＊数据的取值为有限个数
第三页，共39页。
08-2
计数(jìshù)型 术语
＊ 缺陷: 。不满足规格要求的质量特性 。一个产品会具有一个或多个缺陷 。 它可能(kěnéng)会也可能(kěnéng)不会影响产品性能或对客户规格的
例题(lìtí)1: Minitab创建P图
打开文件ATC.mtw
1.选择图表类型: p-chart 2.选择变量(biànliàng):不良 品数
第十五页，共39页。
08-8
例题(lìtí)1: Minitab创建P图
Proportion
生产过程质量控制技术之SPC
是
是
样本容量是 否 否恒定？
使用p图
样本容量是 否桓定？
否
使用u图
是
是
使用np或p图
性质上是否是均
匀或不能按子组
取样—例如：化 否 学槽液、批量油
子组均值是 否 否能很方便
漆等？
地计算？
使用c或u图
使用中 位数图
是
使用单值图
是
X-MR
接上页
子组容量
否
是否大于
或等于9？
是
是否能方便
否
地计算每个
子组的S值？
过程的单个输出之间不可避免的差别；变差的原因 变差（Variation） 可分为两类：普通原因和特殊原因。
特殊原因 （Special Cause）
一种间断性的，不可预计的，不稳定的变差根源。 有时被称为可查明原因，它存在的信号是：存在超 过控制限的点或存在在控制限之内的链或其它非随 机性的图形。
2.3 术语解释——SPC常用术语
因引起的正常波动, 但不能告知此异常是什么因素引 起的
2. SPC的基本概念
2.2 SPC 可以做什么?
1、确保制程持续稳定、可预测。 2、提高产品质量、生产能力、降低成本。 3、为制程分析提供依据。 4、区分变差的特殊原因和普通原因，作为采取局
部措 施或对系统采取措施的指南。
2.3 术语解释——六西格玛术语
是
使用
X— s图
注：本图假设测量系统 已经过评价并且是适用 的。
使用 X—R图
使用 X—R图
4. SPC控制图的制作
SPC-Statistical Process Control
应用SPC控制图的5个步骤
1-样本准备阶段
【品质管理资料】SPC常用术语(doc 17)精编版
SPC常用术语1、高级统计方法（Advanced Statistical Methods）-比基本的统计方法更复杂的统计过程分析及控制技术，包括更高级的控制图技术、回归分析、试验设计、先进的解决问题的技术等。
2、计数型数据（Attributes Data）可以用来记录和分析的定性数据，例如：要求的标签出现，所有要求的紧固件安装，经费报告中不出现错误等特性量即为计数型数据的例子。
其他的例子如一些本来就可测量（即可以作为计量型数据处理）只是其结果用简单的“是/否”的形式来记录，例如：用通过/不通过量规来检验一根轴的直径的可接受性，或一张图样上任何设计更改的出现。
计数型数据通常以不合格品或不合格的形式收集，它们通过p、np、c和u 控制图来分析（参见计量型数据）。
3、均值（Average）（参见平均值Mean）数值的总和被其个数（样本容量）除，在被平均的值的符号上加一横线表示。
例如，在一个子组内的x值的平均值记为X，X（X两横）为子组平均值的平均值，X（X上加一波浪线）为子组中位数的平均值。
R 为子组极差的平均值。
4、认知（AwarenesS个人对质量和生产率相互关系的理解，把注意力引导到管理义务的要求和达到持续改进的统计思想上。
5、基本的统计方法（Basic Statistical Methods）通过使用基本的解决问题的技术和统计过程控制来应用变差理论，包括控制图的绘制和解释（适用于计量型数据和计数型数据）和能力分析。
6、二项分布（Binomial Distribution）应用于合格和不合格的计数型数据的离散型概率分布。
是p和np控制图的基础。
7、因果图（Cause-Effect Diagram）一种用于解决单个或成组问题的简单工具，它对各种过程要素采用图形描述来分析过程可能的变差源。
也被称作鱼刺图（以其形状命名）或石川图（以其发明者命名）。
8、中心线（Central Line）控制图上的一条线，代表所给数据平均值。
SPC精髓总结汇总
SPC精髓总结汇总目录：一、SPC基础知识介绍二、计量型数据控制图：X-R 图三、其它计量型数据控制图四、计数型数据控制图：P 图五、其它计数型数据控制图六、停止灯控制图一、SPC基础知识介绍1、什么是SPC⏹统计过程控制（Statistical Process Control）⏹第二版2005年7月发布（1992/2005）⏹版权由戴姆勒克莱斯勒公司、福特汽车公司和通用汽车公司所有2、SPC的目的利用统计技术：控制过程、持续改进过程3、常见的统计技术⏹旧QC七大手法：柏拉图、因果分析图、直方图、查检表、分层法、控制图、散布图⏹新QC七大手法：亲和图法、关联图法、系统图法、矩阵图法、矩阵分、析法、PDPC法、箭形图解法4、SPC与检验的区别⏹检验：是事后的行为（产品生产后将不合格品挑选出来），是容忍浪费⏹SPC：是事前或事中的行为（在生产前或生产中有些控制和调整五大生产要素，以避免不合格品的产生），是避免浪费5、正态分布图6、变差的普通原因⏹普通原因：始终作用于过程的变差的原因为变差的普通原因⏹例如：一个机加工轴的直径易于受到由于机器（间隙、轴承磨损）、工具（强度、磨损率）、材料（直径、硬度）、操作人员（进给速率、对中准确度）、维修（润滑、易损零件的更换）及环境（温度、动力供应是否恒定）等原因造成潜在的变差的影响⏹针对普通原因的对策：对系统采取措施⏹通常用来消除变差的普通原因⏹几乎总是要求管理措施，以便纠正⏹大约可纠正85%的过程7、变差的特殊原因⏹特殊原因：不是始终作用于过程的变差的原因⏹即当它们出现时将造成（整个）过程的分布改变。
由于特殊原因造成的过程分布的改变有些有害，有些有利⏹针对特殊原因的对策：局部措施⏹通常用来消除变差的特殊原因⏹通常由与过程直接相关的人员实施⏹大约可纠正15%的过程问题8、控制图的构成USL 上规格线UCL ----------------------------------------------------------------------上控制线CL 中线 LCL ----------------------------------------------------------------------下控制线 LSL 下规格线9、 控制图的类型1、计量型数据控制图1.1、均值和极差图（ R X -图） 1.2、均值和标准差图（s X -图）1.3、中位数图（R X -~图）1.4、单值和移动极差图（ MR X -图） 2、计数型数据控制图2.1、不合格品率控制图（P 图） 2.2、不合格品数控制图（NP 图） 2.3、不合格数控制图（C 图）2.4、单位产品不合格数控制图（U 图）二计量型数据控制图：R X - 图1、 实施步骤A.收集数据:子组大小/子组频率/子组数的大小B.计算控制限:初始控制线/延长控制线C.过程控制解释:4种异常情况的判定及对策D.过程能力解释:PPK/CPK 的计算及要求2、 子组大小⏹ 子组:每次连续取样的样本⏹ 子组大小:每次连续取样的样本数量⏹ 确定子组大小的原则:— 子组要合理,一般为2-10个、— 一个子组内的变差代表很短时间内的零件的变差 — 非常相似的生产条件下生产出来的,相互间不存在其 它的系统的关系— 每个子组内的变差主要应是普通原因造成3、 子组频率⏹ 子组频率:每次取样的间隔时间 ⏹ 确定子组频率的原则:— 在适当的时间收集足够的子组来反映过程中的变化 — 过程的初期研究,很短的时间间隔进行分组,以便发觉 短时间的不稳定因子— 当证明过程已处于稳定状态下(或已对过程进行改 善),子组间的时间间隔可以增加 4、子组数大小⏹ 子组数大小:每张控制图的控制点数量 ⏹ 确定子组数大小的原则:— 在初始阶段不低于100个单值数据 — 在量产阶段一般不少于25个点 5、过程控制解释1、超出控制限的点2、连续7点位于平均值的一侧3、连续7点上升(后点等于或大于前点)或下降4、明显的非随机图形(大约2/3的描点应落在控制限的中间三分之一的区域内,大约1/3的点落在其外的三分之二的区域)6、异常情况对策⏹ 当发现异常时，不要随意对过程做不必要的改变 ⏹ 正确的做法是：— 记录下当时的六大生产要素：人/机/料/法/环/测— 进行原因分析后，若能找到原因采取措施，则记录好所 采取的措施— 进行原因分析后，若不能找到原因采取措施，则密切观察过程的变化 7、过程能力解释⏹ PPK:初始过程能力指数PPK,也叫性能指数,或短期过程能力指数 ⏹ 其要求是：PPK ＞1.67或满足顾客的要求⏹ 计算公式为：Ppk=min( ss XUSL LSL X σσˆ3,ˆ3-- ) s ni I n X X S σˆ1)(12=--=∑= ⏹计算数据为：最少100个数据以上⏹ 计算时间：小批量试生产阶段,为PPAP 重要文件之一,需要提交给顾客 ⏹ CPK:稳定的过程能力指数CPK,也叫长期过程能力指数 ⏹其要求是：CPK ＞1.33或满足顾客要求⏹ 计算公式为:Cpk=min(22ˆ3,ˆ3R R XUSL LSL X σσ-- )⏹ 计算数据为:最好是25组⏹ 计算时间：批量生产阶段,按照控制计划的规定,一般是每张控制图完成后三、其它计量型数据控制图1、均值和标准差控制图⏹标准差s是过程变异性更有效的指针,尤其是对于样本容量较大（n＞10）的情况,一般来说,当出现下列一种或多种情况时用s图代替R图:⏹数据是由计算机按实时时序记录和/或描图的,则s的计算程序容易集成化⏹有方便适用的袖珍计算器使s的计算能简单按程序算出⏹使用子组样本容量较大,更有效的变差量度是合适的2、中位数控制图⏹中位数图用在子组的样本容量小于或等于10的情况,样本容量为奇数时更方便⏹如果子组样本容量为偶数,中位数是中间两个数的均值3、单值和移动极差控制图⏹测试一个产品的数据所化时间很长⏹所选取的样本,属于一种极为均匀一致之产品如像液体或气体,测量几个和一个一样⏹加工一个产品的时间很长⏹产品价值很高,测试一个样本会损失很多钱⏹属破坏性试验,每测试一个产品,就损失一个⏹控制过程参数,如:温度﹑压力﹑时间等四、计数型数据控制图：P图1、不合格品率（P图）实施步骤：A.收集数据:子组大小/子组频率/子组数的大小B.计算控制限:初始控制线/延长控制线C.过程控制解释:4种异常情况的判定及对策D.过程能力解释:产品合格率或不合格率2、子组大小⏹子组:每次连续取样的样本⏹子组大小:每次连续取样的样本数量⏹确定子组大小的原则：●子组要大,如50个到200，甚至更多，以便检验出性能的一般变化●一个子组内要包括几个不合格品●每一个子组代表很长的一段时间的过程操作●子组容量分为恒定或它们变化不超过±25％，以及超出±25%二种图形3、子组频率⏹子组频率:每次取样的间隔时间⏹确定子组频率的原则:—应根据产品的周期确定分组的频率以便帮助分析和纠正发现的问题﹒时间间隔短则反馈快﹐但也许与大的子组容量要求矛盾—一般为每班或每天，用于全检工位的较多4、子组数大小⏹为了子组数大小:每张控制图的控制点数量⏹确定子组数大小的原则：—在初始阶段不低于100个单值数据—在量产阶段一般不少于25个点5、过程控制解释1、超出控制限的点2、连续7点位于平均值的一侧3、连续7点上升(后点等于或大于前点)或下降4、明显的非随机图形(大约的描点应落在控制限的中间三分之一的区域内,大约的点落在其外的三分之二的区域)6、过程能力解释⏹如果对于计数型控制图﹐能力直接被定义为不合格品的平均百分数或比例，如PPM（百万分之一）⏹而计量型控制图的能力指的是将／或不将过程的中心调整到规范的目标值后﹐用PPK和CPK表示五、其它计数型数据控制图1、不合格品数控制图（np图）⏹np图用来衡量一个检验中的不合格（不符合或所谓的缺陷）品的数量⏹与p图不同﹐np图表示不合格品的实际数量而不是与样本的比率⏹p图和np图适用的基本情况相同﹐当满足下列情况时可选用np图—不合格品的实际数量比不合格品率更有意义或更容易报告—各阶段子组的样本容量相同2、不合格数控制图（c图）⏹c图用来测量一个检验批内的不合格（或缺陷）的数量（与描在np图上的不合格品的数量不同）⏹c图要求样本的容量恒定或受检材料的数量恒定﹐它主要应用于以下两类检验﹕—不合格分布在连续的产品流上（例如每匹维尼龙上的瑕疵﹐玻璃上的气泡或电线上绝缘层薄的点）—在单个的产品检验中可能发现许多不同潜在原因造成的不合格3、单位产品不合格数控制图（u图）⏹u图是用来测量具有容量不同的样本（受检材料的量不同）的子组内每检验单位产品之内的不合格数量⏹除了不合格数是按每单位产品为基本量表示以外﹐它是与c图相似的⏹u图和c图适用于相同的数据情况﹐但如果样本含有多于一个“单位产品”的量﹐为使报告值更有意义时﹐可以使用u图六、停止灯控制图1、停止灯控制图的概念⏹无论在停止灯控制图中，目标值区域指定为绿色，警告区域指定为黄色，停止区域指定为红色。
计数型数据SPC
2、计算过程能力的度量指数 对于各计数值数据控制图，能力计算指数如下表：
计数型数据SPC
4
过程能力的度量
控制图种类 P图 Pn图 U图 C图
能力指数
P
P
U
C
计算公式
k
pni
P i1 N
k
pni
P i1 N
k
ci
U i1 N
k
ci
C i1 N
计数型数据SPC
5
过程能力的度量
上图计算公式中 K=子组数
计数型数据SPC
3
过程能力的度量
1、计数值数据控制图控制对象的过程能力的解释计 数值数据控制图的过程能力与计算值数据有所不 同，计数值数据控制图上的所有点直接表明了不 符合客户要求的百分数或不合格品数(或缺陷数)， 而计量值数据控制图上的所有点显示的是过程实 际生产的产品与规格比较的结果。计数值数据控 制图控制对象的过程能力定义为不合格品，缺陷 数的平均不合格率或缺陷率。
制作P图前的准备 为了P图能顺利制作并发挥其应用作用，
在制作P图前应做以下准备： 1.取得高层对推行控制图的认可与支持。 2.确定需用P图控制的过程和特性。 3.定义测量系统。 4.消除明显的过程偏差。
计数型数据SPC
7
控制P控制图
正确制作P控制图，是进行过程控制及改善的基础， 制作P控制图的流程如下： 1、收集数据 (1)进行测量系统分析 (2)确定子组样本容量 一般而言，P图的每个子组的样本容量需大于50。 (3)确定子组额率 适当的子组频率可以区分特殊原因引起的过程变化， 在确定抽样频率时需综合考虑过程稳定性和经济性。 一般而言，P图的子组间时间间隔不可过大。 (4)确定子组数 一般来说，要求子组在25个以上，这样可以全面检 验过程的稳定性。
计数型数据SPC
4
过程能力的度量
控制图种类 P图 Pn图 U图 C图
能力指数
P
P
U
C
计算公式
k
pni
P i1 N
k
pni
P i1 N
k
ci
U i1 N
k
ci
C i1 N
计数型数据SPC
5
过程能力的度量
上图计算公式中 K=子组数
计数型数据SPC
3
过程能力的度量
1、计数值数据控制图控制对象的过程能力的解释计 数值数据控制图的过程能力与计算值数据有所不 同，计数值数据控制图上的所有点直接表明了不 符合客户要求的百分数或不合格品数(或缺陷数)， 而计量值数据控制图上的所有点显示的是过程实 际生产的产品与规格比较的结果。计数值数据控 制图控制对象的过程能力定义为不合格品，缺陷 数的平均不合格率或缺陷率。
制作P图前的准备 为了P图能顺利制作并发挥其应用作用，
在制作P图前应做以下准备： 1.取得高层对推行控制图的认可与支持。 2.确定需用P图控制的过程和特性。 3.定义测量系统。 4.消除明显的过程偏差。
计数型数据SPC
7
控制P控制图
正确制作P控制图，是进行过程控制及改善的基础， 制作P控制图的流程如下： 1、收集数据 (1)进行测量系统分析 (2)确定子组样本容量 一般而言，P图的每个子组的样本容量需大于50。 (3)确定子组额率 适当的子组频率可以区分特殊原因引起的过程变化， 在确定抽样频率时需综合考虑过程稳定性和经济性。 一般而言，P图的子组间时间间隔不可过大。 (4)确定子组数 一般来说，要求子组在25个以上，这样可以全面检 验过程的稳定性。
SPC常用术语汇编(doc 19)
SPC常用术语汇编(doc 19)部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑SPC常用术语1、高级统计方法（Advanced Statistical Methods）-比基本的统计方法更复杂的统计过程分析及控制技术，包括更高级的控制图技术、回归分析、试验设计、先进的解决问题的技术等。
2、计数型数据（Attributes Data）可以用来记录和分析的定性数据，例如：要求的标签出现，所有要求的紧固件安装，经费报告中不出现错误等特性量即为计数型数据的例子。
其他的例子如一些本来就可测量（即可以作为计量型数据处理）只是其结果用简单的“是/否”的形式来记录，例如：用通过/不通过量规来检验一根轴的直径的可接受性，或一张图样上任何设计更改的出现。
计数型数据通常以不合格品或不合格的形式收集，它们通过p、np、c和u控制图来分析（参见计量型数据）。
3、均值（Average）（参见平均值Mean）数值的总和被其个数（样本容量）除，在被平均的值的符号上加一横线表示。
例如，在一个子组内的x值的平均值记为X，X（X两横）为子组平均值的平均值，X（X上加一波浪线）为子组中位数的平均值。
R为子组极差的平均值。
4、认知（AwarenesS个人对质量和生产率相互关系的理解，把注意力引导到管理义务的要求和达到持续改进的统计思想上。
5、基本的统计方法（Basic Statistical Methods）通过使用基本的解决问题的技术和统计过程控制来应用变差理论，包括控制图的绘制和解释（适用于计量型数据和计数型数据）和能力分析。
6、二项分布（Binomial Distribution）应用于合格和不合格的计数型数据的离散型概率分布。
是p和np控制图的基础。
7、因果图（Cause-Effect Diagram）一种用于解决单个或成组问题的简单工具，它对各种过程要素采用图形描述来分析过程可能的变差源。
也被称作鱼刺图（以其形状命名）或石川图（以其发明者命名）。
SPC计数型
当样本数量太大，控制上下限会很窄，大部份数据会 超出范围， 当样本品数量太少，数量很多会是零。 缺点和不合格通常会以排列图来找出重要的少数 要真正减低缺点数或不合格品数通常需要在系统上改变 任何工序上的改变必须记录在控制图上
9
使用控制图的准备工作
1. 建立适合行动的环境 2. 确定工序 3. 确定要管理的特性
2
ATTRIBUTES CONTROL CHART 计数值控制图
• 对于必须收集数据,亦只需要简单的量具(通过 /不通过)
很多向管理层汇报的数据都是计数值的 • 使用控制图可以清楚区分和分析普通原因和
特殊原因 • 计数值控制图只需绘划一张图表 有4种主要计数值控制图
3
ATTRIBUTES CONTROL CHART 计数值控制图
U图
P P C
U
24
控制图的选择
决定要控制 的特性
数据是 计量化 的吗？
是否对不合
否
格品数量有
否
兴趣，如“坏”
零件的百
分比
是
抽样量 是否固定？
否 采用 P图
是
采用nP 或P图
是否对不 合格缺点 有兴趣，如 不符合或
零件？
是
抽样量 否 采用
是否固定？
U图
是 采用C图 或U图
25
性质是否 一致，是否 有利于抽 样分组如 化学浴，油 漆批量等？
考虑 - 客户的需要 - 目前存在的和潜在的问题 - 特性的相互关系 4.以操作角度确定测量系统 5.减少不必要的变化
10
P CHART 不合格品比例图
np - 不合格品数 n - 样本数量 k - 样本的个数 p - 不合格品比例 P - 所有P值的平均数 n - 样本的平均数 UCLp - 控制上限 LCLp - 控制下限
9
使用控制图的准备工作
1. 建立适合行动的环境 2. 确定工序 3. 确定要管理的特性
2
ATTRIBUTES CONTROL CHART 计数值控制图
• 对于必须收集数据,亦只需要简单的量具(通过 /不通过)
很多向管理层汇报的数据都是计数值的 • 使用控制图可以清楚区分和分析普通原因和
特殊原因 • 计数值控制图只需绘划一张图表 有4种主要计数值控制图
3
ATTRIBUTES CONTROL CHART 计数值控制图
U图
P P C
U
24
控制图的选择
决定要控制 的特性
数据是 计量化 的吗？
是否对不合
否
格品数量有
否
兴趣，如“坏”
零件的百
分比
是
抽样量 是否固定？
否 采用 P图
是
采用nP 或P图
是否对不 合格缺点 有兴趣，如 不符合或
零件？
是
抽样量 否 采用
是否固定？
U图
是 采用C图 或U图
25
性质是否 一致，是否 有利于抽 样分组如 化学浴，油 漆批量等？
考虑 - 客户的需要 - 目前存在的和潜在的问题 - 特性的相互关系 4.以操作角度确定测量系统 5.减少不必要的变化
10
P CHART 不合格品比例图
np - 不合格品数 n - 样本数量 k - 样本的个数 p - 不合格品比例 P - 所有P值的平均数 n - 样本的平均数 UCLp - 控制上限 LCLp - 控制下限
SPC-计数型数据控制图
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 2片
如何选择正确的SPC图
计数型 数据
P图
Np 图
U图
C图
计算零件数
N = 固定值或变 值
计算零件数 N = 固定值
计算发生次数 N = 变值
计算发生次数 N = 固定值
World Class Quality Pty Ltd - 1999年9月
第 4片
p图
• 计算 p 图的方法
– 确定子组 的容量，一般大于50个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 把有缺陷的产品的数量记录在P图上。 – 确定有缺陷零件的比率，即有缺陷零件的数量／子组 中
的零件数量。 – 在P图上描绘该值。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 11 片
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 当不合格是分布于整个产品时，如油漆部件 上的缺陷数，装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现，或由多 种原因造成时。
World Class Quality Pty Ltd - 1999年9月
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 7片
不合格品数的
np 图
• 何时使用 np 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 更重要的是，当您必须了解正在检验的一组 产品中不合格品的数量时。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
模块 11 - SPC 计数型数据
第 13 片
c图
• 计算 c 图控制线的示例
确定不合格平均数 c
c = c1 + c2 ++ ck k UCLc c 3 c
LCLc c 3 c
其中 k 为子组 数。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
•
精益求精，追求卓越，因为相信而伟 大。2020年11月16日 星期一 下午9时 23分6秒21:23:0620.11.16
•
让自己更加强大，更加专业，这才能 让自己 更好。2020年11月下 午9时23分20.11.1621:23November 16, 2020
•
这些年的努力就为了得到相应的回报 。2020年11月16日星 期一9时 23分6秒21:23:0616 November 2020
LCLnp np 3 np(1 ) n
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 10 片
np 图
• 课堂练习
– 用附录7中的数据计算np 图的 UCL 和 LCL。
– 把数据标在图上并确定是否有任何超为 出控制范围的情况。
World Class Quality Pty Ltd - 1999年9月
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 8片
np 图
• 计算np 图的方法
– 确定子组 的容量，通常为>50 个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 在 np 图上记录有缺陷的零件数量。 – 在 np 图上描绘该数据。
• 当数据为计数型数据时( 一种可以计数的属性 )。
• 在样本容量不等的情况下，当不合格数的情况分 布于整个产品时（如油漆零件的缺陷数，装配工 序的缺陷数）
• 当不合格现象可从多个来源发现，或由于多种原 因造成时。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 4片
p图
• 计算 p 图的方法
– 确定子组 的容量，一般大于50个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 把有缺陷的产品的数量记录在P图上。 – 确定有缺陷零件的比率，即有缺陷零件的数量／子组 中
的零件数量。 – 在P图上描绘该值。
World Class Quality Pty Ltd - 1999年9月
n
注：如果 LCL 的计算结果为负值，则 LCL 应为默认值 0 。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 6片
p图
• 课堂练习
– 用附录5中的数据计算P 图的 UCL 和 LCL 。
– 把数据标在图上并确定是否有任何超出 控制范围的情况。
•
日复一日的努力只为成就美好的明天 。21:23:0621:23:0621:23Monday, November 16, 2020
•
安全放在第一位，防微杜渐。20.11.1620.11.1621:23:0621:23:06November 16, 2020
•
加强自身建设，增强个人的休养。2020年11月16日 下午9时 23分20.11.1620.11.16
模块 11 - SPC 计数型数据
第 17 片
单位产品不合格数的 u图
• 计算 u 图控制线的示例
确定单位产品的平均不合格数 u
u u u u =
1+ 2 ++ k n1 + n2 + nk
UCLu u 3 u n
其中 c1, c2 等为 单位产品的不合 格数，n1, n2 等 为相应的样本容 量。
LCLu u 3 u n
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 18 片
单位产品不合格数的 u图
• 课堂练习
– 用附录8中的数据计算 u 图的 UCL 和 LCL。
– 在图上描绘数据并确定任何超出控 制范围的情况。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 5片
p图
• 计算P图控制线的示例
确定不合格品的平均比率 - p
p
=
n1p1 + n2p2 + + nkpk n1 + n2 +nk
p(1 p) UCLp p 3
n
注: n1p1 等是所发现 的不合格产品的数量 ，n1, n2 等是相应的 样品容量。
p(1 p) LCLp p 3
模块 11 - SPC 计数型数据
第 19 片
•
生活中的辛苦阻挠不了我对生活的热 爱。20.11.1620.11.16Monday, November 16, 2020
•
人生得意须尽欢，莫使金樽空对月。21:23:0621:23:0621:2311/16/2020 9:23:06 PM
•
做一枚螺丝钉，那里需要那里上。20. 11.1621 :23:062 1:23No v-2016 -No v-2 0
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 9片
np 图
• 计算 np 图控制线的示例
确定不合格品的平均数量 - np
k np = np1 + np2 ++ npk
其中k为子组数 ，n为这些子组 的样本容量。
UCLnp np 3 np(1 np ) n np
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 7片
不合格品数的
np 图
• 何时使用 np 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 更重要的是，当您必须了解正在检验的一组 产品中不合格品的数量时。
• 当各子组样本容量均相等时。
模块 11 - SPC 计数型数据
第 11 片
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时（一种可以计数的属 性）。
• 当不合格是分布于整个产品时，如油漆部件 上的缺陷数，装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现，或由多 种原因造成时。
World Class Quality Pty Ltd - 1999年9月
第 14 片
c图
• 课堂练习
– 用附录7中的数据计算c 图的 UCL 和 LCL。
– 在图上描绘该数据并确定任何超出控制 范围的情况。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 15 片
单位产品不合格数的 u图
• 何时使用 u 图
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 2片
如何选择正确的SPC图
计数
C图
计算零件数
N = 固定值或变 值
计算零件数 N = 固定值
计算发生次数 N = 变值
计算发生次数 N = 固定值
World Class Quality Pty Ltd - 1999年9月
•
爱情，亲情，友情，让人无法割舍。20.11.162020年 11月16日星期 一9时23分6秒 20.11.16
谢谢大家！
模块 11 - SPC 计数型数据
第片
SPC - 计数型数据
模块 11
编制: World Class Quality Pty Ltd 授课人: John Adamek
World Class Quality Pty Ltd - 1999
1
年9月
课程目标
• 到本课程结束时，学员应能识别： 1. 计数型SPC数据控制图
2. 何时使用这些图最合适
第 16 片
单位产品不合格数的 u图
• 计算 u 图的方法
– 定义检验内容。 – 确定检验频率。 – 确定在该样本上发现的不合格数。 – 以样本容量除以所发现的不合格数。 – 在 u 图上记录不合格的比率。 – 在 u 图上描绘此数据。
World Class Quality Pty Ltd - 1999年9月
•
科学，你是国力的灵魂；同时又是社 会发展 的标志 。下午9时23分 6秒下 午9时23分21:23:0620.11.16
•
每天都是美好的一天，新的一天开启 。20.11.1620.11.1621:2321:23:0621:23:06Nov-20
•
相信命运，让自己成长，慢慢的长大 。2020年11月16日星 期一9时 23分6秒Monday, November 16, 2020
模块 11 - SPC 计数型数据
第 12 片
c图
• 计算 c 图的方法
– 确保检验样本的容量都相等，如零件的数量，规定 的面积或体积。
– 确定检验频率。 – 确定在该样本上发现的不合格数。 – 把该不合格数记录在 c 图上。 – 在 c 图上描绘该数据。
World Class Quality Pty Ltd - 1999年9月