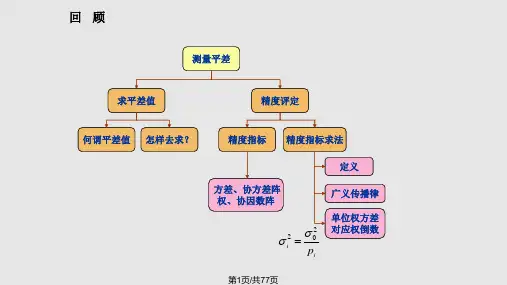
专题3-_平差数学模型与最小二乘原理(实习用—概论与开始统讲)精品PPT课件
- 格式：pptx
- 大小：896.79 KB
- 文档页数：37
下载文档原格式
合集下载
第四章平差数学模型与最小二乘法
图4-2
几何模型中选定元素多于必要元素的元素 2、多余元素——几何模型中选定元素多于必要元素的元素 多余元素 几何模型中选定元素 当几何模型中选定的元素多余必要元素数t 当几何模型中选定的元素多余必要元素数t时，独立量间会产生一个几 作为必要元素， 作为必要元素，则能唯一地确定 ~ ~ ~ ~ ~ ~ ~ ∆ABC形状与大小 。若选定了 L 1、 L 2 、 L 3 和 S 2 ，则有 L1 + L2 + L3 = 180° 形状与大小
函数模型又分为线性模型和非线性模型两类，非线性模型要线性化。 函数模型又分为线性模型和非线性模型两类，非线性模型要线性化。
一、条件平差法的函数模型
条件平差法： 观测值的真值构成的条件方程为函数模型的平差方法。 条件平差法：以观测值的真值构成的条件方程为函数模型的平差方法。 构成的条件方程为函数模型的平差方法 例如，在图 所示水准网中 所示水准网中， 为已知其高程的水准点 为已知其高程的水准点， 、 、 均为 例如，在图4-2所示水准网中，A为已知其高程的水准点，B、C、D均为 未知点。 未知点。网中观测向量的真值为 ~ ~ ~ ~ ~ ~ ~ T L = h1 h2 h3 h4 h5 h6
r ,n n,1 r ,1 r ,1
~ 为常数向量， A0为常数向量，将 L = L + ∆
代入上式， 代入上式，并令
W = AL + A0
(4-2-5) (4-2-6)
则有
A∆ +W = 0
多余观测数r。 （4-2-4）或（4-2-6）式为条件平差的函数模型。条件方程数 多余观测数 。 ） ）式为条件平差的函数模型。条件方程数=多余观测数
若用观测值组成上述两个条件方程，; L2 + L3 − 180° = ω ≠ 0
几何模型中选定元素多于必要元素的元素 2、多余元素——几何模型中选定元素多于必要元素的元素 多余元素 几何模型中选定元素 当几何模型中选定的元素多余必要元素数t 当几何模型中选定的元素多余必要元素数t时，独立量间会产生一个几 作为必要元素， 作为必要元素，则能唯一地确定 ~ ~ ~ ~ ~ ~ ~ ∆ABC形状与大小 。若选定了 L 1、 L 2 、 L 3 和 S 2 ，则有 L1 + L2 + L3 = 180° 形状与大小
函数模型又分为线性模型和非线性模型两类，非线性模型要线性化。 函数模型又分为线性模型和非线性模型两类，非线性模型要线性化。
一、条件平差法的函数模型
条件平差法： 观测值的真值构成的条件方程为函数模型的平差方法。 条件平差法：以观测值的真值构成的条件方程为函数模型的平差方法。 构成的条件方程为函数模型的平差方法 例如，在图 所示水准网中 所示水准网中， 为已知其高程的水准点 为已知其高程的水准点， 、 、 均为 例如，在图4-2所示水准网中，A为已知其高程的水准点，B、C、D均为 未知点。 未知点。网中观测向量的真值为 ~ ~ ~ ~ ~ ~ ~ T L = h1 h2 h3 h4 h5 h6
r ,n n,1 r ,1 r ,1
~ 为常数向量， A0为常数向量，将 L = L + ∆
代入上式， 代入上式，并令
W = AL + A0
(4-2-5) (4-2-6)
则有
A∆ +W = 0
多余观测数r。 （4-2-4）或（4-2-6）式为条件平差的函数模型。条件方程数 多余观测数 。 ） ）式为条件平差的函数模型。条件方程数=多余观测数
若用观测值组成上述两个条件方程，; L2 + L3 − 180° = ω ≠ 0
武汉大学平差第2章平差数学模型PPT课件
增加一个条件方程，因此，共需列 出c=r+u个条件方程，以含有参数
将 L ~L 代入上式，并令
的条件方程为平差函数模型的平差
W(AL A0)
方法，称为附有参数的条件平差法。
参见书中例子。
则得
ABX ~W0
cnn1 cuu1 c1
20.12.2020
上式为附有参数的条件平差的函数 模型。建模方法：找出观测值真值 之间或观测值与参数真值之间应该 满足的 C 个关系式。
一般而言，如果某一平差问题中,观测值
个数为n，必要观测个数为t，多余
观 测 个 数 为 r=n-t ， 再 增 选 u 个 独 立
参 数 ， u=t ， 则 总 共 应 列 出
c=r+u=n 个 函 数 关 系 式 ， 其 一 般 形
式为
L~ F(X~)
n1
或：
L~BX~d
n1 nt t1 n1
将 L ~L代入上式，并令
写成矩阵形式
VTPV VTVmin
将上式对取一阶导数，并令其为零，得
1
dVTV
dxˆ
2VT
B2VT
1 1
2
n 1
vi
0
1 L1
V
n1
1 xˆ
L2
B
n1
xˆ
L
n1
1 Ln
按最小二乘准则，要求：
将 vi xˆLi 代入上式得
n
n
n
vi (x ˆLi)nx ˆLi 0
1
1
1
xˆ 1
C~ xW0
suu1 s1
l LF(X0) B~ xl
n1 ntt1 n1
20.12.2020
第二章测量平差的数学模型及最小二乘原理
5
§2.1 测量平差概述
如图所示水准网，试在以下两种给定几何模型情况下 确定必要元素：
（1）确定A、B、C、D四点间的相对高度：
h1
HB B
h1 h3 h4
h1 h5 h4
（2）确定A、B、C、D四点的高程：
h1 h3 h4
HA
A HA
h4
D
HD
h3
C h6
HC
h5 h2
第二章 测量平差的数学模型及最小二乘原理
L1 L2 L1 L2 S3 L1 L2 S3
L1 L3 S1 S2 L3
XY
L2 L3 S1 S2 S3
必要观测个数： t
C
必要观测元素的特点
L3
S2
S1
给定几何模型，必要观测元素数量及
类型即定，与实际观测量无关； 必要观测元素必须是函数独立量。
A L1 S3
L2 B
第二章 测量平差的数学模型及最小二乘原理
XI’AN UNIVERSITY OF SCIENCE & TECHNOLOGY
第二章 测量平差的 数学模型及最小二乘原理
1
主要内容
§2.1 测量平差概述 §2.2 测量平差的数学模型 §2.3 函数模型的线性化 §2.4 最小二乘原理
第二章 测量平差的数学模型及最小二乘原理
2
§2.1 测量平差概述
6
§2.1测量平差概述
自由度
观测值个数为 n ，必要观测数为 t ，多余观测数为 r ：
r=n-t
h1
HB B
当n<t时： 无法确定几何模型； 当n=t时： 可唯一确定几何模型；
A HA
h4
平差数学模型与最小
教学ppt
1
教学ppt
2
教学ppt
3
教学ppt
4
第二章 平差数学模型与最小二乘原理
§2-1 测量平差概述
在测量工作中，为了确定待定点的高程，需要建 立水准网，为了确定待定点的平面坐标，需要建立 平面控制网（包括测角网、测边网、边角网），我 们常把这些网称为几何模型。每种几何模型都包含 有不同的几何元素，如水准网中包括点的高程、点 间的高差，平面网中包含角度、边长、边的坐标方 位角以及点的二维或三维坐标等元素。这些元素都 被称为几何量。
r=n-t
(2-1-1)
式中n是观测值个数，t是必要观测个数，r称为 多余观测个数，表示有r个多余观测值，在统计学 中也叫自由度。
教学ppt
12
既然一个几何模型能通过t个必要而独立的量唯一 的确定下来，这就意味着在该模型中，其它的量都可 以由这t个量确定下来，即模型中任何一个其它的量 都是这t个独立量的函数，都与这t个量之间存在有一 定的函数关系式。现在模型中有r个多余观测量，因 此，一定也存在着r个这样的函数关系式。
从上面例子可知，一旦几何模型确定了，就能够 唯一地确定该模型的必要观测元素的个数。我们把 能够唯一地确定一个几何模型所必要的元素，称为 必要观测元素。
教学ppt
9
必要观测元素的个数用t表示，称为必要观测个 数。对于上面三种情况，必要观测元素个数分别为 t=2,t=3和t=3。而对于后两种情况，不仅要考虑必 要观测元素的个数，还要考虑到元素的类型，否则 就无法唯一地确定模型。必要观测个数t只与几何模 型有关，与实际观测量无关。
L ~ 1L ~ 2L ~ 31 8 00
(2-1-3)
~~ siSn1L~1 siSn2L~2 0
1
教学ppt
2
教学ppt
3
教学ppt
4
第二章 平差数学模型与最小二乘原理
§2-1 测量平差概述
在测量工作中，为了确定待定点的高程，需要建 立水准网，为了确定待定点的平面坐标，需要建立 平面控制网（包括测角网、测边网、边角网），我 们常把这些网称为几何模型。每种几何模型都包含 有不同的几何元素，如水准网中包括点的高程、点 间的高差，平面网中包含角度、边长、边的坐标方 位角以及点的二维或三维坐标等元素。这些元素都 被称为几何量。
r=n-t
(2-1-1)
式中n是观测值个数，t是必要观测个数，r称为 多余观测个数，表示有r个多余观测值，在统计学 中也叫自由度。
教学ppt
12
既然一个几何模型能通过t个必要而独立的量唯一 的确定下来，这就意味着在该模型中，其它的量都可 以由这t个量确定下来，即模型中任何一个其它的量 都是这t个独立量的函数，都与这t个量之间存在有一 定的函数关系式。现在模型中有r个多余观测量，因 此，一定也存在着r个这样的函数关系式。
从上面例子可知，一旦几何模型确定了，就能够 唯一地确定该模型的必要观测元素的个数。我们把 能够唯一地确定一个几何模型所必要的元素，称为 必要观测元素。
教学ppt
9
必要观测元素的个数用t表示，称为必要观测个 数。对于上面三种情况，必要观测元素个数分别为 t=2,t=3和t=3。而对于后两种情况，不仅要考虑必 要观测元素的个数，还要考虑到元素的类型，否则 就无法唯一地确定模型。必要观测个数t只与几何模 型有关，与实际观测量无关。
L ~ 1L ~ 2L ~ 31 8 00
(2-1-3)
~~ siSn1L~1 siSn2L~2 0
平差模型与最小二乘准则20页
可见 x的方差最小，最有效。
还应有“有效性”要求
最小方差性：
若有一无偏估 ˆ， 计使 D 量ˆ m 2 （ in 最
小方差），则该即估满计足量有效性又满 致性。是最优估值。
•4-４最小二乘准则
一、最小二乘法 设有误差方程： VAx ˆl
n
在满足约束： vi2v12v2 2vn 2m下in，
（2）精度评定－－即是求D(X)的估值。
•4-3 估计值的最优性质
点估计的几种方法： 矩法、最大似然法、最小二乘法、中位数法、截
尾法
用不同的点估计方法对同样的母体进行参数估计 ，会产生不同的估值。
最优估值标准： （1）无偏 性 （2）一致性 （3）有效性
最优估计应具有性质：
估计量ˆ 能在参数真值附近摆动，随着子样容
数理统计问 限题 个： 抽 获 通 样 得 过 x1子 ,有 x2, 样 xn
n有限 构成统 推 计断 量 n母 无体 限
2、常用数理统计方法 （1）参数估计 （2）统计假设检验 （3）回归分析 （4）方差分析
3、对抽样的要求
a、代表性：要求子样的各个分量x i与母体同分布
。即 Exi EX Dxi DX
量的增大，摆幅越来越小，n为时，ˆ 依概率
收敛于 。
一、无偏性
设 ˆ是参数 的 真估 值值，E若 ˆ满
则称 ˆ是 的无偏估计。
问： x是否是母体均估 值计 的？ 无子 偏 s样 2是方
否是母体 Dx方 差 2的无偏估计？
结论
数理统计中
x
1 n
n i1
xi
s 2
1 n
n
(xi
i1
x )2
例：证明子样均值是母体期望的一致性估值。
空间误差分析平差数学模型与最小二乘原理PPT课件
• （3）独立量 一个几何模型的必要观测元素之间是不存在任何确定的函数关系的，即其中的任何一个必要观测元 素不可能表达为其余必要观测元素的函数。这些彼此不存在函数关系的量称为函数独立量。
第8页/共77页
§4-1 测量平差概述
• 5.多余观测 • 假设对模型中的几何量总共观测 n 个， n < t，无法确定模型； n = t，唯一地确定模型，但无法发现粗差 n > t，可以确定模型，还可以发现粗差
条件平差的自由度为多余观测数r，即条件 方程个数。
第22页/共77页
§4-2 函数模型
• 例1：已知点A、B高程；观测值：h1—h5
× hh~~14
~ h5 ~ h5
~ h2 ~ h3
0 0
H
A
~ h3
~ h4
H
B
0
hh~~14
~ h5 ~ h5
~ h2 ~ h3
0 0
h~1
~ h2
~ h3
§4-2 函数模型
h1
B X~1
A
h4
h5
h~~1 h2
X~1 X~1
HA X~2
D X~3 h2
~ h3
X~2
H
A
h3
h6
C X~2
t = 3，选3个参数
X~1 X~2
HB HC
X~3
HD
1 0
1 1
0 1
B
0
0
1 0
0 1
L~
~ h1
~ h2
L~ B X~ d
0
~ h2 ~ h5
~ h3 ~ h6
0 0
h1
~ h3
~ h4
~ h6
第8页/共77页
§4-1 测量平差概述
• 5.多余观测 • 假设对模型中的几何量总共观测 n 个， n < t，无法确定模型； n = t，唯一地确定模型，但无法发现粗差 n > t，可以确定模型，还可以发现粗差
条件平差的自由度为多余观测数r，即条件 方程个数。
第22页/共77页
§4-2 函数模型
• 例1：已知点A、B高程；观测值：h1—h5
× hh~~14
~ h5 ~ h5
~ h2 ~ h3
0 0
H
A
~ h3
~ h4
H
B
0
hh~~14
~ h5 ~ h5
~ h2 ~ h3
0 0
h~1
~ h2
~ h3
§4-2 函数模型
h1
B X~1
A
h4
h5
h~~1 h2
X~1 X~1
HA X~2
D X~3 h2
~ h3
X~2
H
A
h3
h6
C X~2
t = 3，选3个参数
X~1 X~2
HB HC
X~3
HD
1 0
1 1
0 1
B
0
0
1 0
0 1
L~
~ h1
~ h2
L~ B X~ d
0
~ h2 ~ h5
~ h3 ~ h6
0 0
h1
~ h3
~ h4
~ h6
第2章 平差数学模型与最小二乘原理
2.1 测量平差概述1、函数模型是怎样定义的？试举例说明函数模型的作用。
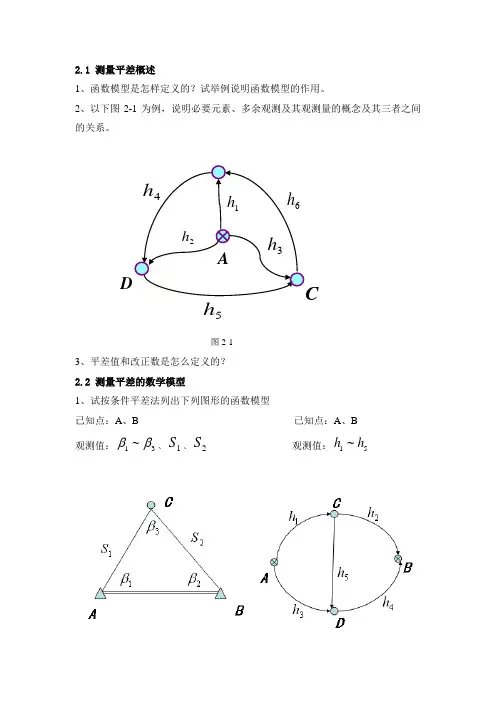
2、以下图2-1为例，说明必要元素、多余观测及其观测量的概念及其三者之间的关系。
图2-13、平差值和改正数是怎么定义的？ 2.2 测量平差的数学模型1、试按条件平差法列出下列图形的函数模型已知点：A 、B 已知点：A 、B 观测值：31~ββ、1S 、2S 观测值：51~h h5h2、试按附有参数的平差法列出下列图形的函数模型已知点：A 、B 已知点：A 、B 观测值：41~h h 观测值：61~L L平差参数：C 点的高程 平差参数：角度ABC ∠、DBC ∠3、试按间接平差法列出下列图形的函数模型已知点：A 已知点：A 、B 、C 观测值：61~h h 观测值：31~S S平差参数：B 、C 、D 点的高程 平差参数：P 点的坐标4、试按附有限制条件的间接平差法列出下列图形的函数模型 已知值：矩形的对角边S 已知点：A 观测值：41~L L 观测值：41~h h平差参数：321~~~L L L 、、 平差参数：43~~h h H B 、、5、在下图所示的水准网中，A 为已知点，B 、C 、D 、E 为待定点，观测了9条路线的高差91~h h ，列出下列四种情况下的函数模型，并指出方程的个数。
（1） 条件平差法的函数模型；（2） 选取B 、C 、D 三点的高程平差值为参数； （3） 选取51~h h 的高差平差值为参数； （4） 选取85~h h 的平差值为参数。
6、试用表格的形式总结四种基本平差方法函数的异同。
7、四种基本平差方法的随机模型是什么？有什么作用？8、同精度观测了下图中的5个角度i L ，A 、B 为已知点，C 点为待定点，CD 边的方位角CD 为已知方位角，试列出条件平差的函数模型。
9、在下图所示的直角三角形中，我们观测了三角形的三个边长1L 、2L 、3L ，选取边长1~L 、2~L 为平差参数，试列出间接平差的观测方程。
第二章-平差数学模型与最小二乘原理2009
ˆ ⎞ d lg sin L i ⎟ ˆ = lg sin( L + v ) = lg sin L + ⎛ ⎜ vi lg sin L i i i i ⎟ ⎜ dL ˆ ˆ =L i ⎠L ⎝ i i ˆ ⎞ ⎛ d lg sin L vi′′ i ⎟ = lg sin Li + ⎜ ⎟ ⎜ dL ˆ ρ ′′ ˆ =L i ⎠L ⎝ i i
§2.1 测量平差的数学模型
在日常生活和科学研究中，时常见到很多模型，一般主要有实物的模拟模型和数学模型。测量 平差的数学模型包括：函数模型和随机模型。一个实际的平差问题，都要建立某种函数模型，函数 模型是描述观测量与未知量之间的数学关系的模型。函数模型分为线性模型和非线性模型两类，测 量平差通常是基于线性模型的，当函数模型为非线性函数时，总是将其用泰勒公式展开，并取其一 次项化为线性形式。
ˆ + l ， l = ( BX 0 + d − L ) V = Bx
其中
⎛ a1 ⎜ B = ⎜ a2 ⎜a ⎝ 3
b1 ⎞ ⎛ S01 − S1 ⎞ ⎟ ⎜ ⎟ b2 ⎟ ， l = ⎜ S02 − S2 ⎟ ⎜S −S ⎟ b3 ⎟ ⎝ 03 3 ⎠ ⎠
这样，就把原来非线性的误差方程化为线性式。解答完毕。 在上面所举的例子中，满足条件方程的改正数 V 都有无穷多组。最小二乘条件平差，即依据条 件方程式，按 V PV = min 求出改正数及其平差值。
（2）方位角条件 1 个。 BA 边及 BC 边的方位角及边长为已知，则由 BA 边的方位角加 2 角及 5 角，应等于 BC 边的方位角。即
v 2 + v5 + w3 = 0 ， w3 = TBA + L2 + L5 − TBC
误差理论与平差基础课件 第3、4章
求函数向量 x = [ x1
x 2 ]T 的方差。
-5-
第三章 协方差传播律 三、两个函数 y ,
r ,1
r ,t
t ,1
z 的互协方差阵
⎡ 4 0 0⎤ ⎢0 2 0⎥ 例3设有观测向量L，已知其协方差阵为，D = ⎢ ⎥ 3, 3 ⎢ 0 0 3⎥ ⎣ ⎦ 求下列函数的协方差。
DYZ = FDXX K T
T DYY = FDXX F T = DYY r ×r
-4-
第三章 协方差传播律
例1已知 L1 ...L3
⎤ ⎡3 DL = ⎢ 2 ⎥ ⎥ ⎢ 3, 3 ⎢ 4⎥ ⎦ ⎣
求函数 x = 5L1 − L2 + 2 L3 − 7 的方差。
例2已知 L1 ...L3
⎡ 3 − 1 1⎤ DL = ⎢− 1 2 0⎥ ⎥ ⎢ 3, 3 ⎢ 1 0 4⎥ ⎦ ⎣ x 2 = − L2 + 3L3 − 2 函数 x1 = 2 L1 − L2 + 5,
单位权中误差 比例因子 权为1的观测值对应的中误差
3
测量中常用的方法
（1）水准测量的权 （2）同精度观测值的算术平均值的权 （3）距离丈量的权 （4）三角高程测量的权
-15-
第三章 协方差传播律 九、协因数和协因数传播律 1 2 3 4 5
协因数 协因数阵 协因数阵的特点 互协因数阵 权阵
-16-
第三章 协方差传播律--协因数和协因数传播律
当观测值互不相关时，权阵为对角阵，主对角 线上的元素为观测值的权。
L = [ L1 ......Ln ]T
2 ⎡σ L1 ⎢ 2 ⎢σ 0 1 = 2 DL = ⎢ ... σ0 ⎢ ⎢ 0 ⎢ ⎣
QLL
平差数学模型与最小二乘原理
t0=3
一个点的坐标、一边方位角
边角三角 网
点数 ×2
t0=3
一个点的坐标、一边方位角
据起算数据情况，把控制网分为：
自由控制网：不足或仅有必要的起算数据 附和控制网：有多余的起算数据
§4-1 测量平差概述
四、计算t和r的例题
1．水准网
2.பைடு நூலகம்角网
B
B 2 C 3 4 5
3 4 C6 8 7
2
1 A
函数模型是指模型(几何、物理)中量(观测量、未知参数)的 真值(或期望值)之间的函数关系式。
函数关系式有线性非线性之分； 线性函数模型与非线性函数模型(线性化后处理)。
随机模型是指描述观测值的先验精度及其相关性的特
征。常用观测值的方差阵或协因数阵或权阵表示。
§4-3 函数模型的线性化
设有函数
设
c1
0 L L L 1 8 0 0 1 2 3 L 0 1 X
X
一般的：
1 2 3 W 0 1 X W c
一、函数模型
3.附有参数的条件平差的函数模型
在具体平差问题中,观测次数n，必要观测次数t，则 多余观测次数r,再增加u个独立参数,且 0 ＜ u ＜ t ， 则总共有r +u = c个条件方程，一般形式是：
(a)
8
5
7
6 D
1 A
D
9
(b)
五、多余观测与平差的关系
多余观测个数：r =n - t 当 n＜ t 时，不能确定平差问题的模型
n = t 时，能确定模型，但无检核、有无粗差不知
n＞ t 时，有多余观测，因观测误差使观测值间产 生矛盾，使模型出现多解。 通过平差处理，让观测值的平差值之间满足相应 的条件关系，消除矛盾，获取模型的唯一最优解。
误差平差：平差数学模型与最小二乘原理
1 3 5
思考：以下是否可行？为什么？
h2 h4 h5 0 h h h 0
1 3 5
H A h3 h4 H B 0
h1 h2 h3 h4 0
二、间接平差的函数模型
1、间接平差的函数模型 观测值与待定参数的数学期望之间的函数关系式。 即：先选定t个独立参数，将每一个观测量表达成所选参数的函 数，这种函数关系式称为“观测方程”。 2、间接平差 以上述的观测方程为平差的函数模型，称为间接平差（又称 为参数平差）。
由于多余观测，将会使观测量真值之间产生一个几何或者物 理的约束方程，即函数模型； 而观测值不可避免地存在偶然误差，使得约束条件因实际存 在闭合差而并不满足； 如何调整观测值，即对观测值合理地加上改正数，使其达到 消除闭合差的目的，这就是测量平差的主要任务！
那么，一个测量平差问题又是怎样来达到消除闭合差的目的呢？ 首先要由观测值和未知量间组成函数模型； 然后采用一定的平差原则对未知量进行估计。
则为：AL A0 0
则为：L BX d
三.附有参数的条件平差的函数模型
1、先仍然按条件平差列r个条件方程；
L1 L2 L3 1800 0
2、然后再增选一个参数，则就会增加 一个条件方程，即
L1 X 0
3、则上式可写成：
X
1 1 1 0 180 A ，B ，A0 1 0 0 1 0
建立不同的函数模型，就有了不同的平差方法： 1、条件平差； 2、间接平差； 3、附有参数的条件平差； 4、附有限制条件的间接平差。
一、条件平差的函数模型
1、条件平差的函数模型 观测值的数学期望之间的函数关系式,又称为条件方程。 2、条件平差 以条件方程为函数模型的平差方法，称为条件平差方法。
思考：以下是否可行？为什么？
h2 h4 h5 0 h h h 0
1 3 5
H A h3 h4 H B 0
h1 h2 h3 h4 0
二、间接平差的函数模型
1、间接平差的函数模型 观测值与待定参数的数学期望之间的函数关系式。 即：先选定t个独立参数，将每一个观测量表达成所选参数的函 数，这种函数关系式称为“观测方程”。 2、间接平差 以上述的观测方程为平差的函数模型，称为间接平差（又称 为参数平差）。
由于多余观测，将会使观测量真值之间产生一个几何或者物 理的约束方程，即函数模型； 而观测值不可避免地存在偶然误差，使得约束条件因实际存 在闭合差而并不满足； 如何调整观测值，即对观测值合理地加上改正数，使其达到 消除闭合差的目的，这就是测量平差的主要任务！
那么，一个测量平差问题又是怎样来达到消除闭合差的目的呢？ 首先要由观测值和未知量间组成函数模型； 然后采用一定的平差原则对未知量进行估计。
则为：AL A0 0
则为：L BX d
三.附有参数的条件平差的函数模型
1、先仍然按条件平差列r个条件方程；
L1 L2 L3 1800 0
2、然后再增选一个参数，则就会增加 一个条件方程，即
L1 X 0
3、则上式可写成：
X
1 1 1 0 180 A ，B ，A0 1 0 0 1 0
建立不同的函数模型，就有了不同的平差方法： 1、条件平差； 2、间接平差； 3、附有参数的条件平差； 4、附有限制条件的间接平差。
一、条件平差的函数模型
1、条件平差的函数模型 观测值的数学期望之间的函数关系式,又称为条件方程。 2、条件平差 以条件方程为函数模型的平差方法，称为条件平差方法。
03 第三章 平差数学模型与最小二乘原理
测量平差讲义第三章：平差数学模型与最小二乘原理本章阐述平差的基本概念，指出：平差数学模型不同，平差方法就不同，但其解是相同的。
平差问题是由多余观测产生的，各类数学模型共同特点是方程数少于未知数个数，所以没有唯一解，只能求特定条件下的特解。
这实际上是参数估计问题。
平差采用的特定条件是最小二乘准则，以后可证明其解符合最优估值的条件。
§3-1 测量平差概述基本概念：1、几何模型：为求某些点的坐标、高程而建立的由角度、边长、高差等观测值和坐标、高程等已知值构成的水准网、导线网、三角网。
2、必要元素是能够唯一确定一个几何模型所必要的元素。
必要元素的个数用t 来表示，通常称为必要观测数。
对于一个确定的几何模型，必要观测数t 是确定的。
t 只与几何模型有关，与实际观测值无关。
例如三角形前方交会确定一个待定点坐标，必要观测数为2，可测两个角、一边一角或两边，都可唯一确定这个几何模型。
但要注意，t 个元素之间必须不存在函数关系，否则实际个数少于t 。
3、多余观测数：设对一个几何模型观测了n 个几何元素，该模型的必要观测数为t ，则：n<t 时,几何模型不能确定，即某些几何元素不能求出。
n=t 时，虽几何模型可唯一确定，但没有检核条件。
即使有错也不能发现，可靠性为零。
测量工作中一般要求必n>t ,此时称r=n-t 为多余观测数，又称自由度。
4、条件方程：一个几何模型若有多余观测值，则观测值的正确值与几何模型中的已知值之间必然产生相应的函数关系，这样的约束函数关系式在测量平差中称为条件方程。
5、闭合差：以观测值代入条件方程，由于存在观测误差，条件式将不能满足。
测量平差中将代入后所得值称为闭合差。
测量平差任务之一，所谓消除不符值，就是合理的调整观测值，对观测值加改正数，达到消除闭合差的目的。
可见消除不符值就是消除闭合差。
§3-2 测量平差的数学模型用数学关系描述几何模型的几何关系和内在联系，称为数学模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
返回目录
（3）在图2-2的水准网中，为 了确定A、B、C、D4点之间高
度个或的高h~4、相差h~对就5、关行h~6 或系了， ，h~1、只如要h~h~、21 、知h~…h6~道3、等其h~等4中。3
它们是同一类型的元素（高 差）。
能够唯一地确定一个几何 模型所必要的元素，简称必要 元素；必要元素的个数用t来表 示。对于上述三种情况，分别 是t=2,t=3和t=3。对于第二种情 况，3个元素中除了角度还至少 要包含一个边长，没有边长仍 然只能确定其形状；
r=n-t
（2-1-1）
式中n为观测值个数，t称为必要观测数，r称为多余观 测数。多余观测数在测量中又称“自由度”。
返回目录
一个几何模型如果有r个多余观测，就产生r个条件方
程。由于观测值不可避免地存在观测误差，由观测值组成
上述条件方程必不能满足，仍以（2）中情况为例，若观
测了角度L1、L2、Lຫໍສະໝຸດ 和边长S1、S2，考虑观测误差，有
返回目录
2-2 测量平差的数学模型
一、条件平差法 二、间接平差法 三、附有参数的条件平差法 四、附有限制条件的间接平差法 五、平差的随机模型
返回目录
在日常生活和科学技术领域中，时常见到许多模型，一 般可将其分为两大类，一类是将实物尺寸放大或缩小而得 的模型，称为实物模型；另一类是用文字、符号、图表或 者对研究的对象进行抽象概括，用数学关系式来描述它的
在测量工程中，最常见的是要确定某些几何量的大小。 例如，为了求定一些点的高程而建立了水准网，为了求定 某些点的坐标而建立了平面控制网或三维测量网。前者包 含点间的高差、点的高程等元素，后者包含角度、边长、 边的方位角以及点的二维或三维坐标等等元素。这些元素 都是几何量，以下统称这些网为几何模型。
为了确定一个几何模型，并不需要知道该模型中所有元 素的大小，而只需要知道其中部分元素的大小就行了，其 它元素可以通过它们来确定。例如：
第二章 平差数学模型与最小二乘原理
本章介绍测量平差的基本概念，简要地给出基本平差
方法的数学模型，为以后各章系统学习各种平差理论打好
基础。最后介绍最小二乘原理，这是测量平差法所遵循的
准则。
第一节
测量平差概述
第二节
测量平差的数学模型
第三节
函数模型的线性化
第四节
参数估计与最小二乘原理
2-1 测量平差概述
（1）在图2-1的△ABC中，为了确定它的形状（相似形），只
要Lˆ3等知。道它其们中都任是意同2个一内类角型的的大元小素就（行角了度，）如。L~1, L~2或L~1, L~3或Lˆ2
（2）为了确定ΔABC的形状和大小（全等形），只要知道其
中如任L~1意、L的~2、2S角~1,1S边~1、、S~22、边L~13,角S~或1、3S~边2、的S~3，大小…就，行等了等，。
Lˆ L , L~ L , L~ L
S~1
1
S
1
, S2~
2
S
2
3
3
3
1
1
S1
2
2
S2
因r=n-t=5-3=2，可组成2个条件方程为
(L11) (L2 2 ) (L3 3 ) 180 （2-1-2）
sin(L )
(S ) (S )
2
2
2
S2
1 S1 sin(L )
（2-1-3）
1
1
若用观测值组成上述两个条件方程，则不能成立，即
L L L 180 0
1
2
3
S2
S1
sin L2 sin L1
返回目录
（2-1-4）
造成条件方程不闭合，或者说存在闭合差，例如 （2-1-4）式中的，就是该三角形角度条件方程的闭合差。
由于观测不可避免地存在偶然误差，当n>t时，几何模型 中应该满足r=n-t个条件方程，实际存在闭俣差而并不满足， 如何调整观测值，即对观测值合理地加上改正数，使其达 到消除闭合差的目的，这是测量平差的主要任务。 一个测量平差问题，首先要由观测值和待求量间组成数 学模型，然后采用一定的平差原则对待求量进行估计，这 种估计要求是最优的，最后计算和分析成果的精度。
返回目录
而无法确定其大小，因此，必要元素不仅要考虑其个数， 而且要考虑以它的类型。由此可知，当某个几何模型给定 之后，能够唯一确定该模型的必要元素的个数t及其类型， t只与几何模型有关，与实际观测量无关。
对于任一几何模型，它的t个必要元素之间必要不存在函 数关系，亦即其只任一元素不能表达成其余（t-1）个元素
在一个几何模型中，除了t个独立量以外，若再增加一个
量中+ L~，，3=则必18必要0º然量，S~2产选若生为再S~1一L~增ss1、ii个nnL~加2LL~~、相一2 S~应1，个返的若量回函目增S~录2数，加关则一系有个式量。L~3 ，仍则以（存2在）L~情1+况L~2 1
由此可知，一个几何模型的独立量个数最多为t个，除 此之外，增加一个量必然要产生一个相应的函数关系式， 这种函数关系式，在测量平差中称为条件方程。
的元选就不函素L~1 、能数，L~说。则2 、tL例~L~=31与3，如，L则~，实2 间对L~际1+无于必L~函（+2要L数~13元）=关1素中8系0只的º；选情，又了况三如两，者在个若之（，以间2）而L存~1和情漏在况L~选函2作中了数为，一关必个系要。，
因此必要元素t个量为函数独立量，简称独立量。
某种特征或内在联系的模型。前者称为模拟模型，后者称 为数学模型。总称为抽象模型。
在测量工程中，涉及的是通过观测量确定某些几何量或 物理量大小等有关的数量问题，因而考虑的模型总是数学 模型。平差的数学模型与一般数学只考虑函数模型不同， 它还要考虑随机模型，因为观测量是一种随机变量。所以 平差的数学模型同时包含函数模型和随机模型两种，在研 究任何平差方法时必须同时予以考虑。
在测量工程中，为了求得一个几何模型中各量的大小就 必须进行观测。如果总共观测了该模型中n个量的大小， 若观测个数少于必要元素的个数，即n<t，显然它无法确定 该模型，即出现了数据不足的情况；若观测了t个独立量， n=t，则可唯一地确定该模型。由于它们都是独立量，故不 存在任何条件方程，在这种情况下，如果观测结果中含有 粗差甚至错误，都将无法发现，在测量工作中是不允许这 样做的。为了能及时发现粗差和错误，并提高测量成果的 精度，就必须使n>t，若令
（3）在图2-2的水准网中，为 了确定A、B、C、D4点之间高
度个或的高h~4、相差h~对就5、关行h~6 或系了， ，h~1、只如要h~h~、21 、知h~…h6~道3、等其h~等4中。3
它们是同一类型的元素（高 差）。
能够唯一地确定一个几何 模型所必要的元素，简称必要 元素；必要元素的个数用t来表 示。对于上述三种情况，分别 是t=2,t=3和t=3。对于第二种情 况，3个元素中除了角度还至少 要包含一个边长，没有边长仍 然只能确定其形状；
r=n-t
（2-1-1）
式中n为观测值个数，t称为必要观测数，r称为多余观 测数。多余观测数在测量中又称“自由度”。
返回目录
一个几何模型如果有r个多余观测，就产生r个条件方
程。由于观测值不可避免地存在观测误差，由观测值组成
上述条件方程必不能满足，仍以（2）中情况为例，若观
测了角度L1、L2、Lຫໍສະໝຸດ 和边长S1、S2，考虑观测误差，有
返回目录
2-2 测量平差的数学模型
一、条件平差法 二、间接平差法 三、附有参数的条件平差法 四、附有限制条件的间接平差法 五、平差的随机模型
返回目录
在日常生活和科学技术领域中，时常见到许多模型，一 般可将其分为两大类，一类是将实物尺寸放大或缩小而得 的模型，称为实物模型；另一类是用文字、符号、图表或 者对研究的对象进行抽象概括，用数学关系式来描述它的
在测量工程中，最常见的是要确定某些几何量的大小。 例如，为了求定一些点的高程而建立了水准网，为了求定 某些点的坐标而建立了平面控制网或三维测量网。前者包 含点间的高差、点的高程等元素，后者包含角度、边长、 边的方位角以及点的二维或三维坐标等等元素。这些元素 都是几何量，以下统称这些网为几何模型。
为了确定一个几何模型，并不需要知道该模型中所有元 素的大小，而只需要知道其中部分元素的大小就行了，其 它元素可以通过它们来确定。例如：
第二章 平差数学模型与最小二乘原理
本章介绍测量平差的基本概念，简要地给出基本平差
方法的数学模型，为以后各章系统学习各种平差理论打好
基础。最后介绍最小二乘原理，这是测量平差法所遵循的
准则。
第一节
测量平差概述
第二节
测量平差的数学模型
第三节
函数模型的线性化
第四节
参数估计与最小二乘原理
2-1 测量平差概述
（1）在图2-1的△ABC中，为了确定它的形状（相似形），只
要Lˆ3等知。道它其们中都任是意同2个一内类角型的的大元小素就（行角了度，）如。L~1, L~2或L~1, L~3或Lˆ2
（2）为了确定ΔABC的形状和大小（全等形），只要知道其
中如任L~1意、L的~2、2S角~1,1S边~1、、S~22、边L~13,角S~或1、3S~边2、的S~3，大小…就，行等了等，。
Lˆ L , L~ L , L~ L
S~1
1
S
1
, S2~
2
S
2
3
3
3
1
1
S1
2
2
S2
因r=n-t=5-3=2，可组成2个条件方程为
(L11) (L2 2 ) (L3 3 ) 180 （2-1-2）
sin(L )
(S ) (S )
2
2
2
S2
1 S1 sin(L )
（2-1-3）
1
1
若用观测值组成上述两个条件方程，则不能成立，即
L L L 180 0
1
2
3
S2
S1
sin L2 sin L1
返回目录
（2-1-4）
造成条件方程不闭合，或者说存在闭合差，例如 （2-1-4）式中的，就是该三角形角度条件方程的闭合差。
由于观测不可避免地存在偶然误差，当n>t时，几何模型 中应该满足r=n-t个条件方程，实际存在闭俣差而并不满足， 如何调整观测值，即对观测值合理地加上改正数，使其达 到消除闭合差的目的，这是测量平差的主要任务。 一个测量平差问题，首先要由观测值和待求量间组成数 学模型，然后采用一定的平差原则对待求量进行估计，这 种估计要求是最优的，最后计算和分析成果的精度。
返回目录
而无法确定其大小，因此，必要元素不仅要考虑其个数， 而且要考虑以它的类型。由此可知，当某个几何模型给定 之后，能够唯一确定该模型的必要元素的个数t及其类型， t只与几何模型有关，与实际观测量无关。
对于任一几何模型，它的t个必要元素之间必要不存在函 数关系，亦即其只任一元素不能表达成其余（t-1）个元素
在一个几何模型中，除了t个独立量以外，若再增加一个
量中+ L~，，3=则必18必要0º然量，S~2产选若生为再S~1一L~增ss1、ii个nnL~加2LL~~、相一2 S~应1，个返的若量回函目增S~录2数，加关则一系有个式量。L~3 ，仍则以（存2在）L~情1+况L~2 1
由此可知，一个几何模型的独立量个数最多为t个，除 此之外，增加一个量必然要产生一个相应的函数关系式， 这种函数关系式，在测量平差中称为条件方程。
的元选就不函素L~1 、能数，L~说。则2 、tL例~L~=31与3，如，L则~，实2 间对L~际1+无于必L~函（+2要L数~13元）=关1素中8系0只的º；选情，又了况三如两，者在个若之（，以间2）而L存~1和情漏在况L~选函2作中了数为，一关必个系要。，
因此必要元素t个量为函数独立量，简称独立量。
某种特征或内在联系的模型。前者称为模拟模型，后者称 为数学模型。总称为抽象模型。
在测量工程中，涉及的是通过观测量确定某些几何量或 物理量大小等有关的数量问题，因而考虑的模型总是数学 模型。平差的数学模型与一般数学只考虑函数模型不同， 它还要考虑随机模型，因为观测量是一种随机变量。所以 平差的数学模型同时包含函数模型和随机模型两种，在研 究任何平差方法时必须同时予以考虑。
在测量工程中，为了求得一个几何模型中各量的大小就 必须进行观测。如果总共观测了该模型中n个量的大小， 若观测个数少于必要元素的个数，即n<t，显然它无法确定 该模型，即出现了数据不足的情况；若观测了t个独立量， n=t，则可唯一地确定该模型。由于它们都是独立量，故不 存在任何条件方程，在这种情况下，如果观测结果中含有 粗差甚至错误，都将无法发现，在测量工作中是不允许这 样做的。为了能及时发现粗差和错误，并提高测量成果的 精度，就必须使n>t，若令