第一节 磁路的基本定律

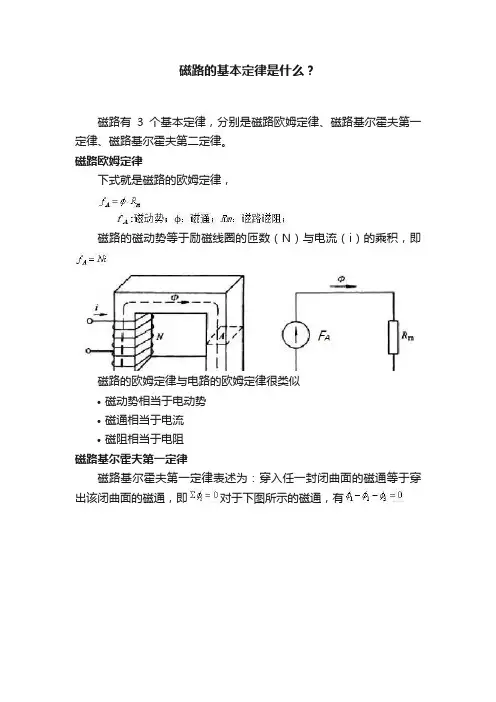
磁路的基本定律是什么？磁路有3个基本定律，分别是磁路欧姆定律、磁路基尔霍夫第一定律、磁路基尔霍夫第二定律。

磁路欧姆定律下式就是磁路的欧姆定律，磁路的磁动势等于励磁线圈的匝数（N）与电流（i）的乘积，即磁路的欧姆定律与电路的欧姆定律很类似•磁动势相当于电动势•磁通相当于电流•磁阻相当于电阻磁路基尔霍夫第一定律磁路基尔霍夫第一定律表述为：穿入任一封闭曲面的磁通等于穿出该闭曲面的磁通，即对于下图所示的磁通，有磁路基尔霍夫第二定律在磁路中沿任何闭合磁路径上，磁动势的代数和等于磁压降的代数和，即对于下图所示的磁通，有题主你好。

磁路是在理想情况下，仿照电路建立的一套理想化的物理模型。

理想化的原因从下面的讨论可以看出。

我们知道，线圈构造成的互感电路在理想情况下有这么几个性质：•不漏磁•电磁感应定律严格成立（如果存在磁荷，这条定律需要修正）•电磁场的变换比较缓慢，电路是似稳的主线圈输入电流是交变电流，那么该线圈就会产生交变的磁场，在不漏磁的假定下，次级线圈里的磁通量就等于主线圈发出的磁通量。

由于电磁场变化很慢，我们可以忽略电磁辐射带走那部分能量，那么这样我们可以用稳恒电路的磁感应强度-电流强度关系式近似表示这里的磁感应强度和电流强度的关系。

简单写为B=4πNI/L（高斯单位制）磁通量φ=BA=4πNIA/L，A是线圈的截面积。

由于主线圈的电流是驱动电流，次级线圈的电流是感应电流，所以我们定义主线圈里的电流与主线圈的匝数乘积为磁动势F，将磁动势与磁通量的比值定义为磁阻。

明显磁阻Rm在数值上等于L/(4πA)，如果考虑铁芯等磁导率不等于真空磁导率的情况时，磁阻改写为L/(4πμA)。

对比电阻表达式，可以发现磁阻和电阻有很多相似的地方，比如都是正比于长度反比于截面积，比例系数是与材料性质有关。

下面我们来讨论磁路基本定律。

如果把φ=BA=4πNIA/L写成φ=F/Rm，那么这个公式就叫磁路的欧姆定律。

由于磁通量的性质，我们可以类比于电路的电流，所以对于串联的线圈之间的磁通量满足φ1=…=φn；对于并联情形有φ0=φ1+…+φn。

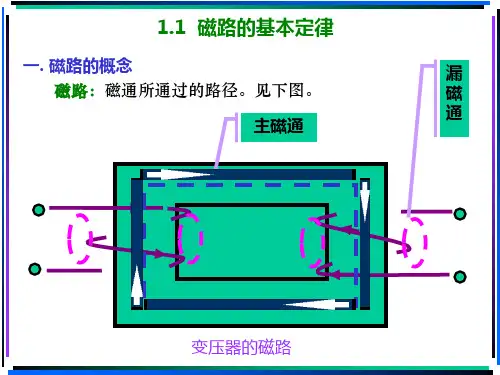
磁路的基本定律磁路的基本定律磁路是指由铁芯和线圈组成的电器元件，在电机、变压器、电磁铁等电气设备中广泛应用。

学习磁路的基本定律对于理解和分析这些设备的工作原理具有重要意义。

一、磁通量1.1 磁通量的定义磁通量是指通过一个闭合曲面内部的总磁场线数，通常用字母Φ表示，单位为韦伯（Wb）。

1.2 磁通量的计算公式根据高斯定理，一个闭合曲面内部的总磁场线数等于该曲面上法向量方向上的磁感应强度积分。

因此，可以用以下公式计算：Φ = ∫B·dS其中，B为磁感应强度（单位为特斯拉），dS为曲面微元（单位为平方米），积分范围为该闭合曲面内部。

二、安培环路定理2.1 安培环路定理的定义安培环路定理是指在一个闭合回路上，沿着任意一条路径积分得到的电流总和相等。

即：∮H·dl = I其中，H为磁场强度（单位为安培/米），dl为路径微元（单位为米），I为该回路内的电流（单位为安培）。

2.2 安培环路定理的应用安培环路定理可以用于分析磁路中的磁通量和磁场强度之间的关系。

例如，在一个闭合回路上，如果有一段铁芯，那么根据安培环路定理，该铁芯内部的磁场强度H应该等于该回路内部电流I所产生的磁通量Φ与铁芯长度l之比。

即：H = Φ / l三、法拉第电磁感应定律3.1 法拉第电磁感应定律的定义法拉第电磁感应定律是指当一个闭合线圈中的磁通量发生变化时，会在线圈中产生感应电动势。

即：ε = -dΦ/dt其中，ε为感应电动势（单位为伏特），Φ为线圈内部的磁通量，t为时间。

3.2 法拉第电磁感应定律的应用法拉第电磁感应定律可以用于分析变压器、发电机等设备中的工作原理。

例如，在一个变压器中，当一侧线圈中的交流电流产生变化时，会在另一侧线圈中产生感应电动势，从而实现电能的传输和变换。

四、磁化曲线4.1 磁化曲线的定义磁化曲线是指在给定条件下，磁通量Φ和磁场强度H之间的关系。

通常用图表或曲线表示。

4.2 磁化曲线的特点磁化曲线的形态取决于铁芯材料的性质和工作状态。

电机学磁路的基本定律电机学磁路是电机学的重要组成部分，它研究的是电机中磁场的产生、分布和作用等问题。

在电机的设计、制造和运行过程中，磁路的分析和计算是必不可少的，因此，了解磁路的基本定律对于电机学的学习和应用都具有重要意义。

一、磁通连续定律磁通连续定律是指在磁路中，磁通量的总和保持不变。

即：任意一段磁路的磁通量之和等于零。

这个定律可以用电流连续定律类比来理解，就是说在任意一段磁路中，磁通量的输入等于输出。

例如，在一个简单的电机中，电流从电源进入线圈，通过线圈产生磁场，磁场又作用于铁芯上，形成磁通量。

然后，磁通量通过空气间隙进入转子，再经过空气间隙进入固定子，最后回到电源。

在这个过程中，磁通量的总和始终保持不变。

二、安培环路定理安培环路定理是指在磁路中，磁通量的变化率等于通过该环路的电流之和。

即：磁通量的变化率等于环路上电流的代数和。

例如，在一个电机中，电流通过线圈产生磁场，磁场又作用于铁芯上，形成磁通量。

如果在铁芯上开一个小孔，通过小孔可以观察到磁通量的变化。

根据安培环路定理，磁通量的变化率等于通过这个小孔的电流之和。

三、法拉第电磁感应定律法拉第电磁感应定律是指在磁路中，电动势的大小等于磁通量变化率的负值。

即：电动势等于磁通量变化率的负值。

例如，在一个变压器中，当一段线圈中的电流变化时，会产生磁场的变化，从而引起另一段线圈中的电动势。

根据法拉第电磁感应定律，电动势的大小等于磁通量变化率的负值。

四、麦克斯韦-安培定理麦克斯韦-安培定理是指在磁场中，磁场的旋度等于该点的磁通量密度与电流密度的代数和。

即：磁场的旋度等于磁通量密度与电流密度的代数和。

例如，在一个电机中，磁场的旋度可以表示为磁通量密度与电流密度的代数和。

如果在电机中的任意一点测量磁场的旋度，可以用该点的磁通量密度与电流密度的代数和来计算。

综上所述，电机学磁路的基本定律包括磁通连续定律、安培环路定理、法拉第电磁感应定律和麦克斯韦-安培定理。

磁路的基本定律磁路有三个基本定律作为分析计算的基础。

1．磁路的基尔霍夫第⼀定律（KCL）
在图1所⽰磁路的分⽀处（⼜称为磁路的节点）作⼀封闭⾯S，若忽略漏磁通并选定主磁通φ1、φ2、φ3的参考⽅向如图所⽰。

图1
①内容：穿进任⼀封闭⾯的磁通⼀定等于穿出该封闭⾯的磁通。

②表达式：
φ1+φ2 -φ3 = 0
写成⼀般形式，有
∑φ = 0 （1）
即汇合于磁路中任⼀节点的磁通的代数和为零，这就是磁路的基尔霍夫第⼀定律。

③正负符号的选取：⼀般选离开节点的磁通项前取正号，反之取负号。

2．磁路的基尔霍夫第⼆定律(KVL)
①磁通势F
铁芯线圈的匝数与通过励磁电流乘积叫做磁通势F，磁通势的SI主单位均为安（A）。

F = NI （2）
②磁位差Um：
磁场强度H与该段磁路平均长度l的乘积，叫做该段磁路的磁位差Um，其单位均为安（A）。

（3）
③内容：磁路的任⼀闭合回路中，各段磁位差的代数和等于磁通势的代数和。

④数学表达式：
推⼴到⼀般情形，有
（4）
⑤正负号的选取：
a. 磁位差的符号:
选⼀绕⾏⽅向，磁通的参考⽅向与绕⾏⽅向⼀致时，该段磁位差项前取正号，反之取负号；
b. 磁通势的符号:
励磁电流的参考⽅向与磁路回线绕⾏⽅向符合右⼿螺旋关系时，该磁通势项前取正号，反之取负号。

3．磁路的欧姆定律
①磁阻：媒质对磁通的阻碍作⽤，称为磁阻。

图2 ⼀段均匀磁路
Rm =
磁阻的SI主单位为每亨（1/H）。

磁路的三个基本定律一、磁路的欧姆定律1. 内容- 磁路中的磁通Φ（单位为韦伯，Wb）与磁动势F（单位为安匝，At）成正比，与磁阻R_m（单位为H^-1）成反比，即varPhi=(F)/(R_m)。

2. 相关概念- 磁动势F：磁动势是产生磁通的激励，等于线圈的匝数N与通过线圈的电流I 的乘积，即F = NI。

例如，一个线圈匝数为100匝，通过的电流为2A，则磁动势F=100×2 = 200安匝。

- 磁阻R_m：磁阻表示磁路对磁通的阻碍作用，它与磁路的长度l（单位为米，m）成正比，与磁路的横截面积S（单位为平方米，m^2）和磁导率μ（单位为亨/米，H/m）成反比，即R_m=(l)/(μ S)。

例如，对于一段长度l = 0.5m，横截面积S=0.01m^2，磁导率μ = 4π×10^-7H/m的磁路，其磁阻R_m=(0.5)/(4π×10^-7)×0.01≈3.98×10^7H^-1。

二、磁路的基尔霍夫第一定律（磁通连续性定律）1. 内容- 对于磁路中的任一闭合面，进入该闭合面的磁通等于离开该闭合面的磁通，即∑varPhi = 0。

2. 理解与示例- 这一定律类似于电路中的基尔霍夫电流定律。

例如，在一个有分支的磁路中，假设一个节点处有三条磁路分支，磁通分别为varPhi_1、varPhi_2和varPhi_3，如果规定进入节点为正，离开节点为负，则varPhi_1-varPhi_2-varPhi_3 = 0。

也就是说，磁通在磁路的节点处是连续的，不会凭空产生或消失。

三、磁路的基尔霍夫第二定律（安培环路定律的推广）1. 内容- 在磁路的任一闭合回路上，磁动势的代数和等于各段磁路磁压降（Hl，其中H为磁场强度，单位为安/米，A/m）的代数和，即∑ F=∑ Hl。

2. 相关概念与示例- 磁场强度H：磁场强度与磁导率μ和磁感应强度B（单位为特斯拉，T）的关系为B = μ H。