期中考试数学命题细则

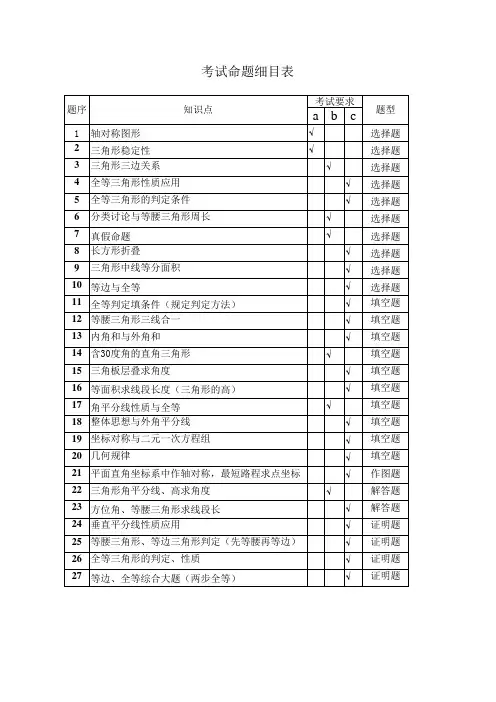
湖北省恩施州高中教育联盟2024-2025学年高二上学期期中考试数学试题（答案在最后）命题单位：考试满分：150分考式用时：120分钟注意事项：1.答题前、考生务必将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码贴在答题卡上的指定位置．2.选择题的作答：每小题选出答案后、用2B 铅笔把答题卡上对应题目的答案标号涂黑．写在试卷、草稿纸和答题卡上的非答题区域均无效．3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内．写在试卷、草稿纸和答题卡上的非答题区域均无效．4.考试结束后，请将本试卷和答题卡一并上交．一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的1.一组数据2，5，3，7，1，6，4的第70百分位数是A.1B.4.9C.4D.52.若圆锥的表面积为4π，底面圆的半径为1，则该圆锥的体积为A.23π3B.C.22π3D.3.在平行六面体1111ABCD A B C D -中，M 为DB 上靠近点D 的三等分点，N 为1CC 的中点.设11111,,A B a A D b A A c === ，则MN =A.211332a b c +- B.211332a b c -- C.211332a b c ++ D.211332a b c -+- 4.从{}1,2,3和{}4,5两个集合中各取一个数组成一个两位数，则这个两位数能被3整除的概率是A.16 B.13 C.12 D.235.已知2sin 3a a +=，则πcos 23a ⎛⎫-= ⎪⎝⎭A.1625- B.79- C.4981 D.456.已知实数x ，y 满足22||||x y x y +=+，则|3|x y +-的最小值与最大值之和为A.4B.5C.6D.77.已知直线a ，b ，c 和平面,,a βγ，则下列命题正确的是A..平面a 内不一定存在和直线a 垂直的直线B.若,a γβγ⊥⊥，则//a βC.若a ，b 异面且,,//,//a a b a b a ββ⊂⊂，则//a βD.若,,a a a b c βγβγ⋂=⋂=⋂=，则直线a ，b ，c 可能两两相交且不过同一点8.设函数22()sin cos ,N*f x x x n ⋅=+∈，下列命题正确的是A.当π2=时，()f x 的最小正周期为πB.当3n =时，()f x 的最大值为14C.()f x 的最小值与n 的取值无关D.()f x 的最大值与n 的取值无关二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分9.已知函数1()cos cos 22f x x x =+，则下列结论正确的是A.2π是()f x 的一个周期B.()f x 在[0.2π]上有2个零点C.()f x 的最大值为32D.()f x 在π0,2⎡⎤⎢⎥⎣⎦上是增函放10.下列命题正确的是A.若事件A ，B ，C 两两互斥．则()()()()P A B C P A P B P C ⋃⋃=++成立B.若事件A ，B ，C 两两独立．则()()()()P ABC P A P B P C =成立C.若事件A ，B 相互独立．则A 与B 不一定相互㹨立D.若()0,()0P A P B >>，则事件A 、B 相互独立与A 、B 互斥不能同时成立11.记C 为圆22:6490C x y x y +--+=的圆心.H 为y 轴上的动点．过点H 作圆C 的两条切线，切点分别是M ，N ，则下列结论正确的是A.MN 的最大值为4B.直线MN 过定点5.23⎛⎫ ⎪⎝⎭C.存在点H ，使得MH NH ⊥D.四边形HMCN 的面积的最小值为三、填室题：本题共3小题，每小题5分，共15分.12.已知单位向量a b ，满足3()(2)2a b a b +⋅-=- ，则a b ⋅= ______.13.已知有3名男生和2名女生，其中3名男生的平均身高为170cm ．方差为30，2名女生的平均身高为165cm ，方差为41，则这5名学生身高的方差为______．14.在正方体1111ABCD A B C D -中，6,AB E =为棱BC 的中点，F 为棱11A D 的三等分点（靠近点1D ），过点A ，E ，F 作该正方体的截面．则该截面的周长是______.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）已知1(12i)112iz +=+（1）求1z ；（2）若复数z 满足12,z z z -=在复平面内对应的点为Z ，且点(1,0),(1,0)A B -，求ZA ZB ⋅ 的取值范围．16.（15分）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos sin 0a C C b c --=.（1）求A ；（2）若ABC 为锐角三角形，且4a =，求ABC 的周长的取值范围.17.（15分）甲、乙两所学校之间进行羽毛球比赛，采用五局三胜制（先赢三局的学校获胜，比赛结束）.约定比赛规则如下：先进行两局男生羽毛球比赛，后进行女生羽毛球比赛.按照以往比赛经验，在男生羽毛球比赛中，每局甲校获胜的概率为35，乙校获胜的概率为25；在女生羽毛球比赛中，每局甲校获胜的概率为13，乙校获胜的概率为23.设各局比赛相互之间没有影响且无平局.（1）求恰好比赛三局，比赛结束的概率；（2）求甲校以3:1获胜的概率.18.（17分）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，PD ⊥底面,22ABCD PD DC AD ===，E 是PC 的中点．（1）求证：//PA 平面EDB .（2）求平面EDB 与平面PAD 夹角的余弦值.（3）在棱PB 上是否存在一点F ，使直线EF ⊥平面EDB ？若存在，求出线段BF 的长；若不存在，说明理由．19.（17分）已知点M 与定点(6,0)A 和点M 与原点O 的距离的比为2，记点M 的轨迹为C .（1）求C 的方程.（2）已知直线:4l x =与x 轴交于点B .①过点B 的直线m 与曲线C 交于D ，E 两点，求线段DE 的中点F 的轨迹方程；②求证BD BE ⋅ 为定值，并求出这个定值.恩施州高中教育联盟2024年秋季学期高二年级期中考试数学参考答案1.D2.C3.A4.B5.B6.C7.C8.D9.ABC 10.AD 11.BD12.1213.40.414.522++15.解：（1）设1i z a b =+，则1i z a b =-，所以(12i)(i)112i a b +-=+，即211,22,a b a b +=⎧⎨-=⎩所以3,4a b ==，即134i z =+.设i,(,)z m n Z m n =+，由12z z -=知，(,)Z m n 在以(3,4)为圆心，2为半径的圆上，即32cos ,42sin ,m n θθ=+⎧⎨=+⎩所以(42cos ,42sin )(22cos ,42sin )ZA ZB θθθθ⋅=----⋅----=16sin 12cos 2820sin()28[8,48]θθθϕ++=++∈，即ZA ZB ⋅ 的取值范围是[8，48].16.解：（1）因为cos sin 0a C C b c --=，所以由正弦定理可知，sin cos sin sin sin 0A C A C B C +--=，即sin cos sin sin 0C A A C C --=.又sin 0C ≠，所以π2sin 16A ⎛⎫-= ⎪⎝⎭，即ππ66A -=或5π6，即π3A =或π（舍去）．（2）由（1）得π3A =，则2π3B C +=.由正弦定理可知,b Bc C ==，所以πsin )8sin6b c B C B ⎛⎫+=+=+ ⎪⎝⎭.因为ABC 为锐角三角，所以π2ππ0,0232B B <<<-<，即ππππ2π,62363B B <<<+<，即π8sin 6B ⎛⎫+∈ ⎪⎝⎭，故ABC的周长的取值范围为(4+.17.解：（1）恰好比赛三局，比赛结束的情况如下：甲校获胜，概率为1331355325P =⨯⨯=；乙校获胜，概率为2222855375P =⨯⨯=．故恰好比赛三局，比赛结束的概率123817257575P P P =+=+=.（2）甲校以3：1获胜的情况如下？①前两局男生羽毛球比赛中甲校全胜，第三局比赛甲校负，第四局比赛甲校胜，概率为23321253325P ⎛⎫=⨯⨯= ⎪⎝⎭；②前两局男生羽毛球比赛中甲校1胜1负，第三局比赛甲校胜，第四局比赛甲校胜，概率为4321142553375P =⨯⨯⨯⨯=.故甲校以3：1获胜的概率34242257515P P P '=+=+=.18.（1）证明：连接AC ，交BD 于点O ，连接OE .因为E 是PC 的中点，O 是AC 的中点，所以//PA OE ，又OE ⊂平面,EDB PA ⊂/平面EDB ，所以//PA 平面EDB.（2）解：如图，以DA DC DP 、、的方向分别为x ，y ，z轴的正方向建立空间直角坐标系，即()()()0,0,0,1,2,0,0,1,1D B E 则(1,2,0),(0,1,1)DB DE == .设平面EDB 的法向量为(,,)m x y z = ，则20,0,DB m x y DE m y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ 令1y =-，得2,1x z ==，所以可取(2,1,1)m =- .易知平面PAD 的一个法向量为(0,1,0)n = .设平面EDB 和平面PAD 的夹角为θ，则||6cos |cos ,|6||||m n m n m n θ⋅=〈〉=== ，所以平面EDB 和平面PAD 夹角的余弦值为6.（3）解：由（2）知(0,0,0),(1,2,0),(0,1,1),(0,0,2)D B E P ，则(1,1,1),(1,2,2),(,2,2)(01),EB BP BF BP EF EBλλλλλ=-=--==--<<= (1,1,1)(,2,2)(1,12,12)BF λλλλλλ+=-+--=---+ .由（2）知平面EDB 的一个法向量可为(2,1,1)m =- ，则直线//EF m ，即12121λλ-=-+，解得35λ=，故当35λ=时，95BF =，则BF 的长为95.19.解：（1）设(,)M x y ，则||2||MA MO =2=，化简得22(2)16x y ++=.（2）①不妨设曲线C 的圆心为C ，所以当C ，F 不重合时，CFB 为直角三角形，取BC 的中点(1,0)G ，则3FG =，所以F 的轨迹方程为222(1)93x y x ⎛⎫-+=< ⎪⎝⎭.（2）由题意知，直线DE 的斜率一定存在，设为k ，则:(4)DE l y k x =-，代入22(2)16x y ++=，得()()222214816120k x k x k ++-+-=，且240,5k ∆><.不妨设()()1122,,,D x y E x y ，则22121222841612,11k k x x x x k k--+==++，故()()()()()[211221212124,4,441BD BE x y x y x x y y k x x ⋅=-⋅-=-⋅-+=+- ()1241620x x ⎤++=⎦.。

小学数学四年级期中考试命题说明文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]小学数学四年级期中考试命题说明一：命题指导思想小学数学毕业考试是是衡量学生是否达到毕业水平的水平性考试小学数学（笔试）的命题，应努力体现课程标准的新理念，有利于调动全体学生学习数学的积极性，有利于提高我县小学数学教学质量.二：命题遵循的原则⒈全面性原则以《小学数学教学大纲（试用修订版）》规定的最低要求为基准以本届毕业班使用的小学数学课本所涉及的内容为考试范围，发挥考查学生数学学科的学习是否达到国家要求的小学毕业合格标准的功能。

⒉科学性原则命题内容无科学性错误，语言准确、简练，答案无歧义。

⒊导向性原则⑴试题注意联系生活实际，突出数学的实践性和应用性.①加强对实际操作能力的考查，如让学生量一量、画一画等。

②加强对估算意识、统计意识的考查，可估算范围、完成对统计表或图的制作和分析等。

⑵试题应重视对知识技能形成过程的考查，引导加强过程教学设计一些反映知识形成过程的试题使那些只重结论不重过程的教学、与注重让学生参与知识形成过程的教学,在测试结果上有区别,以引导教师和学生加强对学习过程的关注。

⒋试题应体现开放性试题的题型要避免程式化适当编制部分开放型题，来测评学生的思维创新能力和问题解决能力，并以此引导学生学习过程之中的探究与创新之风。

①概念、规则等知识的考查，把它们融合在数学问题的解决中去。

②应用题考查, 设计一些开放性试题.如一题多解,一题多问,一题多编,一题多变的题型, 题目的呈现方式也可是多种形式, 使之更接近生活实际.有些应用题的解决过程也不一定非要列出算式, 可以侧重写出解决问题的思维过程。

③设计问题解决方案。

依据问题目标，构思和探索问题解决的思路、策略。

三：考查要点数和数的运算代数初步知识应用题量与计量几何初步知识⒈数和数的运算包括：数的意义，数的读、写法，数的改写，数的大小比较数的整除，分数、小数的基本性质，四则运算的意义和法则四则混合运算，运算定律和简便算法。

期中考试命题制卷工作的一些要求
小学部各教师：
我校小学期中考试时间计划安排在4月24日（周四）。

现就命题制卷工作提出以下具体要求：
1、由各学科组长指定到人员（出题人应为熟悉教材，有经验的老师）命
题制卷，并对试题质量把好第一道关。

2、试题完全定稿后于4月17日晚办公前发电子版到教导处邮箱
【mfzxq@】,并找电脑老师打印出一份付印的样卷上交文印室曾雪映老师，上交样卷前出题教师要做一遍，发现问题及时修改。

3、卷面总分按100分出题（数学不另设附加题，语文如使用城区教育局
试卷请将末尾的“知识拓展”题删掉），考查内容为本学期教材的一半，试卷难易度比例是6:3:1【“6”是基础题，“3”是中等题，“1”是难题。

】
4、
第二行为“小学×年级××期中考试试题”【黑体二号加粗】
第三行为“班级姓名分数”【楷体四号加粗】下面试题部分字体为宋体（不必加粗），字号根据实际情况定，建议一、二年级字号稍大一些，行距根据实际题量调整合理。

要求提交的样卷用8K 纸，试卷中缝部分间隔适宜，方便对折，整张试卷做到排版合理、美观。

5、其他不明之处可到教导处了解。

小学教导处
2014年4月14日。

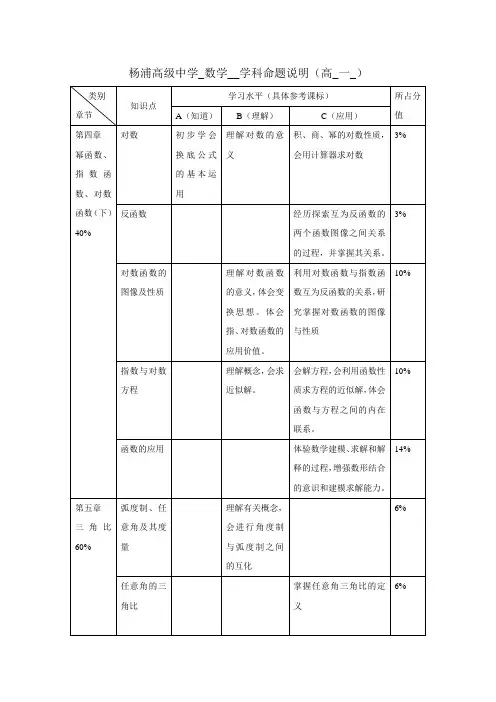
期中考试命题细则
1.备课组交叉命题。

语文、数学、英语、历史和政治学科交叉方式：初一命初三；初二命初一；初三命初二。

地理和生物学科交叉方式：初一命初二；初二命初一。

物理学科交叉方式：初二命初三；初三命初二。

化学学科无交叉，自行命题。

2.学科组长、备课组长负责制。

安排2人命题，一人主命题，一人
主审核，确保试卷质量。

3.考试范围统一（请命题老师相互沟通）；试题结构合理；试题难度
适中。

4.所有学科试卷卷面分值满分100分；
考试时长分配：语文120分钟；数学、英语、物理、化学90分钟；政治、历史、地理、生物60分钟。

5.试卷电子稿务必于10月21日前交至教务处王国伟老师处。

6.参与命题老师计工作量。

感谢您对教导处工作的理解和支持，谢谢！
教导处
2013/10/9。

江西省2024—2025学年上学期第一次模拟选科联考高一数学试卷共4页，19小题，满分150分。

考试用时120分钟。

注意事项：1.考查范围：必修第一册第一章至第三章第二节。

2.答卷前，考生务必将自己的姓名、准考证号等填写在答题卡指定位置上。

3.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

4.考生必须保持答题卡的整洁。

考试结束后，请将答题卡交回。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集，集合，，则A.{2,3,4,5}B.{1,3,4}C.{3,4}D.{3}2.已知命题，，则为A.， B.，C.， D.，3.已知为定义在R 上的奇函数，当时，，则A. B.C. D.4.已知是幂函数，若，则a =A.B.2C.4D.65.若A. B. C. D.6.已知定义在R 上的函数满足，且，且，，则A. B.C. D.7.若关于x 的不等式的解集为，且，则实数m 的值为}{1,2,3,4,5U =2}{1,M =}2,{3,4N =()U M N = ð:1p x ∃>320x ->p ⌝1x ∀…320x ->1x ∀…320x -…1x ∀>320x -<1x ∀>320x -…()f x 0x >31()1f x x x =-+(1)f -=12-1232-3292()(4)m f x m x -=-()2f a =121a <-=5(1)a -+5(1)a +6(1)a -+6(1)a +()f x (5)(5)f x f x +=-12,(5,)x x ∀∈+∞12x x ≠121[(()()x x x f --2]()0f x >(5.5)(4.5)f f >(2.7)(3.2)f f <(7.3)(7.9)f f >(2.7)(5.2)f f >220()21x m x m m +-+-<12(,)x x 12112x x +=A.-4B.-1C.1D.48.已知函数若存在实数x ，使，则实数a 的取值围为A. B.C. D.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.下列计算中正确的是A.C. D.10.使成立的一个充分条件可以是A.且 B.且C.且 D.且11.已知函数的定义域为R ，且的图象关于原点对称，的图象关于y 轴对称，则A. B.C.函数是增函数D.三、填空题：本题共3小题，每小题5分，共15分.12.已知函数，则________.13.已知幂函数的图象过点，则________.14.对于任意实数x ，表示不小于x 的最小整数，例如(1.2)=2，，表示不大于x 的最大整数，例如[1.2]=1，.已知定义在R 上的函数，若集合，则集合A 中所有元素的和为________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）已知函数在上单调递减，其中，且.（1）求的解析式；（2）求函数，的值域.16.（15分）已知集合，，且.23,2,(),2,x ax a x f x a x ⎧-++>⎪=…()0f x <(,1)-∞-(,2)(6,)-∞-+∞(,6)(1,)-∞--+∞(,1)(6,)-∞-+∞ 1144-=2=±23(8)4-=23184-=3a b c ->a c >2b c >-2a c >b c >-2a c >b c>-3a c >2b c>()f x (2)4y f x =+-(4)4y f x x =++(2)4f =(6)12f =-()f x (8)(4)824f x f x x -+-=-30,()()1,0,x f x g x x x x ==-<⎪⎩…((1))g f -=()m f x x =3(3,33[(2)]f =()x (0.2)0-=[]x 0.21[]-=-()(2)[3]f x x x =⋅4|(),23A y y f x x ⎧⎫==-<-⎨⎬⎩⎭…()af x b x=+(0,)+∞24a =(1)1f =()f x 2()2()[()]g x f x f x =+[1,4]x ∈(4,29]A m =+{|2233}B x m x m =-+……12B ∈（1）当时，求实数m 的取值范围；（2）设；，若p 是q 的必要不充分条件，求实数m 的取值范围.17.（15分）已知定义在R 上的奇函数与偶函数满足，若.（1）求的解析式；（2）求关于x 的不等式的解集.18.（17分）某糕点连锁店现有五家分店，出售A ，B 两款糕点，A 为特价糕点，为吸引顾客，按进价销售.已知用16000元购进A 糕点与用22000元购进B 糕点的重量相同，且B 糕点每斤的进价比A 糕点每斤的进价多6元.（1）求A ，B 两种糕点每斤的进价；（2）经市场调查发现，B 糕点每斤售价30元时，每月可售出3120斤，售价每提高1元，则每月少售出120斤，售价每降低1元，则每月多售出120斤，糕点店不会低于进价销售.则B 糕点每斤定价为多少元时，糕点店通过卖B 糕点获得的月利润最大？最大是多少？（3）因为使用进价销售的A 糕点物美价廉，所以深受顾客青睐，五个分店每月的总销量为10000斤.今年年初该连锁店用50万购进一批设备，用于生产A 糕点.已知每斤糕点的原材料价格为8元，若生产A 糕点n 个月（）所用的原材料之外的各种费用总计为万元，若只考虑A 糕点，记该连锁店前n 个月的月平均利润为z 万元，求z 的最大值.19.（17分）对非空数集A 及实数k ，定义，，已知.（1）当时，若集合A 为单元素集，求A ；（2）当时，若集合，求ab 的所有取值构成的集合；（3）若A 中有3个元素，求实数k 的取值范围.16A ∉:p t A ∈:q t B ∈()f x ()g x ()()2||2f x g x x x +=++()()()h x f x g x =⋅()h x 2(3)(3)0h x tx h x t -+-<*n ∈N 211324n n +2{|,}A k x x a k a A ==-∈ {|,}A k x x k a a A ⊗==-∈A k A k =⊗ 1k =3k ={,}A a b =江西省2024—2025学年上学期第一次模拟选科联考高一数学参考答案及评分细则1.【答案】A【解析】，故选A.2.【答案】D【解析】根据存在量词命题的否定是全称量词命题，得，.故选D.3.【答案】B【解析】因为为定义在R 上的奇函数，所以.故选B.4.【答案】C【解析】因为是幂函数，所以，得，故时，.故选C.5.【答案】C【解析】当时，.故选C.6.【答案】D【解析】由题意得函数在上单调递减，在上单调递增.对选项A ，，A 错误；对选项B ，因为函数在上单调递减，所以，B 错误；对选项C ，因为函数在上单调递增，所以，C 错误；对选项D ，因为，函数在上单调递减，故，D 正确.故选D.7.【答案】B【解析】因为关于x 的不等式的解集为，所以关于x 的方程有两个不相等的实数根，所以，解得，且，，所以，解得.故选B.8.【答案】D【解析】当时，，即，因为，所以，故有解，{3,4,5}{2,3,4}{2,3,4,5}()U M N == ð:1p x ⌝∀>320x -…()f x 311(1)(1)1112f f ⎛⎫-=-=--= ⎪+⎝⎭92()(4)m f x m x-=-41m -=5m =12()f x x ==2=4a =1a <-10a +<3(1)a =--3(1)a =+=336(1)(1)(1)a a a --+=-+()f x (,5)-∞(5,)+∞(5.5)(50.5)f f =+=(50.5)(4.5)f f -=()f x (,5)-∞(2.7)(3.2)f f <()f x (5,)+∞(7.3)(7.9)f f >(5.2)(5f f =+0.2)(50.2)(4.8)f f =-=()f x (,5)-∞(2.7)(4.8)(5.2)f f f >=220()21x m x m m +-+-<12(,)x x 220()21x m x m m +-+-=12,x x 22[2(1)]41()440m m m m ∆=--⨯⋅-=-+>1m <122(1)x x m +=--212x x m m =-1221212112(1)2x x m x x x x m m+--+===-1m =-2x >230x ax a -++<23(1)x a x +<-2x >11x ->231x a x +>-即，因为，当且仅当，即时等号成立，故；当时，有解，即有解，也即，因为单调递增，故时，取最大值-1，故.综上，实数a的取值范围为.故选D.9.【答案】ACD （每选对1个得2分）【解析】对于A ，，A 正确；对于B，B 错误；对于C ，，C 正确；对于D ，，D 正确.故选ACD.10.【答案】AC （每选对1个得3分）【解析】充分性成立，即选项能推出，对于A ，，又，同向不等式相加得，A 成立；对于B ，令，，，满足且，但，B 不成立；对于C ，，又，同向不等式相加得，，C 成立；对于D ，令，，，满足且，但，D 不成立.故选AC.11.【答案】ABD （每选对1个得2分）【解析】A 选项，的定义域为R ，因为的图象关于原点对称，所以为奇函数，所以，故，令，得，A 正确；B 选项，由的图象关于y 轴对称，得为偶函数，所以，即，令，得，得，B 正确；C 选项，因为，C 错误；D 选项，因为，所以，因为，令，得，即，故，，D 正确.故选ABD.12.【答案】-8【解析】，.13.【答案】64【解析】由，所以.14.【答案】67【解析】当时，；当时，，，2min31x ax ⎛⎫+>⎪-⎝⎭223(11)341226111x x x x x x +-++==-+++=--- (4)11x x -=-3x =6a >2x …0a +<a <max (a <y =2x =y =1a <-(,1)(6,)-∞-+∞ 1144-=2=23(8)4-==232311848-===3a b c ->22b c b c <-⇒->a c >3a b c ->3a =7b =1c =-2a c >b c >-433a b c -=-<-=b c b c <-⇒->2a c >3a b c ->5a =8b =1c =-3a c >2b c >33a b c -=-=()f x (2)4y f x =+-(2)4y f x =+-(2)4(2)40f x f x --++-=(2)(2)8f x f x -++=0x =(2)4f =(4)4y f x x =++(4)4y f x x =++(4)4(4)4f x x f x x --=++(4)(4)8f x f x x -=++2x =4(2)(6)16f f ==+(6)12f =-(2)(6)f f >(2)(2)8f x f x -++=()8(4)f x f x =--(4)(4)8f x f x x -=++4x t -=()(8)328f t f t t =-+-()(8)328f x f x x =-+-8(4)(8)328f x f x x --=-+-(8)(4)824f x f x x -+-=-(1)112f -=--=-3((1))(2)(2)8g f g -=-=-=-333m =3m =-3()f x x =333(3(36[(2)](22264f ⨯====2x =-()(4)[6](4)(6)24f x =-⋅-=-⨯-=523x -<<-10423x -<<-(2)3x =-，，；当时，，，，，；当时，，，，，.综上，，集合A 中所有元素的和为67.15.解：（1）由得，（2分）因为函数在上单调递减，所以，故.（5分）由得，所以.（7分）（2），（10分）当时，，，，所以函数，的值域为.（13分）【评分细则】值域写成集合或区间形式均给分.16.解：（1）因为，所以，得，（2分）又因为，所以，即，（5分）故当时，m 的取值范围是.（7分）（2）因为，所以，，若p 是q 的必要不充分条件，则B 是A 的真子集，（10分）故（12分）解得.故实数m 的取值范围是.（15分）【评分细则】结果写成集合或区间或不等式形式均给分.17.解：（1）因为，即，又，得，，（4分）635x -<<-[3]6x =-()(2)[3](3)(6)18f x x x =⋅=-⨯-=5332x -- (10)233x --……(2)3x =-9532x --……[3]5x =-()(2)[3](3)(5)15f x x x =⋅=-⨯-=3423x -<<-8323x -<<-(2)2x =-9342x -<<-[3]5x =-()(2)[3](2)(5)10f x x x =⋅=-⨯-={24,18,15,10}A =24a =2a =±()af x b x=+(0,)+∞0a >2a =(1)21f b =+=1b =-2()1f x x=-222424()2()[()]211g x f x f x x x x ⎛⎫=+=-+-=- ⎪⎝⎭[1,4]x ∈2[1,16]x ∈241,44x ⎡⎤∈⎢⎥⎣⎦2131,34x ⎡⎤-∈-⎢⎥⎣⎦2()2()[()]g x f x f x =+[1,4]x ∈3,34⎡⎤-⎢⎥⎣⎦12B ∈221233m m -+……37m ……16A ∉2916m +<72m <16A ∉73,2⎡⎫⎪⎢⎣⎭37m ……A O ≠B O ≠224,3329,m m m ->⎧⎨++⎩…36m <…(3,6]()()2||2f x g x x x -+-=-+-+()()2||2f x g x x x -+=-++()()2||2f x g x x x +=++()2f x x =()||2g x x =+所以.（5分）（2）因为，所以为奇函数，（7分）又当时，单调递增，故函数在R 上单调递增.（9分）则不等式，可化为，即，即，（11分）①若，即时，；②若，即时，不等式无解；③若，即时，，综上，当时，解集为，当时，解集为，当时，解集为.（15分）【评分细则】1.第一问求出和的解析式分别给2分；2.第一问结果写成分段函数形式不扣分；3.第二间结果不写成集合或区间形式扣1分，未总结，但结果正确均给满分，三种情况每少一种情况扣1分.18.解：（1）设A 糕点每斤的进价为a 元，B 糕点每斤的进价为元，所以，解得，所以A 糕点每斤的进价为16元，B 糕点每斤的进价为22元.（4分）（2）设B 糕点每斤涨价元，蛋糕店通过B 糕点获得的月利润为y 元.由题意，（6分）当时，y 有最大值.（8分）所以B 糕点每斤定价为39元时，月利润最大，最大为34680元.（9分）（3）设前n 个月的总利润为w ，因为A 糕点每斤售价为16元，每月可售出10000斤，故每月可收入16万元，其中原材料为8万元，则，（12分）月平均利润万元，（15分）()()()2(||2)h x f x g x x x =⋅=+()2()(||2)2(||2)()h x x x x x h x -=--+=-+=-()h x 0x …2()24h x x x =+()h x 2(3)(3)0h x tx h x t -+-<2(3)(3)(3)h x tx h x t h t x -<--=-23(3)0x t x t +--<(3)(1)0x t x -+<13t <-3t <-13tx <<-13t=-3t =-13t >-3t >-13t x -<<3t <-|13t x x ⎧⎫<<-⎨⎬⎩⎭3t =-∅3t >-|13t x x ⎧⎫-<<⎨⎬⎩⎭()f x ()g x (6)a +16000220006a a =+16a =(8)x x -…22(3022)(3120120)120216024960120(9)34680y x x x x x =+--=-++=--+9x =22*111311685050()324324w n n n n n n n ⎛⎫=--+-=-+-∈ ⎪⎝⎭N 503131215.2532444w n z n n ==--+-+==…当且仅当，即时等号成立，（16分）所以z 的最大值为5.25.（17分）【评分细则】1.第二问未配方，只要结果正确，就给分；2.第三问未说明等号成立条件扣1分.19.解：（1）时，设，由，得，所以，即，得或1，故或.（4分）（2）时，，由，得，得或即或（5分）当时，是方程的两根，故，（6分）当时，两式相减得，由集合中元素的互异性得，所以，故，即，同理，故是方程的两根，所以，（7分）故ab 的所有取值构成的集合为.（8分）（3）设，由，得，①若故是方程的三个不等的实数根，而此方程最多有两个实数根，不可能有三个实数根，故不成立；（11分）②若，当时，，令，得，（12分）对，，两式相减得，因为，所以，代入，得，同理，5032n n=40n =1k ={}A a =11A A =⊗ 2{1}{1}a a -=-211a a -=-220a a +-=2a =-{2}A =-1}{A =3k ={,}A a b =33A A =⊗ 22{3,3}{3,3}a b a b --=--2233,33a a b b ⎧-=-⎨-=-⎩2233,33,a b b a ⎧-=-⎨-=-⎩2260,60a a b b ⎧+-=⎨+-=⎩226,6,a b b a ⎧=-⎨=-⎩2260,60a ab b ⎧+-=⎨+-=⎩,a b 260x x +-=6ab =-226,6a b b a⎧=-⎨=-⎩22a b a b -=-a b ≠1a b +=266(1)5a b a a =-=--=+250a a --=250b b --=,a b 250x x --=5ab =-{6,5}--{,,}A a b c =A k A k =⊗ 222{,,}{,,}a k b k c k k a k b k c ---=---222,,,a k k a b k k b c k k c ⎧-=-⎪-=-⎨⎪-=-⎩,,a b c 220x x k +-=222,,,a k kb b k k ac k k c ⎧-=-⎪-=-⎨⎪-=-⎩2c k k c -=-220c c k +-=180k ∆=+ (1)8k -…2a k k b -=-2b k k a -=-22a b a b -=-a b ≠1a b +=2a k k b -=-2120a a k -+-=2120b b k -+-=故为方程的两个不相等的实根，令，得，（13分）当时，与均有两个不相等的实根，且这两个方程的根不完全相同，故符合题意；（14分）③若则，根据集合中元素的互异性，两两不相等，不妨设，（ⅰ）当时，，又，所以，这与矛盾，故不成立；（ⅱ）当时，，又，所以，这与矛盾，故不成立；（ⅲ）当时，，又，所以，这与矛盾，故不成立；（ⅳ）当时，，又，所以，这与矛盾，故不成立.（16分）综上，实数k 的取值范围是.（17分）【评分细则】1.第一问只得出一种情况，扣2分；结果不写成集合形式，扣1分；2.第二问求出ab 的一个值，给2分，最后结果不写成集合形式，扣1分；3.第三问结果写成不等式、集合或区间形式，结果正确即给满分.,a b 2120x x k -+-=14(12)0k '∆=-->38k >38k >2120x x k -+-=220x x k +-=222,,,a k k b b k k c c k k a ⎧-=-⎪-=-⎨⎪-=-⎩2222a b b c c a k +=+=+=,,a b c a b c >>0a b c >>>22a b >b c >22c a b b ++>22c a b b ++=0a b c >>>22a b >b c >22c a b b ++>22c a b b ++=0a b c >>>22b c <c a <22b c a c ++<22b c a c ++=0a b c >>>22b c <c a <22b c a c ++<22b c a c ++=3,8⎛⎫+∞ ⎪⎝⎭。

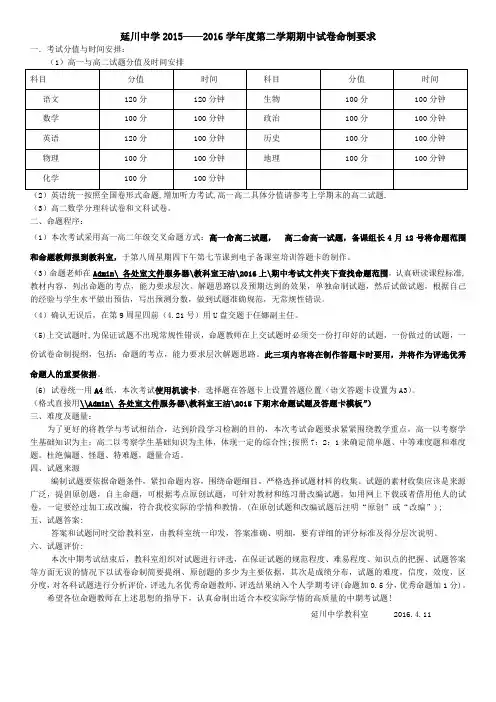
延川中学2015——2016学年度第二学期期中试卷命制要求一．考试分值与时间安排：（1）高一与高二试题分值及时间安排科目分值时间科目分值时间语文 120分120分钟生物100分100分钟数学 100分100分钟政治100分100分钟英语120分100分钟历史100分100分钟物理100分100分钟地理100分100分钟化学100分100分钟（2）英语统一按照全国卷形式命题,增加听力考试,高一高二具体分值请参考上学期末的高二试题.（3）高二数学分理科试卷和文科试卷。

二、命题程序：（1）本次考试采用高一高二年级交叉命题方式：高一命高二试题，高二命高一试题，备课组长4月12号将命题范围和命题教师报到教科室，于第八周星期四下午第七节课到电子备课室培训答题卡的制作。

（3）命题老师在Admin\ 各处室文件服务器\教科室王洁\2016上\期中考试文件夹下查找命题范围，认真研读课程标准,教材内容，列出命题的考点，能力要求层次、解题思路以及预期达到的效果，单独命制试题，然后试做试题，根据自己的经验与学生水平做出预估，写出预测分数，做到试题准确规范，无常规性错误。

（4）确认无误后，在第9周星四前（4.21号）用U盘交题于任娜副主任。

（5)上交试题时,为保证试题不出现常规性错误，命题教师在上交试题时必须交一份打印好的试题，一份做过的试题，一份试卷命制提纲，包括：命题的考点，能力要求层次解题思路。

此三项内容将在制作答题卡时要用，并将作为评选优秀命题人的重要依据。

(6) 试卷统一用A4纸，本次考试使用机读卡，选择题在答题卡上设置答题位置（语文答题卡设置为A3）。

（格式直接用\\Admin\ 各处室文件服务器\教科室王洁\2015下期末命题试题及答题卡模板”）三、难度及题量：为了更好的将教学与考试相结合，达到阶段学习检测的目的，本次考试命题要求紧紧围绕教学重点，高一以考察学生基础知识为主；高二以考察学生基础知识为主体，体现一定的综合性;按照7：2：1来确定简单题、中等难度题和难度题。

宜昌市协作体高一期中考试数学（答案在最后）考生注意：1.本试卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．．．．．．．．．．．．．．．．．．．．．．．．．．．。

4.本卷命题范围：人教A 版必修第一册第一章～第三章第2节。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{}2A x x =∈≤N ，{}23B x x =-<≤，则A B = （）A.{}0,1,2 B.{}1,2 C.{}0,1 D.{}12.设命题p ：0x ∃<，使得20x x+≥，则p ⌝为（）A.0x ∀<，都有20x x +< B.0x ∀≥，都有20x x +≥C.0x ∃<，使得20x x+< D.0x ∃≥，使得20x x+≥3.下列说法正确的是（）A.若0a b >>，则ac bc >B.若a b >，则a b >C.若0a b <<，则2$a ab > D.若a bc >>，则a a cb b c+>+4.下列四个函数中，在()0,+∞上为增函数的是（）A.()3f x x =-B.()2f x x x=+C.()f x x=- D.()31f x x =--5.“21a >”是“10a>”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知函数()()21,2,23,2,f f x x x x x x ⎧->-=⎨+-≤-⎩则()()1ff =（）A.5B.0C.-3D.-47.若函数()21f x x ax =++是定义在(),22b b --上的偶函数，则2b f ⎛⎫=⎪⎝⎭（）A.14B.54C.74D.28.若正数x ，y 满足20xy x y --=，则2yx +的最小值是（）A.2B.C.4D.二、选择题：本题共4小题，每小题5分，共20分。