数列极限的定义(课堂PPT)

当n无限增大时, an无限接近于a . 当n无限增大时, |ana|无限接近于0 . 当n无限增大时, |ana|可以任意小, 要多小就能有多小. 当n增大到一定程度以后, |ana|能小于事先给定的任意 小的正数.
因此, 如果 n 增大到一定程度以后, |ana|能小于事先 给定的任意小的正数, 则当n无限增大时, an无限接近于常 数a.
a1
an a4 a3 a5 a2
2
数列的极限
例如
12,14,18,,21n,;
2,3,4,L,n1,L; 23 n
{
1 2n
}
{n 1} n
14 n(1)n1
2, , ,,
,;
23
n
n (1)n1
{
}
n
观 察 数 列 { a n } 当 n 时 的 变 化 趋 势 .
3
当n无限增大时, 如果数列{an}的一般项an无限接近 于常数a, 则数列{an}收敛a.
4
通过观察:
当 n 无 限 增 大 时 ,a n 1 ( 1 n ) n 1无 限 接 近 于 1 .
问题: “无限接近”意味着什么?如何用数学语言刻划
它.
我们可用两个数之间的‘距离’来刻化两个数
的
接近程度. Qan1
1
(1)n1 n
1
(1)n1 1 1 nn
随着n的增加，1/n会越来越小.
注意: (1)由于N 不唯一,不要求最小的N,故可把 |ana|适当放大,得到一个新的不等式,再寻找 N.
(2)从 |ana|< 找 N 与解不等式 |ana|< 意义不同.
12
例3 证li明 q m n0 ,其 |q中 |1 . n
证 任给 0, 若q0, 则lim qnlim 0 0;
n
n
a 2 a
a 2 a 1 a N 1 a a N 2 a 3
x
当 n N 时 ,所 有 的 点 a n 都 落 在 (a ,a )内 ,
只 有 有 限 个 (至 多 只 有 N 个 )落 在 其 外 . 9
例1 ， 数列 2n1， (1)n1都没有极限.
如果当n无限增大时，数列 a n 不能接近于一个确定的常数，
收敛于
a，
a
称
为
它
的
极
限
，
记
作
lim
n
an
a
或
an a (n )．
如果数列 an 没有极限，则称它是发散的或发
散数列．
注意: N 定 义 的 要 点 . 0,存在 N（），使得 nN ， 时当 ，
ana成立
(
)
a a a
8
N定义 :
0,存在 N（），使得 nN ， 时当 ， ana成立
几何解释:
若 0|q|1, |an0||q|n,
nln |q|ln ,n
ln
ln| q
|
,
对 10,取N ln , 则n 当 N时 ,
ln|q|
恒|有 qn0|,
lim qn0. n
13
证明 lim(1)n不存.在 n
只要n无限增大，an 无法与始终和1无限靠近, 也无法和始终和－1无限靠近。
0 | q | 1
5
Qan1
1 (1)n1 n
1
(1)n1 1 n
1 n
随着n的增加，1/n会越来越小.例如
给定 1,
由 1 1, n
只要n1时,
有an11,
给定 1 , 由 1 1 ,
10
n 10
只 要n10时 ,
有
an
1
1, 10
给 给定 定11100100,0,由只 n1 110n 要 0 , 1 只 0时 n 0要 ,01 有0 时 an,0 1有1a0n1001,
7 9n
1 n
对 0, 取N1 , 则n 当 N时 ,
总2 有 n121,
3n1 3 n
lim 2n12.
n3n1 30,存在 N（），使得 nN ， 时当 ，
ana成立
11
用定义证明
lim
n
an=
a，就是证明对
>0，N存在.
证明的步骤：
(1) 对于任意给定的正数 , 令 |ana|< ; (2) 由上式开始分析倒推, 推出 n > () ; (3)取N=[ ()] , 再用 N语言顺述结论.
1, 100
给定10100,0只要 n100时 0, 有 0 an1100100,
[x]为取整函数
任 意 给 定0,
只要nN([1])时,
有an1成立.6
Qan1
1
(1)n1 n
1
(1)n1 1 1 nn
只要n无限增大，an 就会与1无限靠近,即 an1可 任 意 小
引入符号和N来刻化无限靠近和无限增大.
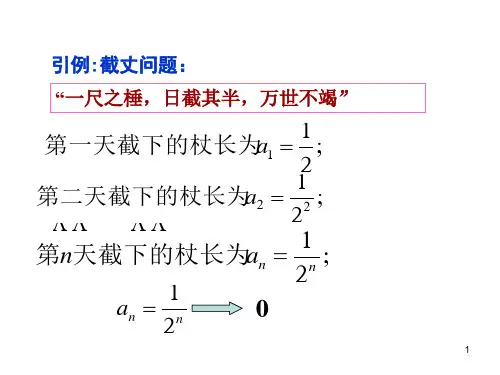
引例:截丈问题：
“一尺之棰，日截其半，万世不竭”
第一天截下的杖a长 1 为 12;
第 二 天截 下的杖a长 2 为 212 ;
第n天截下的杖an长 2为 1n ;
1
an 2n
0
1
2、数列
数列{an }.
注意: 数列对应着数轴上一个点列,可看作一动
点在数轴上依次取 a 1,a 2,L ,a n ,Lq1
不存q在 1
14
n
an充分接近1
nN 确保 an 1
(刻 画 a n 与 1 的 接 近 程 度 )
给定 0, 只要 nN([1]时 ) ,有an1成 立 . 7
定义 1( N 定义) 设 an 是一个数列， a 是一
个确定的数，若对任给的正数 ，相应地存在正整数
N，使得当n N 时，总有 an a ，则称数列 an
lim 则称数列an 没有极限，或称数列
a n
发散，记作
n
an不
存在.
当 n 无限增大时，如果 a n 无限增大，则数列没有极限.这时，
习惯上也称数列 a的n 极限是无穷大，记作
liman
n
10
例2 证l明 im 2n12. n 3n1 3
证
an a
2n1 2 7 3n1 3 3(3n 1)