配套K12全效学习2016版中考数学 第十单元 相似形 第33课时 相似形的应用练习(含解析)

相似形的应用(60分)一、选择题(每题6分，共24分)1．为了测量被池塘隔开的A ，B 两点之间的距离，根据实际情况，作出如图33－1所示的图形，其中AB ⊥BE ，EF ⊥BE ，AF 交BE 于D ，C 在BD 上．有四位同学分别测量出以下四组数据： ①BC ，∠ACB ；②CD ，∠ACB ，∠ADB ；③EF ，DE ，BD ；④DE ，DC ，BC .能根据所测数据，求出A ，B 间距离的有(C)图33－1 A ．1组 B ．2组 C ．3组 D ．4组 【解析】 此题比较综合，要多方面考虑．①因为知道∠ACB 和BC 的长，所以可利用∠ACB 的正切来求AB 的长； ②可利用∠ACB 和∠ADB 的正切求出AB ； ③因为△ABD ∽△FED ，可利用FE AB ＝DEDB求出AB ； ④无法求出A ，B 间距离．故共有3组数据可以求出A ，B 间距离．2．如图33－2是小明设计的用手电来测量某古城墙高度的示意图，点P 处放一水平的平面镜，光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处，已知AB ⊥BD ，CD ⊥BD ，且测得AB ＝1.2 m ，BP ＝1.8 m ，PD ＝12 m ，那么该古城墙的高度是 (B)A ．6 mB ．8 mC ．18 mD ．24 m【解析】 由平面镜的入射角等于反射角， 易得∠APB ＝∠CPD .又∵∠B ＝∠D ＝90°，∴△ABP ∽△CDP ，∴PB PD ＝AB CD ，即1.812＝1.2CD， 解得CD ＝8 m.3．[2014·达州]如图33－3，以点O 为支点的杠杆，在A 端用竖直向上的拉力将重为G 的物体匀速拉起，当杠杆OA 水平时，拉力为F ；当杠杆被拉至OA 1时，拉力为F 1，过点B 1作B 1C ⊥OA ，过点A 1作A 1D ⊥OA ，垂足分别为点C ，D.图33－2图33－3①△OB 1C ∽△OA 1D ；②OA ·OC ＝OB ·OD ； ③OC ·G ＝OD ·F 1；④F ＝F 1.上述4个结论中，正确结论有 (D)A ．1个B ．2个C ．3个D ．4个 4．[2015·聊城模拟]如图33－4，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为1 m 的竹竿的影长是0.8 m ，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，她先测得留在墙壁上的影高为1.2 m ，又测得地面的影长为2.6 m ，请你帮她算一下，树高是 (C)A ．3.25 mB ．4.25 mC ．4.45 mD ．4.75 m 【解析】 设BD 是BC 在地面的影子，树高为x ，根据竹竿的高与其影子的比值和树高与其影子的比值相同得CB BD ＝10.8，而CB ＝1.2，∴BD ＝0.96，∴树在地面的实际影子长是0.96＋2.6＝3.56， 再竹竿的高与其影子的比值和树高与其影子的比值相同得x3.56＝10.8.解得x ＝4.45.∴树高为4.45 m.二、填空题(每题6分，共24分)5．[2015·新疆]如图33－5，李明打网球时，球恰好打过网，且落在离网4 m 的位置上，则网球拍击球的高度h 为__1.4__m.图33－5【解析】 由题意得，DE ∥BC ， ∴△ABC ∽△AED ， ∴DE BC ＝AE AB，图33－4即0.8h ＝44＋3， 解得h ＝1.4 m ．∴击球高度为1.4 m.6．如图33－6，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上．若光源到幻灯片的距离为20 cm ，到屏幕的距离为60 cm ，且幻灯片中图形的高度为6 cm ，则屏幕上图形的高度为__18__cm.【解析】 根据相似三角形的性质，对应高的比等于相似比进行解答．7．[2014·遵义]“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》．意思是说：如图33－7，矩形城池ABCD ，东边城墙AB 长9里，南边城墙AD 长7里，东门点E ，南门点F 分别是AB ，AD 中点，EG ⊥AB ，FH ⊥AD ，EG ＝15里，HG 经过A 点，则FH ＝__2120__里．图33－78．[2015·达州]如图33－8，将矩形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，点D 落在D ′处，C ′D ′交AE 于点M .若AB ＝6，BC ＝9，则AM 的长为__94__.【解析】 ∵C ′是AB 的中点，AB ＝6， ∴AC ′＝BC ′＝3，∵四边形DCFE 沿EF 翻折至D ′C ′FE ， ∴CF ＝C ′F ，∠C ＝∠MC ′F ， ∴BC ＝BF ＋FC ＝BF ＋FC ′＝9， ∴FC ′＝9－BF ，在Rt △BC ′F 中，根据勾股定理，得BF 2＋BC ′2＝FC ′2，即32＋BF 2＝(9－BF )2， 解得BF ＝4，∴FC ′＝5，又∵∠BFC ′＋∠BC ′F ＝90°，∠AC ′M ＋∠BC ′F ＝90°， ∴∠BFC ′＝∠AC ′M ，∵∠A ＝∠B ＝90°，∴△FC ′B ∽△C ′MA ， ∴BF AC ′＝BC ′AM ，即43＝3AM， ∴AM ＝94.三、解答题(共20分) 图33－6图33－89．(10分)[2014·岳阳]如图33－9，矩形ABCD 为台球桌面．AD ＝260 cm ，AB ＝130 cm.球目前在E 点位置，AE ＝60 cm.如果小丁瞄准BC 边上的点F 将球打过去，经过反弹后，球刚好弹到D 点的位置．(1)求证：△BEF ∽△CDF ； (2)求CF 的长．解：(1)由题意，得∠EFG ＝∠DFG ，∵∠EFG ＋∠BFE ＝90°，∠DFG ＋∠CFD ＝90°， ∴∠BFE ＝∠CFD ，∵∠B ＝∠C ＝90°， ∴△BEF ∽△CDF ；(2)∵△BEF ∽△CDF ，∴BE CD ＝BF CF， ∴70130＝260－CF CF，∴CF ＝169. 10．(10分)[2015·菏泽]如图33－10，M ，N 为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞，工程人员为计算工程量，必须计算M ，N 两点之间的直线距离，选择测量点A ，B ，C ，点B ，C 分别在AM ，AN 上，现测得AM ＝1 km ，AN ＝1.8 km ，AB ＝54 m ，BC ＝45 m ，AC ＝30 m ，求M ，N 两点之间的直线距离． 解：连结MN ， ∵AC AM ＝301 000＝3100，AB AN ＝541 800＝3100，∴AC AM ＝AB AN，∵∠BAC ＝∠NAM ，∴△BAC ∽△NAM ， ∴BC MN ＝3100，∴45MN ＝3100，∴MN ＝1 500.答：M ，N 两点之间的直线距离为1 500 m.(20分)11．(10分)[2015·邵阳]如图33－11，某校数学兴趣小组利用自制的直角三角形硬纸板DEF 来测量操场旗杆AB 的高度，他们通过调整测量位置，使斜边DF 与地面保持平行，并使边DE 与旗杆顶点A 在同一直线上，已知DE ＝0.5 m ，EF ＝0.25 m ，目测点D 到地面的距离DG ＝1.5 m ，到旗杆的水平距离DC ＝20 m ，求旗杆的高度．图33－11图33－9图33－10第10题答图【解析】 根据题意可得△DEF ∽△DCA ，进而利用相似三角形的性质得出AC 的长，即可得出答案．解：由题意可得△DEF ∽△DCA ， 则DE DC ＝EF CA，∵DE ＝0.5 m ，EF ＝0.25 m ， DG ＝1.5 m ，DC ＝20 m ， ∴0.520＝0.25AC，解得AC ＝10， 故AB ＝AC ＋BC ＝10＋1.5＝11.5(m)， 答：旗杆的高度为11.5 m.12．(10分)如图33－12，四边形ABCD 中，AC 平分∠DAB ，∠ADC ＝∠ACB ＝90°，E 为AB 的中点．(1)求证：AC 2＝AB ·AD ； (2)求证：CE ∥AD ；(3)若AD ＝4，AB ＝6，求AC AF的值． 解：(1)证明：∵AC 平分∠DAB ， ∴∠DAC ＝∠CAB .又∵∠ADC ＝∠ACB ＝90°， ∴△ADC ∽△ACB ， ∴AD AC ＝AC AB，∴AC 2＝AB ·AD ；(2)证明：∵在Rt △ACB 中，E 为AB 的中点， ∴CE ＝12AB ＝AE ，∴∠EAC ＝∠ECA . 又∵∠CAD ＝∠CAB ， ∴∠DAC ＝∠ECA ， ∴CE ∥AD ； (3)∵CE ∥AD .∴∠DAF ＝∠ECF ，∠ADF ＝∠CEF ， ∴△AFD ∽△CFE ， ∴AD CE ＝AF CF.∵CE ＝12AB ，AB ＝6，∴CE ＝12×6＝3.又∵AD ＝4，由AD CE ＝AF CF 得43＝AFCF ，∴AF AC ＝47，∴AC AF ＝74. 图33－12(12分)13．(12分)[2015·德州] (1)问题如图33－13①，在四边形ABCD 中，点P 为AB 上一点，∠DPC ＝∠A ＝∠B ＝90°. 求证：AD ·BC ＝AP ·BP ； (2)探究如图②，在四边形ABCD 中，点P 为AB 上一点，当∠DPC ＝∠A ＝∠B ＝θ时，上述结论是否依然成立？说明理由； (3)应用请利用(1)(2)获得的经验解决问题：如图③，在△ABD 中，AB ＝6，AD ＝BD ＝5.点P 以每秒1个单位长度的速度，由点A 出发，沿边AB 向点B 运动，且满足∠DPC ＝∠A .设点P 的运动时间为t (s)，当以D 为圆心，以DC 为半径的圆与AB 相切，求t 的值．图33－13解：(1)证明：∵∠DPC ＝∠A ＝∠B ＝90°， ∴∠ADP ＋∠APD ＝90°， ∠BPC ＋∠APD ＝90°， ∴∠ADP ＝∠BPC . ∴△ADP ∽△BPC . ∴AD BP ＝AP BC.∴AD ·BC ＝AP ·BP ；(2)结论AD ·BC ＝AP ·BP 仍成立． 理由：∵∠BPD ＝∠DPC ＋∠BPC ， 又∵∠BPD ＝∠A ＋∠ADP ， ∴∠DPC ＋∠BPC ＝∠A ＋∠ADP . ∵∠DPC ＝∠A ＝θ， ∴∠BPC ＝∠ADP ， 又∵∠A ＝∠B ＝θ， ∴△ADP ∽△BPC ， ∴AD BP ＝AP BC，∴AD ·BC ＝AP ·BP ；(3)如答图，过点D 作DE ⊥AB 于点E . ∵AD ＝BD ＝5，AB ＝6.∴AE ＝BE ＝3.由勾股定理得DE ＝4.∵以D 为圆心，以DC 为半径的圆与AB 相切．第13题答图∴DC＝DE＝4.∴BC＝5－4＝1，又∵AD＝BD，∴∠A＝∠B.∵∠DPC＝∠A，∴∠DPC＝∠A＝∠B.由(1)，(2)的经验可知AD·BC＝AP·BP. 又AP＝t，BP＝6－t，∴t(6－t)＝5×1.解得t1＝1，t2＝5.∴t的值为1 s或5 s.。

2016年全国中考数学真题分类相似形及应用一、选择题1．（2016安徽，8，4分）如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（）A．4 B．4C．6 D．4【考点】相似三角形的判定与性质．【分析】根据AD是中线，得出CD=4，再根据AA证出△CBA∽△CAD，得出=，求出AC即可．【解答】解：∵BC=8，∴CD=4，在△CBA和△CAD中，∵∠B=∠DAC，∠C=∠C，∴△CBA∽△CAD，∴=，∴AC2=CD•BC=4×8=32，∴AC=4；故选B．2．（2016甘肃定西，7，3分）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16 B．1：4 C．1：6 D．1：2【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答即可．【解答】解：∵两个相似三角形的面积比是1：4，∴两个相似三角形的相似比是1：2，∴两个相似三角形的周长比是1：2， 故选：D ．【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方是解题的关键．3. （2016浙江杭州，2,3分） 如图，已知直线a ∥b ∥c ，直线m 交直线a ，b ，c 于点A ,B ,C ，直线n 交直线a ，b ，c 于点D ,E ,F ,若12AB BC=,则DE EF=（ ）FE D CB A cb a nmA. 13B.12C. 23D.1 【答案】B4．（2016新疆生产建设兵团，7，5分）如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，下列说法中不正确的是（ ）A ．DE=BCB ． =C ．△ADE ∽△ABCD ．S △ADE ：S △ABC =1：2【考点】相似三角形的判定与性质；三角形中位线定理．【分析】根据中位线的性质定理得到DE ∥BC ，DE=BC ，再根据平行线分线段成比例定理和相似三角形的性质即可判定． 【解答】解：∵D 、E 分别是AB 、AC 的中点， ∴DE ∥BC ，DE=BC ， ∴=，△ADE ∽△ABC ，∴，∴A，B，C正确，D错误；故选：D．【点评】该题主要考查了平行线分线段成比例定理和相似三角形的性质即可判定；解题的关键是正确找出对应线段，准确列出比例式求解、计算、判断或证明．5.（2016河北，15，2分）如图，△ABC中，∠A=78°，AB=4，AC=6.将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似．．．的是（ C ）第15题图答案：Ｃ解析：只要三个角相等，或者一角相等，两边成比例即可。

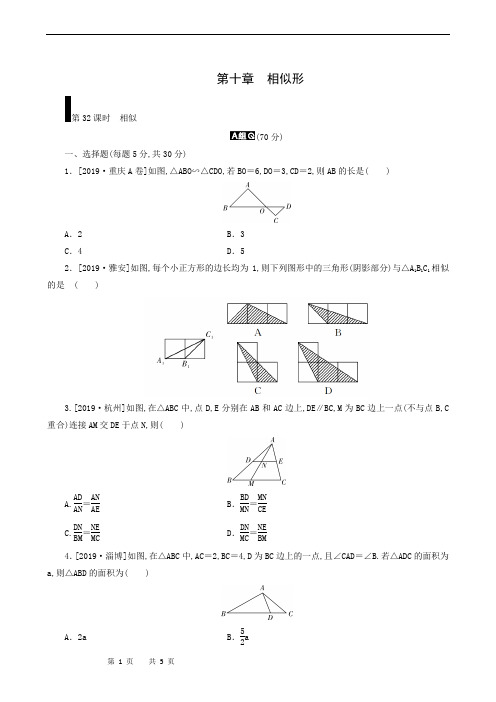
第十章 相似形第32课时 相似(70分)一、选择题(每题5分,共30分)1．[2019·重庆A 卷]如图,△ABO ∽△CDO,若BO ＝6,DO ＝3,CD ＝2,则AB 的长是( )A ．2B ．3C ．4D ．52．[2019·雅安]如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A 1B 1C 1相似的是 ( )3.[2019·杭州]如图,在△ABC 中,点D,E 分别在AB 和AC 边上,DE ∥BC,M 为BC 边上一点(不与点B,C 重合)连接AM 交DE 于点N,则( )A.AD AN ＝AN AE B ．BD MN ＝MN CE C.DN BM ＝NE MCD ．DN MC ＝NE BM4．[2019·淄博]如图,在△ABC 中,AC ＝2,BC ＝4,D 为BC 边上的一点,且∠CAD ＝∠B.若△ADC 的面积为a,则△ABD 的面积为( )A ．2aB ．52aC ．3aD ．72a 5．[2019·安徽]如图,在Rt △ABC 中,∠ACB ＝90°,AC ＝6,BC ＝12.点D 在边BC 上,点E 在线段AD 上,EF ⊥AC 于点F,EG ⊥EF 交AB 于点G,若EF ＝EG,则CD 的长为( )A ．3.6B ．4C ．4.8D ．56．[2019·巴中]如图,在▱ABCD 中,F 为BC 的中点,延长AD 至点E,使DE ∶AD ＝1∶3,连接EF 交DC 于点G,则S △DEG ∶S △CFG ＝( )A ．2∶3B ．3∶2C ．9∶4D ．4∶9二、填空题(每题4分,共20分)7．[2018·成都]已知a 6＝b 5＝c4,且a ＋b －2c ＝6,则a 的值为________．8．[2018·北京]如图,在矩形ABCD 中,E 是边AB 的中点,连接DE,交对角线AC 于点F.若AB ＝4,AD ＝3,则CF ＝____________.9．[2017·潍坊]如图,在△ABC 中,AB≠AC ,D,E 分别为边AB,AC 上的点,AC ＝3AD,AB ＝3AE,点F 为BC 边上一点,添加一个条件：________________________,可以使得△FDB 与△ADE 相似(只需写出一个即可)．10．[2019·包头]如图,BD 是⊙O 的直径,A 是⊙O 外一点,点C 在⊙O 上,AC 与⊙O 相切于点C,∠CAB ＝90°,若BD ＝6,AB ＝4,∠ABC ＝∠CBD,则弦BC 的长为________．11．[2019·荆州]如图,AB 为⊙O 的直径,C 为⊙O 上一点,过B 点的切线交AC 的延长线于点D,E 为弦AC 的中点,AD ＝10,BD ＝6,若点P 为直径AB 上的一个动点,连接EP,当△AEP 是直角三角形时,AP 的长为________．三、解答题(共20分)12．(10分)[2019·自贡改编]如图,在Rt △ABC 中,∠ACB ＝90°,AB ＝10,BC ＝6,CD ∥AB,∠ABC 的平分线BD 交AC 于点E,求DE.13．(10分)[2019·达州]如图,在Rt △ABC 中,∠ACB ＝90°,AC ＝2,BC ＝3. (1)尺规作图：不写作法,保留作图痕迹．①作∠ACB 的平分线,交斜边AB 于点D; ②过点D 作BC 的垂线,垂足为点E; (2)在(1)作出的图形中,求DE 的长．(20分)14．(10分)[2018·雅安]如图,四边形ABCD 和四边形ACED 都是平行四边形,点R 为DE 的中点,BR 分别交AC,CD 于点P,Q.(1)求证：△ABC ≌△DCE; (2)求PQPR的值．15．(10分)[2019·菏泽]如图,BC 是⊙O 的直径,CE 是⊙O 的弦,过点E 作⊙O 的切线,交CB 的延长线于点G,过点B 作BF ⊥GE 于点F,交CE 的延长线于点A.(1)求证：∠ABG ＝2∠C;(2)若GF ＝33,GB ＝6,求⊙O 的半径．(10分)16．(10分)[2019·凉山]如图,∠ABD ＝∠BCD ＝90°,DB 平分∠ADC,过点B 作BM ∥CD 交AD 于点M,连接CM 交DB 于点N.(1)求证：BD 2＝AD·CD ; (2)若CD ＝6,AD ＝8,求MN 的长．参考答案1．C 2.B 3.C 4.C 5.B 6.D 7．12 8.1039．∠A ＝∠BDF 或∠A ＝∠BFD 或∠ADE ＝∠BFD 或∠ADE ＝∠BDF 或DF ∥AC 或BD EA ＝BF ED 或BD ED ＝BFEA10．2 6 11.4或2.56 12.95513．(1)略 (2)65 14.(1)略 (2)1315．(1)略 (2)6 16.(1)略 (2)475关闭Word 文档返回原板块。

课时03 图形的相似一、本节课的知识点1.相似图形定义：形状相同的图形叫做相似图形。

2.相似多边形定义：两个边数相同的多边形，如果它们的角分别相等，边成比例，那么这两个多边形叫做相似多边形。

相似多边形对应边的比叫做相似比。

3.性质相似多边形的对应角相等，对应边成比例。

二、对理解本节课知识点的例题及其解析【例题1】如图，在四边形ABCD与四边形EFGH中，∠A=80°，∠B=90°，∠C=120°，∠F=90°，∠G=120°，∠H=70°，四边形ABCD与四边形EFGH相似吗？【答案】见解析【解析】给出错解和正解两种情况的分析。

错解：在四边形ABCD中，由∠A=80°，∠B=90°，∠C=120°，得∠D=70°；在四边形EFGH中，由∠F=90°,∠G=120°，∠H=70°，得∠E=80°.∴∠A=∠E，∠B=∠F，∠C=∠G，∠D=∠H.∴四边形ABCD与四边形EFGH相似.剖析：不能准确地由相似形的定义判定相似.要判定两个图形是否相似，要看对应角是否相等，对应边是否成比例，二者缺一不可.正解：在四边形ABCD中，由∠A=80°，∠B=90°，∠C=120°，得∠D=70°；在四边形EFGH中，由∠F=90°∠G=120°，∠H=70°，得∠E=80°.∴∠A=∠E，∠B=∠F，∠C=∠G，∠D=∠H，但是根据已知条件无法判定对应边是否成比例.∴四边形ABCD与四边形EFGH不一定相似.【例题2】要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm，6cm和9cm，另一个三角形的最短边长为2.5cm，则它的最长边为（）A．3cm B．4cm C．4.5cm D．5cm【答案】C．【解析】根据相似三角形的对应边成比例求解可得．设另一个三角形的最长边长为xcm ， 根据题意，得：=，解得：x=4.5，即另一个三角形的最长边长为4.5cm ，故选：C ．【例题3】如图，AB ∥CD ∥EF ，AF 与BE 相交于点G ，且AG=2，GD=1，DF=5，那么BC/CE 的值等于 ．【答案】3/5．【解析】首先求出AD 的长度，然后根据平行线分线段成比例定理，列出比例式BC/CE=AD/DF 即可得到结论．∵AG=2，GD=1，∴AD=3，∵AB ∥CD ∥EF ，BC/CE=AD/DF=3/5【例题4】如图：AD 平分BAC ∠交BC 于D ，求证：BD AB DC AC=．321ED C AB【答案】见解析【解析】过C 作CE AD ∥，交BA 的延长线于E ．∴1E ∠=∠，23∠=∠．∵12∠=∠，∴3E ∠=∠．∴AC AE =．∵AD CE ∥，∴BD BA BA DC BE AC==． 注意：过B 作AC 的平行线，交AD 的延长线于E ．也可以证明。

相似形第32课时相似形(60分)一、选择题(每题5分，共30分)1．丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥，比例尺为1∶500的图纸上的大桥的长度约为1.04 m，则大桥的实际长度约是 (D)A．104 m B．1 040 mC．5 200 m D．520 m【解析】设大桥的实际长度为x，依题意，得1∶500＝1.04∶x；得x＝1.04×500＝520(m)．2．[2015·南京]如图32－1，在△ABC中，DE∥BC，ADDB＝12，则下列结论中正确的是 (C)A.AEAC＝12B.DEBC＝12C.△ADE的周长△ABC的周长＝13D.△ADE的面积△ABC的面积＝133．[2015·永州]如图32－2，下列条件不能判定△ADB∽△ABC的是(D)A．∠ABD＝∠ACB B．∠ADB＝∠ABCC．AB2＝AD·AC D.ADAB＝ABBC【解析】在△ADB和△ABC中，∠A是它们的公共角，那么当ADAB＝ABAC时，才能使△ADB∽△ABC，不是ADAB＝ABBC.故答案选D.4．[2014·河北]在研究相似问题时，甲乙同学的观点如下：甲：将边长为3，4，5的三角形按图32－3①的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．①②图32－3乙：将邻边为3和5的矩形按图32－3②的方式向外扩张，得到新矩形，它们的对应边间距图32－1图32－2为1，则新矩形与原矩形相似．对于两人的观点，下列说法正确的是 (C)A ．两人都对B ．两人都不对C ．甲对，乙不对D ．甲不对，乙对 5．如图32－4，在平行四边形ABCD 中，E是AB 的中点，CE 和BD 交于点O ，设△OCD 的面积为m ，△OEB 的面积为5，则下列结论中正确的是 (B) A ．m ＝5 B ．m ＝4 5 C ．m ＝3 5 D ．m ＝10【解析】 ∵AB ∥CD ，∴△OCD ∽△OEB ， 又∵E 是AB 的中点，∴2EB ＝AB ＝CD ，∴S △OEB S △OCD ＝⎝ ⎛⎭⎪⎫BE CD 2，即5m ＝⎝ ⎛⎭⎪⎫122， 解得m ＝4 5. ∴m 的值为4 5.6．[2015·武威]如图32－5，D ，E 分别是△ABC 的边AB ，BC 上的点，DE ∥AC ，若S △BDE ∶S △CDE ＝1∶3，则S △DOE ∶S △AOC 的值为 (D) A.13 B.14 C.19D.116【解析】 ∵S △BDE ∶S △CDE ＝1∶3， ∴BE ∶EC ＝1∶3， ∴BE ∶BC ＝1∶4，∵DE ∥AC ，∴△DOE ∽△COA ，△BED ∽△BCA ，∴DE AC ＝BE BC ＝14， ∴S △DOE ∶S △AOC ＝⎝ ⎛⎭⎪⎫DE AC 2＝116.二、填空题(每题5分，共20分)7．[2015·东莞]若两个相似三角形的周长比为2∶3，则它们的面积比是__4∶9__．8．[2015·金华]如图32－6，直线l 1，l 2，…，l 6是一组等距的平行线，过直线l 1上的点A 作两条射线，分别与直线l 3，l 6相交于B ，E ，C ，F ，若BC ＝2，则EF 的长是__5__.图32－69．[2015·梅州]如图32－7，△ABC 中，点E 是AB 边的中点，点F 在AC 边上，若以A ，E ，F 为顶点的三角形与△ABC 相似，则需要增图32－4图32－5加的一个条件是__AF ＝12AC或∠AFE ＝∠ABC __．(写出一个即可) 【解析】 分两种情况： ①∵△AEF ∽△ABC ， ∴AE ∶AB ＝AF ∶AC ， 即1∶2＝AF ∶AC ， ∴AF ＝12AC ；②∵△AEF ∽△ACB ， ∴∠AFE ＝∠ABC .∴要使以A ，E ，F 为顶点的三角形与△ABC 相似，则AF ＝12AC 或∠AFE ＝∠ABC .10．[2015·泰州]如图32－8，△ABC 中，D 为BC 上一点， ∠BAD ＝∠C ，AB ＝6，BD ＝4，则CD 的长为__5__．【解析】 ∵∠BAD ＝∠C ，∠B ＝∠B ，∴△BAD ∽△BCA ， ∴BA BC ＝BD BA. ∵AB ＝6，BD ＝4， ∴6BC ＝46， ∴BC ＝9，∴CD ＝BC －BD ＝9－4＝5. 三、解答题(共20分)11．(10分)[2015·泰安]如图32－9，在△ABC 中，AB ＝AC ，点P ，D 分别是BC ，AC 边上的点，且∠APD ＝∠B .(1)求证：AC ·CD ＝CP ·BP ；(2)若AB ＝10，BC ＝12，当PD ∥AB 时，求BP 的长．图32－9解：(1)证明：∵AB ＝AC ， ∴∠B ＝∠C . ∵∠APD ＝∠B ， ∴∠APD ＝∠B ＝∠C . ∵∠APC ＝∠BAP ＋∠B ， ∠APC ＝∠APD ＋∠DPC ， ∴∠BAP ＝∠DPC ， ∴△ABP ∽△PCD ， ∴BP CD ＝AB PC， ∴AB ·CD ＝PC ·BP .图32－7图32－8∵AB ＝AC ，∴AC ·CD ＝CP ·BP ；(2)∵PD ∥AB ，∴∠APD ＝∠BAP . ∵∠APD ＝∠C ，∴∠BAP ＝∠C . ∵∠B ＝∠B ， ∴△BAP ∽△BCA ， ∴BA BC ＝BP BA.∵AB ＝10，BC ＝12， ∴1012＝BP 10， ∴BP ＝253.12．(10分)[2015·滨州]如图32－10，已知B ，C ，E 三点在同一条直线上，△ABC 与△DCE 都是等边三角形，其中线段BD 交AC 于点G ，线段AE 交CD 于点F ，求证： (1)△ACE ≌△BCD ； (2)AG GC ＝AF FE.证明：(1)∵△ABC 与△DCE 都为等边三角形， ∴AC ＝BC ，CE ＝CD ，∠ACB ＝∠DCE ＝60°，∴∠ACB ＋∠ACD ＝∠DCE ＋∠ACD ，即∠ACE ＝∠BCD ， 在△ACE 和△BCD 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACE ＝∠BCD ，CE ＝CD ，∴△ACE ≌△BCD (SAS )； (2)∵△ACE ≌△BCD ， ∴∠BDC ＝∠AEC ， 在△GCD 和△FCE 中， ⎩⎪⎨⎪⎧∠GCD ＝∠FCE ＝60°，CD ＝CE ，∠BDC ＝∠AEC ， ∴△GCD ≌△FCE (ASA )， ∴CG ＝CF ，∴△CFG 为等边三角形， ∴∠CGF ＝∠ACB ＝60°， ∴GF ∥CE ， ∴AG GC ＝AF FE.(20分)13．(10分)如图32－11，在△ABC 和△ADE 中，∠BAD ＝∠CAE ，图32－10∠ABC ＝∠ADE .(1)写出图中两对相似三角形(不得添加辅助线)； (2)请分别说明两对三角形相似的理由．【解析】 由两个角对应相等得两三角形相似，关键是得到∠BAC ＝∠DAE . 解：(1)△ABC ∽△ADE ，△ABD ∽△ACE ； (2)∵∠BAD ＝∠CAE ，∴∠BAD ＋∠DAC ＝∠CAE ＋∠DAC ， 即∠BAC ＝∠DAE . 又∵∠ABC ＝∠ADE ， ∴△ABC ∽△ADE . ∴AB AD ＝AC AE.又∵∠BAD ＝∠CAE ，∴△ABD ∽△ACE .14．(10分)[2014·资阳]如图32－12，AB 是⊙O 的直径，过点A 作⊙O 的切线并在其上取一点C ，连结OC 交⊙O 于点D ，BD 的延长线交AC 于E ，连结AD . (1)求证：△CDE ∽△CAD ；(2)若AB ＝2，AC ＝22，求AE 的长．解：(1)∵AB 是⊙O 的直径，∴∠ADB ＝90°， ∴∠ABD ＋∠BAD ＝90°.又∵AC 是⊙O 的切线，∴AB ⊥AC ，∴∠BAC ＝90°， ∴∠CAD ＋∠BAD ＝90°，∴∠ABD ＝∠CAD . ∵∠ABD ＝∠BDO ＝∠CDE ， ∴∠CAD ＝∠CDE ，又∵∠C ＝∠C ，∴△CDE ∽△CAD ； (2)在Rt △OAC 中，∠OAC ＝90°， ∴OA 2＋AC 2＝OC 2，即12＋(22)2＝OC 2， ∴OC ＝3，则CD ＝2.又∵△CDE ∽△CAD ，得CD CE ＝CA CD ，即2CE ＝222， ∴CE ＝2，∴AE ＝AC －CE ＝22－2＝ 2.(10分)15．(10分)[2015·巴中]如图32－13，AB 是⊙O 的直径，OD ⊥弦BC 于点F ，交⊙O 于点E ，连结CE ，AE ，CD ，若∠AEC ＝∠ODC . (1)求证：直线CD 为⊙O 的切线；(2)若AB ＝5，BC ＝4，求线段CD 的长． 解：(1)证明：如答图，连结CO ，∵圆周角∠AEC 与∠ABC 所对弧相同，∴∠ABC ＝∠AEC .又∠AEC ＝∠ODC ，∴∠ABC ＝∠ODC . ∵OC ＝OB ，OD ⊥BC ，∴∠OCB ＝∠OBC ，且∠OCB ＋∠COD ＝90°.∴∠ODC ＋∠COD ＝90°.∴∠OCD ＝180°－∠ODC －∠COD ＝90°，即OC ⊥CD .图32－12图32－13第15题答图又OC 为半径，∴直线CD 为⊙O 的切线； (2)在⊙O 中，OD ⊥弦BC 于点F ， ∴BF ＝CF ＝12BC ＝2.又OB ＝12AB ＝52，∴OF ＝OB 2－BF 2＝32.由(1)知∠OBF ＝∠CDF ，且∠OFB ＝∠CFD ，∴△OFB ∽△CFD .∴OF OB ＝CF CD ，∴CD ＝OB ·CF OF ＝52×232＝103. ∴线段CD 的长为103.。

图形与几何一、选择题1．(荆州中考)已知：直线l1∥l2，一块含30°角的直角三角板如图Y2－1所示放置，∠1＝25°，则∠2等于(B)A．30°B．35°C．40°D．45°【易错分析】(1)不能从实物中建立几何模型；(2)不了解三角板各角的度数；(3)不能通过作平行线把∠1与∠2联系起来．图Y2－1 图Y2－22．如图Y2－2，H是△ABC的高AD，BE的交点，且DH＝DC，则下列结论：①BD＝AD；②BC ＝AC；③BH＝AC；④CE＝CD中正确的有(B)A．1个B．2个C．3个D．4个【易错分析】找不到三角形全等的条件．∵DH＝DC，∠C＝∠DHB，∠ADC＝∠BDH，∴△BDH ≌△ADC.求出①BD＝AD；③BH＝AC，结论②，④为错误结论．3．已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为(C)A．40°B．100°C．40°或100°D．70°或50°【易错分析】容易忽视分两种情况讨论：40°是等腰三角形的底角或40°是等腰三角形的顶角．当40°是等腰三角形的顶角时，则顶角就是40°；当40°是等腰三角形的底角时，则顶角是180°－40°×2＝100°.4．(绥化中考)如图Y2－3，在平行四边形ABCD中，E是CD上的一点，DE∶EC＝2∶3，连结AE，BE，BD，且AE，BD交于点F，则S△DEF∶S△EBF∶S△ABF＝(D)A．2∶5∶25 B．4∶9∶25C．2∶3∶5 D．4∶10∶25【易错分析】(1)不能找到图中的相似三角形；(2)把相似三角形面积比与等高的三角形面积比混淆．根据平行四边形的性质求出DC＝AB，DC∥AB，求出DE∶AB＝2∶5，根据相似三角形的判定推出△DEF∽△BAF，求出△DEF和△ABF的面积比，根据三角形的面积公式求出△DEF和△EBF的面积比，即可求出答案．5．(黔西南中考)一直角三角形的两边长分别为3和4.则第三边的长为 (D)A．5 B.7 C. 5 D．5或7【易错分析】已知边长为4的边可能是斜边，也可能是直角边或者说所求的边长可能是斜边也可能是直角边，所以需要分类讨论．图Y2－36．(玉林中考)如图Y2－4，在⊙O 中，直径CD ⊥弦AB ，则下列结论中正确的是 (B)A ．AC ＝ABB ．∠C ＝12∠BOD C ．∠C ＝∠BD ．∠A ＝∠BOD【易错分析】 垂径定理、圆周角定理理解模糊．A ．根据垂径定理不能推出AC ＝AB ，故A 选项错误；B ．∵直径CD ⊥弦AB ，∴AD ︵＝BD ︵，∵AD ︵对的圆周角是∠C ，BD ︵对的圆心角是∠BOD ，∴∠BOD ＝2∠C ，故B 正确；C ．不能推出∠C ＝∠B ，故C 错误；D ．不能推出∠A ＝∠BOD ，故D 错误．二、填空题7．(呼和浩特中考)如图Y2－5，在△ABC 中，∠B ＝47°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC ＝__66.5°__.【易错分析】 不能把三角形的外角与内角和进行转换．根据三角形内角和定理、角平分线的定义以及三角形外角定理求得12∠DAC ＋12ACF ＝12(∠B ＋∠ACB )＋12(∠B ＋∠BAC )＝12(∠B ＋∠B ＋∠BAC ＋∠ACB )＝227°2；最后在△AEC 中利用三角形内角和定理可以求得∠AEC 的度数．8．(锦州月考)如图Y2－6，△ABC 中AB ＝AC ，AB 的垂直平分线MN 交AC 于点D(1)若∠A ＝38°，则∠DBC ＝__33°__．(2)若AC ＋BC ＝10 cm ，则△DBC 的周长为__10__cm__．【易错分析】 掌握线段垂直平分线上任意一点，到线段两端点的距离相等，是本题易错点．(1)∵AB ＝AC ，∠A ＝38°，∴∠ABC ＝12(180°－∠A )＝12(180°－38°)＝71°， ∵MN 垂直平分线AB ，∴AD ＝BD ，∴∠ABD ＝∠A ＝38°，∴∠DBC ＝∠ABC －∠ABD ＝71°－38°＝33°；(2)∵MN 垂直平分AB ，∴DA ＝DB .∴△DBC 的周长＝BC ＋BD ＋DC＝BC ＋DA ＋DC ＝BC ＋AC ＝10 cm.图Y2－4图Y2－5图Y2－69．(淮安中考)若菱形的两条对角线长分别为2和3，则此菱形的面积是__3__．【易错分析】 易错点“菱形的面积公式是两对角线乘积的一半”，记忆中忘记了“一半”．10．(烟台中考)如图Y2－7，将弧长为6π，圆心角为120°的扇形纸片AOB 围成圆锥形纸帽，使扇形的两条半径OA 与OB 重合(接缝粘连部分忽略不计)，则圆锥形纸帽的高是__．图Y2－7【易错分析】 圆锥的侧面展开图的扇形的半径、弧长、圆心角与圆锥的母线长、底面圆半径、高等之间的对应关系模糊．11．(平阴二模)如图Y2－8，线段AB 是⊙O 上一点，∠CDB ＝20°，过点C 作⊙O 的切线交AB 的延长线于点E ，则∠E 等于__50°__．【易错分析】 不懂得遇到直线与圆相切，连结圆心与切点，利用切线的性质得垂直，根据直角三角形的性质来解决问题．连结OC ，∵圆心角∠BOC 与圆周角∠CDB 都对弧BC ，∴∠BOC ＝2∠CDB ，又∠CDB ＝20°，∴∠BOC ＝40°，又∵CE 为圆O 的切线，∴OC ⊥CE ，即∠OCE ＝90°，则∠E ＝90°－40°＝50°. 12．(哈尔滨中考)如图Y2－9，四边形ABCD 是矩形，点E 在线段CB 的延长线上，连结DE 交AB 于点F ，∠AED ＝2∠CED ，点G 是DF 的中点，若BE ＝1，AG ＝4，则AB 的长为．【易错分析】 不善于把矩形的性质，等边对等角的性质，等角对等边的性质，以及勾股定理进行综合运用，求不出AE＝AG 最关键的一步． 三、解答题13．(娄底中考)为了安全，请勿超速．如图Y2－10一条公路建成通车，在某直线路段MN 限速60 km/h ，为了检测车辆是否超速，在公路MN 旁设立了观测点C ，从观测点C 测得一小车从点A 到达点B 行驶了5 s ，已知∠CAN ＝45°，∠CBN ＝60°，BC ＝200 m ，此车超速了吗？请说明理由．(参考数据：2≈1.41，3≈1.73)【易错分析】 画不出辅助线，构造直角三角形． 解：如答图，过点C 作CD ⊥MN ，垂足为D .∵CD ⊥MN ，∠DBC ＝60°，∴∠BCD ＝30°，∴BD ＝12BC ＝12×200＝100， 由特殊锐角三角函数得：DC ＝1003≈100×1.73＝173 m.∵CD ⊥MN ，∠CAD ＝45°，∴∠DCA ＝∠DAC ＝45°，∴AD ＝DC ＝173 m，图Y2－8图Y2－9图Y2－10AB ＝173－100＝73 m ，73÷5＝14.6 m/s ，60 km/h ＝1623m/s ， 14．6 m/s ＜1623m/s 故此车没有超速．14．如图Y2－11，在△ABC 中，∠C ＝90°，点D ，E 分别在AC ，AB 上，BD 平分∠ABC ，DE⊥AB ，AE ＝6，cos A ＝35.求：(1)DE ，CD 的长；(2)tan ∠DBC 的值． 【易错分析】 不能综合应用解直角三角形、直角三角形性质、相似三角形的性质、三角函数值的定义进行逻辑推理和运算，从而不知如何解答．解：(1)在Rt △ADE 中，由AE ＝6，cos A ＝AE AD ＝35， ∴AD ＝10，由勾股定理，得DE ＝AD 2－AE 2＝102－62＝8，∵BD 平分∠ABC ，DE ⊥AB ，∠C ＝90°，根据角平分线性质，得DC ＝DE ＝8；(2)方法一：由(1)知AD ＝10，DC ＝8，得AC ＝AD ＋DC ＝18.在△ADE 与△ABC 中，∠A ＝∠A ，∠AED ＝∠ACB ，∴△ADE ∽△ABC ， ∴DE BC ＝AE AC ，即8BC ＝618，BC ＝24， ∴tan ∠DBC ＝CD BC ＝824＝13. 方法二：由(1)得AC ＝18，又∵cos A ＝AC AB ＝35，∴AB ＝30， 由勾股定理，得BC ＝24，∴tan ∠DBC ＝13. 15．如图Y2－12，四边形ABCD 是正方形，点G 是BC 边上任意一点，DE ⊥AG 于E ，BF ∥DE 交AG 于F .(1)求证：AF －BF ＝EF ；(2)将△ABF 绕点A 逆时针旋转，使得AB 与AD 重合，记此时点F 的对应点为点F ′，若正方形边长为3，求点F ′与旋转前的图中点E 之间的距离．【易错分析】 对正方形的性质，全等三角形的判定与性质，矩形的判定与性质，以及旋转的性质综合运用能力不够，找不出解题思路．解：(1)证明：如答图，∵四边形ABCD 是正方形，∴AB ＝AD ，∠2＋∠3＝90°，∵DE ⊥AG ，∴∠AED ＝90°，∴∠1＋∠3＝90°，∴∠1＝∠2，又∵BF ∥DE ，图Y2－11图Y2－12∴∠BFA ＝∠AED ＝90°.在△AED 和△BFA 中，⎩⎪⎨⎪⎧∠1＝∠2，∠AED ＝∠BFA ，AD ＝AB ，∴△AED ≌△BFA ，∴BF ＝AE ，∵AF －AE ＝EF ，∴AF －BF ＝EF ；(2)如答图，根据题意，得∠FAF ′＝90°，DE ＝AF ′＝AF ， ∴四边形AEDF ′为矩形，∴EF ′＝AD ＝3. 16．(宜宾中考)如图Y2－13，CE 是⊙O 的直径，BD 切⊙O 于点D ，DE ∥BO ，CE 的延长线交BD 于点A .(1)求证：直线BC 是⊙O 的切线；(2)若AE ＝2，tan ∠DEO ＝2，求AO 的长．【易错分析】 (1)不知道连结半径OD ，通过证明Rt △BDO ≌Rt △BCO 证明∠BCO ＝90°；(2)不能综合运用相似三角形，直角三角形，三角函数解决问题． 解：(1)如答图①，连结DO ，∵BD 切⊙O 于点D ， ∴∠BDO ＝90°，∵DE ∥BO ，∴∠BOC ＝∠DEO ，∠EDO ＝∠BOD ，∵OD ＝OE ，∴∠DEO ＝∠EDO ，∴∠BOC ＝∠BOD . 在Rt △BDO 和Rt △BCO 中，OD ＝OC ，∠BOC ＝∠BOD ，BO ＝BO ， ∴Rt △BDO ≌Rt △BCO ，∴∠BCO ＝∠BDO ＝90°，∴直线BC 是⊙O 的切线；(2)如答图②，连结CD ，设⊙O 的半径为r ，∵CE 是⊙O 的直径，∴∠CDE ＝90°，∵DE ∥BO ，∴∠BOC ＝∠DEO ，即tan ∠BOC ＝tan ∠DEO ＝2，∵OC ＝OE ＝r ，∴BC ＝2r ，则BO ＝3r ，∵tan ∠DEO ＝2，∴DC ＝2DE ，第15题答图 图Y2－13第16题答图①在Rt △CDE 中，由勾股定理得：DC 2＋DE 2＝CE 2，即2DE 2＋DE 2＝(2r )2，∴DE ＝233r ， ∵DE ∥BO ，∴△ADE ∽△ABO ，∴AE AO ＝DE BO ，即22＋r ＝233r 3r，解得r ＝1. ∴AO ＝AE ＋OE ＝2＋1＝3.∴AO 的长为3.。

相似三角形——“K字型”相似模型教学目标：1、理解“K型图”的特征与其中两个三角形相似的条件，2、利用“K型图”中两个三角形的相似性解决一些计算、证明等问题；教学重点难点：1、在已知图形中观察关键特征——“K型”；2、在非“K型”图形中画辅助线，得到“K型”图形；3、在“K型”图的两个三角形中，探索其相似条件。

教学过程：一、前测练习1.如图，在矩形ABCD中，E在AD上，EF⊥BE ，交CD于F，连结BF，则∆∽∆2.在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,则∆∽∆二、模型探究课前完成填空，上课请学生回答答案，根据答案回答以下问题：问题1判定这两个三角形相似的依据是什么？学生答：两个角对应相等的两个三角形相似。

问题2图中已知角有什么共同特征？学生答：图1中顶点共线三角都是直角，图2中顶点共线三角都是60°。

问题3若顶点共线三等角的度数不是90°也不是60°，对应两个三角形还相似吗？图形演示，提问：此时这两个三角形相似吗？请同学们自己画图并证明。

请学生叙此时述证明过程：已知：nCADEB=∠=∠=∠求证：ABD∆∽DEC∆证明：nB=∠nADBBAD-=∠+∠∴180ABn ADE =∠n ADB CDE -=∠+∠∴180CDE BAD ∠=∠∴C B ∠=∠ABD ∆∴∽DEC ∆（或者依据外角等于不相邻的两内角之和）展示学生书写，教师分析，该同学找出的两三角形相似的第一个条件是（C B ∠=∠）第二个条件是（CDE BAD ∠=∠），他是怎么证明这两个角相等呢？方法1、外角等于不相邻的两内角之和；方法2、三角形的内角和等于平角求解，都可行。

问题4若保持共线三等角的度数不变，改变边的长度，对应两个三角形还相似吗？学生答：相似。

因为我们是依据两个角对应相等判定两个三角形相似的。

问题5由此你得到了什么结论？学生答：只要满足共线三角的度数相等，则这两个三角形相似的。

九年级数学上册18《相似形》相似三角形的判定（一）课后作业（新版）北京课改版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（九年级数学上册18《相似形》相似三角形的判定（一）课后作业（新版）北京课改版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为九年级数学上册18《相似形》相似三角形的判定（一）课后作业（新版）北京课改版的全部内容。

相似三角形的判定（一）课后作业1、如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E,在不添加辅助线的情况下，与△AEF相似的三角形有( ）A．0个B．1个C．2个D．3个2、如图,∠A=∠B=90°,AB=7，AD=2，BC=3,在边AB上取点P，使得△PAD与△PBC相似，则这样的P点共有（）A．1个B．2个C．3个D．4个3、如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B，那么下列说法中,错误的是（）A．△ADE∽△ABC B．△ADE∽△ACD C．△ADE∽△DCB D．△DEC∽△CDB4、如图所示，图中共有相似三角形（）A．5对B．4对C．3对D．2对5、已知图(1)、（2）中各有两个三角形，其边长和角的度数已在图上标注，图（2）中AB、CD交于O点，对于各图中的两个三角形而言，下列说法正确的是( ）A．只有(1)相似B．只有（2）相似C．都相似D．都不相似6、如图,在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC∽△AED的是（）A．∠AED=∠B B．∠A DE=∠C C．AD:AE=AC:AB D。