固体物理第5章
- 格式:ppt
- 大小:880.50 KB
- 文档页数:44

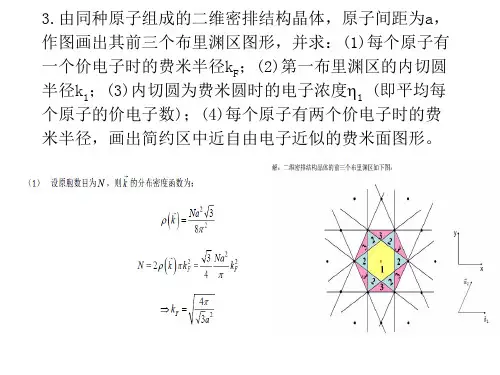









第五章 晶体中电子能带理论 习题1.晶体常数为a 的一维晶体中,电子的波函数为(1)()x ai x k πψ3cos =,(2)()f la x f x k,)(-l ∑∞∞=-=ψ是某一函数,求电子在以上状态中的波矢.[解 答]由《固体物理教程》(5.14)式()()r e R r k R r i n k nψψ∙=+可知,在一维周期势场中运动的电子的波函数满足()()x e a x k ika k ψψ=+由此得(1) ()()()()x e x x ai x a i a x a i a x k ika k k ψψππππψ=-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+=+3cos 3cos 3cos于是1-=ikae因此得 ,5,3,aa akπππ±±±= 若只取布里渊区内的值:ak aππ<-,则有ak π=(2) ()].)1([)(a l x f la a x f a x l l k ∑∑∞-∞=∞-∞=--=++=+ψ令1+='ll得 ()()()()x e x a l x f a x k ika k k ψψψ==-=+∑'.由上式知 ikae =1所以有 ,6,4,2,0aa a kπππ±±±= 因此得在布里渊区内的值为0=k2.一维周期势场为()()[]()⎪⎩⎪⎨⎧-≤≤+-+≤≤---=.1,0,21222b na x b a n b na x b na na x b mW x V 当当其中b a 4=,W 为常数,试画出此势能曲线,并求出势能的平均值.[解 答]图5.1 一维周期势场如图5.1所示,由于势能具有周期性,因此只能在一个周期内求平均即可,于是得V=a 1 ()dx x V a a ⎰-22=()dx x V b bb ⎰-2241 =dx x b mW b b b ⎰--][2141222 =b b x x b b mW --]31[8322 =2261b mW . 3.用近自由电子模型求解上题,确定晶体的第一及第二个禁带宽度. [解 答]根据教科书(5.35)式知禁带宽度的表示式为 ng V E 2=,其中n V 是周期势场()x V傅里叶级数的系数,该系数可由《固体物理教程》(5.22)式n V = a 1 ()dx e x V nx ai a a π222--⎰求得,第一禁带宽度为112V E g ==2()dxex V a a x ai ⎰--222a 1π=2⎰---b b x ai dxex b mW b π2222][241=2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b 2cos ][241222π=3228πb mW .第二禁带宽度为222V E g ==2()dxex V a a x ai ⎰--224a 1π=2⎰---b b x bi dx e x b mW b π][241222 =2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b πcos ][241222=222πb mW4.已知一维晶格中电子的能带可写成()⎪⎭⎫⎝⎛+-=ka ka ma k E 2cos 81cos 8722 , 式中a是晶格常数.m 是电子的质量,求(1)能带宽度,(2)电子的平均速度,(3)在带顶和带底的电子的有效质量. [解 答](1)能带宽度为 .min max E E E -=∆由极值条件 ()0=dkk dE 得上式的唯一解是0sin =ka 的解,此式在第一布里渊区内的解为 ak π,0=.当()k E k ,0时=取极小值min E ,且有 min E =()00=E当()k E ak,时π=,E(k)取极大值max E ,且有.222max ma a E E=⎪⎭⎫ ⎝⎛=π由以上可得能带宽度为.222m i nm a x ma E E E =-=∆(2)由《固体物理教程》(5.81)式,得电子的平均速度为 ().2sin 41sin 1⎪⎭⎫⎝⎛-==ka ka ma dk k dE v(3)由《固体物理教程》(5.87)式得,带顶和带底电子的有效质量分别为.322cos 21cos 1222m ka ka m k E mak ak ak -=⎪⎭⎫⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂=±=-±=*±=πππ.22cos 21cos 012220m ka ka m k E m k k k =⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==-==*5.对简立方结构晶体,其晶格常数为a .(1)用紧束缚方法求出对应非简并s态电子的能带;(2)分别画出第一布里渊区[110]方向的能带﹑电子的平均速度、有效质量以及沿[110]方向有恒定电场时的加速度曲线.[解 答](1)非简并s态电子的能带().e n R k ∑∙--=ns s ats s J C E k E式中n R是晶体参考格点最近邻格矢.对于简单立方晶体,任一格点有6个最近邻.取参考格点的坐标为(0,0,0),则6个最近邻点的坐标为()()().,0,0,0,,0,0,0,a a a ±±±简单立方体非简并s 态电子的能带则为()().cos cos cos 2a k a k a k J C E k E z y x s s at s s ++--=(2)在[110]方向上 ,22,0k k k k y x z === 能带变为(),22cos 40⎪⎪⎭⎫⎝⎛-=ka J E k E s s其中 ,20ss at s J C E E --=在[110]方向上,在第一布里渊区内,电子的能带如图5.2所示.图5.2[110]方向电子的能带电子的平均速度.22sin 221⎪⎪⎭⎫⎝⎛=∂∂=ka a J k E v s 平均速度曲线如图5.3所示.图5.3 平均速度曲线电子的有效质量,22cos 222222⎪⎪⎭⎫ ⎝⎛=∂∂=*ka a J k E m s 有效质量曲线如图5.4所示.图5.4 有效质量曲线 在[110]方向有恒定电场情况下,电子的受力 εe F -=电子的加速度2222cos 2⎪⎪⎭⎫⎝⎛-==*ka a J e m F a s ε.设电场方向与[110]方向相反,加速度曲线则如图5.5所示.图5.5加速度曲线6.用紧束缚方法处理面心立方体晶格的s 态电子,试导出其能带⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E E x z z y y x s s atss ,并求出能带底的有效质量. [解 答]用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,根据《固体物理教程》(5.60)式,其能带表示式为()∑∙--=ns s ats s J C E k E n R k e ,n R 是最近邻格矢.对面心立方晶格,取参考点的坐标为(0,0,0),则12个最近邻格点的坐标为 (2a ±,2a ±,0),( 2a ±,0, 2a ±),(0, 2a ±,2a±). 将上述12组坐标带入能带的表示式,得()∑∙--=ns s ats s J C E k E n R k es s ats J C E --=()()()()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡+++---+-+---+-++---+-z y z y z y z k y k a i z k x k a i z k x k a i z k x k a i z x y x y x y x y x k k a i k k a i k k a i k k a i k k a i k k a i k k a i k k a i e e e e e e e e e e e e 222222222222()()()()()()⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧++++-+++-++--=z y z y z x z x y x y x s s ats k k a k k a k k a k k a k k a k k a J C E 2cos 2cos 2cos 2cos 2cos 2cos⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E x z z y y x s s ats .能带底即()k E 的最小值对应的k为(0,0,0),有《固体物理教程》(5.87)可得在能带底处电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*.同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.7.用紧束缚方法处理体心立方晶体,求出 (1) s 态电子的能带为()2cos 2cos 2cos 8a k a k a k J C E k E z y x s s ats s --= ; (2) 画出第一布里渊区[111]方向的能带曲线;(3) 求出带顶和带底电子的有效质量. 【解 答】(1)用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,其能带的表示式为().e n R k ∑∙--=ns s ats s J C E k E n R 是最近邻格矢.对体心立方晶格,取参考格点的坐标为(0,0,0),则8个最近邻格点的坐标为 (2,2,2aa a ±±±). 将上述8组坐标代入能带的表示式,的().e n R k ∑∙--=ns s ats s J C E k E()()()()()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++--=---+---+---++-+--+++z k y k x k a i z k y k x k a i z k y k x k a i z k y k x k ai z k y k x k a i z k y k x k a i z k y k x k a i z y x e e e e e e e e J C E k k k a i s s ats 22222222()()()()⎥⎦⎤⎢⎣⎡+++--=--+--+2cos 2cos 2cos 2cos 22222a k e a k e a k e a k e J C E z zz z k k a i s s atsy k x k ai y k x k a i y k x k a i y x ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--=-2cos 2cos 422a k a k e e J C E z y k a i s s at s x k ai x 2cos 2cos 2cos 8ak a k a k J C E z y x s s at s --=.(2)在[111]方向上k k k k z y x 33=== , 且第一布里渊区边界在 ak k k z y x π±===,于是能带化成⎪⎪⎭⎫⎝⎛-=ka J E E s 63cos 830,其中s ats C E E -=0.图5.6为第一布里渊区[111]方向的能带曲线.图5.6 [111]方向的能带曲线(3)由能带的表示式及余弦函数的性质可知,当===z y x k k k 时,sE 取最小值,即0===z y x k k k 是能带底,电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.而在布里渊区边界上的⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±a a a πππ2,0,0,0,2,0,0,0,2处是能带顶,电子的有效质量为222a J m m m s zzyyxx-===***.其它交叉项的倒数也全为零.8.某晶体电子的等能面是椭球面⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E ,坐标轴1,2,3相互垂.(1) 求能态密度;(2)今加一磁场B , B与坐标轴的夹角的方向余弦分别为γβα,,,写出电子的运动方程;(3) 证明电子在磁场中的回旋频率*=m eB c ω, 其中2132********⎥⎦⎤⎢⎣⎡++=*m m m m m m m γβα.【解 答】(1) 由已知条件可将波矢空间内电子能带满足的方程化为1222232322222121=++ E m k E m k E m k .将上式与椭球公式1222222=++c z b y a x 比较可知,在波矢空间内电子的等能面是一椭球面.与椭球的体积abc π34比较可得到,能量为E 的等能面围成的椭球体积 2332132234E m m m πτ= 由上式可得dE E m m m d 21321324 πτ=.能量区间内电子的状态数目()dE E m m m V d V dz cc 1321323222πτπ== 是晶体体积.电子的能态密度()21321322E m m m VdE dz E N cπ==(2) 根据《固体物理教程》中(5.86)式得⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂∂+∂∂=331222121212211F k k EF k k E F k E a ,⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂+∂∂∂=332222221122221F k k E F k E F k k E a,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂+∂∂∂=323222321132231F k E F k k E F k k E a .将⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E代入上述三式得运动方程为 333222111,,m F a m Fa m F a ===.即333222111,,F dtdvm F dt dv m F dt dv m ===. (1)当存在磁场B时,电子受到洛仑兹力B v e F⨯-=.其分量形式为 ()()23323223321v B v B v e B v B v e F ωνωβγ-=--=--=,()()31131331132v B v B v e B v B v e F ωνωγα-=--=--=, ()()12212112213v B v B v e B v B v e F ωνωαβ-=--=--=式中B B=,γωβωαωeB eB eB ===321,,.将上述结果代入运动方程(1)得.,,122133311322233211v v dt dvm v v dt dvm v v dt dv m ωωωωωω-=-=-= (2)(3)上述方程可用不同的方法求解.解法一:对(2)式两边作拉普拉斯变换,并采用如下初始条件 ()1010v v =,()2020v v =,().0303v v =得[]11v pL m +[]23v L ω-[]32v L ω=101v m ,-[]13v L ω+[]22v pL m +[]31v L ω=202v m ,[]12v L ω-[]21v L ω+[]33v pL m =303v m .由此解出[]∆∆=11v L . 其中()()B p Ap m m m p m m m pm p m p m +≡+++=---=∆22332222113321312123231ωωωωωωωωω.321m m m A =,321233222211m m m m m m B ωωω++=.()()322130313202121021120332302323103213130312202231011C p C p C v m v m v m pv m m v m m p v m m m pm v m p m v m v m ++≡+++-+=--=∆ωωωωωωωωωωω()203302322103211,v v m m C v m m m C ωω+==,3031320212102113v m v m v m C ωωωωω++=.因此得[]()Bp A C B p p AB C B C p AB C B p Ap C p C p C v L +++-+=+++=22231323221111.上式两边取逆拉普拉斯变换得t B BA Ct B AB C B C p AB C v sin cos 123131+-+=.同理可得t B B A C t B AB C B C p AB C v sin cos 123132'+'-'+'=.()301103312203211,v v m m C v m m m C ωω+='=', 1021130323202223v m v m v m C ωωωωω++='.及t B B A C t B AB C B C p AB C v sin cos 123133''+''-''+''=.()102201212303211,v v m m C v m m m C ωω+=''=''2032210311302333v m v m v m C ωωωωω++=''.可见电子回旋频率为B .解法二:由于电子作周期运动,将试探解t i c e v v ω101=, t i c e v v ω202=t i c e v v ω303=(这里302010,,v v v 一般为复数,电子的真实速度应为321,,v v v 的实部或虚部.) 代入(2)式得 101v m i c ω+302v ω-203v ω=0,103v ω+202v m i c ω-301v ω=0,102v ω-201v ω+303v m i c ω=0.302010,,v v v 有不全为零的解的充要条件是0312123231=----m i m i m i c c c ωωωωωωωωω. 由此得 ()02332222113321=++-c c m m m m m m ωωωωω.于是B m m m m m m c=++=3212332222112ωωωω.这样,两种方法均给出电子回旋频率为21321233222211⎪⎪⎭⎫ ⎝⎛++==m m m m m m B c ωωωω.再将γωβωαωeB eB eB ===321,,,代入上式即得*=meBc ω, 其中2132********⎪⎪⎭⎫⎝⎛++=*m m m m m m m γβα.9.求出一维、二维金属中自由的能态密度.[解 答](1)一维情况自由电子的色散关系为 mk E 222 =.由此得dk E m dk m kdE 2121222⎪⎪⎭⎫ ⎝⎛== ,即dE E m dk 212122-⎪⎭⎫⎝⎛= . 对应同一个dE ,在k ±方向各有一个dk ,因此空间中dE E E +与之间的区间为dE E m dk d 2121222-⎪⎭⎫⎝⎛== τ,在该范围内的状态数为dE E m L d LdZ 212122-⎪⎭⎫⎝⎛== πτπ,其中L 是晶格长度.于是,态密度()12122-⎪⎭⎫ ⎝⎛==E m L dE dZ E N π.(2)二维情况参照《固体物理教程》(5.102)式可知,二维情况下态密度的一般表示式为()⎰∇=Lk EdLS E N 22π.其中S 是晶格的面积,积分沿能量为E 的等能线进行.由()2222y x k k m E += 得 ()mk k k m E y x k 221222 =+=∇.于是有()21222222 mS k m k S E dL S E N Lk ππππ=⎪⎪⎭⎫ ⎝⎛=∇=-⎰.10.二维金属晶格,晶胞为简单矩形,晶格常数A a2=,A b 4=,原子为单价的.(1) 试画出第一、二布里渊区; (2) 计算自由电子费密半径;(3) 画出费密面在第一、二布里渊区的形状.【解 答】(1) 倒格子原胞基矢j bb i a b ππ2,221==.选定一倒格点为原点,原点的最近邻倒格矢有4个,它们是21,b b ±±这4个倒格矢的中垂线围成的区间即是第一布里渊区.即图5.7中Ⅰ所示区间.原点的次近邻倒格矢有4个,它们是21b b ±±这4个倒格矢的中垂线围成的区间与第一布里渊区边界围成的区间即是第二布里渊区.即图5.7中Ⅱ所示区间.图5.7 二维矩形晶格第一、二布里渊区(2)在绝对零度时,二维金属中导电电子若看成自由电子,电子的能量mk E 222 =,能量dE E E+→区间的电子占据波矢空间dk 的范围.在此范围内的波矢数目为图5.8二维波矢空间kdk S ππ2)2(2∙,其中2)2(πS是二维金属中导电电子的波矢密度,S 是金属面积。