任务七平面图形的几何性质

初中数学知识点归纳——平面几何图形的性质平面几何图形是初中数学中的重要内容，其中包括了很多与图形性质相关的知识点。

本文将对初中数学中平面几何图形的性质进行详细归纳和介绍。

首先，我们来讨论三角形的性质。

三角形是由三条线段组成的图形，具有以下特点：1. 三边关系：三角形的任意两边之和大于第三边，任意两边之差小于第三边。

2. 三角形的角关系：三角形的三个内角之和为180度，其中每个内角小于180度。

3. 三角形的边对角关系：如果两个三角形的两边及夹角分别相等，则两个三角形全等；而如果两个三角形的两边及其夹角分别相等，则两个三角形相似。

接下来，我们来讨论四边形的性质。

四边形是由四条线段组成的图形，具有以下特点：1. 四边形对角线关系：四边形的对角线互相平分，即对角线的交点处于对角线上的点被平分为两等分。

2. 四边形的内角和关系：四边形的内角和为360度。

3. 平行四边形的性质：平行四边形的对边互相平行且相等，对角线互相平分。

4. 矩形的性质：矩形是一种特殊的平行四边形，有四个直角，对边相等。

5. 正方形的性质：正方形是一种特殊的矩形，有四个相等的边和四个直角。

此外，还有一些其他平面几何图形的性质也需要了解：1. 直线的性质：直线是由无数个点组成的，无宽度和无端点。

两个互不重合的直线在平面上最多只有一个交点。

2. 射线的性质：射线是由一个端点和一个方向所确定的线段，可以延伸到无穷远。

两个射线共线时，它们有一个公共端点。

3. 角的性质：角是由两条射线共享一个端点而形成的图形。

角的大小可以用度数来表示，一个完整的角是360度。

4. 圆的性质：圆是由一组等距离于圆心的点组成的。

圆的周长公式是C=2πr，其中C代表周长，r代表半径。

圆的面积公式是S=πr^2，其中S代表面积。

最后，我们来讨论一下平面几何图形的应用。

在实际生活中，平面几何图形的知识经常被用于解决各种问题，比如测量房屋面积、计算行驶的路径等。

掌握了平面几何图形的性质，可以帮助我们更好地理解和解决实际问题。

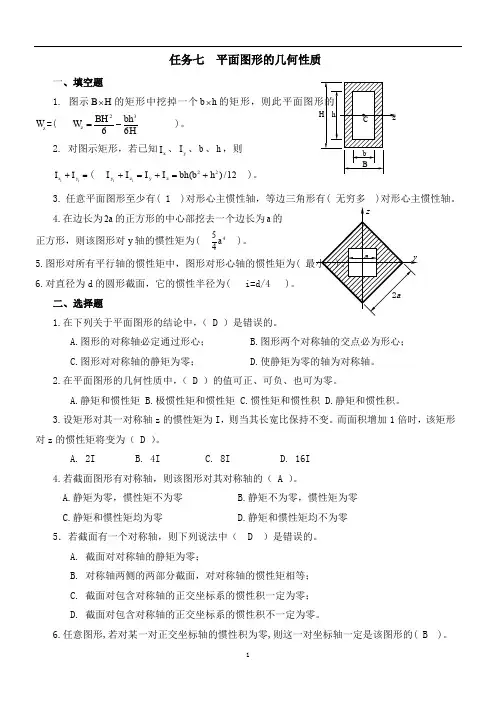
任务七 平面图形的几何性质一、填空题1. 图示B H ⨯的矩形中挖掉一个b h ⨯的矩形，则此平面图形的z W =( 2366z BH bh W H=- )。

2. 对图示矩形，若已知x I 、y I 、b 、h ，则11x y I I +=( 1122()/12y z y z I I I I bh b h +=+=+ )。

3. 任意平面图形至少有( 1 )对形心主惯性轴，等边三角形有( 无穷多 )对形心主惯性轴。

4.在边长为2a 的正方形的中心部挖去一个边长为a 的 正方形，则该图形对y 轴的惯性矩为( 454a )。

5.图形对所有平行轴的惯性矩中，图形对形心轴的惯性矩为( 最小 )。

6.对直径为d 的圆形截面，它的惯性半径为( i=d/4 )。

二、选择题1.在下列关于平面图形的结论中，（ D ）是错误的。

A.图形的对称轴必定通过形心；B.图形两个对称轴的交点必为形心；C.图形对对称轴的静矩为零；D.使静矩为零的轴为对称轴。

2.在平面图形的几何性质中，（ D ）的值可正、可负、也可为零。

A.静矩和惯性矩B.极惯性矩和惯性矩C.惯性矩和惯性积D.静矩和惯性积。

3.设矩形对其一对称轴z 的惯性矩为I ，则当其长宽比保持不变。

而面积增加1倍时，该矩形对z 的惯性矩将变为（ D ）。

A. 2IB. 4IC. 8ID. 16I 4.若截面图形有对称轴，则该图形对其对称轴的（ A ）。

A.静矩为零，惯性矩不为零B.静矩不为零，惯性矩为零C.静矩和惯性矩均为零D.静矩和惯性矩均不为零 5．若截面有一个对称轴，则下列说法中（ D ）是错误的。

A. 截面对对称轴的静矩为零；B. 对称轴两侧的两部分截面，对对称轴的惯性矩相等；C. 截面对包含对称轴的正交坐标系的惯性积一定为零；D. 截面对包含对称轴的正交坐标系的惯性积不一定为零。

6.任意图形,若对某一对正交坐标轴的惯性积为零,则这一对坐标轴一定是该图形的( B )。

——材料力学教案§A-1 引言不同受力形式下杆件的应力和变形，不仅取决于外力的大小以及杆件的尺寸，而且与杆件截面的几何性质有关。

当研究杆件的应力、变形，以及研究失效问题时，都要涉及到与截面形状和尺寸有关的几何量。

这些几何量包括：形心、静矩、惯性矩、惯性半径、极惯性短、惯性积、主轴等，统称为“平面图形的几何性质”。

研究上述这些几何性质时，完全不考虑研究对象的物理和力学因素，作为纯几何问题加以处理。

§A-2 静矩、形心及相互关系任意平面几何图形如图A-1所示。

在其上取面积微元dA ，该微元在Oxy 坐标系中的坐标为x 、y 。

定义下列积分：⎰=Ax A y S d ⎰=Ay A y S d （A-1）分别称为图形对于x 轴和y 轴的截面一次矩或静矩，其单位为3m 。

如果将dA 视为垂直于图形平面的力，则ydA 和zdA 分别为dA 对于z 轴和y 轴的力矩；x S 和y S 则分别为dA 对z 轴和y 轴之矩。

图A-1图形的静矩与形心图形几何形状的中心称为形心,若将面积视为垂直于 图形平面的力，则形心即为合力的作用点。

设C x 、C y 为形心坐标，则根据合力之矩定理⎭⎬⎫==C y C x Ax S Ay S (A-2)或⎪⎪⎭⎪⎪⎬⎫====⎰⎰A ydA AS y A xdA A S x A x CAyC (A-3) 这就是图形形心坐标与静矩之间的关系。

根据上述定义可以看出：1.静矩与坐标轴有关，同一平面图形对于不同的坐标轴有不同的静矩。

对某些坐标轴静矩为正；对另外某些坐标轴为负；对于通过形心的坐标轴，图形对其静矩等于零。

2.如果已经计算出静矩，就可以确定形心的位置；反之，如果已知形心位置，则可计算图形的静矩。

实际计算中，对于简单的、规则的图形，其形心位置可以直接判断。

例如矩形、正方形、圆形、正三角形等的形心位置是显而易见的。

对于组合图形，则先将其分解为若干个简单图形(可以直接确定形心位置的图形)；然后由式(A-2)分别计算它们对于给定坐标轴的静矩，并求其代数和；再利用式(A-3),即可得组合图形的形心坐标。

平面图形的性质与判定导语：平面图形是几何学中的重要概念，它们具有不同的性质和特点。

本文将探讨平面图形的性质与判定，包括图形的对称性、角度、边长、面积等方面。

通过深入研究这些性质，我们可以更好地理解和应用平面图形。

一、对称性对称性是平面图形的一个重要性质，它可以分为轴对称和中心对称两种。

轴对称是指图形可以通过一条直线进行折叠，两边完全重合。

而中心对称是指图形可以通过一个点进行旋转，旋转180度后与原图形完全一致。

对称性的判定对于解题和构图都有重要意义。

例如，正方形就具有轴对称性。

当我们将正方形沿着中心线折叠时，两边完全重合。

而圆形则具有中心对称性，因为它可以通过旋转180度后与原图形完全一致。

二、角度角度是平面图形的重要性质之一，它可以分为直角、锐角和钝角。

直角是指两条线段相互垂直，形成90度的角。

锐角是指两条线段夹角小于90度，而钝角则是指两条线段夹角大于90度。

通过角度的判定，我们可以确定图形的性质和特点。

例如，在三角形中，如果有一个角是直角，则这个三角形是直角三角形。

如果三个角都是锐角，则这个三角形是锐角三角形。

而如果有一个角是钝角，则这个三角形是钝角三角形。

三、边长边长是平面图形的另一个重要性质，它可以帮助我们判断图形的大小和形状。

例如，在矩形中，如果四条边的长度相等，则这个矩形是正方形。

而如果四条边的长度不相等，则这个矩形是长方形。

另外，边长还可以用来计算图形的周长。

周长是指图形的边界长度，可以通过将所有边长相加来计算。

例如，在正方形中，如果一条边的长度是a，则它的周长是4a。

四、面积面积是平面图形的一个重要性质，它可以帮助我们计算图形所占的空间大小。

面积的计算方法因图形而异。

例如，在矩形中，面积可以通过将长和宽相乘来计算。

在三角形中，面积可以通过将底边长度与高相乘再除以2来计算。

面积的计算不仅可以帮助我们理解图形的大小，还可以应用于各种实际问题中。

例如，在建筑设计中，我们需要计算各种房间的面积，以确定材料的使用量。

平面图形的性质与特征一、点、线、面的基本概念及关系1.点：平面上的位置，没有长度、宽度和高度。

2.线：点的移动轨迹，有长度，没有宽度和高度。

3.面：线的移动轨迹，有长度和宽度，没有高度。

4.点、线、面的关系：点构成线，线构成面。

二、直线与射线的性质1.直线：无端点，无限长，同一平面内，直线外一点与直线上一点确定一条直线。

2.射线：有一个端点，无限长，从端点出发，沿直线方向延伸。

三、线段的性质1.线段：有两个端点，有限长。

2.线段的长度：两个端点之间的距离。

3.线段的垂直平分线：线段的中垂线，将线段平分为两个相等的部分，且与线段垂直。

四、角度的性质1.角度：由两条射线的公共端点和这两条射线的非公共部分组成的图形。

2.角度的度量：用度（°）作为单位，180°为直角，90°为锐角，小于90°为锐角，大于90°小于180°为钝角。

3.角度的补角：两个角的度数之和为180°。

4.角度的余角：两个角的度数之和为90°。

五、平行线的性质1.平行线：在同一平面内，永不相交的两条直线。

2.平行线的性质：同位角相等，内错角相等，同旁内角互补。

3.平行线的判定：同位角相等，内错角相等，同旁内角互补。

六、三角形的性质1.三角形：由三条边和三个角组成的多边形。

2.三角形的内角和：180°。

3.三角形的分类：根据边长关系，分为等边三角形、等腰三角形和普通三角形；根据角度关系，分为锐角三角形、直角三角形和钝角三角形。

4.三角形的高：从顶点到对边的垂线段。

七、四边形的性质1.四边形：由四条边和四个角组成的多边形。

2.四边形的内角和：360°。

3.四边形的分类：根据边长关系，分为矩形、正方形、平行四边形和普通四边形；根据角度关系，分为锐角四边形、直角四边形和钝角四边形。

4.四边形的角度性质：对角线互相平分，对边平行。

八、圆的性质1.圆：平面上所有到圆心距离相等的点组成的图形。

平面图形的性质在我们的日常生活中，平面图形无处不在。

从我们居住的房屋形状，到书本页面的轮廓，再到手机屏幕上的图标，平面图形构成了我们所见世界的一部分。

那么，什么是平面图形？平面图形又具有哪些独特的性质呢？平面图形，简单来说，就是在一个平面内由线段、曲线等构成的封闭或不封闭的图形。

常见的平面图形包括三角形、四边形、圆形、多边形等等。

先来说说三角形。

三角形是最为基础和常见的平面图形之一。

它具有稳定性，这一性质在建筑和工程领域有着广泛的应用。

比如，很多桥梁的结构中就运用了三角形的稳定性来确保桥梁的稳固。

三角形的内角和总是180 度，无论其形状大小如何。

根据边的长度和角的大小，三角形又可以分为等边三角形、等腰三角形和直角三角形等不同类型。

等边三角形的三条边长度相等，三个角也都为 60 度；等腰三角形有两条边长度相等，对应的两个角也相等；直角三角形则有一个角为90 度，其两条直角边的平方和等于斜边的平方，这就是著名的勾股定理。

四边形是另一种常见的平面图形。

其中，平行四边形具有两组对边分别平行且相等的性质。

矩形是一种特殊的平行四边形，它的四个角都是直角。

菱形也是特殊的平行四边形，其四条边长度相等。

正方形则更加特殊，它既是矩形又是菱形，具有矩形和菱形的所有性质。

圆形是一种优美而独特的平面图形。

圆上任意一点到圆心的距离都相等，这个距离被称为半径。

圆的周长与直径的比值是一个固定的数，称为圆周率，通常用π表示。

圆的面积等于π乘以半径的平方。

在实际生活中，我们常见的车轮、井盖等很多物品都做成圆形，这是因为圆形在滚动时能够保持平稳，而且在相同周长的情况下，圆形所围成的面积最大。

多边形也是平面图形家族中的重要成员。

多边形可以根据边的数量分为三角形（三边）、四边形（四边）、五边形（五边）等等。

多边形的内角和公式为：（n 2) × 180 度，其中 n 为多边形的边数。

平面图形的性质在数学、科学、工程、艺术等多个领域都发挥着重要作用。

平面图形的性质课件平面图形的性质平面图形是我们学习数学的重要内容之一。

它不仅在几何学中有广泛的应用，还是我们日常生活中常见的形状。

本文将探讨平面图形的性质，以帮助读者更好地理解和应用它们。

一、点、线和面在几何学中，点是最基本的概念。

它没有大小和形状，只有位置。

线由无数个点构成，它们在空间中延伸而成。

线的长度是无限的，但我们通常通过两点来确定一条线的位置。

面是由多条线构成的，它们在空间中形成了一个封闭的区域。

面有无数个点和线，但它没有厚度。

我们常见的平面图形，如矩形、三角形和圆形，都是由线和面组成的。

二、多边形的性质多边形是由直线段构成的封闭图形。

它有以下几个重要的性质：1. 边的数量：多边形至少有三条边。

具体而言，三角形有三条边，四边形有四条边，五边形有五条边，以此类推。

2. 角的数量：多边形的内角数等于其边数减去2。

例如，三角形有3个内角，四边形有4个内角，五边形有5个内角。

3. 内角和：多边形内所有的内角和等于360度。

这意味着无论多边形的形状如何，内角的度数总和都是固定的。

4. 外角和：多边形的外角和总是等于360度。

外角是指由一条边和相邻内角的补角组成的角度。

三、矩形和正方形的性质矩形和正方形是常见的平面图形，它们有特殊的性质：1. 矩形的对角线相等且互相平分：对于任意矩形ABCD，其两条对角线AC和BD相等，且互相平分。

2. 矩形的内角为直角：矩形的四个内角都是直角（90度角）。

3. 正方形是一种特殊的矩形：正方形是边长相等的矩形，因此它也具备矩形的性质。

此外，正方形的内角也都是直角。

四、三角形的性质三角形是最简单的多边形，它有以下几个重要的性质：1. 三角形的内角和为180度：任意三角形的三个内角的度数之和等于180度。

2. 等边三角形的特点：等边三角形的三条边都相等，且三个内角都是60度。

3. 等腰三角形的特点：等腰三角形的两条边（腰）相等，且两个内角也相等。

4. 直角三角形的特点：直角三角形有一个内角是直角（90度），其他两个内角则相加等于90度。

平面图形的性质与应用在数学中，平面图形是指由点和线构成的二维几何图形。

它们具有独特的性质，广泛应用于几何学、工程学、建筑学等领域。

本文将探讨平面图形的一些主要性质，并介绍它们在实际生活中的应用。

一、点、线和平面在平面图形中，点是最基本的要素。

它没有大小和形状，只具有位置信息。

线由两个点确定，可以看作是一条无限延伸的路径。

而平面由无数个点和线组成，是一个无限大的二维空间。

二、多边形的性质多边形是由线段相连而成的封闭图形。

它有许多重要的性质，如：边数、顶点数、内角和外角等。

1. 边数和顶点数一个多边形的边数等于它的顶点数，代表了多边形的复杂程度。

例如，三角形有三个边和三个顶点，矩形有四个边和四个顶点。

2. 内角和外角内角是多边形内部的角度，而外角则是多边形内部一条边的延长线与相邻边之间的角度。

对于一个n边形（n≥3），它的内角和外角满足以下关系：内角和= (n-2) × 180°，外角和= 360°。

这些性质有助于我们计算多边形内部和外部的角度。

三、常见平面图形的性质与应用除了多边形，还有许多其他常见的平面图形，它们也具有自己独特的性质和应用。

1. 圆形圆形是由一条固定半径的弧线围成的平面图形。

它有以下重要性质：半径、直径、周长和面积。

- 半径是由圆心到圆上任意一点的线段，它决定了圆的大小。

- 直径是通过圆心并且两端均在圆上的线段，等于两倍的半径。

- 周长是圆的边界长度，等于2πr（r为半径）。

- 面积是圆内部的空间大小，等于πr²。

圆形的应用非常广泛，如在建筑设计中，圆形的柱子可以提供更好的支撑力；在工程中，圆形的轮胎可以减少摩擦力。

2. 正方形正方形是一种具有四个相等边的矩形，它具有许多特点性质，并广泛应用于实际生活中。

- 边长和周长：正方形的四条边长度相等，周长等于4a（a为边长）。

- 面积：正方形的面积等于a²。

- 对角线：正方形的对角线相等，长度为√2a。

平面图形的性质及相关定理平面图形是几何学中的重要概念，大致可以分为线段、直线、角和面。

每种图形都有其独特的性质及相关定理，本文将针对这些内容展开论述。

1. 线段线段是由两个端点构成的有限部分直线。

线段的性质包括长度、方向和位置等方面。

其中最基本的定理是线段的长度可以通过两个端点的坐标计算得出，即欧几里得距离公式。

此外，线段的方向可以用斜率来描述。

若两线段的斜率相同，则它们平行；若两线段互为负倒数，则它们垂直。

2. 直线直线是没有端点的最长线段，也是平面几何中最基本的图形之一。

直线的性质主要有长度无穷大、方向唯一和位置平行等特点。

对于平行直线，我们可以利用同位角、内错角等相关定理进行证明。

同时，两直线交角的大小与它们的斜率有密切关系，通过求解斜率方程可得到直线之间的关系。

3. 角角是由两条射线共享一个端点所形成的图形。

角的性质包括大小、内外角和相互关系几个方面。

其中最重要的定理是角的度量可以通过弧度或角度计算。

弧度是一个非常重要的新单位，它的定义是角所对应的圆弧长度与圆的半径之比。

此外，角的内外角关系也是值得研究的，例如内错角之和等于180度。

4. 面面是由三条边围成的平面图形。

面的性质包括面积、形状和位置等方面。

最常见的面包括三角形、矩形和圆形。

对于三角形而言，海伦公式可以帮助我们计算其面积，它要求已知三边长度。

另外，矩形具有特殊的性质，如相邻边互相垂直且对角线相等。

而圆是一种特殊的面，它具有无限多个对称轴、周长和面积计算公式等。

总结：平面图形的性质及相关定理是数学研究的重要内容。

通过对线段、直线、角和面的研究，我们可以深入了解它们各自的特点及内在关系。

这些性质及定理的应用广泛，涉及到数学、物理、工程等领域。

在实际生活中，我们也能发现许多与平面图形相关的现象，比如日常用品的设计、城市规划等。

因此，深入掌握平面图形的性质及相关定理对于我们的学习和实践具有重要意义。

平面形的性质知识点总结平面形是几何学中一类常见的二维图形，包括了许多不同的图形，如矩形、正方形、三角形、梯形等。

了解平面形的性质对于解题和分析几何问题非常重要。

本文将对平面形的性质进行总结，并提供一些实例进行说明。

一、矩形的性质矩形是一种特殊的四边形，它的对边相等且平行，且内角均为直角。

以下是矩形的几个重要性质：1. 两对对边分别相等且平行。

2. 对角线相等并且相交于中点。

3. 任意一条边均与其相对的边垂直。

例如，ABCD为矩形，AB＝CD，BC＝AD，AC＝BD，AC和BD为对角线。

二、正方形的性质正方形是一种特殊的矩形，它的四条边相等且平行，且内角均为直角。

以下是正方形的几个重要性质：1. 所有边长相等且平行。

2. 所有角均为直角。

3. 对角线相等且垂直于彼此。

例如，ABCD为正方形，AB＝BC＝CD＝DA，AC＝BD，AC和BD为对角线。

三、三角形的性质三角形是一个有三条边和三个角的平面形。

以下是三角形的一些重要性质：1. 三角形的内角之和为180度。

2. 三角形的外角之和为360度。

3. 三角形的三边满足任意两边之和大于第三边的三角不等式。

例如，ABC为三角形，∠A+∠B+∠C＝180度。

四、梯形的性质梯形是一个有两个平行边的四边形。

以下是梯形的一些重要性质：1. 两个底角（梯形两边且不与平行边相邻的内角）之和等于180度。

2. 两个顶角（梯形两边且与平行边相邻的内角）之和等于180度。

3. 非平行边（腰）不等。

例如，ABCD为梯形，AB平行于CD，∠A+∠B＝180度。

五、圆的性质圆是由一条曲线（圆周）上的所有点与一个固定点（圆心）的距离相等的图形。

以下是圆的一些重要性质：1. 圆心到圆上任意一点的距离相等。

2. 圆周上的弧度等于圆心角所对的弧度。

3. 圆上的切线与半径垂直。

例如，O为圆心，AB为圆上的一条弧，OA与OB为半径，∠AOB为圆心角。

六、五边形和六边形的性质五边形和六边形是常见的多边形，它们具有一些共同的性质：1. 五边形的内角之和为540度，六边形的内角之和为720度。