九年级数学下册263实践与探索《最大面积是多少》典型例题素材(新版)华东师大版.docx

《最大面积是多少》中考题例析利用二次函数知识解决有关几何图形面积最大问题，已成为近年来中考的一个亮点．现例举亮例，供读者赏析．例1如图，要在底边BC = 10CM ，高AD = 120c M 的△ABC 铁皮余料上截取一个矩形EFGH ，使点H 在AB 上，点G 在AC 上，点E 和F 在BC 上，AD 交HG 于点M ，此时AD AM =BC HG ． （1）设矩形EFGH 的长HG = y ， 宽HE = x ，确定y 与x 的函数关系式．（2）当x 为何值时，矩形EFGH 的面积S 最大？ （3）以面积最大的矩形EFGH 为侧面，围成一个圆柱形的铁桶．怎样围时，才能使铁桶的体积较大？请说明理由．（注：围铁桶侧面时，接缝无重叠，底面另有材料配备）解析：（1）∵AD AM =BC HG ，即 120120x -=160y ， ∴y =－34x ＋160． （2）∵S = xy ， ∴S =x ·（－34x ＋160）=－34x 2＋160x =－34（x －60）2＋4800． 所以当x = 60时，矩形EFGH 的面积S 最大，即S = 4800cm 2．（3）围成圆柱形铁桶有两种情形：①以矩形EFGH 的宽HE = 60cm 作为铁桶的高，长HG = 80cm 作为铁桶的底面周长，则底面半径为R =802π． 故铁桶的体积为V 1 =л·（802π）2·60 =96000πcm 3． ②以矩形EFGH 的长HG = 80cm 作为铁桶的高，宽HE = 60cm 作为铁桶的底面周长，则底面半径为r =602π． 故铁桶的体积为V 2 =л·（602π）2·80 =72000πcm 3． 由V 1> V 2，所以以矩形EFGH 的宽HE = 60cm 作为铁桶的高，长HG = 80cm 作为铁桶的底面周长，围成的圆柱形铁桶的体积较大．例2 学校为了美化校园环境，在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃．（1）若请你在这块空地上设计一个长方形花圃，使它的面积比学校计划新建的长AB C E FG HD M方形花圃的面积多1平方米，请你给出你认为合适的三种不同的方案．（2）在学校计划新建的长方形花圃周长不变的情况下，长方形花圃的面积能否增加2平方米？如果能，请求出长方形花圃的长和宽；如果不能，请说明理由．解析：（1）方案1：长为971米，宽为7米． 方案2：长为9米，宽为971米． 方案3：长=宽=8米．（2）在长方形花圃周长不变的情况下，长方形花圃面积不能增加2平方米．由题意得长方形长与宽的和为16米．设长方形花圃的长为x 米，则宽为（16-x ）米．S 长方形=x （16-x ）=-x 2+16x =-（x -8）2+64．∴在长方形花圃周长不变的情况下，长方形的最大面积为64平方米，因此不能增加2平方米．。

《最大面积是多少》典型例题有许多面积的最大(小)值问题, 是中考的重点题型，常常是例用二次函数的最大(小)值来解决的,现举例说明这类问题的解法.例1.现有一块矩形场地，如图1所示，长为40m ，宽为30m ，要将这块地划分为四块分别种植：A .兰花；B .菊花；C .月季；D .牵牛花.(1)求出这块场地中种植B 菊花的面积y 与B 场地的长x 之间的函数关系式，并写出自为量的取值范围.(2)当x 是多少时，种植菊花的面积最大？最大面积是多少？分析：这是花草种植面积的最值问题，先根据矩形的面积公式列出y 与x 之间的函数关系式，再利用配方法或公式法求得最大值.解：(1)由题意知，B 场地宽为(30)m x -，∴2(30)30y x x x x =-=-+， 自变量x 的取值范围为030x <<.(2)2230(15)225y x x x =-+=--+，当15m x =时，种植菊米的面积最大， 最大面积为225m 2.例 2.某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现在两种方案：①围成一个矩形(如图2)；②围成一个半圆形(如图3).设矩形的面积为1S 平方米,宽为x 米, 半圆形的面积为2S 平方米,半径为x 米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(3π≈).分析：这是一道实际应用问题，方案②中半圆的面积是固定不变的，解决本题的关键是确定方案①中矩形面积的最大值，然后再比较.因此，对于方案①，需要根据矩形的面积构造二次函数，通过求二次函数的最值解决.图2 图3解: 方案①：221(302)2302(7.5)112.5S x x x x x =-=-+=--+当x=7.5米时，1S 取最大值112.5平方米.方案②：由30x π=得10x =米， 所以2211310015022S x π==⨯⨯=平方米. ∵112.5<150， ∵12S S <，∴应选方案②.例3.在某市开展的创城活动中，桃园小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD ，花园的一边靠墙，另三边用总长为40m 的栅栏围成(如图4所示).若设花园的BC 的边长为x (cm )，花园的面积为y (m 2).(1)求y 与x 之间的函数关系式，并写出自变量是x 的取值范围；(2)满足条件的花园面积能达到200m 2吗？若能，求出此时x 的值；若不能，说明理由；(3)根据(1)中求得的函数关系式,描述其图象的变化趋势；并结合题意判断当x 取何值时，花园的面积最大？最大面积为多少？分析：(1)根据矩形的面积可以确定函数表达式,根据墙长可确定自变量的范围；(2)假设可到200m 2矩形,根据函数值构造方程,求出x 的值与墙长比较,从而判断是否面积可达到200m 2；(3)通过求二次函数的最值可求到花园的最大面积.解：(1)根据题意得：(40)2x y x -=, 所以y =－21x 2+20x (0< x ≤15)； (2)假设面积可以为200m 2,则y=200时，21202002x x -+=,2404000x x -+=,解得：x =20. 因为20m>15m,所以此花园的面积不能达到200m 2.(3)因为21202y x x =-+的图像是开中向下的抛物线，对称轴为x =20. 所以当0<x≤15时，y 随x 的增大而增大,所以当x =15时,y 有最大值.221152015187.5()2y m =-⨯+⨯=最大值. 即：当x=15时，花园面积最大，最大面积为187.5m 2.注意：顶点横坐标在自变量的取值范围内时，二次函数在顶点处取得最值；顶点横坐标不在自变量的取值范围内时，要根据题目条件，结合函数的性质，进行具体分析，才能求出符合题意的最值.本题应在x的取值范围0<x≤15中确定函数最大值.。

26.3.2 几何图形面积最值问题【同步测试】一．选择题（共2小题）1．用长40m的篱笆围成一个矩形菜园，则围成的菜园的最大面积为（）A．400m2B．300m2C．200m2D．100m2【答案】D【解析】解：设矩形的面积为S平方米，长为xm，由题意，得S＝x（20﹣x），s最大＝100．故选：D．【点睛】本题考查了运用待定系数法求二次函数的解析式的运用，抛物线的顶点式的运用，矩形的面积公式，解答时求出矩形的面积表达式是关键．2．如图，一边靠校园围墙，其他三边用总长为40米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（）A．10米B．15米C．20米D．25米【答案】A【解析】解：设矩形ABCD的边AB为x米，则宽为（40﹣2x）米，S＝（40﹣2x）x＝﹣2x2+40x．要使矩形ABCD面积最大，则x10米，即x的长为10米．故选：A．【点睛】求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y＝﹣x2﹣2x+5，y＝3x2﹣6x+1等用配方法求解比较简单．二．填空题（共3小题）3．如图，用长20m的篱笆，一面靠墙（墙足够长）围成一个长方形的园子，最大面积是________m2．【答案】50m2【解析】解：设与墙平行的一边长为xm，则另一面为，其面积x x2﹣10x，∴最大面积为50即最大面积是50m2．【点睛】求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y＝﹣x2﹣2x+5，y＝3x2﹣6x+1等用配方法求解比较简单．4．周长为13cm的矩形铁板上剪去一个等边三角形（这个等边三角形的一边是矩形的宽），则矩形宽为_____cm，长为____cm时，剩下的面积最大，这个最大面积是_________．【答案】见解析经整理，得：y x2x，当x4时，y取得最大值，y最大（4），此时长为（）．【点睛】本题考查了二次函数在实际生活中的运用，重点是求最值问题．5．如图，在△ABC中，∠B＝90°，AB＝8cm，BC＝6cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以1cm/s的速度移动，如果P，Q分别从A，B同时出发，当△PBQ的面积为最大时，运动时间t为______s．【答案】2∵由以上函数图象知∴当t＝2时，△PBQ的面积最大为4cm2．【点睛】求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y＝﹣x2﹣2x+5，y＝3x2﹣6x+1等用配方法求解比较简单．三．解答题（共3小题）6．一养鸡专业户计划用长116m的竹篱笆靠墙（如图）围成一个长方形鸡舍，怎样设计才能使围成的长方形鸡舍的面积最大？最大面积为多少？【答案】见解析【解析】解：∵四边形ABCD是矩形，∴AB＝CD．设BC＝xm，则AB＝CD（116﹣x）m，矩形的面积为S．由题意，得S＝x•x2+58x（x﹣58）2+1682．∴当x＝58m时，S最大＝1682m2．【点睛】本题考查了矩形的性质的运用，矩形的面积公式的运用，二次函数的解析式的顶点式的运用．解答时求出S与x之间的关系式是关键．7．如图等腰梯形ABCD中，AB＝4，CD＝9，∠C＝60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中以个动点到达端点时，另一个动点也随之停止运动（1）求AD的长；（2）设CD＝x，问当x为何值时△PDQ的面积达到最大？并求出最大值．【答案】见解析【解析】解：（1）如图1在Rt△ADE中，AD2＝5；（2）如图1∵CP＝x，h为PD边上的高，依题意，△PDQ的面积S可表示为：（x）2．（0≤x≤5）∴a0，∴当x时（满足0≤x≤5），S最大值．学科&网【点睛】本题考查了学生的分析作图能力和考查学生综合运用平行线、等腰梯形、等边三角形、菱形、二次函数等知识．这里设计了一个开放的、动态的数学情境，为学生灵活运用基础知识、分析问题、解决问题留下了广阔的探索、创新的思维空间．8．如图等腰梯形花圃ABCD的底边AD靠墙，另三边用长为40m的铁栏围成，设AB的长为xm，该花圃的面积为Sm2（1）求出底边BC的长．（用含x的代数式表示）（2）若∠BAD＝60°，求S与x之间的函数关系式；（3）在（2）的条件下，若墙长为24m，试求S的最大值．【答案】见解析【解析】解：（1）∵AB＝CD＝x米，∴BC＝40﹣AB﹣CD＝（40﹣2x）米．（2）如图，过点B、C分别作BE⊥AD于E，CF⊥AD于F，在Rt△ABE中，AB＝x，∠BAE＝60°∴AE x，BE x，∴S（40﹣2x+40﹣x）•x x（80﹣3x）（0＜x＜20），当S＝93时，，解得：x1＝6，x2＝20（舍去）．∴x＝6（3）由题意，得40﹣x≤24，解得x≥16，结合（2）得16≤x＜20．由（2），S∵a∴函数图象为开口向下的抛物线的一段（附函数图象草图如左）．其对称轴为x，∵16，由左图可知，当16≤x＜20时，S随x的增大而减小，∴当x＝16时，S取得最大值，此时S最大值162+2016＝128m2．【点睛】本题考查了二次函数的性质的运用，等腰梯形的性质的运用．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．本题主要考查二次函数的运用，运算较复杂，难度偏难．。

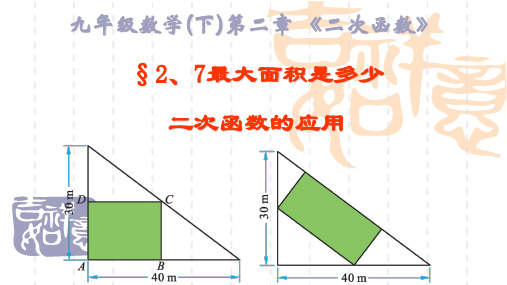
北师大版初中数学九年级下册《2.7最大面积是多少》精品学案导学目标： 学会分析和表示不同背景下实际问题中的变量之间的二次函数关系，并运用二次函数的知识解决实际问题．教学目标：1．经历探究长方形最大面积问题的过程，进一步获得利用数学方法解决实际问题的经验，并进一步感受数学模型思想和数学知识的应用价值。

2．能够对解决问题的基本策略进行反思，形成个人解决问题的风格。

3．进一步体会数学与人类社会的密切联系，了解数学的价值，增进对数学的理解和学好数学的信心，具有初步的创新精神和实践能力。

一．指导自学：（一） 知识储备 1．求二次函数y=43x 2+30x 的（1）开口方向；（2）对称轴；（3）顶点坐标；（4）增减性；（5）x 取何值时，y 取最大或最小值？ .2.有一块三角形余料△ABC ，∠C=90°，AC=30cm ，BC=40cm ，要利用这块余料截出一个矩形，使矩形的四个顶点在三角形的边上，问矩形的边长分别是多少时，矩形的面积为300cm 2？二．精讲导学：（二）典型例题例1．有一块三角形余料，∠C=90°，AC=30cm，BC=40cm，要利用这块余料截出一个如图所示的矩形DECF，使矩形四个顶点落在三角形的边上，，问怎样截，矩形的面积最大？(三)随堂练习1有一块三角形余料，∠C=90°，AC=30cm，BC=40cm，要利用这块余料截出一个矩形，还有其他截法吗？怎样截，所得矩形的面积最大？最大是多少？（四）拓展提高如图假设篱笆（虚线）的长度为15米，两面靠墙围成一个矩形，若墙AB长7米，BC边长10米，如何围才能使围成的矩形的面积最大达标评价（五）随堂测试有一块三角形土地如图，它的底边BC=100米，高AD=80米，某单位沿着BC修一座底面是矩形的大楼，设EH=x米，矩形EFGH的面积为y米2，则（1）EF=______________米；（2）y=_________________（3）当这座大楼的地基面积最大时，这个矩形的长和宽各是多少米？作业:A 必做：同步P1、2382B: 必做：书P68B1.如图张伯伯准备利用现有的一面墙和40ｍ长的篱笆，把墙外的空地围成四个相连且面积相等的矩形养兔场。

[科目]数学
[关键词]面积/几何/割补法
[标题]面积
[内容]
面积
面积的概念很早就形成了。

在古代埃及，尼罗河每年泛滥一次，洪水给两岸带来了肥沃的淤泥，但也抹掉了田地之间的界限标志。

水退了，人们要重新划出田地的界限，就必须丈量和计算田地，于是逐渐有了面积的概念。

在数学上是这样来研究面积问题的：首先规定边长为1的正方形的面积为1，并将其作为不证自明的公理。

然后用这样的所谓单位正方形来度量其他平面几何图形。

较为简单的正方形和长方形的面积是很容易得到的，利用割补法可以把平行四边形的面积问题转化为长方形的面积问题，进而又可以得到三角形的面积。

于是多边形的面积就可以转化为若干三角形的面积。

大家一定很熟悉圆的面积公式，即πr2，其中r是圆的半径，但得到这个公式却不是很容易的，实际上圆面积的严格定义要用到极限的概念。

对面积的深入研究导致了近代测度理论的诞生和发展。