ANSYS中简支梁的模拟计算

基于ANSYS的钢筋混凝土简支梁桥极限承载力分析研究一、本文概述随着现代工程技术的飞速发展，钢筋混凝土简支梁桥作为桥梁工程中的重要结构形式，其极限承载力分析对于确保桥梁的安全性和稳定性具有至关重要的意义。

本文旨在通过基于ANSYS的数值模拟方法，深入研究钢筋混凝土简支梁桥的极限承载力，以期为实际工程应用提供理论依据和技术支持。

本文首先介绍了钢筋混凝土简支梁桥的基本结构特点和应用现状，阐述了进行极限承载力分析的必要性。

接着，详细介绍了ANSYS 有限元分析软件在桥梁工程中的应用及其优势，为后续的研究工作奠定了理论基础。

在研究方法上，本文采用ANSYS软件建立钢筋混凝土简支梁桥的数值模型，通过施加不同的荷载工况，模拟桥梁在实际运营过程中的受力状态。

在此基础上，对桥梁的极限承载力进行分析，探究其破坏模式、应力分布及变形特征。

本文还将考虑不同因素（如材料性能、截面尺寸、配筋方式等）对桥梁极限承载力的影响，以期获得更为全面和准确的分析结果。

本文将对所得的研究结果进行总结，提出钢筋混凝土简支梁桥极限承载力分析的关键问题和改进措施，为实际工程设计和施工提供有益的参考和借鉴。

通过本文的研究，不仅能够加深对钢筋混凝土简支梁桥极限承载力的认识和理解，还能够推动桥梁工程领域的科技进步和创新发展。

二、钢筋混凝土简支梁桥的基本原理钢筋混凝土简支梁桥，作为桥梁工程中的一种基本结构形式，其基本原理主要基于材料力学和结构力学的理论。

简支梁桥是一种静定结构，其特点是梁的两端搁置在支座上，梁端无水平推力，当梁上作用有荷载时，梁内产生的弯矩和剪力仅与荷载的大小和分布有关，而与两端支承处的约束情况无关。

在钢筋混凝土简支梁桥中，混凝土主要承担压应力，而钢筋则主要承受拉应力。

这种组合使得钢筋混凝土结构既具有混凝土的高抗压强度，又具有钢筋的高抗拉强度，从而实现了优势互补，提高了结构的整体承载能力。

钢筋混凝土简支梁桥的设计还需考虑桥梁的使用功能、荷载等级、材料性能、施工工艺等因素。

瞬态缩减法分析简支梁－质量系统实例在这个实例中要用缩减法进行瞬态动力学分析以确定对有有限上升时间的恒定力的动力学响应。

问题的实际结构是一根钢梁支撑着集中质量并承受一个动态载荷。

钢梁长为，支撑着一个集中质量。

这根梁承受着一个上升时间为，最大值为的动载荷。

梁的重量可以忽略，确定产生最大位移响应时的时间及响应。

同时要确定梁中的最大弯曲应力。

求解过程中用不到梁的特性，其截面积可随意输入一个单位值。

取加载结束时间为0.1秒以使质量体达到最大弯曲。

在质量体的侧向设定一个主自由度。

第一个载荷步用于静力学求解。

可以在此模型中可以使用对称性。

选定在最大响应时间（0.092秒）处做扩展处理计算。

已知下列数据：材料特性：=30×103=0.0259067几何数据：载荷：图9钢梁支撑集中质量的几何模型§1GUI方式分析过程第 1步：指定分析标题1.选取菜单途径Utility Menu>File>Change Title。

2.输入文字“瞬态response to a constant force with a finite rise time.”单击OK。

第 2步：指定单元类型1.选取菜单途径Main Menu>Preprocessor>ElementType>Add/Edit/Delete。

Element Type对话框将出现。

2.单击Add。

Library of Element Types对话框出现。

3.在左边的滚动框中，单击“Structural Beam”。

4.在右边的滚动框中，单击“2D elastic 3”，然后单击Apply。

5.在左边的滚动框中，单击“Structural Mass”。

6.在右边的滚动框中，单击“3D mass21”，然后单击OK。

7.在Element Types对话框中，在“Type2”上单击仅一次，然后单击Options。

8.在Rotary inertia options下拉列表中，滚动到“2-D w/o rot iner”并选中它。

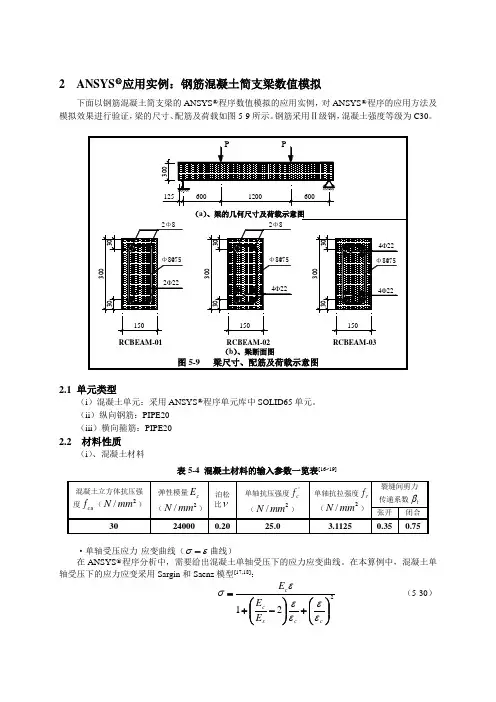
（ii ）纵向钢筋：PIPE20 （iii ）横向箍筋：PIPE202.2 材料性质（i ）、混凝土材料表5-4 混凝土材料的输入参数一览表[16~19]·单轴受压应力-应变曲线（εσ-曲线）在ANSYS ○R程序分析中，需要给出混凝土单轴受压下的应力应变曲线。

在本算例中，混凝土单轴受压下的应力应变采用Sargin 和Saenz 模型[17,18]：221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-+=c c s c c E E E εεεεεσ （5-30）式中取4'4')108.0028.1(c c c f f -=ε；断面图配筋图断面图配筋图断面图配筋图RCBEAM-01 RCBEAM-02 RCBEAM-03图5-12 各梁FEM模型断面图（a）单元网格图（b）钢筋单元划分图图5-13 算例（一）的FEM模型图2.4 模型求解在ANSYS○R程序中，对于非线性分析，求解步的设置很关键，对计算是否收敛关系很大，对于混凝土非线性有限元分析，在计算时间容许的情况下，较多的求解子步（Substeps）或较小的荷载步和一个非常大的最大子步数更容易导致收敛[2]。

在本算例中，设置了100个子步。

最终本算例收敛成功，在CPU为P41.6G、内存为256MB的微机上计算，耗时约为8小时。

2.5 计算结果及分析2.5.1 荷载—位移曲线图5-14为ANSYS○R程序所得到的各梁的荷载-跨中挠度曲线，从图中可以看出：（i）、梁RCBEAM-01：曲线形状能基本反映钢筋混凝土适筋梁剪切破坏的受力特点，而且荷载-跨中挠度曲线与钢筋混凝土梁的弯剪破坏形态非常类似，即当跨中弯矩最大截面的纵筋屈服后，由于裂缝的开展，压区混凝土的面积逐渐减小，在荷载几乎不增加的情况下，压区混凝土所受的正应力和剪应力还在不断增加，当应力达到混凝土强度极限时，剪切破坏发生，荷载突然降低。

（ii）、梁RCBEAM-02：荷载-跨中挠度曲线与超筋梁的试验荷载-跨中挠度曲线很相似，在荷载达到极限情况下，没有出现屈服平台，而是突然跌落。

lsel,s,loc,z,0
lsel,r,loc,y,0
dl,all,,uy
dl,all,,uz
lsel,all
lsel,s,loc,z,3பைடு நூலகம்00
lsel,r,loc,y,0
dl,all,,uy
lsel,all
ksel,s,loc,x,0
ksel,r,loc,y,0
!方法：分离式；solid65和link8
!材料：混凝土采用concr和钢筋为弹性材料，但不考虑压碎
!---------------------------------------------------
!为方便，假定钢筋置于梁底两侧.
!===================================================
lesize,all,,,20
lmesh,all
lsel,s,loc,z,0
lesize,all,,,4
vsel,all
vatt,1,1,1
mshape,0,3d
mshkey,1
vmesh,all
allsel,all
finish
/solu
!施加约束
/config,nres,2000
/prep7
!定义单元及其材料特性等
rd0=20.0 !钢筋直径
et,1,solid65
et,2,link8
mp,ex,1,33e3
mp,prxy,1,0.20
r,1
hntra=28
hntrl=2.6
tb,concr,1
/post1
pldisp,1

（整理）ansys简支梁分析.图b所示的矩形截面的简支梁，受到竖直向下的2q 均布载荷作用。

100mKN图b 梁受力情况及截面尺寸表1 梁的几何参数及材料参数（三）研究方法及模型的建立（包括单元的选取，边界条件的简化等）。

1.梁单元⑴建模：由于对称性，取梁的右半部分为研究对象。

①选择梁单元，设置材料常数定义梁的横截面面积、惯性矩及截面高度。

②建立2个关键点：1（0，0，0）；2（8，0，0）。

③生成直线：ANSYS Main Menu>Preprocessor>Modeling>Lines>Lines>Stright Line，依次连接关键点，点击ok即可。

④划分单元：ANSYS Main Menu>Preprocessor>Meshing>SizeCntrls>ManualSize>Lines>Picked Lines，选择直线，将梁划分为80份；ANSYS Main Menu>Preprocessor>Meshing>MeshTool>Shape>Mech>pickall，完成划分。

⑤施加约束：ANSYS Main Menu>Solution>Difine Loads>Apply>Structural>Displacement>On Nodes，选取对称轴上的节点，施加x方向的约束；选取右下角的节点施加y方向约束。

⑥施加载荷：ANSYS Main Menu>Solution>Difine Loads>Apply>Pressure>On Beams>Pick All，V ALI Pressure Value at I输入100000，V ALJ Pressure Value at J输入100000，即施加了均布载荷。

建好的模型如图1.1所示。

有限元大作业计算
依据已知条件，将梁转化为平面实体模型，可得梁的面荷载等效为4000N/m，弹性模量为28E9N/㎡，泊松比为0.16，梁长8m，高1m，定义实体模型厚度为0.4m。

利用solid材料选项命令建立实体模型，添加各项材料属性，建立实体模型后，以0.1m作为单元长度进行剖分，在模型中轴线左端加上位移X和Y方向的约束，右端加上位移Y方向的约束，加上4000N/m的线荷载后进行模型求解，通过后处理器中PLOT命令导出计算应力云图（如图1所示）和位移图（如图2所示），通过query命令中的Subgrid Solu命令对下边中点处的应力值进行提取（如图3所示）。

图1 实体单元建模应力云图
图2 实体单元建模位移图
图3 实体单元建模中值点应力值
采用beam命令对进行梁单元材料定义，并输入对应参数，之后进行对应建模计算，导出计算结果，应力云图（如图4所示）、位移图（如图5所示）和中
值点应力值（如图6所示）。

图4 梁单元建模应力云图
图5 梁单元建模位移图
图6 梁单元建模中值点应力值
可知，在实体单元建模中，中点处位移为：m 410954.0-⨯，中点处应力值为：192655N/㎡；在梁单元建模中，中点处位移为：m 310227.0-⨯，中点处应力值为：457840N/㎡。

（手算结果见附页）
姓名：吴 小 超
学号：2140720060
班级：研1420班
任课教师：简 政。

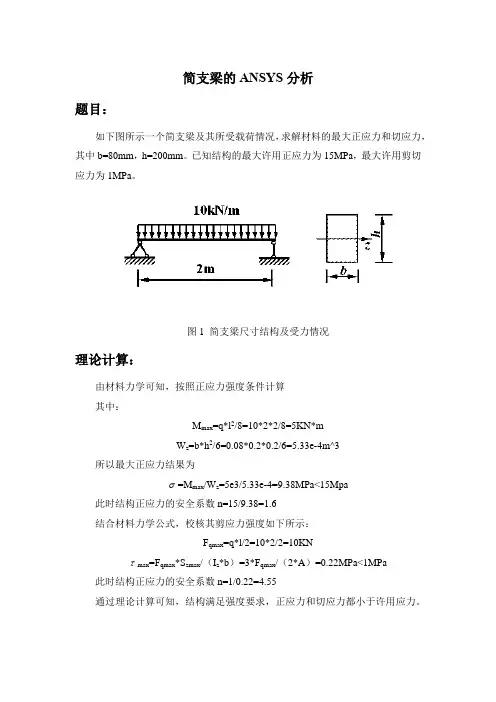
简支梁的ANSYS分析题目：如下图所示一个简支梁及其所受载荷情况，求解材料的最大正应力和切应力，其中b=80mm，h=200mm。

已知结构的最大许用正应力为15MPa，最大许用剪切应力为1MPa。

图1 简支梁尺寸结构及受力情况理论计算：由材料力学可知，按照正应力强度条件计算其中：M max=q*l2/8=10*2*2/8=5KN*mW z=b*h2/6=0.08*0.2*0.2/6=5.33e-4m^3所以最大正应力结果为σ=M max/W z=5e3/5.33e-4=9.38MPa<15Mpa此时结构正应力的安全系数n=15/9.38=1.6结合材料力学公式，校核其剪应力强度如下所示：F qmax=q*l/2=10*2/2=10KNτmax=F qmax*S zmax/（I z*b）=3*F qmax/（2*A）=0.22MPa<1MPa 此时结构正应力的安全系数n=1/0.22=4.55通过理论计算可知，结构满足强度要求，正应力和切应力都小于许用应力。

有限元分析：采用ANSYS软件对上述结构进行分析，得出结构的受力情况。

有限元分析流程如下所示：建立几何模型，该结构为梁结构，在ANSYS中采用梁单元来模拟，那么几何模型为线体，即长度为2m的线，然后赋予梁的截面形状。

单元类型选择beam188单元类型。

该单元类型具有两个节点，每个节点具有六个自由度，分别为空间坐标系下的三个平动自由度和三个转动自由度。

图2 beam188单元类型操作流程如下：GUI：Utility Menu→Preprocessor→Element Type→Add/Edit/Delete，弹出【Element Types】对话框，单机Add按钮，弹出【Library of Element Types】对话框，设置下面选项：左边列表框中选择Beam；右边列表框中选择 2 node 188；图3 单元类型定义定义梁单元的截面属性，操作流程如下：GUI：Utility Menu→Preprocessor→Sections →Beam→Common Sections，弹出如下对话框，并进行如下所示设置，点击Ok。

ANSYS对简支梁的数值模拟
段敬民;冯波涛;李伟
【期刊名称】《低温建筑技术》
【年(卷),期】2009(031)012
【摘要】采用Solid65单元和Link8单元对钢筋混凝土简支梁进行了数值模拟计算,模拟结果表明用Solid65单元和Link8单元模拟钢筋混凝土简支梁破坏是可行的,基本上能反映梁破坏时的力学特征,说明了利用ANSYS有限元程序作为辅助的研究手段来模拟试验过程的可行性的,也是可靠的.
【总页数】3页(P53-55)
【作者】段敬民;冯波涛;李伟
【作者单位】河南理工大学土木工程学院,河南,焦作,454000;河南理工大学土木工程学院,河南,焦作,454000;河南理工大学土木工程学院,河南,焦作,454000
【正文语种】中文
【中图分类】TU311.41
【相关文献】
1.基于ANSYS的简支梁桥柔性墩纵向力分配研究 [J], 丁剑霆;庞静;刘春川
2.基于ANSYS的简支T梁桥桥面连续结构的空间仿真分析 [J], 凌青松
3.基于ANSYS有限元法的简支梁力学计算与优化设计 [J], 吕凯;张文辉
4.基于ANSYS的单跨简支梁钢桥的谐响应分析 [J], 王冬丽;袁朝庆
5.基于ANSYS钢筋混凝土简支梁极限荷载研究 [J], 周广强;王康入
因版权原因，仅展示原文概要，查看原文内容请购买。

图b所示的矩形截面的简支梁，受到竖直向下的2q 均布载荷作用。

100mKN图b 梁受力情况及截面尺寸表1 梁的几何参数及材料参数（三）研究方法及模型的建立（包括单元的选取，边界条件的简化等）。

1.梁单元⑴建模：由于对称性，取梁的右半部分为研究对象。

①选择梁单元，设置材料常数定义梁的横截面面积、惯性矩及截面高度。

②建立2个关键点：1（0，0，0）；2（8，0，0）。

③生成直线：ANSYS Main Menu>Preprocessor>Modeling>Lines>Lines>Stright Line，依次连接关键点，点击ok即可。

④划分单元：ANSYS Main Menu>Preprocessor>Meshing>Size Cntrls>ManualSize>Lines>Picked Lines，选择直线，将梁划分为80份；ANSYS Main Menu>Preprocessor>Meshing>MeshTool>Shape>Mech>pick all，完成划分。

⑤施加约束：ANSYS Main Menu>Solution>Difine Loads>Apply>Structural>Displacement>On Nodes，选取对称轴上的节点，施加x方向的约束；选取右下角的节点施加y方向约束。

⑥施加载荷：ANSYS Main Menu>Solution>Difine Loads>Apply>Pressure>On Beams>Pick All，V ALI Pressure Value at I输入100000，V ALJ Pressure Value at J输入100000，即施加了均布载荷。

建好的模型如图1.1所示。

图1.1 梁单元模型图⑵分析计算：ANSYS Main Menu>Solution>Solve>Current LS ⑶计算结果：图1.2 梁单元计算位移云图由图2.1可以看出，最大位移发生在梁的对称轴即中点处，m y 3-max 10190.0⨯=，支座处位移为0。

例1简支梁的有限元建模与变形分析计算分析模型如图1-1 所示, 习题文件名: beam。

（梁单元表示实体）梁承受均布载荷：1KN/m图1-1梁的计算分析模型梁截面矩形，183*183单位mm面积335cm2惯性矩9.3e-5 m4EX:2.06e11Pa PRXY:0.3 （计算中需要的参数，注意单位）1.1进入ANSYS 设置工作名和标题并在窗口显示程序→ANSYSED 10.0→ANSYS（启动）→file →change jobname（更改工作名）→enter the new jobname: beam（输入工作名）→file→change title（更改标题）→enter new title: beam（输入新标题）→ok→plot （绘制）→replot（重新绘制）1.2ANSYS偏好设置（把与本例无关的可能出现的选项都屏蔽）ANSYS Main Menu: Preferences →选择Structural（结构）→OK1.3选择单元类型ANSYS Main Menu: Preprocessor（前处理器）→Element Type（单元类型）→Add/Edit/Delete… （添加/编辑/删除）→Add…（添加）→选择Beam 2D elastic 3 →OK →Close1.4定义单元实参数ANSYS Main Menu: Preprocessor →REAL Constants（材料实参数）→Add/Edit/Delete… （添加/编辑/删除）→add →ok →AREA（面积，注意换算）3.35e-6，IZZ （惯性矩）9.3e-5，HEIGHT0.183（高）→OK1.5定义材料参数Material Props（材料参数）→Material Models（材料模型）→Structural→Linear→Elastic→Isotropic→input EX:2.06e11, PRXY:0.3（输入弹性模量和泊松比）→OK1.6生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling（建模）→Create →Keypoints（创建关键点）→In Active CS （在当前坐标系）→依次输入三个点的坐标：input:1(0,0),2(1,0)（连续输入选择apply，最后一次输入选择ok）→OK✓生成梁ANSYS Main Menu: Preprocessor →Modeling →Create →Lines →lines →Straight lines →连接两个特征点，1(0,0),2(1,0) →OK1.7网格划分ANSYS Main Menu: Preprocessor →Meshing（网格）→Mesh Attributes（网格特性）→all lines →OK→Meshing（网格）→SIZE CNTRLS（尺寸）→manualsize（手工设置）lines →alllines→→element edge length(单元长度)输入0.1→OK→Mesh(划分网格)→lines→pick all →OK1.8模型施加约束✓最左端节点加约束ANSYS Main Menu: Solution（求解）→Define Loads（定义载荷）→Apply（施加）→Structural →Displacement（位移）→On KEYPOINTS（在关键点处）→pick the keypoints at (0,0) （选择原点）→OK→select UX, UY（施加自由度约束）→OK✓最右端节点加约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement →On keypoints→pick the keypoints at (1,0) →OK→select UY →OK✓施加y方向的载荷ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Pressure（压力）→On Beams→Pick All→V ALI:1000 →OK1.9 分析计算ANSYS Main Menu: Solution →Solve （求解）→Current LS（当前坐标系）→OK(to close the solve Current Load Step window) →OK1.10 结果显示ANSYS Main Menu: General Postproc（通用后处理器）→Plot Results（绘制结果）→Deformed Shape…→select Def + Undeformed（显示变型）K (back to Plot Results window) →Contour Plot→Nodal Solu（节点解）→Stress→1st Principal stress（第一强度理论）1.11 退出系统ANSYS Utility Menu: File→Exit →Save Everything→OK。

实验八 应用ANSYS 对简支梁的仿真计算
一、实验目的
1、掌握ANSYS 的基本操作。

2、将有限元计算结果与理论值进行比较。

二、实验仪器、设备和工具
1、硬件：计算机。

2、软件：ANSYS。

三、数值仿真试验原理
应用有限元方法，以ANSYS 软件为工具。

四、数值试验步骤
1、建立几何模型
2、选择单元类型
3、定义实常数
4、定义材料属性
5、划单元
6、加约束及其它边界条件
7、加载
8、求解
9、后处理
五、问题描述
图为简支梁的示意图。

设集中力N 100=F ，梁的截面直径，梁长度。

材料的弹性模量。

求梁中心处的挠度。

mm 10=d mm 100=l GPa 210=E
六、实验报告要求
1、应用材料力学计算出理论值。

2、应用ANSYS进行计算并与理论值进行比较。

3、理论值实验值相比较计算误差。

并将计算结果填入表中。

附表1 实验值和理论值比较
数值试验值 理论值 相对误差%
七、思考题
1、数值试验计算结果与理论值误差产生的原因？
2、影响数值试验计算结果计算精度的主要因素是什么？
3、简支梁约束简化的合理原因是什么？。

一、用钢筋混凝土简支梁的数值模拟为实例，对ANSYS的使用方法进行说明钢筋混凝土简支梁，尺寸为长2000mm，宽150mm，高300mm。

混凝土采用C30，钢筋全部采用HRB335，跨中集中荷载P作用于一刚性垫板上，垫板尺寸为长150mm，宽100mm。

建立分离式有限元模型，混凝土采用SOLID65单元，钢筋采用LINK8单元，不考虑钢筋和混凝土之间的粘结滑移。

创建分离式模型时，将几何实体以钢筋位置切开，划分网格时将实体的边线定义为钢筋即可。

加载点以均布荷载近似代替钢垫板，支座处则采用线约束和点约束相结合。

单元尺寸以50mm左右为宜。

二、命令流!钢筋混凝土简支梁数值分析!分离式模型FINISH/CLEAR/PREP7!1.定义单元与材料属性ET,1,SOLID65,,,,,,,1ET,2,LINK8MP,EX,1,13585 !混凝土材料的初始弹模以及泊松比MP,PRXY,1,0.2FC=14.3 !混凝土单轴抗压强度和单轴抗拉强度FT=1.43TB,CONCR,1TBDA TA,,0.5,0.95,FT,-1 !定义混凝土材料及相关参数，关闭压碎TB,MISO,1,,11 !定义混凝土应力应变曲线，用MISO模型TBPT,,0.0002,FC*0.19TBPT,,0.0004,FC*0.36TBPT,,0.0006,FC*0.51TBPT,,0.0008,FC*0.64TBPT,,0.0010,FC*0.75TBPT,,0.0012,FC*0.84TBPT,,0.0014,FC*0.91TBPT,,0.0016,FC*0.96TBPT,,0.0018,FC*0.99TBPT,,0.002,FCTBPT,,0.0033,FC*0.85MP,EX,2,2.0E5 !钢筋材料的初始弹模以及泊松比MP,PRXY,2,0.3TB,BISO,2TBDA TA,,300,0 !钢筋的应力应变关系，用BISO模型PI=ACOS(-1)R,1R,2,0.25*PI*22*22R,3,0.25*PI*10*10TBPLOT,MISO,1 !混凝土材料的数据表绘图TBPLOT,BISO,2 !钢筋材料的数据表绘图!2.创建几何模型BLC4,,,150,300,2000*DO,I,1,19 !切出箍筋位置WPOFF,,,100VSBW,ALL*ENDDOWPCSYS,-1WPOFF,,,950 !切出拟加载面VSBW,ALLWPOFF,,,100VSBW,ALLWPCSYS,-1WPROTA,,-90WPOFF,,,30VSBW,ALLWPOFF,,,240VSBW,ALLWPCSYS,-1WPOFF,30WPROTA,,,90VSBW,ALLWPOFF,,,45VSBW,ALLWPOFF,,,45VSBW,ALLWPCSYS,-1!3.划分钢筋网格ELEMSIZ=50 !网格尺寸变量，设置为50mm LSEL,S,LOC,X,30LSEL,R,LOC,Y,30LA TT,2,2,2LESIZE,ALL,ELEMSIZLMESH,ALLLSEL,S,LOC,X,75 LSEL,R,LOC,Y,30LA TT,2,2,2LESIZE,ALL,ELEMSIZ LMESH,ALLLSEL,S,LOC,X,120 LSEL,R,LOC,Y,30LA TT,2,2,2LESIZE,ALL,ELEMSIZ LMESH,ALLLSEL,S,LOC,X,30 LSEL,R,LOC,Y,270LA TT,2,3,2LESIZE,ALL,ELEMSIZ LMESH,ALLLSEL,S,LOC,X,120 LSEL,R,LOC,Y,270LA TT,2,3,2LESIZE,ALL,ELEMSIZ LMESH,ALLLSEL,S,TAN1,Z LSEL,R,LOC,Y,30,270 LSEL,R,LOC,X,30,120 LSEL,U,LOC,X,75 LSEL,U,LOC,Z,0 LSEL,U,LOC,Z,2000 LSEL,U,LOC,Z,950 LSEL,U,LOC,Z,1050 LA TT,2,3,2LESIZE,ALL,ELEMSIZ LMESH,ALLLSEL,ALL!4.划分混凝土网格V A TT,1,1,1 MSHKEY,1ESIZE,ELEMSIZ VMESH,ALLALLSEL,ALL!5.施加荷载和约束LSEL,S,LOC,Y,0LSEL,R,LOC,Z,100DL,ALL,,UYLSEL,S,LOC,Y,0LSEL,R,LOC,Z,1900DL,ALL,,UYDK,KP(0,0,100),UX,,,,UZDK,KP(0,0,1900),UXP0=180000Q0=P0/150/100ASEL,S,LOC,Z,950,1050ASEL,R,LOC,Y,300SFA,ALL,1,PRES,Q0ALLSEL,ALLFINISH!6.求解控制设置与求解/SOLUANTYPE,0NSUBST,60OUTRES,ALL,ALLAUTOS,ONNEQIT,20CNVTOL,U,,0.015ALLSEL,ALLSOLVEFINISH!7.进入POST1查看结果/POST1SET,LASTPLDISP,1 !设定最后荷载步，查看变形ESEL,S,TYPE,,2ETABLE,SAXL,LS,1PLLS,SAXL,SAXL !绘制钢筋应力图ESEL,S,TYPE,,1/DEVICE,VECTOR,ONPLCRACK,1,1 !绘制裂缝和压碎图三、计算结果图1 混凝土材料的数据表绘图图2 钢筋材料的数据表绘图图3 钢筋的模拟图4 混凝土梁的模拟图5 梁在荷载作用下Y方向上的位移图图5 梁在荷载作用下Z方向上的应力图。

简支箱梁约束扭转算例一、工程背景已知某预应力混凝土简支箱梁，计算跨径为40m，沿梁长等截面。

截面尺寸如图1所示。

采用C40混凝土，剪切模量G=1.445×104MPa，弹性模量E=3.40×104MPa。

荷载为跨中作用一偏心荷载P=451.0kN，偏心距e=2.35m(计算约束扭转时，可以简化为集中力矩M k=1060.0kN)。

具体分两个工况进行：（1）跨中截面腹板位置作用一对对称集中竖向荷载，荷载大小为P/2=225.5kN；（2）跨中截面腹板位置作用一对反对称集中竖向荷载，荷载大小为P/2=225.5kN。

分别计算跨中截面、1/4跨位置截面上的正应力与剪应力分布，并绘制相应的正应力和剪应力分布曲线。

图1 箱梁截面尺寸(尺寸单位：cm)二、Ansys计算分析采用壳单元计算，荷载采用一对称荷载和反对称荷载加载。

1、Ansys命令流命令流见附录。

2、计算结果图a.工况一(a) 1/2跨正应力云图和应力曲线图(b) 1/2跨剪应力云图和应力曲线图b.工况二(a) 1/4跨正应力云图和应力曲线图(b) 1/4跨剪应力云图和应力曲线图注：由于路径选择时重复了一段，因此右翼缘由应力重叠现象附录命令流finish/clear/PREP7 ANTYPE,STATIC !定义箱梁厚度（单位：米）t1=0.22t2=0.30t3=0.34ET,1,SHELL63!定义单元R,1,t1R,2,t2R,3,t3!定义实常数跟所选单元有关本单元采用壳单元只需要厚度MP,EX,1,3.4E10!弹性模量1为材料参考号MP,PRXY,1,0.3!泊松比K,1,-4.75,0.955K,2,-2.35,0.955K,3,-2.35,-1.165K,4,2.35,-1.165K,5,2.35,0.955K,6,4.75,0.955K,7,2.35,0.955,40!创建关键点L,1,2$L,2,3$L,3,4L,4,5$L,5,6$L,5,2$L,5,7!连接各点ADRAG,1,6,5,,,,7ADRAG,2,3,4,,,,7!创建面根据直线编号2,3 路径线7ASEL,S,LOC,Y,0.955$AATT,1,1,1!选择面S选择新面作为子集loc按坐标值选择ASEL,S,LOC,X,-2.35$AA TT,1,2,1!Y中心坐标y值为0.955的面ASEL,S,LOC,X,2.35$AATT,1,2,1!设置面的单元属性相应定义点线体的命令不同ASEL,S,LOC,Y,-1.165$AATT,1,3,1!材料号，实常数，单元类型ALLSEL,ALL!选择所有图素NUMMRG,ALL !合并实体单元NUMCMP,ALL!压缩定义编号/PNUM,LINE,1/PNUM,AREA,1!显示面和线的编号LSEL,S,LENGTH,,40!选择长度为40的线段LESIZE,ALL,,,100!将所有的线每根分成100份即上述长度为40的线段LSEL,S,LENGTH,,2.4,4.7!选择长度在2.4-4.7长度单位内的线段LESIZE,ALL,,,5ALLSEL,ALLAMESH,ALL!划分网格FINISH!施加边界条件/SOLU!工况1对称集中竖向荷载DL,3,,UX$DL,3,,UY$DL,3,,UZDL,16,,UY!对线进行约束!F,662,FY,-225500!F,57,FY,-225500!加上集中荷载节点力F,662,FY,-225500!工况2反对称集中竖向荷载F,57,FY,225500SOLVEFINISH/POST1PATH,STRESS1,7!由于这个箱梁的特点，使得选路径时重复了一段，在应力图中有反映PPA TH,1,,-4.75,0.955,20$PPATH,2,,-2.35,0.9 55,20PPA TH,3,,-2.35,-1.165,20$PPATH,4,,2.35,-1.1 65,20PPA TH,5,,2.35,0.955,20$PPATH,6,,4.75,0.955 ,20PPA TH,7,,-2.35,0.955,20!七个路径点PDEF,STRESS1,S,ZPLPAGM,STRESS1,5.0!跨中截面正应力云图PLPATH,STRESS1!跨中截面正应力曲线PDEF,STRESS1,S,XYPLPAGM,STRESS1,5.0!跨中截面剪应力云图PLPATH,STRESS1!跨中截面剪应力曲线PATH,STRESS2,7PPA TH,1,,-4.75,0.955,10$PPATH,2,,-2.35,0.9 55,10PPA TH,3,,-2.35,-1.165,10$PPATH,4,,2.35,-1.1 65,10PPA TH,5,,2.35,0.955,10$PPATH,6,,4.75,0.955 ,10PPA TH,7,,-2.35,0.955,10PDEF,STRESS2,S,ZPLPAGM,STRESS2,5.0!1/4跨截面正应力云图PLPATH,STRESS2!1/4跨截面正应力曲线PDEF,STRESS2,S,XYPLPAGM,STRESS2,5.0!1/4跨截面剪应力云图PLPATH,STRESS2!1/4跨截面剪应力曲线。

第一章简支梁有限元结构静力分析0前言本文利用ANSYS软件中BEAM系列单元建立简支梁有限元模型，对其进行静力分析与模态分析，来比较建模时不同单元类型的选择和网格划分精细程度不同所带来的不同结果，以便了解和认识ANSYS对于分析结果准确性的影响。

1.1梁单元介绍梁是工程结构中最为常用的结构形式之一。

ANSYS程序中提供了多种二维和三维的梁单元，分别具有不同的特性，是一类轴向拉压、弯曲、扭转单元，用以模拟各类结构中的平面以及空间的梁构件。

常用的梁单元中BEAM3、BEAM23和BEAM54为二维梁单元，BEAM4、BEAM24、BEAM344、BEAM188和BEAM189为三维梁单元。

下文将简单介绍常用的梁单元BEAM3、BEAM4、BEAM44、BEAM188以及BEAM189。

1.1.1BEAM3单元：图1.1Beam3单元几何图形BEAM3是具有拉伸、压缩和弯曲的单轴2-D弹性梁单元。

上图给出了单元的几何图形、节点位置及坐标系统。

单元由两个节点、横截面面积、横截面惯性矩、截面高度及材料属性定义。

初始应变通过Δ/L给定，Δ为单元长度L（由I，J节点坐标算得）与0应变单元长度之差。

该单元在每个节点处有三个自由度，可以进行忽略环箍效应的轴对称分析，例如模拟螺栓和槽钢等。

在轴对称分析中，单元的面积和惯性矩必须给出360°范围内的值。

剪切变形量SHERAR是可选的，如给SHERAR赋值为0则表示忽略剪切变形，当然剪切模量（GXY）只有在考虑剪切变形时才起作用。

同时可以运用实常数中的ADDMAS命令为单位长度梁单元施加附加质量。

1.1.2BEAM4单元：图1.2Beam4单元几何图形BEAM4是具有拉伸、压缩、扭转和弯曲的单轴3-D弹性梁单元。

关于本单元的几何模型，节点座标及座标系统详见上图。

该单元在每个节点处有六个自由度。

单元属性包括应力刚化与大变形。

单元方向由两或三个节点确定，实常数有横截面面积，两个方向的惯性矩（IZZ和IYY），梁的高和宽，与单元轴X轴的方向角和扭转惯性矩（IXX），如果没有给出IXX的值或赋予0时，程序自动假设IXX=IYY+IZZ，IXX必须为正同时一般情况下小于弯曲惯性矩，因此最好能够给出IXX的值。

《土木工程有限元》结课作业学生学号：xxxxxxxxxx学生姓名：XXX专业班级：土木13-3班学生成绩：2016~2017年秋季学期问题描述：现有一悬臂梁，其长m ，横截面为圆形，横截面半径，材料的弹性模量，泊松比。

在均布荷载的作用下，请用ANSYS 有限元分析软件计算此悬臂梁的弯矩图、剪力图、位移变形图。

注：均布荷载为每个学生学号的后3位。

*************************************************************************建模思路：（字体均为小四，正文内容不加粗）1.由于结构和受力都处在平面内，所以采用整个平面梁模型。

2.在ANSYS 环境中，设置静力分析类型，单元类型选择BEAM3，输入梁的截面实常数及材料参数。

3.根据坐标生成关键点，有关键点连成线，再对几何线进行相应的单元划分。

4.采用命令（LSEL),(ESLL)进行几何位置及单元的选择，采用命令（SFBEAM)对梁单元施加均布载荷。

5.在后处理中，通过命令（/ESHAPE),对线形单元梁按实体效果进行显示；通过命令（/EXPAND)命令，显示完整的有限元模型。

6.在后处理中，通过命令（ETABLE)定义线性单元的节点剪力，弯矩，通过命令（PLLS)画出线性单元的剪力，弯矩图，通过命令（PRESOL)打印单元结果。

建模流程：（概述主要的建模步骤）1.打开ansys 软件:设定工作目录和工作文件2.设置截面为圆截面：section3.设置计算类型：structure 定义分析类型4.选择单元类型：beam5.定义实常数：（截面积、惯性矩等）6.设定材料参数：preprocessor->material->models （弹性模量和泊松比）7.生成模型，有限元模型，物理模型l =0.5m r =210GPa E =0.25υ=q q8.对模型施加约束和荷载：solution->define loads->apply->structural （displacement->on keypoint（约束））9.分析计算:solution->solve->currentLS10.结果显示：general postproc(后处理)->plot result->deformed shape（变形形状）General postproc->plot result->contour plot->nodal solu（显示位移)->Y-component of displacement：显示Y方向位移UY(1)变形位移显示ANSYS Main Menu:General Postproc->Plot Results->DeformedShap->select Def + Undeformed->OK(2)对线性单元梁按实体效果进行显示（以3倍比例）Utility Menu->PlotCtrls->Style->Size andShape>ESHAPE,[√] ON,SCALE:3->OK(3)显示Y方向的位移云图Main Menu-> General Postproc->Plot Results->Contour Plot->Nodal Solu->DOF Solution,Y-Component of Displacement->OK(4)将所显示的图形存入一个文件中（效果为黑白反相，JPEG格式，文件名：brigde001.jpg）,如图所示。

弹性力学a n s y s求解实例详解Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】ANSYS 上机实验报告一、题目描述如图1所示，一简支梁横截面是矩形，其面积202.0m A =，对弯曲中性轴的惯性矩451067.6m I zz -⨯=，高m h 2.0=，材料的pa E 11101.2⨯=，横向变形系数3.0=μ。

该梁的自重就是均布载荷N q 4000=和梁中点处的集中力N F 2000=，试讨论在均布荷载作用下，简支梁的最大挠度。

二、问题的材料力学解答由叠加法可知：梁上同时作用几个载荷时，可分别求出每一载荷单独作用时的变形，把各个形变叠加即为这些载荷共同作用时的变形。

在只有均布载荷q 作用时，计算简支梁的支座约束力，写出弯矩方程，利用EI M dxw d =22积分两次，最后得出： 铰支座上的挠度等于零，故有0=x 时，0=w ，因为梁上的外力和边界条件都对跨度中点对称，挠曲线也应对该点对称。

因此，在跨度中点，挠曲线切线的斜率等于零，即：2l x =时，0=dx dw ，把以上两个边界条件分别代入w 和0=dxdw 的表达式，可以求出243ql C -=，0=D ，于是得转角方程及挠曲线方程为： x ql x q x ql EIw ql x q x ql EI dx dw EI 2424122464343332--=--==θ （1） 在跨度中点，挠曲线切线的斜率等于零，挠度为极值，由（1）中式子可得：即EIql w q c 3845)(4-=。

在集中力F 单独作用时，查材料力学中梁在简单载荷作用下的变形表可得EIFl w F c 48)(3-=。

叠加以上结果，求得在均布载荷和集中力共同作用下，梁中点处的挠度是EIFl EI ql w w w F c q c c 483845)()(34--=+=，将各参数代入得m w c 410769.0-⨯=三、问题的ansys 解答建立几何模型此问题为可采用Beam 分析，所以该几何模型可用线表示。

实验三简支梁的变形分析实验目的：了解和掌握简支梁的变形分析的方法和步骤。

实验内容：完成工字梁端面受力分析。

图1 是一工字梁受力简图，工字梁型号为32a，其跨度为1.0m，求其在集中力P1和P2作用下O点的挠度。

该工字梁材料的弹性模量为220GPa，泊松比为0.3，集中力P1=8000N，P2=5000N。

要求采用自顶向下的建模方法即采用3D体素建立起几何模型。

图1 工字梁受力简图该问题属于梁的弯曲问题。

由于该工字梁属于标准型材，在分析过程中选择图2所示的几何模型，通过选择相应的梁单元进行求解，这样就简化了3D模型复杂的建模过程和求解步骤。

图2 几何模型实验步骤：⒈定义工作文件名和工作标题1）选择Utility Menu→File→Change Jobname 命令，出现Change Jobname对话框，在[/FILNAM] Enter new jobname 输入栏中输入工作文件名exercise3，并将New log and error files 设置为Yes,单击【OK】按钮关闭该对话框。

2）选择Utility Menu→File→Change Title命令，出现Change Title对话框，在[/TITLE]Enter new title 栏中输入I BEAM SUBJECTED TO CONCENTRATED FORCE，单击【OK】按钮关闭该对话框。

⒉定义单元类型1）选择Main Menu→Preprocessor→ElementType→Add/Edit/Delete命令,出现ElementTypes 对话框，单击【Add】按钮, 出现Library of ElementTypes对话框。

2）在Library of ElementTypes复选框中选择Structural Beam 2D elastic 3,在Element type reference number 输入栏中输入1，如图3所示，单击【OK】按钮关闭该对话框。