1.3.1柱体、锥体、台体的表面积

§1.3.1柱体、锥体、台体的表面积（第一课时）
呼伦贝尔市莫旗尼尔基一中鲍喜良
（一）教学目标
1．知识与技能
（1）了解柱体、锥体与台体的表面积的计算公式（不要求记忆公式）.
（2）能运用公式求柱体、锥体和台体的表面积.
（3）培养学生空间想象能力、思维能力和运算能力
2．过程与方法
让学生经历几何体的侧面展开过程，感知几何体的形状，培养转化化归能力. 3．情感、态度与价值观
通过学习，培养学生的理性精神，渗透辩证法的思想，增强探究意识，激发学习的积极性.
（二）教学重点、难点
重点：了解柱体、锥体、台体的表面积计算公式及其应用.
难点：表面积计算公式的应用
（三）教学方法：自主探究式
S=
SBC
∴四面体
22
π'++'+
(r r r l
.
由左视图知正三棱柱的底面三角形的高为。

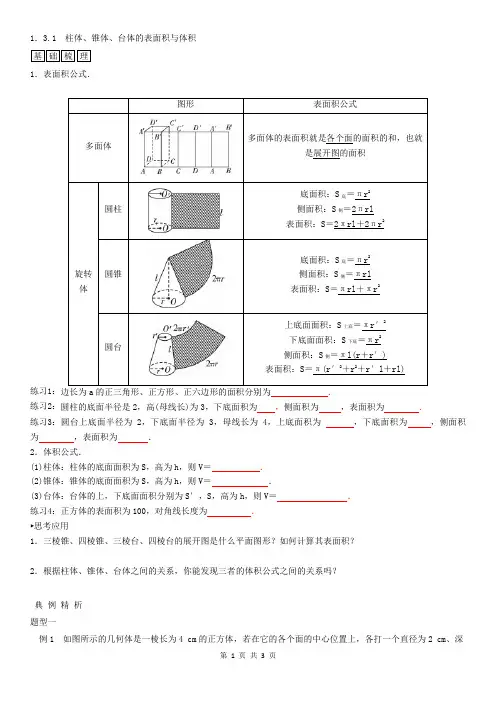
1．3.1 柱体、锥体、台体的表面积与体积基础梳理1．表面积公式．图形表面积公式多面体多面体的表面积就是各个面的面积的和，也就是展开图的面积旋转体圆柱底面积：S底＝πr2侧面积：S侧＝2πrl表面积：S＝2πrl＋2πr2圆锥底面积：S底＝πr2侧面积：S侧＝πrl表面积：S＝πrl＋πr2圆台上底面面积：S上底＝πr′2下底面面积：S下底＝πr2侧面积：S侧＝πl(r＋r′)表面积：S＝π(r′2＋r2＋r′l＋rl)练习1：边长为a的正三角形、正方形、正六边形的面积分别为．练习2：圆柱的底面半径是2，高(母线长)为3，下底面积为，侧面积为，表面积为 .练习3：圆台上底面半径为2，下底面半径为3，母线长为4，上底面积为，下底面积为，侧面积为，表面积为．2．体积公式．(1)柱体：柱体的底面面积为S，高为h，则V＝．(2)锥体：锥体的底面面积为S，高为h，则V＝．(3)台体：台体的上，下底面面积分别为S′，S，高为h，则V＝．练习4：正方体的表面积为100，对角线长度为．►思考应用1．三棱锥、四棱锥、三棱台、四棱台的展开图是什么平面图形？如何计算其表面积？2．根据柱体、锥体、台体之间的关系，你能发现三者的体积公式之间的关系吗？典例精析题型一例1 如图所示的几何体是一棱长为4 cm的正方体，若在它的各个面的中心位置上，各打一个直径为2 cm、深为1 cm的圆柱形的孔，求打孔后的几何体的表面积是多少？(π取3.14)►跟踪训练1．如下图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为( )A．3πB．2π C.πD．4π题型二求空间几何体的体积例2 三棱台ABCA1B1C1中，AB∶A1B1＝1∶2，则三棱锥A1ABC，BA1B1C，CA1B1C1的体积之比为( ) A．1∶1∶1 B．1∶1∶2 C．1∶2∶4 D．1∶4∶4。

题型三几何体表面积与体积公式的综合应用例3一个正三棱柱的三视图如图所示(单位：cm)，求这个正三棱柱的表面积与体积．►跟踪训练3．下图是一个空间几何体的三视图，这个几何体的体积是( ）A．2πB．4πC．6πD．8π。

《柱体、锥体、台体的表面积与体积》说课稿各位老师：大家上午好!我说课的题目是《柱体、锥体、台体的表面积与体积》，下面我将从教材的地位和作用，内容分析，教学目标及重难点，教法和学法以及教学过程等几个方面进行阐述。

一．教材的地位和作用《柱体、锥体、台体的表面积与体积》是新人教版高中数学必修2第一章第3节的第一小节。

本节内容是在学生已从结构特征和视图两个方面感性认识空间几何体的基础上，进一步从度量的角度来认识空间几何体，它属于立体几何入门的内容，所以教学的目的在于使学生了解空间几何体的表面积和体积的计算方法，但不要求记忆公式，并能进一步计算简单组合体的表面积和体积。

二．内容分析本节一开始的“思考”从学生熟悉的正方体和长方体的展开图入手，分析展开图与其表面积的关系，其作用有二：一，复习表面积的概念，即表面积是各个面的面积的和；二，介绍求表面积的方法，即把它们展成平面图形，通过求平面图形的面积的方法，求立体图形的表面积，然后通过“探究”和“思考”引导学生探究柱体，锥体，台体的展开图，并在讨论过程中归纳圆柱，圆锥和圆台的表面积公式，在整个表面积研究过程中，教材都传达了将立体问题平面化的思想，因此在表面积教学过程中应注意引导学生体会这一点。

关于体积的教学，课本是由初中学过的正方体，长方体及圆柱的体积公式推广到一般柱体的体积公式，然后由三棱柱和三棱锥的关系，得到并推广到一般锥体的体积公式，最后由台体的概念，得出台体的体积公式。

从整体上看，教材体现了探究问题的一般思路，即由特殊到一般，再由一般到具体的应用，因此在教学过程中，我们要注重培养学生的转化和类比的思想，并让学生体会探究问题的乐趣，另外还应通过对圆柱，圆锥和圆台的表面积公式，柱体，锥体和台体的体积公式的统一过程培养学生归纳总结的能力。

三．教学目标和重难点根据以上分析，结合高一学生的特点，我制订了如下教学目标及重、难点：1.知识与技能目标：通过对柱体、锥体、台体的研究，了解柱体、锥体、台体的表面积和体积的求法。

1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积课后篇巩固提升基础巩固1.圆台的上、下底面半径分别是3和4,母线长为6,则其表面积等于( )A.72B.42πC.67πD.72π圆台表=S 圆台侧+S 上底+S 下底=π(3+4)·6+π·32+π·42=67π.2.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积的比值为( ) A.1B.12C.√32D.34R ,圆锥底面半径为r ,高都为h ,由已知得2Rh=rh ,∴r=2R ,V 柱∶V 锥=πR 2h ∶13πr 2h=3∶4,故选D .3.一个几何体的三视图如图所示,则该几何体的体积为( )A.83 B.163C.203D.88,高为2的四棱锥,如图所示:∴该几何体的体积V=13×8×2=163.4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36√5B.54+18√5C.90D.81,且四棱柱的底面是边长为3的正方形,侧棱长为3√5,所以所求表面积为(3×3+3×6+3×3√5)×2=54+18√5,故选B .5.若一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比是( ) A .1+4π2πB .1+2π4πC .1+2ππD .1+2π2πa ,圆柱的底面圆的半径为r ,则2πr=a ,r=a 2π,所以圆柱的底面积为a 24π,侧面积为a 2,表面积与侧面积的比是2×a 24π+a 22=1+2π.6.若半径为2的半圆卷成一个圆锥,则它的体积为 .,如图,设圆锥底面半径为r ,高为h ,则{2πr =2π,ℎ2+r 2=4. 解得{r =1,ℎ=√3.故它的体积为1×π×12×√3=√3π.7.一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积为.,底面是侧视图的三角形,底边为6、腰为5,一个底面的面积是12,三棱柱高是4,则侧面积为(5+5+6)×4=64,所以表面积为24+64=88.8.如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,则圆柱被截后剩下部分的体积是.a+b的圆柱,则拼接成的圆柱的体积V=πr2(a+b),所以所求几何体的体积为πr 2(a+b).9.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段中点,Q 为顶点,求在几何体表面上,从P 到Q 点的最短路径的长.由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12×2πa×√2a=√2πa 2, S 圆柱侧=2πa×2a=4πa 2, S 圆柱底=πa 2,所以S 表=√2πa 2+4πa 2+πa 2=(√2+5)πa 2. (2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ=√AP 2+AQ 2=√a 2+(πa )2=a √1+π2,所以从P 点到Q 点在侧面上的最短路径的长为a √1+π2.10.已知正四棱锥底面正方形的边长为4,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积.,正四棱锥的高PO ,斜高PE ,底面边心距OE 组成Rt △POE.∵OE=2,∠OPE=30°, ∴PE=2OE=4.因此S 侧=4×12PE×BC=4×12×4×4=32,S 表面=S 侧+S 底=32+16=48.能力提升1.已知某几何体的三视图如图所示,则该几何体的体积为( )A.1B.2C.3D.6解析依题意,题中的几何体是一个直三棱柱(其底面左、右相对),其中底面是直角边长分别为1、2的直角三角形,侧棱长为3,因此其体积为12×1×2×3=3.2.某几何体的三视图如图所示(单位: cm),则该几何体的体积是( )A .8 cm 3B .12 cm 3C .323 cm 3D .403 cm 3,该几何体是由一个棱长为2的正方体与一个底面边长为2,高为2的正四棱锥组合而成,故其体积为V=23+13×22×2=8+83=323(cm 3),故选C .3.如图,在四边形ABCD 中,∠DAB=90°,∠ADC=135°,AB=5,CD=2√2,AD=2,则四边形ABCD 绕AD 所在直线旋转一周所成几何体的表面积为( ) A.(60+4√2)π B.(60+8√2)π C.(56+8√2)πD.(56+4√2)πABCD 绕AD 所在直线旋转一周所成的几何体,如图.S 表面=S 圆台下底面+S 圆台侧面+S 圆锥侧面=πr 22+π(r 1+r 2)l 2+πr 1l 1=π×52+π×(2+5)×5+π×2×2√2=(60+4√2)π.故选A .4.我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异”,“幂”是截面积,“势”是几何体的高,意思是两等高立方体,若在每一等高处的截面积都相等,则两立方体体积相等.已知某不规则几何体与如图所对应的几何体满足“幂势同”,则该不规则几何体的体积为()A.4-π2B.8-4π3C.8-πD.8-2π,该不规则几何体的体积与已知三视图的几何体体积相等.根据题设所给的三视图,可知题图中的几何体是从一个正方体中挖去半个圆柱,正方体的体积为23=8,半圆柱的体积为12×(π×12)×2=π,因此该不规则几何体的体积为8-π.5.如图,圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的侧面积为.r,则下底面半径为4r,高为4r.由母线长为10可知10=√(3r)2+(4r)2=5r,解得r=2.则圆台的上、下底面半径和高分别为2,8,8.故圆台的侧面积为π×(2+8)×10=100π.π6.一个封闭的正三棱柱容器,高为3,内装水若干(如图甲,底面处于水平状态),将容器放倒(如图乙,一个侧面处于水平状态),这时水面与各棱交点E,F,F1,E1分别为所在棱的中点,则图甲中水面的高度为.E ,F ,F 1,E 1分别为所在棱的中点,所以棱柱EFCB-E 1F 1C 1B 1的体积V=S EFCB ×3=34S △ABC ×3=94S △ABC ,设图甲中水面的高度为h ,则S △ABC ×h=94S △ABC ,所以h=94,故答案为94.7.如图,一圆锥形封闭容器高为h ,圆锥内水面高为h 1,且h 1=13h ,若将圆锥倒置后,圆锥内水面高为h 2,求h 2.因为V圆锥SOV圆锥SO '=(23ℎℎ)3=827,所以V 水V 圆锥SO '=1927. 倒置后的体积关系为V水V圆锥S 'O 1=ℎ23ℎ3=1927,所以h 2=√19ℎ3273=√1933h.8.已知正三棱锥V-ABC 的正视图、俯视图如图所示,其中VA=4,AC=2√3,求该三棱锥的表面积.,且VA=VB=VC=4,AB=BC=AC=2√3. 取BC 的中点D ,连接VD ,则VD ⊥BC ,有 VD=√VB 2-BD 2=√42-(√3)2=√13,则S △VBC =12×VD×BC=12×√13×2√3=√39, S △ABC =12×(2√3)2×√32=3√3, 故三棱锥V-ABC 的表面积为3S △VBC +S △ABC =3√39+3√3=3(√39+√3).9.(选做题)如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x 的内接圆柱. (1)试用x 表示圆柱的高;(2)当x 为何值时,圆柱的侧面积最大,最大侧面积是多少?设所求的圆柱的底面半径为x ,它的轴截面如图,BO=1,PO=3,圆柱的高为h , 由图得x1=3-ℎ3,即h=3-3x (0<x<1). (2)∵S 圆柱侧=2πxh=2πx (3-3x )=6π(x-x 2), 当x=12时,圆柱的侧面积取得最大值为32π.∴当圆柱的底面半径为12时,它的侧面积最大为32π.。