八年级下册数学周报答案

八年级下册数学周报答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、填空题：（20分，每空一分）1、一个数，它的百分位，万位和百位上都是5，其余各位上的数字都是0，这个数写作（），改写成万作单位的数是（）。

2、2:8= =（）%3、在a÷b=7……3中，把a和b同时扩大3倍，商是（），余数是（）。

4、4.02吨=（）吨（）千克3小时12分=（）小时5、把5千克糖平均分成6袋，每袋重（），每袋占总重量的（）。

6、把 :3.75化成最简整数比是( )，比值是（）。

7、两个质数的和是45，这两个质数是（）和（）。

8、甲乙两人走同一段路，甲需4小时，乙需3小时。

甲乙两人所需的时间比是（），速度比是（）。

9、在一个减法算式中，被减数、减数、差三个数的和是216，减数与差的比是4:5，减数是（），差是（）。

10、一个圆柱和一个圆锥等底等高，体积一共是48CM3，这个圆柱的体积是（）CM3，圆锥是（）CM3。

二、判断题：（5分，每题1分）1、一个三角形至少有两个锐角。

（）2、两个连续自然数的积一定是合数。

（）3、圆的面积与半径成正比例。

（）4、可能性很大的事件就是一定会发生的事件。

（）5、2010年的第一季度有90天。

（）三、选择题：（5分，每题1分）1、小明家离学校大约1KM，他从家步行到学校，大约要（）。

A. 100分钟B.60分钟C.15分钟D.1分钟2、一幅地图的线段比例尺是0 50 100 150 200 250KM，这幅地图的比例尺是（）。

A.1:500B.1:5000C.1:50000D.1:50000003、一个半圆形纸片的直径是d,它的周长是( )。

A. πdB. πd+dC. (πd+d)D.πd+d4、男生人数是女生人数的，女生人数比男生人数少（）。

新课标第一网A. B. C. D.5、在右图的长方形中，甲乙甲乙两部分的面积关系是（）。

A.甲>乙B.甲<乙C.甲=乙四、计算1、直接写出得数。

中国教育学会中学数学教学专业委员会“《数学周报》杯”2008年全国初中数学竞赛试题参考答案答题时注意：1．用圆珠笔或钢笔作答.2．解答书写时不要超过装订线.3．草稿纸不上交.一、选择题（共5小题，每小题6分，满分30分. 以下每道小题均给出了代号为A，B，C，D的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填都得0分）1．已知实数满足，则的值为（）．（A）7 （B）（C）（D）5【答】（A）解：因为，≥0，由已知条件得，，所以 7．另解：由已知得：，显然，以为根的一元二次方程为，所以故＝2．把一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷2次，若两个正面朝上的编号分别为m，n，则二次函数的图象与x轴有两个不同交点的概率是（）．（A）（B）（C）（D）【答】（C）解：基本事件总数有6×6＝36，即可以得到36个二次函数. 由题意知＝＞0，即＞4.通过枚举知，满足条件的有17对. 故.3．有两个同心圆，大圆周上有4个不同的点，小圆周上有2个不同的点，则这6个点可以确定的不同直线最少有( )．（A）6条（B）8条（C）10条（D）12条【答】（B）解：如图，大圆周上有4个不同的点A，B，C，D，两两连线可以确定6条不同的直线；小圆周上的两个点E，F中，至少有一个不是四边形ABCD的对角线AC与BD的交点，则它与A，B，C，D的连线中，至少有两条不同于A，B，C，D的两两连线．从而这6个点可以确定的直线不少于8条．当这6个点如图所示放置时，恰好可以确定8条直线．所以，满足条件的6个点可以确定的直线最少有8条．4．已知是半径为1的圆的一条弦，且．以为一边在圆内作正△，点为圆上不同于点A 的一点，且，的延长线交圆于点，则的长为（）．（A）（B）1 （C）（D）a【答】（B）解：如图，连接OE，OA，OB．设，则．又因为，所以≌，于是．另解：如图，作直径EF，连结AF，以点B为圆心，AB为半径作⊙B，因为AB＝BC＝BD，则点A，C，D都在⊙B 上，由所以5．将1，2，3，4，5这五个数字排成一排，最后一个数是奇数，且使得其中任意连续三个数之和都能被这三个数中的第一个数整除，那么满足要求的排法有（）．（A）2种（B）3种（C）4种（D）5种【答】（D）解：设是1，2，3，4，5的一个满足要求的排列．首先，对于，不能有连续的两个都是偶数，否则，这两个之后都是偶数，与已知条件矛盾．又如果（1≤i≤3）是偶数，是奇数，则是奇数，这说明一个偶数后面一定要接两个或两个以上的奇数，除非接的这个奇数是最后一个数．所以只能是：偶，奇，奇，偶，奇，有如下5种情形满足条件：2，1，3，4，5；2，3，5，4，1；2，5，1，4，3；4，3，1，2，5；4，5，3，2，1．二、填空题（共5小题，每小题6分，满分30分）6．对于实数u，v，定义一种运算“*”为：．若关于x的方程有两个不同的实数根，则满足条件的实数a的取值范围是．【答】，或．解：由，得，依题意有解得，，或．7．小王沿街匀速行走，发现每隔6分钟从背后驶过一辆18路公交车，每隔3分钟从迎面驶来一辆18路公交车．假设每辆18路公交车行驶速度相同，而且18路公交车总站每隔固定时间发一辆车，那么发车间隔的时间是分钟．【答】4．解：设18路公交车的速度是米/分，小王行走的速度是米/分，同向行驶的相邻两车的间距为米．每隔6分钟从背后开过一辆18路公交车，则．①每隔3分钟从迎面驶来一辆18路公交车，则．②由①，②可得，所以．即18路公交车总站发车间隔的时间是4分钟．8．如图，在△中，AB=7，AC=11，点M是BC的中点，AD是∠BAC的平分线，MF∥AD，则FC的长为．【答】9．解：如图，设点N是AC的中点，连接MN，则MN∥AB．又，所以，所以．因此9．另解：如图，过点C作AD的平行线交BA的延长线为E，延长MF交AE于点N.则所以.又，所以四边形是等腰梯形，即9．△ABC中，AB＝7，BC＝8，CA＝9，过△ABC的内切圆圆心I作DE∥BC，分别与AB，AC相交于点D，E，则DE的长为．【答】．解：如图，设△ABC的三边长为a，b，c，内切圆I的半径为r，BC边上的高为，则，所以．因为△ADE∽△ABC，所以它们对应线段成比例，因此，所以，故．另解：＝（这里）所以，由△ADE∽△ABC，得，即10．关于x，y的方程的所有正整数解为．【答】解：因为208是4的倍数，偶数的平方数除以4所得的余数为0，奇数的平方数除以4所得的余数为1，所以x，y都是偶数．设，则，同上可知，a，b都是偶数．设，则，所以，c，d都是偶数．设，则，于是＝，其中s，t都是偶数．所以≤．所以可能为1，3，5，7，9，进而为337，329，313，289，257，故只能是＝289，从而＝7．于是因此另解：因为则有又y正整数，所以令因为任何完全平方数的个位数为：1，4，5，6，9由知的个位数只能是1和1或6和6；当的个位数是1和1时，则的个位数字可以为1或9但个位数为1和9的数的平方数的十位数字为偶数，与的十位数字为3矛盾。

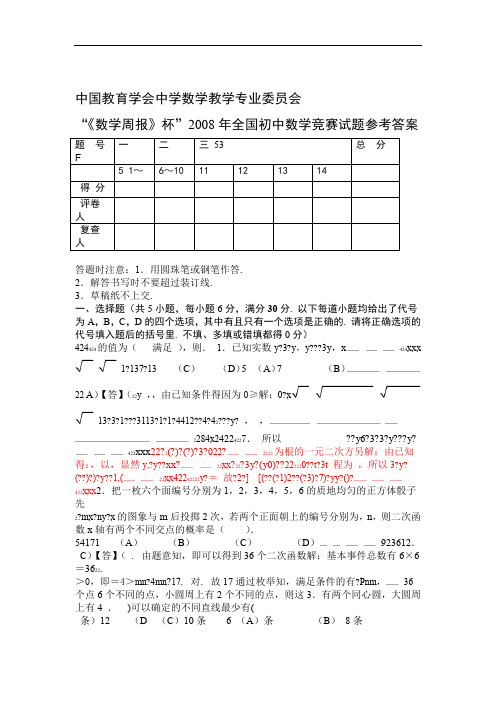
中国教育学会中学数学教学专业委员会“《数学周报》杯”2008年全国初中数学竞赛试题参考答案答题时注意：1．用圆珠笔或钢笔作答.2．解答书写时不要超过装订线.3．草稿纸不上交.一、选择题（共5小题，每小题6分，满分30分. 以下每道小题均给出了代号为A，B，C，D的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填都得0分）424424的值为（满足），则．1．已知实数y?3?y，y???3y，x424xxx 1?137?13（C）（D）5 （A）7 （B）22 A）【答】（22y，，由已知条件得因为0≥解：0?x13?3?1???3113?1?1?4412??4?42???y?，，2284x24224227．所以??y6?3?3?y???y?422xxx22?2(?)?(?)?3?022?2222为根的一元二次方另解：由已知得：，以，显然y,?y??xx?22xx?22?3y?(y0)??222220??t?3t程为，所以3?y? (??)?)?y??1,(22xx42242222y?＝故?2?][(??(?1)2??(?3)?7)?yy?()?422xxx2．把一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先2?mx?ny?x的图象与m后投掷2次，若两个正面朝上的编号分别为，n，则二次函数x轴有两个不同交点的概率是（）．54171 （A）（B）（C）（D）923612．C）【答】（ . 由题意知，即可以得到36个二次函数解：基本事件总数有6×6＝3622.＞0，即＝4＞mn?4mn?17. 对. 故17通过枚举知，满足条件的有?Pnm，36个点6个不同的点，小圆周上有2个不同的点，则这3．有两个同心圆，大圆周上有4 ．)可以确定的不同直线最少有(条）12 （D （C）10条 6 （A）条（B）8条）（B【答】，两两连线DC，个不同的点A，B，解：如图，大圆周上有4中，至少有一FE，可以确定6条不同的直线；小圆周上的两个点，CB，BD的交点，则它与A，个不是四边形ABCD的对角线AC与的两两连线．从而这DC，A，B，D的连线中，至少有两条不同于条．个点可以确定的直线不少于86 3题）（第条直线．个点如图所示放置时，恰好可以确定8当这6 8条．所以，满足条件的6个点可以确定的直线最少有内作正△．以为一边在圆4．已知是半径为1的圆的一条弦，且O?1OAB?aABAB，则的延长线交圆于点A的一点，且，，点为圆上不同于点ODCDB?ABABC?OaED）．的长为（AE35a D）a1 （C（A））（（B）22（B）【答】?设，则OA，OB．解：如图，连接OE，?D??．EAC?120????ECA?4题）（第11????又因为，2180?????ABO?ABD??60???12022≌所以，于是．1?AE?ACE△OA△ABO AFAB为半径，以点B为圆心，另解：如图，作直径EF，连结FO上，，则点＝BC＝BDA，C，D都在⊙B ，因为作⊙BAB ECD11??60?30??EDA??CBA???F由22AB1??30??AE?EFsim?F2?sim所以3，4，，5这五个数字排成一排，最后一个数是奇数，且使得其中任意连续，．将512 ．）三个数之和都能被这三个数中的第一个数整除，那么满足要求的排法有（．5种（D）种（C）4种（A）2种（B）3 D）【答】（5的一个满足要求的排列．，4，是1，2，3解：设aa，，a，a，a51432，不能有连续的两个都是偶数，否则，这两个之后都是偶数，首先，对于a，a，a，a4123与已知条件矛盾．是奇数，这说明一个偶数后面一定要是奇数，则≤3）是偶数，又如果（1≤i aaa2ii?1i?接两个或两个以上的奇数，除非接的这个奇数是最后一个数．种情形满足条件：所以只能是：偶，奇，奇，偶，奇，有如下5a，a，a，a，a54213；1，4，3；2，5，，，，1，34，5；2，3，5，41 2 ．，1，3，25；4，54，3，1，2，30分）6二、填空题（共5小题，每小题分，满分1的方程x*”为：．若关于．对于实数u，v，定义一种运算“6??a?x)x?(vu?v?uv?4．有两个不同的实数根，则满足条件的实数a的取值范围是【答】，或．1a?0?a?112，解：由，得0?1)x??(a?1)x??(a?x?(a?x)44，01?a??依题意有?2，?0(?a?1)??(a?1)?，或．解得，1a??a?0分钟从迎路公交车，每隔36分钟从背后驶过一辆187．小王沿街匀速行走，发现每隔路公交车总站每隔路公交车行驶速度相同，而且1818路公交车．假设每辆18面驶来一辆分钟．固定时间发一辆车，那么发车间隔的时间是．【答】4y x分，同向行驶的相邻两车/路公交车的速度是米米/分，小王行走的速度是解：设18s的间距为米．①．每隔6分钟从背后开过一辆18路公交车，则s6xy??6②．分钟从迎面驶来一辆18路公交车，则3每隔sy3x?3?s4?，所以由①，②可得．xs?4x分钟．418即路公交车总站发车间隔的时间是题）8（第BC的中点，，点M是．如图，在△中，AB=7，AC=118ABC FC的长为AD是∠BAC 的平分线，MF∥AD，则．9．【答】AB，则MN∥如图，设点N是AC的中点，连接MN解：．又，所以MFN????BAD?MF//AD?DAC?FMN，1．所以?FNAB?MN2 8题答案）（第119．因此?NC?AB?AC?FC?FN E22交BA的延长线为E，延长MF另解：如图，过点C作AD的平行线交N.于点AE N则ACE??DAC???E??BAD A F CENF//CEAE?AC?11FN是等腰梯形，，所以四边形所以.又11B911)??BE?(7CF?EN??C即MD22，分别与DE∥BC的内切圆圆心CA＝9，过△ABCI作．△9ABC中，AB＝7，BC＝8，．，则AB，AC相交于点D，EDE的长为16【答】．3 r，b，c，内切圆I的半径为解：如图，设△ABC的三边长为a，h，则BC边上的高为a11，r?c)?ahS?(a?b ABCa△22（第9题答案）ar?．所以cah?b?a r?hDE a?，，所以它们对应线段成比例，因此因为△ADE∽△ABC BCh a rh?)?ca(bar a)a?(?1??a?DE?(1a)?，所以c?b?ahhc?b?a aa619?（7?）8?DE?．故37?9?812?4?3?5?125另解：＝cb?a?125S25?122?p5?r?△ABC???35h所以（这里，）a2128a r?h25DE35?a，得ADE∽△ABC，由△???3BCh a216即?DE??BC3322的所有正整数解为．关于x，y的方程．10)?y?208(xx?y x?48，x?160，??【答】??y?32，y?32.??解：因为208是4的倍数，偶数的平方数除以4所得的余数为0，奇数的平方数除以4所得的余数为1，所以x，y都是偶数．设，则b?2?2a,yx22，)?b?104(aa?b同上可知，a，b都是偶数．设，则d?22c,ba?22，)d?52(cc??d所以，c，d都是偶数．设，则t2s,d?c?222?26(st?ts)?，22213)??((s?13)t，＝于是132?其中s，t都是偶数．所以22222213)13??(s(?13)t?2?．≤11?1315?2?213?s13)?(t为337，329，进而，313，289，257所以，故只能，可能为1，3，57，9s?6，s?20，??2s?1313)t?(＝7．于是，从而＝289是??t?4；t?4，??，x?16，0x?48??因此??，y?32.y?32?? 2222?104)21632,y?210421632?(?104)y104)x(??(??则有因为另解：又y正整数，所以43?y?1．22令21632by?104|,则a???a|x?104|,b?|95，6，因为任何完全平方数的个位数为：1，4，2222 6和6；的个位数只能是1和由1或知ba,21632a??b229的个位数字可以为1当或和的个位数是11时，则ba,ba,22的十位数字为但个位数为1和9的数的平方数的十位数字为偶数，与3矛盾。

课程导报网 1第1期有效学案参考答案第1课时 11.1全等三角形【检测1】C.【检测2】△ABO ，△CDO.【检测3】BD 和CE ，AD 和AE 是对应边，∠A 和∠A ，∠ADB 和∠AEC ，∠B 和∠C 是对应角.【问题1】（1）由AC ∥DE ，AB ∥DF ，得 ∠C ＝∠DEF ，∠F ＝∠ABC ，所以对应边是AC 与DE ，AB 与DF ，CB 与EF ；对应角是∠ACB 与∠DEF ，∠ABC 与∠DFE ，∠CAB 与∠EDF ； （2）由AC 是∠BAD 的平分线，得∠BAC ＝∠DAC ，所以对应边是AB 与AD ，AC 与AC ，BC 与DC ，对应角是∠ABC 与∠ADC ，∠BCA 与∠DCA ，∠BAC 与∠DAC. 【问题2】因为△ABC ≌△DEF ，所以∠B ＝∠E ，∠C ＝∠F ，∠A ＝∠D ，DF ＝AC ＝2cm. 因为∠B ＝50°，∠C ＝70°，所以∠A ＝180°－50°－70°＝60°，∠D ＝∠A ＝60°. 1．D. 2．7．3．OA ＝OC ，AB ＝CD ，OB ＝OD ，∠B ＝∠D ，∠AOD ＝∠COB. 4．C ．5．（1）对应边是FG 和MH ，EF 和NM ，EG 和NH ；对应角是∠E 和∠N ，∠EGF 和∠NHM;（2）根据全等三角形的性质，得NM ＝EF ＝2.4cm ， HG ＝FG －FH ＝MH －FH ＝3.5－1.9＝1.6cm. 6．∠CAE ＝∠BAD ，理由如下： 由旋转可知△ABC ≌△ADE ， 所以∠BAC ＝∠DAE ，所以∠BAC －∠BAE ＝∠DAE －∠BAE ， 所以∠CAE ＝∠BAD. 7．（6）；（3），（5）.8．因为△ABC ≌△ADE ，所以∠BAC ＝∠DAE ， 所以∠BAC －∠EAC ＝∠DAE －∠EAC ， 所以∠BAE ＝∠DAC ，因为∠BAD ＝100°，∠CAE ＝40°， 所以∠BAE ＝∠DAC ＝2BAD CAE∠-∠＝30°，所以∠BAC ＝∠BAE ＋∠CAE ＝30°＋40°＝70°. 9．BM ∥EN ，理由如下： 因为△ABC ≌△FED ，所以∠ABC ＝∠FED ，∠ACB ＝∠FDE ， 又因为∠ABM ＝∠FEN ，所以∠ABC －∠ABM ＝∠FED －∠FEN ， 即∠MBC ＝∠NED ， 又因为∠ACB ＝∠FDE ，所以∠BMC ＝∠END ，所以BM ∥EN. 10．B.11．（1）由已知条件可知∠BAD ＝∠CAE ，所以∠BAD ＋∠DAE ＝∠CAE ＋∠DAE ，所以∠BAE ＝∠CAD ； （2）由已知条件可知BD ＝CE ，所以BD ＋DE ＝CE ＋DE ，所以BE ＝CD.第2课时 11.2三角形全等的判定（1）【检测1】B. 【检测2】AB ＝DC. 【检测3】∵AD ＝FC ，∴AD ＋DC ＝FC ＋DC ，即AC ＝FD. 在△ABC 和△FED 中，,,,BC ED AC FD AB FE =⎧⎪=⎨⎪=⎩∴△ABC ≌△FED （SSS ）. 【问题1】在△ABC 与△DCB 中，,,,AB DC BC CB AC DB =⎧⎪=⎨⎪=⎩∴△ABC ≌△DCB （SSS ）.∴∠ABC ＝∠DCB ，∠ACB ＝∠DBC. ∴∠ABC －∠DBC ＝∠DCB －∠ACB. ∴∠1＝∠2.【问题2】有道理，理由如下： 在△ACB 与△ACD 中，,,,AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩∴△ACB ≌△ACD （SSS ）.∴∠BAC ＝∠DAC ，即AE 是∠DAB 的平分线. 1．D.2．△ADC ，△BCD ；△ABD ，△BAC. 3．AD ⊥BC 符合要求，理由如下： ∵点D 是BC 的中点，∴BD ＝CD. 在△ABD 和△ACD 中，,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩课程导报网 2∴△ABD ≌△ACD （SSS ）. ∴∠ADB ＝∠ADC.又∵∠ADB ＋∠ADC ＝180°， ∴∠ADB ＝∠ADC ＝90°. ∴AD ⊥BC. 4．D ．5．∵AF ＝DC ，∴AF －CF ＝DC －CF.∴AC ＝DF. 在△ABC 与△DEF 中，,,,AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩∴△ABC ≌△DEF （SSS ）. ∴∠A ＝∠D. ∴AB ∥DE.6．在△ADC 与△AEB 中，,,,AC AB AD AE CD BE =⎧⎪=⎨⎪=⎩∴△ADC ≌△AEB （SSS ）. ∴∠DAC ＝∠EAB.∴∠DAC －∠BAC ＝∠EAB －∠BAC. ∴∠DAB ＝∠EAC. ∵△ADC ≌△AEB ， ∴∠B ＝∠C.∴∠B ＋∠BAC ＝∠C ＋∠BAC. ∴∠BMC ＝∠CNB. 7．4．8．连接AC ，在△ADC 与△CBA 中， AB ＝CD ，AD ＝CB ，AC ＝CA ， ∴△ADC ≌△CBA （SSS ）， ∴∠ACD ＝∠CAB ， ∴AB ∥CD ， ∴∠A ＋∠D ＝180°.9．因为所作三角形的一边DE 等于已知△ABC 的一边BC ，则有下列情况：如图（1）中，DE ＝BC ，DM ＝BA ，ME ＝AC ；如图（2）中，DE ＝BC ，DM ＝CA ，ME ＝AB ；如图（3）中，DE ＝BC ，DM ＝BA ，ME ＝AC ；如图（4）中，DE ＝BC ，DM ＝CA ，ME ＝AB.故这样的三角形最多可以画出4个.10．连接BD ，在△ABD 和△CBD 中，,,,AB CB BD BD AD CD =⎧⎪=⎨⎪=⎩∴△ABD ≌△CBD （SSS ）. ∴∠C ＝∠A.11．在△ABD 与△ACE 中，,,,AE AD AB AC BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE （SSS ）. ∴∠ADB ＝∠AEC.∵∠ADB ＋∠CDB ＝∠AEC ＋∠BEC ＝180°， ∴∠CDB ＝∠BEC.第3课时 11.2三角形全等的判定（2）【检测1】SAS.【检测2】BC ＝DC ，SSS ；∠BAC ＝∠DAC ，SAS. 【检测3】在△ABE 和△ACD 中，AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ABE ≌△ACD （SAS ）.【问题1】证明：∵AB ∥ED ，∴∠B ＝∠E. 在△ABC 和△CED 中，AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ABC ≌△CED （SAS ）.∴AC ＝CD.3【问题2】AB ∥CF.理由如下： 在△AED 与△CEF 中，,,,DE FE AED CEF AE CE =⎧⎪∠=∠⎨⎪=⎩∴△AED ≌△CFE （SAS ）. ∴∠A ＝∠FCE. ∴AB ∥CF. 1．B.2．B ，C ；AB ，CD.3．∵∠1＝∠2，∴∠1＋∠BAE ＝∠2＋∠BAE. ∴∠BAC ＝∠DAE. 在△BAC 与△DAE 中，,,,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△BAC ≌△DAE （SAS ）. ∴BC ＝DE. 4．90°.5．∵D ，E 分别是AC ，AB 的中点， ∴AD ＝12AC ，AE ＝12AB. 又∵AB ＝AC ，∴AE ＝AD. 在△ADB 与△AEC 中，AD ＝AE ，∠A ＝∠A ，AB ＝AC ， ∴△ADB ≌△AEC （SAS ）. ∴BD ＝CE.6．（1）∵C 为BD 的中点， ∴CD ＝CB.在△ABC 和△EDC 中，,,,AC EC ACB ECD BC DC =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△EDC （SAS ）. ∴AB ＝ED.（2）∵CD ＝140m ，∴CB ＝140m.在△ACB 中，根据两边之和大于第三边，两边之差小于第三边，所以（140－100）m ＜AB ＜（140＋100）m ，即40m ＜AB ＜240m. 7．D.8．相等，理由如下：在△ABC 与△ADC 中，,,,AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC （SSS ）. ∴∠BAC ＝∠DAC. 在△BAE 与△DAE 中，,,,AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△BAE ≌△DAE （SAS ）. ∴BE ＝DE.9．（1）△ABE ≌△ACD ，证明如下： ∵△ABC 与△AED 均为等腰直角三角形， ∴AB ＝AC ，AE ＝AD ，∠BAC ＝∠EAD ＝90°. ∴∠BAC ＋∠CAE ＝∠EAD ＋∠CAE ， 即∠BAE ＝∠CAD. ∴△ABE ≌△ACD （SAS ）.（2）证明：由（1）△ABE ≌△ACD ，知 ∠ACD ＝∠ABE ＝45°. 又∠ACB ＝45°，∴∠BCD ＝∠ACB ＋∠ACD ＝90°， ∴DC ⊥BE. 10．A.11．证明：在△AOC 与△BOC 中， ∵AO ＝BO ，∠1＝∠2，OC ＝OC ， ∴△AOC ≌△BOC ，∴AC ＝BC.第4课时 11.2三角形全等的判定（3）【检测1】D.【检测2】AOB ，COD.【检测3】在△ACB 与△ADB 中，12,,,C D AB AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ACB ≌△ADB （AAS ）. ∴AC ＝AD.【问题1】证明：∵AC ∥DF ，∴∠ACE ＝∠DFB.又∵∠ACE ＋∠ACB ＝180°，∠DFB ＋∠DFE ＝180°，∴∠ACB ＝∠DFE.又BF ＝EC ，∴BF －CF ＝EC －CF ，即BC ＝EF.课程导报网 4在△ABC 与△DEF 中，,,,ACB DFE A D BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF （AAS ）. ∴AB ＝DE.【问题2】证明：在△ABC 和△ADC 中，12,,34,AC AC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△ADC （ASA ）. ∴AB ＝AD.又∵∠1＝∠2，AO ＝AO ， ∴△ABO ≌△ADO （SAS ）. ∴BO ＝DO. 1．D.2．∠ACB ＝∠DFE ；AB ＝DE ；∠A ＝∠D. 3．∵∠BAD ＝∠EAC ，∴∠BAD －∠CAD ＝∠EAC －∠CAD. ∴∠BAC ＝∠EAD ， 在△ABC 和△AED 中，,,,B E BAC EAD AC AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△AED （AAS ）. ∴AB ＝AE. 4．B.5．∵点O 为AB 的中点，∴AO ＝BO. ∵AD ∥BC ，∴∠ADO ＝∠BEO ，∠DAO ＝∠EBO. 在△AOD 与△BOE 中，,,,ADO BEO DAO EBO AO BO ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AOD ≌△BOE （AAS ）. ∴OD ＝OE.6．∵BF ⊥AC ，DE ⊥AC ， ∴∠DEC ＝∠BFA ＝90°. 在△BFA 与△DEC 中，,,,B D BF DE BFA DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BFA ≌△DEC （ASA ）. ∴AF ＝CE.∴AF ＋EF ＝CE ＋EF. ∴ AE ＝CF. 7．1.8．OM ＝ON 成立．理由是：∵△BOD 绕点O 旋转180°后得到△AOC ， ∴△BOD ≌△AOC ． ∴∠A ＝∠B ，AO ＝BO ． 又∵∠AOM ＝∠BON ， ∴△AOM ≌△BON (ASA)． ∴OM ＝ON ．9．（1）△ACD ≌△CBE ，证明：∵∠ACB ＝90°，∴∠ACD ＋∠BCE ＝90°. 又∵AD ⊥l ，∴∠CAD ＋∠ACD ＝90°. ∴∠BCE ＝∠CAD.∵BE ⊥l ，∴∠ADC ＝∠CEB ＝90°. 在△ACD 与△CBE 中，∠CAD ＝∠BCE ，∠ADC ＝∠CEB ，AC ＝CB ， ∴△ACD ≌△CBE （AAS ）. （2）由（1）可知△ACD ≌△CBE ， ∴AD ＝CE ，CD ＝BE ，∴AD ＝CE ＝CD ＋DE ＝BE ＋DE ＝3＋5＝8. 10．C.11．证明：∵AB ∥DE ，∴∠B ＝∠DEF. ∵BE ＝CF ，∴BC ＝EF. 在△ABC 与△DEF 中，∠B ＝∠DEF ，BC ＝EF ，∠ACB ＝∠F ， ∴△ABC ≌△DEF （ASA ）.11.1~11.2（1）测试题基础巩固一、精挑细选，一锤定音1．D ．2．D ．3．C ．4．D ．5．D ．6．C ．提示：A 中的条件不能构成三角形；B 中的条件可画出两个三角形；D 中的条件可画出无数个三角形． 二、慎思妙解，画龙点睛7．4．8．CD =CB 或∠DAC =∠BAC ．9．65． 10．22．5提示：先证△ABC ≌△DCB ，则∠A ＝∠D ＝78°，∠ABC ＝180°－(∠A ＋∠ACB )＝62°．∠ABD ＝∠ABC －∠DBC ＝22°． 三、过关斩将，胜利在望11．解：依题意，∠B ＝∠C ＝30°． ∴∠BFC ＝∠A ＋∠B ＝80°， ∴∠BOC ＝∠BFC ＋∠C ＝110°． 12．证明：∵AB ⊥BE ，DE ⊥BE ， ∴∠B ＝∠E ＝90°． ∵BF ＝CE ，∴BF ＋FC ＝CE ＋FC ，即BC ＝EF ． 又∵AB ＝DE ，∴△ABC ≌△DEF (SAS)． ∴∠A ＝∠D ．13．证明：∵OA ＝OB ，OC ＝OD ，AC ＝BD ， ∴△OAC ≌△OBD (SSS)． ∴∠AOC ＝∠BOD ．∴∠AOC －∠BOC ＝∠BOD －∠BOC ， 即∠AOB ＝∠COD ． ∵OA ⊥OB ， ∴∠AOB ＝90°．∴∠COD ＝90°，即OC ⊥OD ．14．(1)如果①、③，那么②或如果②、③，那么①； (2)下面选择“如果①、③，那么②”加以证明． 证明：∵BE ∥AF ， ∴∠AFD ＝∠BEC ． 又∵∠A ＝∠B ，AD ＝BC ， ∴△ADF ≌△BCE (AAS)． ∴DF ＝CE ．∴DF －EF ＝CE －EF ，即DE ＝CF ．15．（1）∵∠ABC ＝90°，点F 为AB 延长线上一点， ∴∠ABC ＝∠CBF ＝90°. 在△ABE 与△CBF 中，,,,AB CB ABE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CBF （SAS ）. ∴AE ＝CF.（2）由题意知，△ABC 和△EBF 都是等腰直角三角形， ∴∠ACB ＝∠EFB ＝45°. ∵∠CAE ＝30°，∴∠AEB ＝∠CAE ＋∠ACB ＝30°＋45°＝75°. 由（1）知△ABE ≌△CBF ， ∴∠CFB ＝∠AEB ＝75°，∴∠EFC ＝∠CFB －∠EFB ＝75°－45°＝30°.能力提高1．①②③．2．证明：∵∠AEC =180°-∠DEC =100°，∠ADB =100°， ∴∠AEC =∠ADB ．∵∠BAD +∠CAE =80°，∠ACE +∠CAE =∠CED =80°， ∴∠BAD =∠ACE ． 又∵AB =AC ，∴△ABD ≌△CAE (AAS) ． ∴AD =CE ，AE =BD ． ∴ED =AD -AE =CE -BD ． 3．全等三角形还有：△AA ′E ≌△C ′CF ，△A ′DF ≌△CB ′E. 选△AA ′E ≌△C ′CF 进行说明.∵AD ＝CB ，∠D ＝∠B ＝90°，AB ＝CD ， ∴△ABC ≌△CDA （SAS ）.由平移的性质可得∴△A ′B ′C ′≌△ABC. ∴△A ′B ′C ′≌△ABC ≌△CDA ，∴∠A ＝∠C ′，∴△AA ′E ≌△C ′CF （ASA ）. 4．（1）∵∠A ＋∠APB ＝90°，∠APB ＋∠QPC ＝90°， ∴∠A ＝∠QPC.（2）当BP ＝3时，PC ＝BC －BP ＝2＝AB ，则△BAP ≌△CPQ （ASA ），∴PA ＝PQ.当BP ＝7时，点P 在C 的延长线上，如图所示，则PC ＝BP －BC ＝2＝AB.则△BAP ≌△CPQ （ASA ），∴PA ＝PQ ，综上可知，当BP ＝3或BP ＝7时，PA ＝PQ.A BQClP课程导报网6第2期有效学案参考答案第5课时11.2三角形全等的判定（4）【检测1】斜边、直角边，HL.【检测2】SSS ，SAS ，ASA ，AAS ；HL ． 【检测3】A.【问题1】（1）∵AB ⊥AC ，AC ⊥DC ， ∴∠BAC ＝∠DCA ＝90°. 在Rt △BAC 与Rt △DCA 中，,,BC DA AC CA =⎧⎨=⎩ ∴Rt △BAC ≌Rt △DCA （HL ）.（2）由（1）知Rt △BAC ≌Rt △DCA （HL ）， ∴∠ACB ＝∠CAD ，∴AD ∥BC.【问题2】∵BF ＝EC ，∴BF ＋FC ＝EC ＋FC ，即BC ＝EF. 在Rt △ABC 和Rt △DEF 中，,,AC DF BC EF =⎧⎨=⎩ ∴Rt △ABC ≌Rt △DEF （HL ）. ∴AB ＝DE. 1． AB ＝AC.2. ∵AB ⊥BC ，ED ⊥DC ，∴∠B ＝∠D ＝90°. ∵点C 是BD 的中点，∴BC ＝DC. 在Rt △ABC 与Rt △EDC 中，,,AC EC BC DC =⎧⎨=⎩∴Rt △ABC ≌Rt △EDC （HL ）. ∴ AB=ED.3．CB ＝DA ，理由如下： 由题意易知AC ＝BD.∵CB ⊥AB ，DA ⊥AB ，∴∠DAB ＝∠CBA ＝90°. 在Rt △DAB 与Rt △CBA 中，,,BD AC AB BA =⎧⎨=⎩ ∴Rt △DAB ≌Rt △CBA （HL ）. ∴DA ＝CB. 4．2.5．证明：∵AE ＝DB ，∴AE ＋EB ＝DB ＋EB ，即AB ＝DE . 又∵∠C ＝∠F ＝90°，AC ＝DF ， ∴Rt △ABC ≌Rt △DEF (HL)． ∴∠ABC ＝∠DEF ．∴BC ∥EF ．6．证明：∵DE ⊥AB ，DF ⊥AC ，∴∠BED ＝∠CFD ＝90°.又∵点D 是BC 的中点，∴BD ＝CD. 在Rt △BDE 和Rt △CDF 中，,,BD CD BE CF =⎧⎨=⎩ ∴Rt △BDE ≌Rt △CDF （HL ）.∴DE=DF. 在Rt △ADE 和Rt △ADF 中，,,AD AD DE DF =⎧⎨=⎩ ∴Rt △ADE ≌Rt △ADF （HL ）. 7．D.8．∵AC ⊥CF ，DF ⊥CF ，∴∠ACB ＝∠DFE ＝90°. 又∵EC ＝BF ，∴EC ＋EB ＝BF ＋EB ，∴CB ＝FE. 在Rt △ACB 与Rt △DFE 中，,,CB FE AB DE =⎧⎨=⎩ ∴Rt △ACB ≌Rt △DFE （HL ）.∴AC ＝DF. 在△ACE 与△DFB 中，,,,AC DF ACE DFB CE FB =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△DFB （SAS ）. ∴AE ＝DB.9．答案不唯一，如AD ＝AE ，AB ＝AC ，AD ⊥DC ，AE ⊥BE ，求证：AM ＝AN.证明：∵AD ⊥DC ，AE ⊥BE ，∴∠D ＝∠E ＝90°. 又∵AD ＝AE ，AB ＝AC ，∴Rt △ADC ≌Rt △AEB. ∴∠C ＝∠B. ∵∠CAM ＝∠BAN ，AC ＝AB ，∴△CAM ≌△BAN （ASA ）. ∴AM ＝AN.10．由题意可知：∠A ＝∠D ＝90°，AB ＝CD ，EG ＝FG ， 又∵点E ，F 分别是AB ，DC 的中点， ∴AE ＝12AB ，DF ＝12DC ，∴AE ＝DF. 在Rt △AGE 与Rt △DGF 中，7,,AB DE EG FG =⎧⎨=⎩ ∴Rt △AGE ≌Rt △DGF （HL ）. ∴AG ＝DG ，即G 是AD 的中点.11．∵AC ⊥BD ，∴∠ACB ＝∠DCE ＝90°. ∴∠A ＋∠B ＝90°.在Rt △ACB 和Rt △DCE 中，,,AB DE CB CE =⎧⎨=⎩ ∴Rt △ACB ≌Rt △DCE （HL ）， ∴∠A ＝∠D ， ∴∠D ＋∠B ＝90°. ∴DE ⊥AB.第6课时11.2三角形全等的判定习题课【检测1】D.【检测2】答案不唯一，如∠A ＝∠D 或AC ＝DF 等. 【检测3】∵∠1＝∠2，∠3＝∠4， ∴∠1＋∠3＝∠2＋∠4，∴∠ABC ＝∠DCB. 在△ABC 与△DCB 中，∠4＝∠3，BC ＝CB ，∠ABC ＝∠DCB ， ∴△ABC ≌△DCB （ASA ）. ∴AB ＝CD.【问题1】∠BAD ＝∠CAD ，理由如下： ∵AE ＝13AB ，AF ＝13AC ，AB ＝AC ，∴AE ＝AF. 又∵OE ＝OF ，AO ＝AO ， ∴△AOE ≌△AOF （SSS ）.∴∠EAO ＝∠FAO ，即∠BAD ＝∠CAD.【问题2】如图，在AF 上截取AG=AD ，连接EG ,EF. 在△ADE 和△AGE 中，,,,AD AG DAE GAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△AGE(SAS). ∴DE=GE, ∠AGE=∠ADE=90°. ∵DE=CE, ∴CE=GE. 在Rt △EGF 和Rt △ECF 中，,,GE CE EF EF =⎧⎨=⎩ ∴Rt △EGF ≌Rt △ECF(HL). ∴GF=CF. ∵AF=AG+GF, ∴AF=AD+CF. 1．D.2．答案不唯一，如AE ＝BF 或DE ＝CF 等. 3．∵OP 是∠AOC 和∠BOD 的平分线， ∴∠BOP ＝∠DOP ，∠AOP ＝∠COP ， ∴∠AOP －∠BOP ＝∠COP －∠DOP ， ∴∠AOB ＝∠COD. 在△AOB 与△COD 中，,,,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△COD(SAS). ∴AB ＝CD. 4．B.5．(1)证明：∵∠1＝∠2，∴∠1＋∠CAD ＝∠2＋∠CAD ，即∠BAD ＝∠CAE ． 又∵AB ＝AC ，AD ＝AE ， ∴△BAD ≌△CAE (SAS) ．（2）∵△BAD ≌△CAE ，∴∠B ＝∠C ． ∴∠COB ＝∠B ＋∠E ＝∠C ＋∠E ＝∠1＝60°． 6．（1）∵BG ∥AC ，∴∠DBG ＝∠C. 又∵BD ＝CD ，∠BDG ＝∠CDF ， ∴△BGD ≌△CFD(AAS)，∴BG ＝CF. （2）BE ＋CF ＞EF ，证明：由△BGD ≌△CFD ，得GD ＝FD ，BG ＝CF. 又∵DE ⊥GF ，ED ＝ED ，∴△EDG ≌△EDF(SAS)， ∴EG ＝EF.在△BEG 中，BE ＋BG ＞EG ，即BE ＋CF ＞EF. 7．1m.8．(4，－1)，(－1，3)或(－1，－1) ． 9．在EA 上截取EF ＝EB ，连接FC. ∵CE ⊥AB ，∴∠FEC ＝∠BEC ＝90°. 又∵EC ＝EC ，∴△CFE ≌△CBE （SAS ）. ∴∠B ＝∠CFE.又∵∠CFE ＋∠AFC ＝180°，∠B ＋∠D ＝180°， ∴∠CFA ＝∠D.又∵∠FAC ＝∠DAC ，AC ＝AC ， ∴△AFC ≌△ADC （AAS ）. ∴AF ＝AD.又∵AE ＝AF ＋EF ，EF ＝EB ，∴AE ＝AD ＋BE.10．答案不唯一，如AB＝DC或AF＝DE等.11．图中∠CBA＝∠E.证明：∵AD＝BE，∴AD＋DB＝BE＋DB，即AB＝DE.∵AC∥DF，∴∠A＝∠FDE.又∵AC＝DF，∴△ABC≌△DEF（SAS），∴∠CBA＝∠E.第7课时11.3角的平分线的性质（1）【检测1】C.【检测2】相等，角的平分线上.【检测3】(1)成立，因为由“AAS”可证△OPD≌△OPE，可得PD=PE；(2)成立，因为由“HL”可证△OPD≌△OPE，得∠DOP=∠EOP．【问题1】作DE⊥AB于点E，∵∠C＝90°，∴DC⊥AC.又∵AD为∠BAC的角平分线，∴DC＝DE.∵BC＝64，BD:DC＝9:7，∴DC＝716×64＝28，∴DE＝28.【问题2】∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE＝DF.在△DEB与△DFC中，∠B＝∠C，∠BED＝∠CFD＝90°，DE＝DF，∴△DEB≌△DFC（AAS）.∴BD＝CD.1．B．2．C．3．MD⊥OA且ME⊥OB．4．55°.5．连接AD，在△ABD和△ACD中，AB＝AC，BD＝CD，AD＝AD，∴△ABD≌△ACD（SSS）.∴∠BAD＝∠CAD，即AD平分∠BAC.又∵DE⊥AB，DF⊥AC，∴DE＝DF.6．∵DE⊥AB，DF⊥AC，∴∠BED＝∠CFD＝90°.∵BE＝CF，DB＝DC，∴Rt△BED≌Rt△CFD（HL）.∴DE＝DF.又∵DE⊥AB，DF⊥AC，∴AD是∠BAC的平分线.7．C.8．PD＝PC.证明：过点P作PF⊥OA于点F，PE⊥OB于点E，∵OM是∠AOB的平分线，∴PE＝PF.∵∠CPF＋∠FPD＝90°，∠DPE＋∠FPD＝90°，∴∠DPE＝∠CPF. 在△PDE和△PCF中，∠DPE＝∠CPF，PE＝PF，∠DEP＝∠CFP，∴△PDE≌△PCF（ASA），∴PD＝PC.9．（1）∵∠C＝90°，∴DC⊥AC.∵AD平分∠BAC，DE⊥AB，∴DC＝DE.在Rt△DCF与Rt△DEB中，DF＝DB，DC＝DE，∴Rt△DCF≌Rt△DEB（HL），∴CF＝EB.（2）AE＝AF＋EB，理由如下：∵CE=DE，AD=AD, ∠C=∠DEA=90°，∴Rt△ACD≌Rt△AED（HL）.∴AC＝AE.又∵AC＝AF＋CF＝AF＋EB，∴AE＝AF＋EB.10．D.11．(1)如图；(2)轮船航行时没有偏离预定航线.理由如下：∵P A＝PB，OA＝OB，OP＝OP，∴△OP A≌△OPB(SSS)．∴∠AOP＝∠BOP，即点P在∠AOB的平分线上．故轮船航行时没有偏离预定航线．第8课时11.3角的平分线的性质（2）【检测1】C.【检测2】在三角形内部分别作出两条角平分线，其交点O就是小亭的中心位置，如图1所示.图1【问题1】过点P作PD，PE，PF分别垂直于AB，BC，CA，垂足分别为点D，E，F.∵BM是△ABC的角平分线，点P在BM上，PD⊥AB，PE⊥BC，∴PD＝PE.PCOABA BC•O课程导报网89同理PE ＝PF.∴PD ＝PF ，∴点P 在∠BAC 的平分线上. 【问题2】过点E 作EF ⊥AB ，垂足为点F ．则 EC ＝EF ．∵ED ＝EC ，∴ED ＝EF ．∵ED ⊥AD ，EF ⊥AB ，∴AE 平分∠BAD ． 1．B ．2．C ．3．4．4．D ．5．过点O 作OE ⊥AB ，OF ⊥AC ，垂足点E ，F.∵OB ，OC 分别平分∠ABC ，∠ACB ，OD ⊥BC ， ∴OD ＝OE ＝OF ＝2， ∴ABCS＝AOB S ＋AOC S ＋BOC S＝12×AB ×OE ＋12×AC ×OF ＋12×BC ×OD ＝12（AB ＋AC ＋BC ）×OD ＝12×24×2＝24. 6．∵PC ⊥AC ，PB ⊥AB ，PB ＝PC ， ∴AP 平分∠BAC ，即∠BAP ＝∠CAP.∵∠BAP ＋∠BPA ＝90°，∠CAP ＋∠CPA ＝90°， ∴∠BPD ＝∠CPD. 在△PBD 和△PCD 中，PB ＝PC ，∠BPD ＝∠CPD ，PD ＝PD ， ∴△PBD ≌△PCD （SAS ），∴∠BDP ＝∠CDP. 7．120.8．⑴作∠BAC 、∠ACB 的平分线，它们的交点P 为符合要求的点，如图2所示，作PF ⊥BC ，PE ⊥AB ，PG ⊥AC ，垂足分别为点F ，E ，G .证明：∵AP 是∠BAC 的平分线，∴PE ＝PG .∵CP 是∠ACB 的平分线，∴PF ＝PG ，∴PE ＝PG ＝PF.图2⑵连接BP ，设PE ＝PG ＝PF ＝x ， ∵APC BPC APB ABCS S S S ∆∆∆∆++=，∴21AB ×BC ＝21AB x •＋21AC x •＋21BC x •. ∴7×24＝（7＋24＋25）x . ∴3=x ，即这个距离为3.9．（1）作OM ⊥AB 于点M ，ON ⊥AC 于点N ，连接OA. 在Rt △OMB 和Rt △ONC 中，∵OM ＝ON ，OB ＝OC ，∴Rt △OMB ≌Rt △ONC （HL ），∴∠B ＝∠C.又∵OM ⊥AB ，ON ⊥A ，OM ＝ON ，∴∠MAO ＝∠NAO. 在△ABO 和△ACO 中，∵∠B ＝∠C ，∠BAO ＝∠CAO ，OA ＝OA ， ∴△ABO ≌△ACO （AAS ）.∴AB ＝AC.（2）作OM ⊥AB 于点M ，ON ⊥AC 于点N ，连接OA ， 在Rt △OMB 和Rt △ONC 中， ∵OB ＝OC ，OM ＝ON ，∴Rt △OMB ≌Rt △ONC （HL ），∴∠MBO ＝∠NCO. ∵OM ⊥AB ，ON ⊥AC ，OM ＝ON ，∴∠BAO ＝∠CAO. ∵∠MBO ＝∠NCO ，∠BAO ＝∠CAO ，OA ＝OA ， ∴△ABO ≌△ACO （AAS ），∴AB ＝AC. 10．＝.11．过点D 作DF ⊥BC 于点F.∵BD 平分∠ABC ，DE ⊥AB 于点E ，DF ⊥BC 于点F ， ∴DF ＝DE ＝2cm.又AB ＝9cm ，BC ＝6cm ， ∴ABD S＝12×AB ×DE ＝12×9×2＝9（cm 2）， BCD S＝12×BC ×DF ＝12×6×2＝6（cm 2）. ∴ABCS＝ABD S＋BCDS＝9＋6=15（cm 2）.11.2（2）~11.3测试题基础巩固一、精挑细选，一锤定音1．B ．2．C ．3．B ．4．A ．5．A ．6．B ． 二、慎思妙解，画龙点睛7．HL ．8．152cm ．9．5．10．4处． 三、过关斩将，胜利在望(共50分)11．提示：∠AOB 的平分线与MN 的交点即为所求作的点C ． 12．提示：先用“HL ”证明Rt △AEF ≌Rt △BCD ，从而得到AF ＝BD ，进而得到AD ＝BF ．13．证明：过点D 作DM ⊥AB 于点M ，DN ⊥AC 于点N ， ∵△DEB 与△DFC 的面积相等，BE ＝CF ， ∴DM ＝DN ． ∴AD 平分∠BAC ．14．BF ＝CG .理由如下：连接EB ，EC ， ∵ED ⊥BC ，∴∠BDE ＝∠CDE ＝90°. 在△BDE 与△CDE 中，A G C FB E P课程导报网 10BD ＝CD ，∠BDE ＝∠CDE ，DE ＝DE ， ∴△BDE ≌△CDE （SAS ）. ∴EB ＝EC.∵EF ⊥AB ，EG ⊥AC ，AE 平分∠BAC ， ∴EF ＝EG .在Rt △BEF 与Rt △CEG 中，,,EF EG EB EC =⎧⎨=⎩ ∴Rt △BEF ≌Rt △CEG （HL ）. ∴BF ＝CG . 15．⑴△CDF ，证明：∵AD 平分∠BAC ，DE ⊥AB 于点E ，DF ⊥AC 于点F ， ∴DE ＝DF ，∠BED ＝∠CFD ＝90°. 又∵BD ＝CD ，∴Rt △BDE ≌Rt △CDF （HL ）. ⑵∵AD ＝AD ，DE ＝DF ， ∴Rt △ADE ≌Rt △ADF （HL ）. ∴AE ＝AF.又∵AE ＝6cm ，∴AF ＝6cm. ∵AC ＝4cm ，∴CF ＝AF －AC ＝2cm. 由⑴可得Rt △BDE ≌Rt △CDF ， ∴BE ＝CF ＝2cm.能力提高1．A ．2．互补. 理由如下：作CH ⊥AD 交其延长线于点H ， ∵CE ⊥AB ，∴∠AHC ＝∠AEC ＝90°. 又AC 平分∠BAD ，∴∠CAH ＝∠CAE. 又∵AC ＝AC ，∴△ACH ≌△ACE （AAS ）， ∴AH ＝AE ，CE ＝CH. ∵AD ＋AB ＝2AE ， ∴AD ＋AE ＋BE ＝2AE ， AH －DH ＋AE ＋BE ＝2AE ， AE －DH ＋AE ＋BE ＝2AE ， ∴DH ＝BE.又∵∠CHD=∠CEB,CH ＝CE ，∴△CHD ≌△CEB （SAS ），∴∠B ＝∠CDH.又∵∠CDH ＋∠ADC ＝180°，∴∠B ＋∠ADC ＝180°. 即∠B 与∠ADC 互补. 3．⑴PB ＝PQ. 理由如下：过点P 作PE ⊥BC 于点E ，PF ⊥CD 于对点F ，在正方形PBCQ 中，∠BPQ ＝∠BCQ ＝90°， ∴∠PBC+∠PQC ＝180°.又∵∠PQC ＋∠PQD ＝180°，∴∠PBC ＝∠PQD.又∵AC 为正方形ABCD 的对角线，PE ⊥BC ，PF ⊥CD ，∴PE ＝PF.∴△PBE ≌△PQF(AAS)，∴PB ＝PQ. ⑵结论还成立，理由同上.4．（1）FE 与FD 之间的数量关系是FE=FD ； (2) (1)中的结论FE=FD 仍然成立. 证明：在AC 上截取AG=AE,连接FG . 在△AEF 和△AGF 中，,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△AEF ≌△AGF(SAS). ∴∠AFE=∠AFG ，FE=FG .∵∠B=60°，AD,CE 分别平分∠BAC, ∠BCA ， ∴∠GAF+∠FCA=60°. ∴∠AFE=∠CFD=∠AFG=60°. ∴∠CFG=60°. 在△CFG 和△CFD 中，60,,,CFG CFD CF CF FCG FCD ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△CFG ≌△CFD (ASA). ∴FG=FD.又∵FE=FG ,∴ FE=FD.第3期有效学案参考答案第9课时 第十一章复习课【检测1】B. 【检测2】D.【检测3】答案不唯一，如AC ＝DF 或∠B ＝∠E 或∠A ＝∠D. 【问题1】这个命题是假命题，添加的条件可以是： AC ＝DF 或∠C ＝∠F 或∠CBA ＝∠E. 以添加条件AC ＝DF 证明.∵AD ＝BE ，∴AD ＋DB ＝BE ＋DB ，∴AB ＝DE. 在△ACB 与△DFE 中，,,,AB DE A FDE AC DF =⎧⎪∠=∠⎨⎪=⎩11∴△ACB ≌△DFE （SAS ）.【问题2】（1）图中满足条件的全等三角形是 ：△AGF ≌△DGB ，理由如下： ∵△ABC ≌△DFC ，∴∠A ＝∠D ，AC ＝DC ，CB ＝CF ， ∴AF ＝DB.又∵∠AGF ＝∠DGB ，∴△AGF ≌△DGB.（2）AB ⊥CD ，理由如下：由题意可知△ABC ≌△DCE ， ∴∠B ＝∠ECD.又∵∠ECD ＋∠GCB ＝90°，∴∠GCB ＋∠B ＝90°，即∠CGB ＝90°，∴AB ⊥CD. 1．A. 2．10.3．∵DC 是∠ACE 的平分线，DE ⊥CE ，DF ⊥AC ， ∴∠DEC ＝∠DFC ＝90°，∴DE ＝DF. 在Rt △DFC 和Rt △DEC 中，,,DC DC DF DE =⎧⎨=⎩∴Rt △DFC ≌Rt △DEC （HL ），∴CE ＝CF. 4．A.5．DC ＝PC 且DC ⊥PC ；理由如下：∵∠DAC ＝∠PBC ，∠D ＝∠BPC ，AC ＝BC ， ∴△ACD ≌△BCP （AAS ），∴DC ＝PC ，∠DCA ＝∠PCB. ∵∠PCB ＋∠ACP ＝90°，∴∠DCA ＋∠PCA ＝90°，∴DC ⊥PC.6．（1）证明：连接AD ，可证得Rt △ABD ≌Rt △ACD （HL ），得BD ＝CD.由E ，F ，G ，H 为中点及AB ＝AC ，BD ＝CD ，得 BE ＝CF ，BH ＝CG .又∠B ＝∠C ＝90°，∴△BEH ≌△CFG ，∴EH ＝FG . （2）AD 垂直平分BC ，证明如下：由（1）知Rt △ABD ≌Rt △ACD ，∴∠BAD ＝∠CAD. ∵AB ＝AC ，AO ＝AO ，∴△ABO ≌△ACO （SAS ）. ∴BO ＝CO ，∠AOB ＝∠AOC. 又∠AOB ＋∠AOC ＝180°，∴∠AOB ＝∠AOC ＝90°，∴AD ⊥BC. 7．B.8．BE 是∠ABC 的平分线，理由如下： 延长BC ，AE 交于点F ，AC ⊥BC ，AE ⊥BE ， ∴∠AED ＝∠BCD ＝90°.∵∠ADE ＝∠BDC ，∴∠CBD ＝∠CAF. 在△BCD 与△ACF 中，∠CBD ＝∠CAF ，BC ＝AC ，∠BCD ＝∠ACF ，∴△BCD ≌△ACF （ASA ），∴BD ＝AF. 又∵BD ＝2AE ，∴EF ＝EA. 在△BEA 与△BEF 中，∵BE ＝BE ，∠BEA ＝∠BEF ，EA ＝EF ， ∴△BEA ≌△BEF （SAS ），∴∠ABE ＝∠FBE ，即BE 平分∠ABC. 9．（1）∵BD ⊥DE 于点D ，CE ⊥DE 于点E ， ∴∠ADB ＝90°，∠CEA ＝90°. 又∵AD ＝CE ，AB ＝CA ，∴Rt △ABD ≌Rt △CAE （HL ），∴∠BAD ＝∠ACE. 又∵∠CAE ＋∠ACE ＝90°，∴∠CAE ＋∠BAD ＝90°， ∴∠BAC ＝90°，∴BA ⊥AC.（2）垂直，理由如下：易证Rt △ABD ≌Rt △CAE （HL ）， ∴∠BAD ＝∠ACE.又∵∠ACE ＋∠CAE ＝90°， ∴∠BAD ＋∠CAE ＝90°， ∴∠BAC ＝90°，即BA ⊥AC. 10．D.11．（1）作图略；（2）△BDE ≌△CDE ；理由如下： ∵ DC 平分∠ACB ，∴ ∠DCE =12∠ACB.∵∠ACB =2∠B ， ∴ ∠B =12∠ACB ，∴ ∠DCE =∠B. ∵ DE ⊥BC ，∴∠DEC ＝∠DEB ＝90°. 又∵DE ＝DE ，∴ △BDE ≌△CDE （AAS ）.第十一章综合测试题（一）一、精挑细选，一锤定音1．D. 2．B. 3．C. 4．C. 5．A. 6．C. 7．C. 8．B. 9．C. 10．D. 二、慎思妙解，画龙点睛 11．27°. 12．60°. 13．150°.14．答案不唯一，如EH ＝BE 或AE ＝CE 或AH ＝BC. 15．垂直. 16．100°．17．10. 18．（8,6），（8,8），（8,-6）或（8,-8）. 三、过关斩将，胜利在望19．证明：在△AEB 与△ADC 中， AB ＝AC ，∠A ＝∠A ，AE ＝AD ， ∴△AEB ≌△ADC ，∴∠B ＝∠C ． 20．△A 1B 1C 1与△ABC 不一定全等，图略. 21．△ADF ≌△ABE ，理由：∵AC 平分∠BCD ，AE ⊥BE ，AF ⊥DF ，课程导报网12∴AE ＝AF ，∠AEB ＝∠AFD ＝90°. 又AB ＝AD ，∴Rt △ABE ≌Rt △ADF （HL ）. 22．连接ME ，MF ，∵AB ∥CD ，∴∠B ＝∠C. 在△BEM 与△CFM 中，BE ＝CF ，∠B ＝∠C ，BM ＝CM ，∴△BEM ≌△CFM （SAS ）.∴∠BME ＝∠CMF. ∴∠EMF ＝∠BME ＋∠BMF ＝∠CMF ＋∠BMF ＝∠BMC ＝180°， ∴E ，M ，F 在一直线上.23．⑴证明：∵∠BDE ＝∠CDE ，∴∠ADB ＝∠ADC. 又∵AE 为角平分线，∴∠BAE ＝∠CAE ，且AD ＝AD ， ∴△ABD ≌△ACD （ASA ），∴AB ＝AC.⑵结论还成立，∵AE 为高线，∴∠AEB ＝∠AEC ＝90°. 又∠BDE ＝∠CDE ，且DE ＝DE ， ∴△BDE ≌△CDE. ∴BE ＝CE.又∠AEB ＝∠AEC ＝90°，且AE ＝AE ， ∴△ABE ≌△ACE （SAS ），∴AB ＝AC.24．（1）∵BD ，CE 分别是△ABC 的边AC ，AB 上的高， ∴∠ADB ＝∠AEC ＝90°.∴∠ABP ＝90°－∠BAD ，∠ACE ＝90°－∠DAB ， ∴∠ABP ＝∠ACE. 在△ABP 和△QCA 中，,,,BP CA ABP ACE AB QC =⎧⎪∠=∠⎨⎪=⎩∴△ABP ≌△QCA （SAS ），∴AP ＝AQ. （2）∵△ABP ≌△QCA ，∴∠P ＝∠CAQ. 又∵∠P ＋∠PAD ＝90°，∴∠CAQ ＋∠PAD ＝90°，∴∠PAQ ＝90°，∴AP ⊥AQ. 四、附加题 25．（1）∵1t= s ，∴BP ＝CQ ＝3×1＝3cm.∵AB ＝10cm ，点D 为AB 的中点，∴BD ＝5cm. 又∵PC ＝BC －BP ，BC ＝8cm ， ∴PC ＝8－3＝5cm ，∴PC ＝BD. 又∵∠B ＝∠C ，∴△BPD ≌△CQP. （2）∵PQ v v ≠， ∴BP ≠CQ.又∵△BPD ≌△CPQ ，∠B ＝∠C ，则 BP ＝PC ＝4，CQ ＝BD ＝5， ∴点P ，点Q 运动的时间433BP t== s ， ∴515443QCQ v t===cm/s ． 26．图②成立，图③不成立．证明图②．延长DC 至点K ，使CK ＝AE ，连接BK ，则 △BAE ≌△BCK ，∴BE ＝BK ，∠ABE ＝∠KBC. ∵∠FBE ＝60°，∠ABC ＝120°，∴∠FBC ＋∠ABE ＝60°，∴∠FBC ＋∠KBC ＝60°， ∴∠KBF ＝∠FBE ＝60°， ∴△KBF ≌△EBF ，∴KF ＝EF ， ∴KC ＋CF ＝EF ，即AE ＋CF ＝EF.图③不成立，AE ，CF ，EF 的关系是AE －CF ＝EF.第十一章综合测试题（二）一、精挑细选，一锤定音1．C ．2．A ．3．C ．4．D ．5．C ． 6．B ．7．C ．8．C ．9．C ．10．C ． 二、慎思妙解，画龙点睛 11．∠DBE ，AC ．12．30°． 13．答案不唯一，如∠B ＝∠D ．14．答案不唯一，如Rt △ACD ≌Rt △BCE ，AC ＝BC ， ∠DAC ＝∠EBC ，∠ADC ＝∠BEC ，从中任选两个. 15．145°．16．78°．17．7．18．①②④． 三、过关斩将，胜利在望19．∵BC ＝BD ，点E 是BC 的中点，点F 是BD 的中点， ∴BE ＝BF.又∵∠ABE ＝∠ABF ，AB ＝AB ，∴△ABE ≌△ABF. 20．全等．由折叠可知△BDE ≌△BDC ． ∴DE ＝DC ，∠E ＝∠C ＝90°． ∵AB ＝DC ，∴AB ＝ED ．又∵∠A ＝∠E ＝90°，∠AFB ＝∠EFD ， ∴△ABF ≌△EDF (AAS) ．21．在四边形A BCD 中，已知CD ＝BC ，∠D ＋∠B ＝180°，求证：对角线AC平分∠BAD.证明：过点C 作AB ，AD 的垂线，垂足分别为点E ，F ， ∵∠ADC ＋∠B ＝180°，∠ADC ＋∠CDF ＝180°， ∴∠B ＝∠CDF.在△CDF 和△CBE 中，,,,F CEB CDF B CD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CDF ≌△CBE （AAS ），∴CF ＝CE. 又∵CF ⊥AD ，CE ⊥AB ，∴点C 在∠BAD 的平分线上，即对角线AC 平分∠BAD. 22．(1)FC ；(2)FC＝EA；(3)提示：用SAS证△ABE≌△CDF．23．∵∠B＝90°，ED⊥AC于点D，BE＝DE，∴AE平分∠BAC，∴∠EAD＝12∠BAC.过点B作BF⊥AC于点F，则∠BFA＝∠BFC. ∵AB＝BC，BF＝BF，∴Rt△BFA≌Rt△BFC（HL），∴∠BAC＝∠C，∴∠EAD＝12∠C.24．（1）垂直，相等；（2）当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD＝AF，∠DAF＝90°.∵∠BAC＝90°，∴∠DAF＝∠BAC，∴∠DAB＝∠FAC.又AB＝AC，∴△DAB≌△FAC，∴CF＝BD，∠ACF＝∠ABD.又∵∠ABD＋∠ACB＝90°，∴∠ACF＋∠ACB＝45°，即CF⊥BD.四、附加题25．（1）作图略；在OA和OB上截取OE＝OF，在OP上任取一点C，连接CE，CF，则△COE≌△COF；（2）在AC上截取AM＝AE，连接FM，AD是∠BAC的平分线，∴∠EAF＝∠MAF.又∵AF＝AF，∴△AEF≌△AMF，∴EF＝MF.∵CE是∠BCA的平分线，∠ACB＝90°，∴∠DCF＝45°.又∵∠B＝60°，∴∠BAD＝15°，∴∠CDF＝75°，∴∠AMF＝∠AEF＝105°，∴∠FMC＝75°，∴∠CDF＝∠CMF.又∵CF＝CF，∠DCF＝∠MCF.∴△CDF≌△CMF，∴FD＝FM，∴EF＝DF.26．（1）90；（2）①α＋β＝180°.理由：∵∠BAC＝∠DAE，∴∠BAC－∠DAC＝∠DAE－∠DAC，即∠BAD＝∠CAE.又AB＝AC，AD＝AE，∴△ABD≌△ACE，∴∠B＝∠ACE，∴∠B＋∠ACB＝∠ACE＋∠ACB，∴∠B＋∠ACB＝β.∵α＋∠B＋∠ACB＝180°，∴α＋β＝180°.②当点D在射线BC上时，α＋β＝180°，当点D在射线BC的反射延长线时，α＝β.第4期有效学案参考答案第1课时 12.1轴对称（1）【检测1】（1）互相重合，对称轴；（2）与另一个图形重合，对称点.【检测2】A.【问题1】解：中国银行标志是轴对称图形，而且有2•条不同的对称轴.其对称轴如图1中的直线AB和直线CD.【问题2】解：乙组图形中的两个图案是成轴对称的，其对称轴如图2中的直线MN.对称点见红色标记.1．C.2．C.3.（1）对称轴是过点A的一条铅垂线（画图略）；（2）点A，B，C，D的对称点分别是点A，G，F，E；（3）答案不唯一，图略.4．D.5．虚线a，d是图形的对称轴，虚线b，c，e，f不是.6．答：图（1）不是轴对称图形，图（2）、（3）、（4）是轴对称图形，且图（2）有1条对称轴，图（3）有6条对称轴，图（4）有2条对称轴（画图略）.7．与第1个三角形关于直线AC对称；与第3个三角形关于直线EG对称；与第5个三角形关于直线BD对称；与第7个三角形关于直线FH对称.8．B.9．.10．如图3.11．A.12．（1）如图4；图3方法三方法二方法一课程导报网13（2）第（1）个图是正方体的表面展开图，第（2）个图不是.第2课时 12.1轴对称(2)【检测1】（1）垂直平分线，垂直平分线；（2）两个端点，两个端点，两个端点.【检测2】(1)如图1；(2)直线l垂直平分线段AA′.【问题1】如图2：图2作法：（1）连接AD；（2）分别以点A，D为圆心，以大于12AD的长为半径作弧，两弧交于M，N两点．（3）作直线MN，则MN即为所求的直线.【问题2】（1）DE=CD．∵BD平分∠ABC，∠C=90°，且DE⊥AB于点E，∴DE=CD．（2）AD=BD．∵DE是斜边AB的垂直平分线，∴AD=BD．（3）△ABC的周长为a+2b．1．C. 2．D.3．连接AC．∵点A在线段BC的垂直平分线MN上，∴AB＝AC．∵AB＝AD，∴AC＝AD．∴点A在线段CD的垂直平分线上.4．5cm. 5．第(1)、(2)、(3)幅图中的图形A与图形B成轴对称，第(1)幅图中的对称轴是铅直的(注意：水平的那条对称轴不符合题意)，第(2)幅图中的对称轴是水平的，第(3)幅图中的对称轴是倾斜的．第(4)图中的图形A与图形B不是成轴对称．画图略.6．（1）对称点有：C与C′，A与A′，B与B′；（2）m垂直平分AA′；（3）AC与A′C′的交点在直线m上，AB与A′B′的交点也在直线m上，BC与B′C′的交点都在直线m上；发现的规律：两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．7．D.8．如图3．理由：到两公路距离相等的点在两公路所成角的平分线上，到两个村庄距离相等的点在连结两个村庄所得线段的垂直平分线上，因此，货运站是以上角平分线与垂直平分线的交点.9.连接DB，DC，∵AD是∠A的角的平分线，且DE⊥AB，DF⊥AC，∴DE=DF．∵MD是BC的垂直平分线，∴DB=DC．在Rt△DEB和Rt△DFC中，,,DE DFDB DC=⎧⎨=⎩∴Rt△DEB≌Rt△DFC（HL）．∴EB＝FC．10．A.11．∵DE垂直平分BC，∴DB＝DC．∵AD＋DC＋AC＝14，∴AB＋AC＝14 (1)又AB－AC＝2…………(2)．于是由方程组(1)、(2)解得AB＝8，AC＝6．答：AB和AC的长分别为8cm和6cm.第3课时 12.2作轴对称图形(1)【检测1】（1）形状、大小，对称点，垂直平分；（2）点，对应点，直线、线段、或射线，对称点.【检测2】如图1.图3PMNOl图1 A′A l（1）（2）图4课程导报网1415BlAB C图3【问题1】(1)过点O 作l 的垂线，垂足为O ；延长AO 到A ′，使OA ′＝OA ．则点A ′即为所求作的点；(2)如图2；(3)AB ∥A ′B ′，对应线段所在直线的交点位于对称轴l 上.【问题2】如图3,作点B 关于直线l 的对称点B ′,连接AB ′交直线l 于点C,则沿路线A —C —B 运球可使同学们的用时尽可能少.1．B. 2．如图4.3．如图5，过点D 作AB 的垂线交圆周于点D ′，连接CD ′交AB 于点P ，则点P 即为所求.4．错误. 5．D.6．(1)步骤2，3，4中的对称轴分别是线段d 、b 、a （或c ）所在的直线；(2)略.7．①264×21，√；②429×21，×；③198×81，√. 8．(1)特征1：都是轴对称图形；特征2：图案的总面积都是6；特征3：都有两条互相垂直的对称轴．(2)答案不唯一，如图3．9．如图7，作点B 关于HE 的对称点B ′，点A 关于EF 的对称点A ′，连接B ′A ′分别交HE ，EF 于点C ，D ，则B →C →D →A 即为白球撞击黑球的路线.10．C. 11．(1)如图8；(2)PP 2与AB 平行且相等．理由：设PP 1分别交l 1，l 2于点O 1，O 2．∵P 、P 1关于l 1对称，点P 2在PP 1上，∴PP 2⊥l 1． 又∵AB ⊥l 1，∴PP 2∥AB ．依题意可知O 1O 2＝AM ＝a ，P 1O 1＝PO 1＝b ，P 2O 2＝P 1O 2＝P 1O 1－O 1O 2＝b －a ．∴PP 2＝PP 1－P 1P 2＝2PO 1－2P 1O 2＝2b －2(b －a )＝2a ．故PP 2与AB 平行且相等.第4课时 12.2作轴对称图形(2)【检测1】(x ，－y )，(－x ，y ).【检测2】(1)点A 和点D 、点B 和点C 关于x 轴对称，点A 和点B 、点C 和点D 关于y 轴对称(描点略)； (2)x ，y .【问题1】画图略，(1)A ，B ，C ，D 的坐标分别为(－2，2)、(－1，1)、(－3，－2)、(－4，1)，它们的对称点A ′，B ′，C ′，D ′的坐标分别是(2， 2)、(1，1)、(3，－2)、(4，1)；图6图8O 2P 2O 1P 1l 2l 1ABM P图7B 'A 'GHFEBDA C 图4lll图2lO D 'C 'B 'A 'CADB图1(1) (2)图5PD 'BDAC(2)M′(－a，b).【问题2】解：若两点关于横轴对称，则它们的横坐标不变，而纵坐标变为相反数．于是39,23 5.a ba b-=⎧⎨+=-⎩解得a＝2，b＝－3.1．B. 2．二.3．画图略.(1)A，B，C的坐标分别为(－3，2)，(－2，0)，(3，3)，它们的对称点A′，B′，C′的坐标分别是(－3，－2)，(－2，0)，(3，－3)；(2)M′(a，－b).4．(1，－2). 5．(9，9).6．(1)图略，A1(0，4)，B1(2，2)，C1(1，1)；(2)图略，A2(6，4)，B2(4，2)，C2(5，1)；(3)它们关于某条直线对称，对称轴是一条经过(3，0)且与x轴垂直的直线.7.（-1，1）.8．2，3.9．(1)点A，B，C，D关于x＝－2对称的点分别是A′(－4，1)，B′(－1，4)，C′(1，4)，D′(1，1)，画图略；(2)AB与A′B′交于点E(－2，3)，且S△A′AE＝4.10．D.11．(1)S△ABC＝12×5×3＝152(或7.5)(平方单位)；(2)图略；(3)A1(1，5)，B1(1，0)，C1(4，3)．12．1~12．2测试题基础巩固1．C．2．B．3．A．4．C．5．C．6．B.7．答案不唯一，如：中，喜，目，善，工，田，等等．8．3. 提示：A′D＝AD，A′E＝AE .9．115°．10．(－1，－4) ．提示：m－1＝2，n＋1＝－3．11．（1）点A与点D, 点B与点E, 点C与点F；（2）90°；（3）周长为30cm,面积为30 cm2.12．如图1．13．(1)略；(2)A′(2，3)，B′(3，1)，C′(－1，－2) ．14．(1)AC垂直平分BD．∵AB＝AD，∴点A在线段BD的垂直平分线上．∵BC＝DC，∴点C在线段BD的垂直平分线上．由于两点确定一条直线，∴AC垂直平分BD．(2)S四边形ABCD＝S△ABD＋S△CBD＝12BD·AO＋12BD·CO＝12BD·(AO＋CO)＝12BD·AC＝12×4×5＝10．15．如图2．能力提高1．C．2．151＋25＋12＝188．3．.4．如图3.5．(1)连接B′B′′，B′B′′的垂直平分线即是直线EF；(2)∠BOB′′＝2α．C HHHC C CHHHHHH H图1图2A′P图3方法一方法二方法三方法四课程导报网16课程导报网17。

第5期有效学案参考答案第5课时 等腰三角形(1)【检测1】等边对等角；顶角平分线、底边上的中线、底边上的高. 【检测2】提示：用“SAS ”证明△ADB ≌△ADC . 【问题1】证明：∵AB ＝AC ，AO ＝AO ，OB ＝OC ． ∴△AOB ≌△AOC (SSS)． ∴∠OAB ＝∠OAC ． ∵AB ＝AC ，∴AO ⊥BC .【问题2】设∠ACD ＝α，则∠EDC ＝α，∠A ＝∠AED ＝2α， ∠ACB ＝∠B ＝∠BDC ＝∠A ＋∠ACD ＝3α．在△ABC 中，由内角和定理得2α＋3α＋3α＝180°， ∴α＝°．∴∠A ＝2α＝45°. 1．D. 2．D .3．40°，40°；30°，120°或75°，75°. 4. 25. 5．105°. 6.（1）70°；（2）40°. 7．∠A=∠E ．理由：∵CB=CE ，∴∠E=∠CBE ．又∵AD ∥BC ，∴∠A=∠CBE ，∴∠A=∠E ． 8．∵DB=DC ，∴∠DBC=∠C=40°， ∴∠ADB=∠DBC+∠C=80°． ∵AB=DB ，∴∠A=∠ADB=80°． ∴∠ABD=180°-∠A-∠ADB=20°． 9．解：此题分三种情况．(1)当底边上的高与一腰的夹角是40°时，如图①，顶角是80°，从而两个底角是50°，50°；(2)当一腰上的高与另一腰的夹角是40°且高在三角形内部时，如图②，顶角是50°，从而两个底角是65°，65°；(3)当一腰上的高与另一腰的夹角是40°且高在三角形外部时，如图③，顶角是130°，从而两个底角是25°，25°．综上所述，三个角的度数为80°，50°，50°或50°，65°，65°或130°，25°，25°.10．（1）∵DA= DC ，∴∠A=∠ACD=30°，∴∠CDB=60°．∵DB=DC ，∴∠B=∠DCB=60°，∴∠ACB=90°； （2）∠ACB=90°；（3）不论∠A•等于多少度（小于90°），∠ACB 总等于90°. 11．B.12．证明：连接DE ，DF ．∵AB ＝AC ，∴∠B ＝∠C ． 又∵BD ＝CF ，BE ＝CD ，∴△BDE ≌△CFD (SAS)． ∴DE ＝DF ．∵EG ＝GF ，∴DG ⊥EF ．第6课时 等腰三角形(2)【检测1】D.【检测2】证明：过点A 作AD ⊥BC ，垂足为D ． ∵∠B ＝∠C ，∠ADB ＝∠ADC ，AD ＝AD ，∴△ADB ≌△ADC (AAS)．∴AB ＝AC ；(2)如果一个三角形有两个角相等，那么这两个角所对的边也相等或“等角对等边”.【问题1】已知：如图，∠DAC 是△ABC 的外角，且∠DAC ＝2∠B ． 求证：△ABC 是等腰三角形．证明：∵∠DAC ＝2∠B ，又∵∠DAC ＝∠B ＋∠C ， ∴∠B ＝∠C ．∴△ABC 是等腰三角形 【问题2】∵BD ⊥EF ，∴∠F ＋∠FCD ＝90°，∠B ＋∠E ＝90°. ∵AB ＝AC ，∴∠B ＝∠ACB. ∵∠FCD ＝∠ACB,∴∠B ＝∠FCD.∴∠E ＝∠F.∴AE ＝AF.∴△AEF 是等腰三角形. 1．是. 2．C. 3．D. 4．2cm. 5．∵PD ∥OB ，∴∠DPO=∠BOC ． ∵OC 平分∠AOB ，∴∠BOC=∠AOC.∴∠DPO=∠AOC ． ∴DP=DO ，即△DOP 是等腰三角形 . 6．∵AD 平分∠BAC ，∴∠BAD=∠CAD ． 又∵AD ∥EG ，∴∠G=∠CAD ，∠AFG=∠BAD. ∴∠G=∠AFG ，∴△AGF 是等腰三角形． 7．连接CD ．∵AD ＝BC ，AC ＝BD ，DC ＝CD ． ∴△ADC ≌△BCD ．∴∠ACD ＝∠BDC ．∴OD ＝OC . 8．6.9．证明：在DC 上截取DE ＝DB ，连接AE ．则AB ＝AE ， ∴∠B ＝∠AEB ．∵∠B ＝2∠C ，∴∠AEB ＝2∠C ．∵∠AEB ＝∠C ＋∠EAC ，∴∠C ＝∠EAC ． ∴AE ＝EC ．∴DC ＝DE ＋EC ＝BD ＋AB .10．D.11．(1)证明：∵AB ＝BA ，AC ＝BD ，∠C ＝∠D ＝90°，∴Rt △ABC ≌Rt △BAD (HL)．∴∠EAB ＝∠EBA ．∴AE ＝BE . (2)∵∠AEC ＝45°，∠C ＝90°，∴∠CAE ＝45°．∴∠CAE ＝∠CEA ．∴CE ＝AC ＝1.第7课时 等腰三角形(3)【检测1】相等，60；等边三角形，60，60. 【检测2】一，三，作图略.【问题1】∵△ABC 是等边三角形，∴∠A=60°． 又∵AD=AE ，∴△ADE 是等腰三角形．CABD ① ② ③40︒BD ACCADB40︒C AD B 40︒∴△ADE 是等边三角形．【问题2】DE=DB ，理由：∵CD=CE ，∴∠E=∠EDC ． 又∵∠ACB=60°，∴∠E=30°．又∵∠DBC=30°，∴∠E=∠DBC ，∴DB=DE ． 1．都. 2．150m. 3．4．4．C. 5．D. 6．∵△ABC 是等边三角形，∴∠BAC =60°． ∵AD ⊥BC ，∴∠DAC =30°．∵AE =AD ， ∴∠ADE =12×(180°－30°)=75°． ∴∠CDE =∠ADC －∠ADE =15° .7．∵AP ＝PQ ＝AQ ，∴△APQ 是等边三角形． ∴∠PAQ ＝∠APQ ＝∠AQP ＝60°．∵AP ＝BP ，∴∠BAP ＝∠B ＝12∠APQ ＝30°． 同理，∠CAQ ＝30°．∴∠BAC ＝∠BAP ＋∠PAQ ＋∠CAQ ＝30°＋60°＋30°＝120°. 8．证明：如图，延长AE 到M ，使EM ＝AB ，连接DM ． ∵△ABC 为等边三角形，∴∠A ＝60°，且AB ＝AC ．∴EM ＝AC ． ∵CD ＝AE ，∴CD ＋AC ＝AE ＋EM ．即AD ＝AM ． ∴△ADM 是等边三角形． ∴DA ＝DM ，且∠M ＝60°． 在△DAB 和△DME 中，,,,DA DM A M AB ME =⎧⎪∠=∠⎨⎪=⎩∴△DAB ≌△DME (SAS)． ∴DB ＝DE .9．(1)∵△ACD 和△BCE 都是等边三角形， ∴CA ＝CD ，CE ＝CB ，∠ACD ＝∠BCE ＝60°． 于是∠DCE ＝60°．∠ACE ＝∠DCB ＝120°． ∴△ACE ≌△DCB (SAS). ∴AE ＝DB . (2)由第(1)问的结论得∠CAE ＝∠CDB ． ∵CA ＝CD ，∠ACG ＝∠DCH ＝60°． ∴△ACG ≌△DCH (ASA)． ∴CG ＝CH ．而∠DCE ＝60°． ∴△CGH 是等边三角形. 10．B.11．证明：(1)∵AB ⊥BC ，DC ⊥BC ， ∴∠ABC ＝∠BCD ＝90°．∵△PBC 和△QCD 是等边三角形， ∴∠PBC ＝∠PCB ＝∠QCD ＝60°. ∴∠PBA ＝∠ABC －∠PBC ＝30°， ∠PCD ＝ ∠BCD －∠PCB ＝30°． ∴∠PCQ ＝∠QCD －∠PCD ＝30°． ∴∠PBA ＝∠PCQ ＝30°．(2)∵AB ＝DC ＝QC ，∠PBA ＝∠PCQ ，PB ＝PC ，∴△PAB ≌△PQC ，∴PA ＝PQ ．第8课时 等腰三角形(4)【检测1】一半. 【检测2】4cm.【问题1】连接AD ．∵AB ＝AC ，点D 为BC 的中点， ∴AD ⊥BC ，∠BAD ＝60°．从而∠ADE ＝30°. ∴AD ＝2AE .由∠B ＝30°得AB ＝2AD . ∴AB ＝4AE ，BE ＝3AE ． ∴AE ∶EB ＝1∶3. 【问题2】有触礁的危险． 过点P 作PC ⊥AB ，垂足为点C ． ∵∠BPA ＝∠PBC －∠A ＝15°，∴∠BPA ＝∠A ，∴AB ＝PB ＝15×2＝30． 在Rt △PBC 中，PC ＝12PB ＝15海里＜18海里. 故不改变方向，继续向前航行有触礁的危险. 1.2cm. 2．18cm ，120°. 3．4． 4．2cm ． 5．1．6．∵△ABC 是等边三角形，∴∠ACB ＝60°． ∵AD ∥BC ，∴∠DAC ＝∠ACB ＝60°． ∵CD ⊥AD ，∴∠ACD ＝90°－∠DAC ＝30°． ∴AD ＝6AC 21＝cm. 7．连接AE ，在Rt △ABC 中，∠B ＝90°－∠BAC ＝90°－60°＝30°.∵DE 是AB 的垂直平分线，∴AE ＝BE. ∴∠EAD ＝∠B ＝30°.∴∠CAE ＝30°. ∴AE ＝2CE ＝3×2＝6cm.∴BE=6cm. 8．能求出PD 的长. 过点P 作PE ⊥OB.∵∠AOP ＝∠BOP ，PD ⊥OA ，∴PD ＝PE ． ∵PC ∥OA ，∴∠CPO ＝∠POA ＝15°．∴∠ECP ＝∠BOP ＋∠CPO ＝15°＋15°＝30°． ∴PE ＝2421PC 21＝＝⨯．∴PD ＝2． 9．(1)当∠BQP ＝90°时，BQ ＝12BP ．即t ＝12(3－t )，t ＝1(s)；(2)当∠BPQ ＝90°时，BP ＝12BQ ．即3－t ＝12t ，t ＝2(s)．故当t ＝1 s 或t ＝2 s 时，△PBQ 是直角三角形.10．225a . 提示：过点B 作BD ⊥AC ，垂足为D ．则∠BAD ＝30°，BD ＝12AB ＝15m. 11．(1)如图2； (2)∵l 垂直平分AB ，C ADBEM∴∠EDB ＝90°，EA ＝EB ．∴∠EBA ＝∠A ＝30°． ∵∠ACB ＝90°，∴∠ABC ＝60°． ∴∠EBC ＝∠EBD ＝30°．∴DE ＝CE ＝12BE ．又∵∠F ＝90°－∠ABC ＝30°，∴EF ＝2CE ．∴EF ＝2DE ．12．3测试题基础巩固1．D. 2．D. 3．B ．4．C ．5．A ．6．B ． 7．480．8．等腰. 9．1．10．85°．11．∵AB ＝AC ， BD 平分∠ABC ，∴∠C ＝∠ABC ＝2∠DBC ． 在△DBC 中，∠C ＋∠DBC ＋∠BDC ＝180°， ∴2∠DBC ＋∠DBC ＋84°＝180°． ∴∠DBC ＝32°．∴∠ABD ＝32°．∴∠A ＝∠BDC －∠ABD ＝84°－32°＝52°． 12．证明：∵BA=BC ，∴∠A=∠C ．又∵DF ⊥AC ，∴∠A +∠D =90°，∠C+∠CEF =90°． ∴∠D =∠CEF ．又∵∠CEF=∠BED ，∴∠D =∠BED ，∴BD=BE ． 13.∵CD 平分∠ACB ，∠ACB=120°， ∴∠1=∠2=12022ACB ∠︒==60°． ∵AE ∥DC ，∴∠4=∠2=60°，∠E=∠1=60°， ∴∠3=∠4=∠E=60°，∴△ACE 是等边三角形． 14．证明：连接FA ，∵AB ＝AC ，∠A ＝120°，∴∠B ＝∠C ＝30°． ∵EF 垂直平分AC ，∴FA ＝FC . 于是∠FAC ＝∠C ＝30°，∠BAF ＝90°． 在Rt △BAF 中得，∵BF ＝2FA ．∴BF ＝2CF ．15．过点D 作DG ∥AE 交BC 于点G ．则∠DGB ＝∠ACB ． ∵AB ＝AC ，∴∠B ＝∠ACB ． ∴∠B ＝∠DGB ．∴DB ＝DG ． ∵BD ＝CE ，∴DG ＝CE ．∵∠FDG ＝∠FEC ，∠DFG ＝∠EFC ， ∴△FDG ≌△FEC ．∴DF ＝EF ． 能力提高 1．D ．2．C ．提示：两条对角线的交点P 0满足条件．以AB 为边向正方形内作等边三角形P 1AB ，则P 1也满足条件．同理可作出P 2、P 3、P 4．因此，在正方形内共可找到5个满足条件的点P (注：在正方形外还可以找到4个满足条件的点P ) ．3．40°．提示：∠APQ ＋∠AQP ＝2(∠B ＋∠C )＝2(180°－110°)＝140°． 4．①②③④．提示：连接AC ，由SAS 知△PCA ≌△PCB ，于是可知PC 平分等腰三角形CAB 的顶角，所以PC ⊥AB ． 5．解：过点A 作AG ⊥DE 于点G ，则 AG ∥BC ，∠FGA ＝∠FEB ，∠AFG ＝∠BFE ． ∵FA ＝FB ．∴△FAG ≌△FBE ． ∴FG ＝FE ＝3，AG ＝BE ＝4．易知△CDE 是等腰直角三角形，从而可知△AGD 是等腰直角三角形， ∴DG ＝AG ＝4．∴DF ＝DG ＋FG ＝4＋3＝7．6．答：AB 与AF ，CF 之间的等量关系是：AB ＝AF ＋CF ．证明：分别延长AE ，DF 相交于点M ．则△EAB ≌△EMC ．∴AB ＝CM ，∠BAE ＝∠FMA ． ∵∠BAE ＝∠FAM ， ∴∠FAM ＝∠FMA ． ∴AF ＝FM ．∴AB ＝CM ＝CF ＋FM ＝CF ＋AF ．第6期有效学案参考答案第9课时第十二章复习课【检测1】相等；相等；重合；两；两. 【检测2】相等；相等；60°；三；三；60°.【检测3】（1）是轴对称图形，有3条对称轴；（2）是轴对称图形，有5条对称轴；（3）不是轴对称图形；（4）是轴对称图形，有1条对称轴；（5）是轴对称图形，有2条对称轴；（6）不是轴对称图形；（7）是轴对称图形，有1条对称轴；（8）是轴对称图形，有4条对称轴．【问题1】(1)∵∠BAC ＝30°，∠BCD ＝60°， ∴∠ABC ＝∠BCD －∠BAC ＝30°．∴∠ABC ＝∠BAC ．∴AC ＝BC ＝20，20÷10＝2(小时). 故该船到达C 处时的时间是13时30分. (2)∵∠CBD ＝30°，∠BDC ＝90°， ∴CD ＝12BC ＝10(海里)，10÷10＝1(小时). 故14时30分到达海岛B 的正南D 点处. 【问题2】连接OP ．(1)由对称性可知MP ＝MP 1，NP ＝NP 2， ∴P 1P 2＝△PMN 的周长＝5(cm)． (2)△OP 1P 2是等边三角形，理由是：由对称性可知∠MOP ＝∠MOP 1，∠NOP ＝∠NOP 2，∴∠P 1OP 2＝2∠AOB ＝60°．而OP 1＝OP ，OP 2＝OP ，∴OP 1＝OP 2，∴△OP 1P 2是等边三角形1．D. 2．3，－4. 3．B. 4．C. 5. 60°. 6．如图1，点A 关于MN 的对称点A ′与点A 重合．过点B 作BO ⊥MN 于点O ，延长BO 到B ′，使OB ′＝BO ；同理作出点C 关于MN 的对称点C ′．连接A ′B ′，B ′C ′，C ′A ′，则△A ′B ′C ′即为所求. 7．证明：连接AE ，CE ， ∵NE 垂直平分BD ，∴BE ＝DE ． ∵ME 垂直平分AC ，∴AE ＝CE ．l图2D EFBAC∵AB＝CD，∴△EAB≌△ECD(SSS)．∴∠ABE＝∠CDE . 8．（1）20，45，60；（2）∠A=2∠DBC；（3）作AE⊥BC，垂足为点E.∵AB=AC，∴∠CAE=12∠BAC，∠CAE+∠C=90°.又∵BD⊥AC，∴∠DBC+∠C=90°.∴∠DBC=∠CAE=12∠BAC.9．如图2.10.（-1，3）.11．△AFC是等腰三角形．证明：∵ BD＝BE，∠BAD＝∠BCE，∠B＝∠B，∴△BAD≌△BCE．∴∠BAC＝∠BCA．∵∠BAD＝∠BCE，∴∠DAC＝∠ECA．∴FA＝FC．∴△AFC是等腰三角形．第十二章综合测试题(一)一、精挑细选，一锤定音1．Ａ. 2．B．3．C．4.Ａ. 5．D．6．D．7．D.8．D．9．B．提示：需经过6次反射．10．Ｂ.提示：AＯ既可以作底边，也可以作腰.二、慎思妙解，画龙点睛11．2.12．21∶05．13．20.14．答案不唯一，如BD＝CE或∠BAD＝∠CAE等．°．16.5. 17.5cm.18．70°或20°．提示：有锐角三角形和钝角三角形两种情况．三、过关斩将，胜利在望19．如图1.20．如图2.21．（1）图略；（2）A′（2，2），B′（3，1），C′（-1，-2）．22．延长AD，BC相交于点E，则△CDE是等边三角形．在Rt△ABE中，∵∠A＝30°，∴AE＝2BE．设CD＝x，则4＋x＝2(1＋x)．解得x＝2．故CD的长为2．23.同意. 理由：∵点E在BO的垂直平分线上，∴BE OE=.∵△ABC是等边三角形,∴∠ABC=60°.∵OB平分∠ABC，∴∠OBE=∠ABO=30°.∴∠OBE=∠EOB=30°.∴∠OEF=60°.同理∠OFE=60°.∴△OEF是等边三角形．24.（1）①与③；①与④；②与③；②与④.（2）答案不唯一，如选①与③.已知：∠EBO=∠DCO，BE=CD；求证：△ABC是等腰三角形。

八年级下册数学课本人教版答案合集数学是一门需要不断练习和巩固的学科，而对于学生来说，及时查阅课本答案是很有必要的。

因此，我们整理了八年级下册数学课本人教版的答案合集，方便同学们在学习过程中进行参考和对照。

第一单元有理数的加减。

1. 有理数的概念。

2. 有理数的加法。

3. 有理数的减法。

4. 有理数的加减混合运算。

5. 有理数的加减法应用题。

第二单元有理数的乘法。

1. 有理数的乘法。

2. 有理数的乘法性质。

3. 有理数的乘法应用题。

第三单元有理数的除法。

1. 有理数的除法。

2. 有理数的除法性质。

3. 有理数的除法应用题。

第四单元二次根式。

1. 二次根式的概念。

2. 二次根式的加减。

3. 二次根式的乘除。

4. 二次根式的应用题。

第五单元一元一次方程。

1. 一元一次方程的概念。

2. 一元一次方程的解。

3. 一元一次方程的应用题。

第六单元一元一次不等式。

1. 一元一次不等式的概念。

2. 一元一次不等式的解。

3. 一元一次不等式的应用题。

第七单元图形的相似。

1. 图形的相似概念。

2. 图形的判定。

3. 图形的性质。

4. 图形的应用题。

第八单元勾股定理。

1. 勾股定理的概念。

2. 勾股定理的证明。

3. 勾股定理的应用题。

第九单元圆。

1. 圆的概念。

2. 圆的性质。

3. 圆的应用题。

第十单元统计。

1. 统计调查。

2. 统计图。

3. 统计应用题。

以上是八年级下册数学课本人教版的全部内容，每个单元都包含了知识点的讲解和大量的习题。

通过及时查阅答案，同学们可以更好地巩固所学知识，提高解题能力。

在学习数学的过程中，遇到难题是很正常的，但是要注意及时查漏补缺。

有时候我们可能会在一道题上卡壳，但是通过查看答案，我们就能找到解题的关键所在，从而更好地理解知识点。

同时，通过对照答案，我们还能够及时发现自己的错误，从而避免形成错误的习惯。

除了及时查阅答案，同学们还应该注重课后习题的巩固练习。

只有通过不断地练习和总结，才能够真正掌握数学知识，提高解题能力。

红旗中学八年级下册数学第3周B 班培优学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在等腰ABC 中，120BAC ∠=︒，DE 是AC 的垂直平分线，线段1cm DE =，则BD 的长为（ ）A ．6cmB ．8cmC ．3cmD ．4cm2．如图，在△ABC 中，AB=AC ，∠C=65°，AB 的垂直平分线MN 交于AC 于D 点，则∠DBC 的度数是 （ ）A ．15°B ．20°C ．25°D ．30°3．到三角形三个顶点距离相等的点是（ ）A ．三条角平分线的交点B ．三边中线的交点C ．三边上高所在直线的交点D ．三边的垂直平分线的交点4．如图，在ABC 中，90C ∠=︒．用直尺和圆规在边BC 上确定一点P ，使点P 到点A 、点B 的距离相等，则符合要求的作图痕迹是（ ）A ．B ．C ．D ．5．如果三角形三条垂直平分线的交点刚好在三角形的一边上，那么这个三角形是（ ） A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．等腰三角形6．如图，点E 是BC 的中点，AB ⊥BC ，DC ⊥BC ，AE 平分∠BAD ，下列结论：①∠AED ＝90°；②∠ADE ＝∠CDE ；③DE ＝BE ；④AD ＝AB ＋CD ，四个结论中成立的是（ ）A ．①③B ．①②③C ．②③④D ．①②④7．如图，直线AC ∥BD ，AO 、BO 分别是∠BAC 、∠ABD 的平分线，那么∠BAO 与∠ABO 之间的大小关系一定为（ ）A ．互余B ．相等C ．互补D ．不等 8．如图，OP 平分AOB ∠，PD OA ⊥于点D ，点E 是射线OB 上的一个动点，若3PD =，则PE 的最小值（ ）A ．等于3B ．大于3C ．小于3D ．无法确定 二、填空题9．如图，OP 平分∠AOB ，PA ⊥OA ，PB ⊥OB ，垂足分别为A ，B ．下列结论中成立的有____________(填写正确的序号)．①PA=PB ；②AB 垂直平分OP ；③OA=OB ；④PO 平分∠APB ．10．如图，已知AB CD ∥，点P 到AB 、BC 、CD 的距离相等，则P ∠的度数是______. 11．如图，在直角ABC 中，90C ∠=︒，16AB =，AD 平分BAC ∠交BC 于点D ，若4CD =，则ABD △ 的面积为__________．12．如图，在ABC 中，3,4,,AB AC AB AC EF ==⊥垂直平分BC ，点P 为直线EF 上一动点，则ABP △周长的最小值是________．13．点P 在AOB ∠的内部，点M 、N 分别是点P 关于直线OA 、OB 的对称点，线段MN 交OA 、OB 于点E 、F ，若PEF ∆的周长是20cm ，则线段MN 的长是______.14．如图，在Rt △ABC 中，∠ACB ＝90°，AB 的垂直平分线DE 交BC 的延长线于F ，若∠F ＝30°，DE ＝1，则EF 的长是_____．三、解答题15．如图，ABC 是等腰三角形，AB AC =，36A ∠=.（1）尺规作图：作B 的角平分线BD ，交AC 于点D （保留作图痕迹，不写作法）；（2）判断BCD △是否为等腰三角形，并说明理由.16．已知∠AOB，试在∠AOB内确定一点P，如图，使P到OA、OB的距离相等，并且到M、N两点的距离也相等.17．在△ABC中，∠ABC和∠ACB的平分线相交于点O，（1）若∠ABC=60°，∠ACB=40°，求∠BOC的度数；（2）若∠ABC=60°，OB=4，且△ABC的周长为16，求△ABC的面积18．如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F.(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.(2)如图②,若AB≠AC，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC 交AB于E，交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.参考答案1．D【分析】首先连接AD，由在等腰△ABC中，AB=AC，∠BAC=120°，可求得∠B=∠C=30°，又由DE是AC的垂直平分线，即可求得∠DAC与∠BAD的度数，然后由含30°角的直角三角形的性质，求得答案．【详解】解：连接AD，∵在等腰△ABC中，AB=AC，∠BAC=120°，∴∠B=∠C=30°，∵DE是AC的垂直平分线，∴AD=CD，∴∠DAC=∠C=30°，∠AED=90°，∴AD = CD =2DE=2×1=2（cm），∵∠BAD=∠BAC-∠CAD=90°，∴BD=2AD=4（cm）．故选：D．【点睛】本题考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段两个端点的距离相等．2．A【分析】根据等腰三角形的性质求出∠ABC及∠A的度数，再根据线段垂直平分线性质得到AD＝BD，从而得到∠ABD＝∠A，然后求∠DBC的度数即可．【详解】∵AB=AC，∠C=65°，∴∠ABC=∠C=65°，∠A=180°－2∠C=50°，∵MN垂直平分AB，∴DA=DB，∴∠ABD =∠A =50°，∴∠DBC=∠ABC－∠ABD=65°－50°=15°．故选：A．【点睛】本题主要考查了等腰三角形的性质及垂直平分线的性质，熟记性质是解题的关键．3．D【分析】根据垂直平分线的性质定理的逆定理即可做出选择．【详解】∵到一条线段两端点的距离相等的点在这条线段的垂直平分线上，∴到三角形三个顶点距离相等的点是三边的垂直平分线的交点，故选：D．【点睛】本题考查了线段垂直平分线，理解线段垂直平分线的性质的逆定理是解答的关键．4．C【分析】点P到点A、点B的距离相等知点P在线段AB的垂直平分线上，据此可得答案．【详解】解：∵点P到点A、点B的距离相等，∴点P在线段AB的垂直平分线上，故选：C．【点睛】本题主要考查作图−复杂作图，解题的关键是掌握线段中垂线的性质与尺规作图．5．A【分析】根据三种三角形线段垂直平分线上的交点的位置解答即可．【详解】解：∵锐角三角形三边垂直平分线的交点在三角形的内部，钝角三角形三边垂直平分线的交点在三角形的外部，直角三角形三边垂直平分线的交点在三角形的斜边上，∴该三角形是直角三角形．故选：A．【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，熟记三种三角形线段垂直平分线的交点的位置是解题的关键．6．D【分析】过E作EF⊥AD于F，易证得Rt△AEF≌Rt△AEB，得到BE＝EF，AB＝AF，∠AEF＝∠AEB；而点E是BC的中点，得到EC＝EF＝BE，则可证得Rt△EFD≌Rt△ECD，得到DC＝DF，∠FDE＝∠CDE，也可得到AD＝AF＋FD＝AB＋DC，∠AED＝∠AEF＋∠FED＝1∠BEC＝90°，即可判断出正确的结论．2【详解】解：过E作EF⊥AD于F，如图，∵AB⊥BC，AE平分∠BAD，∴Rt△AEF≌Rt△AEB．∴BE＝EF，AB＝AF，∠AEF＝∠AEB．而点E是BC的中点，∴EC＝EF＝BE．所以③错误；∴Rt△EFD≌Rt△ECD．∴DC＝DF，∠FDE＝∠CDE．所以②正确；∴AD＝AF＋FD＝AB＋DC．所以④正确；∴∠AED＝∠AEF＋∠FED＝12∠BEC＝90°．所以①正确．故选：D．【点睛】本题考查了角平分线的性质：角平分线上的点到角的两边的距离相等．也考查了三角形全等的判定与性质．7．A【解析】试题解析：∵AC∥BD，∴∠CAB+∠ABD=180°，∵AO、BO分别是∠BAC、∠ABD的平分线，∴∠CAB=2∠OAB，∠ABD=2∠ABO，∴∠OAB+∠ABO=90°，∴∠AOB=90°，∴OA⊥OB，故选A.考点：1.平行线的性质；2.余角和补角．8．A【分析】过P点作PH⊥OB于H，利用角平分线的性质得到OH＝OD＝3，然后根据垂线段最短可得到PE的最小值．【详解】解：过P点作PH⊥OB于H，如图，∵OP平分∠AOB，PD⊥OA，PH⊥OB于H，∴OH＝OD＝3，∵点E 是射线OB 上的一个动点，∴点E 与H 点重合时，PE 有最小值，最小值为3．故选：A ．【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了垂线段最短．掌握角平分线的性质是解题关键．9．①③④【分析】根据角平分线的意义及其性质可以对各项的正确性质作出判断．【详解】解：由角平分线的定义可知PA=PB ，∴OP 垂直平分AB ，①正确，②错误；又在△OPA 和△OPB 中，∠AOP=∠BOP ，∠OAP=∠OBP ，OP=OP ，∴△AOP ≌△BOP ，∴OA=OB ，PO 平分∠APB ，③、④正确；故答案为①、③、④．【点睛】本题考查三角形的应用，熟练掌握角平分线、中垂线的意义和性质以及全等三角形的判定和性质是解题关键．10．90°【分析】根据点P 到AB 、BC 、CD 的距离都相等，得BP 、CP 分别是ABC ∠和BCD ∠的平分线，再由AB CD ∥，算出∠BPC 的度数即可.【详解】∵点P 到AB 、BC 、CD 的距离都相等，BP ∴、CP 分别是ABC ∠和BCD ∠的平分线，12CBP ABC ∴∠=∠，12BCP BCD ∠=∠， ()12CBP BCP ABC BCD ∴∠+∠=∠+∠. AB CD ∥，180ABC BCD ∴∠+∠=︒，1180902CBP BCP ∴∠+∠=⨯︒=︒， ()1801809090P CBP BCP ∴∠=︒-∠+∠=︒-︒=︒，故答案为：90°. 【点睛】本题是对角平分线逆定理的考查，熟练掌握平行线的性质及角平分线的逆定理是解决本题的关键.11．32【解析】试题解析：如图，过D 点作DE ⊥AB 于点E ，90C ∠=，AD 平分∠BAC 交BC 于点D ， ∴CD =DE (角的平分线上的点到角的两边的距离相等)，∵CD =4，∴DE =4.1116432.22ABD S AB DE =⋅⋅=⨯⨯= 故答案为32.点睛：角平分线上的点到角两边的距离相等.12．7【分析】根据题意知点B 关于直线EF 的对称点为点C ，故当点P 与点D 重合时，AP+BP 的最小值，求出AC 长度即可得到结论．【详解】解：∵EF 垂直平分BC ，∴B ，C 关于直线EF 对称．设AC 交EF 于点D ，∴当P 和D 重合时，AP BP +的值最小，最小值等于AC 的长，∴ABP △周长的最小值是437+=．【点睛】本题考查了勾股定理，轴对称-最短路线问题的应用，解题的关键是找出P 的位置． 13．20cm【分析】根据“点M 、N 分别是点P 关于直线OA 、OB 的对称点”可知ME PE =，PF FN =，再根据PEF ∆的周长即可求出MN 的长度.【详解】∵点M 、N 分别是点P 关于直线OA 、OB 的对称点，∴ME PE =，PF FN =，∵PEF ∆的周长是20cm ，即20cm PE EF PF ++=.∴20cm MN ME EF FN =++=.【点睛】本题考查的是对称的性质，中垂线的性质，能够判断出ME PE =，PF FN =是解题的关键.14．2【分析】连接BE ，根据垂直平分线的性质、直角三角形的性质，说明∠CBE ＝∠F ，进一步说明BE ＝EF ，，然后再根据直角三角形中，30°所对的直角边等于斜边的一半即可.【详解】解：如图：连接BE∵AB的垂直平分线DE交BC的延长线于F，∴AE＝BE，∠A+∠AED＝90°，∵在Rt△ABC中，∠ACB＝90°，∴∠F+∠CEF＝90°，∵∠AED＝∠FEC，∴∠A＝∠F＝30°，∴∠ABE＝∠A＝30°，∠ABC＝90°﹣∠A＝60°，∴∠CBE＝∠ABC﹣∠ABE＝30°，∴∠CBE＝∠F，∴BE＝EF，在Rt△BED中，BE＝2DE＝2×1＝2，∴EF＝2．故答案为：2．【点睛】本题考查了垂直平分线的性质、直角三角形的性质，其中灵活利用垂直平分线的性质和直角三角形30°角所对的边等于斜边的一半是解答本题的关键.△为等腰三角形15．（1）作图见解析（2）BCD【分析】（1）作角平分线，以B点为圆心，任意长为半径，画圆弧；交直线AB于1点，直线BC 于2点，再以2点为圆心，任意长为半径，画圆弧，再以1点为圆心，任意长为半径，画圆弧，相交于3点，连接3点和O点，直线3O即是已知角AOB的对称中心线.△的三个角，看是否有两个角相等，进而判断是否为等腰三角形. （2）分别求出BCD【详解】（1）具体如下：（2）在等腰ABC 中，36A ∠=，BD 为∠ABC 的平分线，故72ABC C ∠=∠=︒，36DBC ∠=︒，那么在DBC △中，72BDC ∠=︒∵72BDC C ∠=∠=︒∴BCD △是否为等腰三角形.【点睛】本题考查角平分线的作法，以及判定等腰三角形的方法.熟悉了解角平分线的定义以及等腰三角形的判定方法是解题的关键所在.16．见解析.【分析】作出线段MN 的垂直平分线和∠AOB 的平分线，其交点P 即为所求．【详解】解：如图所示：线段MN 的垂直平分线与∠AOB 的平分线的交点P 即为所求：【点睛】本题考查的是角平分线的性质、线段垂直平分线的性质的运用，熟练掌握尺规作图的方法是解答此题的关键．17．（1）∠COB=130°；（2）16.【分析】（1）利用角平分线的定义及三角形内角和即可得出答案；（2）过O 作OD ⊥BC 于D 点，连接AO, 通过O 为角平分线的交点，得出点O 到三边的距离相等，利用特殊角的三角函数值求出距离，然后利用ABC AOC AOB BOC SS S S =++和周长即可得出答案.【详解】（1）解：∵BO 、CO 分别平分∠ABC 和∠ACB∵∠ABC=60°，∠ACB=40°∴∠OBC=12ABC ∠=30°,12OCB ACB ∠=∠=20° 180BOC OBC OCB ∠+∠+∠=︒180()180(3020)130BOC OBC OCB ∴∠=︒-∠+∠=︒-︒+︒=︒（2）过O 作OD ⊥BC 于D 点，连接AO∵O 为角平分线的交点∴点O 到三边的距离相等又∵∠ABC=60°，OB=4∴∠OBD=30°，OD=2即点O 到三边的距离都等于2∴ABC AOC AOB BOC S S S S =++111222222AC AB BC =⨯+⨯+⨯ AC AB BC =++又∵△ABC 的周长为16∴ 16ABC S AB AB BC ∆=++=【点睛】本题主要考查角平分线的性质，掌握角平分线的性质是解题的关键.18．（1）△AEF、△OEB、△OFC、△OBC、△ABC共5个，EF=BE+FC；（2）有，△EOB、△FOC，存在；（3）有，EF=BE-FC．【分析】（1）由AB=AC，可得∠ABC=∠ACB；又已知OB、OC分别平分∠ABC、∠ACB；故∠EBO=∠OBC=∠FCO=∠OCB；根据EF∥BC，可得：∠OEB=∠OBC=∠EBO，∠FOC=∠FCO=∠BCO；由此可得出的等腰三角形有：△AEF、△OEB、△OFC、△OBC、△ABC；已知了△EOB和△FOC是等腰三角形，则EO=BE，OF=FC，则EF=BE+FC．（2）由（1）的证明过程可知：在证△OEB、△OFC是等腰三角形的过程中，与AB=AC的条件没有关系，故这两个等腰三角形还成立．所以（1）中得出的EF=BE+FC的结论仍成立．（3）思路与（2）相同，只不过结果变成了EF=BE-FC．【详解】解：（1）图中是等腰三角形的有：△AEF、△OEB、△OFC、△OBC、△ABC；EF、BE、FC的关系是EF=BE+FC．理由如下：∵AB=AC，∴∠ACB=∠ABC，△ABC是等腰三角形；∵BO、CO分别平分∠ABC和∠ACB，∴∠ABO=∠OBC=12∠ABC，∠OCB=∠ACO=12∠ACB，∵EF∥BC，∴∠EOB=∠OBC，∠FOC=∠OCB，∴∠ABO=∠OBC=∠EOB=∠OCB=∠FOC=∠FCO，∴△EOB、△OBC、△FOC都是等腰三角形，∵EF∥BC，∴∠AEF=∠ABC，∠AFE=∠ACB，∴∠AEF=∠AFE，∴△AEF是等腰三角形，∵OB、OC平分∠ABC、∠ACB，∴∠ABO=∠OBC，∠ACO=∠OCB；∵EF∥BC，∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO；即EO=EB，FO=FC；∴EF=EO+OF=BE+CF；（2）当AB≠AC时，△EOB、△FOC仍为等腰三角形，（1）的结论仍然成立．∵OB、OC平分∠ABC、∠ACB，∴∠ABO=∠OBC，∠ACO=∠OCB；∵EF∥BC，∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO；即EO=EB，FO=FC；∴EF=EO+OF=BE+CF；（3）△EOB和△FOC仍是等腰三角形，EF=BE-FC．理由如下：同（1）可证得△EOB是等腰三角形；∵EO∥BC，∴∠FOC=∠OCG；∵OC平分∠ACG，∴∠ACO=∠FOC=∠OCG，∴FO=FC，故△FOC是等腰三角形；∴EF=EO-FO=BE-FC．【点睛】本题主要考查了等腰三角形的判定和性质，平行线、角平分线的性质等知识．进行线段的等量代换是正确解答本题的关键．。

2020-2021学年人教版八年级下学期数学练习题及答案
4．（3分）已知一个平行四边形相邻的两边长不相等且都为整数，若它的两条对角线长分别为8cm和12cm，则它相邻两边长的长度可以分别是（）
A．4cm，6cm B．5cm，6cm C．6cm，8cm D．8cm，10cm 【分析】首先根据题意画出图形，然后由平行四边形的性质得出OA＝4cm，OB＝6cm，利用三角形的三边关系，即可求得答案．
【解答】解：如图所示，
∵平行四边形的两条对角线长分别为8cm和12cm，
∴OA＝OC＝4cm，OB＝OD＝6cm，
∴2＜AB＜10，
同理：2＜AD＜10，
∵AB+AD＞12，
∴相邻两边长的长度可以分别是6cm，8cm；
故选：C．
【点评】此题考查了平行四边形的性质以及三角形三边关系．熟练掌握平行四边形的性质，运用三角形的三边关系是解决问题的关键．
第1页共1页。