(完整word版)职高数学基础模块下册复习题

中职数学基础模块（下）期末试卷一、选择题（10⨯4＝40分）1、在等差数列{}n a 中，d a a 则公差,12,462==等于 （ ） A 、1 B 、2 C 、2± D 、82、若,22,2,4==-=⋅b a b a 则向量b a,的夹角θ 是 （ ） A 、 0 B 、 90 C 、 180 D 、 270 3、经过点)3,4(-A 与)9,1(-B 的直线方程是（ ） A.0112=--y x B.052=--y x C.052=-+y x D.0112=-+y x 4、直线012=+-y x 与直线6121-=x y 的位置关系是（ ） A.垂直 B.重合 C.平行 D.相交而不垂直 5、等比数列1,2,4,8.....的前10项和是（ ）A .63B .1008C .1023D .10246、直线0102=-+y x 与圆422=+y x 的位置关系 （ ）A 、相离B 、相切C 、过圆心D 、相交但不过圆心 7、已知A 、B 两点坐标为A （3，-1），B （2,1） ，且B 是线段AC 的中点则 点C 的坐标为 （ ）A 、（2,6）B 、（1,3）C 、（2.5，0）D 、（-1,2） 8、经过点A(-1,4) ,且斜率是1/2 的直线方程为 （ ）A 、092=+-y xB 、092=--y xC 、0102=++y xD 、0102=-+y x9、直线)1(32+-=-x y 的倾斜角和所过的定点分别是 （ ） A ．)2,1(,60-- B. )2,1(,120- C.)2,1(,150- D.)2,1(,120- 10、过点)3,2(A ，且与y 轴平行的直线方程为（ ）A.2=xB.2=yC.3=xD.3=y 二、填空题（4⨯4＝16分）1、直线0623=--y x 的斜率为 ，在y 轴上的截距为2、方程062622=-+-+y x y x 化为圆的标准方程为3、已知==-=a b a 则),2,21(),3,2( ，=⋅b a 。

中职数学基础模块（下）期末试卷一、选择题（10⨯4＝40分）1、在等差数列{}n a 中，d a a 则公差,12,462==等于 （ ） A 、1 B 、2 C 、2± D 、82、若,22,2,4==-=⋅b a b a则向量b a ,的夹角θ 是 （ ） A 、 0 B 、 90 C 、 180 D 、 270 3、经过点)3,4(-A 与)9,1(-B 的直线方程是（ ） A.0112=--y x B.052=--y x C.052=-+y x D.0112=-+y x 4、直线012=+-y x 与直线6121-=x y 的位置关系是（ ） A.垂直 B.重合 C.平行 D.相交而不垂直 5、等比数列1,2,4,8.....的前10项和是（ ） A .63 B .1008 C .1023 D .10246、直线0102=-+y x 与圆422=+y x 的位置关系 （ ）A 、相离B 、相切C 、过圆心D 、相交但不过圆心 7、已知A 、B 两点坐标为A （3，-1），B （2,1） ，且B 是线段AC 的中点则 点C 的坐标为 （ ）A 、（2,6）B 、（1,3）C 、（2.5，0）D 、（-1,2） 8、经过点A(-1,4) ,且斜率是1/2 的直线方程为 （ ）A 、092=+-y xB 、092=--y xC 、0102=++y xD 、0102=-+y x9、直线)1(32+-=-x y 的倾斜角和所过的定点分别是 （ ） A ．)2,1(,60-- B. )2,1(,120- C.)2,1(,150- D.)2,1(,120- 10、过点)3,2(A ，且与y 轴平行的直线方程为（ ）A.2=xB.2=yC.3=xD.3=y 二、填空题（4⨯4＝16分）1、直线0623=--y x 的斜率为 ，在y 轴上的截距为2、方程062622=-+-+y x y x 化为圆的标准方程为3、已知==-=a b a 则),2,21(),3,2( ，=⋅b a 。

中职数学(基础模块)下册第六章数列单元考试卷(含答案)中职数学（基础模块）下册第六章数列单元考试卷含答案一、选择题1.数列{an}的通项公式an=（-1）^3*(n+1)*9，因此a2=9，选B。

2.选A，因为2，6，10，14，18是公差为4的等差数列。

3.已知a1=-3，d=2，所以a5=-3+4*2=5，选B。

4.已知a5=9，d=2，所以a(n)=a5+(n-5)*d=9+(n-5)*2=2n-1，选D。

5.已知a1=-3，d=3，所以S8=(a1+a8)*4/2=（-3+a1+7d）*4/2=（-3+21）*4/2=36，选A。

6.已知a4+a7=16，又a4=a1+3d，a7=a1+6d，所以a1+9d=16，又S10=(a1+a10)*10/2=（a1+a1+9d）*10/2=5(a1+9d)=5*16=80，选B。

7.已知a1=2，q=-3，所以a3=a1*q^2=-18，选A。

8.已知a1=-8，a4=1，所以q=(a4/a1)^(1/3)=2，选A。

9.已知a1=2，q=-3，所以S5=(a1*(1-q^5))/(1-q)=（2*(1-(-3)^5))/(1-(-3))=122，选B。

10.已知2，a，8成等差数列，所以a=5，选C。

11.已知，a，8成等比数列，所以a=-2，选D。

12.“a+c=2b”是“a，b，c组成等差数列”的必要不充分条件，选B。

二、填空题13.公差d=5，an=-1+(n-1)*5=5n-6.14.通项公式an=n+1.15.设a2=x，所以a6=x^3，代入等比数列的通项公式an=a1*q^(n-1)，得到a1*x^5=16，即a1=16/x^5.16.公差d=3.三、解答题17.（1）已知a1=-5，d=6，所以an=-5+(n-1)*6=6n-11.2）S5=(a1+a5)*5/2=(-5+19)*5/2=35.18.设三个数为a-d，a，a+d，根据题意得到以下两个方程：a-d+a+a+d=12，解得a=4；a-d)*a*(a+d)=28，代入a=4，解得d=2；因此三个数为2，4，6.19.题目：已知成等比数列的三个数和为13，积为27，求这三个数。

中职学业水平考试数学（基础模块）下册 第5章指数函数与对数函数单元测试卷班级_______姓名__________座号_____成绩________ 一、选择题(每小题3分，共45分) 1.下列哪个函数是对数函数（ ）A. 3xy = B.2y x -=C. 10x y =D. log a y x =(a>0且a ≠1) 2.指数函数图像经过定点（ ）A.（0，0）B.（0，1）C.（1，0）D.（1，1） 3.对数log a a =（ ）A.0B.1C.aD.2a4.将416x =化成对数式可表示为（）A. x =16log 4B. 4log 16x =C.16log 4x =D.4log 164=5. 下列各函数中，为指数函数的是（ ） A.32y x= B. 3log yx =C. 2x y =D. y x =6.下列运算中，正确的是（ ） A.3443222⋅= B. 3443222÷=C. 3443(2)2= D. 3344220-⋅=7.已知a>0且a ≠0，下列式子中，错误的是（ ）A.32a = B.2log 2aa =C.351a-=D. 1x yy xaa --=8.下列各指数函数中，在区间（－∞，+∞）内为减函数的是（ ）A. 3xy = B. ()4x yπ= C. 10x y = D. 5x y = 9．若函数log a y x =的图像经过点（2，－1），则底a ＝（ ） A.2 B.-2 C. 12D. -1210.下列各函数中，在区间（0，+∞）内为增函数的是（ ）A. 2y x -= B.2log y x =C. 2x y -=D.23xy ⎛⎫= ⎪⎝⎭11. 下列各角中，与330°角终边相同的角是( ) A. 510° B. 150° C. －150° D. －30° 12.已知函数1()1x f x x +=-，则(2)f -=( )A.13- B. 13C.1D.313. 下列各式中正确的是（ ）A 、7ln 2ln )72ln(+=+B 、7ln 2ln )72ln(•=•C 、7ln 2ln )72ln(+=•D 、7ln 2ln 72ln =14. 若4log 3-=x ，则=x （ ） A 、34- B 、－12 C 、81 D 、81115.已知x y a log =（0>a 且1≠a ）的图像经过定点P ，则点P 的坐标可能是（ ）A 、（0，1）B 、（1，0）C 、（1，1）D 、（0，0） 二、填空题(每小题3分，共15分) 16. -34=________ (-3)4=_____ 17.212>x ,求x 的取值范围是__________18.把根式写成分数指数幂的形式：＝___________19.指数式131273-=写成对数式为___________________ 20.函数lg(1)yx =-的定义域为__________________三、解答题(每题8分，共40分)21. 求值：（1） lg4+lg25 （2）lg500-lg5 22. 已知一段公路的弯道半径是30m, 转过的圆心角是120度，求该弯道的长度。

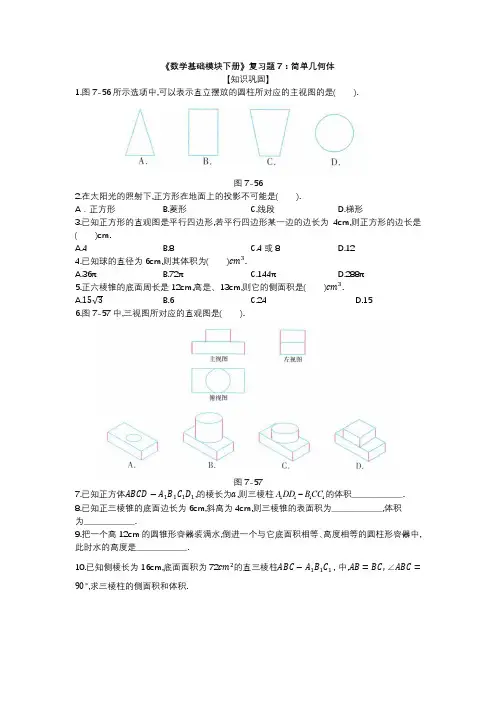
《数学基础模块下册》复习题7：简单几何体【知识巩固】1.图7-56所示选项中,可以表示直立摆放的圆柱所对应的主视图的是( ).图7-562.在太阳光的照射下,正方形在地面上的投影不可能是( ).A ．正方形 B.菱形 C.线段 D.梯形3.已知正方形的直观图是平行四边形,若平行四边形某一边的边长为4cm,则正方形的边长是( )cm.A.4B.8C.4或8D.124.已知球的直径为6cm,则其体积为( )cm 3.A.36πB.72πC.144πD.288π5.正六棱锥的底面周长是12cm,高是、13cm,则它的侧面积是( )cm 3.A.15√3B.6C.24D.156.图7-57中,三视图所对应的直观图是( ).图7-577.已知正方体ABCD −A 1B 1C 1D 1,的棱长为a ,则三棱柱1111A DD B CC 的体积______________.8.已知正三棱锥的底面边长为6cm,斜高为4cm,则三棱锥的表面积为______________,体积 为______________.9.把一个高12cm 的圆锥形容器装满水,倒进一个与它底面积相等、高度相等的圆柱形容器中,此时水的高度是______________.10.已知侧棱长为16cm,底面面积为72cm 2的直三棱柱ABC −A 1B 1C 1，中,AB =BC,∠ABC =90°,求三棱柱的侧面积和体积.11.已知圆柱的轴截面是正方形,面积为S,求圆柱的侧面积和体积.12.已知圆柱的侧面展开图是一个长为12cm、宽为8cm的矩形,求圆柱的体积.【能力提升】1.圆柱形水槽的底面半径是8cm,一个铁块完全浸没在水中,当铁块取出时,水面下降了5cm,求铁块的体积.2.过球半径的中点作一个垂直于半径的截面,该截面的面积与球的大圆面积之比是多少?3.某粮库现有一个用于储藏粮食的圆柱形仓库,仓库的底面直径为12m,高为4m,为存放更多粮食,拟建一个更大的圆柱形仓库.现有两种方案:一是新建仓库的底面半径比原来大4m,高不变;二是高度增加4m,底面半径不变.(1)分别计算这两种方案所建仓库的体积;(2）仅就仓库墙面(即仓库的侧面)而言,若每平方米成本为α元,分别计算这两种方案的墙面建造成本;(3）从建造成本和容量大小角度比较,哪一个方案效益更好?。

全国中等职业教育数学基础模块下册数学练习题 一、填空题 1． 如果直线l 经过点(2,0),(5,3)--，那么直线l 的倾斜角是_______________2． 已知(3,4),(5,2)A B --，则AB =_____________3．2246120x y x y +---=的半径=_______________4.已知点A (1,2)、B (3,1),则线段AB 的垂直平分线的方程是_______________5．方程220x y -=表示的图像是_______________6．(1,2)C -为圆心，且与直线3490x y -+=相切的圆的方程为_______________ {7．若直线0x y a ++=（其中a 是常数）经过圆222460x y x y +-+-=的圆心，则a =________8．设直线过点(0,)a ,其斜率为1，且与圆222x y +=相切，则a 的值为_______________9. 若直线x －y =2被圆(x －a )2+y 2=4所截得的弦长为22,则实数a 的值为_______________10. 在正方体ABCD A B C D ''''-中，,M N 分别是AB ，DD '的中点，则异面直线B M '与CN 所成的角为_______________11. 三条直线10,280x y x y ++=-+=x 和350ax y +-=只有两个不同的交点，则a =____________12. 已知直线3420x y ++=与圆2240x y y ++=交于,A B 两点，则线段AB 的垂直平分线方程是_______________13. 一束光线从点(1,1)A -出发，经x 轴反射到圆22:(2)(3)1C x y -+-=上的最短路径是 ．14. 已知圆1C ：2(1)x ++2(1)y -=1，圆2C 与圆1C 关于直线10x y --=对称，则圆2C 的方程为 ．%15. 直线3410x y --=与圆22(1)(2)9x y -++=的位置关系是_______________16. 若方程220x y x y k +-++=表示圆，则k 的取值范围是_______________17.设圆2220x y ax ++-=的圆心是(1,0)，则圆的半径等于________18．过原点且倾斜角为60︒的直线被圆 2240x y y +-=所截得的弦长为19．过点(2,3)且平行于直线250x y +-=的直线方程为_______________二、计算题1．求以直线34120x y -+=在坐标轴间所截的线段为直径的圆的方程.2．已知(3,5),(1,2),(0,0)A B O ---,求（1）直线AB 的方程；（2）求ABO ∆的面积. ~3．过原点O 作圆C ：22(1)(2)1x y -+-=的切线，求原点与切线切点之间的距离.4．如图，四棱锥P ABCD -的底面是正方形，PD ABCD ⊥底面，点E 在棱PB 上。

加满油！ 跑得更远！数学基础模块下册复习题第一章 数列1.数列112，223，334，445，…的一个通项公式是 （ ） （A ）21n n a n =+ （B ）221n n n a n +=+ （C ）211n n n a n ++=+ （D ）221n n n a n +=+ 2.数列通项是n n a n ++=11，当其前n 项和为9时，项数n 是 （ ）（A ）9 （B ）99 （C ）10 （D ）1003.在数列2，5，9，14，20，x ，…中，x 的值应当是 （ ）（A ）24 （B ）25 （C ）26 （D ）274.数列{a n }通项公式a n =log n+1(n+2)，则它的前30项之积是 （ ）（A ）51 （B ）5 （C ）6 （D ）231log 3log 3215+ 5.已知数列{a n }满足a 1=1,且121(2)n n a a n -=+≥，则数列的第五项a 5= 6.已知数列{a n }前n 项之和S n =1n n +，则a n= 7.一数列的通项公式为a n = 30 + n －n 2.①问－60是否为这个数列中的一项.②当n 分别为何值时，a n = 0, a n >0, a n <08.等差数列8，5，2…的第20项为9.数列{a n }的通项公式为25n a n =+，则此数列的公差为10.在等差数列｛a n ｝中，已知a 1=2,a 2+a 3=13，则a 4+a 5+a 6等于 （ ）（A ）40 （B ）42 （C ）43 （D ）4511.若等差数列共有10项，其奇数项之和为15，偶数项之和为30，则d= ( )（A ）5 （B ）4 （C ）3 （D ）212.方程lgx+lgx 3+lgx 5+….+lgx 2n-1=2n 2的解是13.等差数列{ a n }，a 1=1, a 1+a 2+…+a 10 =100，则此数列的通项a n = ．14.在等差数列{ a n }中，（1）已知a 3+a 11=20，则a 7=（2）已知3a +4a +5a +6a +7a ＝450, 求2a +8a 及前9项和9S ．15.等差数列{a n }的前n 项和记为S n .已知a 10=30，a 20=50. （1）求通项a n ； （2）若S n =242,求n ．16.在等差数列{}n a 中,已知.,63,6,994n S a a n 求=-==17.在等比数列{a n }中a 2＝2， a 5＝54，则q ＝ ；18.在等比数列{a n }中a 5＝1， a n ＝256，q ＝2，则n ＝ .19.公差不为0的等差数列第二、三、六项成等比数列，则公比等于20.等比数列的前三项和等于首项的3倍，则该等比数列的公比为 （ ）（A ）-2 （B ）1 （C ）-2或1 （D ）2或-121.11的等比中项是 ．22.lgx+lgx 2+lgx 3+…+lgx 10=110，则lgx+lg 2x+…+lg 10x=23.在2与32之间插入三个实数，使这5个数成等比数列，则插入的3个数为24.在数列{a n }中，a 3、a 10是方程 x 2- 3x -5 = 0的两个根，则 a 6.a 7= ．25.数列{a n }中，若a n+1=2a n(1)n ≥，且a 1=2，则S 5= 第二章 向量1.______OA OB CO BO +++=，______CE AC DE AD +--=。

高教版职高数学基础模块下期末测试题一、选择题（36分）1、数列-1,1，-1,1，…的一个通项公式是（ ）．（A ）n n a )1(-= （B ）1)1(+-=n n a （C ）n n a )1(--= （D ）2sin πn a n =2．一个等比数列的第3项是45，第4项是-135，它的公比是（ ）．（A ）3 （B ）5 （C ） -3 （D ）-53 ．如果圆的方程为034222=++-+y x y x ,则该圆的圆心坐标和半径分别是 （ ）A ．(1,-2),2B ．(1,-2),2 C ．(-1,2),2 D ．(-1,2),24.10y -+=的倾斜角为 A ．0150 B ．0120 C ．060 D ．0305．以A （１，３）和Ｂ（－５，１）为端点的线段AB 的中垂线方程是A ．380x y -+=B ．340x y ++=C ．260x y --=D ．380x y ++=6、已知线段AB 的端点A （3，4）及中点0（0，3），则点B 的坐标为（ ）A 、（27,23）B 、（-3，2）C 、（3，2）D 、（3，10）7、已知a =（3，1），b=（32-，5），则a 与b 的夹角等于（ ）A 、30oB 、60oC 、120oD 、60o 或120o8、已知a （3，-2）b （-3，-4），则a?b=（ ）A 、0B 、1C 、-1D 、29.如果空间两条直线互相垂直，那么它们（ ）A.一定相交B.异面直线C.共面直线D.一定不平行10.下面图形中不一定是平面图形的是（ ）A.三角形B.平行四边形C.四条线段首尾连接成的四边形D.梯形11、如果平面外一条直线上有两点到这个平面的距离相等，那么这条直线与平面的位置关系是（ ）。

A 、平行B 、相交C 、垂直D 、平行或相交12、如图，是一个正方体，则? B1AC= （ ）A 、30oB 、45oC 、60oD 、75o二、填空题（16分）13.数列{}n a 是等比数列， ,3,11==q a 则=5a _________ .14. 已知三个数13,,13-+A 成等差数列，则A =_________15、 若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于_________16.已知：a = ( 3, 2) , b = ( - 4 , x ) ,若a ⊥b , 则x=_________三、解答题（48分）17．等差数列{}n a 中，64=a ，484=S ，求1a ．（6分）18、求以直线x+y-2=0与直线x-2y+1=0的交点为圆心，且半径为4的圆的方程（6分）19、如图、直线AB 、BC 、CA 两两相交，交点分别为A 、B 、C ，判断这三条直线是否共面，并说明理由. （7分）20．已知三点A （1，－1），B （3，3），C （4，5）。

中职数学基础模块（下）期末试卷一、选择题（10⨯4＝40分)1、在等差数列{}n a 中，d a a 则公差,12,462==等于 （ ） A 、1 B 、2 C 、2± D 、82、若,22,2,4==-=⋅b a b a则向量b a ,的夹角θ 是 （ ）A 、 0B 、 90C 、 180D 、 270 3、经过点)3,4(-A 与)9,1(-B 的直线方程是（ ） A.0112=--y x B 。

052=--y x C 。

052=-+y x D 。

0112=-+y x4、直线012=+-y x 与直线6121-=x y 的位置关系是（ )A 。

垂直 B.重合 C.平行 D 。

相交而不垂直 5、等比数列1，2,4,8。

.。

..的前10项和是（ ） A 。

63B 。

1008C 。

1023 D.1024 6、直线0102=-+y x 与圆422=+y x 的位置关系 （ ) A 、相离 B 、相切 C 、过圆心D 、相交但不过圆心7、已知A 、B 两点坐标为A(3，—1），B(2,1） ,且B 是线段AC 的中点则点C 的坐标为 ( ) A 、（2，6) B 、（1,3） C 、（2.5,0） D 、（-1，2)8、经过点A(—1,4) ，且斜率是1/2 的直线方程为 （ ）A 、092=+-y xB 、092=--y xC 、0102=++y xD 、0102=-+y x9、直线)1(32+-=-x y 的倾斜角和所过的定点分别是 （ ） A ．)2,1(,60-- B 。

)2,1(,120- C.)2,1(,150- D 。

)2,1(,120-10、过点)3,2(A ，且与y 轴平行的直线方程为（ ） A.2=x B.2=y C.3=x D 。

3=y二、填空题（4⨯4＝16分）1、直线0623=--y x 的斜率为 ，在y 轴上的截距为2、方程062622=-+-+y x y x 化为圆的标准方程为3、已知==-=a b a 则),2,21(),3,2( ，=⋅b a。