一个相似三角形基本图形在解题中的应用

专题12 相似三角形的性质及应用知识网络重难突破知识点一相似三角形的性质①对应角相等，对应边成比例．②周长之比等于相似比；面积之比等于相似比的平方．③对应高线长之比、对应角平分线长之比、对应中线长之比都等于相似比．【典例1】（2020•衢州模拟）如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR分别交AC，CD于点P，Q．平行四边形ABCD的面积为6，则图中阴影部分的面积为．【点拨】由四边形ABCD和四边形ACED都是平行四边形，易证得△BCP∽△BER，△ABP∽△CQP∽△DQR，又由点R为DE的中点，可求得各相似三角形的相似比，继而求得答案．【解析】解：∵四边形ABCD和四边形ACED都是平行四边形，∴AD＝BC＝CE，AB∥CD，AC∥DE，∴平行四边形ACED的面积＝平行四边形ABCD的面积＝6，△BCP∽△BER，△ABP∽△CQP∽△DQR，∴△ABC的面积＝△CDE的面积＝3，CP：ER＝BC：BE＝1：2，∵点R为DE的中点，∴CP：DR＝1：2，∴CP：AC＝CP：DE＝1：4，∵S△ABC＝3，∴S△ABP＝S△ABC＝，∵CP：AP＝1：3，∴S△PCQ＝S△ABP＝，∵CP：DR＝1：2，∴S△DQR＝4S△PCQ＝1，∴S阴影＝S△PCQ+S△DQR＝．故答案为：．【点睛】此题考查了平行四边形的性质以及相似三角形的判定与性质．熟记相似三角形的面积比等于相似比的平方是解题的关键．【典例2】（2019秋•河北区期末）如图在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC．（1）求证：△ADE∽△ABC；（2）如AF＝3，AG＝5，求△ADE与△ABC的周长之比．【点拨】（1）由于AG⊥BC，AF⊥DE，所以∠AFE＝∠AGC＝90°，从而可证明∠AED＝∠ACB，进而可证明△ADE∽△ABC；（2）依据△ADE∽△ABC，利用相似三角形的周长之比等于对应高之比，即可得到结论．【解析】解：（1）∵AG⊥BC，AF⊥DE，∴∠AFE＝∠AGC＝90°，∵∠EAF＝∠GAC，∴∠AED＝∠ACB，∵∠EAD＝∠BAC，∴△ADE∽△ABC；（2）由（1）可得△ADE∽△ABC，又∵AG⊥BC于点G，AF⊥DE于点F，∴△ADE与△ABC的周长之比＝＝．【点睛】本题考查相似三角形的判定，解题的关键是熟练运用相似三角形的判定，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．【变式训练】1．（2020春•甘州区校级月考）两个相似三角形面积比是4：9，其中一个三角形的周长为24cm，则另一个三角形的周长是（）cm．A．16 B．16或28 C．36 D．16或36【点拨】根据相似三角形的性质求出相似比，得到周长比，根据题意列出比例式，解答即可．【解析】解：∵两个相似三角形面积比是4：9，∴两个相似三角形相似比是2：3，∴两个相似三角形周长比是2：3，∵一个三角形的周长为24cm，∴另一个三角形的周长是16cm或36cm，故选：D．【点睛】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方是解题的关键．2．（2019秋•慈溪市期末）如图所示，若△ABC∽△DEF，则∠E的度数为（）A．28°B．32°C．42°D．52°【点拨】先求出∠B，根据相似三角形对应角相等就可以得到．【解析】解：∵∠A＝110°，∠C＝28°，∴∠B＝42°，∵△ABC∽△DEF，∴∠B＝∠E．∴∠E＝42°．故选：C．【点睛】本题考查相似三角形的性质的运用，全等三角形的对应角相等，是基础知识要熟练掌握．3．（2019秋•奉化区期末）如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB，若AB＝3BD，则S△ADE：S△EFC的值为（）A．4：1 B．3：2 C．2：1 D．3：1【点拨】由题意可证四边形BDEF是平行四边形，可得BD＝EF，AD＝2EF，通过证明△ADE∽△EFC，可求解．【解析】解：∵AB＝3BD，∴AD＝2BD，∵DE∥BC，EF∥AB，∴四边形BDEF是平行四边形，∴BD＝EF，∴AD＝2EF，∵DE∥BC，EF∥AB，∴∠AED＝∠C，∠FEC＝∠A，∴△ADE∽△EFC，∴S△ADE：S△EFC的＝（）2＝4：1，故选：A．【点睛】本题考查了相似三角形的判定和性质，平行四边形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．4.（2020•下城区模拟）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D，如果＝，AD＝9，那么BC的长是（）A．4 B．6 C．2D．3【点拨】证明△ADC∽△CDB，根据相似三角形的性质求出CD、BD，根据勾股定理求出BC．【解析】解：∵∠ACB＝90°，∴∠ACD+∠BCD＝90°，∵CD⊥AB，∴∠A+∠ACD＝90°，∴∠A＝∠BCD，又∠ADC＝∠CDB，∴△ADC∽△CDB，∴＝，＝，∴＝，即＝，解得，CD＝6，∴＝，解得，BD＝4，∴BC＝＝＝2，故选：C．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．5.（2019•纳溪区模拟）如图，已知矩形ABCD，AB＝6，BC＝10，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（）A．6 B．7 C．8 D．9【点拨】延长AF交DC于Q点，由矩形的性质得出CD＝AB＝6，AB∥CD，AD∥BC，得出＝1，△AEI∽△QDE，因此CQ＝AB＝CD＝6，△AEI的面积：△QDI的面积＝1：16，根据三角形的面积公式即可得出结果．【解析】解：延长AF交DC于Q点，如图所示：∵E，F分别是AB，BC的中点，∴AE＝AB＝3，BF＝CF＝BC＝5，∵四边形ABCD是矩形，∴CD＝AB＝6，AB∥CD，AD∥BC，∴＝1，△AEI∽△QDE，∴CQ＝AB＝CD＝6，△AEI的面积：△QDI的面积＝（）2＝，∵AD＝10，∴△AEI中AE边上的高＝2，∴△AEI的面积＝×3×2＝3，∵△ABF的面积＝×5×6＝15，∵AD∥BC，∴△BFH∽△DAH，∴＝＝，∴△BFH的面积＝×2×5＝5，∴四边形BEIH的面积＝△ABF的面积﹣△AEI的面积﹣△BFH的面积＝15﹣3﹣5＝7．故选：B．【点睛】本题考查了矩形的性质、相似三角形的判定与性质、三角形面积的计算；熟练掌握矩形的性质，证明三角形相似是解决问题的关键．6.（2020•杭州）如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB．（1）求证：△BDE∽△EFC．（2）设，①若BC＝12，求线段BE的长；②若△EFC的面积是20，求△ABC的面积．【点拨】（1）由平行线的性质得出∠DEB＝∠FCE，∠DBE＝∠FEC，即可得出结论；（2）①由平行线的性质得出＝＝，即可得出结果；②先求出＝，易证△EFC∽△BAC，由相似三角形的面积比等于相似比的平方即可得出结果．【解析】（1）证明：∵DE∥AC，∴∠DEB＝∠FCE，∵EF∥AB，∴∠DBE＝∠FEC，∴△BDE∽△EFC；（2）解：①∵EF∥AB，∴＝＝，∵EC＝BC﹣BE＝12﹣BE，∴＝，解得：BE＝4；②∵＝，∴＝，∵EF∥AB，∴△EFC∽△BAC，∴＝（）2＝（）2＝，∴S△ABC＝S△EFC＝×20＝45．【点睛】本题考查了相似三角形的判定与性质、平行线的性质等知识；熟练掌握相似三角形的判定与性质是解题的关键．知识点二相似三角形的应用【典例3】（2019秋•解放区校级期中）一块直角三角形木板的面积为1.5m2，一条直角边AB为1.5m，怎样才能把它加工成一个无拼接的面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用所学的知识说明哪位木匠的方法符合要求（加工损耗不计，计算结果中的分数可保留）【点拨】结合相似三角形的判定与性质进而得出两个正方形的边长，进而求出面积比较得出答案．【解析】解：由AB＝1.5m，S△ABC＝1.5m2，可得BC＝2m，由图甲，过点B作Rt△ABC斜边AC上的高，BH交DE于P，交AC于H．由AB＝1.5m，BC＝2m，得AC＝＝2.5（m），由AC•BH＝AB•BC可得：BH＝＝1.2（m），设甲设计的桌面的边长为xm，∵DE∥AC，∴Rt△BDE∽Rt△BAC，∴＝，即＝，解得x＝（m），由图乙，若设乙设计的正方形桌面边长为ym，由DE∥AB，得Rt△CDE∽Rt△CBA，∴＝，即＝，解得y＝（m），∵x＝，y＝，∴x＜y，即x2＜y2，∴S正方形甲＜S正方形乙，∴第二个正方形面积大【点睛】此题主要考查了相似三角形的应用，正确表示出正方形的边长是解题关键．【变式训练】1．（2019秋•嘉兴期末）如图，小明在打乒乓球时，为使球恰好能过网（设网高AB＝15cm），且落在对方区域桌子底线C处，已知小明在自己桌子底线上方击球，则他击球点距离桌面的高度DE为（）A．15cm B．20cm C．25cm D．30cm【点拨】证明△CAB∽△CDE，然后利用相似比得到DE的长．【解析】解：∵AB∥DE，∴△CAB∽△CDE，∴＝，而BC＝BE，∴DE＝2AB＝2×15＝30（cm）．故选：D．【点睛】本题考查了相似三角形的应用：利用视点和盲区的知识构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．2．（2019秋•鹿城区月考）如图，AB和CD表示两根直立于地面的柱子，AC和BD表示起固定作用的两根钢筋，AC与BD相交于点M，已知AB＝8m，CD＝12m，则点M离地面的高度MH为（）A．4 m B．m C．5m D．m【点拨】根据已知易得△ABM∽△DCM，可得对应高BH与HD之比，易得MH∥AB，可得△MDH∽△ADB，利用对应边成比例可得比例式，把相关数值代入求解即可．【解析】解：∵AB∥CD，∴△ABM∽△DCM，∴＝＝＝，（相似三角形对应高的比等于相似比），∵MH∥AB，∴△MCH∽△ACB，∴＝＝，∴＝，解得MH＝．故选：B．【点睛】此题主要考查了相似三角形的应用；用到的知识点为：平行于三角形一边的直线与三角形另两边相交，截得的两三角形相似；相似三角形的对应边成比例；对应高的比等于相似比；解决本题的突破点是得到BH与HD的比．3．（2019秋•滨江区期末）如图，小华同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，使斜边DF与地面保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝30cm，EF＝15cm，测得边DF离地面的高度AC＝120cm，CD＝600cm，则树AB的高度为420cm．【点拨】利用直角三角形DEF和直角三角形BCD相似求得BC的长，再加上AC的长即可求得树高AB．【解析】解：∵∠DEF＝∠BCD＝90°，∠D＝∠D，∴△DEF∽△DCB，∴BC：EF＝DC：DE，∵DE＝30cm，EF＝15cm，AC＝120cm，CD＝600cm，∴，∴BC＝300cm，∴AB＝AC+BC＝120+300＝420cm，故答案为：420．【点睛】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．4.（2020•秦皇岛一模）如图所示，AD、BC为两路灯，身高相同的小明、小亮站在两路灯杆之间，两人相距6.5m，小明站在P处，小亮站在Q处，小明在路灯C下的影长为2m，已知小明身高1.8m，路灯BC 高9m．①计算小亮在路灯D下的影长；②计算建筑物AD的高．【点拨】解此题的关键是找到相似三角形，利用相似三角形的性质，相似三角形的对应边成比例求解．【解析】解：①∵EP⊥AB，CB⊥AB，∴∠EP A＝∠CBA＝90°∵∠EAP＝∠CAB，∴△EAP∽△CAB∴∴∴AB＝10BQ＝10﹣2﹣6.5＝1.5；②∵FQ⊥AB，DA⊥AB，∴∠FQB＝∠DAB＝90°∵∠FBQ＝∠DBA，∴△BFQ∽△BDA∴＝∴∴DA＝12．【点睛】本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求出建筑物AB的高与小亮在路灯D下的影长，体现了方程的思想．巩固训练1．（2019秋•连州市期末）两个相似三角形的对应边分别是15cm和23cm，它们的周长相差40cm，则这两个三角形的周长分别是（）A．45cm，85cm B．60cm，100cm C．75cm，115cm D．85cm，125cm【点拨】根据题意两个三角形的相似比是15：23，可得周长比为15：23，计算出周长相差8份及每份的长，可得两三角形周长．【解析】解：根据题意两个三角形的相似比是15：23，周长比就是15：23，大小周长相差8份，所以每份的周长是40÷8＝5cm，所以两个三角形的周长分别为5×15＝75cm，5×23＝115cm．故选：C．【点睛】本题考查对相似三角形性质的理解：（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．2．（2018秋•临安区期末）如图，在△ABC中，BC＝8，高AD＝6，点E，F分别在AB，AC上，点G，H 在BC上，当四边形EFGH是矩形，且EF＝2EH时，则矩形EFGH的周长为（）A．B．C．D．【点拨】通过证明△AEF∽△ABC，可得，可求EH的长，即可求解．【解析】解：如图，记AD与EF的交点为M，∵四边形EFGH是矩形，∴EF∥BC，∴△AEF∽△ABC，∵AM和AD分别是△AEF和△ABC的高，∴∴∴EH＝，∴EF＝，∴矩形EFGH的周长＝2×（+）＝故选：C．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，灵活运用相似三角形的性质是本题的关键．3．（2019秋•庐阳区校级期中）如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE＝1：4，则S△DOE：S△AOC的值为（）A．B．C．D．【点拨】由已知条件易求BE：BC＝1：5；证明△DOE∽△AOC，得到DE：AC的值，由相似三角形的性质即可解决问题．【解析】解：∵S△BDE：S△CDE＝1：4，∴BE：EC＝1：4，∴BE：BC＝1：5，∵DE∥AC，∴△DOE∽△AOC，∴DE：AC＝BE：BC＝1：5，∴S△DOE：S△AOC＝（）2＝，故选：D．【点睛】本题主要考查了相似三角形的判定及其性质的应用问题；熟练掌握相似三角形的判定与性质，证出BE：BC＝1：5是解决问题的关键．4．（2020•上城区一模）如图，△ABC中，D，E两点分别在边AB，BC上，若AD：DB＝CE：EB＝3：4，记△DBE的面积为S1，△ADC的面积为S2，则S1：S2＝16：21．【点拨】过点E、C分别作EF⊥AB于点F，CG⊥AB于点G，根据相似三角形的性质与判定即可求出答案．【解析】解：过点E、C分别作EF⊥AB于点F，CG⊥AB于点G，∴EF∥CG，∴△BEF∽△BCG，∴，∵CE：EB＝3：4，∴，∴，∴＝＝，∴S1：S2＝16：21，故答案为：16：21．【点睛】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．5．（2019秋•江干区期末）如图，已知▱ABCD中，E是BC的三等分点，连结AE与对角线BD交于点F，则S△BEF：S△ABF：S△ADF：S四边形CDFE＝1：3：9：11．【点拨】由E是BC的三等分点，得到＝，根据平行四边形的性质得到AD∥BC，AD＝BC，根据相似三角形的性质得到＝＝设S△BEF＝k，S△ABF＝3k，S△ADF＝9k，求得S△ABF+S△ADF＝S四边形ABCD＝S△BEF+S四边形CDFE＝12k，得到S四边形CDFE＝12k﹣k＝11k，于是得到结论．【解析】解：∵E是BC的三等分点，∴＝，在▱ABCD中，∵AD∥BC，AD＝BC，∴△ADF∽△EBF，∴＝＝，∴S△BEF：S△ABF：S△ADF＝1：3：9，设S△BEF＝k，S△ABF＝3k，S△ADF＝9k，∴S△ABF+S△ADF＝S四边形ABCD＝S△BEF+S四边形CDFE＝12k，∴四边形CDFE＝12k﹣k＝11k，∴S△BEF：S△ABF：S△ADF：S四边形CDFE＝1：3：9：11，故答案为：1：3：9：11．【点睛】本题考查了平行四边形的性质、相似三角形的判定与性质以及面积的计算方法；熟练掌握平行四边形的性质，证明三角形相似是解决问题的关键．6．（2020•晋安区一模）如图，利用镜子M的反射（入射角等于反射角），来测量旗杆CD的长度，在镜子上作一个标记，观测者AB看着镜子来回移动，直到看到旗杆顶端在镜子中的像与镜子上的标记相重合，若观测者AB的身高为1.6m，量得BM：DM＝2：11，则旗杆的高度为8.8m．【点拨】根据题意抽象出相似三角形，然后利用相似三角形的对应边的比相等列式计算即可．【解析】解：根据题意得：△ABM∽△CDM，∴AB：CD＝BM：DM，∵AB＝1.6m，BM：DM＝2：11，∴1.6：CD＝2：11，解得：CD＝8.8m，故答案为：8.8．【点睛】本题考查了相似三角形的知识，解题的关键是根据实际问题抽象出相似三角形，难度不大．7．（2019秋•竞秀区期末）如图，路灯距地面的高度PO＝8米，身高1.6米的小明在点A处测量发现，他的影长AM＝2.4米，则AO＝9.6米；小明由A处沿AO所在的直线行走8米到点B时，他的影子BN 的长度为0.4米．【点拨】如图，设OA＝x，BN＝y．利用相似三角形的性质构建方程组即可解决问题．【解析】解：如图，设OA＝x，BN＝y．∵EB∥OP∥F A，∴△MAF∽△MOP，△NBE∽△NOP，∴＝，＝，∴＝，＝，解得x＝9.6，y＝0.4，故答案为9.6，0.4．【点睛】本题考查相似三角形的应用，解题的关键是学会利用参数构建方程组解决问题，属于中考常考题型．8．（2019秋•开江县期末）如图，学校操场旁立着一杆路灯（线段OP）．小明拿着一根长2m的竹竿去测量路灯的高度，他走到路灯旁的一个地点A竖起竹竿（线段AE），这时他量了一下竹竿的影长AC正好是1m，他沿着影子的方向走了4m到达点B，又竖起竹竿（线段BF），这时竹竿的影长BD正好是2m，请利用上述条件求出路灯的高度．【点拨】根据相似三角形的性质即可得到结论．【解析】解：由于BF＝DB＝2m，即∠D＝45°，∴DP＝OP＝灯高．在△CEA与△COP中，∵AE⊥CP，OP⊥CP，∴AE∥OP．∴△CEA∽△COP，∴．设AP＝xm，OP＝hm，则，①，DP＝OP＝2+4+x＝h，②联立①②两式，解得x＝4，h＝10．∴路灯有10m高．【点睛】本题考查了相似三角形的性质，熟练掌握相似三角形的性质是解题的关键．9．（2019秋•余杭区期末）如图，在△ABC中，点D，E分别在边AC，AB上且AE•AB＝AD•AC，连结DE，BD．（1）求证：△ADE∽△ABC．（2）若点E为AB中点，AD：AE＝6：5，△ABC的面积为50，求△BCD的面积．【点拨】（1）由已知得出AE：AC＝AD：AB，由∠A＝∠A，即可得出：△ADE∽△ABC．（2）设AD＝6x，则AE＝5x，AB＝10x，由已知求出AC＝＝x，得出CD＝AC﹣AD＝x，得出＝，由三角形面积关系即可得出答案．【解析】（1）证明：∵AE•AB＝AD•AC，∴AE：AC＝AD：AB，∵∠A＝∠A，∴△ADE∽△ABC．（2）解：∵点E为AB中点，∴AE＝BE，∵AD：AE＝6：5，∴设AD＝6x，则AE＝5x，AB＝10x，∵AE•AB＝AD•AC，∴AC＝＝＝x，∴CD＝AC﹣AD＝x，∴＝，∵△ABC的面积为50，∴△BCD的面积＝×50＝14．【点睛】本题考查了相似三角形的判定与性质、三角形面积关系等知识；熟练掌握相似三角形的判定与性质是解题的关键．10．（2018秋•江干区期末）如图，在菱形ABCD中，点E在BC边上（不与点B、C重合），连接AE、BD 交于点G．（1）若AG＝BG，AB＝4，BD＝6，求线段DG的长；（2）设BC＝kBE，△BGE的面积为S，△AGD和四边形CDGE的面积分别为S1和S2，把S1和S2分别用k、S的代数式表示；（3）求的最大值．【点拨】（1）证明△BAG∽△BDA，利用相似比可计算出BG＝，从而得到DG的长；（2）先证明△ADG∽△EBG，利用相似三角形的性质得＝（）2＝k2，＝＝k，所以S1＝k2S，根据三角形面积公式得到S△ABG＝，再利用菱形的性质得到S2＝S1+﹣S＝k2S+kS﹣S＝（k2+k﹣1）S；（3）由于＝＝1+﹣，然后根据二次函数的性质解决问题．【解析】解：（1）∵AG＝BG，∴∠BAG＝∠ABG，∵四边形ABCD为菱形，∴AB＝AD，∴∠ABD＝∠ADB，∴∠BAG＝∠ADB，∴△BAG∽△BDA，∴＝，即＝，∴BG＝，∴DG＝BD﹣BG＝6﹣＝；（2）∵四边形ABCD为菱形，∴BC＝AD＝kBE，AD∥BC，∵AD∥BE，∴∠DAE＝∠BEA，∠ADG＝∠BEG∴△ADG∽△EBG，∴＝（）2＝k2，＝＝k，∴S1＝k2S，∵＝＝k，∴S△ABG＝，∵△ABD的面积＝△BDC的面积，∴S2＝S1+﹣S＝k2S+kS﹣S＝（k2+k﹣1）S；（3）∵＝＝1+﹣＝﹣（﹣）2+，∴的最大值为．【点睛】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．注意相似三角形面积的比等于相似比的平方．也考查了菱形的性质．。

相似三角形的应用ppt课件contents •相似三角形基本概念与性质•相似三角形在几何问题中应用•相似三角形在三角函数中应用•相似三角形在物理问题中应用•相似三角形在建筑设计中应用•总结与展望目录01相似三角形基本概念与性质定义AAA 相似SAS 相似SSS 相似定义及判定方法01020304两个三角形如果它们的对应角相等，则称这两个三角形相似。

如果两个三角形的三组对应角分别相等，则这两个三角形相似。

如果两个三角形有两组对应边成比例且夹角相等，则这两个三角形相似。

如果两个三角形的三组对应边都成比例，则这两个三角形相似。

相似比与对应边长成比例关系相似比两个相似三角形的对应边之间的比值称为相似比。

对应边长成比例关系在相似三角形中，任意两边之间的比值等于其他两边之间的比值，即a/a'=b/b'=c/c'，其中a、b、c和a'、b'、c'分别是两个相似三角形的对应边长。

相似三角形面积比关系面积比公式两个相似三角形的面积之比等于它们对应边长之比的平方，即(S1/S2)=(a/a')^2=(b/b')^2=(c/c')^2，其中S1和S2分别是两个相似三角形的面积，a、b、c和a'、b'、c'分别是它们的对应边长。

应用举例利用相似三角形的面积比关系可以解决一些实际问题，如测量高度、计算距离等。

02相似三角形在几何问题中应用利用相似三角形对应边成比例的性质，通过已知线段长度求解未知线段长度。

结合图形变换（如平移、旋转等）和相似三角形的性质，构造新的相似三角形，进而求解线段长度。

通过相似三角形的性质，建立比例关系，求解未知线段长度。

利用相似三角形求线段长度利用相似三角形证明角相等或互补通过相似三角形的性质，证明两个角相等或互补。

利用相似三角形对应角相等的性质，证明两个角相等。

结合图形变换和相似三角形的性质，构造新的相似三角形，证明两个角互补。

相似三角形题型讲解相似三角形是初中几何的重要内容，包括相似三角形的性质、判定定理及其应用，是中考必考内容，以相似三角形为背景的综合题是常见的热点题型，所以掌握好相似三角形的基础知识至关重要，本讲就如何判定三角形相似，以及应用相似三角形的判定、性质来解决与比例线段有关的计算和证明的问题进行探索。

一、如何证明三角形相似例1、如图：点G 在平行四边形ABCD 的边DC 的延长线上,AG 交BC 、BD 于点E 、F ，则△AGD ∽ ∽ 。

分析：关键在找“角相等”，除已知条件中已明确给出的以外，还应结合具体的图形，利用公共角、对顶角及由平行线产生的一系列相等的角。

本例除公共角∠G 外,由BC ∥AD 可得∠1=∠2，所以△AGD ∽△EGC 。

再∠1=∠2（对顶角），由AB ∥DG 可得∠4=∠G ，所以△EGC ∽△EAB 。

评注：（1）证明三角形相似的首选方法是“两个角对应相等的两个三角形相似”。

（2）找到两个三角形中有两对角对应相等，便可按对应顶点的顺序准确地把这一对相似三角形记下来。

例2、已知△ABC 中，AB=AC ，∠A=36°，BD 是角平分线， 求证：△ABC ∽△BCD分析：证明相似三角形应先找相等的角，显然∠C 是公共角，而另一组相等的角则可以通过计算来求得。

借助于计算也是一种常用的方法。

证明：∵∠A=36°，△ABC 是等腰三角形，∴∠ABC=∠C=72° 又BD 平分∠ABC ，则∠DBC=36°在△ABC 和△BCD 中，∠C 为公共角，∠A=∠DBC=36° ∴△ABC∽△BCD例3：已知，如图，D 为△ABC 内一点连结ED 、AD ，以BC 为边在△ABC 外作∠CBE=∠ABD，∠BCE=∠BAD 求证：△DBE∽△ABCA B C DEF G 1234ABCD分析：由已知条件∠ABD=∠CBE，∠DBC公用。

所以∠DBE=∠ABC，要证的△DBE和△ABC，有一对角相等，要证两个三角形相似，或者再找一对角相等，或者找夹这个角的两边对应成比例。

“一线三等角”模型在初中数学中的应用相似三角形在初中几何的教学中发挥着不可小觑的作用，在中考考题中常有涉及和渗透，笔者在初三的教学中发现掌握相似三角形的基本图形，对培养学生分析问题和解决问题的能力有一定的促进作用。

本文以相似三角形中的“一线三等角”这一基本图形为载体，研究这一基本图形背景下的相关题型，并进行了收集与整理，希望对学生灵活应用这一模型有所帮助。

一、弄清基本模型定义和解题原理二、应用举例1.在“动点问题”中的应用例1：如图2，正方形ABCD的边长为1cm，M、N分别是BC、CD上两个动点，且始终保持AM⊥MN，设BM的长为x cm，CN的长为y cm.求点M在BC上的运动过程中y的最大值。

分析：由图可知∠B=∠C=∠AMN=90°，Rt△ABM与Rt△MCN成“一线三等角”模型，所以Rt△ABM∽Rt△MCN，从而，所以，.所以y的最大值为。

【变式】如“例1”的条件，将问题改为“当BM=cm时，四边形ABCN的面积最大，最大面积为 cm2.”分析：四边形ABCN的面积为，BC，AB的长都为1，是定值，只有CN在变化，要使四边形ABCN的面积最大，则CN最大，即转化为“例1”的问题.2.与反比例函数联手例2：（2015?孝感）如图3，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y=的图象上.若点B在反比例函数y=的图象上，则k的值为（）A.-4B.4C.-2D.2分析：看到反比例函数图像上的点A，并且要求的点B也在反比例函数图像上，从而联想反比例函数解析式中“k”的几何意义解决问题.过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D.根据“一线三等角”模型，很容易得到△ACO∽△ODB，从而==4，然后用反比例函数解析式中“k”的几何意义即可.3.在“直角三角形存在性问题”中的应用点的存在性问题始终是中考考查的热点和难点，对学生的思维能力和模型思想等基本数学素养有着较高的要求，所以一直困扰着学生.数学解题研究中一直很关注一题多解的研究，多一种解决问题的方法，能让学生步入考场有更多的选择，直角三角形的存在性问题多数教师在讲解的时候是引导学生利用解析式法“”和勾股定理解决.笔者在教学中发现，利用“一线三等角”模型解决直角三角形的存在性问题也是一种通用方法，即便这个点在抛物线上也能使用（当点在抛物线上时，利用勾股定理会出现四次情形，初中学生无法解决），能为学生解决这类问题提供了一种新的选择。

由一个基本图形的衍生所想到的……—— “相似三角形性质应用的专题研究课”课堂实录与评析1 引言解综合题的关键在于思路.一道综合题,往往可以分解成若干个基本问题(基本图形).分解好了,解题思路的形成也就水到渠成.因此,基本图形(基本方法)的重要性就凸显出来.但如何才能让学生对此有深刻的体验与感悟呢?2011年4月,浙江省教育厅“百人千场”数学学科送教下乡活动在浙江磐安县安文初中举行.笔者以此为设计思路,执教了一节“相似三角形性质应用的专题研究课”,受到了与会教师和送教专家的好评.现将课堂教学实录与点评整理如下,供各位同仁参考.2 教学实录2.1 原题呈现,感知模型引例 如图1所示,有一块锐角三角形余料ABC,它的边BC=12cm ,高线AD=8cm ,现要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB,AC 上.问加工成的正方形边长为多少cm ?（学生经过几分钟的思考,基本都可以得出答案）生1:设正方形的边长为x cm .∵PN ∥BC,∴△APN ∽△ABC,∴PN AE BC AD =(相似三角形的对应高之比等于相似比) 即8812x x -=,得8.4=x ,∴正方形的边长为4.8cm . 师:回答的很好,是否还有其它建立等量关系的方法?生2:我用面积法.设正方形的边长为x mm .由S △ABC = S △APN + S 正方形PQMN + S △PBQ + S △MNC 得,12821)8(21)12(212⨯⨯=-++-x x x x x ,解得8.4=x ,∴正方形的边长为4.8cm . 师:真棒!对于数学问题,我们常常可以尝试从不同的途径进行思考.一题多解,有助于拓展我们的思维,开阔我们的视野.当然,希望同学们结合下面的变化图,思考这个基本图形的本质是什么?[点评]通过课本典型例题的复现与解决,为学生运用基础知识,感知基本模型营造了和谐的氛围,间接的消除了学生上公开课的紧张感,使学生能轻松的投入到学习过程之中.而引导思考解决问题的不同策略,既有效发展了学生思维的灵活性,也意在消除学生的思维定势.2.2 适度变化,理解模型例1 已知△ABC 中,BC=12,BC 边上的高AD=8,(1) 若并排放置的2个相等的小正方形组成的矩形,内接于△ABC(如图2),则小正方形的边长为多少? 并排放置3个小正方形呢?(有了与前面问题的类比,学生很快就举手了)生3:作AD ⊥BC 于D(如图3),设正方形边长为x ,则PN=2x ,AE=8x -.由△APN ∽△ABC 可得,247x =. 类似的,并排放置3个小正方形时,小正方形的边长为924. (2)如图4,若并排放置小正方形有n 个,则这时小正方形的边长又为多少?（部分学生马上举手示意）生4:小正方形的边长为2423n +. 师:你是怎么得到的呢？生4:看到前面的答案分别是245,247,249,就猜想内接n 个时,边长应为2423n +. 师:很好!通过数据的变化特点去发现规律,是数学归纳的重要方式.但合理的猜想仍需要严密的推理证实,同学们能证明吗？生4:设正方形边长为x ,则PN=nx .由相似得8812x nx -=,∴2423x n =+,故猜想正确. 师:太棒了.观察分析、尝试猜想、推理证明是学习数学的基本方法,同学们平时要经常加以运用.下面让我们把问题更一般化.例2 如图5,已知△ABC 中,BC=12,BC 边上的高AD=8,四边形PQMN 为△ABC 的内接矩形.(1)设PQ=x ,你能求出PN 的长吗?(用含x 的代数式表示）生5:还是采用上面的方法.由相似得8812x PN -=,解得1223+-=x PN (2)记矩形PQMN 的面积为S,求S 的最大面积.生5:S=PQ ·PN=x x 12232+-(0＜x ＜8),则当42=-=a b x 时,max 24S =. 师:由上述解答可以清晰的发现,在这个基本图形中,因PN ∥BC,故有△APN ∽△ABC,于是由性质可知PN 与AE 之间便存在等量关系,从而PQ(ED)与PN 之间也存在等量关系.若这两者之间自身还存在数量关系,就可利用方程模型求解.[点评]这两个变式,看似变化不多,难度不大,却使学生进一步体验到基本图形与基础知识的重要性,初步理解了基本图形所蕴含的本质,突出了本课的主题.而从特殊到一般,从类比到猜想,从方程到函数模型等数学思想方法的有机渗透,则较好实现了数学教学中知识与方法,过程与结果的和谐统一,润物无声.2.3 动中求静,应用模型例3 如图6,在锐角△ABC 中,BC=12,△ABC 的面积为48,D ,E 分别是边AB ,AC 上的两个动点（D 不与A ,B 重合）,且保持DE ∥BC ,以DE 为边,在点A 的异侧作正方形DEFG .(1)当正方形DEFG 的边GF 在BC 上时,求正方形DEFG 的边长. 图4 图 5图 6F G E D CB A师:请同学们画出图形,并求解.生6(黑板上画出图7后):就是原题呈现的情况,这时边长应为4.8.（下面的学生纷纷表示赞同） 师:我发现同学们对这个基本图形印象深刻!好,请继续看下面的问题.(2)设DE =x ,△ABC 与正方形DEFG 重叠部分的面积为y ,试求y 关于 x 的函数关系式及x 的取值范围,并求出y 的最大值. 师:请同学们思考,随着DE 的运动,重叠部分会有哪些变化,（一位学生上黑板画出了图8-1和8-2）生7:有两种不同的情况,所以要进行分类讨论.师:很好!那应该如何分类？生7:以边GF 所在位置进行分类,有边GF 在△ABC 内部和△ABC 外部两种,以边GF 在BC 上为临界.师:回答的真好!那就请同学们来解决这个问题,并思考与前面问题之间的联系.生8:①当正方形DEFG 在△ABC 内部(含边界)时,0 4.8x <≤,此时y 就是正方形DEFG 的面积,即2y x =,最大值为24.823.04=;②当边GF 在正方形外部时,就是例2的情况,此时4.812x <<,过A 作AP ⊥BC 于P,交DE 于H,由△ADE ∽△ABC 可得,PH=x 328-, ∴x x x x y 832)328(2+-=-=,当62=-=ab x 时,y 有最大值,且最大值为24. 因24＞23.04,所以重叠部分的最大面积为24.师:看来,熟悉了基本图形确实能使我们在解题时如虎添翼.那么,这个基本图形还可以作哪些变化呢,让我们继续加以体会.[点评]由静到动,看似一小步,实则是多数学生数学学习过程中的一大难点.但王老师在教学中没有直接展开讲解,而是先让学生动手实践来感知图形的变化特点,从而产生了分类解决的方法,于是难点突破就变得顺理成章,也为后续问题的解决奠定了方法基础.同时,在前后问题的比较中也让学生进一步体会到基本模型的应用价值,强化了本课主题.2.4 深化模型,提高认知例4 如图9,锐角△ABC 中,BC=12,AH ⊥BC 点H,且AH=8,点D 为AB 的任意一点,过点D 作DE ∥BC,交AC 于点E,AH 于F.设AF 为x (0＜x ＜8)以DE 为折线将△ADE 翻折,所得△DE A '与梯形DBCE 重叠部分的面积记为 y (点A 的对称点A '落在AH 所在直线上）.请问,当x 取何值时,y 的值最大?最大值是多少？ 师:请仔细理解题意,并思考随着DE 的运动,重叠部分图形有哪些变化,分界点在哪里,C B 图 8-2图 8-1CB 图 9A A能画出来吗?生9:有两种情形.一种如图9,重叠部分是三角形;另一种如图10,重叠部分为梯形,DE 是三角形的中位线时分界.师:看来,理解了图形的变化规律也就掌握了分类的方法.但是如何来求这个梯形的面积呢?前面的基本图形还适用吗?生10:适用.用两次基本图,即用△ADE ∽ABC 求DE,用△'''E D A ∽△DE A '求''E D . (见学生都表示理解了)师:那下面就请大家具体的求一下吧.(过了一会)生10:当0＜x ≤4时,y 就是△ADE 的面积,由相似知DE=x 23,所以243x y =,故当4=x 时,y 有最大值12.当4＜x ＜8时,利用△'''E D A ∽△DE A '可得F A H A DE E D ''''=,即xx x x E D )8(5.1''--=,∴123''-=x E D . 则482449)8)(12323(212-+-=--+=x x x x x y ,故当316=x 时,y 有最大值16. 因16＞12,所以当8=x 时,重叠部分的最大面积为16.师:这么繁琐的数据计算居然没有一点问题,这位同学的运算能力真强.但老师还是想请大家再思考下,是否有直接计算面积的方法呢?生11:用面积比与相似比的关系呀!由△'''E D A ∽△DE A '得22''')82(43x x x S E D A -=∆, 所以2''')4(3-=∆x S E D A ,于是482449)4(343222-+-=--=x x x x y .…… 师:这位同学的知识掌握得很全面,这也说明根据目标来选择方法可以使我们少走弯路. 下面让我们再用几何画板演示一下动态的变化过程,希望能加深大家的理解(过程略).[点评]从矩形面积过渡到梯形面积的计算,就不仅仅是模仿运用了,它能有效促进学生的抽象能力,模型识别能力与迁移能力的提高,提升了思维的深度,也使学生在图形的变化过程中感悟了万变不离其宗的道理,而问题解决过程中的方法优化,则强化了学生的目标意识与思维监控能力.而最后几何画板工具的使用,既给学生的几何直觉以有力的支撑,又关注了数学学习中的“弱势群体”,体现了王老师面向全体的教学理念.2.5 归纳小结,反思提高请同学们就本节课的学习情况进行一下回顾与总结.……师:同学们都说得很好,把这些发言归纳起来,主要是:运用性质“相似三角形的对应高之比等于相似比”,可以解决了一类长度(面积)而在具体的解决问题过程中,我们还运用了从特殊到一般,类比、猜想、归纳,分类讨论等数学基本思想方法.通过学习,我们对基本模型的重要性想必有了更新的认识,希望同学们在今后的学习中勤于观察,善于比较,提炼本质,有效运用.唯有如此,才能真正提高数学学习的效率,才能有效发展思维能力.3 总评对基本图形(基本方法)的感悟、理解与运用,主要靠学生在平时的学习过程中,通过有意识的观察思考、实践比较、分析提炼、有效运用等才能得以实现,这也正是衡量学生数学能力与数学素养的重要依据.但这样的工作能否以专题研究课的形式予以强化与指导,王老师的这节课给我们带来了可供借鉴的研究样本.3.1 谋篇布局,构思精巧高效的课堂源自于有效的教学设计.纵观本节课,王老师以“相似三角形对应高之比等于相似比”这一重要性质的应用为主要认知线索,以教材中的范例(求三角形的内接正方形边长)为原型,并精心选择了与此相关联的四个变式问题展开研究,层层深入,变化有度,衔接自然.其中,从水平变式到垂直变式的渐变,突出了过程体验,强化了对基本图形的本质理解.而从几何到代数的综合,从方程到函数模型的构建,从静态图形到动态图形的变化,从图形的平移到折叠变换,则能使学生完善认知网络,丰富图形认知,促进方法理解,提高思维能力.这样的设计,较好地遵循了学生的学习规律,为达成本课的学习目标创设了适切的载体,也有利于促进学生主动的学习,彰显了教师的教学智慧.3.2 方法为先,思维为本数学不仅仅是一种重要的“工具”和“方法”,更重要的是一种思维模式.因此,增强学生的数学概括和抽象能力,提升其思维能力是数学教学的重要任务.就本课而言,较好的体现了这一点.一是学生亲历了问题的发生与发展过程,对基本图形本质及其作用的理解是在充分的体验过程中得以逐步领悟的,这些数学思维活动留给学生的感受是非常深刻的,对于学生今后深入理解图形性质,关注图形之间联系,从复杂图形中分离基本图形,提高图形分析能力等都会带来积极的影响;二是在具体解决问题的过程中,有机的渗透从特殊到一般,分类讨论,数形结合,方程及函数等思想方法,让学生在必要的观察、猜想、类比、推理与交流中感悟这些思想方法的概括与内化过程,对于唤醒学生的认知内驱力,促进他们的思维发展,进而形成有效的思维策略有着显著的效果,也充分体现了数学教育的价值.3.3 过程流畅,氛围和谐在课堂上可以看到,在以变式生成的问题串的科学引领下,伴随着问题解决过程中不断的成功体验,以及教师适时的激励评价,激发了学生积极的情感体验与学习热情,使得绝大多数学生都被卷入到积极的数学思维活动中来,这种和谐学习氛围的创设,极大提高了学生的自主学习能力与主动参与意识.而本课中问题的思路基本都是学生提出,方法由学生补充,解答由学生完成,而教师则退居幕后,仅在思维展开的疑难处,思路形成的困惑点及时介入、点拨指导.这种教与学的方式,看似平淡,却于无深处有惊雷,真实体现了数学学习的基本规律与数学思维方式的基本特点,也较好贯彻了“学为主体、教为主导”的教学理念.3.4 值得思考的问题教学永远是一门遗憾的艺术,没有最好,只有更好.从这个意义上讲,下面几个问题或许值得我们深思.3.4.1 更好理解变式教学的内涵.设计变式的目的,意在更好促进学生感悟数学方法,理解数学本质.就本课而言,让学生感悟、提炼基本图形的本质,并迁移运用应是教学的核心目标,为此,设计从引例到例2的三个变式,就是承载此目标的工具.但在教学中我们遗憾的看到,这里的提炼与概括都是教师帮助完成的.从教学行为分析,主要是老师担心学生讲不好而怕耽误时间,因为后面2个例题的安排显然是本课的重头戏.而从学生角度分析,虽然三个系列变式彼此相关,但要从中提炼本质,恐怕也还是有一定难度的.因此,是否可以考虑把这三个例题整合成引例的三个系列问题,即从求内接正方形边长→求两邻边长存在等量关系的内接矩形边长(如PQ:PN=2:5)→变任意内接矩形(用几何画板演示),问这些矩形中是否最大面积的矩形?这样就能使问题之间更连贯,内在结构更紧密,层次之间更清晰,也更符合学生的认知规律.从而也就有利于学生领悟图形本质,也能为后续学习留出必要的时间与空间.3.4.2 正确把握铺垫的意义.在学生的认知障碍点、思维困惑处进行适当的铺垫,其目的在于为学生搭建“思维的脚手架”,从而为教师引导学生自主探究、突破教学难点提供一条思维通道.因此,设置铺垫必须认真考虑学生原有的认知起点与认知能力.从这个意义上讲,本课设置的一些铺垫就值得商榷.如例2中为求矩形的最大面积,先设计了用x表示PN的长.这样的设计过于直白,同时也把本题蕴藏的教育功能(模型意识,关系意识等)异化成机械的运算操练,这显然不是编制本题的用意所在.实际上,求内接矩形的最大面积,自然会引发学生联想函数模型,而要构建函数模型,自然也能想到用x表示PN的长.同样,例3中先求临界状态时正方形边长的设计,有为求而求的嫌疑.从逻辑上讲,要求重叠部分的图形面积,首先要思考图形的形状是否有变化,若无变化,该如何求?若有变化,则必须考虑有哪几类变化,分界点分别在哪里?这样的引导,才能赋予学生一般有用的思维策略,也是数学教学的本质所在.故此,正确认识铺垫的意义,才能科学合理的进行问题设计,也能更好促进学生的思维发展. 另外,本课教学中教师若能更大胆一些,在适当的引领与启发下放手让学生参与问题变式的引申或改编,或许能激发学生更为浓厚的学习兴趣与更强的主体参与意识,从而亦使教学效果更加优化.当然,这也是一个非常值得研究的课题.作者简介:[1]王宝金.1981年11月出生,浙江绍兴人,现为浙江绍兴县柯岩中学数学教研组长.主要从事初中数学课堂教学研究.联系电话:[2]张宏政.1968年3月出生,浙江定海人,现为浙江舟山南海实验初中教学管理处主任,是舟山市学科带头人,曾在省级以上数学期刊发表学术文章30多篇,参编竞赛书籍多本.主要从事初中数学教学研究.联系电话:。

4.5相似三角形的性质及应用一、相似三角形的性质1．相似三角形的对应角相等，对应边的比相等. 2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高，对应中线，对应角平分线的比都等于相似比. 要点：要特别注意“对应”两个字，在应用时，要注意找准对应线段. 3. 相似三角形周长的比等于相似比∽，则由比例性质可得：4. 相似三角形面积的比等于相似比的平方∽，则分别作出与的高和，则21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D '''''''⋅⋅⋅⋅=='''''''''⋅⋅△△要点：相似三角形的性质是通过比例线段的性质推证出来的. 二、三角形的重心三角形三条中线的交点叫做三角形的重心，三角形的重心分每一条中线成1:2的两条线段.OEFDABC即12OD OE OF OA OB OC === . 要点：H OEFDAB C过点E 作EH ∥BC 交AD 于H ，根据三角形的中位线平行于第三边并且等于第三边的一半可得CD=2EH ，从而得到BD=2EH ，再根据△BDO 和△EHO 相似，利用相似三角形对应边成比例列出比例式计算即可得证1=2OE HE OB BD ，同理其他比例也可以得到． 三、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点：测量旗杆的高度的几种方法：平面镜测量法 影子测量法 手臂测量法 标杆测量法2.测量距离测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。

1．如甲图所示，通常可先测量图中的线段DC 、BD 、CE 的距离（长度），根据相似三角形的性质，求出AB 的长.2．如乙图所示，可先测AC 、DC 及DE 的长，再根据相似三角形的性质计算AB 的长.要点：1．比例尺：表示图上距离比实地距离缩小的程度，比例尺= 图上距离/ 实际距离;2．太阳离我们非常遥远，因此可以把太阳光近似看成平行光线．在同一时刻，两物体影子之比等于其对应高的比;3．视点：观察事物的着眼点（一般指观察者眼睛的位置）; 4. 仰（俯）角：观察者向上（下）看时，视线与水平方向的夹角． 一、单选题1．两三角形的相似比是2：3，则其对应角的角平分线之比是（ ） A ．2:3 B ．2：3 C ．4：9 D ．8：27 【解答】B【提示】根据相似三角形对应角平分线的比等于相似比解答即可． 【详解】解：∵两三角形的相似比是2：3， ∴相似三角形对应角平分线的比是2：3，故选：B ．【点睛】本题考查了相似三角形的性质，主要利用了相似三角形对应角平分线的比，对应高的比，对应中线的比都等于相似比的性质．2．已知ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2，若BC 边上的中线长为1，则EF 边上的中线长是（ ） A ．2 B ．2 C ．3D ．4【解答】A【提示】由ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2可知：相似比为1:2，则对应中线的比为1:2，即可求出答案．【详解】∵ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2 ∴相似比为1:2 ∴其对应中线的比为1:2 ∵BC 边上的中线长为1 ∴EF 边上的中线长是2 故选：A【点睛】本题主要考查了相似三角形的相似比的相关知识点，熟练掌握相似三角形面积比、相似比、对应边的高线、中线的比的关系是解题的关键，属于基础知识题．3．如图点D 、E 分别在△ABC 的两边BA 、CA 的延长线上，下列条件能判定ED ∥BC 的是（ ）．A ．AD DEAB BC =； B ．AD AE AC AB =；C ．AD AB DE BC ⋅=⋅； D ．AD AC AB AE ⋅=⋅． 【解答】D【提示】根据选项选出能推出ADE ABC ∆∆∽，推出D B ∠=∠或E C ∠=∠的即可判断． 【详解】解：A 、∵AD DEAB BC =，EAD BAC ∠=∠，不符合两边对应成比例及夹角相等的相似三角形判定定理. 无法判断ADE ∆与ABC ∆相似，即不能推出//DE BC ，故本选项错误；B 、AD AE AC AB =EAD BAC ∠=∠， ADE ACB ∴∆∆∽，E B ∴∠=∠，D C ∠=∠，即不能推出//DE BC ，故本选项错误；C 、由AD AB DE BC ⋅=⋅可知AB DEBC AD =，不能推出DAE BAC ∆∆∽，即不能推出D B ∠=∠，即不能推出两直线平行，故本选项错误；D 、∵AD AC AB AE ⋅=⋅，AD AEAB AC ∴=，EAD BAC ∠=∠， DAE BAC ∴∆∆∽，D B ∴∠=∠，//DE BC ∴，故本选项正确；故选：D ．【点睛】本题考查了相似三角形的性质和判定和平行线的判定的应用，主要考查学生的推理和辨析能力，注意：有两组对应边的比相等，且这两边的夹角相等的两三角形相似． 4．已知ABC 与DEF 相似，且A D ∠=∠，那么下列结论中，一定成立的是（ ） A ．B E ∠=∠ B ．AB ACDE DF =C ．相似比为AB DED ．相似比为BCEF【解答】D【提示】根据相似三角形的性质对不同的对应角和对应边进行分类讨论．【详解】解：∵B 可以与E 对应，也可以与F 对应，∴∠B=∠E 或∠B=∠F ，A 不一定成立； 同上，AB 可以与DE 对应，也可以与DF 对应，∴AB AC DE DF =或AB ACDF DE =，B 不一定成立；同上，AB 可以与DE 对应，也可以与DF 对应，∴相似比可能是AB DE ，也可能是ABDF ，C 不一定成立；∵∠A=∠D ，即∠A 与∠D 是对应角，∴它们的对边一定是对应比，即BC 与EF 是对应比，∴相似比为BCEF ，∴D 一定成立， 故选D ．【点睛】本题考查相似三角形的性质，注意相似三角形的性质是针对对应角和对应边而言的． 5．如图，小明站在 C 处看甲、乙两楼楼顶上的点 A 和点 E ．C ，E ，A 三点在同一直线上，B ，C 相距 20 米，D ，C 相距 40 米，乙楼的高 BE 为 15 米，小明的身高忽略不计，则甲楼的高 AD 为 （ ）A ．40 米B ．20 米C ．15 米D ．30 米【解答】D【提示】证明ADC EBC ∽△△，利用相似三角形的性质解答即可． 【详解】解：由题意可知：90ADC ∠=︒，90EBC ∠=︒，C ∠是公共角，∴ADC EBC ∽△△， ∴AD DCEB BC =， ∵20m BC =，40m DC =，15m BE =， ∴40=15=30m 20DC AD EB BC =⨯⨯．故选：D【点睛】本题考查相似三角形的判定及性质，解题的关键是熟练掌握相似三角形的判定及性质． 6．如图，在Rt △ABC 中，90ACB ∠=，CD AB ⊥垂足为D ，那么下列结论错误的是（ ）A ．22AC BD BC AD ⋅=⋅B ．22BC BD CD AB ⋅=⋅C ．AD BC AC CD ⋅=⋅ D ．CD BC AC BD ⋅=⋅ 【解答】B【提示】根据直角三角形的性质与相似三角形的判定可知△ADC ∽△CDB ∽△ACB ，利用相似三角形的对应线段成比例即可求解. 【详解】∵∠ACB=90°，CD ⊥AB ， ∴△ADC ∽△CDB ∽△ACB ∴AC2=AD·AB ，BC2=BD·AB ，故22AC BD BC AD ⋅=⋅，A 正确，B 错误；∵△ADC ∽△CDB∴AD AC CDCD BC BD == ∴AD BC AC CD ⋅=⋅，CD BC AC BD ⋅=⋅,C,D 选项正确； 故选B.【点睛】此题主要考查相似三角形的判定与性质，解题的关键是熟知直角三角形的性质及相似三角形的判定.7．如图，E ，F 是平行四边形ABCD 对角线AC 上两点，AE=CF=14AC ．连接DE ，DF 并延长，分别交AB ，BC 于点G ，H ，连接GH ，则ADG BGHS S △△的值为（ ）A ．12B ．23C ．34D ．1【解答】C【提示】首先证明AG ：AB=CH ：BC=1：3，推出GH ∥AC ，推出△BGH ∽△BAC ，可得223924ADC BAC BGHBGHS S BA SSBG （）（）====,13ADG ADCSS=，由此即可解决问题．【详解】∵四边形ABCD 是平行四边形 ∴AD=BC ，DC=AB ， ∵AC=CA ， ∴△ADC ≌△CBA ， ∴S △ADC=S △ABC ，∵AE=CF=14AC ，AG ∥CD ，CH ∥AD ，∴AG ：DC=AE ：CE=1：3，CH ：AD=CF ：AF=1：3， ∴AG ：AB=CH ：BC=1：3， ∴GH ∥AC ， ∴△BGH ∽△BAC ， ∴223924ADC BAC BGHBGHS S BA S SBG （）（）====，∵13ADG ADCS S=，∴913434ADG BGHS S=⨯=.故选C ．【点睛】本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识，解题的关键是灵活运用所学知识解决问题，属于中考选择题中的压轴题．8．如图，在正方形ABCD 中，ABP 是等边三角形，AP 、BP 的延长线分别交边CD 于点E 、F ，联结AC 、CP 、AC 与BF 相交于点H ，下列结论中错误的是（ ）A ．AE=2DEB ．CFP APHC ．CFP APCD ．2CP PH PB =⋅【解答】C【提示】A.利用直角三角形30度角的性质即可解决问题． B.根据两角相等两个三角形相似即可判断．C.通过计算证明∠DPB≠∠DPF ，即可判断．D.利用相似三角形的性质即可证明． 【详解】解：∵四边形ABCD 是正方形， ∴∠D=∠DAB=90°， ∵△ABP 是等边三角形， ∴∠PAB=∠PBA=∠APB=60°， ∴∠DAE=30°， ∴AE=2DE ，故A 正确; ∵AB ∥CD ，∴∠CFP=∠ABP=∠APH=60°，∵∠PHA=∠PBA+∠BAH=60°+45°=105°， 又∵BC=BP ，∠PBC=30°， ∴∠BPC=∠BCP=75°， ∴∠CPF=105°，∴∠PHA=∠CPF ，又易得∠APB=∠CFP=60°， ∴△CFP ∽△APH ，故B 正确; ∵∠CPB=60°+75°=135°≠∠DPF ， ∴△PFC 与△PCA 不相似，故C 错误; ∵∠PCH=∠PCB-∠BCH=75°-45°=30°， ∴∠PCH=∠PBC ， ∵∠CPH=∠BPC ， ∴△PCH ∽△PBC ，∴PC PHPB PC =,∴PC2=PH•PB ，故D 正确， 故选：C ．【点睛】本题考查相似三角形的判定和性质，等边三角形的性质，正方形的性质，直角三角形30度角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．9．如图所示，D 、E 分别是ABC ∆的边AB 、BC 上的点，且//DE AC ，AE 、CD 相交于点O ．若45::2DOE COA S S ∆∆=，则BDES ∆与CDE S ∆的比是（ ）A ．1：2B ．1： 3C ．2：3D ．2：5 【解答】C【提示】利用相似三角形的性质解决问题即可． 【详解】解：∵//DE AC ， ∴DEO CAO ∆∆∽， ∵45::2DOE COA S S ∆∆=，∴2425DE AC ⎛⎫=⎪⎝⎭，∴25DE AC =， ∵//DE AC ， ∴25BE DE BC AC ==， ∴23BE EC =，∴BDES ∆与CDE S ∆的比2:3=，故选：C ．【点睛】本题主要考查的是相似三角形的性质和判定，熟练掌握相似三角形的性质和判定定理是解题的关键．10．如图，正方形ABCD 和正方形CGFE 的顶点,,C D E 在同一条直线上，顶点, ,B C G 在同一条直线上．O 是EG 的中点，EGC ∠的平分线GH 过点D ，交BE 于点H ，连接FH 交EG 于点M ，连接OH 交EC 于点N ．则BCCG 的值为（ ）A ．31-B ．3C ．21-D ．2【解答】C【详解】∵四边形ABCD 和四边形CGFE 是正方形，,,BC DC CE CG BCE DCG ∴==∠=∠．在BCE和DCG △中，,,(),,BC DC BCE DCG BCE DCG SAS BEC BGH CE CG =⎧⎪∠=∠∴∴∠=∠⎨⎪=⎩≌．90BGH CDG ∠+∠=︒，,90CDG HDE BEC HDE ∠=∠∴∠+∠=︒．GH BE ∴⊥．GH 平分,EGC BGH EGH ∠∴∠=∠．()BGH EGH ASA ∴≌．BH EH ∴=．又O 是EG 的中点，//HO BG ∴．D C DHN G ∴∽△△．DN HN DC CG ∴=．设HN a =，正方形ECGF 的边长是2b ，则2BC a =，22,,22b a aCD a NC b a b -==∴=，即2220a ab b +-=，解得(12)a b =-+或(12)a b =--（舍去），则221,212a BCb CG =-∴=-．二、填空题11．若两个相似三角形的面积比是9：25，则对应边上的中线的比为 _________． 【解答】3：5【提示】根据相似三角形的性质：相似三角形对应边上的中线之比等于相似比即可得出答案． 【详解】∵两个相似三角形的面积比是9：25 ∴两个相似三角形的相似比是3：5 ∴对应边上的中线的比为3：5 故答案为：3：5．【点睛】本题主要考查相似三角形的性质，掌握相似三角形的性质是解题的关键． 12．如图，△ABC ∽△CBD ，AB=9，BD=25，则BC=______．【解答】15【提示】根据相似三角形的性质列出比例式，代入计算即可求解． 【详解】解：∵△ABC ∽△CBD ，∴AB CBCB BD =，即2BC AB BD =⨯， AB=9，BD=25，2292522515BC AB BD ∴=⨯=⨯==，15BC =∴， 故答案为：15【点睛】本题考查了相似三角形的性质，根据相似三角形的性质列出比例式是解题的关键． 13．一个三角形三边长度之比为2：5：6，另一个与它相似的三角形最长边为24，则三角形的最短边为_________． 【解答】8【提示】首先设与它相似的三角形的最短边的长为x ，然后根据相似三角形的对应边成比例，即可得方程，解此方程即可求得答案．【详解】解：设与它相似的三角形的最短边的长为x ，则 2624x =，∴8x =；∴三角形的最短边为8． 故答案为：8．【点睛】此题考查了相似三角形的性质．此题比较简单，注意掌握相似三角形的对应边成比例定理的应用．14．如图，在矩形ABCD 中，E 是BC 的中点，连接AE ，过点E 作EF AE ⊥交DC 于点F ．若4AB =，6BC =，则DF 的长为______．【解答】74【提示】结合矩形的性质证明BAECEF ∆∆可求得CF 的长，再利用DF CD DF =-可求解．【详解】解：四边形ABCD 为矩形，90B C ∴∠=∠=︒，4CD AB ==，90BAE AEB ∴∠+∠=︒，EF AE⊥，90AEF∴∠=︒，90AEB CEF∴∠+∠=︒，BAE CEF∴∠=∠，BAE CEF∴∆∆，::AB CE BE CF∴=，E是BC的中点，6BC=，3BE CE∴==，4AB=，4:33:CF∴=，解得94CF=，97444DF CD DF∴=-=-=．故选：7 4．【点睛】本题主要考查矩形的性质，相似三角形的判定与性质，证明BAE CEF∆∆是解题的关键．15．用杠杆撬石头的示意图如图所示，P是支点，当用力压杠杆的A端时，杠杆绕P点转动，另一端B向上翘起，石头就被撬动．现有一块石头要使其滚动，杠杆的B端必须向上翘起8cm，已知杠杆的动力臂AP与阻力臂BP之比为4：1，要使这块石头滚动，至少要将杠杆的A端向下压_____cm．【解答】32【提示】首先根据题意画出图形，然后根据△APM∽△BPN有AP AMBP BN=，然后再利用动力臂AP与阻力臂BP之比为4：1和8BN≥即可求出AM的最小值．【详解】解：如图：AM、BN都与水平线垂直，即AM∥BN；∴△APM∽△BPN；∴APBP＝AMBN，∵杠杆的动力臂AP与阻力臂BP之比为4：1，∴AMBN＝41，即AM＝4BN；∴当BN≥8cm时，AM≥32cm；故要使这块石头滚动，至少要将杠杆的端点A 向下压32cm ． 故答案为：32．【点睛】本题主要考查相似三角形的判定及性质的应用，掌握相似三角形的判定及性质是解题的关键． 16．如图，已知,20,60AB BC ACBAD DAE AD DE AE ︒︒==∠=∠=，则DAC ∠的度数为_________．【解答】40°【提示】由AB BC ACAD DE AE ==可判定△ABC ∽△ADE ，得到∠BAC=∠DAE ，再根据20BAD ︒∠=，60DAE ︒∠=，可得出∠DAC 的度数.【详解】解：∵AB BC ACAD DE AE ==， ∴~ABC ADE ， ∴60BAC DAE ︒∠=∠=， 又∵20BAD ︒∠=， ∴40DAC ︒∠=． 故答案为：40°.【点睛】本题考查了相似三角形的判定和性质，解题的关键是能根据AB BC ACAD DE AE ==判定出△ABC ∽△ADE.17．如图，已知在ABC 中，90C ∠=︒，10AB =，1cot 2B =，正方形DEFG 的顶点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长为_____．【解答】207【提示】作CM ⊥AB 于M ，交GF 于N ，由勾股定理可得出AB ，由面积法求出CM ，证明△CGF ∽△CAB ，再根据对应边成比例，即可得出答案． 【详解】作CM ⊥AB 于M ，交GF 于N ，如图所示： ∵Rt △ABC 中，∠C ＝90°，AB ＝10，1cot B 2=，∴设BC ＝k ，则AC ＝2k ，AB2＝AC2＋BC2，即：102＝（2k ）2＋k2，解得：k ＝25， ∴BC ＝25，AC ＝45， ∴CM ＝AC BC AB ⋅＝452510⨯＝4，∵正方形DEFG 内接于△ABC ， ∴GF ＝EF ＝MN ，GF ∥AB ， ∴△CGF ∽△CAB ，∴CN GF =CM AB ，即4EF EF410-=， 解得：EF ＝207；故答案为：207．【点睛】本题考查的是相似三角形的判定和性质、正方形的性质、勾股定理等知识；正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键．18．如图，在ABC 中，90ACB ∠=︒，AC BC =，点E 是边AC 上一点，以BE 为斜边往BC 侧作等腰Rt BEF △，连接,CF AF ，若6AB =，四边形ABFC 的面积为12，则AE =_________，AF =_________．【解答】 234【提示】如图，过点E 作EH AB ⊥于H ，过点F 作FQ AC ⊥，交AC 的延长线于Q ，由面积和差关系可求3BCF S ∆=，通过证明ABE CBF ∆∆∽，可得2()ABE BCF S AB S BC∆∆=，可求2EH =，由勾股定理可求AE ，BE ，EF 的长，通过证明BEH EFQ ∆∆∽，可得2BE EH BH EF QF EQ ===，可求22EQ =，2QF =，由勾股定理可求解．【详解】解：如图，过点E 作EH AB ⊥于H ，过点F 作FQ AC ⊥，交AC 的延长线于Q ，90ACB ∠=︒，AC BC =，2AB BC ∴，=6AB ，32AC BC ∴==四边形ABFC 的面积为12，12ABC BCF S S ∆∆∴+=， 3BCF S ∆∴=，等腰Rt BEF ∆，2BE BF ∴，45EBF∠=︒，=45ABC ∠︒，ABE CBF ∴∠=∠，2AB BE BC FB == ABE CBF ∴∆∆∽，∴2()ABE BCF S AB S BC ∆∆=， 326ABE S ∆∴=⨯=，∴162AB EH ⨯=，2EH ∴=，45CAB ∠=︒，EH AB ⊥，45CAB AEH ∴∠=∠=︒，2AH EH ∴==，222AE EH ==，4BH ∴=，2CE =，2221825BE CE BC ∴=+=+=，10EF ∴=，180AEH BEH FEB QEF ∠+∠+∠+∠=︒， 90BEH FEQ ∴∠+∠=︒，且90BEH EBH ∠+∠=︒EBH QEF ∴∠=∠，且90Q BHE ∠=∠=︒，BEH EFQ ∴∆∆∽， ∴2BE EH BHEF QF EQ ===， 22EQ ∴=，2QF =， 42AQ ∴=，2232234AF AQ QF ∴=+=+=，故答案为：22，34．【点睛】本题考查了相似三角形的判定和性质，等腰直角三角形的性质，勾股定理等知识，利用相似三角形的性质求出EH 的长是本题的关键．三、解答题19．如图，在ABP 中，C ，D 分别是,AP BP 上的点．若4,5,6,3CD CP DP AC BD =====．(1)求证：ABP DCP ∽△△； (2)求AB 的长． 【解答】(1)见解析(2)AB＝8【提示】（1）△ABP与△DCP有公共角，分别计算PDPC与APBP的值，得到PD PCPA PB=，根据相似三角形的判定定理得出结论；（2）运用相似三角形的性质计算即可．（1）证明：∵CD＝CP＝4，DP＝5，AC＝6，BD＝3，∴AP＝AC+CP＝6+4＝10，BP＝BD+DP＝3+5＝8，∴54PDPC=，10584APBP==，∴PD APPC BP=，即PD PCPA PB=，∵∠DPC＝∠APB，∴△ABP∽△DCP；（2）解：∵△ABP∽△DCP，∴AB PBCD PC=，即844AB=，∴AB＝8．【点睛】本题考查了相似三角形的判定与性质，属于基础题．解决问题的关键是掌握：有两边对应成比例且夹角相等的两个三角形相似．20．如图，在矩形ABCD中，AB：BC＝1：2，点E在AD上，BE与对角线AC交于点F．(1)求证：△AEF∽△CBF；(2)若BE⊥AC，求AE：ED．【解答】(1)见解析(2)1：3【提示】（1）根据矩形的性质得到AD∥BC，然后根据相似三角形的判断方法可判断△AEF∽△CBF；（2）设AB=x，则BC=2x，利用矩形的性质得到AD=BC=2x，∠BAD=∠ABC=90°，接着证明△ABE∽△BCA，利用相似比得到AE=12x，则DE=32x，从而可计算出AE：DE．（1）解：证明：∵四边形ABCD为矩形，∴AD∥BC，∴△AEF∽△CBF；（2）设AB=x，则BC=2x，∵四边形ABCD为矩形，∴AD=BC=2x，∠BAD=∠ABC=90°，∵BE⊥AC，∴∠AFB=90°，∵∠ABF+∠BAF=90°，∠BAC+∠ACB=90°，∴∠ABF=∠ACB，∵∠BAE=∠ABC，∠ABE=∠BCA，∴△ABE∽△BCA，∴AE ABAB BC=，即2AE xx x=，∴AE=12x，∴DE=AD-AE=32x，∴AE：DE=13:22x x=1：3．【点睛】本题考查了三角形相似的判定与性质，应注意利用图形中已有的公共角、公共边等条件，同时利用相似三角形的性质进行几何计算．也考查了矩形的性质．21．如图，为了测量平静的河面的宽度EP，在离河岸D点3.2米远的B点，立一根长为1.6米的标杆AB，在河对岸的岸边有一根长为4.5米的电线杆MF，电线杆的顶端M在河里的倒影为点N，即PM PN=，两岸均高出水平面0.75米，即0.75DE FP==米，经测量此时A、D、N三点在同一直线上，并且点M、F、P、N N共线，点B、D、F共线，若AB、DE、MF均垂直与河面EP，求河宽EP是多少米？【解答】河宽为12米【提示】连接DF ，根据题意可得出四边形DEPF 为矩形，由ADB NDF ∽△△可求得DF ，便可解决问题．【详解】解：如图，连接DF ，∵点B 、D 、F 共线，DE 、MF 均垂直与河面EP ，且0.75DE FP ==， 4.5MF =， ∴四边形DEPF 为矩形， ∴DF EP =，∴ 4.50.75 5.25PN FM FP =+=+=， ∴ 5.250.756FN PN FP =+=+=， ∵AB 、DE 、MF 均垂直与河面EP ， ∴90ABD NFD ∠=∠=︒， ∵ADB NDF ∠=∠， ∴ADB NDF ∽△△； ∴AB NFBD DF =， ∵ 1.6AB =， 3.2BD =， ∴1.663.2DF =，∴12DF =， ∴12EP =（米）． 答：河宽EP 是12米．【点睛】本题主要考查了相似三角形的性质与判定，矩形的判定和性质等知识．关键是构造和证明三角形相似．22．如图，已知AD ，BC 相交于点E ，且△AEB ∽△DEC ，CD ＝2AB ，延长DC 到点G ，使CG ＝12CD ，连接AG ．(1)求证：四边形ABCG 是平行四边形；(2)若∠GAD ＝90°，AE ＝2，CG ＝3，求AG 的长． 【解答】(1)证明见解析； (2)35AG =【提示】（1）根据相似三角形的性质可得AB ∥CD ，再由CD ＝2AB ，CG ＝12CD ，可得AB ＝CG ，即可证明；（2）由平行四边形的性质可得AG ∥BC ，可得∠AEB ＝90°，再由CG ＝3可得AB ＝3，利用勾股定理可得BE ，再由相似三角形的性质可得CE ，从而得出BC ，即可求解． （1）证明：∵△AEB ∽△DEC ， ∴∠B ＝∠BCD ， ∴AB ∥CD ， 即AB ∥CG ，∵CD ＝2AB ，CG ＝12CD ，∴AB ＝CG ，∴四边形ABCG 是平行四边形； （2）解：∵四边形ABCG 是平行四边形，AE ＝2，CG ＝3， ∴AG ∥BC ，AG ＝BC ，AB ＝CG ＝3， ∵∠GAD ＝90°， ∴∠AEB ＝90°，在Rt △ABE 中，由勾股定理可得：BE 22AB AE -即BE ＝22325-=，∵△AEB ∽△DEC ， ∴12BE AB CE CD ==， ∴CE ＝25，∴BC ＝BE+CE ＝35， ∴AG ＝BC ＝35．【点睛】本题考查相似三角形的性质，勾股定理，平行四边形的判定与性质，解题的关键是熟练掌握相似三角形的性质，勾股定理的运用，平行四边形的判定与性质．23．如图，在△ABC 中，AD 是角平分线，点E 是边AC 上一点，且满足ADE B ∠=∠．(1)证明：ADB AED ∆∆；(2)若3AE =，5AD =，求AB 的长． 【解答】(1)见解析(2)253【提示】（1）证出∠BAD=∠EAD ．根据相似三角形的判定可得出结论； （2）由相似三角形的性质可得出AD ABAE AD =，则可得出答案． （1）∵AD 是∠BAC 的角平分线， ∴∠BAD=∠EAD ． ∵∠ADE=∠B ， ∴△ADB ∽△AED ． （2）∵△ADB ∽△AED ， ∴AD ABAE AD =，∵AE=3，AD=5， ∴535AB =， ∴253AB =． 【点睛】本题考查了相似三角形的判定与性质以及三角形内角和定理，熟练掌握相似三角形的判定定理和性质定理是解题的关键．24．已知：平行四边形ABCD ，E 是BA 延长线上一点，CE 与AD 、BD 交于G 、F ．求证：2CF GF EF =⋅．【解答】见解析【提示】根据平行四边形的性质得到AD BC ∥，AB CD ∥，得到△DFG ∽△BFC ，△DFC ∽△BFE ，根据相似三角形的性质列出比例式，计算即可． 【详解】证明：∵四边形ABCD 是平行四边形， ∴AD BC ∥，AB CD ∥，∴△DFG ∽△BFC ，△DFC ∽△BFE ∴GF DF CF BF =，CF DFEF BF =， ∴GF CFCF EF =， 即2CF GF EF =⋅．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．25．如图，已知cm,cm,23,36,117AD a AC b BC AC B D ===∠∠=︒=︒，ABC DAC △∽△．（1）求AB 的长；（2）求DC 的长； （3）求BAD ∠的度数．【解答】（1）32cm a ；（2）2cm3b ；（3）153︒【提示】（1）由ABC DAC △∽△，可得：,AB BCAD AC =再代入数据可得答案；（2）由ABC DAC △∽△，可得：,AC BCDC AC =再代入数据可得答案；（3）由ABC DAC △∽△，可得：117,36,BAC D B DAC ∠=∠=︒∠=∠=︒再利用角的和差可得答案； 【详解】解：（1）23,,BC AC AD a ==3,2BC AC ∴= ABC DAC △∽△，,AB BCAD AC ∴= 3,2AB a ∴= 3.2AB a ∴=（2） ABC DAC △∽△，,AC BCDC AC ∴= 而3,,2BC AC b AC == 3,2b DC ∴=2.3DC b ∴=（3） ABC DAC △∽△，36,117,B D ∠=︒∠=︒117,36,BAC D B DAC ∴∠=∠=︒∠=∠=︒11736153.BAD BAC DAC ∴∠=∠+∠=︒+︒=︒【点睛】本题考查的是相似三角形的性质，掌握相似三角形的对应角相等，对应边成比例是解题的关键.26．如图，在四边形ABCD 中，AC ，BD 交于点F ．点E 在BD 上，且BAE CAD ∠=∠，AB ACAE AD =．(1)求证：ABC AED ∽△△． (2)若20BAE ∠=︒，求∠CBD 的度数． 【解答】(1)证明见解析 (2)20︒【提示】（1）根据两边对应成比例，且夹角相等，两个三角形相似，即可证明．（2）根据（1）中ABC AED ∽△△，得出ADB ACB ∠=∠，再根据对顶角相等，AFD BFC ∠=∠，证得AFD BFC ∽△△，得出CBD CAD BAE ∠=∠=∠，即可求解． （1）∵BAE CAD ∠=∠∴BAE EAF CAD EAF ∠+∠=∠+∠， ∴BAC DAE ∠=∠， AB ACAE AD =，∵在ABC 和AED △中， AB ACAE AD BAC DAE ⎧=⎪⎨⎪∠=∠⎩，∴ABC AED ∽△△． （2）∵ABC AED ∽△△， ∴ADB ACB ∠=∠，又∵AFD BFC ∠=∠，对顶角相等，∴AFD BFC ∽△△， ∴CBD CAD ∠=∠，∵BAE CAD ∠=∠，20BAE ∠=︒，∴20CAD ∠=︒， 故答案为：20︒．【点睛】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键． 27．如图，四边形ABCD 为正方形，且E 是边BC 延长线上一点，过点B 作BF ⊥DE 于F 点，交AC 于H 点，交CD 于G 点．(1)求证：△BGC ∽△DGF ； (2)求证：GD AB DF BG ⋅=⋅； (3)若点G 是DC 中点，求GFCE 的值．【解答】(1)见解析 (2)见解析 (3)5GF CE=【提示】（1）由正方形性质和题干已知垂直条件得直角相等，后由对顶角相等，进而得到△BGC ∽△DCF ．（2）由第一问的结论可得到相似比，既有DG BC DF BG ⋅=⋅，然后因为正方形四边相等，进行等量代换即可求出证明出结论．（3）通过ASA 判定出△BGC ≌△DEC ，进而根据第一问结论可得△BGC ∽△DGF ，然后通过相似比设未知数，赋值CG x =，即可求出GFCE 的值．（1）证明：∵四边形ABCD 是正方形 ∴90BCD ADC ∠=∠=︒ ∵BF DE ⊥ ∴90GFD ∠=︒ ∴BCD GFD ∠=∠，又∵BGC DGF ∠=∠， ∴△BGC ∽△DCF ． （2）证明：由（1）知△BGC ∽△DGF ， ∴BG BCDG DF =， ∴DG BC DF BG ⋅=⋅ ∵四边形ABCD 是正方形， ∴AB BC =∴DG AB DF BG ⋅=⋅． （3）解：由（1）知△BCC ∽△DGF ， ∴FDG CBG ∠=∠，在△BGC 与△DEC 中，,{,=,CBG CDE BCG DCE BC CD ∠=∠∠=∠ ∴△BGC ≌△DEC （ASA ） ∴CG EC = ∵G 是CD 中点 ∴CG DG = ∴::GF CE CF DC = ∵△BGC ∽△DGF ∴::GF DG CG BG =在Rt △BGC 中，设CG x =，则2BC x =，BC =∴CG BG =∴GF CE=【点睛】本题主要考查了正方形的性质，全等三角形判定和性质，相似三角形判定和性质等知识点，熟练运用相似三角形判定和性质是解题的关键．28．如图1，在ABC 中，90ACB ∠=︒，AC BC =，点D 是AB 边上一点（含端点A 、B ），过点B 作BE 垂直于射线CD ，垂足为E ，点F 在射线CD 上，且EF BE =，连接AF 、BF ．（1）求证：ABF CBE ∽；（2）如图2，连接AE ，点P 、M 、N 分别为线段AC 、AE 、EF 的中点，连接PM 、MN 、PN ．求PMN ∠的度数及MNPM 的值；（3）在（2）的条件下，若2BC =PMN 面积的最大值．【解答】（1）证明见解析；（2）135PMN ∠=；=2MN PM 3）14 【提示】（1）根据两边对应成比例，夹角相等判定即可．（2）PMN ∠的值可以根据中位线性质，进行角转换，通过三角形内角和定理求解即可，MNPM 的比值转换为AFCE 的比值即可求得.（3）过点P 作PQ 垂直于NM 的延长线于点Q ，12PMN S MN PQ =△，将相关线段关系转化为CE ，可得关系218PMN S CE =△，观察图象，当2CE BC == 【详解】（1）证明：∵90ACB ∠=︒，AC BC = ∴2AB BC =,45ABC BAC ∠=∠= ∵BE 垂直于射线CD , ∴90,BEF ∠= 又∵EF BE =∴2FB EB =,45FBE EFB ∠=∠= ∵+ABC ABE ABE FBE ∠∠=∠+∠ 即：ABF CBE ∠=∠又∵2AB BFCB BE == ∴ABF CBE ∽（2）解：∵点P 、M 、N 分别为线段AC 、AE 、EF 的中点∴//PM CN ，//MN AF ，11,22PM CE MN AF== ∴MPN CNP ∠=∠,CNM EFA ∠=∠∴+MPN MNP CNP MNP CNM EFA ∠∠=∠+∠=∠=∠ 又∵ABF CBE ∽ ∴90AFB CEB ∠=∠= 又∵45EFB ∠=∴904545EFA AFB BFE ∠=∠-∠=-= ∴+45MPN MNP ∠∠=又∵++180MPN MNP PMN ∠∠∠= ∴18045135PMN ∠=-=又∵12=12AFMN AFPM CECE = 又∵ABF CBE ∽ ∴=2AF AB CE CB = ∴=2MNPM（3）如下图：过点P 作PQ 垂直于NM 的延长线于点Q , 135,PMN ∠=︒ 45,PMQ MPQ ∴∠=︒=∠,PQ ∴= 111221222228216PMNS MN PQ AF PM AF CE AF CE ==⨯⨯==△又∵BC =∴AF =∴221168PMN S CE ==△∴当CE 取得最大值时，PMN 取得最大值， ,BE CE ⊥E ∴在以BC 的中点为圆心，BC 为直径的圆上运动，∴当CE CB ==CE 最大，∴11=2=84S ⨯， 【点睛】本题考查的是三角形相似和判定、以及三角形面积最大值的求法，根据题意找见相关的等量是解题关键．。

数学解题中相似三角形性质的妙用362133 福建省惠安岩峰中学 陈硕清362100 福建省惠安高级中学 杨苍洲很早开始,人们就懂得利用相似三角形的有关性质来计算那些不能直接测的物体的高度.古希腊数学家,天文学家泰勒斯曾利用相似三角形的原理,测出金字塔的高度.其所用的方法是:在金字塔顶部的影子处立一根竹子,借住太阳光线构成两个相似三角形,塔高与竿高之比等于两者影长之比,由此便可算出金字塔的高度.测量物体的高度的方法究竟有哪些方法?利用相似三角形的性质还能解决什么问题?在初中数学解题中,适当地运用相似三角形的性质,常有意想不到的效果.现归纳如下.1利用相似三角形测量物体的高度图1方法1 利用太阳光的影子基本图形1测量数据:标杆高DE,标杆影长EF,物体影长BC,测量原理:因为太阳光AC M DF,所以N ACB =N DFE,又因为N B =N DEF =90b ,所以v ABC V v DEF,所以AB DE =BCEF.例1 为了测量学校旗杆的高度,身高1.65m 的小华和小东来到操场上,他让小东到体育室借来皮尺,量出小华的影长为0.5m,旗杆的影长为2.3m,运用这些数据,你能帮他们算出旗杆的大约高度吗?解析 设旗杆高为x m ,则有1.650.5=x2.3,解得x =7.59(m ),即旗杆的高度约为7.59m .方法2利用标杆图2基本图形2测量数据:眼(E )与地面的距离EF,人(EF )与标杆(CD )的距离,人(EF )与物体(AB )的距离BF.测量原理:因为CD M AB,所以v AEG V v CEH,所以AGCH =EGEH,所以AB =AG +EF,其中DF =EH,BF =EG.图3例2 (华东师大版九年级(上)第24章复习题C 组第17题)三国魏人刘徽,自撰5海岛算经6,专论测高望远,其中一题,是数学史上有名的测量问题,今译如下:如图,要测量海岛上一座山峰A 的高度A H,立两根高三丈的标杆BC 和DE,两竿相距BD =1000步,D,B,H 成一线,从BC 退行123步到F,人目着地观察A.A,C,F 三点共线;从DE 退行127步到G,从G 看A.A,E,G 三点也共线.试算出山峰的高度AH 和HB 的距离.(古制1步=6尺,1里=180丈=1800尺=300步.结果用里和步来表示)解析 设A H =x ,B H =y ,由v FBC V v FHA,可得 BF HF =BC AH,即123y +123=5x.¹由v GDE V v GA H ,可得DG H G =DEAH,即127y +1000+127=5x.º由¹,º联立方程组,解得x =1255,y =30750.故山峰的高度为1255步或4里55步.方法3 利用镜子的反射图4基本图形3测量数据:眼(D )到地面距离DE,人(DE )与平面镜(C )的距离CE,平面镜(C )与物体距离BC.测量原理:因为N ACB =N DCE,N B =N E,所以v ABC V v DEC,所以AB DE =BCCE.例3 王林想用镜子测量一棵古松树的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他30(2011年第1期#初中版)#解题研究#图5两次利用镜子,如图,第一次把镜子放在C 点,人在F 点正好在镜子中看到树尖A ;第二次他把镜子放在G 处,人在M 处正好看到树尖A .已知王林眼睛距地面1.7m ,量得CG 为12m ,CF 为1.8m ,GM 为3.84m ,求这棵古松树的高.解析 设树高AB =x m ,BC =y m ,由v ABC V v EFC 得EF AB =CF BC,即 1.7x =1.8y .¹由v ABG V v NMG 得NM AB =GMBG,即1.7x =3.84y +12.º由¹,º联立方程组解得x =10,即这棵松树的高为10m .2 利用相似三角形求面积问题运用性质/相似三角形的面积比等于它们的相似比的平方0解决某些面积问题常能使问题迎刃而解,这类题也是中考和数学竞赛命题的热点之一.基本图形4 如图6,在v ABC 中,DE M BC 则v ADE V v ABC,所以S 1S 2=DE BC2(其中S 1,S 2分别表示v ADE和v ABC 的面积).图6图7例4 (美国数学邀请赛试题)如图7所示,在v ABC 的内部选取一点P,过P 点作3条分别与v ABC 的三边平行的直线,这样所得的3个三角形t 1,t 2,t 3的面积分别为4,9和49,求v ABC 的面积.解析 设v ACB 的面积为t ,由DE M BC,FG M AB,I H M AC 得v FDP V v I PE V v P H G V v ACB,所以t 1t =PD BC 2,t 2t =PE BC 2,t 3t=H G BC 2,所以2+3+7t=PD +PE +H G BC =1,解得t =144.图8例5 (2004年江苏省竞赛题)如图8所示,在v ABC 中,DE M FG M BC,GI M EF M AB,若v ADE,v EFG,v GI C 的面积分别为20c m 2,45c m 2,80c m 2,求v ABC 的面积.解析 由DE M FG M BC,GI M EF M AB,得 v ADE V v EFG V v GI C.所以S v ADE S v A BC =DE BC 2,S v EFG S v ABC =FGBC 2,S v GI C S v ABC =I CBC2.又DE =BH ,FG =H I ,所以20+45+80S v ABC=B H +H I +I CBC=1,_S v ABC =405c m 2.图9基本图形5如图9所示,在v ABC 中,D 是AB 上的一点,若N AD E =N C (或N AED =N B 等等)则v ADE V v ACB,得 S v ADE Sv A BC =DE BC2.图10例6 如图10所示,设v ABC 的面积是1,D 是边BC 上的一点且CD AC =23,若在边AC 上取一点E,3CE =2BC,求四边形ABDE 的面积的值.解析 由3CE =2BC,得CE BC =23,得 CE BC =CD AC =23.31#解题研究#(2011年第1期#初中版)又N ACB =N DCE,_v CDE V v CAB._S v CDE S v CBA =CD AC 2=232=49._1-S ABDE 1=49,解得S ABDE=59.图11例7 (2007年浙江省竞赛题)如图11所示,v ABC 中,AB =AC,N A =36b ,CD 是N C 的平分线,则v DBC 的面积与v ABC 的面积的比值是 .解析 由N BCD =N A =36b ,N B =N B 得v BCD V v BAC所以BD BC =BCAB ,又BC =CD =AD,BD =AB -AD =AB -BC所以,BC 2=AB #(AB -BC ),解得BC =-1+52AB._S v DBC S v CBA =BD BC2=-1+522=3-52.3 利用相似三角形巧解折叠图形问题用相似的方法解决某些图形的折叠问题,可以达到事半功倍的效果.这类题,有利于考查学生的空间想象能力和动手操作能力,是数学竞赛命题的热点之一.图12例8 (1995年希望杯竞赛题)如图12所示,沿AE 折叠长方形ABCD,使D 点落在BC 边的点F 处,若AB =12c m ,BC =13c m ,求FC 的长度.解析 折叠后v ADE T v AFE,N AFE =N D =90b ,所以N BFA +N EFC =90b ,N BFA +N BAF =90b ,_N BAF =N EFC,又N B =N C =90b ,_v ABF V v FCE,_AB CF =AFEF,由AF =AD =BC =13,再根据勾股定理求得BF =5,所以FC =8.从而求得EF =263.图13例9 (1994年广州等城市联赛题)如图13所示,一边长AB 为25c m ,宽BC 为86c m 矩形ABCD 纸片,AD 上有一点P,且AP =66c m ,折这张纸片使点B 落在点P 上,求折痕EF 的长.解析 过F 作FM L AB 于M ,因为EF 为折痕,点B 和点P 对应,所以PB L EF,由此可得N EFM =N ABP.又N A =N AMF =90b ,_v APB V v M EF,_AB MF =PBEF .由勾股定理得BP =AP 2+AB 2=662+252=29,又M F =BC =86所以6686=29EF ,EF =1163.例10 如14图是一矩形的纸片,其中AB =12c m ,AD =16c m ,按下列步骤:将其对折,使AB 落在AD 上,得折痕AF (如图15);将v AFB 沿BF 折叠,AF 与DC 交于点G (如图15),求GC 的长.图14 图15解析 如图14中,BD =16-12=4,在图15中,AD =12-4=8,如图15中,由AB M CF,得v ADG V v FCG,_AD CF =DG CG,_84=12-CG CG,解得CG =4.(收稿日期:20101005)32(2011年第1期#初中版)#解题研究#。

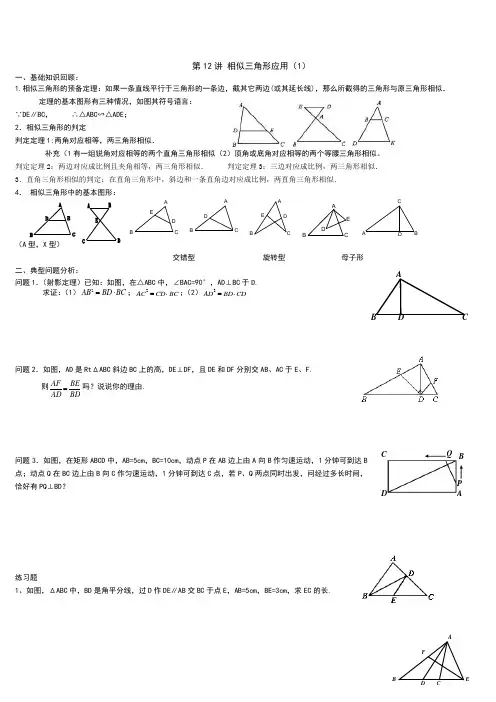
ABCDD ABCDABCA BCD E第12讲 相似三角形应用（1）一、基础知识回顾：1.相似三角形的预备定理：如果一条直线平行于三角形的一条边，截其它两边(或其延长线)，那么所截得的三角形与原三角形相似． 定理的基本图形有三种情况，如图其符号语言： ∵DE ∥BC ， ∴△ABC ∽△ADE ； 2．相似三角形的判定判定定理1:两角对应相等，两三角形相似．补充（1有一组锐角对应相等的两个直角三角形相似（2）顶角或底角对应相等的两个等腰三角形相似。

判定定理2：两边对应成比例且夹角相等，两三角形相似． 判定定理3：三边对应成比例，两三角形相似． 3．直角三角形相似的判定：在直角三角形中，斜边和一条直角边对应成比例，两直角三角形相似． 4． 相似三角形中的基本图形：（A 型，X 型）交错型 旋转型 母子形二、典型问题分析：问题1．（射影定理）已知：如图，在△ABC 中，∠BAC=90°，AD ⊥BC 于D.求证：（1）2AB BD BC =⋅；2AC CD BC =⋅；（2）2AD BD CD =⋅问题2．如图，AD 是Rt ΔABC 斜边BC 上的高，DE ⊥DF ，且DE 和DF 分别交AB 、AC 于E 、F.则BDBE AD AF =吗？说说你的理由.问题3．如图，在矩形ABCD 中，AB=5cm ，BC=10cm ，动点P 在AB 边上由A 向B 作匀速运动，1分钟可到达B 点；动点Q 在BC 边上由B 向C 作匀速运动，1分钟可到达C 点，若P 、Q 两点同时出发，问经过多长时间，恰好有PQ ⊥BD ？ 练习题1、如图，ΔABC 中，BD 是角平分线，过D 作DE ∥AB 交BC 于点E ，AB=5cm ，BE=3cm ，求EC 的长.BA BCD EQ P DCB A2.如图，已知AD 为△ABC 的角平分线，AD 的垂直平分线交BC 的延长线于点E ，交AB 与F ，试判定△BAE 与△ACE 是否相似，并说明理由。