第5章 线性系统的频域分析法[198页]
- 格式：ppt
- 大小：8.33 MB
- 文档页数：100
下载文档原格式
合集下载
第5章-线性系统的频域分析法
0.1 0.2
0.5
1
2
5
10
20
50
（） -96.3 -102.5 -116.6 -140.7 -164.7 -195.3 -219.3 -240.6 -257.5
5-4 频率域稳定判据
一、奈氏判据的数学基础 1、幅角原理
设F(s)为复变函数，F(s)
在s平面上任一点 K*(s z1)(s z2) (s zm)
G( j) j L() 20lg () 90
L(dB) 40 20
0 0.01 0.1
1
20
20dB / dec
10
-40
( ) 90
0 0.01 0.1
1
90
10
4、一阶惯性环节
G(
j)
1
Tj
1
1
e arctgT
1 T 22
L() 20 lg 1 T 22
() arg tgT
5-1 引言
频率特性是研究自动控制系统的一种工程方法，它 反映正弦信号作用下系统性能。应用频率特性可以 间接地分析系统的动态性能与稳态性能。频率特性 法的突出优点是组成系统的元件及被控对象的数学 模型若不能直接从理论上推出和计算时，可以通过 实验直接求得频率特性来分析系统的品质。其次， 应用频率特性法分析系统可以得出定性和定量的结 论，并且有明显的物理意义。在应用频率特性法分 析系统时，可以利用曲线，图表及经验公式，因此， 用频率特性法分析系统是很方便的。
1
T
() 45
L(dB) 0
20
40
60 ( )
0
1 T
精确特性
45
90
渐进特性
20dB/ dec
第5章线性系统的频域分析法
1 的对数幅相曲线 1 j0.5
0
5.2
典型环节频率特性曲线的绘制
5.1.1
频率特性的基本概念与定义
先考查图 5.1 所示的 RC 滤波网络为例，说明频率特性的基本概念．
R
ui
C
uo
图 5.1 RC 滤波网络
设 RC 网络的输入信号是幅值为 A 的正弦信号 ui A sin t ，当输出 uo 呈稳态时,记录
ui 、 uo 的曲线如图 5.2 所示．由图可见, RC 网络的稳态输出信号仍为正弦信号，频率与
5.8 为 RC 网络 T 0.5 时的尼科尔斯图．后面我们会进一步学习如何利用对数幅相曲线和 系统开环和闭环传递函数的关系，绘制关于闭环幅频特性的等 M 图和闭环相频特性的等 图．
0
5
2 3 4 7
1
L( ) / dB
10
15
20
10
100 80
图 5.8
60 40 20 ( ) /
输入信号的频率相同，只是幅值有所衰减，相位存在一定延迟．
ui
A
2
0
uo
t
0
2
t
图 5.2 RC 网络的输入和稳态输出信号
RC 网络的微分方程如下:
T
duo uo ui dt
(5.1)
式中, T RC 为时间常数．将式(5.1)取拉普拉斯变换，并代入初始条件 uo (0) uo0 ,得：
uo ( s )
1 1 A Tuo0 ui ( s) Tuo0 2 2 Ts 1 Ts 1 s
(5.2)
再将式(5.2)取拉普拉斯反变换得：
0
5.2
典型环节频率特性曲线的绘制
5.1.1
频率特性的基本概念与定义
先考查图 5.1 所示的 RC 滤波网络为例，说明频率特性的基本概念．
R
ui
C
uo
图 5.1 RC 滤波网络
设 RC 网络的输入信号是幅值为 A 的正弦信号 ui A sin t ，当输出 uo 呈稳态时,记录
ui 、 uo 的曲线如图 5.2 所示．由图可见, RC 网络的稳态输出信号仍为正弦信号，频率与
5.8 为 RC 网络 T 0.5 时的尼科尔斯图．后面我们会进一步学习如何利用对数幅相曲线和 系统开环和闭环传递函数的关系，绘制关于闭环幅频特性的等 M 图和闭环相频特性的等 图．
0
5
2 3 4 7
1
L( ) / dB
10
15
20
10
100 80
图 5.8
60 40 20 ( ) /
输入信号的频率相同，只是幅值有所衰减，相位存在一定延迟．
ui
A
2
0
uo
t
0
2
t
图 5.2 RC 网络的输入和稳态输出信号
RC 网络的微分方程如下:
T
duo uo ui dt
(5.1)
式中, T RC 为时间常数．将式(5.1)取拉普拉斯变换，并代入初始条件 uo (0) uo0 ,得：
uo ( s )
1 1 A Tuo0 ui ( s) Tuo0 2 2 Ts 1 Ts 1 s
(5.2)
再将式(5.2)取拉普拉斯反变换得：
线性系统的频域分析法
转折频率：
n 1 T
+20dB/dec
2 2
L( ) 20 lg 1 T
20 0 -20
1 T
• 低频段：T 1时，
G ( j ) j T 1 1 2T 2 e j arctanT
0
幅相曲线：
Im
∞
ω=0
1 Re
A( ) 1 T 幅频特性：
2
2
( ) arctanT 相频特性：
伯德图：
1）对数幅频图
A( ) 1 2T 2
L(ω)/dB
L( ) 20 lg
20dB/dec
ω
( )
90 0 0.1 1 10
2）对数相频图
( ) G( j ) 90
ω
微分环节的对数坐标图
（4）惯性环节
1 传递函数： G ( s ) Ts 1
频率特性： G ( j )
1 1 j T j T 1 1 2 T 2 1 e j arctanT 1 2T 2 1 幅频特性： A( ) 1 2T 2
1 G( s ) Ts 1
解: 将s=jω代入，求得频率特性为：
1 G( j ) G( s ) s j jT 1 1 T j 2 2 2 2 1 T 1 T
1 1 2T 2
11
e j arctanT
2 2T 22 1 1 T ( ) G( j ) arctan T 相频特性： T 虚频特性： Q( ) Im[ G ( j )] 1 2T 2
R(s) C(s)
G(s)
结论： 稳定的系统，在正弦信号作用下其稳态 输出也是同频率的正弦信号，但振幅和相 位不同。
自动控制原理-胡寿松-第五章-线性系统的频域分析法
第四象限
第三象限
Mr
注意： （特殊点与趋势） 1. A(0) 1, (0) 0; A() 0, () 180 2. 与虚轴的交点 （转折点，是阻尼比的减函数） 2 (0 ) 3.有谐振时， 2 r , M r 为 的减函数 。当 2 0.707 时，谐振峰值 M r 1 。 2
7.延迟环节和延迟系统
1.典型环节
2.最小相位环节的频率特性
（考试、考研重点，nyquist图与bode图必须会画，概率图）
考试的标准画法
L(dB)
20
10
20 lg k
0
10
1
10
100
1000
o
( )
10
0
1
10
100
1000
10
比例环节的nyquist图与bode图
本节目录 1.典型环节 2.最小相位环节的频率特性（Nyquist图与bode图） 3.非最小相位环节的频率特性（Nyquist图与bode图） 4.系统的开环幅相曲线（Nyquist图） 5.系统的开环对数频率特性曲线（bode图）
重点掌握最小相位情况的各个知识点，非最小相位情况的考试不考，考研可能考。 6.传递函数的频域实验确定
考试的标准画法
o
注意考察几个特殊点： A(0), (0);
积分环节的nyquist图与bode 图
A(), ()
与横轴的交点。 注意横竖坐标交点处的的横坐标值（如果交点处没标横坐标值，则斜线不到头）
比较交点不标记的情况
0
0
纯微分环节的Bode图
半对数坐标系中的直线方程（重要，bode图解计算时经常用到）
第五章线性系统的频域分析法
对 A(ω ) 求导并令等于零，可解得 A(ω ) 的极值对应的频率 ω r 。
ω r = ω n 1 2ζ 2
该频率称为谐振峰值频率。可见，当 ζ = 当ζ
> 1 2
s = jω
G( jω) =| G( jω) | e
j∠G( jω)
= A(ω)e
j (ω)
G( jω) = G(s) |s= jω
G( jω) = G(s)|s= jω =| G( jω)| e j∠G( jω) = A(ω)e j(ω)
A A j (ω ) k1 = G( jω ) e k2 = G( jω ) e j (ω ) 2j 2j
可以作为系统模型
G( jω) = G(s) |s= jω = G( jω) e j(ω)
定义 幅频特性
A(ω ) =| G( jω ) |
(ω ) = ∠G ( jω )
它描述系统对不同频率输入信号在稳态时的放大特性； 它描述系统对不同频率输入信号在稳态时的放大特性； 相频特性
它描述系统的稳态响应对不同频率输入信号的相位移特性； 它描述系统的稳态响应对不同频率输入信号的相位移特性； 幅频特性和相频特性可在复平面上构成一个完整的向量 G ( jω ), 频率特性。 频率特性 G ( jω ) = A(ω )e j (ω ) ，它也是 ω 的函数。G( jω) 称为频率特性 还可将 G ( jω ) 写成复数形式，即
A(ω ) = 1 1 + T 2ω 2 ,
G (s) =
1 Ts + 1
G ( jω ) =
1 jT ω + 1
(ω ) = tg 1T ω
幅频特性 L(ω) = 20log A(ω) = 20log K 20log 1+ T 2ω2 低频段：当Tω << 1时，ω 高频段：当 Tω >> 1时， ω
第五章 线性系统的频域分析法
-20dB
( ) 90
20dB/dec 1
20dB/dec
振荡环节 (0 1)
2 n 2 2 1 传递函数： G(s) 2 2 s 2 n s n T s 2Ts 1
频率特性： G(j )
幅频特性：
1 T 2 2 j 2 T 1
L() 20lg 22 1
() tg1 ()
结论 ① 非最小相位环节和对应的最小相位环节 幅频特性相同，相频特性符号相反，幅相曲线关于实轴对称。 对数幅频曲线相同，对数相频曲线关于0o线对称。
A( ) 1 1 T 2 2
1 例如，最小相位的惯性环节 Ts 1 :
3 对数幅频渐进特性曲线
近似表示对数幅频曲线，可简化作图，分低频和高频两部分。 以惯性环节为例，其对数幅频特性为： 1 L( ) 20 lg 20 lg 1 T 2 2 1 T 2 2
1 当T 1即 时， L() 20lg1 0 低频部分，零分贝线。 T 1 高频部分，斜率为 当T 1即 时， L() 20lg T -20db/dec的直线。 T 令L(ω( 0，得 ω 1 ，因此 T 两条线交于 1 处，称 1 为惯性环节的交接频率。
式中 A( )
幅值比
1 1 T
2 2
,
( ) arctanT
相位差
为了得到频率特性的定义，我们将其与传递函数联系起来。
1 RC网络的传递函数为：G ( s ) Ts 1
取s=jω，则：
1 分子分母同乘 1 jT 1 G( j ) (1 jT ) 2 2 2 2 jT 1 jT 1 1 T 1 T
对数相频
( ) 90
20dB/dec 1
20dB/dec
振荡环节 (0 1)
2 n 2 2 1 传递函数： G(s) 2 2 s 2 n s n T s 2Ts 1
频率特性： G(j )
幅频特性：
1 T 2 2 j 2 T 1
L() 20lg 22 1
() tg1 ()
结论 ① 非最小相位环节和对应的最小相位环节 幅频特性相同，相频特性符号相反，幅相曲线关于实轴对称。 对数幅频曲线相同，对数相频曲线关于0o线对称。
A( ) 1 1 T 2 2
1 例如，最小相位的惯性环节 Ts 1 :
3 对数幅频渐进特性曲线
近似表示对数幅频曲线，可简化作图，分低频和高频两部分。 以惯性环节为例，其对数幅频特性为： 1 L( ) 20 lg 20 lg 1 T 2 2 1 T 2 2
1 当T 1即 时， L() 20lg1 0 低频部分，零分贝线。 T 1 高频部分，斜率为 当T 1即 时， L() 20lg T -20db/dec的直线。 T 令L(ω( 0，得 ω 1 ，因此 T 两条线交于 1 处，称 1 为惯性环节的交接频率。
式中 A( )
幅值比
1 1 T
2 2
,
( ) arctanT
相位差
为了得到频率特性的定义，我们将其与传递函数联系起来。
1 RC网络的传递函数为：G ( s ) Ts 1
取s=jω，则：
1 分子分母同乘 1 jT 1 G( j ) (1 jT ) 2 2 2 2 jT 1 jT 1 1 T 1 T
对数相频
第五章线性系统的频域分析法
① 对数相频特性曲线 在半对数坐标系中 对于( 0, -90°)点 是斜对称的。 ② 对数幅频特性曲线 有峰值。
对 A( ) 求导并令等于零，可解得 A( ) 的极值对应的频率 r 。
r n 1 2 2
该频率称为谐振峰值频率。可见，当
当
1 2
时，无谐振峰值。当
K 10
当K 1时， 1, L( ) 0;
当 10时，L( ) 20
1
10 100
K 1
可见斜率为－20/dec
当K 0时， 1, L( ) 20 log K ;
( )
1
10 100
当 K时，L( ) 0
90
当有两个积分环节时可见斜率为 －40/dec
K K K G( j ) j e 2 j
L( ) 20 log A( ) 20 log 20 log K 20 log , K
A( )
K
( ) tg 1 ( / 0)
2
L( ) / dB 40 20
20 40
0 L( ) 20lg K 常数 0 0
K 1 K 1 K 1
相频特性：
0 ( ) K 180 K 0 K 0
( )
180
K 0 K 0
log
180
K ⒉ 积分环节的频率特性：G ( s ) s
( ) arctan T
( ) 0
0
A( ) K
A( ) 0
( ) 90
j
第5章线性系统的频域分析法课件
+
+
RC
duo dt
uo
ui
ui(t)
i (t) C
uo(t)
-
-
G(s) Uo(s) 1 1 Ui (s) 1 RCs 1 Ts
其中：T=RC
设 ui (t) Asin t
Ui (s)
A s2 2
U
o
(s)
1 Ts
1
Ui
(s)
1 Ts
1
s
2
A
2
Uo (s) 经拉氏反变换，可得
1 A F
tan T--稳态输出幅值 --稳态输出相位
正弦输入与稳态输出之间： 频率相同；幅值不同；相位不同。
i
o
0
t
ui
u0
A
2
0
线性系统G(s)
t
0
2
t
u输0 出仍为正弦信号，频率与输入信号相同，幅值较输入 0 信号有 一2 定 衰减，相t 位存在一定延迟。
A() Uo 1
第五章 线性系统的频域分析法
5.1 引言 5.2 频率特性 5.3 典型环节和开环频率特性曲线的绘制 5.4 频率域稳定判据 5.5 稳定裕度 5.6 闭环系统的频域性能指标
5.1 引言
1.时域分析法的优缺点
时域法是分析和设计控制系统的直接方法，它的主要优点是： 1）直观、容易理解。借助于MATLAB仿真，可以直接得到 系统的时域响应曲线，以及各种时域指标。 2）典型二阶系统的参数与系统性能指标的关系明确。当系 统的闭环零、极点满足二阶近似条件时，可用主导极点对应 的典型二阶系统的指标来近似估计高阶系统的技术指标。
5）延迟系统的开环传递函数包含延迟环节，其闭环特征方 程是超越方程，不能用劳斯判据判断稳定性，也不能用 MATLAB绘制根轨迹，系统分析很困难。
第五章(5) 线性系统的频域分析法
Mr 1 2 1 2
谐振频率为： r n 1 2 2
0.707时， Mr与是单调 关系，Mr小 大 % 小
Mr
3db
r B
3)、系统带宽 b
度量闭环系统具有或保持一定的信号复现能力的频率范围。
设一阶系统的闭环传递函数为 ( j 0) 1， 因为开环系统为1型，
基本题型2 1.由系统的开环奈奎斯特图或者bode图，反求系统的开环传递函数。 2.由图判断系统的稳定性及稳定裕度。
其它灵活题型1
本章知识点 1．频率特性的概念，根据某正弦输入求解已知系统的输出响应。 2．典型环节的频率特性，比例、惯性、一阶微分、振荡、二阶微分、积分、 微分、延迟环节的Nyquist图和Bode图绘制。 3．传递函数互为倒数的环节的Nyquist图和Bode图绘制。 4．最小相位惯性、一阶微分、振荡、二阶微分环节及其对应的非最小相位环 节的Nyquist图和Bode图绘制。 5．开环传递函数形式与Nyquist图起点和终点的对应关系。 6．开环传递函数形式与Bode图低频段、中频段、高频段的对应关系。开环传 递函数与Bode图L特性之间互相求解。 7．Nyquist图ω从0-至0至0+、ω从ωn-至ωn至ωn+补虚线弧方法。Bode图ω 从0至0+、ω从ωn-至ωn至ωn+补虚线段方法。 8．频率域稳定性判据，Nyquist稳定判据R=2N=P-Z，Bode稳定判据N=N+N-=(P-Z)/2。 9．根据Nyquist稳定判据判定系统稳定时的开环参数范围。 10．截止频率ωc，闭环相角裕度γ，截止频率ωx，闭环幅值裕度h、h(dB)。 11．闭环带宽频率ωb，闭环频率特性M(ω)，α(ω)。闭环谐振频率ωr、谐振峰 值M(ωr)。 12．闭环等M圆、等N圆、Nichols图线。 13．闭环性能指标，频率域指标与时域指标的联系。
谐振频率为： r n 1 2 2
0.707时， Mr与是单调 关系，Mr小 大 % 小
Mr
3db
r B
3)、系统带宽 b
度量闭环系统具有或保持一定的信号复现能力的频率范围。
设一阶系统的闭环传递函数为 ( j 0) 1， 因为开环系统为1型，
基本题型2 1.由系统的开环奈奎斯特图或者bode图，反求系统的开环传递函数。 2.由图判断系统的稳定性及稳定裕度。
其它灵活题型1
本章知识点 1．频率特性的概念，根据某正弦输入求解已知系统的输出响应。 2．典型环节的频率特性，比例、惯性、一阶微分、振荡、二阶微分、积分、 微分、延迟环节的Nyquist图和Bode图绘制。 3．传递函数互为倒数的环节的Nyquist图和Bode图绘制。 4．最小相位惯性、一阶微分、振荡、二阶微分环节及其对应的非最小相位环 节的Nyquist图和Bode图绘制。 5．开环传递函数形式与Nyquist图起点和终点的对应关系。 6．开环传递函数形式与Bode图低频段、中频段、高频段的对应关系。开环传 递函数与Bode图L特性之间互相求解。 7．Nyquist图ω从0-至0至0+、ω从ωn-至ωn至ωn+补虚线弧方法。Bode图ω 从0至0+、ω从ωn-至ωn至ωn+补虚线段方法。 8．频率域稳定性判据，Nyquist稳定判据R=2N=P-Z，Bode稳定判据N=N+N-=(P-Z)/2。 9．根据Nyquist稳定判据判定系统稳定时的开环参数范围。 10．截止频率ωc，闭环相角裕度γ，截止频率ωx，闭环幅值裕度h、h(dB)。 11．闭环带宽频率ωb，闭环频率特性M(ω)，α(ω)。闭环谐振频率ωr、谐振峰 值M(ωr)。 12．闭环等M圆、等N圆、Nichols图线。 13．闭环性能指标，频率域指标与时域指标的联系。
第五章 线性系统的频域分析法
第五章 线性系统的频域分析法思考题5-1 已知系统如图5-1])2)(1(/[1,221K s s s G s G +++=+=试用奈氏判据确定使系统稳定的K 值范围。
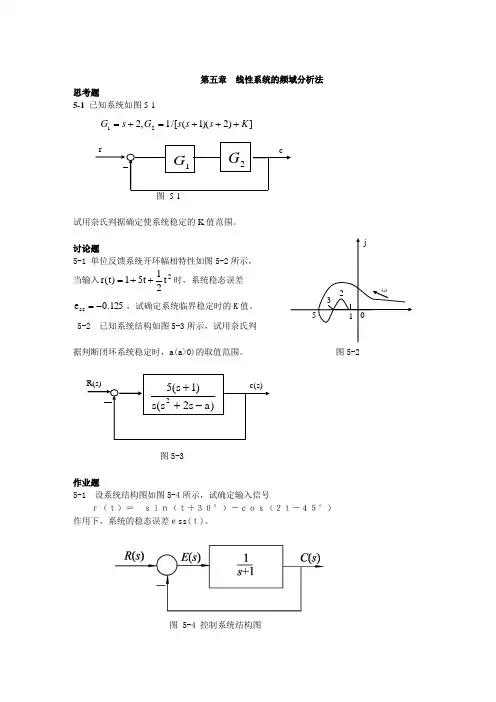
讨论题5-1 单位反馈系统开环幅相特性如图5-2所示， 当输入2t 21t 51)t (r ++=时，系统稳态误差 125.0e ss -=，试确定系统临界稳定时的K 值。
5-2 已知系统结构如图5-3所示，试用奈氏判据判断闭环系统稳定时，a(a>0)的取值范围。
图5-2图5-3作业题5-1 设系统结构图如图5-4所示，试确定输入信号ｒ（ｔ）＝ｓｉｎ（ｔ＋３０°）－ｃｏｓ（２ｔ－４５°）作用下，系统的稳态误差ｅss(ｔ)。
图 5-4 控制系统结构图 1G 2G r c -5 -3-1 -2 ω j0 )a s 2s (s )1s (52-++ R(s) c(s)5-2 典型二阶系统的开环传递函数为 )2s (s )s (G n 2n ζω+ω= 当取r(t)=2sint 时，系统的稳态输出为ｃss(t)＝２sin(t-45°)试确定系统参数ωｎ、ζ。
5-3已知系统开环传递函数;)1Ts (s )1s (K )s (H )s (G 2++τ= （Ｋ、τ、Ｔ＞０）试分析并绘制τ＞Ｔ和T ＞τ情况下的概略开环幅相曲线。
5-4 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;（Ｋ、Ｔ1、Ｔ2＞０）当取ω＝１时， o 180)j (G -=ω∠,|Ｇ(ｊω)|＝０.５。
当输入为单位速度信号时，系统的稳态误差为0.1，试写出系统开环频率特性表达式G(ｊω)。
5-5 已知系统开环传递函数为)1s 5.0s )(1s 2(s 10)s (H )s (G 2+++= 试分别计算ω＝０.５和ω＝２时，开环频率特性的幅值A(ω)和相位φ（ω）。
5-6 绘制下列传递函数的对数幅频渐近特性曲线：(1) )1s 8)(1s 2(2)s (G ++= （2）)12s )(1s s (s )11.0s (8)s (G 2++++=5-7 已知最小相位系统的对数幅频渐近特性曲线如图5-5所示，试确定系统的开环传递函数。
自动控制原理：第五章 线性系统的频域分析法
对不同频率正弦信号的跟踪能力或复现能力； G(jw)只与系统或环节本身的结构参数有关,是 系统或环节本身的属性； 与输入信号和初始条件无关。
『例1』某系统结构图如图，求 rt作 用下的稳态输出 c;t
(1) rt 3cos 2t 30
(2) rt 3sin 8t 20
r(t)
6
c(t)
L 20lg 1 20lg
L
0.1
20
1
0
10
-20
每增加十倍时， L减少20dB
积分环节的对数幅频曲线是一条斜率为－20dB/dec的直 线，该直线与零分贝线相交于w=1的地方。
b) 微分环节
传递函数 频率特性 幅频特性 相频特性 对数幅频特性
Gs s G j j
A
90
L 20 lg
二. 频率特性的几何表示方法
常用的频率特性图有极坐标图与伯德图。 1. 幅相频率特性曲线(极坐标图)
G(jw)为复数, 在坐标图中，它是一个矢量, 既可用模值和 幅角表示,也可在直角坐标中用实部和虚部表示。即:
G j A e j Re G j jI mG j
当输入正弦信号频率从0变到+∞,矢量 A 的e j终
G j 1
jRC 1
A G j 1
T 2 2 1
arctan RC
『注』幅频特性是w的偶函数，相频特性是w的奇函数，
故w从0到-∞的极坐标图与w从0到+∞的极坐标图对称 于实轴，因此通常只需绘制w从0到∞时的极坐标图。
Im
0 0 Re
2. 对数频率特性曲线 (伯德图)
rt A1 sin(t 时1)
系统稳态输出为同频率的正弦信号 ct A2 sin(t 2 ) 。
『例1』某系统结构图如图，求 rt作 用下的稳态输出 c;t
(1) rt 3cos 2t 30
(2) rt 3sin 8t 20
r(t)
6
c(t)
L 20lg 1 20lg
L
0.1
20
1
0
10
-20
每增加十倍时， L减少20dB
积分环节的对数幅频曲线是一条斜率为－20dB/dec的直 线，该直线与零分贝线相交于w=1的地方。
b) 微分环节
传递函数 频率特性 幅频特性 相频特性 对数幅频特性
Gs s G j j
A
90
L 20 lg
二. 频率特性的几何表示方法
常用的频率特性图有极坐标图与伯德图。 1. 幅相频率特性曲线(极坐标图)
G(jw)为复数, 在坐标图中，它是一个矢量, 既可用模值和 幅角表示,也可在直角坐标中用实部和虚部表示。即:
G j A e j Re G j jI mG j
当输入正弦信号频率从0变到+∞,矢量 A 的e j终
G j 1
jRC 1
A G j 1
T 2 2 1
arctan RC
『注』幅频特性是w的偶函数，相频特性是w的奇函数，
故w从0到-∞的极坐标图与w从0到+∞的极坐标图对称 于实轴，因此通常只需绘制w从0到∞时的极坐标图。
Im
0 0 Re
2. 对数频率特性曲线 (伯德图)
rt A1 sin(t 时1)
系统稳态输出为同频率的正弦信号 ct A2 sin(t 2 ) 。
第5章线性系统的频域分析方法
最小相位环节：
特点:某个参数的符号相反
除积分微分外，最小相位环 节有对应的非最小相位环节
非最小相位环节:
非最小相位环节和与之相对 应的最小相位环节的区别在 于其零极点在s平面的位置。
不稳定环节
设有两个系统
1 Ts G1 ( s ) 1 10Ts
和
1 Ts G2 ( s) 1 10Ts
1 典型环节 根据零极点，将开环传递函数的分子和分母多项式分解 成因式，再将因式分类，得到典型环节。 开环系统可表示为若干典型环节的串联形式
设典型环节的频率特性为
幅值相乘， 相角相加
则系统开环频率特性
系统的开环幅频特性和相频特性
系统开环频率特性为组成系统的各典型环节频率特性的合成 系统开环对数幅频特性
A 1 U o (s) [U i ( s ) Tuo 0 ] 代入 U i ( s ) L[ A sin t ] 2 s 2 Ts 1
U o ( s) Tu 1 A A [ 2 Tuo 0 ] o 0 再由拉氏逆变换 Ts 1 s 2 (Ts 1)(s 2 2 ) Ts 1
(1) 幅相频率特性曲线 (Nyquist图，极坐标图)
将频率特性表示为复平面上的向量，其长度为A(ω) ， 向量与正实轴夹角为 (ω)，则ω变化时，相应向量的矢端 曲线即为幅相曲线。
G( jω)=A(ω)e j(ω) ，G(-jω)=A(ω)e -j(ω)
A(ω)偶, (ω)奇
ω：0→+∞和ω：0→ -∞的幅相曲线关于实轴对称 只绘制ω从零变化至+∞的幅相曲线。 用箭头表示ω增大时幅相曲线变化方向 对于RC网络 G ( j )
j
cos j sin
第五章线性系统的频域分析法
第五章 线性系统的频域分析法重难点：1. 频率特性⎧⎨⎩定义与传递函数之间的关系2. 频率特性的几种图示方法⎧⎧⎨⎪⎨⎩⎪⎩奈氏曲线的绘制奈氏曲线由图确定系统伯德图（Boder)3. 奈奎斯特稳定判据⎧⎧⎪⎨⎨⎩⎪⎩幅值裕度稳定裕度相角裕度稳定判据频率特性（线性定长系统的频率特性）：指在零初始条件下，稳态输出的正弦信号与输出的正弦信号的复数比。
1.例子：00i 00i ()()()()()()d t RCt t dtRCS S S S U U U U U U +=+= ()0i()1()1S G S S RCS U U ==+ 令()1,RC T G s TS ==22i i ()sin .()A t A t s U U S ωωω==+则100()()t s U UL-=R UU 0C()220i 1()()1s G S S TS U U ASωωωωω==++=２２ＡＢＳＡＢＣ ＋＝＋＋１１ｓ＋ｊｓ－ｊ＋ｓ＋ｓ＋ＴＴｓ()0()t arctgT ωω+-ｔ－ＴＡＡＵ()()()s j j arctgT G S G j ωωω=-==ＡarctgT ϕω=-1）输出电压的稳态值是与输入信号同频率的正弦信号。
2）幅值与相角和输入信号不同，与ω，T 有关。
()()()0it U U ω∞=1A ＝幅频特性()()()0iarctgT t U U ϕωω=-=-∞相角相角2.幅频特性与传递函数之间的关系： ()()A G j ωω= ()()G j ϕωω= 证明： ()()()()()()()111......Y S N S G S X S S S S P P P ==+++()()22sin ,X x t X t X S S ωωω==+()()()()()()()22111......N S X Y S X S G S S S S P P P S ωω==++++()()()()()()111......N S X S j s j S S S P P P ωωω=+-+++()()1nc c j jajS j s j s k k p ωω-==+++-+∑ ()1jnt j t j t c c j p y t aj e k e k e ωω--==++∑()()()22j t j tX X y G j G j j je e ωωωω-∞=-+- ()()()22j j j tj tX G j X G j y jje e eeϕϕωωωω--∞=+-()()()()[]22j t j t y G j X jjeeϕωϕωω-++∞=+-()()()()[]2j t j t y G j X jeeϕωϕωω-+++∞=-()()()()()()cos sin cos sin ()[]2t j t t j t y G j X jωϕωϕωϕωϕω-+-+++-+∞=()()()2sin ()]()sin 2j t y G j XG j X t jωϕωωωϕ+∞==+()()A G j ωω= ()()G j ϕωϕω== 3.实部，虚部表示：()()j G j G j e ϕωω=()()()()()()cos ()sin G j p jQ p G j Q G j ωωωωωϕωωϕ=+==()G j ω=Q arctgPϕ= 总结：1.频率特性适合于线性定长系统，他也是一种数学模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N(s) D(s)
A s2 2
(s
N (s) p1)(s p2 )
(s
pn
)
A s2
2
p1, p2 , , pn 为G(s)的极点
6
若系统无重极点，则（5-1）式可写为
n
C(s)
ai
b1
b2
i1 s pi s j s j
(5-2)
对（5-2）式求拉氏反变换，则得系统的输出信号
n
(s
A j )(s
j )
(s
j )
s j
G(
j )
A 2j
若系统稳定，pi 均具有负实部， t 时，上式中的暂态
分量将衰减为零，这时，可得到系统的稳态响应：
lim c(t)
t
b1e
jt
b2e jt
将 b1, b2 代入上式，并利用欧拉公式，可求得稳态响应为
8
c(t) |t
b1e jt
b2e jt
5.1.1 频率特性的概述
频率特性又称频率响应，它是系统（或元件）对不同 频率正弦输入信号的响应特性（图5-1）。
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
0.5
1
1.5
2
2.5
3
线性系统
5
4
3
2
1
0
-1
-2
-3
-4
-5
0
0.5
1
1.5
2
2.5
3
图5-1 正弦信号对线性系统的作用
3
一、系统对正弦输入信号的稳态输出
G(
j )
A e jt 2j
G(
j )
A 2j
e jt
G( j) e j A e jt G( j) e j
A
e jt
G(
j )
e jt A
e jt
2j
2j
2j
G( j) Asin(t )
在正弦信号的作用下，系统的稳态响应仍然是一个 正弦函数，其频率与输入信号的频率相同，振幅为输 入信号幅值的 G( j) 倍，相位移为 G( j)
实频-虚频形式： G( j) U() jV()
16
jV
V () 0
A() ( )
U () U
G( j) A()e j() U () jV ()
u(t)
y(t)
1
2
3
4
5
t/s
图5-2 输入输出信号的对比
6
5
设系统的传递函数为：
C(s) G(s) N(s)
N (s)
R(s)
D(s) (s p1)(s p2 ) (s pn )
已知输入 r(t) Asin(t)，其拉氏变换 R(s) A
s2 2
A为常量，则系统输出为
C(s)
G(s)R(s)
T
() 90
!频率特性反映了系统(电路)的内在性质,与 外界因素无关。
15
5.1.4 频率特性表示法
频率特性可用解析式或图形来表示。 （一）解析表示
系统开环频率特性可用以下解析式表示：
幅频-相频形式： G( j) G( j) G( j) 指数形式(极坐标) ： G( j) G( j) e j 三角函数形式：G( j) G( j) cos() j G( j) sin()
c(t) b1e jt b2e jt aie pit
(5-3)
i 1
其中 b1,b2和ai (i 1, 2, n)
待定系数
7
b1
G(s)
A s2 2
(s
j )
s j
G(
j )
(s
A j)(s
(s
j )
j )
s j
G(
j )
A 2j
b2
G(s)
A s2 2
(s
j )
s j
G(
j )
1
（2）系统的频率特性可用实验方法测出。 （3）用频率法设计系统，可以忽略噪声的影响。
本章主要讨论频率响应法的基本概念、典型环节 及系统频率特性的求法、频率特性与时域响应的关 系和闭环系统的频率特性等。
5.1 频率特性的基本概念
从讨论系统在正弦信号作用下的稳态响应出发， 掌握频率特性的基本概念。
2
14
G(s)
U 2
(s)
1
R
U (s) 1 Ts 1
T RC
u (t) 1
i(t) C
u (t) 2
G(
j)
U 2
(
j)
1
A()e j()
U ( j) 1 jT
1
A() 1 1 (T)2
() tg1T
幅值A()随着频率升高而衰减
对于低频信号 (T 1)
A() 1
() 0
对于高频信号 (T 1) A() 1 0
设输入r(t)为正弦信号， 作用于线性定常系统 G(s) ，输出响应为c(t)，则输出信号为同频率 的正弦信号，但输出的振幅和相位不同于输入 量，且随着输入信号频率的变化而变化，如图 5-2所示：
4
6
r(t) 2cos(t) 4
2 幅值 0
c(t) 4.8cos(t ) -2
-4
-6
-8 0
红 —输 入 ， 蓝 —全 响 应 ， 黑 —稳 态 响 应 yss(t)
式中, G( j) 是稳态输出信号的幅值与输入 信号的幅值之比，称为幅频特性。 () 是稳 态输出信号的相角与输入信号相角之差(相
移)，称为相频特性。
11
5.1.3 频率特性的求取
在系统传递函数G(s)中，令s= j，即可得到 系统的频率特性。有开环频率特性与闭环频 率特性之分。 1 已知系统的系统方程，输入正弦函数求其稳态 解，取输出稳态分量和输入正弦的复数比；
第五章线性系统的频域分析法
频率响应法(Frequency-response analysis)
是二十世纪三十年代发展起来的一种经典工程实用 方法,是一种利用频率特性进行控制系统分析的图 解方法,可方便地用于控制工程中的系统分析与设 计。频率法用于分析和设计系统有如下优点： （1）不必求解系统的特征根，采用较为简单的图解 方法就可研究系统的稳定性。
2 根椐传递函数来求取 G( j) G(s) s j
3 通过实验测得。
12
5.1.4 频率特性的物理意义
频率特性与传递函数的关系: G(jω)=G(s)|s=jω 频率特性表征了系统或元件对不同频率正弦
输入的响应特性。
(ω)大于零时称为 相角超前，小于零 基本思路：实际 施加于控制系统的周期或非周期信号都可表示成 由许多谐波分量组成的傅立叶级数或用傅立叶积 分表示的连续频谱函数，因此根据控制系统对于 正弦谐波函数这类典型信号的响应可以推算出它 在任意周期信号或非周期信号作用下的运动情况。
9
5.1.2 频率特性的定义 1、频率响应
在正弦输入信号作用下，系统输出的稳态值 称为系统的频率响应，记为c(t)。
2、频率特性
系统频率响应c(t)与输入正弦信号r(t)的复数比称 为系统的频率特性，是随输入正弦信号角频率 变化而变化的复变函数，
10
•
记为G(j)，即
G
(
j
)
c
•
r
G( j) G( j) e j