32动量算符和角动量算符

i ( p p )r ห้องสมุดไป่ตู้


2 p ( r ) p ( r ) d c e
* 2
d dxdydz
c





i

e
[( p x p x ) ( p y p y ) y ( p z p ) z ] x z
3 2
p (r )
1
e
i p r
量子力学
函数为

(x) px
1 ( 2 )
1/ 2
i
e
pxx
3、箱归一化
如果我们仍然要求按通常的归一化方式 对动量本征函数归一化，就必须放弃无穷空 间的积分，采用箱归一化方法。以一维为例 [ L , L ] 中运 讨论。设粒子只能在有限空间 2 2 动。由
(x) pn
1 L
i 2 n x
e
L
则满足归一化条件



* pn

pn
dx 1
讨论： h L , p n p n 1 p n L 0 1）当 h 则本征谱由分立谱变成了连续谱 L dp 2）三维情况：粒子被限制的边长为 L 的一个 正方形箱中，取箱的中心为坐标原点，波函 数满足的周期性边界条件为：在两个相对的
L

i L

dx

L 2
i
*

dx
2
L 2
) (
L 2
)
所以对于任意的 ,
(L) 2
*
都有
const 1
( L ) 2
*

角动量算符平方与动量分量的对易关系角动量算符和动量算符是量子力学中的两个重要算符，它们描述了粒子的运动和旋转性质。

在量子力学中，一个物理量A的算符表示为^A，而物理量B的算符表示为^B。

首先，我们来定义角动量算符和动量算符：1. 角动量算符：在量子力学中，角动量算符通常用L表示，其三个分量的算符分别为^L_x，^L_y和^L_z。

2. 动量算符：动量算符通常用p表示，其三个分量的算符分别为^p_x，^p_y和^p_z。

然后，我们来讨论角动量算符平方和动量算符分量的对易关系。

在量子力学中，对易关系可以用来描述两个算符的关系，对易关系为[ ^A, ^B ] = ^A ^B - ^B ^A。

首先，我们来计算角动量算符平方和角动量分量的对易关系：( ^L_x )^2 = ^L_x ^L_x = ( ^L_x ^L_x - ^L_x ^L_x ) + ^L_x^L_x= ^L_x ( ^L_x ^L_x - ^L_x ^L_x ) + ^L_x ^L_x= [ ^L_x, ^L_x ] ^L_x + ^L_x ^L_x= 0 + ^L_x ^L_x= ^L_x ^L_x同理，可得( ^L_y )^2 = ^L_y ^L_y 和 ( ^L_z )^2 = ^L_z ^L_z。

接下来，我们来计算角动量平方与动量算符分量的对易关系：[ ( ^L_x )^2, ^p_x ] = ^L_x ^L_x ^p_x - ^p_x ^L_x ^L_x根据量子力学中的对易关系，角动量算符和动量算符的分量满足对易关系：[ ^L_i, ^p_j ] = iħ ε_ijk ^L_k其中ε_ijk是三维Levi-Civita符号，i，j，k可以取x，y，z。

带入上式：[ ( ^L_x )^2, ^p_x ] = ^L_x ^L_x ^p_x - ^p_x ^L_x ^L_x= ^L_x ħ ε_xyz ^L_z - ħ ε_xyz ^L_z ^L_x= ħ ε_xyz ( ^L_x ^L_z - ^L_z ^L_x )同理可得：[ ( ^L_y )^2, ^p_y ] = ħ ε_xyz ( ^L_y ^L_z - ^L_z ^L_y )[ ( ^L_z )^2, ^p_z ] = ħ ε_xyz ( ^L_z ^L_z - ^L_z ^L_z )可见，角动量算符平方和动量算符分量并不对易。

球坐标系的动量算符
在原子物理学和量子力学的教学中都会遇到动量算符，其表达
形式p =-inV,它是量子力学中的一个基本算符。它的的直角坐标
a , a , a 系下的形式为
i5
=
-
itt(i —
Bx
+J
—
函
+k —Bz )，各分量 九
=
a a -in — ，凡 = -iii — , 祁彻
仇 =-in. —a 是大家都熟悉的，学生们也没有疑惑，但是对于在球坐
az az ar az ae az J (Jl
ar r ae
我们
通
过直
角
坐标
系
可用e,<p
表
示出
.^l,
)l^.,
^K 在球面
坐标系
下的
形式：
oo ,,^l、
,^J
\ K^ J
f .g \ eo0sg,cspcoos0 coscp
= .gi
cos0 sin cp
c。
- sin0
一二rn
我们把上面的结果代入下式
2.2动量各分量的算符表示
2.2.1 - in —B 和
1 iii
a 不是厄密算符，不能作为动量的分量
祈
r汾
各分量的 P^,,^ Pa,^P叩算符形式就产生了疑惑，而一般的量子力学教材 [1~3]对此也没有过多说明，本文试图从在量子力学中表示力学量的
算符必须是厄密算符的要求出发解决这一疑惑。
1.直角坐标系中动量及其各分量的算符表示
P= -ihv'= -in(立； 十二＋立 k)= - in(~
函 By oz
OX
6
立

，都是厄米算符。
对于任意量子态
，
。所以，动量算符确实是一个厄米算符。 动量算符确实是一个厄米算符
返回目录
4/52
1.2 （位置算符）本征值与本征函数
假设，位置算符 的本征值为 的本征函数是 。用方程表达， 这方程的一般解为，
其中， 虽然
是常数， 无法归一化：
是狄拉克δ函数。
设定
= 1，我们可以使
满足下述方程：
们立刻再测量可观察量

，得到的答案必定是
可是，假若，我们改为测量可观察量 为
，则量子态不会停留于本征态
的本征态。假若，得到的测量值为其本征值
，则量子态几率地坍缩为本征态

根据不确定性原理， 的不确定性与 与 之间， 与 的不确定性的乘积 之间，也有类似的特性。 ，必定大于或等于 。
返回目录
19/52
返回目录
13/52
3.1 角动量算符 简介
角动量促使在旋转方面的运动得以数量化。在孤立系 统里，如同能量和动量，角动量是守恒的。在量子力 学里，角动量算符的概念是必要的，因为角动量的计 算实现于描述量子系统的波函数，而不是经典地实现 于一点或一刚体。在量子尺寸世界，分析的对象都是 以波函数或量子幅来描述其几率性行为，而不是命定 性(deterministic)行为。
量子力学
算 符
目录
一、位置算符
1.1 厄米算符 1.2 （位置算符）本征值与本征函数 1.3 正则对易关系
七、自旋算符
7.1 概论 7.2 发展史 7.3 自旋量子数
7.3.1 基本粒子的自旋 7.3.2 亚原子粒子的自旋 7.3.3 原子和分子的自旋 7.3.4 自旋与统计
二、动量算符

作 换 px ⇔ x，p′ ⇔ x0， 代 ： 则 x 1 δ ( px − p′ ) = x ∫−∞ e 2πh i
∞ i ( px − p′ ) x x h
dx
1 ∞ h px ( x−x0 ) δ (x − x0 ) = dpx ∫−∞ e 2πh
性质
f (x)δ (x − a) = f (a)δ (x − a)
周期性边界条件
在箱子边界的对应点A, A’上加上其波函数相等的条件，此边 界条件称为周期性边界条件。
r L rA′ ≡ − , y, z 2
y A
r L rA ≡ , y, z 2
ce
i L [ px + py y+ pz z] h 2 i −L [ px + py y+ pz z] h 2
x = r sin θ cosφ, tanφ = y / x sin φ 1 ∂φ x tanφ = y, +x =0 cosφ cos2 φ ∂x
∂f ∂f ∂r ∂f ∂θ ∂f ∂φ = + + ∂xi ∂r ∂xi ∂θ ∂xi ∂φ ∂xi
∂ ∂ ∂r ∂ = + ∂x ∂r ∂x ∂θ ∂ ∂ ∂r ∂ 或 = + ∂r ∂y ∂θ ∂y ∂ ∂ ∂r ∂ = + ∂r ∂z ∂θ ∂z ∂θ ∂ + ∂φ ∂x ∂θ ∂ + ∂y ∂φ ∂θ ∂ + ∂z ∂φ ∂φ ∂x ∂φ ∂y ∂φ ∂z
∂r n ∂x = si θ cosφ ∂r n n = si θ si φ ∂y ∂r = cosθ ∂z
∂θ 1 = cosθ cosφ r ∂x 1 ∂θ = cosθ sinφ r ∂y ∂θ 1 = − sinθ r ∂z

动量算符和角动量算符的对易关系
动量算符和角动量算符的对易关系是量子力学中一个重要的基本原理。

在物理学中，对易关系是指两个算符A和B，它们的对易子是0，即[A,B]=AB-BA=0。

如果两个算符A和B的对易子不等于0，那么它们是不对易的。

在量子力学中，动量算符和角动量算符的对易关系是：
[Px, Lz]=iħYx
[Py, Lz]=iħYy
[Pz, Lz]=iħYz
其中Px、Py和Pz分别表示沿着X、Y和Z方向的动量算符，Lz表示沿着Z方向的角动量算符，ħ是普朗克常数除以2π，而Yx、Yy和Yz 表示一个轨道角动量算符在X、Y和Z方向上的本征值，它们称为
“本征矢”。

这个对易关系告诉我们，在量子力学中，动量算符和角动量算符是互
相影响的。

如果我们测量一个粒子的动量，就会影响其角动量，并且
在测量其角动量时，会影响其动量。

这个关系是量子力学的基本原理
之一，它描述了物理世界的量子性质。

总的来说，动量算符和角动量算符的对易关系是量子力学中一个非常
重要的基本原理，它不仅仅涉及到动量和角动量的测量，还涉及到粒
子的本质结构和量子性质。

因此，对于每一个学习量子力学的人来说，理解动量算符和角动量算符的对易关系是非常必要的。

动量算符的本征方程
本征方程
力学量算符
本征值波函数 本征值
本征值和本征波函数由本征值方程得到 动量算符
动量算符的本征态
解以上方程得
c为归一化常数
归一化出现问题,发散 px = px’ 两种归一方法
利用
( x)
x
这样一来
同时我们从解本征方程看，动量的本征值可取任意值， 连续谱，在处理动量问题时，常把动量的连续本征值变 为分立值，最后在把分立体征值实回到连续本征值。
箱中粒子波函数是动量取分立值的平面波
角动量算符
角动量平方算符
角动量平方算符
角动量算符——球坐标系中的表示
球坐标中P点，直角坐标表示（x,y,z) 球坐标（ r, , ），
z
p
r

y
ห้องสมุดไป่ตู้
在球坐标下，以上算符
有怎样的具体形式？
x
角动量算符——球坐标系中的表示
例如
由
角动量算符——球坐标系中的表示
定轴转动呢？
本征方程
方程求解是困难的 物理要求在整个区域有限
在直坐标 球坐标
角动量算符的本征值和本征函数
有限条件 解是球函数
勒让德多项式
角动量算符的本征函数的归一化
球谐函数
角动量算符的本征值和本征函数
L为角量子数
m为磁量子数
量子数？
角动量算符的本征值问题的应用
应用转动问题 刚性转子 定态薛方程 刚体运动分解 为平动和转动
角动量算符——球坐标系中的表示
这样就求得了 同样方法可求得 带入
角动量算符——球坐标系中的表示
(1)
(2)
(3)
角动量算符——球坐标系中的表示

这时，方程(19)的解是球谐函数 Ylm ( ,) ： Ylm(,) NlmPl m (cos)eim m 0, 1, 2, l (21) Pl m (cos ) 是缔合勒让德多项式，Nlm 是归一化常数。
Nlm由Ylm ( ,) 的归一化条件定出：
0
2 0
Ylm ( ,)Ylm ( ,) sin d d
2 1
sin
(sin
)
1 sin2
2
2
(18)
３、角动量 z 分量算符 Lˆz ：
Lˆz i
(16)
Lˆ2z
2 2
2
４、角动量平方算符的本征值方程：
2
1
sin
(sin
)
1
sin2
2
2
Y
(
,)
2Y ( ,) (18)
或 sin1
(sin
)
1 sin2
§3.2 动量算符和角动量 算符
一、动量算符
１、动量算符的本征值方程
i p (r ) p p (r ) (1)
函p 是数。动分量量算式符：的本征i 值，xpp((rr))是属px于 p此(r本) 征值的本征
i
y
p (r )
py
p (r )
i
z
p (r )
pz
p (r )
它们的解是 p (r ) C exp( i p r ) (2)
二、角动量算符
１、定义：角动量算符 L rˆ pˆ (12)
分量式为
Lˆx ypˆ z zpˆ y
( y z ) i i z y
(y z ) z y
Lˆy zpˆ x xpˆ z
(z x ) i i x z

显然有如下性质
lˆ++ = lˆ− ， lˆ−+ = lˆ+
这两个算符不是厄密算符。 (II) 对易关系
[lˆz , lˆ± ] = ±hlˆ± ， [lvˆ 2 , lˆ± ] = 0 ， lˆ+lˆ− = lvˆ 2 − lˆz2 + hlˆz ， lˆ−lˆ+ = lvˆ 2 − lˆz2 − hlˆz ④ Lˆ2 在球坐标中的表示
exp⎢⎣⎡
i h
( px
−
px′ )⎥⎦⎤dx
=
2πhδ
( px
−
px′ )
∫∞ −∞
exp⎢⎣⎡
i h
(py
−
p y′ )⎥⎦⎤dy
=
2πhδ
(
py
−
py′ )
∫∞ −∞
exp⎢⎣⎡
i h
( pz
−
pz′ )⎥⎦⎤dz
=
2πhδ ( pz
−
pz′ )
式中 δ ( px − p′x ) 是以 px − p′x 为宗量的 δ 函数，故有
§3.2 动量算符和角动量算符 1．动量算符和本征方程 1). 动量算符
当波函数ψ 表示为坐标 x 、y 、z 的函数时，动量 p 和动量算符 − ih∇ 相对应，定义动量算符 pˆ ：
pr → prˆ = −ih∇
px
=
−ih
∂ ∂x
py
=
−ih
∂ ∂y
pz
=
−ih
∂ ∂z
本征方程： 各分量方程：
∂ ∂x
−
x
∂ )
∂z
lˆz
=
xpˆ y
−

函
即

p
(rv)
p (rv)d
( pv
pv) (3)
其中
p (rv)

1
3
(2 h) 2
exp( i h
pv rv) (4)
这是为由什于么动 量p (rv本) 征不值能可归以一取化连为续1，值而，是pv归的一各化分为量可函取数任：
意实数，动量本征值构成连续谱。
Lˆ2z

h2
2
2
４、角动量平方算符的本征值方程：
h2
1

sin


(sin
)

1
sin2
2
2

Y
(
,)

h2Y ( ,) (18)
或 sin1
(sin


)

1 sin2

2
2

Y
(
,

数中断成为多项式： l(l 1) l 0,1, 2,L (20)
这时，方程(19)的解是球谐函数 Ylm ( ,) ： Ylm(,) NlmPl m (cos)eim m 0, 1, 2,L l (21) Pl m (cos ) 是缔合勒让德多项式，Nlm 是归一化常数。
Y1,0
3 cos 4
Y1,1
3 sin ei 8

(x,
y,

L)

(x,
y,
L)
2
可得到
2
2
2
py
ny
2 h
L
, n
y
0, 1, 2,L

0
得归一化的波函数为
1 imϕ Φm (ϕ) = e 2π
(m = 0, ±1, ±2,⋯ )
L2的本征值问题
ˆ L2Y (θ , ϕ ) = λ ℏ 2Y (θ , ϕ )
L2 的本征值方程可写为：
1 ∂ ∂ 1 ∂2 −ℏ [ (sin θ )+ 2 ]Y (θ , ϕ ) = λ ℏ 2Y (θ , ϕ ) (3.2.16) sin θ ∂θ ∂θ sin θ ∂φ 2 或：
的本征方程 L2的本征方程
ˆ L2Ylm (θ , ϕ ) = l (l + 1)ℏ 2Ylm (θ , ϕ )
(3.2.22） ） Lz的本征方程
ˆ LzYlm (θ , ϕ ) = mℏYlm (θ , ϕ )
(3.2.23） ）
→
l z = mℏ
m = 0,±1,±2, ⋯
例: 若体系的波函数就是球谐函数 Y20 (θ , ϕ ) (1)求其角动量矢量与 z 轴的加角. 求其角动量矢量与 轴的加角
2
1 ∂ ∂ 1 ∂2 [ (sin θ )+ 2 ]Y (θ , ϕ ) = −λY (θ , ϕ ) 2 sin θ ∂θ ∂θ sin θ ∂φ
(3.2.17)
其中 Y(θ,ϕ) 是 L2 属于本征值 Y(θ λℏ2 的本征函数。此方程就是球谐函数方程 ℏ 的本征函数。 为使 Y(θ,ϕ) 在θ 变化的区域(0, π)内是有限的， 则必须满足：λ = ℓ（ℓ + 1), 其中 ℓ = 0, 1, 2, ... (3.2.18） ）
− iℏ∇ψ p (r ) = pψ p (r )
求解 采用分离变量法，令： 采用分离变量法，
（3.2.1） ）
ψ p ( r ) = ψ ( x )ψ ( y )ψ ( z )

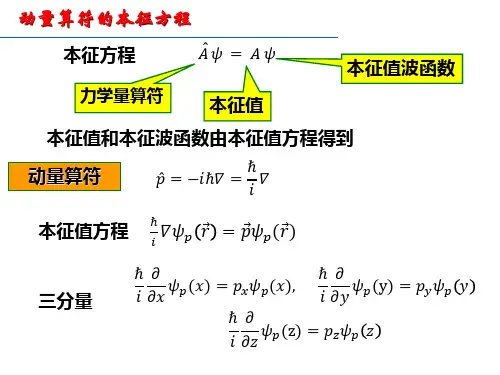
§3.2 动量算符和角动量算符一．动量算符。

1. 动量算符的本征值方程：()()r p r ip p ψψ=∇，三个分量方程是 （3.2.1） ()()r p r xi p x p ψψ=∂∂ ， +∞<<∞-x ()()r p r yi p y p ψψ=∂∂ ， +∞<<∞-y （3.2.2） ()()r p r zi p z p ψψ=∂∂ ， +∞<<∞-z 通解是()r p i pCe r∙=ψ，C 是归一化常数。

（3.2.3） 2.动量本征函数的归一化。

()()()()()[]⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-'-+'-+'-∙∞+∞-=dxdydze C d r r z p p y p p x p p ip pz z y y x x2τψψ因为()()x x x p p ip p dx ex x '-=⎰∞+∞-'-δπ2，所以有()()()()()()()()p p C p p p p p p C d r r z z y y x x p p'-='-'-'-=∙+∞∞-⎰δπδδδπτψψ323222如果取()232-= πC ，则()r pψ归一化为δ函数。

()()()()()r p i pp per p p d r r∙∙+∞∞-='-=⎰2321;πψδτψψ（3.2.4）（3.2.5）3.箱归一化在A （L/2,y,z ）和A '(-L/2,y,z)点, ()r p i p Ce r∙=ψ的值应相同。

即⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛++-=z p y p L p i z p y p L p i z y x z y x CeCe2121()1=L p ix e所以πx xn L p 2=，x n 是正负整数或零。

,1,0,2±==x xx n Ln p π （3.2.6）,1,0,2±==y yy n Ln p π （3.2.7）,1,0,2±==z zz n Ln p π （3.2.8） 当L ∞→时，z y x p p p ,,的本征值就变为连续谱。

i
2
exp[ ( px p x ) x ]dx exp[ ( p y p y ) y ]dy exp[ ( p z p z )z ]dz

i

i
2 3 C 2 (2 )3 ( px p ) ( p p ) ( p p ) C (2 ) ( p p) ( p p) x y y z z
一、 动量算符 (Momentum operator)
ˆ i p
x p i ( , x, y, z )
ˆx p ˆxx i xp ˆ x i p ˆy p ˆyy i yp x ˆ ˆzz i zp z p ˆ y i p ˆy p ˆyx 0 y xp ˆz p ˆz y 0 yp ˆ z i zp p ˆxz 0 z ˆ x p
§3.2 动量算符和角动量算符
p (r ) 本征值方程: i p (r ) p
i x p px p p p y p 三个分量方程: i y p pz p i z
解之得:
p (r ) Ce
i
pr
第三章 量子力学中的力学量
3/34
Quantum mechanics
§3.2 动量算符和角动量算符
归一化常数的确定:


* p (r )dxdydz p ( r )
2
C C




exp[ ( px p x ) x ( p y p y ) y ( p z p z ) x ]dxdydz i
ˆ x F Fp ˆ x i p ˆ y F Fp ˆ y i p ˆ z F Fp ˆ z i p F x F y F z

量子力学中的角动量和角动量算符量子力学是一门研究微观世界的学科，其理论框架是由一系列的数学工具和基本原理构成的。

其中，角动量是量子力学中一个重要的概念之一。

本文将深入探讨量子力学中的角动量和角动量算符。

一、经典力学中的角动量在深入讨论量子力学中的角动量之前，我们首先要回顾一下经典力学中的角动量。

在经典力学中，角动量是描述物体旋转运动的物理量。

它的大小等于物体的转动惯量乘以角速度，即L=Iω。

根据角动量公式，我们可以得知，当物体的转动惯量变大或角速度增大时，其角动量也会随之增大。

二、角动量的量子化然而，在量子力学中，角动量与经典力学有所不同。

根据量子力学的原理，物理量是以量子的形式存在的，即具有能级的离散取值。

角动量便是其中之一。

量子力学中的角动量是由波函数描述的，而波函数是角动量算符的本征函数。

三、角动量算符在量子力学中，角动量算符用J表示，可以分为轨道角动量算符L和自旋角动量算符S两部分。

轨道角动量算符L与物体的形状和运动有关，描述的是物体的转动运动；而自旋角动量则是描述粒子自身的性质，与其内在特性有关。

这两者的和即为总角动量算符J。

四、角动量算符的本征函数和本征值由于角动量算符是具有量子性质的，所以它的本征函数和本征值是量子力学研究中的重要问题之一。

角动量算符的本征函数可以用球谐函数表示，它们具有特定的轨道和角动量量子数。

这些本征函数对应的本征值则是角动量的取值。

五、角动量的算符性质角动量算符具有一些特殊的代数性质，比如它们之间的对易关系和升降算符。

对易关系给出了角动量算符之间的相互关系，如[Lx,Ly]=iħLz。

而升降算符则可以用来改变角动量的量子态。

这些性质使得我们可以更好地研究和描述量子力学中的角动量现象。

六、角动量的应用角动量在量子力学中具有广泛的应用。

例如，我们可以通过角动量算符来描述原子、分子和固体中的电子的运动状态。

此外，角动量还可以用于解释和预测粒子的自旋现象，如自旋磁矩和自旋共振等。

f ( x ) ( x x0 )dx f ( x0 ) 推广到三维： r ( x ) ( y ) z



0
x0
x
2.性质：
( x ) ( x )
( ax )
1 |a|
( x)
f ( x ) ( x x0 ) f ( x0 ) ( x x0 )
d dx dx
d dx i dx

*

ˆ p * dx

ˆ 若当 x 时 ， 0， 0， 则 p 是厄密算符
。
(8)量子力学中力学量算符的构成
• 量子力学中表示力学量的算符必需是线性,厄密算符,且它 的本征函数构成完备系. • 经典力学中力学量是坐标r和动量p的函数,把坐标保持不 变,动量换为动量算符就构成了量子力学中相应的力学量 ˆ ˆ 算符. F ( r , p ) F ( r , p )
F (x)

n0

F
(n)
(0)
n!
x
n
则可定义算符 Û 的函数 F(Û)为:
ˆ F (U )
n 0

F
(n)
(0)
n!
ˆn U
例如:
i ˆ Ht
e


n 0

1 n!
[
i
ˆ t ]n H
（6）算符的本征值方程
ˆ F x x
是常数
这样形式的方程称为算符的本征值方程。 本征值方程的解： 求得满足方程的一系列本征值： , , , 1 2 n
i
px py pz

量子力学中的角动量算符在量子力学中，角动量是一个非常重要的物理量。

它描述了粒子的旋转运动和自旋状态。

为了描述和计算量子系统中的角动量，我们使用角动量算符。

本文将介绍量子力学中的角动量算符以及其相关特性。

一、角动量算符的定义角动量算符是量子力学中用来描述角动量的数学表达式。

对于自然界中的粒子，其角动量算符由三个互相独立的分量组成：Lx、Ly和Lz。

它们分别对应了角动量在x、y和z方向上的投影。

这些算符可以写成以下形式：Lx = yLz - zLyLy = zLx - xLzLz = xLy - yLx其中，x、y和z是坐标系中的轴。

二、角动量算符的性质角动量算符具有一些重要的性质，其中一些是经典力学中角动量的推广，而另一些则是由量子力学的性质决定的。

1. 对易关系角动量算符满足对易关系，即：[Lx, Ly] = iħLz[Ly, Lz] = iħLx[Lz, Lx] = iħLy其中ħ是普朗克常量的约化版本。

2. 共同本征态角动量算符有一组共同的本征态，即轨道角动量的本征态和自旋的本征态。

这些本征态由量子数来标记，分别是轨道角动量量子数l、角动量的z分量量子数m以及自旋量子数s。

对于每一个量子数组合，都对应着一个特定的本征态。

3. 角动量的取值范围轨道角动量的量子数l可以取零或正整数值，如0、1、2等，而z分量量子数m的取值范围为-l到l的整数，例如l为1时，m可以是-1、0或1。

自旋量子数s只能取0或1/2。

这些量子数的取值范围决定了角动量算符的本征值。

三、角动量算符的应用角动量算符在量子力学中的应用非常广泛。

下面将介绍一些常见的应用。

1. 角动量的量子数通过角动量算符，我们可以得到一些重要的物理量，如角动量的大小和方向。

通过计算角动量算符的本征值，可以确定量子系统的角动量取值。

2. 角动量的叠加当将两个或多个角动量相加时，我们需要使用角动量算符来描述。

通过对角动量算符的叠加，可以得到合成系统的总角动量。

[Ô, Û] = 0 (Ô Û)+ = Ô Û
1．指出下列算符哪个是线性的，说明其理由。 ．指出下列算符哪个是线性的，说明其理由。
d d d2 (1) 4 x 2 2 (c1u1 + c2u2 ) = 4 x 2 2 (c1u1 ) + 4 x 2 2 (c2u2 ) dx dx dx d2 d2 = c1 ⋅ 4 x 2 2 u1 + c2 ⋅ 4 x 2 2 u2 是线性算符 dx dx
（3Байду номын сангаас算符之和
若两个算符 Ô、Û 之和定义为：对体系的任何波函数 有： 、 之和定义为：对体系的任何波函数ψ
(Ô＋Û)ψ=Ôψ+ Ûψ
Hˆ = Tˆ + V ˆ 算符 Hamilton 体系动能算符 势能算符 表明 Hˆ 等于 Tˆ 和 V ˆ 之和。 之和。
显然，算符求和满足交换率和结合率。 显然，算符求和满足交换率和结合率。
4 掌握氢原子的量子力学处理方法和相关的结果。了 解 掌握氢原子的量子力学处理方法和相关的结果 氢原子的量子力学处理方法和相关的结果。 氢原子内电子坐标取值的概率分布、 氢原子内电子坐标取值的概率分布、电流密度分布和原 子磁矩的概念。 子磁矩的概念。 5 掌握厄密算符的性质：本征值为实数，本征函数的正 掌握厄密算符的性质 本征值为实数， 厄密算符的性质： 交性和完备性。 交性和完备性。 6 理解和掌握测不准关系。 理解和掌握测不准关系。 测不准关系
例如： 例如：算符 x ∂ ˆ px = −iℏ ∂x 不对易。 不对易。
证：
ˆ (1) xpxψ = x(−iℏ ∂∂x )ψ = − iℏx ∂∂x ψ
ˆ (2) px xψ = (−iℏ ∂∂x )xψ = −iℏψ − iℏx ∂∂x ψ