下载文档原格式
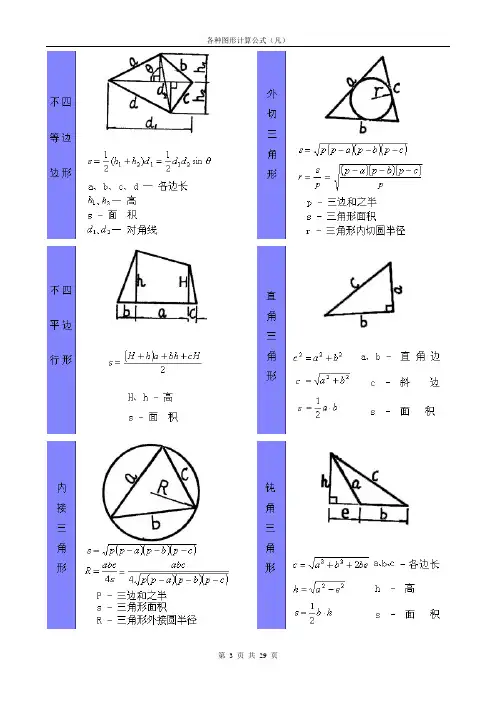
多面体的体积和表面积图形尺寸符号立方体长方体∧棱柱∨三棱柱棱锥棱台圆柱和空心圆柱∧管∨斜线直圆柱直圆锥圆台球球扇形∧球楔∨球缺圆环体∧胎∨球带体桶形椭a,b,c-半轴球体交叉圆柱体梯形体常用图形求面积公式图形尺寸符号面积（F）表面积（S）正方形长方形三角形平行四边形任意四边形正多边形菱形梯形圆形椭a·b-主轴F= (π/4) a·b 圆形扇形弓形圆环部分圆环新月形L d/10 2d/10 3d/10 4d/10 5d/10 6d/10 7d/10 P 0.40 0.79 1.18 1.56 1.91 2.25 2.55抛物线形等多边形土方开挖体积：V=（长+2垫层超出基础长度+2工作面宽+放坡系数×高度）×（宽+2垫层超出基础长度+2工作面宽+放坡系数×高度）×高度+1/3×放坡系数²×高度³几何图形及计算公式大全平面图形名称符号周长C和面积S正方形a—边长C＝4a S＝a2长方形a和b－边长C＝2(a+b) S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－角其中s＝(a+b+c)/2S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高S＝ah＝absinαα－两边夹角菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα)＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－圆半径D－外圆直径d－圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2 V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h积空心圆柱R－外圆半径r－圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)d－桶底直径h－桶高V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物线形)。
几何体的表面积计算在几何学中，几何体的表面积是指该几何体的各个表面的总面积。
计算几何体的表面积对于解决实际问题具有重要的意义，例如在建筑设计中，计算建筑物的表面积有助于确定材料的用量和成本预算。
下面将介绍几种常见几何体的表面积计算方法：1. 立方体的表面积计算立方体是一种具有六个相等正方形面的几何体。
其表面积计算公式为：A = 6a^2，其中a为立方体的边长。
例如，边长为5cm的立方体的表面积为：A = 6 * 5^2 = 150cm^2。
2. 圆柱的表面积计算圆柱是一种由一个圆和与该圆平行的一个曲面所组成的几何体。
其表面积计算公式为：A = 2πr(r + h)，其中r为圆的半径，h为圆柱的高度。
例如，半径为3cm，高度为6cm的圆柱的表面积为：A = 2π * 3(3 + 6) = 108π cm^2。
3. 球体的表面积计算球体是一种所有点到球心的距离相等的几何体。
其表面积计算公式为：A = 4πr^2，其中r为球的半径。
例如，半径为5cm的球体的表面积为：A = 4π * 5^2 = 100π cm^2。
4. 圆锥的表面积计算圆锥是一种由一个圆和从该圆上一点到该圆内所有点的连线所组成的几何体。
其表面积计算公式为：A = πr(r + l)，其中r为圆的半径，l 为圆锥的斜高。
例如，半径为4cm，斜高为6cm的圆锥的表面积为：A = π * 4(4 + 6) = 40π cm^2。
5. 正方体的表面积计算正方体是一种所有面都为正方形的几何体。
其表面积计算公式为：A = 6a^2，其中a为正方体的边长。
例如，边长为7cm的正方体的表面积为：A = 6 * 7^2 = 294cm^2。
6. 圆台的表面积计算圆台是一种由一个圆和与该圆平行的一个曲面，以及连接两个底圆上各点的连线所组成的几何体。
其表面积计算公式为：A = π(r_1 +r_2)l + πr_1^2，其中r_1和r_2分别为两个底圆的半径，l为圆台的斜高。
空间几何体的表面积计算空间几何体的表面积计算是几何学中的一个重要概念。
通过计算几何体的表面积，我们可以了解几何体的形状和大小，为实际问题的解决提供依据。
本文将介绍如何计算一些常见空间几何体的表面积，并提供相应的计算公式和实例。
一、立方体的表面积计算立方体是最简单的空间几何体之一。
它的六个面都是正方形，边长为a。
计算立方体的表面积可以使用以下公式：表面积 = 6 × a^2例如，如果立方体的边长为5cm，那么它的表面积就是6 × 5^2 = 150cm^2。
二、长方体的表面积计算长方体是另一个常见的几何体，它的六个面分别是矩形。
其中，底面的长为a，宽为b，高为h。
计算长方体的表面积可以使用以下公式：表面积 = 2ab + 2bh + 2ah例如，如果长方体的长为4cm，宽为3cm，高为6cm，那么它的表面积就是2 × 4 × 3 + 2 × 3 × 6 + 2 × 4 × 6 = 120cm^2。
三、圆柱体的表面积计算圆柱体是一个具有两个平行圆底面的几何体，它的侧面是一个矩形。
其中，底面的半径为r，高为h。
计算圆柱体的表面积可以使用以下公式：表面积= 2πr^2 + 2πrh例如，如果圆柱体的半径为2cm，高为5cm，那么它的表面积就是2π × 2^2 + 2π × 2 × 5 = 56π cm^2。
四、球体的表面积计算球体是一个完全由曲面组成的几何体，其表面积是其最基本的属性之一。
其中，球的半径为r。
计算球的表面积可以使用以下公式：表面积= 4πr^2例如，如果球体的半径为3cm，那么它的表面积就是4π × 3^2 = 36π cm^2。
五、锥体的表面积计算锥体是一个由一个圆形底面和一个顶点相连而成的几何体。
其中，底面的半径为r，斜高为l（即底面上一点到顶点的距离）。
计算锥体的表面积可以使用以下公式：表面积= πr^2 + πrl例如，如果锥体的半径为4cm，斜高为6cm，那么它的表面积就是π × 4^2 + π × 4 × 6 = 64π cm^2。
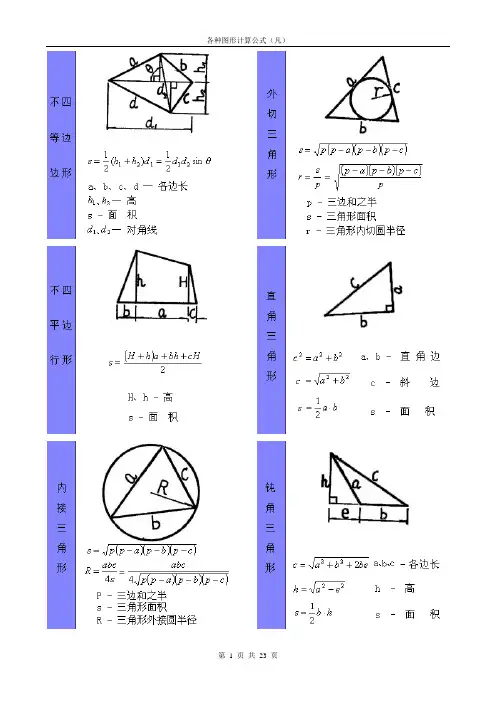
多面体的体积和表面积图形尺寸符号立方体长方体∧棱柱∨三棱柱棱锥棱台圆柱和空心圆柱∧管∨斜线直圆柱直圆锥圆台球球扇形∧球楔∨球缺圆环体∧胎∨球带体桶形椭a,b,c-半轴球体交叉圆柱体梯形体常用图形求面积公式图形尺寸符号面积（F）表面积（S）正方形长方形三角形平行四边形任意四边形正多边形菱形梯形圆形椭a·b-主轴F= (π/4) a·b 圆形扇形弓形圆环部分圆环新月形L d/10 2d/10 3d/10 4d/10 5d/10 6d/10 7d/10 P 0.40 0.79 1.18 1.56 1.91 2.25 2.55抛物线形等多边形土方开挖体积：V=（长+2垫层超出基础长度+2工作面宽+放坡系数×高度）×（宽+2垫层超出基础长度+2工作面宽+放坡系数×高度）×高度+1/3×放坡系数²×高度³几何图形及计算公式大全平面图形名称符号周长C和面积S正方形a—边长C＝4a S＝a2长方形a和b－边长C＝2(a+b) S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα)＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径S＝π(R2-r2)＝π(D2-d2)/4D－外圆直径d－内圆直径椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2 V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长C＝2πrS底＝πr2S侧＝ChS底—底面积S侧—侧面积S表—表面积S表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径V＝2π2Rr2＝π2Dd2/4d－环体截面直径桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15(母线是抛物线形)。
几何体的表面积计算在几何学中，表面积是描述一个物体外部覆盖的总面积。
这在许多实际问题中都是一个重要的指标，如建筑、制造、设计等领域。
计算几何体的表面积可以帮助我们了解其空间占有和形状特征。
本文将介绍一些常见几何体表面积的计算方法。
一、立方体的表面积计算立方体是最简单的几何体之一，它有六个相等的正方形表面。
要计算一个立方体的表面积，只需将六个正方形的面积相加。
设立方体的边长为a，则其表面积S可以表示为：S = 6a²二、长方体的表面积计算长方体是由三个相对平行的长方形组成的几何体。
它的表面积计算公式如下：S = 2lw + 2lh + 2wh其中l、w和h分别表示长方体的长、宽和高。
三、圆柱体的表面积计算圆柱体是一个由两个平行圆底之间的曲面和两个底面构成的几何体。
要计算圆柱体的表面积，需要计算两个底面的面积和侧面的面积之和。
表面积公式如下：S = 2πr² + 2πrh其中r表示圆柱体的底面半径，h表示圆柱体的高度。
四、球体的表面积计算球体是一个完全由曲面组成的几何体，其表面积计算公式如下：S = 4πr²其中r表示球体的半径。
五、正方体的表面积计算正方体是由六个相等的正方形构成的几何体。
每个正方形的边长均为a。
要计算正方体的表面积，只需将六个正方形的面积相加。
表面积公式如下：S = 6a²其中a表示正方体的边长。
六、棱柱的表面积计算棱柱是一个由两个相等的底面和连接底面的多边形侧面构成的几何体。
要计算棱柱的表面积，需要计算底面的面积和侧面的面积之和。
设底面的面积为B，侧面的面积为L，则表面积可表示为：S = B + L七、棱锥的表面积计算棱锥是由一个封闭基和连接基和顶点的三角形侧面构成的几何体。
要计算棱锥的表面积，需要计算封闭基的面积和侧面的面积之和。
设封闭基的面积为B，侧面的面积为L，则表面积可表示为：S = B + L八、棱台的表面积计算棱台是由一个上底、一个下底和连接上下底的多边形侧面构成的几何体。
简单常见几何图形的计算方法几何学是数学的一个重要分支，研究的是空间中的形状和大小关系。
在我们日常生活中，常常会遇到一些简单的几何图形，如圆、矩形、三角形等。
本文将介绍一些常见几何图形的计算方法，帮助读者更好地理解和应用几何学知识。
一、圆的计算方法圆是几何学中最基本的图形之一，它具有无限多个点，且到圆心的距离都相等。
在计算圆的相关问题时，我们通常会用到以下几个重要的参数：1. 半径（r）：圆心到圆上任意一点的距离。
2. 直径（d）：穿过圆心的线段，两端点在圆上。
3. 周长（C）：圆的周长，也称为圆周长或圆周。
4. 面积（A）：圆所包围的平面区域。
对于圆的计算，有以下几个常用公式：1. 直径和半径的关系：d = 2r。
2. 周长和直径的关系：C = πd，其中π≈3.14159，是一个无理数。
3. 周长和半径的关系：C = 2πr。
4. 面积和半径的关系：A = πr²。
二、矩形的计算方法矩形是一个有四个直角的四边形，它的对边长度相等。
在计算矩形的相关问题时，我们通常会用到以下几个重要的参数：1. 长度（L）：矩形的长边。
2. 宽度（W）：矩形的短边。
3. 周长（P）：矩形的周长，也称为矩形周长。
4. 面积（A）：矩形所包围的平面区域。
对于矩形的计算，有以下几个常用公式：1. 周长和长度、宽度的关系：P = 2(L + W)。
2. 面积和长度、宽度的关系：A = LW。
3. 长度和面积的关系：L = A/W。
4. 宽度和面积的关系：W = A/L。
三、三角形的计算方法三角形是一个有三个顶点和三条边的多边形，它的内角和为180度。
在计算三角形的相关问题时，我们通常会用到以下几个重要的参数：1. 底边（b）：三角形的底边。
2. 高（h）：从底边到对顶顶点的垂直距离。
3. 边长（a、b、c）：三角形的三条边。
4. 周长（P）：三角形的周长，也称为三角形周长。
5. 面积（A）：三角形所包围的平面区域。
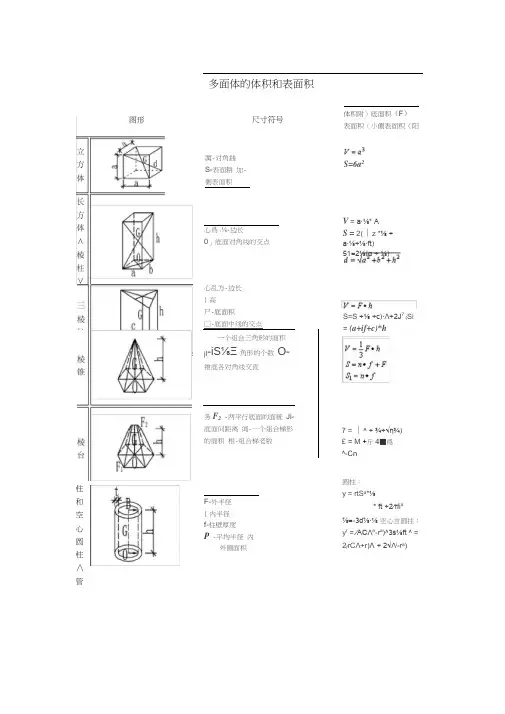
多面体的体积和表面积心乱方-边长 1高 尸-底面积 □-底面中线的交点一个组合三角形的面积jl -iS⅛Ξ角形的个数 O-锥底各对角线交直务F 2 -两平行底面的面粧 Ji-底面间距离 闻-一个爼合梯形的面积 相-组合梯老数7 = ∣^ + ¾÷√η¾) £ = M +斤4■爲 ^-Cn厲-对角銭S-表面耕 加-侧表面积尺寸符号心爲1⅛-边长0」底面对角线的交点体积附）底面积（F ） 表面积（小侧表面积（阳S=6a 2V = a∙⅛* AS = 2(∣z *⅛ +a∙⅛+⅛∙ft)51=2⅛(α + ⅛)柱和 空 心 圆 柱 ∧ 管F-外半径1内半径f-柱壁厚度P -平均半径 内外侧面积圆柱：y = rtS a *⅛* ft +2∕τfi a⅞=-3d⅞∙⅛ 空心言圆拄： y r = ∕ACΛa -r a )^3s⅛ft ^ = 2f rC Λ+r)Λ + 2√Λi -r a )S=S +⅛ +c)∙Λ+2J 7 (Si = (a+if+c)*hVy = ψ∙(j⅞2 3 + √+⅛) 5*1 = KHR+r)I= y ∣(R-r)2+h 2 £ =址十疔(0+/)y = -jιr⅛ =2W44r⅛3 y=^(4ft+rf) = 157f(⅛?+^£斜 线 直 圆 柱 ⅛-≡小高度¾-盘大高度T -底面半径^-^c⅛+⅛>rtf 1∙α+J —) cc≤ αS l - πr(⅛ +¾)r-廐面半径卜母线长+⅛2 =鈕球半径 d ・弓定底11直径A-弓形高一半径d-直径4 3皿'— L.PV = Lf I f =——=0.5236 护36 S=A f tr 2 ==V⅛-球駛的高J--球銭半径d-平切圆直径=曲面面积S-球缺表而稅R -圆球擁平均半径D-圆环体平均半径d-圆怀体截面直径T-匾!环∙⅛⅛⅛面半径尺-球半径①孩-底面半径沟-腰高⅞-⅛∣i<≡Φ底圆⅛3L的距离^ = n fi∖r-¾3¾ -⅛A-rr(^ + A3)护土畋彷-附3⅛ -√D⅛ -3P 478⅛Pr = ^(3⅛+3⅛ + ⅛i) ⅛¾ = 2∕⅛⅛。
