SPSS单因素和多因素方差分析法

格式：ppt
大小：749.50 KB
文档页数：46

下载文档原格式

SPSS统计分析—差异分析

显著性水平： 0.05——显著 0.001——非常显著 0.0001——极其显著
t检验的类型
• 单样本t检验——样本均值与总体均值的比较 • 独立两样本t检验——独立两样本均值比较 • 配对样本t检验——配对设计的差数均值与总体均值0的比较
单样本t检验
统计学上的定义和计算公式
定义：SPSS单样本T检验是检验某个变量的总体均值和某指定值之间是否存在显著差异。统计的前提是样本总体服从正态分布。也就是说单样本本身无法比较，进行的是其均数与已知总体均数间的比较。
较样本差值的均值和总体均值0之间的关系。如果两组数据没有差别，那么其样本差值的均值应该在0附近波动。否则为两组数据是有差别的。这种方法的本质就是在对配对样本的差值同总体均值0做单样本t检验。
两配对样本T检验的零假设H0为两总体均值之间不存在显著差异。
◆注意单样本t检验和独立两样本t检验样本内部数据的顺序是可以任意调换。而配对样本t检验的样本必须是一一对应的。样本内数据的顺序不能随意交换顺序。
数学 99.00 88.00 99.00 89.00 94.00 90.00 79.00 56.00 89.00 99.00 70.00 89.00 55.00 50.00 67.00 67.00 56.00 56.00
组别 0 0 0 0 0 0 2 2 2 2 2 2 1 1 1 1 1 1
实现步骤
SPSS中实现过程
分析——比较均值——单因素ANOVA
SPSS中实现过程
研究问题
三组学生的数学成绩
人名 hxh yaju yu shizg hah s watet jess wish
2_new1 2_new2 2_new3 2_new4 2_new5 2_new6 2_new7 2_new8 2_new9

单因素分析的spss操作

单因素分析的spss操作
在SPSS中进行单因素分析的操作步骤如下：
1. 打开SPSS软件并加载数据集。

2. 选择菜单栏中的“分析”（Analyze）选项，并从下拉菜单中选择“比较均值”（Compare Means）。

3. 在弹出的子菜单中选择“独立样本T检验”（Independent-Samples T Test）或“单因素方差分析”（One-Way ANOVA），具体选择哪一种方法根据数据类型来决定。

4. 将需要进行分析的变量从“因素”的文本框中移动到“因素”框中，或将其从“因素”框中移除，具体操作根据需要来决定。

5. 点击“选项”（Options）按钮，根据需要选择不同的选项，如描述统计数据、置信区间、效应大小等。

6. 点击“确定”（OK）按钮，开始进行单因素分析。

7. SPSS将生成分析结果的输出窗口，其中包括各种统计指标，如均值、标准差、频数等，并进行相关的统计检验。

8. 可以利用SPSS提供的图表功能，如直方图、箱线图等，对数据进行可视化分析。

以上是在SPSS中进行单因素分析的一般步骤。

具体操作方法可能因SPSS版本的不同而略有差异，也可以根据数据类型和分析需求来调整具体的参数设置。

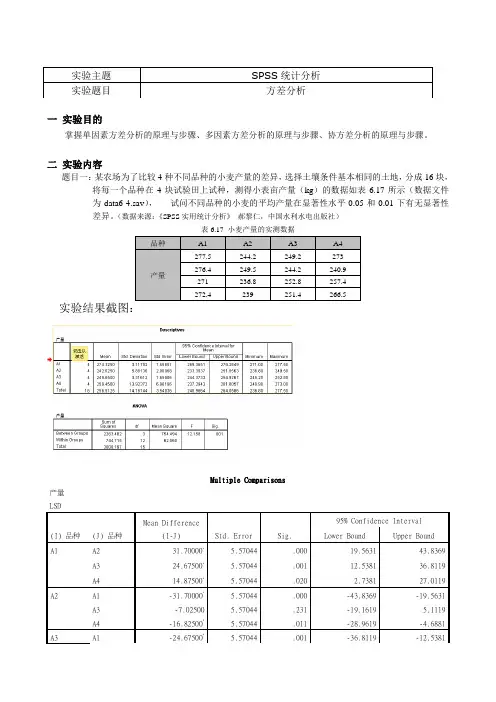
spss方差分析

一实验目的掌握单因素方差分析的原理与步骤、多因素方差分析的原理与步骤、协方差分析的原理与步骤。

二实验内容题目一：某农场为了比较4种不同品种的小麦产量的差异，选择土壤条件基本相同的土地，分成16块，将每一个品种在4块试验田上试种，测得小表亩产量（kg ）的数据如表6.17所示（数据文件为data6-4.sav ），试问不同品种的小麦的平均产量在显著性水平0.05和0.01下有无显著性差异。

（数据来源：《SPSS 实用统计分析》郝黎仁，中国水利水电出版社）表6.17 小麦产量的实测数据品种A1 A2 A3 A4 产量277.5244.2 249.2 273 276.4 249.5 244.2 240.9 271 236.8 252.8 257.4 272.4239251.4266.5实验结果截图：Multiple Comparisons产量 LSD(I) 品种 (J) 品种 Mean Difference(I-J) Std. ErrorSig.95% Confidence IntervalLower BoundUpper BoundA1A2 31.70000*5.57044 .000 19.5631 43.8369 A3 24.67500* 5.57044 .001 12.5381 36.8119 A414.87500* 5.57044 .020 2.7381 27.0119 A2A1 -31.70000* 5.57044 .000 -43.8369 -19.5631 A3 -7.02500 5.57044 .231 -19.1619 5.1119 A4-16.82500* 5.57044 .011 -28.9619 -4.6881 A3A1-24.67500*5.57044.001-36.8119-12.5381实验主题 SPSS 统计分析实验题目方差分析实验结果分析：根据不同小麦的平均产量在显著性水平0.05和0.01下的奇性检验结果、方差检验结果、多重比较结果、均值折线图可以看出，不管是方差还是均值，差异较大，而它的均值折线图分布比较陡峭。

用SPSS进行单因素方差分析和多重比较

方差分析方差分析可以用来检验来多个均值之间差异的显著性，可以看成是两样本t检验的扩展。

统计学原理中涉及的方差分析主要包括单因素方差分析、两因素无交互作用的方差分析和两因素有交互作用的方差分析三种情况。

虽然Excel可以进行这三种类型的方差分析，但对数据有一些限制条件，例如不能有缺失值，在两因素方差分析中各个处理要有相等的重复次数等；功能上也有一些不足，例如不能进行多重比较。

而在方差分析方面SPSS的功能特别强大，很多输出结果已经超出了统计学原理的范围。

用SPSS检验数据分布的正态性方差分析需要以下三个假设条件：（1）、在各个总体中因变量都服从正态分布；（2）、在各个总体中因变量的方差都相等；（3）、各个观测值之间是相互独立的。

在SPSS中我们很方便地对前两个条件进行假设检验。

同方差性检验一般与方差分析一起进行，这一小节我们只讨论正态性的检验问题。

[例7.4] 检验生兴趣对考试成绩的影响的例子中各组数据的正态性。

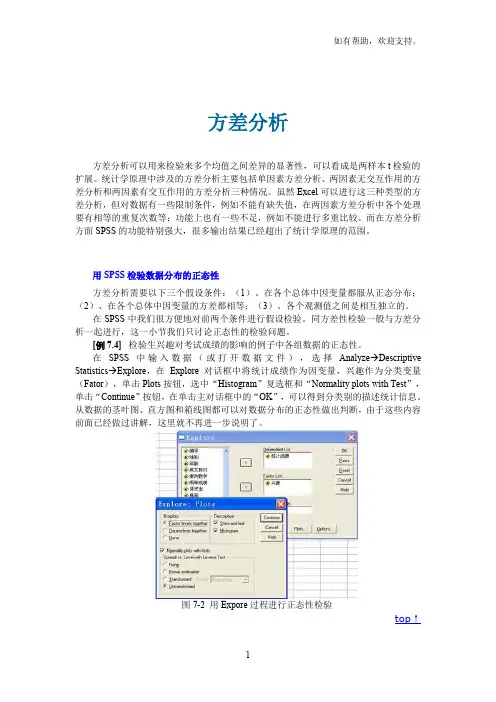
在SPSS中输入数据（或打开数据文件），选择Analyze→Descriptive Statistics→Explore，在Explore对话框中将统计成绩作为因变量，兴趣作为分类变量（Fator），单击Plots按钮，选中“Histogram”复选框和“Normality plots with Test”，单击“Continue”按钮，在单击主对话框中的“OK”，可以得到分类别的描述统计信息。

从数据的茎叶图、直方图和箱线图都可以对数据分布的正态性做出判断，由于这些内容前面已经做过讲解，这里就不再进一步说明了。

图7-2 用Expore过程进行正态性检验top↑输出结果中的Q-Q图是观察数据分布正态性的一种常用图形。

这类图形大致是这样绘制的：计算数据在样本中对应的经验分布函数值（类似于累积分布的函数值，取值在0-1之间）；然后计算标准正态分布（或者均值、方差相同的正态分布）对应于经验分布函数值的分位数。

数据统计及SPSS应用-方差分析

–提出Ｈ０假设 –选择检验统计量 –计算统计量的观测值和概率值 –根据给出的显著性水平做出决策
单因素方差分析--假设条件
• 单一因素影响试验结果，该因素各水平：I=1， 2，…K • 各水平下样本均值为： x1 , x 2 ,...x k • 方差为： 2 2 2 σ1 ,σ 2 ...σ k • 前提条件：样本正态分布，方差差异不显著 • H0假设：均值差异不显著，x = x = ... = x (i ≠ j ) • H1假设：至少有， x i ≠ x j • 方差分析的实质：相同方差下，正态分布样本的 K个水平下的观测值的均值差异的检验。
单因素方差分析--Contrast选项
• 先验对照检验
–使用Ｔ检验检验用户定义的样本组合的均值差异 –系数之和应等于０ –显著性水平＜０．０５对比组差异显著 –如：μ１＋μ ２＝ μ ３
单因素方差分析--Contrast选项
多因素方差分析--基本概念
• 当作用在一个过程的因素不只一个时，对不同因素或因素的不同水平造成不同结果的研究将采用多因素方差分析的研究方法。 • 研究多个因素的各个水平对试验结果的影响，以及各因素相互作用对试验的影响。
组内数据与该组均值间的离差平方和反映数据抽样误差为随机误差各组均值与总均值间的离差平方和反映各样本组均值的差异为系统误差ssssss由于离差平方和的值与其项数k与n有关因此在方差分析中不能作为比较组间差异与组内差异的依据应当去掉项数影响求其均方来比较组间与组内差异
数据管理与分析
数据统计及ＳＰＳＳ应用
• 注意：
多因素方差分析--基本引用
• 【分析】【一般线性模型】【单变量】
–因变量：实验结果 –固定因素：不同水平来线性地影响因变量的值（一般是可认为控制的，如温度，品种）。 –随机因素：通过随机大量取值来影响过程变化的因素（一般不可控，比如身高，体重）。 –协变量：与因变量相关，用来控制影响过程变化的干扰因素。

SPSS操作—方差分析

• 实际工作中往往需要两两的组间均值比较。这就需要使用 One-way ANOVA进行单因素方差分析时使用选择项从而获得更丰富的信息，使分析更深入。
例题进一步分析
析中剔除
实例-单因素方差分析各处理重复数不等的方差分析
用四种饲料喂养19头猪比较，四种饲料是否不同。
饲料 A 133.8 B 151.2 C 193.4 D 225.8
125.3
143.1 128.9 135.7
149.0
162.7 143.8 153.5
185.3
182.8 188.5 198.6
Post Hoc（均数的多重比较选项）
• 进行多重比较是对每两个组的均值进行如下比较：MEAN(i)MEAN(j)≥4.6625×RANGE×SQRT(1/N(i)+1/N(j))；其中i、j分别为组序号， MEAN(i)、MEAN(j)分别为第i、j组均值， N(i)、N(j) 分别为第i、j组中的观测数。各组均值的多重比较方法的算法不同RANGE值也不同。
• Hochberg’s GT2(霍耶比GT2法)：用正态最大系数进行多重比较
• Gabriet(盖比理法)：用正态标准系数进行配对比较，在单元数较大时，这种方法较自由； • Waller-Duncan(瓦尔-邓肯法)：用t统计量进行多重比较检验。
使用贝耶斯接近；
• Dunnett(邓尼特法)：最小显著差数测验法，进行各组与对照组的均值，默认的对照组是最后一组；选定此方法后，激活下面的Control Catetory参数框，展开小菜单，选择对照组 • Tamhane‘s T2(塔海尼T2法)：t检验进行配对比较； • Dunnett’s T3(邓尼特T3法)：正态分布下的配对比较； • Games-Howell(盖门-霍威尔法)：各组均值的配对比较，该方法较灵活；

SPSS中的方差分析法(1)

方差分析（多因素，协方差）一、方法名称单因素二、定义（方法及结果）三、用途四、实现过程1、格式数据整理2、提交显示3、分析变量处理：自变量、因变量ANOVA检验：显示表，是否齐次1 方差分析法方差分析是一种是一种假设检验，它把观测总变异的平方和自由度分解为对应不同变异来源的平方和自由度，将某种控制性因素所导致的系统性误差和其他随机性误差进行对比，从而判断各组样本之间是否存在显著性差异，以分析该因素是否对总体存在显著性影响。

2 样本数据要求方差分析法采用离差平法和对变差进行度量，从总离差平方分解出可追溯到指定来源的部分离差平方和。

方差分析要求样本满足以下条件：2.1 可比性样本数据各组均数本身必须具有可比性，这是方差分析的前提。

2.2 正态性方差分析要求样本来源于正态分布总体，偏态分布资料不适用方差分析。

对偏态分布的资源要考虑先进行对数变换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法变换为正态或接近正态后再进行方差分析。

2.3 方差齐性。

方差分析要求各组间具有相同的方差，满足方差齐性。

3 单因素分析法实验操作单因素分析用于分析单一控制变量影响下的多组样本的均值是否存在显著性差异。

单因素分析法的原理，单因素方差分析也称为一维方差分析,用于分析单个控制因素取不同水平时因变量的均值是否存在显著差异。

单因素方差分析基于各观测量来自于相互独立的正态样本和控制变量不同水平的分组之间的方差相等的假设。

单因素方差分析将所有的方差划分为可以由该因素解释的系统性偏差部分和无法由该因素解释的随机性偏差,如果系统性偏差明显超过随机性偏差,则认为该控制因素取不同水平时因变量的均值存在显著差异。

3.1 实验数据描述某农业大学对使用不同肥料的实验数据对比。

产量（千克/亩产）施肥类型864 普通钾肥875 普通钾肥891 普通钾肥873 普通钾肥883 普通钾肥859 普通钾肥921 控释肥944 控释肥986 控释肥929 控释肥973 控释肥963 控释肥962 复合肥941 复合肥985 复合肥974 复合肥977 复合肥在SPSS的变量视图中建立变量“产量”和“施肥类型”，分别表示实验田产量和实验田的施肥类型。

spss方差分析理论概念及实际操作分析

给定显著性水平α，并与检验统计量的概率p值进行比较。如果p<α，则拒绝原假设，即认为控制变量的不同水平下观测变量个总体的均值存在差异，当控制变量的各个效应不同时为0时，控制变量的不同水平对观测变量产生了显著影响；如果p>α，则接受原假设，认为控制变量不同水平下观测变量各总体的均值无显著差异，控制变量的各个效应同时为0，控制变量的不同水平对观测变量没有产生显著影响。
实例操作
采用“*******”数据，分析不同身份的旅游者对“政府及相关部门的政策充分地照顾到遗产地资源开发各利益群体的实际情况”的认同是否存在显著性差异。 D1政府及相关部门的政策充分地照顾到遗产地资源开发各利益群体的实际情况 1不同意 2稍微不同意 3中立 4稍微同意 5同意您的身份： A. 一般居民（旅游者） B. 学生 C. 专家、学者 D. NGO E. 媒体工作者
多因素方差分析适用案例
• 不同年龄、职业的旅游者对旅游形式的选择是否存在显著性差异？即，年龄与职业队旅游者选择旅游形式是否存在显著影响？ • 不同教育背景、地区的旅游者对成都市内旅游满意度是否存在显著性差异？
多因素方差分析分析步骤
1. 提出原假设 H0：各控制变量不同水平下观测变量总体的均值无显著性差异，控制变量各效应和交互作用效应同时为0，即控制变量和它们的交互作用没有对观测变量产生显著性影响
方差齐次性检验
上表为方差齐性检验表，Levene值为1.480，自由度分别为4 和612，显著性水平P值=0.207 > 0.05，可以认为不同身份的游客对“政府及相关部门的政策充分地照顾到遗产地资源开发各利益群体的实际情况”的认同程度具有方差齐性，即各种身份的游客样本所在总体方差相同。
单因素方差分析结果

SPSS统计分析教程多因素方差分析

多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。

SPSS调用“Univariate”过程，检验不同水平组合之间因变量均数，由于受不同因素影响是否有差异的问题。

在这个过程中可以分析每一个因素的作用，也可以分析因素之间的交互作用，以及分析协方差，以及各因素变量与协变量之间的交互作用。

该过程要求因变量是从多元正态总体随机采样得来，且总体中各单元的方差相同。

但也可以通过方差齐次性检验选择均值比较结果。

因变量和协变量必须是数值型变量，协变量与因变量不彼此独立。

因素变量是分类变量，可以是数值型也可以是长度不超过8的字符型变量。

固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。

[例子]研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。

分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。

表5-7 不同温度与不同湿度粘虫发育历期表数据保存在“”文件中，变量格式如图5-1。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量历期“历期”变量，因素变量温度“A”，湿度为“B”变量，重复变量“重复”。

然后输入对应的数值，如图5-6所示。

或者打开已存在的数据文件“”。

图5-6 数据输入格式2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“General Linear Model”项，在右拉式菜单中点击“Univariate”项，系统打开单因变量多因素方差分析设置窗口如图5-7。

图5-7 多因素方差分析窗口3）设置分析变量设置因变量:在左边变量列表中选“历期”，用向右拉按钮选入到“Dependent Variable：”框中。

设置因素变量:在左边变量列表中选“a”和“b”变量，用向右拉按钮移到“Fixed Factor(s):”框中。

可以选择多个因素变量。

由于内存容量的限制，选择的因素水平组合数(单元数)应该尽量少。

SPSS方差分析

SPSS⽅差分析实验⽬的：1、学会使⽤SPSS的简单操作。

2、掌握⽅差分析。

实验内容：1.单因素⽅差分析；2.双因素⽅差分析。

实验步骤： 1.单因素⽅差分析，⽅差分析是基于变异分解的思想进⾏的，在单因数⽅差分析中，整个样本的变异可以看成由两个部分构成：总变异=随机变异+处理因数导致的变异，其中随机变异是永远存在的，确定处理因数导致的变异是否存在就是所要达到的研究⽬标，即只要能证明它不等于0，就等同于证明了处理因数的确存在影响。

这样可采⽤⼀定的⽅法来⽐较组内变异和组间变异的⼤⼩，如果后者远远⼤于前者，则说明处理因数的影响的确存在，如果两者相差⽆⼏，则说明该影响不存在。

SPSS操作：【分析】→【⼀般线性模型-单变量】，将因变量选⼊【因变量】，将⾃变量选⼊【固定因⼦】。

如果需要均值图⽰，【绘图】，将因⼦选⼊【⽔平轴】，【图】→【添加】。

如果需要多重⽐较时，【事后多重⽐较】，将因⼦选⼊【两两⽐较检验】，【假定⽅差齐性】→【LSD】。

如果需要相关统计量时，【选项】→【显⽰】→【描述统计量】。

如果需要⽅差齐性检验时，【选项】→【输出】→【齐性检验】。

如果需要对模型的参数进⾏估计时，【选项】→【输出】→【参数估计值】。

如果需要预测值时，【保存】→【预测值】→【未标准化】。

1 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /CRITERIA=ALPHA(0.05)5 /DESIGN=超市位置.⽅差单变量分析11 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /PLOT=PROFILE(超市位置) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO5 /CRITERIA=ALPHA(0.05)6 /DESIGN=超市位置.单因数⽅差分析2轮廓图1 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /POSTHOC=超市位置(LSD)5 /CRITERIA=ALPHA(0.05)6 /DESIGN=超市位置.单因数⽅差分析31 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /PRINT DESCRIPTIVE5 /CRITERIA=ALPHA(.05)6 /DESIGN=超市位置.单因数⽅差分析41 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /PRINT HOMOGENEITY5 /CRITERIA=ALPHA(.05)6 /DESIGN=超市位置.单因数⽅差分析51 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /PRINT PARAMETER5 /CRITERIA=ALPHA(.05)6 /DESIGN=超市位置.单因数⽅差分析61 UNIANOVA 销售额 BY 超市位置2 /METHOD=SSTYPE(3)3 /INTERCEPT=INCLUDE4 /SAVE=PRED5 /CRITERIA=ALPHA(.05)6 /DESIGN=超市位置.单因数⽅差分析7 2.双因数⽅差分析：分析两个因数对实验结果的影响。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4．因素的主效应和因素间的交互效应

如果一个因素的效应大小在另一个因素不同水平下明显不同，则称两因素间存在交互作用
表5-1 某公司产品销售方式所对应的销售量
序号销售方式 1 2 3 4 5 水平均值
方式一
方式二方式三
77
95 71
86
92 76
81
78 68
88
96 81
83
89 74

2．水平

因素的不同等级称作水平。例如，性别因素在一般情况下只研究两个水平：男、女。应该特别注意的是在SPSS数据文件中，作为因素出现的变量不能是字符型变量，必须是数值型变量。例如性别变量SEX，定义为数值型，取值为0、1。换句话说，因素变量的值实际上是该变量实际值的代码，代码必须是数值型的。可以定义值标签F、M（或Fema1e、 ma1e）来表明0、1两个值的实际含义，以便在打印方差分析结果时使用。使结果更加具有可读性。
2.基本原理方差分析认为： SST（总的离差平方和）=SSA（组间离差平方和） +SSE（组内离差平方和）如果在总的离差平方和中，组间离差平方和所占比例较大，说明观测变量的变动主要是由因素的不同水平引起的，可以主要由因素的变动来解释，系统性差异给观测变量带来了显著影响；反之，如果组间离差平方和所占比例很小，说明观测变量的变动主要由随机变量因素引起的。
第5章 SPSS的方差分析
5.1 方差分述析概念
5.1.1 方差分析的概念
在上节课中我们讨论了如何对一个总体及两个总体的均值进行检验，如我们要确定两种销售方式的效果是否相同，可以对零假设进行检验。但有时销售方式有很多种，这就是多个总体均值是否相等的假设检验问题了，所采用的方法是方差分析。
2. 实例操作
Step01 ：打开或建立数据文件 5-2.sav ，选择菜单栏中的【Analyze （分析）】 →【Compare Means( 比较均值 )】→【One-Way ANOVA( 单因素 ANOVA)】命令，弹出【One-Way ANOVA( 单因素ANOVA) 】对话框。这里“rate”变量表示基金的费用比率；“fund”变量表示基金的类型，其中，“ 1”表示中等规模的资本股票基金，“2”表示小额资本股票基金，“3”表示混合型股票基金，“4”表示专项股票基金。
Step05：单击【Post Hoc】按钮，弹出【Post Hoc(两两比较) 】对话框。由于这里已计划好对这4组均值进行两两比较，则在其对话框中勾选【LSD】复选框。单击【Continue】按钮，返回主对话框。
LSD（最小显著差异法）：用
t检验完成各组均值间的配对比较。对多重比较误差率不进行调
83
90 74
方式四
80
84
79
70
82
79
81.5
总均值
5.1.2 方差分析的基本思想
在表 5-1 中，要研究不同推销方式的效果，其实就归结为一个检验问题，设为第i（i=1,2,3,4）种推销方式的平均销售量，即检验原假设是否为真。从数值上观察，四个均值都不相等，方式二的销售量明显较大 H 0 : 1 2 3 4 。从表5-1可以看到，20个数据各不相同，这种差异可能是由以下两方面的原因引起的。一是推销方式的影响，不同的方式会使人们产生不同消费冲动和购买欲望，从而产生不同的购买行动。这种由不同水平造成的差异，称之为系统性差异。

5.2.4 实例进阶分析：股票基金的费用比率
1. 实例内容 Money杂志报告了股票和债券基金的收益和费用比率。10种中等规模的资本股票基金、10种小额资本股票基金、10种混合型股票基金和10种专项股票基金的费用比率的数据见表5-5所示（单位：％）。（1）请检验这4种类型股票基金之间的平均费用比率的差异性。（2）混合型股票基金的费用比率是其他三种类型基金费用比率的平均水平吗？
5.2 SPSS在单因素方差分析中的应用
单因素方差分析也叫一维方差分析，它用来研究一个因素的不同水平是否对观测变量产生了显著影响，即检验由单一因素影响的一个（或几个相互独立的）因变量由因素各水平分组的均值之间的差异是否具有统计意义。 1.使用条件应用方差分析时，数据应当满足以下几个条件：在各个水平之下观察对象是独立随机抽样，即独立性；各个水平的因变量服从正态分布，即正态性；各个水平下的总体具有相同的方差，即方差齐；
Coefficients：为多项式指定各组均值的系数。因素变量分为几组，输入几个系数，多出的无意义。如果多项式中只包括第一组与第四组的均值的系数，必须把第二个、第三个系数输入为0值。如果只包括第一组与第二组的均值，则只需要输入前两个系数，第三、四个系数可以不输入。多项式的系数需要由读者自己根据研究的需要输入。
（2）方差齐性检验表5-7是方差齐性检验结果表。表中显示Levene 统计量等于2.086。由于概率P值0.119大于显著性水平0.05，故认为这四种类型基金费用比率的方差是相同的，满足方差分析的前提条件。
（3）单因素方差分析表表5-7为单因素方差分析表。可以看到，费用比率总的离差平方总和为13.320；不同基金的组间离差为1.772；组内离差为11.548；它们的方差比分别为0.591和0.321，相除得F统计量的观测值为1.841，对应的概率P值为0.157。这里显著性水平为0.05，由于P值大于显著性水平0.05，所以接受零假设，认为不同类型基金的费用比率没有显著性差异。
4.各组均值的精细比较多重比较检验只能分析两两均值之间的差异性，但是有些时候需要比较多个均值之间的差异性。具体操作是将其转化为研究这两组总的均值是否存在显著差异。这种比较是对各均值的某一线性组合结构进行判断，即上述检验可以等价改写为对进行统计推断。这种事先指定均值的线性组合，再对该线性组合进行检验的分析方法就是各组均值的精细比较。显然，可以根据实际问题，提出若干种检验问题。
5.1.3 方差分析的基本假设
（1）各样本的独立性。即各组观察数据，是从相互独立的总体中抽取的。（2）要求所有观察值都是从正态总体中抽取，且方差相等。在实际应用中能够严格满足这些假定条件的客观现象是很少的，在社会经济现象中更是如此。但一般应近似地符合上述要求。水平之间的方差（也称为组间方差）与水平内部的方差（也称组内方差）之间的比值是一个服从F分布的统计量 F = 水平间方差 / 水平内方差 = 组间方差 / 组内方差
整；
Step06：单击【Options】按钮，在弹出的对话框中勾选【Descriptive(描述性)】复选框表示输出描述性统计量，选择
此项，会计算并输出：观测量数目、均值、标准差、标准误、最小值、最大值、各组中每个因变量的95％
勾选【Homogeneity-of-variance (方差同质性)】复选框表示输出方差齐性检验表；勾选【Mean plot(均值图)】复选框表示输出各水平的均值折线图。再单击【Continue】按钮，返回主对话框。 Step07：单击【One-Way ANOVA(单因素ANOVA)】对话框中的【 OK】按钮，完成操作。
1 ( 1 2 ) 2
1 ( 3 4 ) 2

One-way过程就是单因素简单方差分析过程，它在Analyze菜单中的Compare Means过程组中，用 One-way ANOVA菜单项调用，可以进行单因素方差分析、均值多重比较和相对比较。

One-way ANOVA过程要求因变量属于正态分布总体；如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程；如果几个因变量之间彼此不独立，应该用GLM过程。
第一栏：方差来源；第二栏：离均差平方和；第三栏：自由度第四栏：均方差（第二栏与第三栏之比）；第五栏：F值（组间均方与组内均方之比）；第六栏：F值对应的概率即P值
（4）多重比较检验结果表5-8显示了两两基金之间费用比率均值比较结果。表中的星号表示在显著性水平0.05的条件下，相应的两组均值存在显著性差异。表中第四列Mean Difference表示两两不同基金费用比率差值的均值。第六列是进行t检验的概率P值，可以通过比较P值大小来判断两两基金之间的费用比率是否有显著差异。从结果来看，只有第一种和第四种基金费用比率的概率P值（0.033）小于显著性水平。因此这四种基金中，只有它们之间的费用比率存在显著性差异，其他基金的费用比率之间都没有显著差异。
SPSS将自动计算检验统计量和相伴概率P值，若P值小于等于显著性水平α ，则拒绝原假设，认为因素的不同水平对观测变量产生显著影响；反之，接受零假设，认为因素的不同水平没有对观测变量产生显著影响。 3.多重比较检验问题多重比较是通过对总体均值之间的配对比较来进一步检验到底哪些均值之间存在差异。
H 0 : 1 2 3 4
方差分析中的术语
因素与处理（Factor and Treament）水平（Level）单元（Cell）因素的主效应和因素间的交互效应均值比较协方差分析

1．因素与处理

因素(Factor)是影响因变量变化的客观条件；例如影响农作物产量的因素有气温、降雨量、日照时间等；
置1）描述性统计量表SPSS的结果报告中首先输出了描述性统计量，如表56所示。首先，中等规模的资本股票基金的平均费用比率（1.440）最低，而专项股票基金的平均费用比率（2.000）最高，但各类型基金的平均值差距不大。其次，从标准差大小来看，中等规模的资本股票基金（0.3806）最低，而混合型股票基金（0.7379）最高。最后，表5-6还列出了各种类型基金的最大值、最小值及95％水平的置信区间。
Step02：在【候选变量】列表框中选择“rate”变量作为因变量，将其添加至【Dependent List(因变量列表)】列表框中。 Step03：在【候选变量】列表框中选择“fund”变量作为水平值，将其添加至【Factor(因子)】列表框中。