人教版九年级数学讲义二次函数与一元二次方程(含解析)(2020年最新)
- 格式:pdf
- 大小:259.98 KB
- 文档页数:14



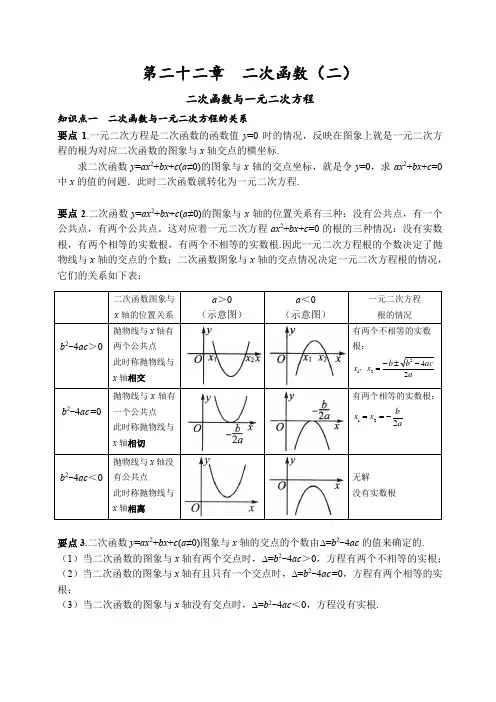
第二十二章二次函数(二)二次函数与一元二次方程知识点一二次函数与一元二次方程的关系要点1.一元二次方程是二次函数的函数值y=0时的情况,反映在图象上就是一元二次方程的根为对应二次函数的图象与x轴交点的横坐标.求二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点坐标,就是令y=0,求ax2+bx+c=0中x的值的问题.此时二次函数就转化为一元二次方程.要点2.二次函数y=ax2+bx+c(a≠0)的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点。
这对应着一元二次方程ax2+bx+c=0的根的三种情况:没有实数根,有两个相等的实数根,有两个不相等的实数根.因此一元二次方程根的个数决定了抛物线与x轴的交点的个数;二次函数图象与x轴的交点情况决定一元二次方程根的情况,它们的关系如下表:要点3.二次函数y=ax2+bx+c(a≠0)图象与x轴的交点的个数由∆=b2-4ac的值来确定的.(1)当二次函数的图象与x轴有两个交点时,∆=b2-4ac>0,方程有两个不相等的实根;(2)当二次函数的图象与x轴有且只有一个交点时,∆=b2-4ac=0,方程有两个相等的实根;(3)当二次函数的图象与x轴没有交点时,∆=b2-4ac<0,方程没有实根.课堂练习1.在平面直角坐标系xOy中,二次函数y=x2-4x的图象与x轴的交点坐标是()A.(0,0)B.(4,0)C.(4,0)、(0,0)D.(2,0)、(-2,0)2.已知关于x的一元二次方程ax2+bx+c=0有两个相等的实数根,则抛物线y=ax2+bx+c与x轴的交点个数是()A.0B.1C.2D.33.若函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是()A.k<3B.k<3且k≠0C.k≤3D.k≤3且k≠04.已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,那么关于x的一元二次方程ax2+bx+c=0的两个解为()A.-1,3B.-2,3C.1,3D.3,45.二次函数y=x2-6x-7的图象与x轴的交点坐标是,与y轴的交点坐标是.6.已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(5,0),则一元二次方程ax2+bx+c =0(a≠0)的根是.7.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行与y轴的直线,则关于x的方程x2+bx=5的解为()A.x1=0,x2=4B.x1=1,x2=5C.x1=1,x2=-5D. x1=-1,x2=58.已知抛物线y=2(k+1)x2+4kx+2k-3,求k为何值时,抛物线与x轴有两个交点、有唯一交点、没有交点.9.已知关于x 的一元二次方程:x 2-(t -1)x +t -2=0. (1)求证:对于任意实数t ,方程都有实数根;(2)当t 为何值时,二次函数y =x 2-(t -1)x +t -2的图象与x 轴的两个交点的横坐标互为相反数?请说明理由.知识点二 抛物线与x 轴两交点之间的距离 要点1.抛物线与x 轴两交点之间的距离公式:若抛物线y =ax 2+bx +c (a ≠0)与x 轴两交点为A (x 1,0),B (x 2,0)由于x 1、x 2是方程ax 2+bx +c =0的两个根,.有2121acx x a b x x =-=+,则结合两点之间的距离公式:22)()(B A B A x x y y AB -+-=(勾股定理).a a acb a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=-+=-=-=444)()(222122122121.课堂练习1.已知抛物线y =43x 2415-x +3经过与x 轴相交于A ,B 两点,与y 轴相交于C 点,顶点为D 点,分别求出△ABC 和△ABD 的面积.知识点三利用二次函数的图象求一元二次方程的近似解要点1.我们可以利用二次函数的图象求一元二次方程的解.由于作图或观察可能有误差,由图象求得的解一般是近似的.利用二次函数的图象求一元二次方程的近似解的一般步骤如下:(1)作出二次函数y=ax2+bx+c(a≠0)的图象,由图象确定与x轴交点的个数,即方程解的个数;(2)观察图象与x轴的交点在哪两个数之间,即确定交点的横坐标的取值范围;(3)在两个数之间取值估计,并用计算器估算近似解近似解出现在对应y值正负交替的地方.当x由x1到x2,对应的y值出现y1>0,y2<0(或y1<0<y2)时,则x1,x2中必有一个是方程的近似解.再比较|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似解;若|y1|>|y2|则x2是方程的近似解.利用二次函数的图象求一元二次方程的近似解的常用方法如下表:方法步骤结论方法一直接作出二次函数y=ax2+bx+c(a≠0)的图象图象与x轴的交点的横坐标就是方程ax2+bx+c=0(a≠0)的根方法二先将一元二次方程变为ax2+bx=-c(a≠0),再在同一直角坐标系中画出抛物线y=ax2+bx和直线y=-c两图象交点的横坐标就是方程ax2+bx+c=0(a≠0)的根方法三先将一元二次方程化为ax2=-bx-c(a≠0)移项后得再在同一直角坐标系中画出抛物线y=ax2和直线y=-bx-c两图象交点的横坐标就是方程ax2+bx+c=0(a≠0)的根课堂练习1.已知二次函数y=x2-2x-3.(1)请你将函数解析式化成y=a(x-h)2+k的形式,并在平面直角坐标系中画出y=x2-2x-3的图象(2)利用(1)中的图象结合图象变换表示x2-2x-1=0的根,要求保留作图痕迹,指出方程的图形意义.2.如图,点A (2.18,-0.51),B (2.68,0.54),在二次函数y =ax 2+bx +c (a ≠0)的图象上,则方程ax 2+bx +c =0的一个近似值可能是( ) A.2.18 B.2.68C.-0.51D.2.453.根据下列表格的对应值,判断ax 2+bx +c =0(a ≠0,a ,b ,c 为常数)的一个解x 的取值范围是 .知识点四 二次函数与一元二次不等式的关系要点1.二次函数y =ax 2+bx +c (a ≠0)与一元二次不等式ax 2+bx +c >0(a ≠0)及ax 2+bx +c <0(a ≠0)之间的关系如下(x 1<x 2): (1)a <0时:判别式a >0抛物线y =ax 2+bx +c 与x 轴的交点不等式ax 2+bx +c >0 的解集 不等式ax 2+bx +c <0的解集△>01x x <或2x x > 12x x x <<△=01x x ≠(或2x x ≠)无解△<0全体实数 无解x 3.23 3.24 3.25 3.26 ax 2+bx +c-0.06-0.020.030.09(2)a<0时:利用二次函数y=ax2+bx+c(a≠0)的图象解不等式:不等式ax2+bx+c>0(a≠0)的解集是二次函数y=ax2+bx+c(a≠0)的图象位于x轴上方的所有点的横坐标.不等式ax2+bx+c<0(a≠0)的解集是二次函数y=ax2+bx+c(a≠0)的图象位于x轴下方的所有点的横坐标;当二次函数y=ax2+bx+c(a≠0)的函数值y>0时,其自变量x的取值范围是不等式ax2+bx+c>0的解集;当二次函数y=ax2+bx+c(a≠0)的函数值y<0时,其自变量x的取值范围是不等式ax2+bx+c<0的解集.要点2.利用二次函数图象解一元二次不等等式的步骤:(1)将一元二次不等式化为ax2+bx+c>0(或<0)的形式;(2)明确二次项系数a的正负、对称轴在y轴哪侧,并计算b2-4ac的值;(3)作出不等式对应的二次函数y=ax2+bx+c(a≠0)的草图;(4)二次函数在x轴上方的图象对应的函数值大于零,在x轴下方的图象对应的函数值小于零.课堂练习1.解不等式-x2+5x+3>7.2.已知二次函数y=x2-4x+3.(1)求出该二次函数图象的顶点坐标和对称轴;(2)在坐标系中画出该函数的图象;(3)根据图象直接写出不等式x2-4x+3>0的解集.3.已知二次函数y=-x2+2x+3.(1)求其开口方向、对称轴、顶点坐标,并画出这个函数的图象;(2)根据图象,直接写出;①当函数值y为正数时,自变量x的取值范围;②当-2<x<2 时,函数值y的取值范围.4.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是()A.x<-4或x>2B.-4<x<2C.x<0或x>2D.0<x<2。







二次函数与一元二次方程一、知识点二、标准例题:例1:如图,已知二次函数2y ax bx c=++的部分图象,由图象可估计关于x的一元二次方程20ax bx c++=的两个根分别是1 1.6x=,2x=A.-1.6 B.3.2C.4.4 D.5.2【答案】C【解析】由抛物线图象可知其对称轴为x=3,又抛物线是轴对称图象,∴抛物线与x轴的两个交点关于x=3对称,而关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,那么两根满足2×3=x1+x2,而x1=1.6,∴x2=4.4.故选C.总结:此题主要利用抛物线是轴对称图象的性质确定抛物线与x 轴交点坐标,是一道较为简单的试题.例2:如图,二次函数2y ax bx c =++(0a ≠)和一次函数1y x =-的图象交于(2,3)A --,(1,0)B 两点,则方程2(1)10ax b x c +-++=(0a ≠)的根为()A .122,3x x =-=-B .121,0x x ==C .122,1x x =-=D .123,0x x =-= 【答案】C【解析】解:∵2(1)10ax b x c +-++=,∴21ax bx c x ++=-.∴方程2(1)10ax b x c +-++=的根即为二次函数2y ax bx c =++(0a ≠)与一次函数1y x =-的图象交点的横坐标,∵二次函数2y ax bx c =++(0a ≠)和一次函数1y x =-的图象交于(2,3)A --,(1,0)B 两点,∴方程2(1)10ax b x c +-++=(0a ≠)的根为122,1x x =-=.故选C.总结:本题考查了二次函数与一元二次方程的关系,解此题的关键是将方程2(1)10ax b x c +-++=变形为21ax bx c x ++=-,进一步将所求转化为求二次函数2y ax bx c =++(0a ≠)与一次函数1y x =-的图象交点的横坐标,这类题目的求解,重在理解与领悟.最后结合抛物线的增减性进行判断.例3:二次函数y =x 2+bx ﹣t 的对称轴为x =2.若关于x 的一元二次方程x 2+bx ﹣t =0在﹣1<x <3的范围内有实数解,则t 的取值范围是( )A .﹣4≤t <5B .﹣4≤t <﹣3C .t≥﹣4D .﹣3<t <5【答案】A【解析】解:∵抛物线的对称轴x =2b -=2, ∴b =﹣4,则方程x 2+bx ﹣t =0,即x 2﹣4x ﹣t =0的解相当于y =x 2﹣4x 与直线y =t 的交点的横坐标,∵方程x 2+bx ﹣t =0在﹣1<x <3的范围内有实数解,∴当x =﹣1时,y =1+4=5,当x =3时,y =9﹣12=﹣3,又∵y =x 2﹣4x =(x ﹣2)2﹣4,∴当﹣4≤t <5时,在﹣1<x <3的范围内有解.∴t 的取值范围是﹣4≤t <5,故选:A .总结:本题主要考查了二次函数与一元二次方程之间的关系,一元二次方程2ax bx c k ++=的解相当于2y ax bx c =++与直线y=k 的交点的横坐标,解的数量就是交点的个数,熟练将二者关系进行转化是解题的关键.例4:.某班“数学兴趣小组”对函数22||y x x =-的图象和性质进行了探究,探究过程如下:(1)自变量x 的取值范围是全体实数,x 与y 的几组对应值如下表:其中,m =__________.(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象剩下的部分.(3)观察函数图象,写出一条性质__________.(4)进一步探究函数图象发现:①方程22||0x x -=有__________个实数根.②关于x 的方程22||x x a -=有4个实数根时,a 的取值范围是__________.【答案】(1)0(2)(3)当1x >时,y 随x 的增大而增大(4)①3②10a -<<.【解析】(1)x=-2时,m=x 2-2l-2l=0;.(2)如图所示(3)由函数图象知:1x >时y 随x 的增大而增大;函数图像关于y 轴对称;(4)如图:①22||=0x x -时即0y =,∴令x 轴有3个交点,分别是2-、0、2;即答案为3;②由函数图象知:关于x 的方程22||x x a -=有4个交点,∴a 的取值范围是10a -<<.总结:本题考查了抛物线与x 轴的交点:把求二次函数y=ax2+bx+c (a ,b ,c 是常数,a≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.其中观察函数图像的能力是解答本题的关键.三、练习1.已知二次函数(1)(1)37y x a x a a =---+-+(其中x 是自变量)的图象与x 轴没有公共点,且当1x <-时,y 随x 的增大而减小,则实数a 的取值范围是( )A .2a <B .1a >-C .12a -<≤D .12a -≤<【答案】D【解析】(1)(1)37y x a x a a =---+-+22236x ax a a =-+-+,抛物线与x 轴没有公共点, 22(2)4(36)0a a a ∴∆=---+<,解得2a <, 抛物线的对称轴为直线22a x a -=-=,抛物线开口向上, 而当1x <-时,y 随x 的增大而减小,1a ∴≥-,∴实数a 的取值范围是12a -≤<,故选D .2.如图所示,已知二次函数2y ax bx c =++的图象与x 轴交于,A B 两点,与y 轴交于点C ,OA OC =,对称轴为直线1x =,则下列结论:①0abc <;②11024a b c ++=;③10ac b -+=;④2c +是关于x 的一元二次方程20ax bx c ++=的一个根.其中正确的有( )A .1个B .2个C .3个D .4个【答案】B【解析】∵抛物线开口向下,∴0a <, ∵抛物线的对称轴为直线12bx a =-=,∴20b a =->,∵抛物线与y 轴的交点在x 轴上方,∴0c >,∴0abc <,所以①正确;∵2b a =-, ∴102a b a a +=-=,∵0c >, ∴11024a b c ++>,所以②错误;∵(0,)C c ,OA OC =,∴(,0)A c -,把(,0)A c -代入2y ax bx c =++得20ac bc c -+=,∴10ac b -+=,所以③错误;∵(,0)A c -,对称轴为直线1x =,∴(2,0)B c +,∴2c +是关于x 的一元二次方程20ax bx c ++=的一个根,所以④正确;综上正确的有2个,故选B.3.已知0m >,关于x 的一元二次方程()()120x x m +--=的解为1212,()x x x x <,则下列结论正确的是( )A .1212x x <-<<B .1212x x -<<<C .1212x x -<<<D .1212x x <-<<【答案】A【解析】解:关于x 的一元二次方程()()120x x m +--=的解为12,x x ,可以看作二次函数()()12m x x =+-与x 轴交点的横坐标,∵二次函数()()12m x x =+-与x 轴交点坐标为()()1,0,2,0-,如图:当0m >时,就是抛物线位于x 轴上方的部分,此时1x <-,或2x >;又∵12x x <∴121,2x x =-=;∴1212x x <-<<,故选:A .4.对于一个函数,自变量x 取a 时,函数值y 也等于a ,我们称a 为这个函数的不动点.如果二次函数y =x 2+2x +c 有两个相异的不动点x 1、x 2,且x 1<1<x 2,则c 的取值范围是( )A .c <﹣3B .c <﹣2C .c <14D .c <1【答案】B【解析】由题意知二次函数y =x 2+2x+c 有两个相异的不动点x 1、x 2,所以x 1、x 2是方程x 2+2x+c =x 的两个不相等的实数根,整理,得:x2+x+c=0,所以△=1-4c>0,又x2+x+c=0的两个不相等实数根为x1、x2,x1<1<x2,所以函数y= x2+x+c=0在x=1时,函数值小于0,即1+1+c<0,综上则140 110cc-⎧⎨++⎩><,解得c<﹣2,故选B.5.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线一定过原点②方程ax2+bx+c=0(a≠0)的解为x=0或x=4,③a﹣b+c<0;④当0<x<4时,ax2﹣bx+c<0;⑤当x<2时,y随x增大而增大,其中结论正确的个数()A.1 B.2 C.3 D.4【答案】C【解析】①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;②∵抛物线与x轴的交点坐标为:(0,0),(4,0),∴方程ax2+bx+c=0(a≠0)的解为x=0或x=4,正确;③∵当x=﹣1和x=5时,y值相同,且均为正,∴a﹣b+c>0,结论③错误;④当0<x<4时,ax2﹣bx+c<0,结论④正确;⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.综上所述,正确的结论有:①②④.故选:C.6.抛物线23y x bx =++的对称轴为直线1x =.若关于x 的一元二次方程230x bx t ++-=(t 为实数)在14x -<<的范围内有实数根,则t 的取值范围是( )A .211t ≤<B .2t ≥C .611t <<D .26t ≤<【答案】D【解析】∵23y x bx =++的对称轴为直线1x =,∴2b =-,∴223y x x =-+,∴一元二次方程230x bx t ++-=的实数根可以看做223y x x =-+与函数y t =的有交点, ∵方程在14x -<<的范围内有实数根,当1x =-时,6y =,当4x =时,11y =,函数223y x x =-+在1x =时有最小值2,∴26t ≤<,故选D .7.若函数y =(m ﹣1)x 2﹣6x +32m 的图象与x 轴有且只有一个交点,则m 的值为( )A .﹣2或3B .﹣2或﹣3C .1或﹣2或3D .1或﹣2或﹣3 【答案】C【解析】解:当m =1时,函数解析式为:y =﹣6x +32是一次函数,图象与x 轴有且只有一个交点, 当m ≠1时,函数为二次函数,∵函数y =(m ﹣1)x 2﹣6x +32m 的图象与x 轴有且只有一个交点,∴62﹣4×(m ﹣1)×32m =0, 解得,m =﹣2或3,故选:C .8.二次函数y =ax 2+bx +c (a ≠0)和正比例函数y =﹣13x 的图象如图所示,则方程ax 2+(b + 13)x +c =0(a ≠0)的两根之和( )A .大于0B .等于0C .小于0D .不能确定【答案】C 【解析】解:设20(0)ax bx c a ++=≠的两根为x 1,x 2,∵由二次函数的图象可知12x x 0+<,a 0>,0b a∴-<. 设方程210(0)3ax b x c a ⎛⎫+++=≠ ⎪⎝⎭的两根为m ,n ,则1133b b m n a a a++=-=-- 010300a a b am m >∴-<-<∴+<. 故选:C .9.如图,二次函数y =ax 2+bx+c 图象的对称轴是直线x =1,与x 轴一个交点A (3,0),则与x 轴的另一个交点坐标是( )A .(0,12-)B .(12-,0)C .(0,﹣1)D .(﹣1,0)【答案】D【解析】解:∵点A 的坐标为(3,0),∴点A 关于x =1的对称点的坐标为(﹣1,0).故选:D .10.已知二次函数226y x x m =-+的图象与x 轴没有交点,则m 的取值范围是_____. 【答案】92m >【解析】∵二次函数y=2x 2-6x+m 的图象与x 轴没有交点, ∴△<0,∴(-6)2-4×2×m <0, 解得:92m >; 故答案为:92m >.11.抛物线2243y x x =--,当14x -≤≤时,y 的取值范围是__________. 【答案】513y -≤≤【解析】解:根据二次函数的解析式2243y x x =--可得 由a=2>0,可得抛物线的开口向上 对称轴为:41222b x a -=-=-=⨯ 所以可得在14x -≤≤范围内,二次函数在11x -≤≤,y 随x 的增大而减小,在14x <≤上y 随x 的增大而增大.所以当1x =取得最小值,最小值为:2435y =--=- 当4x =取得最大值,最大值为:22444313y =⨯-⨯-= 所以513y -≤≤ 故答案为:513y -≤≤12.抛物线223y x x =--与x 轴的交点坐标是_____【答案】(10)-,,(3,0) 【解析】令y=0,则x 2-2x-3=0, 解得x=3或x=-1.则抛物线y=x 2-2x-3与x 轴的交点坐标是(3,0),(-1,0). 故答案为(3,0),(-1,0).13.已知函数y ={−x 2+2x(x >0)x(x ≤0)的图象如图所示,若直线y =x +m 与该图象恰有两个不同的交点,则m 的取值范围为_____.【答案】0<m <14【解析】解:直线y =x +m 与该图象恰有三个不同的交点, 则直线与y =x 有一个交点, ∴m >0,∵与y =−x 2+2x 有两个交点, ∴x +m =−x 2+2x , Δ=1−4m >0, ∴m <14, ∴0<m <14; 故答案为0<m <14.14.抛物线2y ax bx c =++经过点(3,0)A -、(4,0)B 两点,则关于x 的一元二次方程2(1)a x c b bx-+=-的解是___________ 【答案】12x =-,25x =.【解析】依题意,得:9301640a b c a b c -+=⎧⎨++=⎩,解得:12b ac a =-⎧⎨=-⎩,所以,关于x 的一元二次方程a(x -1)2+c =b -bx 为:2(1)12a x a a ax --=-+, 即:2(1)121x x --=-+, 化为:23100x x --=, 解得:12x =-,25x =,故答案为:12x =-,25x =.15.已知m ,n 是方程(x ﹣a )(x ﹣b )﹣1=0(其中a <b )的两根,且m <n ,则a ,b ,m ,n 的大小关系是_____. 【答案】m <a <b <n【解析】∵函数y =(x ﹣a )(x ﹣b )与x 轴的交点坐标的横坐标为a 与b , 二次函数y =(x ﹣a )(x ﹣b )﹣1相当于y =(x ﹣a )(x ﹣b )向下平移一个单位, 又∵二次项系数为1,开口向上,如图所示:∴由图可得:m <a <b <n . 故答案为:m <a <b <n .16.如图,抛物线2y ax c =+与直线y mx n =+交于A(-1,P),B(3,q)两点,则不等式2ax mx c n ++>的解集是_____.【答案】3x <-或1x >.【解析】解:∵抛物线2y ax c =+与直线y mx n =+交于()1,A p -,()3,B q 两点,∴m n p -+=,3m n q +=,∴抛物线2y ax c =+与直线y mx n =-+交于()1,P p ,()3,Q q -两点,观察函数图象可知:当3x <-或1x >时,直线y mx n =-+在抛物线2y ax bx c =++的下方,∴不等式2ax mx c n ++>的解集为3x <-或1x >. 故答案为:3x <-或1x >.17.如图,直线y =mx +n 与抛物线y =ax 2+bx +c 交于A (﹣1,p ),B (4,q )两点,则关于x 的不等式mx +n <ax 2+bx +c 的解集是____.【答案】﹣1<x <4.【解析】观察函数图象可知:当﹣1<x <4时,直线y =mx+n 在抛物线y =ax 2+bx+c 的下方, ∴不等式mx+n <ax 2+bx+c 的解集为﹣1<x <4. 故答案为:﹣1<x <4.18.已知k 是常数,抛物线y =x 2+(k 2+k -6)x +3k 的对称轴是y 轴,并且与x 轴有两个交点. (1)求k 的值:(2)若点P 在抛物线y =x 2+(k 2+k -6)x +3k 上,且P 到y 轴的距离是2,求点P 的坐标. 【答案】(1)k =-3;(2)点P 的坐标为(2,-5)或(-2,-5). 【解析】(1)∵抛物线y=x 2+(k 2+k -6)x+3k 的对称轴是y 轴,∴26022b k k x a +-=-=-=,即k 2+k -6=0, 解得k=-3或k=2,当k=2时,二次函数解析式为y=x 2+6,它的图象与x 轴无交点,不满足题意,舍去, 当k=-3时,二次函数解析式为y=x 2-9,它的图象与x 轴有两个交点,满足题意,∴k=-3;(2)∵P 到y 轴的距离为2, ∴点P 的横坐标为-2或2, 当x=2时,y=-5; 当x=-2时,y=-5,∴点P 的坐标为(2,-5)或(-2,-5).19.在画二次函数()20y ax bx c a =++≠的图象时,甲写错了一次项的系数,列表如下乙写错了常数项,列表如下:通过上述信息,解决以下问题:(1)求原二次函数()20y ax bx c a =++≠的表达式;(2)对于二次函数()20y ax bx c a =++≠,当x _____时,y 的值随x 的值增大而增大;(3)若关于x 的方程()20ax bx c k a ++=≠有两个不相等的实数根,求k 的取值范围.【答案】(1)2323y x x =-++;(2)13≤;(3)103k <. 【解析】解:(1)由甲同学的错误可知c=3, 由甲同学提供的数据选x=-1,y=6;x=1,y=2,有6323a b a b =-+⎧⎨=++⎩,∴12a b =⎧⎨=-⎩,∴a=1,由甲同学给的数据a=1,c=3是正确的;由乙同学提供的数据,可知c=-1,选x=-1,y=-2;x=1,y=2,有2121a b a b -=--⎧⎨=+-⎩,∴12a b =⎧⎨=⎩,∴a=1,b=2, ∴y=x 2+2x+3;(2)y=x 2+2x+3的对称轴为直线x=-1, 抛物线开口向上,∴当-1x ≥时,y 的值随x 的值增大而增大; 故答案为-1≥;(3)方程()20ax bx c k a ++=≠有两个不相等的实数根,即x 2+2x+3-k=0有两个不相等的实数根, ∴()4-430k ∆=->, ∴2k >;20.已知抛物线232y ax bx c =++.(1)若1a b ==,1c =-,求该抛物线与x 轴公共点的坐标;(2)若1a b ==,且当11x -<<时,抛物线与x 轴有且只有一个公共点,求c 的取值范围.【答案】(1)()1,0-和1,03⎛⎫⎪⎝⎭.(2)13c =或51c -<≤-【解析】(1)当1a b ==,1c =-时,抛物线为2321y x x =+-,方程23210x x +-=的两个根为11x =-,213x =.所以该抛物线与x 轴公共点的坐标是()1,0-和1,03⎛⎫⎪⎝⎭.(2)当1a b ==时,抛物线为232y x x c =++,且与x 轴有公共点.对于方程2320x x c ++=,判别式4120c ∆=-≥,有13c ≤.①当13c =时,由方程213203x x ++=,解得1213x x ==-,此时抛物线为21323y x x =++与x 轴只有一个公共点1,03⎛⎫- ⎪⎝⎭;②当13c <时,11x =-时,1321y c c =-+=+,21x =时,2325y c c =++=+.由已知11x -<<时,该抛物线与x 轴有且只有一个公共点,考虑其对称轴为13x =-,应有1200y y ≤⎧⎨>⎩,即1050c c +≤⎧⎨+>⎩,解得51c -<≤-.综上,13c =或51c -<≤-. 21.已知函数()21y x m x m =-+-+(m 为常数). (1)该函数的图象与x 轴公共点的个数是(). A .0 B .1 C .2 D .1或2(2)求证:不论m 为何值,该函数的图象的顶点都在函数()21y x =+的图象上. (3)当23m -≤≤时,求该函数的图象的顶点纵坐标的取值范围.【答案】(1)D (2)详见解析;(3)当23m -≤≤时,该函数的图象的顶点纵坐标z 的取值范围是04z ≤≤. 【解析】(1)因为()()()2214110m m m ∆=--⋅-⋅=+≥,故选D.(2)配方得()2221(1)124m m y x m x m x -+⎛⎫=-+-+=--+⎪⎝⎭, 所以该函数的图象的顶点坐标为()211,24m m ⎛⎫+- ⎪ ⎪⎝⎭. 把12m x -=代入()21y x =+,得221(1)124m m y -+⎛⎫=+= ⎪⎝⎭. 因此,不论m 为何值,该函数的图象的顶点都在函数()21y x =+的图象上.(3)设函数的图象的顶点纵坐标()214m z +=.当1m =-时,z 有最小值0.当1m <-时,z 随m 的增大而减小;当1m >-时,z 随m 的增大而增大.又当2m =-时,()221144z -+==;当3m =时,()23144z +==.因此,当23m -≤≤时,该函数的图象的顶点纵坐标z 的取值范围是04z ≤≤.。