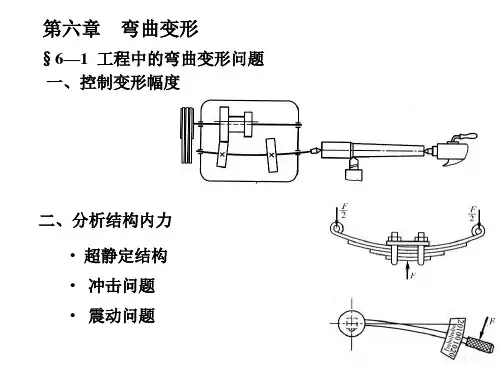
实例
车床主轴：变形过大，会使齿轮啮合不良，轴与轴承产生非均匀磨损
，产生噪声，降低寿命，影响加工精度。
吊车梁：变形过大会出现小车爬坡现象，引起振动。
研究变形目的
建立刚度条件，解决刚度问题
建立变形协调条件，解决超静定问题
为振动计算奠定基础。
概念
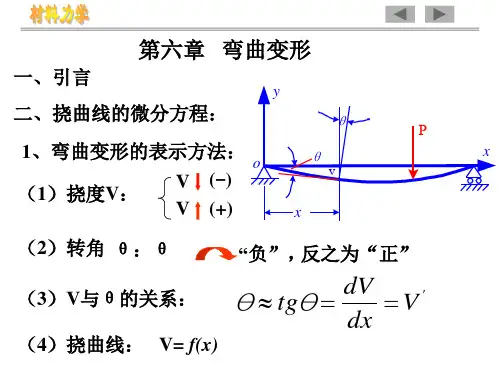
以简支梁为例，以变形前的轴线为x轴，垂直向上为y轴，xoy平面为梁的纵向对称面。
挠曲线：
在对称弯曲情况下，变形后梁的轴线为xoy平面内的一条曲线，此曲线称为挠曲线
挠度：
梁的任一截面形心的竖直位移称为挠度。
挠曲线的方程式：
转角：
弯曲变形中，梁的横截面对其原来位置转过的角度θ，称为截面转角。
根据平面假设，梁的横截面变形前，垂直于轴线，变形后垂直于挠曲线。
故
:
挠度w和转角θ是度量弯曲变形的两个基本量。
挠度与转角符号规定：在图示坐标中，挠度向上为正，反时针的转角为正。
此式为挠曲线的近似微分方程。
挠曲线的曲率表示式：
纯弯曲：
横力弯曲：
“
细长梁,
忽略Fs影响。
挠曲线的曲率表达式
纯弯曲：
（a）
横力弯曲：
对细长梁而言，忽略剪力Fs的影响
（b）
高等数学中对曲率的定义及表达式
于是式（a）转化为
（c）
在我们选定的坐标系内，若弯矩M 为正，则挠曲线向下凸，（如图所示），随着弧长S的增加，θ也是增加的，即正增量d S对应的dθ也是正的，于是考虑符号后，式（c）可写成
（d）因为
所以
注意到
代入式（d）及：
（e）
此为挠曲线的微分方程，适用于弯曲变形的任意情况，它是非线性的。
在小变形的情况下，梁的挠度w一般都远小于跨度，挠曲线w=f(x)是一非常平坦的曲线，转角θ也是一个非常小的角度，于是
（f）
式（e）
,
于是式（e）可写成
（g）
此式为挠曲线的近似微分方程。
挠曲线的近似微分方程
对等直梁而言，EI为常量，于是上式可写成
积分可得转角方程，再积分可得挠曲线方程
边界条件：
在挠曲线的某些点上，挠度或转角有时是已知的这类条件称为边界条件。
连续条件：
挠曲线是一条光滑连续的曲线，在挠曲线的任一点上有唯一确定的挠度和转角这就是连续条件。
刚度条件：
例题
Example1
图示梁受均布载荷，已知，试用积分法求梁的转角和挠度方程，、 .
Solution.
列弯矩方程：
列微分方程及积分
求积分常数
边界条件：当时，
∴
转角方程及挠度方程：
求,
将=0代入以上二式
Example2
内燃机的凸轮轴或齿轮轴计算简图，试求转角方程及挠度方程，及、。
Solution.
求反力：
列弯矩方程：
（AC）
（CB）
列微分方程及积分
（AC）
（CB）
求积分常数
边界条件：
连续条件：
∴
转角方程及挠度方程
（AC）
(a)
(b)
（CB）
(c)
(d)
最大挠度，最大转角
当时，
当时，
若，则,
若，则,
最大挠度
当时,为极值,所以应首先确定为零的截面位置。
.
若在式（a）中，令，可求的
若，则为正值。
可见从截面A到截面C转角由负变正，改变了符号，挠曲线既为光滑连续曲线，=0的截面必然在（AC）段。
令式（a）等于零：
即为挠度为最大值的截面横坐标。
以代入式（b）的最大挠度
当F作用于中点时，即，最大挠度发生在中点。
极端情况，当F无限接近右支座时，以省略，于是
可见即是在这种极端情况下，最大挠度仍然发生在跨度中点附近，也就是最大挠度总在靠近跨度中点。
所以可以用跨度中点的挠度近似代替最大挠度，因此，在式（b）中令
求出跨度中点挠度为：
即是在极端情况下，→0时
误差分析：
用代替所引起的误差
结论
可见在简支梁中，只要挠曲线无拐点，总可用跨度中点的挠度代替最大挠度不会引起很大误差。
优点：
可以求得挠曲线的转角方程和挠曲线方程，因此可求任意截面的转
角和挠度是最基本的方法。
缺点：
积分法比较麻烦。
在小变形，线弹性前提下（材料服从胡克定律），挠度与转
角均与载荷成线性关系。
因此，当梁上有多个载荷作用时，可以分别求出每一
载荷单独引起的变形，把所得变形叠加即为这些载荷共同作用时的变形，这就
是弯曲变形的叠加法。
为了便于工程计算，把简单基本载荷作用下梁的挠曲线方程，最大挠度，
最大转角计算公式编入手册，以便查用。
Example 1
Given：
Find ：,
,
Solution：
查表P190
Example 2
Given：
Find ：,,,
Solution：
P189-190
查表
多余约束(redundant restraint)
多余支反力(redundant reaction)
相当系统（equivalent system）静定基
变形比较法
超静定梁求解步骤
判断梁的静不定度；
解除“多余”约束，代之以相应的多余支反力，得到原静不定梁的相当系统；
基本静定梁变形情况与原超静定梁变形情况应该相同,这就是变形协调条件。
由变形协调条件和力与变形间的物理关系求得补充方程；
由平衡方程和补充方程求得全部支座反力或内力。
三度静不定
支座沉陷
梁的刚度条件
梁的合理刚度设计
梁的变形除了与梁的支承和载荷情况有关外,还与材料、截面和跨度有关。
挠度的最大值可综合概括为：
由上式可见,欲提高梁的抗弯刚度,可采取如下措施。
提高梁弯曲刚度的措施
增大梁的抗弯刚度EI
由于各类钢材的弹性模量E值相差甚少,因此虽采用高强度钢可以大大提高梁
的强度,但对增大梁的刚度却意义不大。
增大截面的惯矩I是提高刚度的主要途径。
与此同时强度也可得以提高。
从刚度方面考虑，应增大整个梁截面的惯矩I。
(在同一强度下，变截面梁比等截面梁的柔性大。
减小梁的跨度或增加支承
梁的挠度(或转角)与跨度的n次幂成正比,因此为减小梁的变形,采取减小梁跨的办法是一个很有效的措施。
利用对梁采取增加支承的办法,会使梁的最大挠度值降低。
增加约束后,原来的静定梁就会变成超静定梁。
减小弯矩数值
由于弯矩是引起梁弯曲变形的主要因素,因此减小弯矩数值也是提高梁弯曲刚度的一项重要措施。
.
图示结构中CD为刚性杆,C、D处为铰接,AD与DE梁的EI相同,试求E端约束反力
解:
一次超静定,去掉钢杆CD,代以反力F,且CD为钢杆,故
,。
