下载文档原格式
晶体结构专题练习1、(2000初赛)最近发现一种由钛原子和碳原子构成的气态团簇分子，如右图所示，顶角和面心的原子是钛原子，棱的中心和体心的原子是碳原子，它的化学式是______。
Ti14C132、(2005初赛)为纪念1905年爱因斯坦连续发表6篇论文导致物理学大变革100周年，今年被定为国际物理年。
本题涉及的“热电效应”机理也是爱因斯坦首先阐释的，如图是化学家合成的能实现热电效应的一种晶体的晶胞模型。
图中的大原子是稀土原子，如镧；小原子是周期系第五主族元素，如锑；中等大小的原子是周期系VIII 族元素，如铁。
按如上结构图写出这种热电晶体的化学式。
给出计算过程。
提示：晶胞的6个面的原子数相同。
设晶体中锑的氧化态为－1，镧的氧化态为＋3，问：铁的平均氧化态多大？化学式：LaFe4Sb12注：写La2Fe8Sb24扣1分。
铁的氧化态：9/4=2.25计算化学式的过程如下：晶胞里有2个La原子(处于晶胞的顶角和体心)；有8个Fe 原子(处于锑形成的八面体的中心)；锑八面体是共顶角相连的，平均每个八面体有6/2=3个锑原子，晶胞中共有8个八面体，8×3=24个锑原子；即：La2Fe8Sb24。
其他合理过程也可。
3、(2004初赛)2004年7月德俄两国化学家共同宣布，在高压下氮气会发生聚合得到高聚氮, 这种高聚氮的N-N键的键能为160 kJ/mol (N2的键能为942 kJ/mol)，晶体结构如图所示。
在这种晶体中，每个氮原子的配位数为；按键型分类时，属于晶体。
这种固体的可能潜在应用是，这是因为：。
3 原子晶体炸药(或高能材料) 高聚氮分解成N2释放大量能量。
4、(1998初赛·改编)钨酸盐是一类重要的钨化合物。
试回答下列问题：(1)Na2WO4晶胞中，O2-以立方最紧密堆积排列，每个立方晶胞中有32个O2-，W6+占据四面体空隙，Na+占据八面体空隙，构成尖晶石结构。
W6+占据四面体空隙的分数是多少？Na+占据八面体空隙的分数是多少？(2)钨酸钠Na2WO4和金属钨在隔绝空气的条件下加热得到一种具有金属光泽的、深色的、有导电性的固体，化学式Na x WO3，用X射线衍射法测得这种固体的立方晶胞的边长a=3.80×10-10 m，用比重瓶法测得它的密度为d=7.36 g/cm3。
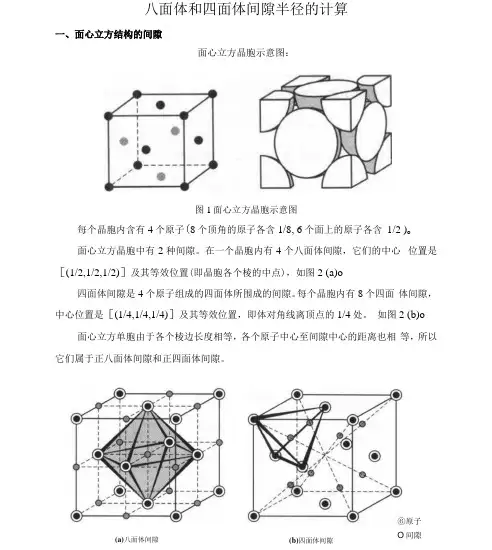
八面体和四面体间隙半径的计算一、面心立方结构的间隙面心立方晶胞示意图：图1面心立方晶胞示意图每个晶胞内含有4个原子(8个顶角的原子各含1/8, 6个面上的原子各含1/2 )o面心立方晶胞中有2种间隙。
在一个晶胞内有4个八面体间隙，它们的中心位置是［(1/2,1/2,1/2)］及其等效位置(即晶胞各个棱的中点)，如图2 (a)o四面体间隙是4个原子组成的四面体所围成的间隙。
每个晶胞内有8个四面体间隙，中心位置是［(1/4,1/4,1/4)］及其等效位置，即体对角线离顶点的1/4处。
如图2 (b)o 面心立方单胞由于各个棱边长度相等，各个原子中心至间隙中心的距离也相等，所以它们属于正八面体间隙和正四面体间隙。
⑥原子O间隙(a)八面体间隙(b)四面体间隙图2面心立方结构的间隙分别以点阵常数a和原子半径R计算面心立方晶体的八面体间隙半径和四面体间隙半径。
1、八面体间隙半径「8半径为R的圆球(相当于原子半径)堆积成正八面体空隙，计算中心到顶点的距离即是八面体间隙的半径。
E(a) (b) (c)图3正八面体间隙示意图正八面体空隙由6个等径圆球密堆积而成，其顶点即圆球的球心，其棱长即圆球的直径。
空隙的实际体积小于八面体体积。
图3中三图分别示出球的堆积情况及所形成的正八面体空隙。
由图3 (c)知，八面体空隙中心到顶点的距离为：OC = -AC = -yf2AB = -^x2R = y/2R22 2 (1)而八面体空隙中心到球面的最短距离为：r8 = OC-R = V2R -R « 0.414R (2)此即半径为R的等径圆球最密堆积形成的正八面体空隙所能容纳的小球的最大半径0.414Ro图4面心立方密排面的示意图如图4,面心立方最紧密排面是{111},密排方向为<110>,原子直径是a/2<110>的长度，即 R = aV2/4o故 a = 4R/V2 = 2V2/?：".146a (3)式(3)也可以直接看出：八面体间隙的原子至间隙中心的距离为乎,原— a-a-—a^0A46a子半径为4 ,所以间隙半径为24。
晶胞中的四面体空隙与八面体空隙下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!晶胞中的四面体空隙与八面体空隙晶体结构中的空隙是指原子或离子形成晶格时未被其他原子或离子占据的空间。
六方最密堆积八面体空隙坐标1. 前言嘿，大家好！今天我们聊聊一个看似高深，但其实挺有意思的话题——六方最密堆积和八面体空隙的坐标。
听起来有点像化学课上老师口中的那些术语，但别担心，咱们就像在喝茶聊天，轻松愉快地来聊聊这个话题。
其实，这个堆积方式在我们日常生活中有不少应用，比如说水晶的排列、某些矿石的结构等等，真的是无处不在呀。
2. 六方最密堆积的基本概念2.1 什么是六方最密堆积？六方最密堆积，顾名思义，就是以六边形的方式将物体堆放得最紧密。
就像你把几颗糖果在桌子上摆放，想让它们贴得更紧，就得想办法让每一颗糖都不浪费空间。
这种堆积方式的一个典型例子就是蜜蜂的蜂巢，那个六角形的结构可真是聪明无比啊，既节省材料又能装下更多的蜂蜜。
2.2 八面体空隙的形成接着说到八面体空隙，想象一下，你把一些球放在一起，球与球之间就会留下小空隙。
而这些空隙形状就像个小小的八面体。
怎么回事呢？就是在六方最密堆积的过程中，空隙的形状和分布会形成特定的几何图形，八面体就是其中之一。
这种空隙的存在，让我们在堆积材料时，不仅可以提升堆积的效率，还有助于理解各种物质的相互作用。
3. 空隙坐标的奇妙之旅3.1 如何找到空隙坐标？这就好比玩拼图游戏，你得找到合适的位置才能让每块拼图都拼上去。
在六方最密堆积中，八面体的空隙坐标就像是拼图的关键点。
首先，咱们要确定几个基本的坐标轴，比如说x、y、z轴。
然后在这些坐标系中，八面体空隙的中心位置可以通过一些简单的公式计算出来。
这样一来，咱们就能找到那些小空隙的“家”了。
3.2 实际应用说到这儿，可能有人会问：“这跟我有什么关系啊？”别急，答案来了！六方最密堆积和空隙坐标的概念其实在很多领域都有用武之地。
比如在材料科学中，研究人员通过这些堆积方式来开发新材料，以达到更高的强度和更轻的重量。
你可以想象一下，未来的汽车、飞机，甚至是手机都可能因为这些堆积结构而变得更加高效，科技真是日新月异啊！4. 结尾总的来说，六方最密堆积和八面体空隙坐标的确是个有趣的领域，虽然它可能看上去很复杂，但其实背后有很多简单而美妙的原理在起作用。
一、立方与六方最密堆积中的正八面体与正四面体空隙从晶体中原子排列的刚球模型和对致密度（致密度指晶胞内原子球所占体积与晶胞体积之比值）分析可知，即使是最密堆积，金属晶体中依然存在空隙，这些空隙对金属的性能有重要影响。
晶体结构中最常见的空隙是八面体空隙（图1）和四面体空隙（图2）。
图1八面体空隙图2四面体空隙八面体空隙由6个原子围成，四面体空隙由4个原子围成，若设金属原子的半径为r A，空隙能容纳的最大外来原子半径为r B，利用几何关系可求出正八面体与正四面体空隙的r B/r A的比值分别为0.414、0.225。
图三八面体空隙计算图四四面体空隙计算小结面心立方最密堆积晶胞原子个数∶四面体空隙数∶八面体空隙数＝4∶8∶4巧记口诀1:2:1，原四八；八角六面当骨架四分之一填四面、棱心体心都填八二、体心立方晶胞的变形八面体与变形的四面体空隙体心立方堆积没有正多面体空隙，但有多种变形的多面体空隙，这里介绍变形的八面体空隙与变形的四面体空隙。
图5 变形的八面体空隙其中心位置位于晶胞每个面的中心与每条边的中心，是一个压扁的八面体，在垂直轴上从中心到顶点的距离为a/2（a为晶胞参数），比水平方向的距离√2a/2要短。
空隙最短处能容纳最大外来原子半径为rB 和堆积原子的半径rA的rB/rA比值为0.154。
图6 变形的四面体空隙每个面上都有4个四面体的中心，如图，这种空隙的rB /rA比值为0.291。
三、其它晶胞八面体与四面体空隙总结图7 体心立方晶胞的空隙体心立方堆积晶胞原子个数∶四面体空隙数∶八面体空隙数＝2∶12∶6各类堆积空隙小结图8 体心立方晶胞的空隙此总结系参考别人的，希望对各位老师有帮助！。
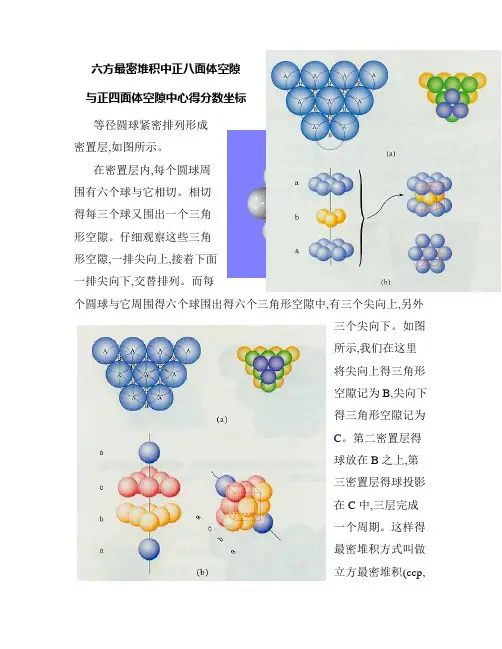
六方最密堆积中正八面体空隙与正四面体空隙中心得分数坐标等径圆球紧密排列形成密置层,如图所示。
在密置层内,每个圆球周围有六个球与它相切。
相切得每三个球又围出一个三角形空隙。
仔细观察这些三角形空隙,一排尖向上,接着下面一排尖向下,交替排列。
而每个圆球与它周围得六个球围出得六个三角形空隙中,有三个尖向上,另外三个尖向下。
如图所示,我们在这里将尖向上得三角形空隙记为B,尖向下得三角形空隙记为C。
第二密置层得球放在B之上,第三密置层得球投影在C中,三层完成一个周期。
这样得最密堆积方式叫做立方最密堆积(ccp,记为A1型),形成面心立方晶胞。
若第三密置层得球投影与第一密置层得球重合,两层完成一个周期。
这样得最密堆积方式叫做六方最密堆积(hcp,记为A3型),形成六方晶胞,如图所示。
在这两种堆积方式中,任何四个相切得球围成一个正四面体空隙;另外,相切得三个球如果与另一密置层相切得三个球空隙对应,它们六个球将围成一个正八面体空隙。
也就就是说,围成正八面体空隙得这六个球可以分为相邻得两层,每层得正三角形中心得连线垂直于正三角形所在得密置层,参瞧下图,黑色代表得不就是球而就是正八面体得中心。
在这两种最密堆积方式中,每个球与同一密置层得六个球相切,同时与上一层得三个球与下一层得三个球相切,即每个球与周围十二个球相切(配位数为12)。
中心这个球与周围得球围出八个正四面体空隙,平均分摊到每个正四面体空隙得就是八分之一个球。
这样,每个正四面体空隙分摊到得球数就是四个八分之一,即半个。
中心这个球周围还围出六个八面体空隙,它平均分摊到每个正八面体空隙得就是六分之一个球。
这样,每个正八面体空隙分摊到得球数就是六个六分之一,即一个。
总之,这两种最密堆积中,球数: 正八面体空隙数: 正四面体空隙数= 1:1:2 。
面心立方最密堆积(ccp, A1型)中正八面体空隙与正四面体空隙得问题比较简单、直观。
下面我们集中讨论六方最密堆积(hcp,A3型)中正八面体空隙与正四面体空隙中心得分数坐标。
五、晶 体 结 构1． 因为立方晶系中，六个面都是等价的，若有底心立方晶胞存在，则必有面心立方晶胞存在，故立方晶系中不存在底心立方晶胞。
不带电荷的分子或原子（金属）之间的相互作用力小，若原子（非金属）以共价键连接，简单立方中的两个原子之间距离又太大，不利于共价键形成，所以不带电荷的分子或原子往往采取六方或立方最紧密堆积或立方体心密堆积结构。
由于六方最紧密堆积结构与立方紧密堆积的空间利用率相同，所以它们具有相同的密度。
在这两种紧密堆积中，原子的配位数为12。
2． Cu 为面心立方晶体，1个晶胞中Cu 原子个数＝8×(18) + 6×(12)＝ 4（1）（2） ＝1.119 Å 3． ∵Fe 原子半径是相同的，在α型中，Fe3A 2M N a ααρ=g ，在γ型中， Fe γ3A γ4M N a ρ=g 在α型中，43r a α=，∴43a rα=；在γ型中，42r a γ=，∴22a r γ=∴Fe 3A (43)N rαρ=g ，Fe γ3A (22)N r ρ=g∴ 33γ(22)360.918682(43)r r αρρ===4． (1)(2) 原子堆积系数(100)=2222(4141)0.78544(22)r a r ππ⨯+=== 原子堆积系数(110)=22(414212)0.5554242r a π⨯+⨯== 原子堆积系数(111)= 22(316312)30.90696(12)(2)sin60r a ππ⨯+⨯==⨯o 23A 324A 463.548.936,8.97110(3.165)10m N V N ρ-⨯===⨯⨯⨯ 解得＝Cu 42,24r a r a =∴=5． (1 ) MgO 与MnO 的d M —O 相差很大，这说明O 2–围成的正八面体空隙小，而Mg 2+、Mn 2+的半径差别大，导致d MnO >d MgO ；而S 2–和Se 2–半径大，围成的正八面体空隙既大于 ，又大于 ，所以d MgS ～d MnS ，d MgSe ＝d MnSe ，相当于Mg 2+和Mn 2+在S 2–和Se 2–围成的正八面体空隙中“扰动”。
一、面心立方最密堆积面心立方最密堆之中，八面体间隙位于棱心和体心，如上图可知，八面体间隙位于体心的计1个，位于12条棱心各计1/4，12×1/4=3，合计4个。
四面体间隙位于晶胞内部，在每条体对角线的1/4和3/4两处，共4×2=8个。
正四面体空隙（1/4，1/4，1/4）（3/4，1/4，3/4）（3/4，3/4，1/4）（1/4，3/4，3/4）（3/4，3/4，3/4）（1/4，1/4，3/4）（1/4，3/4，1/4）（3/4，1/4，1/4）正八面体空隙（1/2，1/2，1/2）（1/2，0，0）（0，1/2，0）（0，0，1/2）球数：正四面体空隙数：正八面体空隙=4：8：4六方最密堆积之中，八面体间隙位于晶胞内部，如上图可知，八面体间隙共计6个。
四面体间隙8个位于晶胞内部，12个位于6条棱心各计1/3，12×1/3＝4，合计12个。
六方最密堆积中：由于六方最密堆积和面心立方最密堆积都是“最密堆积”，所以它们的球与两种间隙比例有相同的关系。
正四面体空隙（0，0，3/8）（0，0，5/8）（2/3，1/3，1/8）（2/3，1/3，7/8）正八面体空隙（1/3，2/3，1/4）（1/3，2/3，3/4）球数：正四面体空隙数：正八面体空隙=6：12：6体心立方堆积之中，八面体间隙与四面体间隙如上图以1个晶胞计：八面体间隙位于棱心与面心，12条棱心各计1/4，12×1/4＝3；6个面心各计1/2，6×1/2＝3，共6个。
四面体间隙都位于面心，共4×6×1/2=12个。
体心立方堆积堆积中：球数：正四面体空隙数：正八面体空隙=2：12：6。
六方最密堆积中正八面体空隙和正四面体空隙This model paper was revised by the Standardization Office on December 10, 2020六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标等径圆球紧密排列形成密置层，如图所示。
在密置层内，每个圆球周围有六个球与它相切。
相切的每三个球又围出一个三角形空隙。
仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。
而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。
如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。
第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。
这样的最密堆积方式叫做立方最密堆积（ccp，记为 A1型），形成面心立方晶胞。
若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。
这样的最密堆积方式叫做六方最密堆积（hcp，记为A3型），形成六方晶胞，如图所示。
在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。
也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。
在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。
中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。
这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。
中心这个球周围还围出六个八面体空隙，它平均分摊到每个正八面体空隙的是六分之一个球。
这样，每个正八面体空隙分摊到的球数是六个六分之一，即一个。
总之，这两种最密堆积中，球数 : 正八面体空隙数 : 正四面体空隙数 = 1:1:2 。
