空间坐标系和投影
- 格式:doc
- 大小:2.60 MB
- 文档页数:20


如何选择适合的坐标系和投影方式选择适合的坐标系和投影方式在地理信息系统(GIS)和空间数据处理中至关重要。
坐标系和投影方式的选择直接影响着地图的精度和可视化效果。
本文旨在介绍如何选择适合的坐标系和投影方式,以便更好地应用于GIS和空间数据处理。
一、了解坐标系和投影方式的概念坐标系是一种地理坐标系统,用于描述地球上任意位置的坐标。
常用的坐标系包括经纬度坐标系、平面直角坐标系、地心坐标系等。
而投影方式是地球表面三维坐标映射到二维平面上的一种方法。
常用的投影方式有等面积投影、等角投影、等距投影等。
二、考虑数据来源和应用目的选择适合的坐标系和投影方式首先需要考虑数据来源和应用目的。
不同的数据来源可能使用不同的坐标系和投影方式。
例如,遥感数据常用的坐标系是地心坐标系(WGS84);而测量数据常使用局部的平面直角坐标系。
根据应用目的,选择坐标系和投影方式能够更好地呈现所需信息。
三、考虑地理范围和形状地理范围和形状也是选择适合的坐标系和投影方式的重要因素。
对于较小的地理范围,可以采用平面直角坐标系,如UTM投影。
而对于全球范围的数据,则需要选择适用于大范围的坐标系和投影方式,如Mercator投影。
此外,根据地球的形状,也需考虑到地球在不同地区的畸变程度,如极地存在极大畸变。
四、考虑数据精度和准确性选择适合的坐标系和投影方式还需要考虑数据的精度和准确性。
对于高精度要求的数据,在选择坐标系和投影方式时需要尽量减小数据的形变和畸变,保证数据的准确性。
同时,要根据实际情况选择合适的投影方式,以符合数据的精度要求。
五、考虑处理软件和技术支持最后,选择适合的坐标系和投影方式还需要考虑处理软件和技术支持。
不同的GIS软件和数据处理工具可能支持不同的坐标系和投影方式。
因此,要确保所选择的坐标系和投影方式能够被处理软件和工具支持,以便进行数据处理和分析。
总结起来,选择适合的坐标系和投影方式需要考虑数据来源和应用目的、地理范围和形状、数据精度和准确性以及处理软件和技术支持等因素。

空间解析几何基本概念空间解析几何是数学中一个重要的分支,它研究的对象是三维空间中的几何图形和几何问题。
在进行空间解析几何的学习和研究之前,我们需要先了解一些基本概念。
一、坐标系空间解析几何中常用的坐标系有直角坐标系和极坐标系两种。
直角坐标系由三个相互垂直的坐标轴构成,通常用x、y、z表示。
极坐标系则由原点、极径和极角组成,极径表示点到原点的距离,极角表示点与正x轴的夹角。
二、点、直线和平面在空间解析几何中,点是最基本的图形概念,用坐标表示为(x,y,z)。
直线可以通过两点或参数方程表示,例如直线L可以表示为:L: {(x,y,z) | x=x0+at, y=y0+bt, z=z0+ct},其中a、b、c为实数,(x0,y0,z0)为直线上的一点。
平面可以通过三点或参数方程表示,例如平面P可以表示为:P: { (x,y,z) | Ax+By+Cz+D=0 },其中A、B、C、D为实数。
三、距离和中点在空间解析几何中,点与点之间的距离可以通过勾股定理计算:d(P_1, P_2) = √((x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2),其中P_1(x_1, y_1, z_1)和P_2(x_2, y_2, z_2)为两点的坐标。
直线上的两点的中点可以通过坐标的平均值计算得到。
四、向量向量是空间解析几何中的重要概念,它可以表示有方向和大小的量。
向量由起点和终点表示,可以用坐标表示为一个有序三元组。
向量的运算包括加法、减法、数量乘法和点乘法。
两个向量的加法等于它们对应坐标的相加,减法等于相减。
数量乘法将向量的大小与一个实数相乘,结果是一个新的向量。
点乘法可以用来判断两个向量是否垂直,它的结果为零表示两个向量垂直。
五、投影在空间解析几何中,投影是指点在坐标轴或平面上的影子。
点在坐标轴上的投影可以通过坐标的部分表示,例如点P的x轴投影为(x, 0,0)。
点在平面上的投影可以通过垂直于平面的直线与平面的交点来表示。


空间坐标系怎么看坐标投影坐标投影是地理信息系统中一个重要的概念,它用于将三维空间中的点投影到一个二维平面上。
在地理定位、地图绘制、导航等领域中,坐标投影起到了至关重要的作用。
本文将介绍空间坐标系的概念,以及如何理解坐标投影。
空间坐标系空间坐标系是用来描述地球表面或其他物体上点的位置的系统。
通常,空间坐标系由坐标轴和坐标原点组成。
常用的空间坐标系有地理坐标系和投影坐标系。
•地理坐标系:地理坐标系使用经度和纬度来表示地球表面上点的位置。
经度表示点相对于本初子午线的东西方向的位置,纬度则表示点相对于赤道的北南方向的位置。
•投影坐标系:为了方便地图绘制和测量,人们发展了各种坐标投影方法,将地球表面上的点投影到一个二维平面上。
不同的投影方法得到的坐标投影方式各有特点,适用于不同的地区和用途。
坐标投影坐标投影是将三维空间中的点通过某种方式映射到二维平面上的方法。
为了能够投影地球表面上的点到平面上,人们发展了多种坐标投影方法,其中最常见的有等角投影、等积投影和等距投影等。
•等角投影:等角投影保持地球表面上的任意两点之间的角度不变,这样可以保证在投影后的平面上保持灵活的角度测量和方向导航。
著名的等角投影包括墨卡托投影和兰伯特投影。
•等积投影:等积投影保持地球表面上区域的面积比例不变,这样可以准确地表示不同区域的地理特征。
常见的等积投影有克里格勒投影和阿尔伯斯投影等。
•等距投影:等距投影保持地球表面上的任意两点之间的距离不变,这样可以保持准确的距离计量特性。
例如,正轴等距圆柱投影就是一种常见的等距投影方法。
在地图中使用坐标投影地图是坐标投影的一个主要应用领域。
使用坐标投影的目的是将地球表面上复杂的三维地理信息转化为容易理解和使用的二维表示,使得我们能够更好地理解地球和进行空间分析。
在地图中使用坐标投影时,我们首先需要选择适合于具体地理区域和使用目的的投影方法。
不同的坐标投影方法适合于不同的地理区域和需要。
我们还需要确定地图的中心点和缩放级别,以便于有效地展示地理信息。

空间直角坐标系的坐标投影法简介空间直角坐标系是描述物体在三维空间中位置的一种方式,它由三条相互垂直的坐标轴组成:x轴、y轴和z轴。
而坐标投影法是一种常用的方法,用于将三维空间中的点位置通过投影映射到二维平面上,以便更直观地表示和分析对象在三维空间中的位置关系。
坐标投影法的基本原理坐标投影法的基本原理是将三维空间中的点在一个二维平面上进行投影。
这个平面可以是任意的,常用的包括水平平面、垂直平面等。
在空间直角坐标系中,通过选择合适的平面和定义相应的坐标系,可以方便地描述物体在三维空间中的位置。
坐标投影法的具体步骤步骤一:选择投影平面首先,需要选择一个合适的投影平面。
这个平面可以根据具体问题和需要进行选择,常用的有水平平面、垂直平面等。
选择时需要考虑保持坐标系的垂直性和方便计算。
步骤二:确定坐标系在选定投影平面后,需要在该平面上建立一个坐标系。
通常情况下,选择投影平面上的两条互相垂直的线作为坐标轴。
这两条线上的点与原空间中的点有一一对应的关系,可以通过坐标值来表示。
步骤三:求投影点坐标在确定了投影平面和坐标系后,需要将原空间中的点进行投影,得到在投影平面上的点坐标。
投影的方法可以根据具体情况而定,常用的有平行投影和透视投影等。
步骤四:记录投影点坐标最后,将求得的投影点坐标记录下来。
这些坐标可以作为二维平面上点的位置,用于分析和表示原空间中的点的位置关系。
应用示例坐标投影法在实际应用中有广泛的使用。
以下是一个简单的应用示例,以帮助更好理解坐标投影法的实际运用。
假设一个球体位于空间直角坐标系的原点(0, 0, 0)处,球心坐标(x, y, z)分别为(2, 3, 4),我们想要求球心在水平平面上的投影坐标。
1.选择水平平面作为投影平面;2.在水平平面上建立一个坐标系,其中x轴和y轴分别与空间直角坐标系中的x轴和y轴平行;3.计算球心投影坐标,即将球心的z坐标设为0,得到投影坐标为(2,3)。
通过这个示例,我们可以看到坐标投影法的实际运用过程,从选择投影平面、建立坐标系,到计算投影点坐标,最终得到在二维平面上的投影坐标。
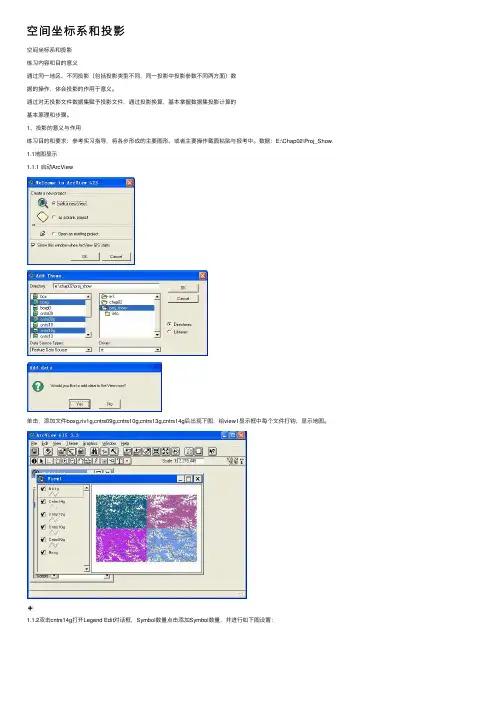
空间坐标系和投影空间坐标系和投影练习内容和⽬的意义通过同⼀地区、不同投影(包括投影类型不同,同⼀投影中投影参数不同两⽅⾯)数据的操作,体会投影的作⽤于意义。
通过对⽆投影⽂件数据集赋予投影⽂件,通过投影换算,基本掌握数据集投影计算的基本原理和步骤。
1、投影的意义与作⽤练习⽬的和要求:参考实习指导,将各步形成的主要图形、或者主要操作截⾯粘贴与报考中。
数据:E:\Chap02\Proj_Show.1.1地图显⽰1.1.1 启动ArcView单击,添加⽂件boxg,riv1g,cntrs09g,cntrs10g,cntrs13g,cntrs14g后出现下图,给view1显⽰框中每个⽂件打钩,显⽰地图。
1.1.2双击cntrs14g打开Legend Edit对话框,Symbol数量点击添加Symbol数量,并进⾏如下图设置:同样的⽅法操作cntrs09g,cntrs10g,cntrs13g,并保持设置与cntrs14g⼀致,结果如下图⽤Text⼯具按钮为图⾯加图幅名,可以⽤Pointer来调整注记的⼤⼩结果图如下:1.2投影信息显⽰1.2.1打开workstation-Arc1.2.2输⼊⼯作路径w+⽂件路径。
如:1.2.3⽤describe+⽂件名语句来查看投影信息。
如1.2.4输⼊各个⽂件投影信息如下:1.3投影⽐较在ArcV iew 中添加⽂件riv1与riv1a 数据并显⽰观察:造成⽂件riv1、riv1a 显⽰差异的原因:其中蓝⾊部分是riv1,红⾊部分是riv1a,可以看到两张图并没有重合在⼀起,彼此之间有缝隙,在1.2实验中已经知道riv1和riv1a 都是ALBERS 投影,但是riv1的第⼆标准纬线为37 100.000中央⼦午线为109 30 0.00,⽽riv1a 的第⼆标准纬线为37 9 30.000中央⼦午线为109 29 30.00,这样就造成了显⽰的差异。
1.4为Coverage 赋予投影1.4.1:1.4.2:显⽰:1.4.3显⽰:完成为为Coverage 赋予投影。

关于坐标系和投影的相关知识探讨坐标系和投影是地理学和地理信息系统(GIS)中的基础概念。
坐标系是用于定位地球上任意点位置的一种方案,而投影则是将地球的曲面表达在平面上的方法。
本文将探讨坐标系和投影的相关知识,包括定义、分类、应用以及优缺点等。
首先,坐标系是地理空间数据基准的一部分,用于描述地球上一些点的位置。
常见的坐标系包括地心坐标系、大地坐标系和平面坐标系等。
其中,地心坐标系以地球的中心作为起点,以地球的表面为参照进行定位。
大地坐标系则以地球表面上的一个点作为起点,以地球的形状和大小为参照进行定位。
平面坐标系是将地球表面投影到平面上的一种方法,常用于地图制作和空间分析中。
投影是将地球的曲面表达在平面上的一种方法。
由于地球是一个近似于椭球体的三维对象,将其表达在平面上时会出现形变。
根据存储项目,地图投影可以分为正形投影和等面积投影。
正形投影是指将地球上各点间的角度关系保持不变的投影方法,可以保持形状的相对准确。
等面积投影则是指将地球上的面积比例保持不变的投影方法,可以保持面积的相对准确。
常见的投影方法包括墨卡托投影、正轴等积圆柱投影和兰勃托投影等。
在GIS应用中,坐标系和投影的选择是非常重要的。
不同的应用需要不同的坐标系和投影方案来满足精度和准确性的要求。
例如,在地图制作中,通常使用平面坐标系和等面积投影来保持地图上各个地区的相对面积准确。
而在空间分析中,通常使用大地坐标系和正形投影来保持地图上各个地区的角度关系准确。
尽管各个坐标系和投影方法都有自己的优点和局限性,但基于特定的应用需求选择合适的坐标系和投影方法是非常重要的。
此外,随着技术的进步和研究的不断深入,也涌现出了一些新的坐标系和投影方法,以更好地满足各种不同应用的需求。
总之,坐标系和投影是地理学和GIS中的基础概念,对于地球定位和地图制作非常重要。
通过理解和应用合适的坐标系和投影方法,可以更准确地表达地球的空间信息,从而支持各种地理空间应用和决策。

空间坐标系分类1. 引言空间坐标系是用来描述和定位物体在空间中位置的数学系统。
它是地理信息系统(GIS)、遥感、导航和测量等领域的基础概念。
在实际应用中,不同的任务需要使用不同类型的空间坐标系。
本文将介绍常见的空间坐标系分类,包括地心坐标系、大地坐标系和投影坐标系。
2. 地心坐标系地心坐标系是以地球为参考对象建立的一种三维坐标系统。
它将地球看作一个理想化的球体,并以地球质心为原点建立直角坐标系。
地心坐标系通常用于天文学、大地测量和卫星导航等领域。
2.1 地心惯性坐标系在地心惯性坐标系中,以地球质心为原点,建立一个固定于宇宙空间的直角坐标系统。
该坐标系统不随时间变化,适用于天体力学研究和卫星轨道计算。
2.2 地心测量坐标系地心测量坐标系是以地球质心为原点,建立一个固定于地球的直角坐标系统。
该坐标系统考虑了地球的形状和重力场的影响,适用于大地测量和地球物理研究。
3. 大地坐标系大地坐标系是以地球表面为参考对象建立的一种三维坐标系统。
它是基于地球椭球体模型和大地测量学原理建立的,用于描述地理位置和测量数据。
3.1 大地水准面大地水准面是一个近似于海平面的参考面,在大部分应用中被作为零高程基准。
在大地水准面上,可以通过经纬度和高程来确定一个点在大地坐标系中的位置。
3.2 大地椭球体模型大地椭球体模型是对地球形状进行近似描述的数学模型。
常用的大地椭球体模型有WGS84、GRS80等,它们通过半长轴、扁率等参数来定义椭球体的形状。
3.3 大地水平坐标系大地水平坐标系使用经度和纬度来表示一个点在水平方向上的位置。
经度表示东西方向上的偏移,纬度表示南北方向上的偏移。
常见的大地水平坐标系有经纬度坐标和UTM坐标。
3.4 大地垂直坐标系大地垂直坐标系使用高程来表示一个点在垂直方向上的位置。
常见的大地垂直坐标系有正高程、椭球高和大地水准面高等。
4. 投影坐标系投影坐标系是将三维空间投影到二维平面上的一种数学变换。
它是为了解决地球表面在平面上展示时产生的形状变形、距离失真等问题而设计的。

关于坐标系和投影的相关知识探讨1、坐标系坐标系由原点和坐标轴组成。
坐标系如笛卡尔坐标系、极坐标系、球面坐标系和柱面坐标系。
我们比较熟悉的为平面坐标系、空间直角坐标系(前两者属于笛卡尔坐标系)和球面坐标系。
比如说一个点坐标是(-2850017.472,4690744.523,3237959.973)就是指空间直角坐标,而我们经常看到的Google Earth上的点的坐标(37°20′17″N,112°33′20″E)就是指球面坐标。
测量学上,坐标系怎样定义的呢?地球是一个不规则的类椭球,怎样用严格的数学方式表示它,应该是测绘学家们所追求的高峰。
为了表示地球上每一个点的位置,是不是要建立一个统一的世界坐标系呢?建立坐标系是不是要确定坐标原点和坐标轴呢?那怎样建立呢?测量学家们把地球当作一个规则的椭球来处理,这下就好办多了,椭球中心就原点呗,长轴短轴就作为坐标轴,这样一个坐标系就出来了啊。
可是有人会问,那这个椭球怎么表示呢?嘛嘛的,我也想问,原来这是科学家们利用天文观测得到的,而且不同的科学家得到的椭球还不一样,比如,一个叫Krasovsky的人搞了个克拉索夫斯基椭球,还有人搞了什么IUGG-1975、WGS-84、GRS80椭球,他们主要特点是长半轴和扁率不同。
可是又有人会问,搞这么多椭球干嘛,有一个不就行啦。
呵呵,我们知道,地球坑坑洼洼的,用严密的椭球来表示肯定有误差,有的国家为了使自己的国家与椭球面吻合(最好大家都站在椭球面上),这样根据各自的情况就定义了不同的参考椭球,比如北京54坐标系就采用了苏联老大哥的克拉索夫斯基椭球。
可是问题又来了,怎样才算吻合得好呢?肯定会有人站在椭球面上,有人站在椭球面下,真头疼。
此时,测量学家们引入了大地基准面(貌似Datum,编者加)来衡量椭球与大地的吻合度。
大地基准面是由大地水准面而来,是指平均海平面延伸到大陆得到的一个封闭曲面。
比如,在建立北京54坐标系时,专家们肯定会选择与中国的大地水准面吻合比较好的椭球。

测绘过程中常用的坐标系和投影方式近年来,随着科技的不断发展,测绘技术也得以飞速发展。
在测绘过程中,坐标系和投影方式是两个非常重要的概念。
坐标系是指用于确定物体位置的一种数学模型,而投影方式则是指将三维地理空间投影到二维平面上的方法。
在本文中,我们将探讨测绘过程中常用的坐标系和投影方式。
一、坐标系在测绘学中,常用的坐标系主要有直角坐标系和球面坐标系两种。
1. 直角坐标系直角坐标系是指以三个相互垂直的坐标轴为基准的坐标系。
它是最常用的坐标系之一,适用于大部分的测绘工作。
直角坐标系可以将地球表面上的点的位置准确地表示出来,具有高精度和高度的可视化效果。
2. 球面坐标系球面坐标系是一种以球体表面上的点为基准的坐标系。
在进行大规模城市建设、地质勘测、海洋测绘等工作时,球面坐标系比直角坐标系更为实用。
球面坐标系可以更好地表示地球表面的复杂形状和曲面,因此在这些需要精确测绘的领域应用广泛。
二、投影方式投影方式是将三维地理空间投影到二维平面上的方式。
在测绘学中,常用的投影方式主要有等角投影、等积投影和等距投影。
1. 等角投影等角投影是指将地球表面上的点通过投影转换到二维平面上时,保持角度不变的一种投影方式。
这种投影方式能够准确地表示地球表面上的角度关系,适用于航空摄影、气象预报等领域。
2. 等积投影等积投影是指在投影转换过程中保持地球表面上面积比例不变的一种投影方式。
这种投影方式能够准确地表示地球表面上地物的相对大小,适用于土地规划、农业统计等领域。
3. 等距投影等距投影是指将地球表面上的点通过投影转换到二维平面上时,保持距离比例不变的一种投影方式。
这种投影方式能够准确地表示地球表面上点之间的距离关系,适用于交通规划、道路建设等领域。
三、总结在测绘过程中,坐标系和投影方式是两个不可或缺的概念。
直角坐标系和球面坐标系是常用的坐标系,分别适用于不同的测绘需求。
等角投影、等积投影和等距投影则是常用的投影方式,分别适用于不同的测绘需求。
坐标系和地图投影是地理信息系统中非常重要的概念初学者或非专业人士往往容易混淆它们之间的区别。
以下是一些常见的问题和它们的不同之处:坐标系与地图投影的区别:坐标系是定义空间位置的参照框架,它使用数值坐标来描述点在空间中的位置。
常见的坐标系包括地理坐标系、投影坐标系等。
地理坐标系使用经纬度来表示地球表面上的位置,而投影坐标系则是将地球表面投影到一个平面坐标系上。
地图投影是将地球表面或球体表面上的地理信息转换到二维平面上的过程。
地图投影涉及到将三维空间的地理信息转换为二维平面上坐标的过程,这个过程中会涉及到一些变形和误差。
不同的投影方法会导致不同的变形和误差,因此需要根据实际应用需求选择合适的投影方法。
常见错误认识:(1)将坐标系和地图投影混淆:有些初学者或非专业人士可能会将坐标系和地图投影混淆,认为它们是同一个概念。
实际上,坐标系是描述空间位置的参照框架,而地图投影是将地理信息转换到二维平面上的过程。
(2)忽视投影方法的选择:不同的投影方法适用于不同的应用场景。
有些初学者或非专业人士可能会忽视根据实际需求选择合适的投影方法,导致地图出现严重的变形和误差。
(3)对变形和误差的认识不足:地图投影过程中会涉及到一些变形和误差,有些初学者或非专业人士可能会忽视这些变形和误差,导致分析和计算出现偏差。
总之,坐标系和地图投影是两个密切相关的概念,它们在地理信息系统中起着重要的作用。
初学者或非专业人士需要准确理解它们的定义和区别,以更好地应用它们来解决实际问题。
除了上述提到的常见错误认识外,还有一些其他需要注意的问题。
例如,一些初学者可能会将地图投影与地图绘制混淆,认为它们是同一个过程。
实际上,地图投影是将地理信息转换为平面坐标的过程,而地图绘制则是将平面坐标转换为可见的地图图像的过程。
这两个过程是相互独立的,但在地理信息系统中常常会一起使用。
另外,一些初学者还可能会忽视地图投影的局限性。
不同的投影方法具有不同的优点和缺点,没有一种投影方法可以适用于所有情况。
三维坐标系与投影解析在几何学中,三维坐标系是用来表示三维空间中的点和图形的工具。
它由三个坐标轴(x、y、z)组成,每个坐标轴上都有正负方向。
通过坐标轴上的数值,我们可以精确地描述点在三维空间中的位置。
三维坐标系可以帮助我们解决许多与空间相关的问题。
例如,在三维坐标系中,我们可以表示一个立方体,球体或者任何其他三维图形。
通过在坐标系中绘制线段、平面和曲线,我们可以更好地理解和分析空间中的几何特征。
投影解析是一种方法,用于将三维空间中的图形投影到一个或多个二维平面上。
在投影解析中,我们通过计算每个三维点在投影平面上的坐标,来表示三维图形在二维平面上的形状和位置。
常用的投影解析方法有平行投影和透视投影。
平行投影是指将三维图形的每个点沿着平行于某个方向的直线投影到一个平面上。
这种投影方法常用于工程制图和计算机图形学中。
平行投影可以使图形保持等比例和直线保持平行,但通常会导致图形失去深度和透视感。
透视投影是指将三维图形的每个点投影到一个视点上,并延长直线到投影平面上。
透视投影模拟了人眼观察物体时的效果,可以使图形具有更真实的逼近感和立体感。
透视投影广泛应用于绘画、建筑设计和影视制作等领域。
除了常用的平行投影和透视投影,还有一些其他的投影解析方法,如轴测投影和斜轴测投影。
轴测投影将三维图形的每个点沿着轴线投影到一个或多个平行于坐标轴的平面上,常用于制图和设计。
斜轴测投影通过调整轴线的角度,可以使图形具有更立体的效果。
总结起来,三维坐标系和投影解析是几何学中重要的工具和方法。
它们可以帮助我们准确地描述和分析空间中的图形,提供更好的理解和可视化效果。
通过学习和应用这些知识,我们可以更深入地探索和研究三维空间的属性和特征。
无论是在科学研究、工程设计还是艺术创作中,三维坐标系和投影解析都具有重要的应用价值。
力在空间直角坐标系的投影方法在空间直角坐标系中,力的投影是指力在坐标轴上的分量。
力的投影方法可以帮助我们计算力在不同方向上的作用效果,从而更好地理解和分析物体受力的情况。
我们需要明确什么是投影。
投影是指一个向量在某个方向上的分量,也可以看作是该向量在该方向上的影子。
在空间直角坐标系中,我们常常使用x轴、y轴和z轴作为坐标轴,分别表示水平方向、垂直方向和竖直方向。
因此,力在空间直角坐标系中的投影即为力在x轴、y轴和z轴上的分量。
以一个力F为例,我们可以将它分解为在x、y、z轴上的三个分量,分别表示为Fx、Fy和Fz。
这三个分量可以通过力的向量和坐标轴的夹角以及力的大小来计算得出。
我们需要计算力F与坐标轴的夹角。
假设力F的向量表示为F = (Fx, Fy, Fz),坐标轴x的单位向量表示为i,坐标轴y的单位向量表示为j,坐标轴z的单位向量表示为k。
那么力F与坐标轴x的夹角θx 可以通过向量的点乘运算得出:θx = arccos((F·i) / |F|),其中"·"表示点乘运算,"|F|"表示力F的大小。
同样地,力F与坐标轴y的夹角θy可以通过向量的点乘运算得出:θy = arccos((F·j) / |F|);力F与坐标轴z的夹角θz可以通过向量的点乘运算得出:θz = arccos((F·k) / |F|)。
接下来,我们可以根据夹角和力的大小来计算力在各个坐标轴上的分量。
力F在x轴上的分量Fx可以通过力的大小与cos(θx)的乘积得出:Fx = |F| * cos(θx)。
力F在y轴上的分量Fy可以通过力的大小与cos(θy)的乘积得出:Fy = |F| * cos(θy)。
力F在z轴上的分量Fz可以通过力的大小与cos(θz)的乘积得出:Fz = |F| * cos(θz)。
通过上述计算,我们可以得到力F在空间直角坐标系中的投影分量Fx、Fy和Fz。
GIS基础知识-坐标系、投影、EPSG:4326、EPSG:3857最近接⼿⼀个GIS项⽬,需要⽤到 PostGIS,GeoServer,OpenLayers 等⼯具组件,遇到⼀堆地理信息相关的术语名词,在这⾥做⼀个总结。
1. ⼤地测量学 (Geodesy)是⼀门量测和描绘地球表⾯的学科,也包括确定地球重⼒场和海底地形。
1.1 ⼤地⽔准⾯ (geoid)是海洋表⾯在排除风⼒、潮汐等其它影响,只考虑重⼒和⾃转影响下的形状,这个形状延伸过陆地,⽣成⼀个密闭的曲⾯。
虽然我们通常说地球是⼀个球体或者椭球体,但是由于地球引⼒分布不均(因为密度不同等原因),⼤地⽔准⾯是⼀个不规则的光滑曲⾯。
虽然不规则,但是可以近似地表⽰为⼀个椭球体,这个椭球体被称为。
⼤地⽔准⾯相对于参考椭球体的⾼度被称为 Undulation of the geoid 。
这个波动并不是⾮常⼤,最⾼在冰岛为85m,最低在印度南部为 −106 m,⼀共不到200m。
下图来⾃,表⽰ EGM96 geoid 下不同地区的 Undulation。
1.2 参考椭球体(Reference ellipsoid)是⼀个数学上定义的地球表⾯,它近似于⼤地⽔准⾯。
因为是⼏何模型,可以⽤长半轴、短半轴和扁率来确定。
我们通常所说的经度、纬度以及⾼度都以此为基础。
⼀⽅⾯,我们对地球形状的测量随着时间迁移⽽不断精确,另⼀⽅⾯,因为⼤地⽔准⾯并不规则,地球上不同地区往往需要使⽤不同的参考椭球体,来尽可能适合当地的⼤地⽔准⾯。
历史上出现了很多不同的参考椭球体,很多还仍然在使⽤中。
国内过去使⽤过“北京54”和“西安90”两个坐标系,其中北京54使⽤的是克拉索夫斯基(Krasovsky)1940的参考椭球,西安80使⽤的是1975年国际⼤地测量与地球物理联合会第16届⼤会推荐的参考椭球。
当前世界范围内更普遍使⽤的是WGS所定义的参考椭球。
2. 坐标系(coordinate system)有了参考椭球体这样的⼏何模型后,就可以定义坐标系来进⾏描述位置,测量距离等操作,使⽤相同的坐标系,可以保证同样坐标下的位置是相同的,同样的测量得到的结果也是相同的。
空间坐标系分类空间坐标系是地理空间数据中最基本的组成部分之一。
它是用于在地球表面定位地理位置的数学模型。
根据坐标系的定义、用途和数据类型,空间坐标系可以分为多种类型。
一、地心坐标系地心坐标系是以地球质心为原点,建立在地心上的坐标系。
它是地球动力学、测量学、大地水准面计算、游戏开发等领域的基础。
地心坐标系通常以X、Y、Z分别表示三个坐标轴。
二、大地坐标系大地坐标系是以地球椭球体上的一个点为原点的坐标系。
其坐标系基准面和大地水准面平行,用于计算地理数据。
大地坐标系可以分为经纬度坐标系和平面直角坐标系等不同类型。
三、投影坐标系投影坐标系是建立在大地坐标系之上的,用来将三维地理对象投影到二维平面上进行处理和显示。
投影坐标系可以分为等角投影、等积投影、等距投影、圆柱投影、圆锥投影等多种类型。
四、本地坐标系本地坐标系是以某个地理实体为原点的坐标系,如一座建筑、一段道路或一个桥梁等。
本地坐标系通常用于建筑、工程、道路、桥梁等领域的测量和设计,可大大提高数据精度和可靠性。
五、象限坐标系象限坐标系又称笛卡尔坐标系,是直角坐标系的一种。
它将平面分为四个象限,以X轴和Y轴上的正方向作为基准。
象限坐标系主要用于GIS、CAD、图形处理等领域的数据处理和显示。
六、局部坐标系局部坐标系是建立在某个特定地点的坐标系。
它包括经过这个点的三个坐标轴,并根据特定的规则确定了其中一个向量的方向。
局部坐标系主要用于机器人、导航、航空航天、地震学等领域的测量和控制。
总之,不同类型的空间坐标系在地理信息系统、测量学、人工智能等领域中都起着重要的作用。
了解并掌握各种坐标系的特点和应用,将有助于提高地理数据的处理和应用能力。
空间坐标系和投影练习内容和目的意义通过同一地区、不同投影(包括投影类型不同,同一投影中投影参数不同两方面)数据的操作,体会投影的作用于意义。
通过对无投影文件数据集赋予投影文件,通过投影换算,基本掌握数据集投影计算的基本原理和步骤。
1、投影的意义与作用练习目的和要求:参考实习指导,将各步形成的主要图形、或者主要操作截面粘贴与报考中。
数据:E:\Chap02\Proj_Show.1.1地图显示1.1.1 启动ArcView单击,添加文件boxg,riv1g,cntrs09g,cntrs10g,cntrs13g,cntrs14g后出现下图,给view1显示框中每个文件打钩,显示地图。
1.1.2双击cntrs14g打开Legend Edit对话框,Symbol数量点击添加Symbol数量,并进行如下图设置:同样的方法操作cntrs09g,cntrs10g,cntrs13g,并保持设置与cntrs14g一致,结果如下图用Text工具按钮为图面加图幅名,可以用Pointer来调整注记的大小结果图如下:1.2投影信息显示1.2.1打开workstation-Arc1.2.2输入工作路径w+文件路径。
如:1.2.3用describe+文件名语句来查看投影信息。
如1.2.4输入各个文件投影信息如下:1.3投影比较在ArcV iew中添加文件riv1与riv1a数据并显示观察:造成文件riv1、riv1a显示差异的原因:其中蓝色部分是riv1,红色部分是riv1a,可以看到两张图并没有重合在一起,彼此之间有缝隙,在1.2实验中已经知道riv1和riv1a都是ALBERS投影,但是riv1的第二标准纬线为37 10 0.000中央子午线为109 30 0.00,而riv1a的第二标准纬线为37 9 30.000中央子午线为109 29 30.00,这样就造成了显示的差异。
1.4为Coverage赋予投影1.4.1:1.4.2:显示:1.4.3显示:完成为为Coverage赋予投影。
2.为无投影文件的数据集添加投影信息(文件)实习内容:掌握在ArcMap环境下为没有投影文件的coverage赋予投影信息实习要求:根据已知投影的地图,为有投影但无投影文件的coverage添加投影信息实习数据:E:\Chap02\Proj_Cal用于练习的数据为高斯投影,西安80坐标系;但是由于多种原因,在数据集中没有投影文件,同时投影单位为KM。
为此,需要给添加投影文件并将单位换算成M2.1练习1换算投影单位2.1.1打开workstation-Arc并进行如下操作:2.2练习2添加投影文件2.2.1打开ArcMap,在ArcTools box中选择Data Management tools/project and transformations/define projection(如下图所示)2.2.2在出现的Define Projection对话框中进行下图中坐标系统的设置2.2.3打开workstation-Arc进行下图操作2.3练习3换算投影(初步)2.3.1打开workstation-Arc进行下图操作完成投影换算:3.为不知投影信息的扫描图像赋予投影信息3.1加载数据3.1.1在ArcMap中加载文L51g009002a.tif。
3.1.2打开workstation-Arc进行下图操作3.2添加"影像配准"工具栏3.3确定控制点坐标3.3.1首先将Georeferencing工具条的Georeferencing菜单下Auto Adjust不选择。
在Georeferencing工具条上,Add Control Point按钮。
使用该工具在L51g009002_0.tif上精确找到同名地物(控制点),用鼠标点左键定位,再击右键选择“Input X and Y…”,打开Enter Coordinates对话框,同时在workstation的界面读取坐标值,将其复制到Enter Coordinates对话框。
如下图用同样的方法,在影像上增加另外3个控制点,保存它们的实际坐标。
如果必要,须考虑再选择一些控制点。
3.3.2点击V iew Link Table 按钮,打开Link Table对话框,讲对话框底边Auto Adjust选择,在输入4个控制点的情况下,Transformation设定为1st Order Polynmial。
如下图所示3.4矫正并重采样栅格生成新的栅格文件3.4.1在Georeferencing菜单下,点击Rectify,对配准的影响根据设定的变换公式重新采样,另存为一个新的影像文件3.5结果检验:加载投影变换后的图形文件,加载等高线和高程度点图层(cntrs,pnts);比较其吻合程度。
4.为ArcView Shape 格式的图形文件计算投影4.1将Shape格式的文件转换成Coverage格式打开workstation-Arc进行下图操作,将Shape格式的文件转换成Coverage格式4.2 加载snow.txt,并为其添加坐标系统4.2.1 打开ArcMap ,向其中加载snow.txt。
点击上方的TOOLS ,选择下方的Add XY Data。
4.2.2弹出的Add XY Data 对话框中,选择X Field 为longitude, Y Field 为latitude。
点击Edit按钮,弹出Spatial Reference Properities 对话框。
点击Selected按钮来添加固定的坐标系统。
选择地理坐标系统(Geographic Coordinate Systems)下的北美(North America)下的North American Datum 1983 坐标系。
4.2.3依次点击确定打开ArcMap中的Arc Toolbox工具箱中的Date Management Tools/Projections and Transformations/Define Projection。
如下图所示:4.3 生成snowutm83.shp4.3.1点击Show/Hide ArcToolbox Window使ArcToolbox显示出来。
打开ArcToolbox下的Data Management Tools / Projections and Transformations / Feature / Project .在弹出的Project 对话框中选择snow.txt Events为Input Database,将Output Feature Class重命名为snowutm83.shp。
将输出坐标系统设为投影坐标系统下NAD 1983下面的NAD 1983 UTM Zone 11N。
点击OK,得到snowutm83.shp。
4.4为生成的83cov定义投影在Define Projection对话框中进行如下设置,定义投影5.为grid文件计算投影实习内容:掌握ArcMap环境下、ARC/INFO workstation环境下对DEM进行投影换算的方法。
实习要求:在某地区DEM的制作过程中,作业人员为了简便,给坐标的X值(理论值)减去36000000M,其实就是没有考虑投影带号;Y值(理论值)减去400000M。
这里要求对其予以纠正。
实习数据:E:\Chap02\GTD_Proj。
5.1投影定义5.1.1打开ArcMap,启动ArcToolbox,选择Data Management Tools,然后选择Projections and Transformation/Define Projection,出现以下界面。
5.1.2选择Coordinate System后的键,选择投影select-Projected Coordinate System-GaussKruger-Beijing 1954-Beijing_1954_Degree_GK_CM_108E在Spatial Reference 属性对话框中选择Modify,修改False_Northing(-40000000),确定后出现以下界面,在确定就可以完成投影的定义。
5.1.3运行workstation-Arc查看投影的描述,具体操作如下图:5.2.1运行workstation-Arc,进行如下操作6.地图数字化过程中的投影计算目的:通过本实习,掌握在地图数字化过程中进行投影计算和地图接边的基本操作方法。
要求:对某地区1:1万标准分幅的河流图进行投影计算,并将其拼接。
数据:提供该地区投影计算的Master Coverage(主控Coverage)。
6.1打开workstation-Arc进行下图操作:按照同样的方法把每一个文件都进行重新编号,得到一组新的数据.6.2然后进行投影转换6.2.1输入create j55 F:\学习\ARCGIS\Chap02\Rivs\Master_Tics\mas_cov,即可创建一个j55的coverage。
6.2.2然后在输入transform F:\学习\ARCGIS\Chap02\Rivs\ed\j55 j55。
同理,将其他各个图幅也做相应处理。
6.2.3完成后,依次输入build j7 line,build j8 line.......build j64 line,再输入append riv_all arc tic。
即创建一个完整的图像,命名为riv_all。
再依次加个各个分幅,j7,j8.....j64。
输入end结束。
6.2.4在arcmap中打开最终的合成图riv_all,即可看到最终效果图。