2011广东各地高三上期末考试题分类解答题汇编—立体几何(文)

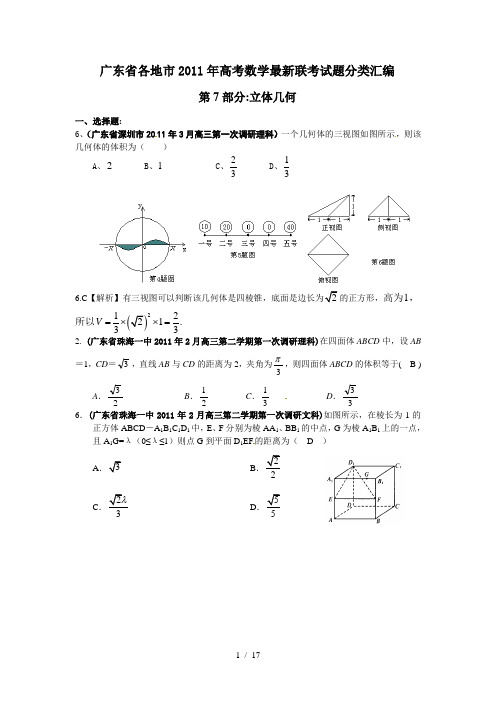
广东省各地市2011年高考数学最新联考试题分类汇编第7部分:立体几何一、选择题: 6、（广东省深圳市2011年3月高三第一次调研理科）一个几何体的三视图如图所示，则该几何体的体积为（ ）A 、2B 、1C 、23D 、136.C 【解析】有三视图可以判断该几何体是四棱锥，底面是边长为2的正方形，高为1，所以()21221.33V =⨯⨯=2. (广东省珠海一中2011年2月高三第二学期第一次调研理科)在四面体ABCD 中，设AB ＝1，CD ＝3，直线AB 与CD 的距离为2，夹角为3π，则四面体ABCD 的体积等于( B ) A ．23 B ．21 C ．31 D ．33 6．(广东省珠海一中2011年2月高三第二学期第一次调研文科)如图所示，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为棱AA 1、BB 1的中点，G 为棱A 1B 1上的一点，且A 1G=λ（0≤λ≤1）则点G 到平面D 1EF 的距离为（ D ）A ．3B ．22 C ．23λD ．53. (广东省珠海一中2011年2月高三第二学期第一次调研文科)一个几何体的三视图如下图所示，其中正视图是一个边长为2的正三角形，俯视图是一正方形，那么该几何体的侧．视图．．的面积为( C )A．1 B．2C．D．4⒌(广东省江门市2011年高考一模文科)某型号儿童蛋糕上半部分是半球，下半部分是圆锥，三视图如图1，则该型号蛋糕的表面积=S( A )A．π115B．π110C．π105D．π100⒌(广东省江门市2011年高考一模理科)一个底部水平放置的几何体，下半部分是圆柱，上半部分是正四棱锥，其三视图如图1所示，则这个几何体的体积=V( D )A．3054+πB．π69C．π66D．2454+π7.(广东省广雅金山佛一中2011年2月高三联考理科)已知某一几何体的正视图与侧视图如图，则下列图形中，可以是该几何体的俯视图的图形有（ D ）正视图侧视图图2侧视图俯视图正视图4x33x 4A ．①②③⑤B ．②③④⑤C ．①②④⑤D ． ①②③④6. (广东省东莞市2011年高三一模理科)一空间几何体的三视图如图2所示, 该几何体的体积为85123π+，则正视图中x 的值为( C ) A. 5 B. 4 C. 3 D. 28．(广东省东莞市2011年高三一模文科)一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积等于( A ) A ．13B ．23C ．156D ．62243．(广东执信中学2011年2月高三考试文科)已知,αβ为不重合的两个平面，直线,m α⊂那么“m β⊥”是“αβ⊥”的（ A ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．(广东执信中学2011年2月高三考试文科)已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 （ B ）A ．383cm B ．343cm C ．323cm D ．313cm二、填空题:2312．（广东省深圳市2011年3月高三第一次调研文科）已知正三棱柱（侧棱与底面垂直，底面是正三角形）的高与底面边长均为2，其直观图和正(主)视图如下，则 它的左(侧)视图的面积是 ．12. 2 3.【解析】画出左(侧)视图如图,其面积为2 3.14. (广东省珠海一中2011年2月高三第二学期第一次调研理科)在0120的二面角内，放一个半径为10cm 的球切两半平面于A,B 两点，那么这两切点在球面上的最短距离是___________310π11．(广东省广雅金山佛一中2011年2月高三联考文科)已知空间四边形ABCD 中，AB ⊥BC ，BC ⊥CD ， CD ⊥AB ，且AB ＝2，BC ＝5，CD ＝7，则AD ＝ 4 。

lαβm广东高考数学真题汇编：立体几何1、（2011•广东文数）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（ ） A 、20 B 、15 C 、12 D 、101解答：解：由题意正五棱柱对角线一定为上底面的一个顶点和下底面的一个顶点的连线，因为不同在任何侧面内，故从一个顶点出发的对角线有2条．正五棱柱对角线的条数共有2×5=10条．故选D2、（2011•广东文数）如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为 （ ） A 、 B 、4 C 、 D 、23、（2011•广东理数）如某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则几何体的体积为（ ） A 、6 B 、9 C 、12 D 、185. （2009广东文科）给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行； ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中，为真命题的是A ．①和②B ．②和③C ．③和④D ．②和④6．（2008广东文数）将正三棱柱截去三个角（如图1所示，AB C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）7．（2007广东文数）若l mn ，，是互不相同的空间直线，αβ，是不重合的平面，则下列命题中为真命题的是（ ）Ａ．若l n αβαβ⊂⊂，，∥，则l n ∥Ｂ．若l αβα⊥⊂，，则l β⊥Ｃ．若l nm n ⊥⊥，，则l m ∥ Ｄ．若l l αβ⊥，∥，则αβ⊥ 8、（2006广东）给出以下四个命题①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;EF DIA H GB C EF DA B C侧视 图1图2B EA ．B EB ．B EC ．B ED ．③如果两条直线都平行于一个平面,那么这两条直线互相平行;④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是A.4B.3C.2D.19. (2005广东)给出下列关于互不相同的直线m 、l 、n 和平面α、β，的四个命题： ①若A l m =⊂αα ,，点m A ∉，则l 与m 不共面；②若m 、l 是异面直线, αα//,//m l , 且m n l n ⊥⊥,，则α⊥n ； ③若βα//,//m l , βα//，则m l //；④若=⊂⊂m l m l ,,αα点A ，ββ//,//m l ，则βα//． 其中为假命题的是A ．①B ．②C ．③D ．④11、（2006广东）若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为13．（2008广东文数）如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，60ABD ∠=，45BDC ∠=，PD 垂直底面ABCD，PD =，E F ，分别是PB CD ，上的点，且PE DFEB FC =，过点E 作BC 的平行线交PC 于G ． （1）求BD 与平面ABP 所成角θ的正弦值； （2）证明：EFG △是直角三角形； （3）当12PE EB =时，求EFG △的面积．13．解：（1）在Rt BAD ∆中，60ABD ∠=，,AB R AD ∴==而PD 垂直底面ABCD ，PA ===PB ===,在PAB ∆中，222PA AB PB +=,即PAB ∆为以PAB ∠为直角的直角三角形。

立体几何1、（山东卷）右图是一个几何体的三视图，依据图中数据，可得该几何体的表面积是(A)9π （ B ） 10π(C)11π(D)12π【分析 】考察三视图与几何体的表面积。

个球和一个圆柱组合而成的，其表面及为从三视图能够看出该几何体是由一S4 12122 21312 .答案： D2、（广东卷）将正三棱柱截去三个角（如图1 所示 A ，B ，C 分别是 △GHI 三边的中点）获得几何体如图2，则该几何体按图 2 所示方向的侧视图（或称左视图）为（ ）HAGABBBBBC 侧视BCIEDEDEEEEF F A ．B ．C ．D ．图 1图 2【分析 】解题时在图 2 的右侧放扇墙 (心中有墙 ),可得答案 A.答案： A3、（海南、 宁夏理科卷） 某几何体的一条棱长为 7 ，在该几何体的正视图中， 这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中， 这条棱的投影分别是长为 a 和 b 的线段，则 a+b 的最大值为（）A ．2 2B ．2 3C ． 4D ．2 5【分析 】联合长方体的对角线在三个面的投影来理解计算。

如图设长方体的高宽高分别为m, n, k ，由题意得m2n2k27 ， m2k26 n 1k n1 k 2a ， 1m 2 b ，所以 (a 21) (b 2 1) 6ma 2b 28，∴ (a b)2a 2 2abb 28 2ab8 a 2 b 2 16a b 4 当且仅当 a b 2 时取等。

答案： C4、（海南、宁夏理科卷）一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的极点都在同一 个球面上，且该六棱柱的体积为9，底面周长为 3，则这个球的体积为．8【 解 析 】 令 球 的 半 径 为 R ， 六 棱 柱 的 底 面 边 长 为 a ， 高 为 h ， 显 然 有a 2( h ) 2R ， 且2V 63 a 2 h 9a 1 4 342R 148VR6a 3h333答案：435、（海南、宁夏文科卷）一个六棱柱的底面是正六边形，其侧棱垂直底面。

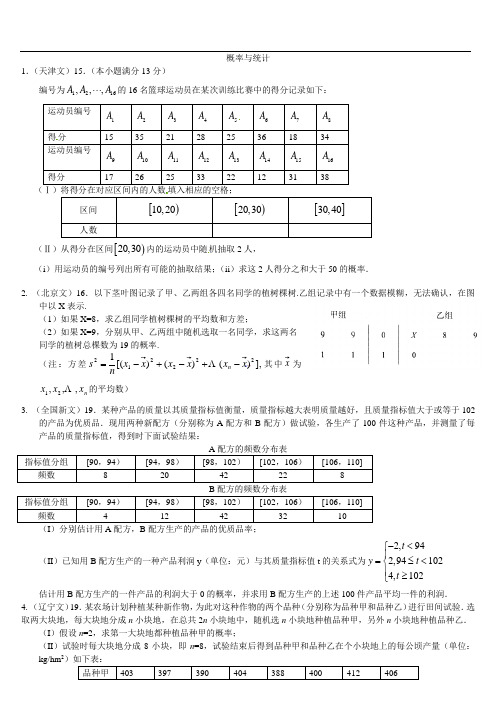
概率与统计1．（天津文）15．（本小题满分13分）编号为1216,,,A A A ⋅⋅⋅的16名篮球运动员在某次训练比赛中的得分记录如下： 运动员编号 1A2A3A4A5A6A7A8A得分 1535212825361834运动员编号 9A10A11A12A13A14A15A16A得分1726253322123138（Ⅰ）将得分在对应区间内的人数填入相应的空格；区间 [)10,20[)20,30[]30,40人数（Ⅱ）从得分在区间[)20,30内的运动员中随机抽取2人，（i ）用运动员的编号列出所有可能的抽取结果；（ii ）求这2人得分之和大于50的概率．2. （北京文）16．以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊，无法确认，在图中以X 表示. （1）如果X=8，求乙组同学植树棵树的平均数和方差；（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率. （注：方差],)()()[(1222212x x x x x x ns n -+-+-=其中x 为n x x x ,,,21 的平均数）3. （全国新文）19．某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A 配方和B 配方）做试验，各生产了100件这种产品，并测量了每产品的质量指标值，得到时下面试验结果：A 配方的频数分布表 指标值分组 [90，94）[94，98）[98，102）[102，106）[106，110]频数 8 20 42 22 8 B 配方的频数分布表指标值分组 [90，94）[94，98）[98，102）[102，106）[106，110]频数 412423210（I ）分别估计用A 配方，B 配方生产的产品的优质品率；（II ）已知用B 配方生产的一种产品利润y （单位：元）与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤<⎨⎪≥⎩估计用B 配方生产的一件产品的利润大于0的概率，并求用B 配方生产的上述100件产品平均一件的利润． 4. （辽宁文）19．某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成n 小块地，在总共2n 小块地中，随机选n 小块地种植品种甲，另外n 小块地种植品种乙．（I ）假设n =2，求第一大块地都种植品种甲的概率；（II ）试验时每大块地分成8小块，即n =8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm 2）如下表：品种甲 403 397 390 404 388 400 412 406 品种乙419403412418408423400413分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？ 附：样本数据n x x x ,,,21⋅⋅⋅的的样本方差])()()[(1222212x x x x x x ns n -+⋅⋅⋅+-+-=，其中x 为样本平均数．5. （江西文）16．某饮料公司对一名员工进行测试以便确定考评级别，公司准备了两种不同的饮料共5杯，其颜色完全相同，并且其中的3杯为A 饮料，另外的2杯为B 饮料，公司要求此员工一一品尝后，从5杯饮料中选出3杯A 饮料。

03 立体几何1. （2011天津卷理）17．（本小题满分13分）如图，在三棱柱111ABC A B C -中，H 是正方形11AA B B的中心，1AA =1C H ⊥平面11AAB B ，且1C H = （Ⅰ）求异面直线AC 与A 1B 1所成角的余弦值； （Ⅱ）求二面角111A AC B --的正弦值； （Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B内，且MN ⊥平面11A B C ，求线段BM 的长．【解析】17．本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识，考查用空间向量解决立体几何问题的方法，考查空间想象能力、运算能力和推理论证能力.满分13分.方法一：如图所示，建立空间直角坐标系，点B 为坐标原点.依题意得(0,0,0),A B C 11(2,0),,22,2,5)A B（I ）解：易得11((AC AB ==- ， 于是111111cos ,3||||AC A B AC A B AC A B ⋅===⋅所以异面直线AC 与A 1B 1所成角的余弦值为3（II ）解：易知111(AA AC ==设平面AA 1C 1的法向量(,,)m x y z =，则11100m AC m AA ⎧⋅=⎪⎨⋅=⎪⎩即0,0.⎧-+=⎪⎨=⎪⎩不妨令x 可得m =， 同样地，设平面A 1B 1C 1的法向量(,,)n x y z =，则11110,0.n AC n A B ⎧⋅=⎪⎨⋅=⎪⎩即0,0.⎧-+=⎪⎨-=⎪⎩不妨令y = 可得n =于是2cos ,,||||7m n m n m n ⋅===⋅从而sin ,m n =所以二面角A —A 1C 1—B（III ）解：由N 为棱B 1C 1的中点，得(,222N 设M （a ，b ，0），则(,22MN a b =--由MN ⊥平面A 1B 1C 1，得11110,0.MN A B MN A C ⎧⋅=⎪⎨⋅=⎪⎩即()(0,2()(()(0.22a a b ⎧-⋅-=⎪⎪⎨⎪-⋅+-⋅+⎪⎩解得24a b ⎧=⎪⎪⎨⎪=⎪⎩故(24M因此BM = ，所以线段BM的长为||BM =方法二：（I ）解：由于AC//A 1C 1，故111C A B ∠是异面直线AC 与A 1B 1所成的角. 因为1C H ⊥平面AA 1B 1B ，又H 为正方形AA 1B 1B 的中心，11AA C H ==可得1111 3.AC B C ==因此2221111111111111cos 2AC A B B C C A B AC A B +-∠==⋅所以异面直线AC 与A 1B 1所成角的余弦值为3（II ）解：连接AC 1，易知AC 1=B 1C 1， 又由于AA 1=B 1A 1，A 1C 1=A 1=C 1，所以11AC A ∆≌11BC A ∆，过点A 作11AR AC ⊥于点R ，连接B 1R ，于是111B R AC ⊥，故1ARB ∠为二面角A —A 1C 1—B 1的平面角. 在11Rt A RB ∆中，11111sin B R A B RA B =⋅∠== 连接AB 1，在1ARB ∆中，2221111114,,cos 2AR B R AB AB AR B R ARB AR B R+-==∠=⋅27=-，从而1sin ARB ∠=所以二面角A —A 1C 1—B 1的正弦值为7（III ）解：因为MN ⊥平面A 1B 1C 1，所以11.MN A B ⊥ 取HB 1中点D ，连接ND ，由于N 是棱B 1C 1中点， 所以ND//C 1H且112ND C H ==又1C H ⊥平面AA 1B 1B ，所以ND ⊥平面AA 1B 1B ，故11.ND A B ⊥ 又,MN ND N =所以11A B ⊥平面MND ，连接MD 并延长交A 1B 1于点E ， 则111,//.ME A B ME AA ⊥故 由1111111,4B E B D DE AA B A B A ===得1DE B E ==EM 交AB 于点F ，可得12BF B E ==连接NE. 在Rt ENM ∆中，2,.ND ME ND DE DM ⊥=⋅故所以24ND DM DE ==可得FM =连接BM ，在Rt BFM ∆中，BM ==2. （2011北京理）16．（本小题共14分） 如图，在四棱锥P ABCD -中，PA ⊥平面A B C D ，底面A B C D 是菱形，2,60AB BAD =∠= .(Ⅰ)求证：BD ⊥平面;PAC （Ⅱ）若,PA AB =求PB 与AC 所成角的余弦值；（Ⅲ）当平面PBC 与平面PDC 垂直时，求PA 的长.【解析】（16）（共14分） 证明：（Ⅰ）因为四边形ABCD 是菱形，所以AC ⊥BD.又因为PA ⊥平面ABCD. 所以PA ⊥BD.所以BD ⊥平面PAC. （Ⅱ）设AC∩BD=O. 因为∠BAD=60°，PA=PB=2,所以BO=1，AO=CO=3.如图，以O 为坐标原点，建立空间直角坐标系O —xyz ，则P （0，—3，2），A （0，—3，0），B （1，0，0），C （0，3，0）. 所以).0,32,0(),2,3,1(=-=AC PB 设PB 与AC 所成角为θ，则4632226cos =⨯=. （Ⅲ）由（Ⅱ）知).0,3,1(-= 设P （0，－3，t ）（t>0）， 则),3,1(t BP --=设平面PBC 的法向量),,(z y x m =, 则0,0=⋅=⋅m m所以⎪⎩⎪⎨⎧-+--=+-03,03tz y x y x 令,3=y 则.6,3t z x ==所以)6,3,3(tm =同理，平面PDC 的法向量)6,3,3(tn -=因为平面PCB ⊥平面PDC, 所以n m ⋅=0，即03662=+-t 解得6=t 所以PA=6 3. （2011辽宁卷理）18．（本小题满分12分）如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA =AB =12P D ．（I ）证明：平面PQC ⊥平面DCQ ； （II ）求二面角Q —BP —C 的余弦值．【解析】18．解：如图，以D 为坐标原点，线段DA 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D —xyz. （I ）依题意有Q （1，1，0），C （0，0，1），P （0，2，0）.则(1,1,0),(0,0,1),(1,1,0).DQ DC PQ ===-所以0,0.PQ DQ PQ DC ⋅=⋅=即PQ ⊥DQ ，PQ ⊥DC. 故PQ ⊥平面DCQ.又PQ ⊂平面PQC ，所以平面PQC ⊥平面DCQ. …………6分（II ）依题意有B （1，0，1），(1,0),(12,1).C B B P ==--设(,,)n x y z =是平面PBC 的法向量，则0,0,20.0,n CB x x y z n BP ⎧⋅==⎧⎪⎨⎨-+-=⋅=⎩⎪⎩即 因此可取(0,1,2).n =--设m 是平面PBQ 的法向量，则0,0.m BP m PQ ⎧⋅=⎪⎨⋅=⎪⎩可取(1,1,1).cos ,m m n =<>=所以 故二面角Q —BP —C的余弦值为 ………………12分 4. （全国大纲卷理）19．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 如图，四棱锥S ABCD -中， AB CD ⊥,BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====．（Ⅰ）证明：SD SAB ⊥平面;（Ⅱ）求AB 与平面SBC 所成角的大小．【解析】19．解法一：（I ）取AB 中点E ，连结DE ，则四边形BCDE 为矩形，DE=CB=2， 连结SE，则,SE AB SE ⊥又SD=1，故222ED SE SD =+，所以DSE ∠为直角。

2011届高考模拟题（课标）分类汇编：立体几何1．（2011·朝阳期末）关于直线l ，m 及平面α，β，下列命题中正确的是 ( C )（A ）若//l α，m αβ=I ，则//l m ； （B ）若//l α，//m α，则//l m ； （C ）若l α⊥，//l β，则αβ⊥； （D ）若//l α，m l ⊥，则m α⊥．2．（2011·朝阳期末）如图，正方体1111ABCD A B C D -中， E ，F 分别为棱AB ，1CC 的中点，在平面11ADD A内且与平面1D EF 平行的直线( A )（A ）有无数条 （B ）有2条（C ）有1条 （D ）不存在 3．（2011·朝阳期末）都是边长为2的正三角形，俯视图半径为1的圆，则这个 几何体的体积为3. 4．（2011·朝阳期末）（本小题满分13分）如图，已知三棱柱111ABC A B C -中，1AA ⊥底面ABC ，2AC BC ==，14AA =，AB =M ，N 分别是棱1CC ，AB 中点.（Ⅰ）求证：CN ⊥平面11ABB A ； （Ⅱ）求证：//CN 平面1AMB ；（Ⅲ）求三棱锥1B AMN -的体积．A BCDA 1BC 1D 1EF正视图 侧视图BA B 1正视图俯视图（Ⅰ）证明：因为三棱柱111ABC A B C -中，1AA ⊥底面ABC又因为CN ⊂平面ABC ， 所以1AA CN ⊥. ………1分 因为2AC BC ==，N 是AB 中点，所以CN AB ⊥. ………………2分因为1AA AB A =I ， ………………3分 所以CN ⊥平面11ABB A ． …………4分（Ⅱ）证明：取1AB 的中点G ，连结MG ，NG ，因为N ，G 分别是棱AB ，1AB 中点，所以1//NG BB ，112NG BB =. 又因为1//CM BB ，112CM BB =，所以//CM NG ，CM NG =.所以四边形CNGM 是平行四边形. ……………6分 所以//CN MG . ……………………… 7分因为CN ⊄平面1AMB ，GM ⊂平面1AMB ， ………8分 所以//CN 平面1AMB ． …………9分（Ⅲ）由（Ⅱ）知GM ⊥平面1AB N . ……10分 所以11MN M N1144323B A AB V V --==⨯=… 13分5．(2011·丰台期末)若一个螺栓的底面是正六边形，它的正视图和俯视图 如图所示，则它的体积是( C ) A3225+π B．3225π C．3225π D．12825πABCA 1B 1C 1M NGAA 1BCDB 1C 1E 6．(2011·丰台期末) （本小题共13分）直三棱柱ABC -A 1B 1C 1中，AB =5，AC =4，BC =3，AA 1=4，D 是AB 的中点．（Ⅰ）求证：AC ⊥B 1C ； （Ⅱ）求证：AC 1∥平面B 1CD ；证明：（Ⅰ）在△ABC 中，因为 AB =5，AC =4，BC =3， 所以 AC ⊥BC ．因为 直三棱柱ABC -A 1B 1C 1，所以 C C 1⊥AC ． 因为 BC ∩AC =C ， 所以 AC ⊥平面B B 1C 1C ． 所以 AC ⊥B 1C ． ………………………7分 （Ⅱ）连结BC 1，交B 1C 于E ．因为 直三棱柱ABC -A 1B 1C 1，所以 侧面B B 1C 1C 为矩形，且E 为B 1C 中点．又D 是AB 中点，所以 DE 为△ABC 1的中位线， 所以 DE // AC 1． 因为 DE ⊂平面B 1CD ， AC 1⊄平面B 1CD ， 所以 AC 1∥平面B 1CD ．7.(2011·东莞期末) 把边长为1的正方形ABCD 沿对角线BD 折起，使得平面⊥ABD 平面CBD ，形成三棱锥ABD C -的正视图与俯视图如右图所示，则侧视图的面积为( D )A.21 B.22 C.42 D.41AA 1B CDB 1C 1在三棱锥ABC S -中，ABC ∆是边长为32的正三角形，平面SAC ⊥平面ABC ，2==SC SA ，M 、N 分别为AB 、SB 的中点。

2011年高考试题解析数学（文科）分项版08 立体几何一、选择题:1.(2011年高考安徽卷文科8)一个空间几何体得三视图如图所示，则该几何体的表面积为（A ） 48 (B)32+817 (C) 48+817 (D) 80 【答案】C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，下底为4，高为4，两底面积和为()12244242⨯+⨯=，四个侧面的面积为()44221724817++=+，所以几何体的表面积为48817+.故选C.【解题指导】：三视图还原很关键，每一个数据都要标注准确。

2．(2011年高考广东卷文科9)如图1-3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别为等边三角形、等腰三角形和菱形，则该几何体体积为（ ）A ．B ．C ．D ． 2【答案】C【解析】由题得该几何体是如图所示的四棱锥P-ABCD ，，棱锥的高，3232322131331233231222=⨯⨯⨯⨯⨯=∴=-=-==∴=-=V PO h AO 所以选择C.3．（2011年高考湖南卷文科4)设图１是某几何体的三视图，则该几何体的体积为A ．942π+ Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+ 答案：D解析：有三视图可知该几何体是一个长方体和球构成的组合体，其体积3439+332=18322V ππ=⨯⨯+（）。

4．（2011年高考湖北卷文科7)设球的体积为V 1,它的内接正方体的体积为V 2，下列说法中最合适的是A. V 1比V 2大约多一半B. V 1比V 2大约多两倍半C. V 1比V 2大约多一倍D. V 1比V 2大约多一倍半答案：D解析：设球半径为R ，其内接正方体棱长为a 2222a a a R ++=，即23,3a R =由 3 32正视图侧视图俯视图图13331248,339v R v a R π===，比较可得应选D.5.（2011年高考山东卷文科11)下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是(A)3 (B)2 (C)1 (D)0 【答案】A【解析】对于①,可以是放倒的三棱柱；容易判断②③可以.6.（2011年高考海南卷文科第8题）在一个几何体的三视图中，正视图和俯视图如右图，则相应的侧视图可以为（ ）解析：D. 由主视图和府视图可知，原几何体是由后面是半个圆锥，前面是三棱锥的组合体，所以，左视图是D 。

广东文科数学历届立体几何高考题集锦2011年广东文科数学9. 如图 1-3,某几何体的正视图(主视图 ,侧视图(左视图和俯视图分别是等边三角形等腰三角形和菱形,则该几何体体积为A. 4B.4C.32D.218. (本小题 13分如图所示的几何体是将高为 2,底面半径为 1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的 ., , , , ' ', , ' ' A A B B CD CD DE DE ''分别为的中点,' '1122, , , O O O O 分别是, ' ' , , C D C D D ED E的中点 . (1 2:', ', , O A O B 证明四点共面;(2 ' ' '111' ' ', O ' ' G AA AOH H AO =设为的中点,延长到使得 , 证明 :'2' ' . BO HBG ⊥平面2012年广东文科数学7. 某几何体的三视图如图 1所示,它的体积为( A. 72π B. 48π C. 30π D. 24π图 1正视图俯视图侧视图PABCFE图 518. (本小题满分 13分如图 5所示, 在四棱锥 P ABCD -中, AB ⊥平面 PAD , //AB CD , PD AD =, E 是PB 的中点, F 是 CD 上的点且 12DF AB=, PH 为△ PAD 中 AD 边上的高 . (1证明:PH ⊥平面 ABCD ;(2若 1PH =, AD =, 1FC =,求三棱锥 E BCF -的体积;(3证明:EF ⊥平面 PAB .解:(1证明:因为 AB ⊥平面 PAD所以 PH AB ⊥因为 PH 为△ PAD 中 AD 边上的高所以 PH AD ⊥因为 ABAD A =所以 PH ⊥平面 ABCD(2连结 BH ,取 BH 中点 G ,连结 EG 因为 E 是 PB 的中点,所以 //EG PH 因为 PH ⊥平面 ABCD所以 EG ⊥平面 ABCD则 1122EG PH ==111332E BC FB C FV S E G F C A D -∆=⋅=⋅⋅⋅⋅=(3证明:取 PA 中点 M ,连结 MD , ME 因为 E 是 PB 的中点,所以 1//2ME AB =因为 1//2DF AB =所以 //ME DF =所以四边形 MEDF 是平行四边形所以 //EF MD 因为 PD AD = 所以 MD PA ⊥因为 AB ⊥平面 PADPABCEM所以 MD AB ⊥因为 PAAB A =所以 MD ⊥平面 PAB 所以 EF ⊥平面 PAB2013年广东文科数学6. 某三棱锥的三视图如图 2所示,则该三棱锥的体积是(A. 16B. 13C. 23D. 18. 设 l 为直线, , αβ是两个不同的平面,下列命题中正确的是( A. 若//, //l l αβ,则//αβ,则//αβ B. 若, l l αβ⊥⊥,则//αβ C. 若, //l l αβ⊥,则//αβ D. 若, //l αβα⊥,则l β⊥18. (本题满分 14分如图 4,在边长为 1的等边三角形 ABC 中, D,E, 分别为AB,AC 上的点, AD=AE, F 是 BC 的中点, AF 与 DE 交于点 G ,将△ ABF 沿 AF 折起,得到如图 5所示的三棱锥 A-BCF,其中 2BC =。

2011年高考试题解析数学（文科）分项版08 立体几何一、选择题:1.(2011年高考安徽卷文科8)一个空间几何体得三视图如图所示，则该几何体的表面积为（A ） 48 (D) 80 【答案】C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，下底为4，高为4，两底面积和为()12244242⨯+⨯=，四个侧面的面积为(44224++=+，所以几何体的表面积为48+故选C.【解题指导】：三视图还原很关键，每一个数据都要标注准确。

2．(2011年高考广东卷文科9)如图1-3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别为等边三角形、等腰三角形和菱形，则该几何体体积为（ ）A． B ． C ． D ． 2【答案】C【解析】由题得该几何体是如图所示的四棱锥P-ABCD ，，棱锥的高，3232322131331233231222=⨯⨯⨯⨯⨯=∴=-=-==∴=-=V PO h AO 所以选择C.3．（2011年高考湖南卷文科4)设图１是某几何体的三视图，则该几何体的体积为A ．942π+ Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+ 答案：D解析：有三视图可知该几何体是一个长方体和球构成的组合体，其体积3439+332=18322V ππ=⨯⨯+（）。

4．（2011年高考湖北卷文科7)设球的体积为V 1,它的内接正方体的体积为V 2，下列说法中最合适的是A. V 1比V 2大约多一半B. V 1比V 2大约多两倍半C. V 1比V 2大约多一倍D. V 1比V 2大约多一倍半答案：D正视图侧视图俯视图图1解析：设球半径为R ，其内接正方体棱长为a2R =，即,a =由333124,3v R v a π==，比较可得应选D.5.（2011年高考山东卷文科11)下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是(A)3 (B)2 (C)1 (D)0 【答案】A【解析】对于①,可以是放倒的三棱柱；容易判断②③可以.6.（2011年高考海南卷文科第8题）在一个几何体的三视图中，正视图和俯视图如右图，则相应的侧视图可以为（ ）解析：D. 由主视图和府视图可知，原几何体是由后面是半个圆锥，前面是三棱锥的组合体，所以，左视图是D 。

2011年最新高考+最新模拟——立体几何1.【2010·浙江理数】设，是两条不同的直线，是一个平面，则下列命题正确的是（）A.若，，则B.若，，则C.若，，则D.若，，则【答案】B【解析】可对选项进行逐个检查.本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察，属中档题.2.【2010·全国卷2理数】与正方体的三条棱、、所在直线的距离相等的点（）A.有且只有1个B.有且只有2个C.有且只有3个D.有无数个【答案】D【解析】直线上取一点，分别作垂直于于则分别作，垂足分别为M，N，Q，连PM，PN，PQ，由三垂线定理可得，PN⊥PM⊥；PQ⊥AB，由于正方体中各个表面、对等角全等，所以，∴PM=PN=PQ，即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件，故选D.3.【2010·全国卷2理数】已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为（）A.1B.C.2D.3【答案】C【解析】本试题主要考察椎体的体积，考察告辞函数的最值问题.设底面边长为a，则高所以体积，设，则，当y取最值时，，解得a=0或a=4时，体积最大，此时，故选C.4.【2010·陕西文数】若某空间几何体的三视图如图所示，则该几何体的体积是（）A.2B.1C.D.【答案】B【解析】本题考查立体图形三视图及体积公式如图，该立体图形为直三棱柱,所以其体积为.5.【2010·辽宁文数】已知是球表面上的点，，，，，则球的表面积等于（）A.4B.3C.2D.【答案】A【解析】由已知，球的直径为，表面积为6.【2010·辽宁理数】有四根长都为2的直铁条，若再选两根长都为a的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a的取值范围是（）A.（0,）B.（1,）C.(,）D.（0,）【答案】A【解析】本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力.根据条件，四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架，有以下两种情况：（1）地面是边长为2的正三角形，三条侧棱长为2，a，a，如图，此时a可以取最大值，可知AD=，SD=，则有<2+，即，即有a<(2)构成三棱锥的两条对角线长为a，其他各边长为2，如图所示，此时a>0;综上分析可知a∈（0,）7.【2010·全国卷2文数】与正方体ABCD—A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点（）A.有且只有1个B.有且只有2个C.有且只有3个D.有无数个【答案】D【解析】本题考查了空间想象能力.∵到三条两垂直的直线距离相等的点在以三条直线为轴，以正方体边长为半径的圆柱面上，∴三个圆柱面有无数个交点.8.【2010·全国卷2文数】已知三棱锥中，底面为边长等于2的等边三角形，垂直于底面，=3，那么直线与平面所成角的正弦值为（）A. B. C.D.【答案】D【解析】本题考查了立体几何的线与面、面与面位置关系及直线与平面所成角.过A作AE垂直于BC交BC于E，连结SE，过A作AF垂直于SE交SE于F，连BF，∵正三角形ABC，∴ E为BC中点，∵ BC⊥AE，SA⊥BC，∴ BC⊥面SAE，∴ BC⊥AF，AF⊥SE，∴ AF⊥面SBC，∵∠ABF为直线AB与面SBC所成角，由正三角形边长3，∴，AS=3，∴ SE=，AF=，∴.9.【2010·江西理数】过正方体的顶点A作直线L，使L与棱,,所成的角都相等，这样的直线L可以作（）A.1条B.2条C.3条D.4条【答案】D【解析】考查空间感和线线夹角的计算和判断，重点考查学生分类、划归转第二类：化的能力.第一类：通过点A位于三条棱之间的直线有一条体对角线AC1，在图形外部和每条棱的外角和另2条棱夹角相等，有3条，合计4条.10.【2010·安徽文数】一个几何体的三视图如图，该几何体的表面积是（）A.372B.360C.292D.280【答案】B【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和. 把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体，画出直观图，得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和..11.【2010·重庆文数】到两互相垂直的异面直线的距离相等的点（）A.只有1个B.恰有3个C.恰有4个D.有无穷多个【答案】D【解析】放在正方体中研究,显然，线段、EF、FG、GH、HE的中点到两垂直异面直线AB、CD的距离都相等，所以排除A、B、C，选D.亦可在四条侧棱上找到四个点到两垂直异面直线AB、CD的距离相等.12.【2010·浙江文数】若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（）A.cm3B.cm3C.cm3D.cm3【答案】B【解析】本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算，属容易题.13.【2010·山东文数】在空间，下列命题正确的是（）A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行【答案】D14.【2010·北京文数】如图，正方体的棱长为2，动点E、F 在棱上.点Q是CD的中点，动点P在棱AD上，若EF=1，DP=x，E=y(x,y 大于零)，则三棱锥P-EFQ的体积（）A.与x，y都有关；B.与x，y都无关；C.与x有关，与y无关；D.与y有关，与x无关；【答案】C15.【2010·北京文数】一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该集合体的俯视图为：（）【答案】C16.【2010·北京理数】如图，正方体ABCD-的棱长为2，动点E、F在棱上，动点P，Q分别在棱AD，CD上，若EF=1，E=x，DQ=y，DＰ＝ｚ（ｘ，ｙ，ｚ大于零），则四面体PEＦＱ的体积（）Ａ.与ｘ，ｙ，ｚ都有关Ｂ.与ｘ有关，与ｙ，ｚ无关Ｃ.与ｙ有关，与ｘ，ｚ无关Ｄ.与ｚ有关，与ｘ，ｙ无关【答案】D17.【2010·四川理数】半径为的球的直径垂直于平面，垂足为，是平面内边长为的正三角形，线段、分别与球面交于点M，N，那么M、N两点间的球面距离是（）A. B.C. D.【答案】A【解析】由已知，AB＝2R,BC＝R,故tan∠BAC＝，cos∠BAC＝，连结OM，则△OAM为等腰三角形，AM＝2AOcos∠BAC＝，同理AN＝，且MN∥CD ，而AC＝R,CD＝R，故MN：CD＝AN:AC MN＝，连结OM、ON，有OM＝ON＝R，于是cos∠MON＝，所以M、N两点间的球面距离是 .18.【2010·广东理数】如图1，△ ABC为三角形，////,⊥平面ABC 且3== =AB,则多面体△ABC -的正视图（也称主视图）是【答案】D19.【2010·广东文数】20.【2010·福建文数】若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )A． B．2C． D．6【答案】D【解析】本题考查立体几何中的三视图，考查同学们识图的能力、空间想象能力等基本能力.由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，所以底面积为，侧面积为，选D．21.【2010·全国卷1文数】已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2,则四面体ABCD的体积的最大值为（）A. B. C. D.【答案】B【解析】本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.过CD作平面PCD，使AB⊥平面PCD,交AB与P,设点P到CD的距离为,则有,当直径通过AB与CD的中点时,,故.22.【2010·全国卷1文数】正方体-中，与平面所成角的余弦值为（）A. B. C. D.【答案】D【解析】本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法，利用等体积转化求出D到平面AC的距离是解决本题的关键所在,这也是转化思想的具体体现.方法一：因为BB1//DD1,所以B与平面AC所成角和DD1与平面AC所成角相等,设DO⊥平面AC，由等体积法得,即.设DD1=a,则,.所以,记DD与平面AC所成角为,则1,所以.方法二：设上下底面的中心分别为；与平面AC所成角就是B与平面AC所成角，.23.【2010·全国卷1文数】直三棱柱中，若，，则异面直线与所成的角等于（）A.30°B.45°C.60°D.90°【答案】C【解析】本小题主要考查直三棱柱的性质、异面直线所成的角、异面直线所成的角的求法.延长CA到D，使得，则为平行四边形，就是异面直线与所成的角，又三角形为等边三角形，.24.【2010·湖北文数】用、、表示三条不同的直线，表示平面，给出下列命题：①若∥，∥，则∥；②若⊥，⊥，则⊥；③若∥，∥，则∥；④若⊥，⊥，则∥.A. ①②B. ②③C. ①④ D.③④25.【2010·山东理数】在空间，下列命题正确的是（）A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行【答案】D【解析】考查空间直线与平面的位置关系及线面垂直与平行的判定与性质，属基础题.由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案.26.【2010·福建理数】所以∥，故∥∥，所以选项A、C正确；因为平面，∥，所以平面，又平面，故，所以选项B也正确，故选D.【命题意图】本题考查空间中直线与平面平行、垂直的判定与性质，考查同学们的空间想象能力和逻辑推理能力.27.【2010·湖北省武汉市四月调研】若a、b是异面直线，、是两个不同平面，，则（）A．l与a、b分别相交 B．l与a、b都不相交C．l至多与a、b中一条相交 D．l至少与a、b中的一条相交【答案】B【解析】假设l与a、b均不相交，则l∥a，l∥b，从而a∥b与a、b是异面直线矛盾.故l至少与a、b中的一条相交选D.28．【2010·北京西城一模】如图，平面平面，=直线，是内不同的两点，是内不同的两点，且直线，分别是线段的中点．下列判断正确的是（）A．当时，两点不可能重合B．两点可能重合，但此时直线与不可能相交C．当与相交，直线平行于时，直线可以与相交D．当是异面直线时，直线可能与平行【答案】B【解析】若两点重合，由知，从而平面，故有，故B正确．29．【2010·宁波市二模】已知表示两个互相垂直的平面，表示一对异面直线，则的一个充分条件是（）A. B. C. D.【答案】D选择【解析】依题意，a⊥α ,则a平行β或在β内，由于b⊥β，则，D.30．【2010·上海市浦东新区4月二模】“直线与平面没有公共点”是“直线与平面平行”的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】C【解析】由直线与平面平行的定义知，选C.31．【2010··北京崇文一模】已知是两条不同直线，是三个不同平面，下列命题中正确的为 ( )A．若则 B．若则C．若，则 D．若则【答案】B【解析】A中可以是任意关系；B正确；C中平行于同一平面，其位置关系可以为任意．D中平行于同一直线的平面可以相交或者平行．32.【2010·甘肃省部分普通高中第二次联合考试】已知直线,平面,且,给出下列命题:①若∥，则m⊥；②若⊥，则m∥;③若m⊥，则∥；④若m∥，则⊥其中正确命题的个数是（）A．1 B．2 C．3D．4【答案】B①正确；对【解析】对于①∵，若∥，∴m⊥β，所以m⊥，于②，若⊥，则m∥β或m在β内，m与l可以平行可以异面还可以相交，所以②错；对于③∵，若m⊥，则与β可以相交，③错；对于④若m ∥，则l⊥，∴⊥，④正确，选择B.33.【2010·湖北六市四月联考】给出互不相同的直线、、和平面、，下列四个命题：①若，，，则与不共面；②若、是异面直线，，，且，，则；③若，，，，，则；④若，，，则其中真命题有（）A.4个B.3个C.2个 D.1个【答案】B【解析】由异面直线的判定定理，易知①是真命题；由线面平行的性质，存在直线，，使得，，∵、是异面直线，∴与是相交直线，又，，∴，，故，②是真命题；由线面平行的性质和判定，知③是真命题；满足条件，，的直线、或相交或平行或异面，故④是假命题，于是选B.34.【2010•河南省郑州市第二次质检】已知α，β，γ是三个不同的平面，命题“α∥β，且α⊥γβ⊥γ”是真命题．如果把α，β，γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有（）A．0个 B．1个 C．2个 D．3个【答案】C【解析】依题意,α与β换成直线后是真命题，γ与β换成直线后是真命题，γ与α换成直线后是假命题，选择C.35．【2010•宁波二模】已知表示两个互相垂直的平面，表示一对异面直线，则的一个充分条件是（）A. B. C. D.【答案】D选择【解析】依题意，a⊥α ,则a平行β或在β内，由于b⊥β，则，D.36．【2010•绵阳三诊】已知，表示两个不同的平面，是一条直线且，则：“”是“”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】若，因是一条直线且，由面面垂直的判定定理，知，反之，若是一条直线且，当时，与平面的位置关系可以为：相交或平行或，故“”是“”的必要不充分条件，选B.37．【2010·吉林市下学期期末质量检测】已知a，b表示两条不同的直线，α、β表示两个不同的平面，则下列命题中正确的是（）A．若B．若所成角等于b与β所成角，则a//b.C．若D．若【答案】D【解析】对于选项A：直线a，b可能平行或异面；对于选项B：只有当平面α与β平行时，才有a//b，故B不对；对于选项C，有可能直线b在平面β内，故C错；故选D.38．【2010·山东德州五月质检】在空间中，给出下面四个命题：(1)过一点有且只有一个平面与已知直线垂直；(2)若平面外两点到平面的距离相等，则过两点的直线必平行于该平面；(3)两条相交直线在同一平面的射影必为相交直线；(4)两个相互垂直的平面，一个平面内的任意一直线必垂直于另一平面内的无数条直线.其中正确的是( )A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)【答案】D【解析】对于(2)可能该直线与平面相交；对于(3)可能两相交直线的射影为一条直线或一点与过该点的一条直线,故选D.39．【2010·江西省重点中学第二次联考】已知一个确定的二面角，和是空间的两条异面直线，在下面给出的四个条件中，能使和所成的角也确定的是（）A．∥且∥ B．∥且C．且 D．且【答案】D【解析】因为二面角的大小是确定的，所以当且时，和所成的角与二面角的大小相等或互补，故而和所成的角也确定,选D.40．【2010·崇文一模】已知是两条不同直线，是三个不同平面，下列命题中正确的为 ( )A．若则 B．若则C．若，则 D．若则【答案】D【解析】A中，垂直于同一平面的平面可能平行或者相交；B中，平行于同一直线的平面可能平行或者相交；C中，平行于同一平面的直线可能是任意关系；D中，垂直于同一平面的直线平行,正确．41．【2010·上海市长宁区二次模】已知α，β表示两个不同的平面，m为平面α内的一条直线，则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】根据是平面与平面垂直的判定定理知：由m⊥βα⊥β，反之不成立.故选B.42．【2010·河北省衡水中学一模】正四棱锥P—ABCD的底面积为3，体积为E为侧棱PC的中点，则PA与BE所成的角为( )A．B． C．D．【答案】B【解析】由V==×3×h，所以h=，从而侧棱长PA=，取AC中点O，连OE，则OE∥PA，且OE=，于是∠OEB为异面直线PA与BE所成的角或其补角.在直角三角形BOE中，BO=，所以tan∠OEB=，所以∠OEB=.43．【2010·湖北省襄樊五中5月调研测试】如图，正三棱锥A-BCD中，E在棱AB上，F在棱CD上．并且==λ（0＜λ<＋∞)，设α为异面直线EF与AC所成的角，β为异面直线EF与BD所成的角，则α＋β的值是（）A． B． C．D．与λ的值有关【答案】C【解析】利用特殊化思想，当λ=1，即E、F分别为AB、CD中点时，取BC中点M，则EM∥AC,FM∥BD,又AC⊥BD，所以三角形EMF为直角三角形，所以α＋β=.44．【2010·甘肃省兰州市五月实战模拟】二面角，A，B是棱l 上的两点，AC，BD分别在平面内，AC⊥l，BD⊥l，且AC=AB=1，BD=2，则CD 的长等于（）A．2 B．C． D．【答案】A【解析】过B作BE∥AC，且BE=1，则∠DBE=60°，从而DE==，在三角形CDE 中，CD==2.45．【2010·泸州二诊】如图，在正三棱柱中，.若二面角的大小为，则点到平面的距离为（）A. B. C. D.【答案】A【解析】取中点，连结，，则是二面角的平面角. ∵，∴，∴在中，，，设点到平面的距离为，则由得，，解得，选A.46．【2010·湖北省年普通高等学校招生全国统一考试模拟训练（二）】如图，在直三棱柱ABC-A1B1C1中，AB＝1，AC＝2，BC＝，D，E分别是AC1和BB1的中点，则直线DE与平面BB1C1C所成的角为（）A． B． C． D．【答案】A【解析】取AC中点F，连DF，BF，则易知BF∥DE，过F作FH⊥BC于H，则FH⊥平面BCC1B1，则角∠FBH为所求，在直角三角形FHB中，FH=,BF=AC=1，所以∠FBH=30°.47．【2010·湖南师大附中第二次月考试卷】如图，在正三棱柱ABC－A1B 1 C1中，点M为侧棱AA1上一动点，已知△BCM面积的最大值是，二面角M―BC―A 的最大值是，则该三棱柱的体积等于（）A. B. C.D.【答案】A【解析】当点M与点A1重合时，△BCM的面积为最大值，此时二面角M―BC―A也为最大.由已知可得，，所以底面正三角形ABC 的边长为2，高为，从而正三棱柱的高AA1＝.所以正三棱柱的体积，故选A.48．【2010·曲靖一中高考冲刺卷数学（八）】如图，正方体中，M,N分别为AB,DC中点，则直线MC与所成角的余弦值为（）A. B. C. D.【答案】B【解析】连NA，D1A，则∠D1NA为所求，在三角形D1NA中由余弦定理可求得cos∠D1NA=.49．【2010·曲靖一中高考冲刺卷数学（四）】一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是那么这个三棱柱的体积是（）A. B. C. D.【答案】D【解析】因为球的体积为π，柱体的高为2r=4，又正三棱柱的底面三角形内=×(4)2×4=.切圆半径与球半径相等，r=2，所以底面边长a=4,所以V柱50.【2010·内蒙古赤峰市四月统一考试】已知正三棱锥的侧棱长是底面边长的2倍，则侧棱与底面所成角的余弦值等于（）A. B. C. D .【答案】A【解析】设底面边长AB=1，则侧棱长SA=2，过顶点S作底面的垂线，垂足O 为底面中心，连结AO，则∠SAO为所求，因为AO=,所以cos∠SAO==.51．【2010·上海市奉贤区4月调研】已知一球半径为2，球面上A、B两点的球面距离为,则线段AB的长度为（）A.1B.C.2D. 2【答案】C【解析】由l=αR=α×2=得，α=，从而知∠AOB=，即△AOB为正三角形，所以AB=OA=R=2.52．【2010·石家庄市教学质量检测（二）】如图，在正三棱锥A-BCD中，E、F分别是AB、BC的中点，EF⊥DE，且BC=1，则正三棱锥A-BCD的体积是（）A. B. C. D.【答案】B【解析】EF∥AC，所以AC⊥DE，又AC⊥BD，所以AC⊥平面ABD，所以侧面三角形为等腰直角三角形，AB=AC=AD=，V=×()3=.53.【2010·甘肃省部分普通高中高三第二次联合考试】如图，在半径为3的球面上有三点，，球心到平面的距离是，则两点的球面距离是（）A．B．C． D．【答案】B【解析】取AC中点H，连OH，则OH垂直于平面ABC，又OA=3，所以AC=2AH=CH=2×=3,又，BC=3，从而三角形OBC为正三角形，∠BOC=60°，所以球面距离为l=×3=.54．【2010·成都石室中学高三“三诊”模拟考试】如图所示，在正三棱锥S—ABC中，M、N分别是SC、BC的中点，且，若侧棱则正三棱锥S—ABC外接球的表面积是（）A．12π B．32π C．36π D．48π【答案】C【解析】因为MN⊥AM，所以SB⊥AM，又SB⊥AC，所以侧面三角形为等腰直角三角形，所以SA=SB=SC=2，所以2R=×(2)=6，所以S=π(2R)2=36π.55．【河南省郑州市2010年高中毕业班第二次质量预测】过球的一条半径的中点作垂直于这条半径的球的截面，则此截面面积是球表面积的（）A． B． C．D．【答案】B【解析】易求得截面圆半径为球半径的倍，所以==.56．【2010·唐山三模】一个与球心距离为1的平面截球所得的圆面面积为4π，则球的表面积为( )A.5πB.17πC.20π D.68π【答案】C【解析】截面圆的半径为2，所以球半径R==，所以S=20π.57．【2010·成都市第37中学五月考前模拟】如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且均为正三角形，EF∥AB，EF=2，则该多面体的体积为（）A. B. C. D.【答案】A【解析】过A、B两点分别作AM、BN垂直于EF，垂足分别为M、N，连结DM、CN，可证得DM⊥EF、CN⊥EF，多面体ABCDEF分为三部分，多面体的体积V为，∵，，∴，作NH垂直于点H，则H为BC的中点，则，∴，∴，， ，∴，故选A ．58.【2010·内蒙古赤峰市一模】四面体ABCD 的外接球球心在CD 上，且CD=2，.在外接球球面上A 、B 两点间的球面距离是（ ）A ．B ．C ．D ．【答案】C【解析】由题意知半径R=1，所以∠AOB=，从而球面距离为l=×1=.59．【2010·江西赣州十一县（市）第二学期期中联考】棱长为1的正方体的8个顶点都在球O 的表面上，E 、F 分别是棱AB 、的中点，则经过E 、F 的球截面的面积最小值是（ ） A ． B ． C ． D ．【答案】C【解析】当截面圆的圆心在直线EF上时，其面积最小.因为EF=，可求得球心O到直线EF的距离为，所以截面圆的半径r===，所以S=.60.【2010·上海文数】已知四棱椎的底面是边长为6 的正方形，侧棱底面，且，则该四棱椎的体积是.【答案】96【解析】考查棱锥体积公式.61.【2010·湖南文数】图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm.【答案】462.【2010·浙江理数】若某几何体的三视图（单位：cm）如上图（右）所示，则此几何体的体积是___________.【答案】144【解析】图为一四棱台和长方体的组合体的三视图，由卷中所给公式计算得体积为144，本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算，属容易题.63.【2010·辽宁理数】如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为___ ___.【答案】【解析】本题考查了三视图视角下多面体棱长的最值问题，考查了同学们的识图能力以及由三视图还原物体的能力.由三视图可知，此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥，所以最长棱长为.64.【2010·江西理数】如图，在三棱锥中，三条棱，，两两垂直，且>>,分别经过三条棱，，作一个截面平分三棱锥的体积，截面面积依次为，，，则，，的大小关系为 .【答案】【解析】考查立体图形的空间感和数学知识的运用能力，通过补形，借助长方体验证结论，特殊化，令边长为1，2，3得.65.【2010·北京文数】如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p（x，y）的纵坐标与横坐标的函数关系是，则的最小正周期为；在其两个相邻零点间的图像与x轴所围区域的面积为 .【答案】4【解析】“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动是指以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续，类似地，正方形PABC可以沿着x轴负方向滚动.66.【2010`四川理数】如图，二面角的大小是60°，线段.，与所成的角为30°.则与平面所成的角的正弦值是 .【答案】【解析】过点A作平面β的垂线，垂足为C，在β内过C作l的垂线.垂足为D，连结AD，由三垂线定理可知AD⊥l，故∠ADC为二面角的平面角，为60°，又由已知，∠ABD＝30°，连结CB，则∠ABC为与平面所成的角，设AD＝2，则AC＝，CD＝1，AB＝＝4，∴sin∠ABC＝.67.【2010·天津文数】一个几何体的三视图如图所示，则这个几何体的体积为 .【答案】3【解析】本题主要考查三视图的基础知识，和主题体积的计算，属于容易题. 正视图和侧视图的高是几何体的高，由俯视图可以确定几何体底面的形状，本题也可以将几何体看作是底面是长为3，宽为2，高为1的长方体的一半.由俯视图可知该几何体的底面为直角梯形，则正视图和俯视图可知该几何体的高为1，结合三个试图可知该几何体是底面为直角梯形的直四棱柱，所以该几何题的体积为.68.【2010·天津理数】一个几何体的三视图如图所示，则这个几何体的体积为 .【答案】【解析】本题主要考查三视图的概念与柱体、椎体体积的计算，属于容易题.利用俯视图可以看出几何体底面的形状，结合正视图与侧视图便可得到几何体的形状，求锥体体积时不要丢掉哦.由三视图可知，该几何体为一个底面边长为1，高为2的正四棱柱与一个底面边长为2，高为1的正四棱锥组成的组合体，因为正巳灵珠的体积为2，正四棱锥的体积为，所以该几何体的体积V=2+= .69.【2010·湖北文数】圆柱形容器内盛有高度为3cm的水，若放入三个相同的珠（球的半么与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是__ __cm.【答案】4【解析】设球半径为r，则由可得,解得r=4.70.【2010·湖南理数】图3中的三个直角三角形是一个体积为20的几何体的三视图，则．71.【2010·福建理数】若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于．【答案】【解析】本题考查立体几何中的三视图，考查同学们识图的能力、空间想象能力等基本能力.由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，所以底面积为，侧面积为，所以其表面积为.72．【2010·甘肃省兰州市五月实战模拟】已知S—ABC是正四面体，M为AB 之中点，则SM与BC所成的角为 .【答案】arccos【解析】设正四面体边长为1，取AC中点N，则MN∥BC，∠SMN为异面直线SM与BC所成的角或其补角，且MN=，SM=SN=，由余弦定理可得cos∠SMN=.73．【2010·石家庄市质量检测（二）】如图，在底面边长为2的正三棱柱ABC-A1B1C1中，若二面角C1-AB-C的大小为60，则点C到平面ABC1的距离为．【答案】【解析】过点C作CD⊥AB交AB于D，连结C1D，则由三垂线定理知∠CDC1为二面角的平面角，则∠CDC1=60°.过点C作CH⊥C1D，交C1D于H，则CH⊥平面ABC1，故CH为所求，在三角形CC1D中，CD=,从而CC1=3，从而CH=.74．【2010·云南曲靖一中高考冲刺卷六】正四面体外接球的体积为，则点A到平面BCD的距离为__________________.【答案】【解析】V=，所以R=，过A作AH⊥平面BCD，则垂足为底面中心，则AH为所求.又由正四面体与外接球的关系知，AH=R=.75．【2010·上海市长宁区二模】棱长为a的正方体ABCD－A1B1C1D1的8个顶点都在球O的表面上，E、F分别是棱AA1、DD1的中点，则直线EF被球O截得的线段长是_________.【答案】a【解析】由题意知球心为正方体对角线的中点，球半径为a，球心到直线EF 的距离为，所以直线EF被球O截得的线段长l=2=a.76.【2010·邯郸市二模】三棱锥A—BCD，AB=a，CD=b，∠ABD=∠BDC，M，N 分别为AD，BC的中点，P为BD上一点，则MP+NP 的最小值是 .。