2015年中考专题复习测试题之一---二次函数复习测试题

中考数学总复习《二次函数压轴题（面积问题）》专题训练-附含答案学校：___________班级：___________姓名：___________考号：___________1．如图，在平面直角坐标系中，抛物线2y ax x c =-+与y 轴交于点()0,4A -，与x 轴交于点()4,0B ，连接AB .(1)求抛物线的解析式．(2)P 是AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点C ，过点P 作PD x ⊥轴于点D ．①求PC PD +的最大值．①连接PA ，PB ，是否存在点P ，使得线段PC 把PAB 的面积分成3:5两部分？若存在，请直接写出点P 的坐标；若不存在，请说明理由．2．综合与探究如图1，抛物线212y x bx c =-++经过点(4,0)B 和(0,2)C ，与x 轴的另一个交点为A ，连接AC ，BC ．(1)求该抛物线的解析式及点A 的坐标；(2)如图1，点D 是线段AC 的中点，连接BD ．点E 是抛物线上一点，若ABE BCD S S =△△，设点E 的横坐标为x ，请求出x 的值；(3)试探究在抛物线上是否存在一点P ，使得45PBO OBC ∠+∠=︒？若存在，请直接写出点P 的坐标；若不存在，请说明理由．3．如图抛物线2y ax bx c =++经过点()1,0A -，点()0,3C ，且OB OC =．(1)求抛物线的解析式及其对称轴；(2)点D 、E 是直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值．(3)点P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA 的面积分为3:5两部分，求点P 的坐标．4．已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ，与x 轴交于另一点B ，抛物线的顶点为D ．(1)求此二次函数解析式；(2)连接DC 、BC 和DB ，判断BCD △的形状并说明理由；(3)在对称轴右侧抛物线上找一点P ，使得P 、D 、C 构成以PC 为底边的等腰三角形，求出点P 的坐标及此时四边形PBCD 的面积．5．如图，抛物线214y x bx c =-++与x 轴交于点,A B 两点（点A 在点B 的右侧），点()()8,02,0A B -、，与y 轴交于点C ．(1)求抛物线的解析式； (2)点D 为抛物线的顶点，过点D 作DE AC ∥交抛物线于点E ，点P 为抛物线上点,D E 之间的一动点，连接,,,,AC AE AP CE CP ，线段,AP CE 交于点G ，记CPG △的面积为1,S AEG △的面积为2S ，且12S S S =-，求S 的最大值及此时点P 的坐标；(3)在（2）的条件下，将拋物线沿射线AC 方向平移5个单位长度后得到新抛物线，点Q 是新拋物线对称轴上一动点，在平面内确定一点R ，使得以点P Q B R 、、、为顶点的四边形是矩形．直接写出所有符合条件的点R 的坐标．6．如图，有一个长为30米的篱笆，一面利用墙（墙的最大可用长度18a =米）围成的中间隔有一道篱笆的长方形花圃设花圃的宽AB 为x 米，面积为y 平方米．(1)求y 与x 的函数关系式，并直接写出自变量x 的取值范围；(2)如何设计才能使长方形花圃面积最大；并求其最大面积．7．如图，过原点的抛物线212y x bx c =-++与x 轴的另一个交点为A ，且抛物线的对称轴为直线2x =，点B 为顶点(1)求抛物线的解析式(2)如图（1），点C 为直线OB 上方抛物线上一动点，连接AB，BC 和AC ，线段AC 交直线OB 于点E ，若CBE △的面积为1S ，ABE 的面积为2S ，求12S S 的最大值 (3)如图（2），设直线()20y kx k k =-≠与抛物线交于D ，F 两点，点D 关于直线2x =的对称点为D ，直线D F '与直线2x =交于点P ，求证：BP 的长是定值．8．抛物线2y x bx c =-++经过点A ，B ，C ，已知()1,0A -和()0,3C ．(1)求抛物线的解析式及顶点E 的坐标；(2)点D 在BC 上方的抛物线上．①如图1，若CAB ABD ∠=∠，求点D 的坐标；①如图2，直线BD 交y 轴于点N ，过点B 作AD 的平行线交y 轴于点M ，当点D 运动时，求CBD AMNS S △△的最大值及此时点D 的坐标． 9．在平面直角坐标系中，O 为坐标原点，抛物线244y ax ax =-+交x 轴于点A 、B （A 左B右），交y 轴于点C ，直线123y x =-+，经过B 点，交y 轴于点D ．(1)如图1，求a 的值；(2)如图2，点P 在第一象限内的抛物线上，过点A 、B 作x 轴的垂线，分别交直线PD 于点E 和F ，若PF DE =，求点P 的坐标；(3)如图3，在（2）的条件下，点Q 在第一象限内的抛物线上，过点Q 作QH DP ⊥于点H ，交直线BD 于点R ，连接EQ 和ER ，当QE ER =时，求ERQ △的面积．10．已知抛物线213222y x x =-++与x 轴交于B 、C 两点（点B 在点C 的左侧），与y 轴交于点A ．(1)判断ABC 的形状，并说明理由．(2)设点(,)P m n 是抛物线在第一象限部分上的点，过点P 作PH x ⊥轴于H ，交AC 于点Q ，设四边形OAPC 的面积为S ，求S 关于m 的函数关系式，并求使S 最大时点P 的坐标和QHC △的面积；(3)在（2）的条件下，点N 是坐标平面内一点，抛物线的对称轴上是否存在点M ，使得以P 、C 和M 、N 为顶点的四边形是菱形，若存在，写出点M 的坐标，并选择一个点写出过程，若不存在，请说明理由．11．已知，如图，在平面直角坐标系中，点O 为坐标原点，直线6y x =+与x 轴相交于点B ，与y 轴交于点C ，点A 是x 轴正半轴上一点，且满足2tan 3ACO ∠=．(1)若抛物线2y ax bx c =++经过A 、B 和C 三点，求抛物线的解析式；(2)若点M 是第二象限内抛物线上的一个动点，过点M 作MP y ∥轴，交BC 于点P ，连接OP ，在第一象限内找一点Q ，过点Q 作⊥OQ OP 且OQ OP =，连接PQ ，MQ ，设MPQ 的面积为S ，点P 的横坐标为t ，求S 与t 的函数关系式，并直接写出自变量的取值范围；(3)在（2）的条件下，设PQ 与y 轴相交于点R ，若53=PR PC 时，求点P 的坐标． 12．已知抛物线22y ax ax c =-+过点()10A -，和()03C ，，与x 轴交于另一点B ．(1)求抛物线的解析式；(2)若抛物线的顶点为D ，在直线BC 上方抛物线上有一点P （与D 不重合），BCP 面积与BCD △面积相等，求点P 的坐标；(3)若点E 为抛物线对称轴上一点，在平面内是否存在点F ，使得以E 、F 和B 、C 为顶点的四边形是菱形，若存在，请直接写出F 点的坐标；若不存在，请说明理由．13．如图，抛物线过点()08D ，，与x 轴交于()20A -，，()40B ，两点．(1)求抛物线的解析式；(2)若点C 为二次函数的顶点，求BCD S △．14．如图，O 为平面直角坐标系坐标原点，抛物线22y ax ax c =-+经过点()6,0B ，点()0,6C 与x 轴交于另一点A ．(1)求抛物线的解析式；(2)D 点为第一象限抛物线上一点，连接AD 和BD ，设点D 的横坐标为t ，ABD △的面积为S ，求S 关于t 的函数解析式（不要求写出自变量t 的取值范围）；(3)在（2）的条件下，P 为第四象限抛物线上一点，连接PA 交y 轴于点E ，点F 在线段BC 上，点G 在直线AD 上，若1tan 2DAO ∠=，四边形BEFG 为菱形，求点P 的坐标． 15．已知抛物线2()20y ax x c a =++≠与x 轴交于点(1,0)A -和点B ，与直线3y x =-+交于点B 和点C ，M 为抛物线的顶点，直线ME 是抛物线的对称轴．(1)求抛物线的解析式及点M 的坐标；(2)点P 为直线BC 上方抛物线上一点，连接PB ，PC ，当PBC 的面积取最大值时，求点P 的坐标．参考答案：1．(1)2142y x x =-- (2)① PC PD +取得最大值254 ① 53,2⎛⎫- ⎪⎝⎭或 316,2⎛⎫+- ⎪⎝⎭2．(1)213222y x x =-++ (1,0)-； (2)3172+或3172-或3332+或3332- (3)存在，517(,)39--或113(,)39-3．(1)故抛物线的表达式为：223y x x =-++，函数的对称轴为：1x =；(2)10113++(3)()4,5-或()8,45-4．(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3，四边形PBCD 的面积为45．(1)213442y x x =-++ (2)S 的最大值为1，()4,6P(3)()7,3或()5,3-6．(1)2330S x x =-+ 410x ≤＜；(2)当宽AB 为5米，长15BC =米时，长方形花圃的最大面积为75平方米.7．(1)2122y x x =-+ (2)188．(1)()1,4(2)①()2,3D ；①CBD AMN S S △△的最大值为916，此时315,24D ⎛⎫ ⎪⎝⎭9．(1)13a =- (2)()4,4P(3)1010．(1)直角三角形(2)244S m m =-++ (2,3)P 1QHC S =(3)存在，点M 坐标为3651(,)22+或3651(,)22-或333(,)22或333(,)22-或31(,)22，理由见解析11．(1)211642=--+y x x (2)()2396042S t t t =---<< (3)()()124,2,2,4P P --12．(1)223y x x =-++(2)()23P ，(3)存在，点F 的坐标为()417，或()417-，或()2314-+，或()2314--，13．(1)228y x x =-++(2)614．(1)211642y x x =-++ (2)2553042S t t =-++ (3)()8,6P -15．(1)抛物线的解析式为223y x x =-++，点M 的坐标为(1,4)(2)315,24P ⎛⎫ ⎪⎝⎭。

中考数学复习《二次函数》专题训练-附带有参考答案一、选择题1．下列函数中，是二次函数的是（）A．y=x2+1x B．y=12x(x-1) C．y=-2x-1 D．y=x(x2+1)．2．抛物线y=(x−2)2−3的顶点坐标是（）A．(2，−3)B．(−2，3)C．(2，3)D．(−2，−3)3．把抛物线y=5x2向左平移2个单位，再向上平移3个单位，得到的抛物线是（）A．y=5(x−2)2+3B．y=5(x+2)2−3C．y=5(x+2)2+3D．y=5(x−2)2−34．函数y＝ax2与y＝﹣ax+b的图象可能是（）A． B． C． D．5．函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是（）A．k<3 B．k<3且k≠0 C．k≤3且k≠0 D．k≤36．若A（−5，y1），B（1，y2），C（2，y3）为二次函数y=x2+2x+m的图象上的三点，则y1，y2，y3的大小关系是（）A．y1<y2<y3B．y2<y3<y1C．y2<y1<y3D．y3<y1<y27．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①b＞0；②当x＞0，y随着x 的增大而增大；③（a+c）2﹣b2＜0；④a+b≥m（am+b）（m为实数）．其中结论正确的个数为（）A．4个B．3个C．2个D．1个8．某服装店购进单价为15元的童装若干件，销售一段时间后发现：当销售价为25元时，平均每天能售出8件，而当销售价每降低2元时，平均每天能多售出4件，为使该服装店平均每天的销售利润最大，则每件的定价为（）A．21元B．22元C．23元D．24元二、填空题9．将二次函数y＝x2－2x化为y＝(x－h)2＋k的形式，结果为10．若抛物线y＝ax2＋bx＋c与x轴的两个交点坐标是（－1，0），（3，0），则此抛物线的对称轴是直线．11．将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位，若得到的函数图象与直线y＝2有两个交点，则a的取值范围是.12．飞机着陆后滑行的距离y （单位：m）关于滑行时间t （单位：s）的函数解析式是y=60t-65t2，从飞机着陆至停下来共滑行米．13．已知如图：抛物线y=ax2+bx+c与直线y=kx+n相交于点A(−52，74)、B(0，3)两点，则关于x的不等式ax2+bx+c＜kx+n的解集是三、解答题14．如图，在平面直角坐标系中，一次函数y1=kx−7的图象与二次函数y2=2x2+bx+c的图象交于A(1，−5)、B(3，t)两点.（1）求y1与y2的函数关系式；（2）直接写出当y1<y2时，x的取值范围；（3）点C为一次函数y1图象上一点，点C的横坐标为n，若将点C向右平移2个单位，再向上平移4个单位后刚好落在二次函数y2的图象上，求n的值.15．某品牌服装公司新设计了一款服装，其成本价为60（元/件）.在大规模上市前，为了摸清款式受欢迎状况以及日销售量y（件）与销售价格x（元/件）之间的关系，进行了市场调查，部分信息如表：销售价格x（元/件）80 90 100 110日销售量y（件）240 220 200 180（1）若y与x之间满足一次函数关系，请直接写出函数的解析式（不用写自变量x的取值范围）；（2）若该公司想每天获利8000元，并尽可能让利给顾客，则应如何定价？（3）为了帮助贫困山区的小朋友，公司决定每卖出一件服装向希望小学捐款10元，该公司应该如何定价，才能使每天获利最大？（利润用w表示）16．如图，抛物线y=−x2+bx+c与x轴交于A，B两点（A在B的左侧），与y轴交于点N，过A点的直线：l：y=−x−1与y轴交于点C，与抛物线y=−x2+bx+c的另一个交点为D(5，−6)，已知P点为抛物线y=−x2+bx+c上一动．点（不与A、D重合）．（1）求抛物线的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的动点，以NC为一边且顶点为N，C，M，P的四边形是平行四边形，直接写出所有符合条件的M点坐标．17．如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线C1：y=−18x2+32x+32近似表示滑雪场地上的一座小山坡，某滑雪爱好者小张从点O正上方A点滑出，滑出后沿一段抛物线C2：y=−14x2+bx+c 运动．（1）当小张滑到离A处的水平距离为8米时，其滑行高度为10米，求出b，c的值；（2）在(1)的条件下，当小张滑出后离的水平距离为多少米时，他滑行高度与小山坡的竖直距离为是5米？2（3）若小张滑行到坡顶正上方，且与坡顶距离不低于4米，求b的取值范围．18．如图，在平面直角坐标系中，抛物线y=ax2+bx−4与x轴交于A(4，0)、B(−3，0)两点，与y轴交于点C．（1）求这条抛物线所对应的函数表达式．（2）如图①，点D是x轴下方抛物线上的动点，且不与点C重合．设点D的横坐标为m，以O、A、C、D 为顶点的四边形面积为S，求S与m之间的函数关系式．（3）如图②，连结BC，点M为线段AB上一点，点N为线段BC上一点，且BM=CN=n，直接写出当n为何值时△BMN为等腰三角形．参考答案 1．B 2．A 3．C 4．B 5．D 6．B 7．B 8．B9．y =(x −1)2−1 10．x ＝1 11．a ＜5 12．75013．x <−52或x >014．（1）解：把点A(1，−5)代入y 1=kx −7得−5=k −7 ∴y 1=2x −7；把点B(3，t)代入y 1=2x −7中，得t =−1 ∴A(1，−5)把点A 、B 分别代入y 2=2x 2+bx +c 中，得{−2=2+b +c−1=18+3b +c 解得{b =−6c =−1∴y 2=2x 2−6x −1； （2）x <1或x >3（3）解：∵点C 为一次函数y 1图象上一点，∴C(n ，2n −7)将点C 向右平移2个单位，再向上平移4个单位后得到点C ′(n +2，2n −3) 把C ′代入y 2=2x 2−6x −1，得2n −3=2(n +2)2−6(n +2)−1 解得n =±1 所以n 的值为1或-1 15．（1）y=-2x+400（2）解：由题意，得：(x −60)(−2x +400)=8000解得x 1=100，x 2=160 ∵公司尽可能多让利给顾客 ∴应定价100元（3）解：由题意，得w =(x −60−10)(−2x +400)=−2x 2+540x −28000 =−2(x −135)2+8450∵−2<0∴当x =135时，w 有最大值，最大值为8450. 答：当一件衣服定为135元时，才能使每天获利最大. 16．（1）解：∵直线l ：y =−x −1过点A∴A(−1，0)又∵D(5，−6)将点A ，D 的坐标代入抛物线表达式可得：{−1−b +c =0−25+5b +c =−6 解得{b =3c =4．∴抛物线的解析式为：y =−x 2+3x +4． （2）解：如图设点P(x ，−x 2+3x +4) ∵PE ∥x 轴，PF ∥y 轴则E(x 2−3x −5，−x 2+3x +4)，F(x ，−x −1) ∵点P 在直线l 上方的抛物线上∴−1<x <5∴PE =|x −(x 2−3x −5)|=−x 2+4x +5，PF =|−x 2+3x +4−(−x −1)|=−x 2+4x +5 ∴PE +PF =2(−x 2+4x +5)=−2(x −2)2+18． ∴当x =2时，PE +PF 取得最大值，最大值为18．（3）符合条件的M 点有三个：M 1(4，−5)，M 2(2+√14，−3−√14)， M 3(2−√14，−3+√14)． 17．（1）解：由题意可知抛物线C 2：y=−14x 2+bx+c 过点(0， 4)和(8， 10) 将其代入得：{4=c10=−14×82+8b +c解得 ∴b=114，c=4（2）解：由(1)可得抛物线Cq 解析式为： y=−14x 2+114x+4设运动员运动的水平距离为m 米时，运动员与小山坡的竖直距离为52米，依题意得： −14m 2+114m +4−(−18m 2+32m +32)=52解得： m 1=10，m 2=0(舍)故运动员运动的水平距离为10米时，运动员与小山坡的竖直距离为为52米． （3）解：∵抛物线C 2经过点(0， 4) ∴c=4抛物线C 1： y=−18x 2+32x +32=−18(x −6)2+6 当x=6时，运动员到达坡项 即−14×62+6b+4≥4+6． ∴b ≥15618．（1）解：把A(4，0)、B(−3，0)代入y =ax 2+bx −4中 得{16a +4b −4=09a −3b −4=0解得{a =13b =−13∴这条抛物线所对应的函数表达式为y =13x 2−13x −4． （2）解：当x =0时y =−4∴C(0，−4)当−3<m <0时S =S △ODC +S △OAC =12×4×(−m)+12×4×4=−2m +8当0<m <4时S =S △ODC +S △OAD =12×4×m +12×4×(−13m 2+13m +4)=−23m 2+83m +8． （3）解：n =52，n =2511，n =3011．。

中考数学总复习《二次函数图像与坐标轴的交点问题》专题测试卷带答案班级：___________姓名：___________考号：___________一、单选题(共12题；共24分)1．抛物线y =x 2−2x +1与坐标轴的交点个数为（ ）A ．无交点B ．1个C ．2个D ．3个2．如图，已知二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴交于点A （﹣1，0），与y 轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x ＝1.下列结论：①abc ＞0；②4a ＋2b ＋c ＞0；③4ac ﹣b 2＞8a ；④13<a <23； ⑤b ＞c.其中含所有正确结论的选项是（ ） A ．①②③B ．②③④C ．①④⑤D ．①③④⑤3．已知二次函数y=ax 2+bx+c （a≠0，a ，b ，c 为常数）的y 与x 的部分对应值如下表：x 3.23 3.24 3.25 3.26 y﹣0.06﹣0.08﹣0.030.09判断方程ax 2+bx+c=0的一个解x 的取值范围是（ ） A ．3＜x ＜3.23 B ．3.23＜x ＜3.24 C ．3.24＜x ＜3.25D ．3.25＜x ＜3.264．已知抛物线y =−3x 2+bx +c 与x 轴只有一个交点，且过点A(m −2，n)和B(m +4，n)，则n 的值为（ ） A ．-9B ．-16C ．-18D ．-275．如图，二次函数y=ax 2+bx+c （a≠0）的图象与x 轴交于点A 、B 两点，与y 轴交于点C ，对称轴为直线x=-1，点B 的坐标为（1，0），则下列结论：①AB=4；②b 2-4ac ＞0；③ab ＜0；④a 2-ab+ac ＜0，其中正确的结论有（ ）个．A．3B．4C．2D．16．坐标平面上某二次函敷图形的顶点为(2，-1)，此函数图形与x轴相交于P、Q两点，且PQ=6若此函数图形通过(1，a)、(3，b)、(-1，c)、(-3，d)四点，则下列结论错误的是() A．a=b B．d>c C．c>a D．d<07．二次函数y＝ax2＋bx＋c的图象如图所示，则下列判断中错误的是()A．图象的对称轴是直线x＝1；B．一元二次方程ax2＋bx＋c＝0的两个根是－1、3；C．当x＞1时，y随x的增大而减小；D．当－1＜x＜3时，y＜0.8．如图，已知抛物线l：y= 12（x-2）2-2与x轴分别交于0、A两点，将抛物线l1向上平移得到l2，过点A作AB⊥x轴交抛物线l2于点B，如果山抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16，则抛物线l2的函数表达式为（）A．y= 12（x-2）2+4B．y= 12（x-2）2+3C．y= 12（x-2）2+2D．y= 12（x-2）2+19．如图，铅球运动员掷铅球的高度y（m）与水平距离x（m）之间的函数关系式是y=﹣112x2+ 23x+ 53，则该运动员此次掷铅球的成绩是（）A．6m B．12m C．8m D．10m10．已知函数y= x2+2x-3，当x=m时，y＜0，则m的值可能是（）.A．-4B．0C．2D．311．对于二次函数y=（x+1）2+2的图象，下列说法正确的是（）A．开口向下B．对称轴是直线x=﹣1C．顶点坐标是（1，2）D．与x轴有两个交点12．已知二次函数y=ax2+bx+c（a，b，c为常数，a≠0）的图象如图所示，有下列结论：①abc＞0，②b2-4ac＜0，③a-b+c＞0，④4a-2b+c＜0，其中正确结论的个数是（）A．1B．2C．3D．4二、填空题(共6题；共6分)13．如图，抛物线y=a(x−4)(x+1)(a>0)与x轴交于A，B两点（点A在点B的左边）与y轴交于点C，连接BC，过点A作直线BC的平行线交抛物线于另一点E，交y轴于点D，则ADDE的值为.14．已知抛物线y＝2x2+bx﹣1与x轴的交点坐标分别是（﹣3，0）和（2，0），那么关于x的一元二次方程2x2+bx﹣1＝0的根是．15．抛物线y=(x+2)2+3上的点到x轴最短的距离是．16．如图，二次函数y＝ax2+bx+c的图象经过点A（﹣1，0），B（3，0）．有下列结论：①图象的对称轴为直线：x＝1；②a：b：c＝﹣1：2：3；③若0＜x＜4，则5a＜y＜﹣3a；④一元二次方程cx2+bx+a＝0的两个根分别为﹣1和13，其中正确的结论有（填序号）．17．如图，二次函数y＝ax2＋bx＋c的图象与x轴的两个交点分别为（﹣1，0），（3，0）对于下列命题：①b﹣2a＝0；②abc＜0；③a﹣2b＋4c＜0④8a＋c＜0，其中正确的有．18．如图，抛物线y=−x2+bx+c与x轴交于点A(1，0)、点B，与y轴相交于点C(0，3)，下列结论：①b=−2﹔②B点坐标为(−3，0)，③抛物线的顶点坐标为(−1，3)，④直线y=ℎ与抛物线交于点D、E，若DE<2，则h的取值范围是3<ℎ<4﹔⑤在抛物线的对称轴上存在一点Q，使△QAC的周长最小，则Q点坐标为(−1，2)．其中正确的有．三、综合题(共6题；共75分)19．已知二次函数y=x2−mx+m−2．（1）求证：不论m为何实数，此二次函数的图象与x轴都有两个不同交点；（2）若此函数y有最小值−54，求这个函数表达式．20．已知y=x2−(m+2)x+(2m−1)是关于x的抛物线解析式.（1）求证：抛物线与x轴一定有两个交点；（2）点A(−2,y1)、B(1,y2)和C(4,y3)是抛物线上的三个点，当抛物线经过原点时，判断y1、y2和y3的大小关系.21．如图，在平面直角坐标系中，抛物线y＝12（x﹣1）2﹣2与x轴交于点A和点B（点A在点B 的左侧），第一象限内的点C在该抛物线上．（1）直接写出A、B两点的坐标；（2）若△ABC的面积为12，求点C坐标；（3）在（2）问的条件下，直线y＝mx+n经过点A、C，12（x﹣1）2﹣2＞mx+n时，直接写出x的取值范围．22．如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x-6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；（3）若球一定能越过球网，又不出边界，求h的取值范围．23．如图，已知抛物线y=−x2+bx+c与x轴、y轴分别相交于点A（－1，0）和B（0，3），其顶点为D．（1）求这条抛物线的解析式；（2）若抛物线与x轴的另一个交点为E，求⊥ODE的面积；抛物线的对称轴上是否存在点P使得⊥PAB的周长最短．若存在请求出点P的坐标，若不存在说明理由．24．已知，如图，二次函数y=−x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C(0, 5)，且经过点(1, 8)（1）求该抛物线的解析式；（2）求该抛物线的顶点坐标和对称轴.（3）求△ABC的面积S△ABC.参考答案1．【答案】C 2．【答案】C 3．【答案】D 4．【答案】D 5．【答案】A 6．【答案】D 7．【答案】D 8．【答案】C 9．【答案】D 10．【答案】B 11．【答案】B 12．【答案】B 13．【答案】1514．【答案】x 1＝−3，x 2＝2 15．【答案】3 16．【答案】①②④ 17．【答案】③18．【答案】①②④⑤19．【答案】（1）证明： Δ=(−m)2−4(m −2)=m 2−4m +8=(m −2)2+4 ，不论 m 为何值时，都有 Δ>0此时二次函数图象与 x 轴有两个不同交点．（2）解： ∵4ac−b 24a =4(m−2)−m 24=−54， m 2−4m +3=0 ， ∴m =1 或 m =3所求函数式为 y =x 2−x −1 或 y =x 2−3x +1 ．20．【答案】（1）证明：y=x 2﹣（m+2）x+（2m ﹣1）.∵⊥=[﹣（m+2）]2﹣4×1×（2m ﹣1）=（m －2）2+4＞0，∴抛物线与x 轴一定有两个交点 （2）解：∵抛物线y=x 2﹣（m+2）x+（2m ﹣1）经过原点，∴2m ﹣1=0.解得：m =12 ，∴抛物线的解析式为y=x 2−52x.当x=﹣2时，y1=9；当x=1时，y2=－3.5；当x=4时，y3=6，∴y2＜y3＜y121．【答案】（1）解：令y=0，则12（x-1）2-2=0解得x1=−1，x2=3∴A（-1，0），B（3，0）（2）解：∵A（-1，0），B（3，0）∴AB=4∵S△ABC=12AB·yC=12∴12×4×y C=12解得y C=6∴12(x−1)2−2=6解得x1=5，x2=−3（不符题意，舍去）∴C（5，6）（3）解：由图象可知，当12(x−1)2−2>mx+n时，x的取值范围是x＜-1或x＞522．【答案】（1）解：∵h=2.6，球从O点正上方2m的A处发出∴抛物线y=a（x-6）2+h过点（0，2）∴2=a（0-6）2+2.6解得：a=- 1 60故y与x的关系式为：y=- 160（x-6）2+2.6（2）解：当x=9时，y=- 160（x-6）2+2.6=2.45＞2.43所以球能过球网；当y=0时解得：x1=6+2 √39＞18，x2=6-2 √39（舍去）故会出界；（3）解：当球正好过点（18，0）时，抛物线y=a（x-6）2+h还过点（0，2），代入解析式得：{2=36a+ℎ0=144a+ℎ解得： {a =−154ℎ=83此时二次函数解析式为：y=- 154 （x-6）2+ 83此时球若不出边界h≥ 83当球刚能过网，此时函数解析式过（9，2.43），抛物线y=a （x-6）2+h 还过点（0，2），代入解析式得：{2.43=a(9−6)2+ℎ2=a(0−6)2+ℎ解得： {a =−432700ℎ=19375此时球要过网h≥19375故若球一定能越过球网，又不出边界，h 的取值范围是：h≥ 83．23．【答案】（1）解：根据题意得{−1−b +c ＝0c ＝3 ，解得 {b ＝2c ＝3∴抛物线解析式为y=-x 2+2x+3； （2）解：当y=0时，-x 2+2x+3=0解得x 1=-1，x 2=3，则E （3，0）； y=-（x-1）2+4，则D （1，4）， ∴S ⊥ODE = 12×3×4=6；连接BE 交直线x=1于点P ，如图，则PA=PE ， ∴PA+PB=PE+PB=BE ， 此时PA+PB 的值最小， 易得直线BE 的解析式为 y=-x+3， 当x=1时，y=-x+3=3， ∴P （1，2）．24．【答案】（1）解：∵二次函数 y =−x 2+bx +c 的图象经过点 (0, 5) 和 B(1, 8)∴{c =5−1+b +c =8 解这个方程组，得 {b =4c =5∴该二次函数的解析式是 y =−x 2+4x +5 ； （2）解： y =−x 2+4x +5=−(x −2)2+9 ∴顶点坐标是 (2, 9) ；对称轴是x=2；（3）解：∵二次函数y=−x2+4x+5的图象与x轴交于A，B两点∴−x2+4x+5=0解这个方程得：x1=−1即二次函数y=−x2+4x+5与x轴的两个交点的坐标为A(−1, 0)和B(5, 0).∴△ABC的面积S△ABC=12AB×OC=12×|5−(−1)|×5=15.。

2015年中考真题初中数学---二次函数（1）一．选择题（共30小题）1．（2015•兰州）下列函数解析式中，一定为二次函数的是（）A ．y=3x﹣1 B．y=ax2+bx+c C．s=2t2﹣2t+1 D．y=x2+2．（2015•宁夏）函数y=与y=﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（）A ．B．C．D．3．（2015•锦州）在同一坐标系中，一次函数y=ax+2与二次函数y=x2+a的图象可能是（）A ．B．C．D．4．（2015•沈阳）在平面直角坐标系中，二次函数y=a（x﹣h）2（a≠0）的图象可能是（）A ．B．C．D．5．（2015•泉州）在同一平面直角坐标系中，函数y=ax2+bx与y=bx+a的图象可能是（）A ．B．C．D．6．（2015•安徽）如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b﹣1）x+c的图象可能是（）A ．B．C．D．7．（2015•咸宁）如图是二次函数y=ax2+bx+c的图象，下列结论：①二次三项式ax2+bx+c的最大值为4；②4a+2b+c＜0；③一元二次方程ax2+bx+c=1的两根之和为﹣1；④使y≤3成立的x的取值范围是x≥0．其中正确的个数有（）A ．1个B．2个C．3个D．4个8．（2015•衢州）下列四个函数图象中，当x＞0时，y随x的增大而减小的是（）A ．B．C．D．9．（2015•湖北）二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示，则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的图象可能是（）A ．B．C．D．10．（2015•泰安）某同学在用描点法画二次函数y=ax2+bx+c的图象时，列出了下面的表格：x …﹣2 ﹣1 0 1 2 …y …﹣11 ﹣2 1 ﹣2 ﹣5 …由于粗心，他算错了其中一个y值，则这个错误的数值是（）A ．﹣11 B．﹣2 C．1 D．﹣511．（2015•泰安）在同一坐标系中，一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是（）A ．B．C．D．12．（2015•梅州）对于二次函数y=﹣x2+2x．有下列四个结论：①它的对称轴是直线x=1；②设y1=﹣x12+2x1，y2=﹣x22+2x2，则当x2＞x1时，有y2＞y1；③它的图象与x轴的两个交点是（0，0）和（2，0）；④当0＜x＜2时，y＞0．其中正确的结论的个数为（）A ．1 B．2 C．3 D．413．（2015•兰州）在下列二次函数中，其图象对称轴为x=﹣2的是（）A ．y=（x+2）2B．y=2x2﹣2 C．y=﹣2x2﹣2 D．y=2（x﹣2）214．（2015•益阳）若抛物线y=（x﹣m）2+（m+1）的顶点在第一象限，则m的取值范围为（）A m＞1B m＞0C m＞﹣1 D﹣1＜m＜0．．．．15．（2015•黔南州）二次函数y=x2﹣2x﹣3的图象如图所示，下列说法中错误的是（）A ．函数图象与y 轴的交点坐标是（0，﹣3）B ．顶点坐标是（1，﹣3）C ．函数图象与x 轴的交点坐标是（3，0）、（﹣1，0）D ．当x＜0时，y 随x的增大而减小16．（2015•甘孜州）二次函数y=x2+4x﹣5的图象的对称轴为（）A ．x=4 B．x=﹣4 C．x=2 D．x=﹣217．（2015•常州）已知二次函数y=x2+（m﹣1）x+1，当x＞1时，y随x的增大而增大，而m的取值范围是（）A ．m=﹣1 B．m=3 C．m≤﹣1 D．m≥﹣118．（2015•玉林）如图，反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点（﹣，m）（m＞0），则有（）A ．a=b+2k B．a=b﹣2k C．k＜b＜0 D．a＜k＜019．（2015•台州）设二次函数y=（x﹣3）2﹣4图象的对称轴为直线l，若点M在直线l上，则点M的坐标可能是（）A ．（1，0）B．（3，0）C．（﹣3，0）D．（0，﹣4）20．（2015•福州）已知一个函数图象经过（1，﹣4），（2，﹣2）两点，在自变量x的某个取值范围内，都有函数值y随x的增大而减小，则符合上述条件的函数可能是（）A ．正比例函数B．一次函数C．反比例函数D．二次函数21．（2015•日照）如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A （1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，其中正确的是（）A ．①②③B．①③④C．①③⑤D．②④⑤22．（2015•毕节市）二次函数y=ax2+bx+c的图象如图所示，则下列关系式错误的是（）A ．a＜0 B．b＞0 C．b2﹣4ac＞0 D．a+b+c＜023．（2015•深圳）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法正确的个数是（）①a＞0；②b＞0；③c＜0；④b2﹣4ac＞0．A ．1 B．2 C．3 D．424．（2015•恩施州）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论：①b2＞4ac；②2a+b=0；③a+b+c＞0；④若点B（﹣，y1）、C（﹣，y2）为函数图象上的两点，则y1＜y2，其中正确结论是（）A ．②④B．①④C．①③D．②③25．（2015•兰州）二次函数y=ax2+bx+c的图象如图，点C在y轴的正半轴上，且OA=OC，则（）A ．ac+1=b B．ab+1=c C．bc+1=a D．以上都不是26．（2015•孝感）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y 轴交于点C，且OA=OC．则下列结论：①abc＜0；②＞0；③ac﹣b+1=0；④OA•OB=﹣．其中正确结论的个数是（）A ．4 B．3 C．2 D．127．（2015•南宁）如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣1，下列结论中：•①ab＞0， ②a+b+c＞0， ③当﹣2＜x＜0时，y＜0．正确的个数是（）A ．0个B．1个C．2个D．3个28．（2015•遂宁）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＞0；②abc＜0；③b2﹣4ac＞0；④a+b+c＜0；⑤4a﹣2b+c＜0，其中正确的个数是（）A ．2 B．3 C．4 D．529．（2015•广安）如图，抛物线y=ax2+bx+c（c≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（）A ．﹣3＜P＜﹣1 B．﹣6＜P＜0 C．﹣3＜P＜0 D．﹣6＜P＜﹣330．（2015•凉山州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0②当﹣1≤x≤3时，y＜0③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2④9a+3b+c=0其中正确的是（）A ．①②④B．①④C．①②③D．③④2015年中考真题初中数学---二次函数（2）一．选择题（共30小题）1．（2015•湘潭）如图，观察二次函数y=ax2+bx+c的图象，下列结论：①a+b+c＞0，②2a+b＞0，③b2﹣4ac＞0，④ac＞0．其中正确的是（）A ．①②B．①④C．②③D．③④2．（2015•枣庄）如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（）A ．①②④B．③④C．①③④D．①②3．（2015•烟台）如图，已知顶点为（﹣3，﹣6）的抛物线y=ax2+bx+c经过点（﹣1，﹣4），则下列结论中错误的是（）A．b2＞4abB ．ax2+bx+c≥﹣6C ．若点（﹣2，m），（﹣5，n）在抛物线上，则m＞nD ．关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣14．（2015•巴中）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=﹣1，下列结论：①abc＜0；②2a+b=0；③a﹣b+c＞0；④4a﹣2b+c＜0其中正确的是（）A ．①②B．只有①C．③④D．①④5．（2015•潜江）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b2=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论有（）A ．1个B．2个C．3个D．4个6．（2015•齐齐哈尔）抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则下列结论：①4ac﹣b2＜0；②2a ﹣b=0；③a+b+c＜0；④点M（x1，y1）、N（x2，y2）在抛物线上，若x1＜x2，则y1≤y2，其中正确结论的个数是（）A ．1个B．2个C．3个D．4个7．（2015•乐山）已知二次函数y=ax2+bx+c的图象如图所示，记m=|a﹣b+c|+|2a+b+c|，n=|a+b+c|+|2a﹣b﹣c|．则下列选项正确的是（）A ．m＜n B．m＞nC ．m=n D．m、n的大小关系不能确定8．（2015•潍坊）已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（﹣1，0），下列结论：①abc＜0；②b2﹣4ac=0；③a＞2；④4a﹣2b+c＞0．其中正确结论的个数是（）A ．1 B．2 C．3 D．49．（2015•黔东南州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b，④4ac﹣b2＜0；其中正确的结论有（）A ．1个B．2个C．3个D．4个10．（2015•包头）如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），对称轴为直线x=1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：①当x＞3时，y＜0；②3a+b＜0；③﹣1≤a≤﹣；④4ac﹣b2＞8a；其中正确的结论是（）A ．①③④B．①②③C．①②④D．①②③④11．（2015•茂名）在平面直角坐标系中，下列函数的图象经过原点的是（）A ．y=B．y=﹣2x﹣3 C．y=2x2+1 D．y=5x12．（2015•天水）二次函数y=ax2+bx﹣1（a≠0）的图象经过点（1，1），则a+b+1的值是（）A ．﹣3 B．﹣1 C．2 D．313．（2015•大庆）已知二次函数y=a（x﹣2）2+c，当x=x1时，函数值为y1；当x=x2时，函数值为y2，若|x1﹣2|＞|x2﹣2|，则下列表达式正确的是（）A ．y1+y2＞0 B．y1﹣y2＞0 C．a（y1﹣y2）＞D．a（y1+y2）＞014．（2015•义乌市）如果一种变换是将抛物线向右平移2个单位或向上平移1个单位，我们把这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后的一条抛物线是y=x2+1，则原抛物线的解析式不可能的是（）A ．y=x2﹣1 B．y=x2+6x+5 C．y=x2+4x+4 D．y=x2+8x+1715．（2015•临沂）要将抛物线y=x2+2x+3平移后得到抛物线y=x2，下列平移方法正确的是（）A ．向左平移1个单位，再向上平移2个单位B ．向左平移1个单位，再向下平移2个单位C向右平移1个．单位，再向上平移2个单位D ．向右平移1个单位，再向下平移2个单位16．（2015•成都）将抛物线y=x2向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为（）A ．y=（x+2）2﹣3B．y=（x+2）2+3 C．y=（x﹣2）2+3 D．y=（x﹣2）2﹣317．（2015•荆州）将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（）A ．y=（x﹣1）2+4 B．y=（x﹣4）2+4 C．y=（x+2）2+6 D．y=（x﹣4）2+618．（2015•河池）将抛物线y=x2向右平移2个单位，再向上平移3个单位后，抛物线的解析式为（）A ．y=（x+2）2+3 B．y=（x﹣2）2+3 C．y=（x+2）2﹣3D．y=（x﹣2）2﹣319．（2015•牡丹江）抛物线y=3x2+2x﹣1向上平移4个单位长度后的函数解析式为（）A ．y=3x2+2x﹣5 B．y=3x2+2x﹣4 C．y=3x2+2x+3 D．y=3x2+2x+420．（2015•攀枝花）将抛物线y=﹣2x2+1向右平移1个单位长度，再向上平移1个单位长度所得的抛物线解析式为（）A ．y=﹣2（x+1）2B．y=﹣2（x+1）2+2C．y=﹣2（x﹣1）2+2D．y=﹣2（x﹣1）2+121．（2015•乐山）二次函数y=﹣x2+2x+4的最大值为（）A ．3 B．4 C．5 D．622．（2014•舟山）当﹣2≤x≤1时，二次函数y=﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（）A ．﹣B．或C．2或D．2或或23．（2014•淄博）如图，二次函数y=x2+bx+c的图象过点B（0，﹣2）．它与反比例函数y=﹣的图象交于点A（m，4），则这个二次函数的解析式为（）A ．y=x2﹣x﹣2 B．y=x2﹣x+2 C．y=x2+x﹣2 D．y=x2+x+224．（2014•成都）将二次函数y=x2﹣2x+3化为y=（x﹣h）2+k的形式，结果为（）A ．y=（x+1）2+4 B．y=（x+1）2+2 C．y=（x﹣1）2+4 D．y=（x﹣1）2+225．（2015•柳州）如图，二次函数y=ax2+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（）A ．x＜﹣2 B．﹣2＜x＜4 C．x＞0 D．x＞426．（2015•陕西）下列关于二次函数y=ax2﹣2ax+1（a＞1）的图象与x轴交点的判断，正确的是（）A．没有交点B ．只有一个交点，且它位于y轴右侧C ．有两个交点，且它们均位于y轴左侧D ．有两个交点，且它们均位于y轴右侧27．（2015•宁波）二次函数y=a（x﹣4）2﹣4（a≠0）的图象在2＜x＜3这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为（）A ．1 B．﹣1 C．2 D．﹣228．（2015•兰州）二次函数y=x2+x+c的图象与x轴的两个交点A（x1，0），B（x2，0），且x1＜x2，点P（m，n）是图象上一点，那么下列判断正确的是（）A ．当n＜0时，m＜0B．当n＞0时，m＞x2C ．当n＜0时，x1＜m＜x2D．当n＞0时，m＜x129．（2015•天津）已知抛物线y=﹣x2+x+6与x轴交于点A，点B，与y轴交于点C．若D为AB的中点，则CD的长为（）A ．B．C．D．30．（2015•苏州）若二次函数y=x2+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解为（）A ．x1=0，x2=4 B．x1=1，x2=5 C．x1=1，x2=﹣5 D．x1=﹣1，x2=5 2015年中考真题初中数学---二次函数（3）一．选择题（共10小题）1．（2015•济南）如图，抛物线y=﹣2x2+8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1向右平移得C2，C2与x轴交于点B，D．若直线y=x+m与C1、C2共有3个不同的交点，则m的取值范围是（）A ．﹣2＜m ＜B．﹣3＜m ＜﹣C．﹣3＜m＜﹣2 D．﹣3＜m ＜﹣2．（2015•杭州）设二次函数y1=a（x﹣x1）（x﹣x2）（a≠0，x1≠x2）的图象与一次函数y2=dx+e （d≠0）的图象交于点（x1，0），若函数y=y1+y2的图象与x轴仅有一个交点，则（）A a（x1﹣x2）=dB a（x2﹣x1）=dC a（x1﹣x2）2=dD a（x1+x2）2=d．．．．3．（2015•达州）若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x1，0）、（x2，0），且x1＜x2，图象上有一点M（x0，y0），在x轴下方，则下列判断正确的是（）A ．a（x0﹣x1）（x0﹣x2）＜0B．a＞0C ．b2﹣4ac≥0 D．x1＜x0＜x24．（2015•贵港）如图，已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A（3，2），与x轴交于点B（2，0），若0＜y1＜y2，则x的取值范围是（）A ．0＜x＜2 B．0＜x＜3 C．2＜x＜3 D．x＜0或x＞35．（2015•泸州）若二次函数y=ax2+bx+c（a＜0）的图象经过点（2，0），且其对称轴为x=﹣1，则使函数值y＞0成立的x的取值范围是（）A ．x＜﹣4或x＞2B．﹣4≤x≤2 C．x≤﹣4或x≥2 D．﹣4＜x＜26．（2015•六盘水）如图，假设篱笆（虚线部分）的长度16m，则所围成矩形ABCD的最大面积是（）A ．60m2B．63m2C．64m2D．66m27．（2015•铜仁市）河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣x2，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（）A ．﹣20m B．10m C．20m D．﹣10m8．（2015•金华）图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可近似看成抛物线y=﹣（x﹣80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴，若OA=10米，则桥面离水面的高度AC为（）A ．16米B．米C．16米D．米9．（2015•潍坊）如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（）A ．cm2B．cm2C．cm2D．cm210．（2015•嘉兴）如图，抛物线y=﹣x2+2x+m+1交x轴与点A（a，0）和B（b，0），交y 轴于点C，抛物线的顶点为D，下列四个命题：①当x＞0时，y＞0；②若a=﹣1，则b=4；③抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6．其中真命题的序号是（）A ．①B．②C．③D．④2015年中考真题初中数学---二次函数（1）参考答案一．选择题（共30小题）1．C 2．B 3．C 4．D 5．C 6．A 7．B 8．B 9．C 10．D 11．D 12．C 13．A 14．B 15．B 16．D 17．D 18．D 19．B20．D 21．C 22．D 23．B 24．B 25．A 26．B 27．D 28．B29．B 30．B2015年中考真题初中数学---二次函数（2）参考答案一．选择题（共30小题）1．C 2．A 3．C 4．D 5．B 6．C 7．A 8．B 9．C 10．B 11．D 12．D 13．C 14．B 15．A 16．A 17．B 18．B 19．C20．C 21．C 22．C 23．A 24．D 25．B 26．D 27．A 28．C29．D 30．D2015年中考真题初中数学---二次函数（3）参考答案一．选择题（共10小题）1．D 2．B 3．A 4．C 5．D 6．C 7．C 8．B 9．C 10．C。

中考数学总复习《二次函数的最值》练习题-附带答案解析一、单选题(共12题；共24分)1．如图，△ABC是直角三角形，△A=90°，AB=8cm，AC=6cm。

点P从点A出发，沿AB方向以2cm/s的速度向点B运动，同时点Q从点A出发，沿AC方向以1cm/s的速度向点C运动，其中一个动点到达终点则另一个动点也停止运动，则△APQ的最大面积是（）A．0cm2B．8cm2C．16cm2D．24 cm2 2．二次函数y=ax2+bx+c（a≠0）的图象如图所示，则在下列各式子：①abc＞0；②a+b+c＞0；③a+c＞b；④2a+b=0；⑤△=b2-4ac＜0；⑥3a+c＞0；⑦（m2-1）a+(m-1)b≥0（m为任意实数）中成立式子（）A．②④⑤⑥⑦B．①②③⑥⑦C．①③④⑤⑦D．①③④⑥⑦3．已知二次函数y=x2﹣2mx（m为常数），当﹣1≤x≤2时函数值y的最小值为﹣2，则m的值是（）A．B．C．或D．- 或4．已知二次函数y＝x2﹣4x+2，关于该函数在﹣1≤x≤3的取值范围内，下列说法正确的是（）A．有最大值﹣1，有最小值﹣2B．有最大值0，有最小值﹣1 C．有最大值7，有最小值﹣1D．有最大值7，有最小值﹣25．二次函数y=−x2+6x−7，当x取值为t≤x≤t+2时有最大值t=2，则t的取值范围为（）A．t≤0B．0≤t≤3C．t≥3D．以上都不对6．如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（）A．√3cm2B．32√3cm2C．92√3cm2D．272√3cm27．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下B．x＞1时y随x的增大而减小C．顶点坐标是（1，2）D．函数有最大值28．如图，一条抛物线与x轴相交于M，N两点（点M在点N的左侧），其顶点P在线段AB上移动，点A，B的坐标分别为（﹣2，﹣3），（1，﹣3），点N的横坐标的最大值为4，则点M的横坐标的最小值为（）A．﹣1B．﹣3C．﹣5D．﹣7 9．我们定义一种新函数：形如y＝|ax2+bx+c|（a≠0，b2﹣4ac＞0）的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y＝|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：其中正确结论的个数是（）①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时函数值y随x值的增大而增大；④当x＝﹣1或x＝3时函数的最小值是0；⑤当x＝1时函数的最大值是4A．4B．3C．2D．110．设实数x＞0，y＞0，且x＋y－2x2y2＝4，则1x+1y的最小值为()A．4 √2B．3 √2C．2 √2D．√2 11．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=-1对称；③当x=-2时函数y的值等于0；④当x=-3或x=1时函数y的值都等于0．其中正确结论的个数是（）A．1B．2C．3D．4 12．如图，已知抛物线y=ax2+bx+c（a＜0）的对称轴为x=1，交x轴的一个交点为（x1，0），且﹣1＜x1＜0，有下列5个结论：①abc＞0；②9a﹣3b+c＜0；③2c＜3b；④（a+c）2＜b2；⑤a+b＞m（am+b）（m≠1的实数）其中正确的结论有（）A．1个B．2个C．3个D．4个二、填空题(共6题；共6分)13．已知二次函数y=ax2+4ax+a2−1，当−4≤x≤1时y的最大值为5，则实数a的值为.14．函数y=2x2-8x+1的最小值是.15．当-2≤x≤1时二次函数若y=−(x−m)2+m2+1有最大值4，则m的值为．16．如图，在△ABC中△B＝90°，AB＝12cm，BC＝24cm，动点P从点A开始向B点以2cm/s的速度移动（不与点B重合）；动点Q从点B开始向点C以4cm/s的速度移动（不与点C重合）.如果P、Q分别从A、B同时出发，那么经过秒四边形APQC的面积最小.17．一条抛物线与x轴相交于A，B两点（点A在点B的左侧），若点M，N的坐标分别为（－1，－2），（1，－2），抛物线顶点P在线段MN上移动．点B的横坐标的最大值为3，则点A的横坐标的最小值为．18．二次函数y=mx2+2x+m−4m2的图象经过原点，则此抛物线的顶点坐标是三、综合题(共6题；共66分)19．如图，在平面直角坐标系中点A、C的坐标分别为（﹣1，0）、（0，﹣√3），点B在x轴上．已知某二次函数的图象经过A、B、C三点，且它的对称轴为直线x=1，点P为直线BC下方的二次函数图象上的一个动点（点P与B、C不重合），过点P作y轴的平行线交BC于点F．（1）求该二次函数的解析式；（2）若设点P的横坐标为m，用含m的代数式表示线段PF的长；（3）求△PBC面积的最大值，并求此时点P的坐标．20．X市与W市之间的城际铁路正在紧张有序地建设中.在建成通车前，进行了社会需求调查，得到一列火车一天往返次数m与该列车每次拖挂车厢节数n的部分数据如下：车厢节数n4710往返次数m16104b（k，b为常数，k≠0）；②y=ax2+bx+c（a，b，c为常数，a≠0）中选取一个合适的函数模型，求出的m关于n的函数关系式是m=（不写n的范围）；（2）结合你求出的函数，探究一列火车每次挂多少节车厢，一天往返多少次时一天的设计运营人数Q最多（每节车厢载容量设定为常数p）.21．在平面直角坐标系xOy中抛物线y=ax2+bx+2（a≠0）经过点A(1，−1)，与y轴交于点B．（1）直接写出点B的坐标；（2）点P(m，n)是抛物线上一点，当点P在抛物线上运动时n存在最大值N．①若N=2，求抛物线的表达式；②若−9<a<−2，结合函数图象，直接写出N的取值范围．22．一商店销售某种商品，平均每天可售出20件，每件盈利50元，为了扩大销售、增加利润，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.（1）当每件商品降价多少元时该商店每天销售利润为1600元？（2）当每件商品降价多少元时该商店每天销售利润最大？最大为多少元？23．某商店购进一批单价为8元的商品，如果按每件10元出售，那么每天可销售100件，经调查发现，这种商品的销售单价每提高1元，其销售量相应减少10件.（1）求销售量y件与销售单价x(x>10)元之间的关系式；（2）当销售单价x定为多少，才能使每天所获销售利润最大？最大利润是多少？24．如图，已知直线y=﹣12x+2与抛物线y=a （x+2）2相交于A、B两点，点A在y 轴上，M为抛物线的顶点．（1）请直接写出点A的坐标及该抛物线的解析式；（2）若P为线段AB上一个动点（A、B两端点除外），连接PM，设线段PM的长为l，点P的横坐标为x，请求出l2与x之间的函数关系，并直接写出自变量x的取值范围；（3）在（2）的条件下，线段AB上是否存在点P，使以A、M、P为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．参考答案1．【答案】C 2．【答案】D 3．【答案】D 4．【答案】D 5．【答案】C 6．【答案】C 7．【答案】C 8．【答案】C 9．【答案】A 10．【答案】A 11．【答案】B 12．【答案】D13．【答案】2−√10 或1 14．【答案】-7 15．【答案】2或- √3 16．【答案】3 17．【答案】-3 18．【答案】（-4，-4）19．【答案】（1）解：设二次函数的解析式为y=ax 2+bx+c （a≠0，a 、b 、c 为常数）由抛物线的对称性知B 点坐标为（3，0） 依题意得： {a −b +c =09a +3b +c =0c =−√3解得： {a =√33b =−2√33c =−√3∴所求二次函数的解析式为 y =√33x 2−2√33x −√3（2）解：∵P 点的横坐标为m∴P 点的纵坐标为 √33m 2−2√33m −√3设直线BC 的解析式为y=kx+b （k≠0，k 、b 是常数） 依题意，得 {3k +b =0b =−√3∴{k=√33b=−√3故直线BC的解析式为y=√33x−√3∴点F的坐标为(m,√33m−√3)∴PF=−√33m2+√3n(0＜m＜3)（3）解：∵△PBC的面积S=S△CPF+S△BPF=12PF⋅BO=12×(−√33m2+√3m)×3=−√32(m−32)2+9√38∴当m=32时△PBC的最大面积为9√38把m=32代入y=√33x2−2√33x−√3得y=−5√34∴点P的坐标为(32,−5√3 4)20．【答案】（1）-2n+24（2）解：由题意得：Q=pmn=pn(−2n+24)=−2pn2+24pn ∵−2p<0∴Q有最大值∴当n=−24p2×(−2p)=6时Q有最大值此时答：一列火车每次挂6节车厢，一天往返12次时一天的设计运营人数最多. 21．【答案】（1）（0，2）（2）解：①依题意，当N=2时该抛物线的顶点为（0，2）.设抛物线的解析式为y=ax2+2.由抛物线过A（1，−1），得a+2=−1解得a=−3∴抛物线的表达式为y=−3x2+2．②2≤N<322．【答案】（1）解：设每件商品应降价x元，根据题意，得(50-x)(20+2x)=1600 解得：x1=10，x2=30因要求每件盈利不少于25元，故x2=30应舍去……答：每件商品应减价10元，该商店每天销售利润为1600元.（2）解：设每件商品应降价x元，销售利润为W元。

第一部分：一次函数考点归纳：一次函数：若y=kx+b(k,b 是常数，k ≠0)，那么y 叫做x 的一次函数，特别的，当b=0时，一次函数就成为y=kx(k 是常数，k ≠0)，这时，y 叫做x 的正比例函数，当k=0时，一次函数就成为若y=b ，这时，y 叫做常函数。

☆A 与B 成正比例 A=kB(k ≠0)直线位置与k ，b 的关系：（1）k ＞0直线向上的方向与x 轴的正方向所形成的夹角为锐角； （2）k ＜0直线向上的方向与x 轴的正方向所形成的夹角为钝角； （3）b ＞0直线与y 轴交点在x 轴的上方； （4）b ＝0直线过原点；（5）b ＜0直线与y 轴交点在x 轴的下方；平移1，直线x y 31=向上平移1个单位，再向右平移1个单位得到直线 。

2， 直线143+-=x y 向下平移2个单位，再向左平移1个单位得到直线________方法：直线y=kx+b ，平移不改变斜率k ，则将平移后的点代入解析式求出b 即可。

直线y=kx+b 向左平移2向上平移3 <=> y=k(x+2)+b+3;（“左加右减，上加下减”）。

练习：直线m:y=2x+2是直线n 向右平移2个单位再向下平移5个单位得到的，而（2a,7）在直线n 上，则a=____________；函数图形的性质例题：1．下列函数中，y 是x 的正比例函数的是（ ）A．y=2x-1 B．y=3xC．y=2x2 D．y=-2x+12，一次函数y=-5x+3的图象经过的象限是（）A．一、二、三 B．二、三、四C．一、二、四 D．一、三、四3，若函数y=（2m+1）x2+（1-2m）x（m为常数）是正比例函数，则m的值为（）A．m>12B．m=12C．m<12D．m=-124、直线y kx b=+经过一、二、四象限，则直线y bx k=-的图象只能是图4中的（）5，若一次函数y=（3-k）x-k的图象经过第二、三、四象限，则k的取值范围是（）A．k>3 B．0<k≤3 C．0≤k<3 D．0<k<36，已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（）A．y=-x-2 B．y=-x-6 C．y=-x+10 D．y=-x-17，已知关于x的一次函数27y mx m=+-在15x-≤≤上的函数值总是正数，则m的取值范围是（）A．7m>B．1m>C．17m≤≤D．都不对8、如图，两直线1y kx b=+和2y bx k=+在同一坐标系内图象的位置可能是（）9，一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（）xyo xyoxyoxyoA B C D10，,已知一次函数（1）当m 取何值时，y 随x 的增大而减小？ （2）当m 取何值时，函数的图象过原点？函数解析式的求法：正比例函数设解析式为： ,一个点的坐标带入求k. 一次函数设解析式为： ；两点带入求k,b1，已知一个正比例函数与一个一次函数的图象交于点A （3,4），且OA=OB（1） 求两个函数的解析式；（2）求△AOB 的面积；第二部分：二次函数（待讲）课前小测：1，抛物线3)2x (y 2-+=的对称轴是（ ）。

中考数学总复习《二次函数图像与一元二次方程的综合应用》专项测试卷-附参考答案一、单选题(共12题；共24分)1．已知抛物线y=ax2+bx+c经过点(1，0)和点(0，−3)，且对称轴在y轴的左侧，有下列结论：①a>0；②a+b=3；③抛物线经过点(−1，0)；④关于x的一元二次方程ax2+bx+c=−1有两个不相等的实数根．其中，正确结论的个数是（）A．0B．1C．2D．32．若关于x的一元二次方程(x−2)(x−3)=m有实数根x1，x2，且x1≠x2，有下列结论：①x1=2，x2=3；②m>−14；③二次函数y=(x−x1)(x−x2)+m的图象与x轴的交点坐标分别为（2，0）和（3，0）.其中正确的个数有（）A．0B．1C．2D．33．如图，抛物线y=-x2+mx的对称轴为直线x=2，若关于x的一元二次方程-x2+mx-t=0 (t为实数)在1<x<3的范围内有解，则t的取值范围是()A．-5<t≤4B．3<t≤4C．-5<t<3D．t>-54．如图，抛物线y=−x2+mx的对称轴为直线x=2，若关于x的一元二次方程−x2+mx−t=0（t为实数）在1≤x≤3的范围内有解，则t的取值错误的是（）A．t=2.5B．t=3C．t=3.5D．t=45．若关于的方程x2+px+q=0没有实数根，则函数y=x2−px+q的图象的顶点一定在（）A．x轴的上方B．x轴下方C．x轴上D．y轴上6．已知二次函数y＝ax2+bx+c（a≠0）图象上部分点的坐标（x，y）的对应值如表所示：x…0√54…y…0.37﹣10.37…A．0或4B．√5或4﹣√5C．1或5D．无实根7．二次函数y=ax2+bx的图象如图所示，若一元二次方程ax2+bx=−m有实数根，则m的最大（）A．3B．−3C．−6D．98．若x1，x2（x1＜x2）是方程（x﹣a）（x﹣b）=﹣1（a＜b）的两根，则实数x1，x2，a，b的大小关系是（）A．a＜x1＜x2＜b B．x1＜a＜x2＜b C．x1＜a＜b＜x2D．x1＜x2＜a＜b9．下列关于二次函数y＝ax2－2ax+1（a＞1）的图象与x轴交点的判断，下确的是（）A．没有交点B．只有一个交点，且它位于y轴右侧C．有两个交点，且它们均位于y轴左侧D．有两个交点，且它们均位于y轴右侧10．已知b>0，二次函数y=ax2+bx+a2−1的图象为下列之一，则a的值为（）A．1B．-1C．−1−√52D．−1+√5211．已知函数y=ax2+bx+c，当y＞0时，−12<x<13．则函数y=cx2﹣bx+a的图象可能是下图中的（）A．B．C．D．12．二次函数y=ax2+bx+c的部分图象如图所示，对称轴方程为x=−1，图象与x轴相交于点（1，0），则方程cx2+bx+a=0的根为（）A．x1=1，x2=−3B．x1=−1C．x1=1，x2=−13D．x1=−1二、填空题(共6题；共6分)13．二次函数y=ax2+bx+c(a≠0)的部分图象如图所示，对称轴为直线x=−1，与x轴的一个交点为(1 ， 0)，与y轴的交点为(0 ， 3)，则方程ax2+bx+c=0(a≠0)的解为．14．如图抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②a﹣b+c＜0；③b+2a＝0；④当y＜0时，x的取值范围是﹣1＜x＜3；⑤当x＜0时，y随x增大而增大；⑥方程ax2+bx+c＝2有两个不等的实数根，其中结论正确的结论的序号是.15．二次函数y=x2+bx的对称轴为x=1，若关于x的一元二次方程x2+bx−c=0（c为实数），在﹣1≤x≤4范围内有解，则c的取值范围为．16．已知二次函数y=ax2+bx+c的图象如图所示，则方程ax2+bx+c=0的两根之和是．17．将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位，若得到的函数图象与直线y＝2有两个交点，则a的取值范围是.18．如图，抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(−2，4)，B(1，1)，则方程ax2=bx+c的解是.三、综合题(共6题；共70分)19．某商场销售一批名牌衬衫：平均每天可售出20件，每件盈利40元，为了扩大销售量，增加盈利，尽快减少库存，商场决定采取适当的降价促销措施，经市场调查发现：如果每件衬衫降价1元，那么平均每天就可多售出2件.（1）求出商场盈利与每件衬衫降价之间的函数关系式；（2）若每天盈利达1200元，那么每件衬衫应降价多少元？20．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，根据图象解答下列问题：（1）写出方程ax2+bx+c＝0的两个根；（2）写出不等式ax2+bx+c＞0的解集；（3）若方程ax2+bx+c＝k有两个不相等的实数根，求k的取值范围．21．已知：二次函数y＝ax2+bx+ 12（a＞0，b＜0）的图象与x轴只有一个公共点A．（1）当a＝12时，求点A的坐标；（2）求A点的坐标（只含b的代数式来表示）；（3）过点A的直线y＝x+k与二次函数的图象相交于另一点B，当b≥﹣1时，求点B的横坐标m 的取值范围．22．已知抛物线y=x2-(m+1)x+m（1）求证：抛物线与x轴一定有交点；（2）若抛物线与x轴交于A(x1,0），B（x2,0）两点，x1﹤0﹤x2,且1OA−1OB=−34,求m的值. 23．十一黄金周期间，某商场销售一种成本为每件60元的服装，规定销售期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=-x+120（1）销售单价定为多少元时，该商场获得的利润恰为500元？（2）设该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少？24．如图，抛物线y=ax2+bx−4a(a≠0)经过A(−1，0)，C(0，4)两点，与x轴交于另一点B，连接AC，BC．（1）求抛物线的解析式；（2）平行于x轴的直线y=−14与抛物线分别交于点D，E，求线段DE的长．参考答案1．【答案】D2．【答案】C3．【答案】B4．【答案】A5．【答案】A6．【答案】B7．【答案】A8．【答案】A9．【答案】D10．【答案】B11．【答案】A12．【答案】C13．【答案】x1=114．【答案】①③⑤⑥15．【答案】−1≤c≤816．【答案】217．【答案】a＜518．【答案】x1=−219．【答案】（1）解：设每件降低x元，获得的总利润为y元则y＝（40﹣x）（20+2x）＝﹣2x2+60x+800（2）解：∵当y＝1200元时，即﹣2x2+60x+800＝1200∴x1＝10，x2＝20∵需尽快减少库存∴每件应降低20元时，商场每天盈利1200元。

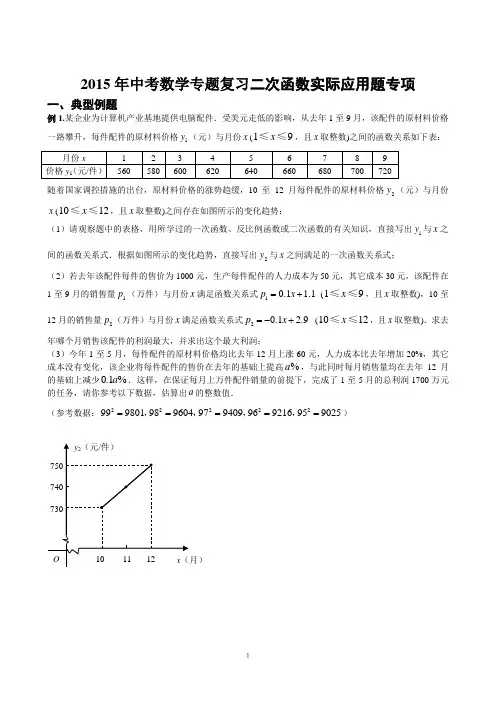
１2015年中考数学专题复习二次函数实际应用题专项一、典型例题例1.某企业为计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格1y （元）与月份x (19x ≤≤，且x 取整数)之间的函数关系如下表：月份x 1 2 3 4 5 6 7 8 9 价格y 1（元/件） 560580600620640660680700720随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格2y （元）与月份x (1012x ≤≤，且x 取整数)之间存在如图所示的变化趋势：（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出1y 与x 之间的函数关系式．根据如图所示的变化趋势，直接写出2y 与x 之间满足的一次函数关系式；（2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量1p （万件）与月份x 满足函数关系式10.1 1.1p x =+ (19x ≤≤，且x 取整数)，10至12月的销售量2p （万件）与月份x 满足函数关系式20.1 2.9p x =-+ (1012x ≤≤，且x 取整数)．求去年哪个月销售该配件的利润最大，并求出这个最大利润；（3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高%a ，与此同时每月销售量均在去年12月的基础上减少0.1%a ．这样，在保证每月上万件配件销量的前提下，完成了1至5月的总利润1700万元的任务，请你参考以下数据，估算出a 的整数值．（参考数据：2999801=，2989604=，2979409=，2969216=，2959025=）y 2（元/件）x （月）750 740 73010 11 12O２例2.星光中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x 米．（1）若平行于墙的一边的长为y 米，直接写出y 与x 之间的函数关系式及其自变量x 的取值范围； （2）垂直于墙的一边的长为多少米时，这个苗圃园的面积最大，并求出这个最大值；（3）当这个苗圃园的面积不小于88平方米时，试结合函数图象，直接写出x 的取值范围．例3.如图是二次函数2122y x =-+的图象在x 轴上方的一部分，若这段图象与x 轴所围成的阴影部分面积为S ，试求出S 取值的一个范围． 例4. 新星电子科技公司积极应对2008年世界金融危机，及时调整投资方向，瞄准光伏产业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）．公司累积获得的利润y （万元）与销售时间第x （月）之间的函数关系式（即前x 个月的利润总和y 与x 之间的关系）对应的点都在如图所示的图象上．该图象从左至右，依次是线段OA 、曲线AB 和曲线BC ，其中曲线AB 为抛物线的一部分，点A 为该抛物线的顶点，曲线BC 为另一抛物线252051230y x x =-+-的一部分，且点A ，B ，C 的横坐标分别为4，10，12（1）求该公司累积获得的利润y （万元）与时间第x （月）之间的函数关系式；（2）直接写出第x 个月所获利润s （万元）与时间x （月）之间的函数关系式（不需要写出计算过程）；（3）前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？y （万元） （月） xAB C440- 10 12 0 （图）３例5. 某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙（墙的长度不限），另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD ．已知木栏总长为120米，设AB 边的长为x 米，长方形ABCD 的面积为S 平方米．（1）求S 与x 之间的函数关系式（不要求写出自变量x 的取值范围）．当x 为何值时，S 取得最值（请指出是最大值还是最小值）？并求出这个最值；（2）学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为1O 和2O ，且1O 到AB BC AD 、、的距离与2O 到CD BC AD 、、的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当（1）中S 取得最值时，请问这个设计是否可行？若可行，求出圆的半径；若不可行，请说明理由．三、能力训练1. 如图，A 、B 、C 、D 为⊙O 的四等分点，动点P 从圆心O 出发，沿O — C — D — O 路线作匀速运动．设运动时间为t （s ），∠APB=y （°），则下列图象中表示y 与t 之间函数关系最恰当的是（ ）2. 如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x 的变化而变化，那么表示y 与x 之间函数关系的图象大致为( )3. 如图，点C D 、是以线段AB 为公共弦的两条圆弧的中点，4AB ，点E F 、OPDCBA y t9045y t9045y t 0904545900t y A B C D围墙A BC D O 1O 2CABxyOB ．x yO C ． xyO A ．xyO D ．４分别是线段CD AB 、上的动点，设22AF x AE FE y =-=，，则能表示y 与x 的函数关系的图象是（ ）4. 某公园草坪的防护栏是由100段形状相同的抛物线形组成的．为了牢固起见，每段护栏需要间距0.4m 加设一根不锈钢的支柱，防护栏的最高点距底部0.5m （如图），则这条防护栏需要不锈钢支柱的总长度至少为（ ） A ．50m B ．100 m C ．160 m D ．200 m5. 农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房如图所示，则需要塑料布y （m 2）与半径R （m ）的函数关系式是（不考虑塑料埋在土里的部分） ．6. 如图，ABC △是一块锐角三角形材料，边6cm BC =，高4cm AD =．要把它加工成一个矩形零件，使矩形的一边在BC 上，其余两 个顶点分别在AB AC ，上，要使矩形EGHF 的面积最大，EG 的长 应为 cm ．7. 如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千．拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米．20.50.4单位：mAB C D E M F G H 2米2.5米 1米0.5米2R 米30米５8. 我市某外资企业生产的一批产品上市后30天内全部售完，该企业对这批产品上市后每天的销售情况进行了跟踪调查．其中，国内市场的日销售量1y （万件）与时间t （t 为整数，单位：天）的部分对应值如下表所示．而国外市场的日销售量2y （万件）与时间t （t 为整数，单位：天）的关系如右图所示． 时间t （天） 051015202530日销售量1y （万件）0 25 40 45 40 25 0（1）请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示1y 与t 的变化规律，写出1y 与t 的函数关系式及自变量t 的取值范围；（2）分别探求该产品在国外市场上市20天前（不含第20天）与20天后（含第20天）的日销售量2y 与时间t 所符合的函数关系式，并写出自变量t 的取值范围；（3）设国内、外市场的日销售总量为y 万件，写出y 与时间t 的函数关系式，并判断上市第几天国内、外市场的日销售总量y 最大，并求出此时的最大值．9. 连接上海市区到浦东国际机场的磁悬浮轨道全长约为30km ，列车走完全程包含启动加速、匀速运行、制动减速三个阶段．已知磁悬浮列车从启动加速到稳定匀速动行共需200秒，在这段时间内记录下下列数据：时间t （秒） 0 50 100 150 200 速度υ（米／秒） 0 30 60 90 120 路程s （米）7503000675012000（1）请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段（0200t ≤≤）速度υ与时间t 的函数关系、路程s 与时间t 的函数关系．（2）最新研究表明，此种列车的稳定动行速度可达180米／秒，为了检测稳定运行时各项指标，在列车达到这一速度后至少要运行100秒，才能收集全相关数据．若在加速过程中路程、速度随时间的变化关系仍然满足（1）中的函数关系式，并且制动减速所需路程与启动加速的路程相同．根据以上要求，至少还．要再建．．．多长轨道就能满足试验检测要求？ （3）若减速过程与加速过程完全相反．根据对问题（2）的研究，直接写出列车在试验检测过程中从启动到停车这段时间内，列车离开起点的距离y （米）与时间t （秒）的函数关系式（不需要写出过程）0 5 10 15 20 25 30 304020 102()y 万件()t 天６10. 红星公司生产的某种时令商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m （件）与时间t （天）的关系如下表： 时间t （天） 1 3 5 10 36 … 日销售量m （件）9490847624…未来40天内，前20天每天的价格1y （元/件）与时间t （天）的函数关系式为11254y t =-（120t ≤≤且t 为整数），后20天每天的价格2y （元/件）与时间t （天）的函数关系式为21402y t =-+（2140t ≤≤且t 为整数）．下面我们就来研究销售这种商品的有关问题：（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m （件）与t （天）之间的关系式；（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a 元利润（4a <）给希望工程．公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t （天）的增大而增大，求a 的取值范围．四、思维拓展11. 如图，把一张长10cm ，宽8cm 的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．（1）要使长方体盒子的底面积为48cm 2，那么剪去的正方形的边长为多少？（2）你感到折合而成的长方体盒子的侧面积会不会有更大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由；（3）如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形，然后折合成一个有盖的长方体盒子，是否有侧面积最大的情况；如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由．12. 某大学毕业生响应国家“自主创业”的号召，投资开办了一个装饰品商店．该店采购进一种今年新上７市的饰品进行了30天的试销售，购进价格为20元/件．销售结束后，得知日销售量P （件）与销售时间x （天）之间有如下关系：280P x =-+（130x ≤≤，且x 为整数）；又知前20天的销售价格1Q （元/件）与销售时间x （天）之间有如下关系：11302Q x =+（120x ≤≤，且x 为整数），后10天的销售价格2Q （元/件）与销售时间x （天）之间有如下关系：145Q =（2130x ≤≤，且x 为整数）． （1）试写出该商店前20天的日销售利润1R （元）与后10天的日销售利润2R （元）分别与销售时间x （天）之间的函数关系式；（2）请问在这30天的试销售中，哪一天的日销售利润最大？并求出这个最大利润． 注：销售利润＝销售收入－购进成本．13. 某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y （元/件）与月销量x （件）的函数关系式为y =1001-x ＋150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w 内（元）（利润 = 销售额－成本－广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a 元/件（a 为常数，10≤a ≤40），当月销量为x （件）时，每月还需缴纳1001x 2元的附加费，设月利润为w 外（元）（利润 = 销售额－成本－附加费）． （1）当x = 1000时，y = 元/件，w 内 = 元；（2）分别求出w 内，w 外与x 间的函数关系式（不必写x 的取值范围）；（3）当x 为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a 的值；（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？14. 某商店以6元/千克的价格购进某种干果1140千克，并对其进行筛选分成甲级干果与乙级干果后同时．．开始销售．这批干果销售结束后，店主从销售统计中发现：甲级干果与乙级干果在销售过程中每天都有销售量，且在同一天卖完；甲级干果从开始销售至销售的第x 天的总销售量．．1y （千克）与x 的关系为８2140y x x =-+；乙级干果从开始销售至销售的第t 天的总销售量．．2y （千克）与t 的关系为221y at bt =+，且乙级干果的前三天的销售量的情况见下表：t 1 2 3 2y214469（1）求a b 、的值；（2）若甲级干果与乙级干果分别以8元/千克和6元/千克的零售价出售，则卖完这批干果获得的毛利润为多少元？（3）问：从第几天起乙级干果每天的销售量比甲级干果每天的销售量至少多6千克？（说明：毛利润＝销售总金额－进货总金额．这批干果进货至卖完的过程中的损耗忽略不计．）15. 某商场经营某种品牌的童装，购进时的单价是60元．根据市场调查，在一段时间内，销售单价是80元时，销售量是200件，而销售单价每降低1元，就可多售出20件． （1）写出销售量y （件）与销售单价x （元）之间的函数关系式；（2）写出销售该品牌童装获得的利润w （元）与销售单价x （元）之间的函数关系式；（3）若童装厂规定该品牌童装销售单价不低于76元，且商场要完成不少于240件的销售任务，则商场销售该品牌童装获得的最大利润是多少元？一、例题精选答案例1. 解：（1）154020(19)y x x x =+≤≤，且取整数．263010(1012)y x x x =+≤≤，且取整数．（2）设去年第x 月的利润为W 万元． 当19x ≤≤，且x 取整数时，1122(10005030)(0.1 1.1)(1000503054020)2164182(4)450W p y x x x x x =∙---=+----=-++=--+．19x ≤≤，∴当4x =时，450W =最大．当1012x ≤≤，且x 取整数时．９222(10005030)(0.1 2.9)(1000503063010)(29)W p y x x x =∙---=-+----=-．1012x ≤≤时，W 随x 的增大而减小．当10x =时，361W =最大．450361>，∴去年4月销售该配件的利润最大，最大利润为450万元．（3）去年12月销售量为：0.112 2.9 1.7-⨯+=（万件）． 今年原材料价格为：750+60=810（元）． 今年人力成本为：50(120%)60⨯+=（元）． 由题意，得[]51000(1%)8106030 1.7(10.1%)1700a a ⨯+---⨯-=．设%t a =，整理，得21099100t t -+=．解得99940120t ±=．2979409=，2969216=，而9401更接近9409． 9401∴=97．10.1t ∴≈或29.8t ≈．110a ∴≈或2980a ≈． 21.7(10.1%)1980a a -∴≥，≈舍去．10a ∴≈．答：a 的整数值为10．例2. 解：（1）()302615.y x x =-<≤（2）设矩形苗圃园的面积为.S 则()2302230Sxy x x x x ==-=-+∴()227.5112.5,S x =--+ 由（1）知，615.x <≤ ∴当7.5x =时，112.5.S =最大值即当矩形苗圃园垂直于墙的边长为7.5米时，这个苗圃园的面积最大，最大值为112.5． （3）611.x ≤≤１０例3. 解：方法一：由题意，可知这段图象与x 轴的交点为A （-2，0）、B （2，0），与y 轴的交点为C （0，2）．显然，S 在ABC ∆面积与过A 、B 、C 三点的⊙O 半圆面积之间． ∵ ABC S △=4， 12O S =2π，∴ 4<S <2π．说明：关于半圆⊙O 的面积大于图示阴影部分面积的证明，如下（对学生不要求）： 设P （x ，y ）在图示抛物线上，则 OP 2=x 2+y 2=（4-2y ）+y 2=（y -1）2+3． ∵ 0≤y ≤2， ∴ 3≤OP 2≤4．∴ 点P 在半圆x 2+y 2=3、x 2+y 2=4所夹的圆环内， 以及点P 为内圆周点（2±，1）与外圆周点A 、B 、C ．∴ 半圆⊙O 的面积大于图示阴影部分的面积． 由于内半圆的面积为12O S -3π2， ∴3π2<S <2π． 如果学生能得出此结论，可在上面结论基础上，加4分．方法二：由题意，可知这段图象与x 轴的交点为A （-2，0）、B （2，0），与y 轴的交点为C （0，2）．显然，这段图象在图示半径为3、2的两个半圆所夹的圆环内，以及过内半圆上点 P （2±，1）与半外圆上点A 、B 、C ． ∴ S 在图示两个半圆面积之间．即21π(3)2⋅<S <2122π⋅．∴ 3π2<S <2π．例4. （1）设直线OA 的方程为y kx =，则由()()00440-，，，在该直线上，404k -=，得10k =-． 10y x ∴=-．设曲线AB 所在的抛物线方程为()2440y a x =--，由于点B 在抛物线252051230y x x =-+-上，设()10B m ，，则320m =． 由于()10320B ，在抛物线上，故()23201040a=--·4． 40a ∴=．即()22104401080120y x x x =--=-+．BC A ＯxyP P A BCＯxy()()()22101234:0123410801205678952051230101112x x x y x x x x x x -==⎧⎪∴=-+=⎨⎪-+-=⎩，，，注写成，，，，亦可，，，，，， （4x =可归为第2段，10x =亦可归为第2段）（2）()()()1012340420905678959102101011121012x x x x s x x x x x x x x ⎧-=⎪⎪∴=-=⎨⎪-+=⎪⎩，，，或≤≤且为整数，，，，或≤≤且为整数，，或≤≤且为整数（注：解析式每对1个给1分，取值范围全正确给1分，共4分）（3）由（2）知，1234x =，，，时，s 均为-10；56789x =，，，，时，2090s x =-，s 有最大值90，而在101112x =，，时，10210s x =-+，在10x =时，s 有最大值110，故在10x =时，s 有最大值110．即第10个月公司所获利润最大，它是110万元．例5. 解：（1）据题意，得1202BC x =-．()212022120S x x x x ∴=-=-+．20-<， ∴当()1203022x =-=⨯-时，()2120180042S -==⨯-最大值（平方米）． （2）由（1），当S 取得最大值时，有30AB =，60BC =. 设1O ⊙的半径为r 米，圆心1O 到AB 的距离为y 米．据题意，得2302260y y r =⎧⎨+=⎩，．解得1515y r =⎧⎨=⎩，．00.5y r -=<，∴这个设计不可行．二、能力训练答案围墙A BC D O 1O 2r1. C2. A3. C4. C5. 230ππy R R =+6. 27.128. 解：（1）21165y t t =-+（030t ≤≤，t 为整数） 3分（2）从图中可知，当020t <≤时，2y 是t 的正比例函数，且图象过点(2040)，， 设2y kt =，把点(2040)，代入2y kt =，得2k =．∴当020t <≤时，22y t =．4分当2030t ≤≤时，2y 是t 的一次函数，且它的图象过点(2040)，，(300)，， 设2y =k 't+b ，把（20，40），（30，0）代入2y =k '+b ，得2040300.k b k b '+=⎧⎨'+=⎩， 解得4120.k b '=-⎧⎨=⎩，24120y t ∴=-+． 5分22(020)4120(2030).t t t y t t t <⎧∴=⎨-+⎩且为整数且为整数 ≤， ≤≤， 6分（3）由12y y y =+，得2218(020)512120(2030)5t t t t y t t t t ⎧-+<⎪⎪=⎨⎪-++⎪⎩且为整数且为整数 ≤， ≤≤，7分当020t <≤时，22118(20)8055y t t t =-+=--+．t 为整数，∴当19t =时，y 最大值为79.8万件．8分当2030t ≤≤时，22112120(5)12555y t t t =-++=--+．y 随t 的增大而减小，∴当20t =时，y 最大值为80万件．9分综上所述，上市后第20天国内外市场日销售总量y 值最大，最大值为80万件． 10分9. （1）通过描点或找规律，确定v 与t 是一次函数，35v t =s 与t 是二次函数，2310s t =． （2）由35v t =得当180v =时，300t =秒，则232700010s t ==米27=千米． 180********⨯=米18=千米因为减速所需路程和启动加速路程相同，所以总路程为2721872⨯+= 所以还需建723042-=千米．（3）当0300t <≤时，2310s t = 当300400t <≤时，18027000s t =-当400700t <≤时，23(700)7200010s t =--+（一般式为234207500010s t t =-+-）．10. 解：（1）将194t m =⎧⎨=⎩，和390t m =⎧⎨=⎩，代入一次函数m kt b =+中，有94903k b k b=+⎧⎨=+⎩，．296k b =-⎧∴⎨=⎩，． 296m t ∴=-+． 经检验，其它点的坐标均适合以上解析式， 故所求函数解析式为296m t =-+．（2）设前20天日销售利润为1p 元，后20天日销售利润为2p 元． 由221111(296)514480(14)578422p t t t t t ⎛⎫=-++=-++=--+ ⎪⎝⎭， 120t ≤≤，∴当14t =时，1p 有最大值578（元）．由2221(296)20881920(44)162p t t t t t ⎛⎫=-+-+=-+=-- ⎪⎝⎭．2140t ≤≤且对称轴为44t =，∴函数2p 在2140t ≤≤上随t 的增大而减小．∴当21t =时，2p 有最大值为2(2144)1652916513--=-=（元）． 578513>，故第14天时，销售利润最大，为578元．（3）2111(296)5(142)4809642p t t a t a t a ⎛⎫=-++-=-+++- ⎪⎝⎭对称轴为(142)142122a t a -+==+⎛⎫⨯- ⎪⎝⎭．120t ≤≤，∴当14220a +≥即3a ≥时，1p 随t 的增大而增大．又4a <，34a ∴<≤．三、思维拓展答案11. 解：（1）设正方形的边长为x cm ，则(102)(82)48x x --=．1分即2980x x -+=．解得18x =（不合题意，舍去），21x =．∴剪去的正方形的边长为1cm ．3分（注：通过观察、验证直接写出正确结果给3分） （2）有侧面积最大的情况．设正方形的边长为x cm ，盒子的侧面积为y cm 2， 则y 与x 的函数关系式为：2(102)2(82)y x x x x =-+-．即2836y x x =-+．5分改写为2981842y x ⎛⎫=--+ ⎪⎝⎭．∴当 2.25x =时，40.5y =最大．即当剪去的正方形的边长为2.25cm 时，长方体盒子的侧面积最大为40.5cm 2．7分（3）有侧面积最大的情况．设正方形的边长为x cm ，盒子的侧面积为y cm 2．若按图1所示的方法剪折，则y 与x 的函数关系式为：1022(82)22xy x x x -=-+． 即213169666y x ⎛⎫=--+ ⎪⎝⎭．∴当136x =时，1696y =最大． 9分 若按图2所示的方法剪折，则y 与x 的函数关系式为：822(102)22xy x x x -=-+．即2798633y x ⎛⎫=--+ ⎪⎝⎭．∴当73x =时，983y =最大． 11分比较以上两种剪折方法可以看出，按图2所示的方法剪折得到的盒子侧面积最大，即当剪去的正方形的边长为73cm 时，折成的有盖长方体盒子的侧面积最大，最大面积为983cm 2．图1图212. 解：（1）根据题意，得111(20)(280)[(30)20]2R P Q x x =-=-++-＝220800(120)x x x x -++≤≤，且为整数22(20)(280)(4520)502000(2130.)R P Q x x x x =-=-+-=-+≤≤且为整数（2）在120x ≤≤，且x 为整数时， ∵21(10)900R x =--+∴当10x =时，1R 的最大值为900. 在2130x ≤≤，且x 为整数时，∵在2502000R x =-+中，2R 的值随x 值的增大而减小， ∴当21x =时，2R 的最大值是950.∵950>900.∴当21x =即在第21天时，日销售利润最大，最大值为950元．13. 解：（1）140 57500；（2）w 内 = x （y -20）- 62500 = 1001-x 2＋130 x 62500-， w 外 = 1001-x 2＋（150a -）x ． （3）当x = )1001(2130-⨯-= 6500时，w 内最大；分由题意得2214()(62500)1300(150)100114()4()100100a ⨯-⨯----=⨯-⨯-，解得a 1 = 30，a 2 = 270（不合题意，舍去）．所以 a = 30． （4）当x = 5000时，w 内 = 337500， w 外 =5000500000a -+． 若w 内 ＜ w 外，则a ＜32.5； 若w 内 = w 外，则a = 32.5； 若w 内 ＞ w 外，则a ＞32.5．所以，当10≤ a ＜32.5时，选择在国外销售； 当a = 32.5时，在国外和国内销售都一样；当32.5＜ a ≤40时，选择在国内销售．14. 解：（1）选取表中两组数据，求得120a b ==，； （2）甲级干果与乙级干果n 天销完这批货． 则224201140n n n n -+++=． 即601140n =．解之得19n =． 当19n =时，1399y =，2741y =．毛利润＝3998741611406798⨯+⨯-⨯=（元）； （3）第n 天甲级干果的销售量为241n -+． 第n 天乙级干果的销售量为219n +．(219)(241)6n n +--+≥．解之得 7n ≥． 答：（略）15. 解：（1）由题意，得：()2008020v x =+-⨯=201800x -+．答：y 与x 之间的函数关系式是2201800y x =-+．（2）由题意，得：()()60201800w x x =--+=2203000108000x x -+-．答：w 与x 之间的函数关系式是203000108000y x x =-+-．（3）由题意，得：20180024076x x -+⎧⎨⎩，．≥≥解得7678x ≤≤．2203000108000w x x =-+-，对称轴为()300075220x =-=⨯-，又0a <，∴当7678x ≤≤时，w 随x 增大而减小． ∴当76x =时，()()7660207618004480w =-⨯-⨯+=最大．答：这段时间商场最多获利4480元．。

中考数学总复习之二次函数专题复习一．选择题（共8小题）1．二次函数y＝2x2+8x+5的图象的顶点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．把二次函数y＝x2+2x﹣6配方成顶点式为（）A．y＝（x﹣1）2﹣7B．y＝（x+1）2﹣7C．y＝（x+2）2﹣10D．y＝（x﹣3）2+33．已知二次函数y＝（a﹣2）x2，当x＞0时，y随x的增大而减小，则实数a的取值范围是（）A．a＞0B．a＞2C．a≠2D．a＜24．关于抛物线y＝（x﹣1）2﹣2，以下说法正确的是（）A．抛物线在直线x＝﹣1右侧的部分是上升的B．抛物线在直线x＝﹣1右侧的部分是下降的C．抛物线在直线x＝1右侧的部分是上升的D．抛物线在直线x＝1右侧的部分是下降的5．2019年在武汉市举行了军运会，在军运会比赛中，某次羽毛球的运动路线可以看作是抛物线y＝x2+x+的一部分（如图），其中出球点B离地面O点的距离是米，球落点的距离是（）A．1米B．3米C．5米D．米6．二次函数y＝x2﹣3x+1的图象大致是（）A．B．C．D．7．无论k为何值，直线y＝kx﹣2k+2与抛物线y＝ax2﹣2ax﹣3a总有公共点，则a的取值范围是（）A．a＞0B．C．或a＞0D．8．如图，已知开口向上的抛物线y＝ax2+bx+c与x轴交于点（﹣1，0），对称轴为直线x＝1．下列结论：①abc＞0；②2a+b＝0；③若关于x的方程ax2+bx+c+1＝0一定有两个不相等的实数根；④a＞．其中正确的个数有（）A．1个B．2个C．3个D．4个二．填空题（共8小题）9．如图，某学校拟建一块矩形花圃，打算一边利用学校现有的墙（墙足够长），其余三边除门外用栅栏围成，栅栏总长度为38m，门宽为2m．这个矩形花圃的最大面积是．10．如图，同学们在操场上玩跳大绳游戏，绳甩到最高处时的形状是抛物线型，摇绳的甲、乙两名同学拿绳的手的间距为6米，到地面的距离AO与BD均为0.9米，绳子甩到最高点C处时，最高点距地面的垂直距离为1.8米．身高为1.4米的小吉站在距点O水平距离为m米处，若他能够正常跳大绳（绳子甩到最高时超过他的头顶），则m的取值范围是．11．二次函数y＝2x2的图象如图所示，点O为坐标原点，点A在y轴的正半轴上，点B、C 在函数图象上，四边形OBAC为菱形，且∠AOB＝30°，则点C的坐标为．12．二次函数的图象如图所示，点A0位于坐标原点，点A1，A2，A3，…，A2023在y轴的正半轴上，点B1，B2，B3，…，B2023在二次函数位于第一象限的图象上，若△A0B1A1，△A1B2A2，△A2B3A3，…，△A2022B2023A2023都为等边三角形，则△A2022B2023A2023的边长为．13．已知二次函数y＝（x﹣3）2+3，当x＝时，y取得最小值．14．已知抛物线y＝x2+bx+c的部分图象如图所示，当y＞0时，x的取值范围是．15．如图，二次函数y＝﹣x2+mx的图象与x轴交于坐标原点和（6，0），若关于x的方程x2﹣mx+t＝0（t为实数）在1≤x＜5的范围内有解，则t的取值范围是．16．二次函数y＝ax2+bx﹣3（a≠0）的图象经过点（1，4），则代数式a+b的值为．三．解答题（共4小题）17．如图，已知二次函数y＝ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A（﹣1，0）和点B，点P是直线BC上方的抛物线上一动点．（1）求二次函数的表达式；（2）求BC所在直线的函数解析式；（3）过点P作PM∥y轴交直线BC于点M，求线段PM长度的最大值．18．如图，直线y＝x+2与x轴交于点B，与y轴交于点D．抛物线y＝ax2+bx﹣4与x轴交于点A（4，0）和点B，与y轴交于点C．（1）求该抛物线的解析式；（2）如图，点P为抛物线在直线AC下方的一动点，作PH∥y轴，PF⊥AC，分别交AC 于点H、F，求PH+PF的最大值和此时点P的坐标；（3）在（2）的条件下，将抛物线y＝ax2+bx﹣4沿射线AC平移个单位长度，得到新抛物线，点R在新抛物线的对称轴上，点S在抛物线y＝ax2+bx﹣4上．当以点D、P、R、S为顶点的四边形是平行四边形时，写出所有符合条件的点R的坐标，并写出求解点R的坐标的其中一种情况的过程．19．如图，已知抛物线y＝﹣x2+mx+3与x轴交于A、B两点，与y轴交于点C，点B的坐标为（3，0）．（1）求m的值及抛物线的顶点坐标；（2）求抛物线与坐标轴的交点所围成的三角形面积；（3）点P是抛物线对称轴l上的一个动点，当P A+PC的值最小时，求点P的坐标．。