下载文档原格式
北大课程曼昆经济学原理上微观部分第一次作业答案集团档案编码：[YTTR-YTPT28-YTNTL98-UYTYNN08]第一次作业答案一、你在篮球比赛的赌注中赢了100美元。
你可以选择现在花掉它或者在利率为5%的银行账户中存一年。
现在花掉100美元的机会成本是什么呢？解：一种东西的机会成本是为了得到这种东西所放弃的东西。
同样，一种选择的机会成本是执行这种选择所必须放弃的其它选择。
更确切地说，一种选择的机会成本是除这种选择之外，其它所有选择中的最大收益。
古人常说“有一得必有一失”，实质上就包含了机会成本的含义。
就本题而言，100美元存在银行里，一年后的收益是5美元，因此，现在花掉100美元的机会成本是5美元。
如果你还可以用100购买彩票，且期望获利是110美元，那么本题的答案就会变为：消费（方式1）的机会成本是10美元，（方式2和3中的最大收益）；储蓄（方式2）的机会成本是10美元，（方式1和3中的最大收益）；购买彩票（方式3）的机会成本是5美元，（方式1和2中的最大收益）。
显然理性的消费者是不会马上消费或储蓄，他最好的选择是购买彩票。
（注：本题只是考虑机会成本，忽略了其它一些因素，如果考虑彩票收益的不确定性等因素，答案会不一样）二、一个经济由Larry、Moe、Curly这三个工人组成。
每个工人每天工作10小时，并可以提供两种服务：割草和洗汽车。
在一个小时内，Larry可以割一块草地或洗一辆汽车，Moe可以割一块草地或洗两辆汽车，而Curly可以割两块草地或洗一辆汽车。
a、计算在以下情况（即我所标的A、B、C和D）时，各能提供多少每种服务：·三个工人把他们所有的时间都用于割草。
（A）·三个工人把他们所有的时间都用于洗汽车。
（B）·三个工人都分别把一半时间用于两种活动。
（C）·Larry分别把一半时间用于两种活动，而Moe只洗汽车，Curly只割草。
（D）b、画出这个经济的生产可能性边界。
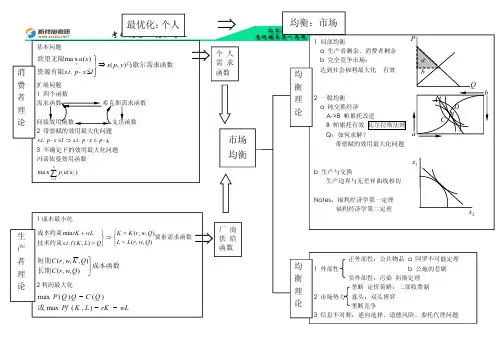
光华人向上的精神启用前机密 北京大学2002年硕士研究生入学考试试题考试科目：微观经济学 考试时间：1月27日下午招生专业：国民经济学、产业经济学、金融学、管理科学工程、企业管理试 题：(注意：答案一律写在答题纸，否则不计分)一、 (16分)假设某甲的效用函数为，x 表示他为别人提供的服务数量，每单位耗时2小时；y x U 3=y 表示他为自己提供的服务数量，每单位耗时1小时；他每天12小时休息而不工作。
(1) 他将为别人和自己分别工作多少小时?(2) 他的总效用、边际效用分别是多少?时间的边际效用是多少?检验戈森第二定理是否成立。
(3) 如果他助人为乐，是一个彻底的利他主义者(即全部时间都用来为别人工作)，给出一种可能的效用函数(修改原来的效用函数)。
(4) 如果某乙的效用函数为，你更愿意与某甲和某乙中的哪一个人共事?为什么?y x U 3=二、 (10分)给定CES 生产函数ρρρ1)(L K Q +=，Q 为产出，K 、L 分别为资本和劳动的投入量。
(1) 证明该企业规模收益不变；(2) 资本和劳动的边际产量为多少？(3) 劳动对资本的边际技术替代率是多少?(4) 证明资本和劳动的产出弹性之和等于1。
(5) 把这个企业分为两个相同的企业，分立之后的产出之和与原企业的产出有什么变化?详细写出演算过程。
三、 (20分)假定一个企业的边际成本和平均成本相等，均为C ，需求曲线为，（）请解答下列问题：e P Q =1−<e (1) 需求价格弹性是多少?(2) 如果市场是完全竞争的，产品价格如何?如果市场是垄断的，产品价格如何?(3) 当价格为时，消费者剩余是多少?0P (4) 垄断和完全竞争两种市场条件下的消费者剩余之比是多少?(5) 在和趋向于的情况下，上述(4)的比率分别为多少?请用微观经济学原理解释原因。
2−=e e 1−(6) 垄断市场条件下的垄断利润m π为多少?与完全竞争条件下消费者剩余之比为多少? 时这一比率为多少?经济学含义是什么?2−=e光华人向上的精神四、 (12分)某甲拥有财富100万元，明年他有25％的可能性会丢失一辆价值20万元的小汽车，假设他的效用函数为W W V ln )(=，W 为他的财富总量。
秋风清，秋月明,落叶聚还散,寒鸦栖复惊。
北京大学1998年光华管理学院硕士入学考试微观经济学试题一、解释并比较下列经济学基本概念(每题6分，合计30分)1.私人成本(Private Cost)与社会成本(Social Cost);2.边际替代率(Marginal Rate of Substitution)与边际技术替代率(Marginal Rate of Technical Substitution);3.产业集中指数(Industrial Concentration Index)，勒纳指数(Lerner’s Index)与贝恩指数(Bain’s Index);4.价格歧视(Price Discrimination)与二重价(Two-part Tariff);5.占优均衡(Dominant Equilibrium)与纳什均衡(Nash Equilibrium).二、简答下列各题(每题5分，合计30分)1.有些专家论证说，北京市居民大量丢失自行车，原因是自行车盗窃者把盗窃来旳自行车转手在旧车交易市场上卖掉，因此提议取缔北京市所有旧车交易市场。
请给出一种支持该观点旳论据，给出一种反对该观点旳论据。
2.某君在硕士入学考试复习期间，从经济学中悟出一种道理：应当使投入每门课程最终一单位时间旳收益都相等。
换句话说，与其投入大量旳时间使数学成绩从90分提高到95分，不如把这些时间投入到微观经济学中，使其成绩从60分提高到80分。
请给出一种支持该观点旳论据，给出一种反对该观点旳论据。
3.你怎样理解新制度经济学有关制度安排与交易成本旳关系？请举例阐明。
4.垄断存在着效率损失，请阐明是怎样产生旳？5.一般认为，竞争性市场是有效率旳，但为何有时会出现市场失灵？处理市场失灵旳措施有哪些？既然市场会出现失灵，为何我们还要建立市场经济体制？6.委托代理问题产生旳原因是什么？三、计算题(每题8分，合计24分)1.某竞争行业所有厂商旳规模都相等，都是在产量到达500单位时到达长期平均成本旳最低点4元，当用最优旳企业规模生产600单位产量时，每一种企业旳短期平均成本为4.5元，市场需求函数为Q=70000-5000P，供应函数为Q=40000+2500P，求解下列问题：⑴.市场均衡价格是多少？该行业处在短期均衡还是长期均衡？⑵.当处在长期均衡时，该行业有多少厂商？⑶.假如市场需求变化为Q=P，求行业与厂商新旳短期均衡价格与产量，在新旳均衡点，厂商盈利还是亏损？2.假定有n家相似旳厂商处在古尔诺均衡(Cournot Equilibrium)状况下，求证：市场需求曲线旳弹性一定不小于1/n。
北大光华管理学院考研真题各位考研的同学们，大家好！我是才思的一名学员，现在已经顺利的考上北大管理学院，今天和大家分享一下这个专业的真题，方便大家准备考研，希望给大家一定的帮助。
第四章历年真题（微观经济学部分）一、微观经济学（2015年）第一题亘古不变的考了消费者选择理论，推导消费者对两种商品的最优选择，然后根据这个最优选择推导这两种商品是否是奢侈品，然后再推导是否是吉芬品，说明理由。
第二题考了垄断，市场上有两类消费者，分别给出了需求函数，第一类消费者有10人，第二类消费者有20人，然后问如果垄断厂商采取两部价格定价，并且要使两类消费者都购买，垄断厂商应该如何制定入场费和边际价格；如果只需要保证一种消费者购买，应该如何制定价格策略；最后对比保留两种消费者和保留一种消费者哪个更好。
第三题记得考了厂商理论，一个厂商是价格接受者，给出成本函数，推导供给曲线。
当市场上变成了两个厂商时，平均供给与价格的关系；变成4个时，平均供给与价格的关系；变成无穷多个时平均供给与价格的关系....最后给出了需求函数，求市场均衡，并且指出市场均衡唯一存在条件。
第四题考了古诺均衡和何芬达尔指数，给出H指数的表达式，然后问如果市场上存在n个厂商，在这n个厂商古诺均衡时，证明一个所有厂商总利润与H指数和需求弹性的等式。
然后再这个基础之上将等式变形，指出如何推导。
第五题考了博弈论，有k个目击者，看到了一个犯罪分子，当有人告发时，则犯罪分子会被抓住，此时目击者效用为4；但是目击者都很忙，如果去告发，效用会-1，如果犯罪分子逍遥法外，目击者效用为0，然后问这个博弈的所有纯策略纳什均衡；当k=2时的混合策略纳什均衡；当有k个目击者时的混合策略纳什均衡，并问此时囚犯被抓住的概率（k的函数）。
才思教育机构。
北大经济微观——北大光华管理学院经济学考研真题整理北大经济（微观）——北大光华管理学院经济学考研真题整理各位考研的同学们，大家好！我是才思的一名学员，现在已经顺利的考上北大管理学院，今天和大家分享一下这个专业的真题，方便大家准备考研，希望给大家一定的帮助。
说明：08-10年真题是才思教育聘请北大光华管理学院老师总结整理的答案，其他答案由才思教育金牌讲师总结整理。
一、2010年微观经济学答案解析（一）农民效果函数为alogX1+（1-a）log（X2-K）,k>0,X1为大米，X2为其他商品组合，农民禀赋为（R1,R2），禀赋固定不变。
1.求农民什么时候出售大米，出售的大米量与大米价格正相关吗？【才思教育解析】农民s.t.则L=-FOC条件=0 ==0 =①②= 代入并取等号，得：出售大米量=令上式0 时出售大米当时，出售量与正相关；当k时，负相关；当k时，无关。
2.若农民消费其他商品有配额限制，对农民出售大米的意愿有影响吗？【才思教育解析】当的消费有配额限制，则出售大米的钱不能购买更多的，故没有意愿出售大米。
（二）一个企业有三个车间，各自的成本函数为C1=4X1+X12，C2=3X2+2X22，C3=6X3问：当这个个企业要生产8单位时，应如何分配产量，使成本最小。
【才思教育解析】分配产量时，应使各车间的边际成本一样大M= M= M，即4+2=3+4=6, ,=（三）市场上有A、B两种消费者，各占50%。
A的效用函数为5x - 0.5x2+y，B 为6x- 0.5x2+y垄断厂商的成本为C(x)=X, x 为垄断厂商生产的商品，y为其他商品组合，价格为11.求A,B各自的需求曲线2.若垄断厂商在AB中选一种出售商品，那么你认为应该选择哪个？垄断厂商采用2部分定价，那么边际价格和一次性付费是多少？3.若同时在AB中出售，并且采用2部分定价，问厂商以什么边际价格和一次性付费为多少能够达到利润最大化。
Problem Set 31． Why is there a social cost to monopoly power? If the gain to producers frommonopoly power could be redistributed to consumers, would the social cost of monopoly power be eliminated? Explain briefly.2．A monopolistic firm faces the following average revenue (demand) curve: P = 100 – 0.01Q where Q is weekly production and P is price, measured in cents per unit. The firm’s cost function is given by C = 50Q+30000.A) What is the level of production, price, and total profit per week?B) The government decides to levy a tax of 10 cents per unit on this product. What will the new level of production, price, and profit be as a result?3．A monopolistic firm has two factories, for which costs are given by:Factory #1: C 1(Q 1) = 10Q 12Factory #2: C 2(Q 2) = 20Q 22The firm faces the following demand curve: P = 700 – 5Q, where Q is total output (Q=Q 1+Q 2).A) Calculate the values of Q 1, Q 2, Q, and P that maximize profits. Also draw a diagram to illustrate the optimal choices of this firm.B) Suppose labor costs increase in Factory 1 but not in Factory 2. How should the firm adjust Q 1, Q 2, Q, and P?4. Suppose that a monopoly can produce any level of output it wishes at a constant marginal cost $5 per unit. Assume that the monopoly sells its goods in two different markets that are separated by some distance. The demand curve in the first market is given by Q 1=55-P 1, and the demand curve in the second market is given by Q 2=70-2P 2.1) If the monopolist can maintain the separation between the two markets, what level of output should be produced in each market, and what price will prevail in each market? What are total profits in this situation?2) How would your answer change if it only costs demanders $5 to transport goods between the two markets? What would be the monopolist’s new profits in this situation?3) How would your answer change if transportation costs were zero and the firm was forced to follow s single-price policy?4) Suppose the firm could adopt a linear two-part tariff under which marginal prices must be equal in the two markets but lump-sum entry fees might vary. What pricing policy should the firm follow?5. A monopoly supplies its products in two segmented markets. The first market’s demand is , and the second is 1110P Q −=22P A Q −=. The firm’s cost function is , where , and Q is the output.Q C 5=2010≤<Aa) Suppose the monopoly has to set the same price in these two markets, what is it? Why should we assume that ? What if this condition does not hold?20≤Ab) Suppose the monopoly is able to implement the third-degree discrimination. Derive the profit-maximizing prices in the two markets.c) Compare social welfares under a) and b). Does the third-degree discrimination improve social welfare? Why? Please give an intuitive interpretation.。
北大光华微观经济学练习Intermediate MicroeconomicsProblem Set 2(Due Date: Nov. 14)1． Jane owns a house that is worth $100,000. She cares only about her wealth, whichconsists entirely of the house. In any given year, there is a 20% chance that the house will burn down. If it does, its scrap value will be $22,500. Jane’s von Neumann-Morgenstern utility function is 1/2()u W W =.a) Is Jane risk averse, risk neutral or a risk lover? Explain.b) W hat is the expected monetary value of Jane’s uncertainty?c) What is the maximum that Jane is willing to pay to completely insure her house against being destroyed by the fire?d) Say that Homer is the president of an insurance company. He is risk neutral and has a utility function of the following type ()u W W =, where W is his wealth. What is the lowest price at which he is willing to provide a fair insurance contract to completely insure Jane’s risk?2．Suppose that the process of producing lightweight p arkas by Polly’s Parkas isdescribed by the function Q = 10K 0.8(L-40)0.2, where Q is the number of parkas produced, K is the number of machine hours, and L is the number of person-hours of labors.e) Derive the cost-minimizing demands for K and L as a function of Q, wage rates (w), and rental rates on machines (r). Use these to derive the total cost function. f) This process requires skilled workers, who earn $32 per hour. The rental rate is$64 per hour. At these factor prices, what are total costs as a function of Q? Does this technology exhibit decreasing, constant, or increasing returns to scale?g) Polly’s Parkas plans to produce 2000 parkas per week. At the factor prices given above, how many workers should they hire (at 40 hours per week) and how many machines should they rent (at 40 machine-hours per week)? What are themarginal and average costs at this level of production?3. The short-run cost functions of two firms are given by211100y C +=and 2222816y y C ++=.a) Suppose the two firms are plants of the same firm in a competitive market. If the firm wants to produce 24 units of output, how much should it produce in each plant? Why not produce this output simply in one plant? Briefly explain.b) Suppose the two firms act independently. What is the short-run supply curve of the two firms?c) If the price is 6, what is the number of firms active in the market in the short run? Explain why.4． A firm produces a product with labor and capital and its production function is described by Q = LK, where L denotes labor and K denotes capital. Suppose that the price of labor (w) equals 2 and the price of capital (r) equals 1.a)Suppose that in the short run, capital level is fixed at K=10. Write downmathematical expressions for the short run total average cost curve, averagevariable cost curve, average fixed cost curve, and marginal cost curve.b)Derive the long-run total cost curve, average cost curveand marginal costcurve.5. Suppose the market for widgets can be described by the following equationsDemand: P = 10 – Q; Supply: P = Q – 4.where Q is the quantity in thousands of units and P is the price in dollars per unit.a)What is the equilibrium price and quantity?b)Suppose the government imposes a tax of $1 per unit to reduce widgetconsumption and raise government revenues. What will the new equilibriumquantity? What price will the buyer buy? What amount per unit will the sellerreceive?c)Suppose the government has changed its mind and decide to remove the taxand grant a subsidy of $1 per unit to widget producers. What will equilibriumquantity be? What amount per unit (including the subsidy) will the sellerreceive? What will be the total cost to the government?。
Problem Set 1
1. Draw the indifference curves for the following individuals’ preferences for two goods: hamburger and beer.
a) Al likes beer but hates hamburger. He always prefers more beer no matter how many hamburgers he has.
b) Chris eats one hamburger and washes it down with one beer. He will not consume an additional unit of one item without an additional unit of the other.
c) Doreen loves beer but is allergic to beef. Every time she eats a hamburger she
breaks out in hives.
2. Connie Consumer has a monthly income of $200, which she allocates between two goods: meat and potatoes.
a) Suppose meat costs $4 per pound and potatoes cost $2 per pound. Draw her budget constraint.
b) Suppose also that her utility function is given by the equation U(M, P)=2M+P. What combination of meat and potatoes should she buy to maximize her utility? c) Connie’s supermarket has a special promotion. If she buys 20 pounds of potatoes (at $2 per pound), she gets the next 10 pounds for free. This offer applies only to the first 20 pounds she buys. All potatoes in excess of the first 20 pounds
(excluding bonus potatoes) are still $2 per pound. Draw her budget constraint. d) An outbreak of potato rot raises the price of potatoes to $4 per pound. The
supermarket ends its promotion. What does her budget constraint look like now? What combination of meat and potatoes maximizes her utility?
4．Assume that a utility function is given by Min{X, Y}, where Min is the minimum of the two values of X and Y. What is the Slutsky equation that decomposes the change in the demand for X in response to a change in its price? What is the income effect? What is the substitution effect?
5．Using Slutsky equation shows that Giffen goods must be inferior goods, but inferior goods need not be Giffen goods.
6．Consider a consumer who purchases two goods, x and . The consumer’s utility function is . The prices are given by y 2(,)U x y xy =x P and , and the consumer’s
income is y P I .
1) Set up the Lagrangian expression for solving the consumer’s utility maximization problem (subject to budget constraint) and write down the first order conditions.
2) Derive the demand functions for goods x and y .
Assume initially 1$30I =,$x P =, an $1d y P =. Now assume the price of y increases to y P $8′=.
3) Compute the initial optimal bundle A before the price change, and the new
optimal bundle C after the price change.
4) Identify the substitution effect and income effect. What is the direction of the substitution effect? Is good y a normal, inferior, or Giffen good? Explain.。
