《直线方程的四种形式》
- 格式:ppt
- 大小:714.00 KB
- 文档页数:29

直线方程公式大全一、一般式方程直线的一般式方程表示为 Ax + By + C = 0,其中 A、B、C 为常数。
直线方程大全中的其他形式可以通过一般式方程推导得出。
二、斜截式方程斜截式方程是直线方程的另一种常见形式。
它表示为 y = mx + c,其中 m 为斜率,c 为截距。
三、截距式方程截距式方程也是直线方程的一种常见形式,表示为 x/a + y/b = 1,其中 a、b 分别为 x 轴和 y 轴的截距。
四、两点式方程两点式方程通过直线上的两个点来表示直线方程。
设直线上的两个点为 (x1, y1) 和 (x2, y2),则两点式方程表示为 (y - y1) = ((y2 - y1)/(x2 - x1))(x - x1)。
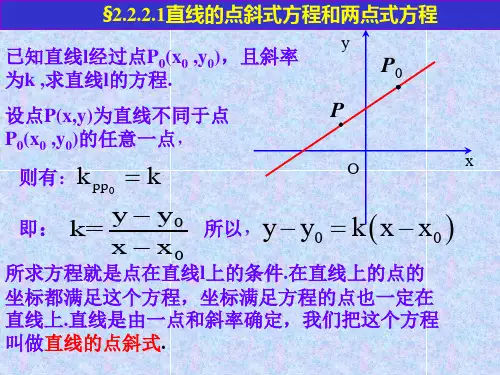
五、点斜式方程点斜式方程利用直线上的一个已知点的坐标和该直线的斜率来表示方程。
设已知点为 (x1, y1),斜率为 m,则点斜式方程表示为 y - y1 = m(x - x1)。
六、垂直线方程垂直线的特点是斜率不存在,所以其方程可以表示为 x = a,其中 a 为与 y 轴垂直的线在 x 轴上的截距。
七、水平线方程水平线的特点是斜率为零,所以其方程可以表示为 y = a,其中 a 为与 x 轴平行的线在 y 轴上的截距。
八、点式方程点式方程是直线方程中最简单的形式,利用直线上的一个已知点的坐标来表示直线方程。
设已知点为 (x1, y1),则点式方程表示为 (y - y1) = m(x - x1),其中 m 为直线的斜率。
九、角平分线方程角平分线是将一个角平分成两个相等的角的线段。
设角的两边斜率分别为 m1 和 m2,角平分线的斜率可表示为 m = (m1 + m2)/2,将平分线上的一个点坐标 (x1, y1) 代入点斜式方程可得到角平分线方程。
十、法线方程直线的法线是与该直线垂直的直线。
设直线的斜率为 m,法线的斜率可表示为-1/m,再通过已知点 (x1, y1) 可以得到法线方程。


直线方程百度百科直线方程是描述平面上一条直线的数学表达式,它是数学中的重要概念之一。
直线方程可以通过多种方法推导和表示,包括点斜式、斜截式、一般式等等。
在本文中,我们将介绍直线方程的基本定义、常见表示方法以及相关概念。
直线方程的基本定义直线方程是通过点和直线的关系来表示的。
在平面几何中,我们知道一条直线可以由两个不同的点唯一确定。
因此,直线方程的基本定义可以简单描述为:给定直线上两个不同的点,通过这两个点可以得到直线方程。
点斜式直线方程点斜式直线方程是直线方程中最常见的一种表示方式。
它利用直线上的一个点的坐标和直线的斜率来表示直线方程。
点斜式直线方程的一般形式为:y - y1 = m(x - x1)在上述方程中,(x1, y1)表示直线上的某一点,m表示直线的斜率。
斜率表示了直线在平面上的倾斜程度,可以通过两个点的坐标来计算得到。
斜截式直线方程斜截式直线方程是直线方程中的另一种常见表示方法。
它通过直线的斜率和截距来表示直线方程。
斜截式直线方程的一般形式为:y = mx + b在上述方程中,m表示直线的斜率,b表示直线在 y 轴上的截距。
斜截式直线方程更加简洁,易于理解和计算。
一般式直线方程一般式直线方程是直线方程中的一种标准形式,它通过直线的一般系数来表示。
一般式直线方程的一般形式为:Ax + By + C = 0在上述方程中,A、B和C都是实数,且A和B不同时为 0。
一般式直线方程可以通过将斜截式直线方程或点斜式直线方程进行变换得到。
直线方程的应用直线方程在数学和实际应用中有着广泛的应用。
在几何学中,直线方程被用于计算直线的斜率、交点等性质。
在物理学和工程学中,直线方程被用于描述物体的运动、电路的行为等。
直线方程也常常和其他数学概念结合使用,比如与曲线方程相结合来求解方程组等。
总结通过本文,我们了解了直线方程的基本定义以及常见的表示方法。
点斜式直线方程、斜截式直线方程和一般式直线方程是直线方程中常用的表示形式。


高二数学直线方程的四种形式(1)练习1. 过点(4,2)-,倾斜角为135ο的直线方程是().A20y++-B360y+++=C.40x+-=D.40x++=2. 已知直线的方程是21y x+=--,则(). A.直线经过点(2,1)-,斜率为1-B.直线经过点(2,1)--,斜率为1C.直线经过点(1,2)--,斜率为1-D.直线经过点(1,2)-,斜率为1-3. 直线l过点(1,1),(2,5)--两点,点(1002,)b在l上,则b的值为().A.2003 B.2004 C.2005 D.20064. 直线y ax b=+(0a b+=)的图象是( )5.方程331--=+xy表示过点______、斜率是____、倾斜角是___、在y轴上的截距是________的直线。
6.过点P(2, 3),并且在两坐标轴上的截距相等的直线的方程为________________________。
7.过点P(2, 3),并且在x轴上的截距是在y轴上的截距2倍的直线的方程___________________。
8. 已知点(1,2),(3,1)A B,则线段A B的垂直平分线的方程是 .9. 在x轴上的截距为2,在y轴上的截距为3-的直线方程 .10.求经过点(1,2),且与直线23y x=-平行的直线方程.___________11.直线48y x=+与坐标轴所围成的三角形的面积__________.12. 直线l的倾斜角比直线122y=+的倾斜角大45ο,且直线l的纵截距为3,则直线的方程是______________13. 已知三角形的三个顶点(5,0),(3,3)A B--,(0,2)C,求B C边所在直线的方程,以及该边上中线所在直线的方程.(写成点斜式)14.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点。
(1)求AB边所在的直线方程;(2)求中线AM的长(3)求AB边的高所在直线方程。



直线方程的几种表达形式直线是二维空间中最基本的图形之一,它可以用不同的方式来表达其方程。
我们下面将探讨一下几种不同的直线表达形式。
1. 坐标式:直线可由其上两点 $(x_1,y_1),(x_2,y_2)$ 来确定。
假设这两点不同,那么直线的坐标式可以表示为:$y-y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x-x_1)$这个式子可以化简为:$y = \frac{y_2 - y_1}{x_2 - x_1}(x-x_1) +y_1$。
2. 斜截式:斜截式直线方程使用直线斜率和一条相交直线的截距来描述。
假设我们知道直线上一点 $(a,b)$ 和直线的斜率 $m$,那么直线的斜截式方程为:$y = mx + b$3. 一般式:一般式是表示直线方程的另一种方式,它通常使用 $Ax+By+C=0$ 的格式。
直线方程的一般式可通过化简 $Ax+By+C=0$ 得到。
例如,假设我们知道直线斜率 $m$ 和 $y$ 截距 $b$,那么直线就可以化简为如下的一般式:$y = mx + b$ 可以简化为 $-mx + y - b = 0$。
4. 向量式:向量方程是直线方程的另一种描述方式。
向量可以表示为 $(x,y)$。
直线的向量方程可由一个点 $(x_0, y_0)$ 和斜率向量 $(a,b)$ 给出:$(x,y) = (x_0, y_0) + t(a,b)$,其中 $t$ 是任意实数,表示从该点开始的直线上的任意点。
最后,需要注意的是,这四种直线表达形式是等效的,因此可以相互转换。
综上所述,我们已经介绍了直线的几种表达形式。
了解它们有助于我们更深入地理解直线的性质和特点。

注意直线方程的适用范围直线方程的四种形式(点斜式、斜截式、两点式、截距式)都有各自的适用范围:点斜式和斜截式适用于斜率存在的情形,而截距式要求直线纵、横截距均存在且不为零,两点式适用于直线的斜率存在且不为零。
当已知直线过两已知点时,其方程简单易求。
而在使用直线方程的点斜式、斜截式、截距式等形式时容易犯如下的错误:一是利用点斜式、斜截式求直线方程时,忽视斜率不存在的情形;一类是应用直线的截距式时,忽视直线过坐标原点。
例1:求过点()3,2P 且被两条直线1l :0633=+-y x ;2l :033=-y x 所截得的线段长为2的直线方程。
错解:两平行直线1l 和2l 之间的距离:3936=+=d ,而所求直线l 被两平行直线截得的线段长为2,故所求直线l 与直线1l 和2l 的夹角为060,设直线l 的斜率为k ,则333133=+-k k ,则得到33-=k 。
则所求直线方程()2333--=-x y ,即013=-+y x 。
剖析:用直线的点斜式方程来解本题,就意味着该直线的斜率一定存在,但是直线2=x 的斜率不存在,但是满足题意,因此上述的解答不全面,正确的答案应该是两条直线013=-+y x 和2=x 。
评注:考虑问题一定要全面细致,特别是针对斜率不存在的直线。
例2:求过点()4,2M 向圆()()13122=++-y x 所引切线方程。
错解: ()()150341222>=++-,∴点()4,2M 在圆外, 设过点M 的切线为()24-=-x k y ,即042=+--k y kx ,则圆心到切线的距离为()1142312=++---⨯=k k k d ,则724=k ,则所求的切线方程为 020724=--y x 。
剖析:过圆外一点作圆的切线应该有两条,若所求的斜率只有一个,应该找出过该点而斜率不存在的另一条切线,本题忽略了直线2=x评注:要注意的规律是过圆外一点作圆的切线应该有两条。
直线方程(直线方程完美总结归纳)一、倾斜角与斜率直线的倾斜角是指直线与x轴正方向的夹角。
当直线与x 轴平行或重合时,其倾斜角规定为0度。
倾斜角的范围是小于等于α,且α小于180度。
直线的斜率是指直线倾斜角的正切值,记作k=tanα(α不等于90度)。
当直线与x轴平行或重合时,斜率为0;当直线与x轴垂直时,斜率不存在。
经过两点P的直线的斜率公式是k=(y2-y1)/(x2-x1)。
每条直线都有倾斜角,但并不是每条直线都有斜率。
求斜率的一般方法有两种:已知直线上两点,根据斜率公式k=(y2-y1)/(x2-x1)求斜率;已知直线的倾斜角α或α的某种三角函数,根据k=tanα来求斜率。
利用斜率证明三点共线的方法:已知A(x1,y1),B(x2,y2),C(x3,y3),若x1=x2=x3或kAB=kBC,则有A、B、C三点共线。
考点一:斜率与倾斜角。
例1.已知直线l的斜率的绝对值等于3,则直线的倾斜角为30度或150度。
例2.已知过两点A(m2+2,m2-3),B(3-m2-m,2m)的直线l的倾斜角为45度,求实数m的值。
考点二:三点共线。
已知三点A(a,2)、B(3,7)、C(-2,-9a)在一条直线上,求实数a的值。
考点三:斜率范围。
例1.已知两点A(-2,-3),B(3,0),过点P(-1,2)的直线l与线段AB始终有公共点,求直线l的斜率k的取值范围。
例2.已知实数x、y满足2x+y=8,当2≤x≤3时,求y的最大值与最小值。
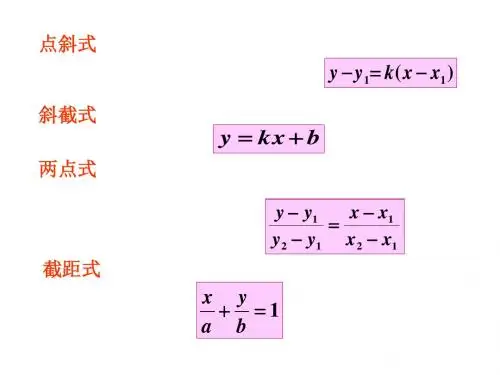
二、直线方程直线方程有四种形式:点斜式、斜截式、两点式和截距式。
其中,点斜式的形式为y-y1=k(x-x1),斜截式的形式为y=kx+b,两点式的形式为(y-y1)/(x-x1)=(y2-y1)/(x2-x1),截距式的形式为xy+a+b=0.点斜式的局限性是不包括垂直于x轴的直线,斜率k为斜率。
斜截式的局限性是不包括垂直于x轴和y轴的直线,k为斜率,b是直线在y轴上的截距。
高一直线方程知识点直线方程是高中数学中的重要内容之一,它在几何图形的研究以及解决实际问题中起着重要的作用。
本文将介绍高一阶段涉及的直线方程知识点,涵盖了一元一次方程、点斜式、两点式和截距式四种形式。
一、一元一次方程一元一次方程是最简单的直线方程形式,也是了解直线方程的基础。
一元一次方程的一般形式为y = kx + b,其中k和b为实数常数。
其中,k表示直线的斜率,b表示直线与y轴的截距。
通过给定的斜率k和截距b,我们可以画出对应的直线。
例如,当k = 2,b = 3时,直线的方程为y = 2x + 3。
这条直线的斜率为2,截距为3,表示一种矢量在平面上的运动轨迹。
二、点斜式点斜式是一种常用的直线方程形式,它利用直线上的一个点和直线的斜率来确定直线方程。
点斜式的一般形式为y - y₁ = k(x -x₁),其中(x₁, y₁)为直线上的一点,k为直线的斜率。
通过给定的点(x₁, y₁)和斜率k,我们可以构造出直线的方程。
例如,当直线上的一点为(2, 4),斜率为3时,直线的方程为y - 4= 3(x - 2)。
这条直线通过点(2, 4),斜率为3。
三、两点式两点式是利用直线上的两个点来确定直线方程的形式。
两点式的一般形式为(y - y₁)/(y₂ - y₁) = (x - x₁)/(x₂ - x₁),其中(x₁, y₁)和(x₂, y₂)为直线上的两个点的坐标。
通过已知的两个点的坐标(x₁, y₁)和(x₂, y₂),我们可以建立直线的方程。
例如,当直线上的两个点为(3, 1)和(5, 4)时,直线的方程为(y - 1)/(4 - 1) = (x - 3)/(5 - 3)。
这条直线通过点(3, 1)和(5, 4)。
四、截距式截距式是直线方程的另一种表示形式,它利用直线与x轴和y 轴的截距值来确定直线方程。
截距式的一般形式为x/a + y/b = 1,其中a和b分别为直线与x轴和y轴的截距。
通过给定的截距值a和b,我们可以写出直线的方程。