正弦、余弦函数的性质(一)

正弦函数、余弦函数的图象和性质（一）●作业导航掌握用“五点法”画正弦函数图象，掌握正弦函数的定义域、值域、最大值和最小值、周期、奇偶性、单调性．一、选择题(本大题共5小题，每小题3分，共15分)1．函数f (x )＝sin(5x ＋27π)是( )A ．奇函数B ．偶函数C ．非奇非偶函数D ．既是奇函数又是偶函数 2．下列函数中，最小正周期为π的偶函数是( )A ．y ＝sin2xB ．y ＝cos 2xC ．y ＝sin2x ＋cos2xD ．y ＝x x22tan 1tan1+- 3．y ＝3sin|x |，x ∈R 的值域为( ) A ．(0，3) B ．［0，3］ C ．(-3，3) D ．［-3，3］4．设函数f (x )是周期为2T 的函数，若f (x )定义域为R ，且图象关于直线x ＝T 对称，那么f (x )是( )A ．奇函数B ．偶函数C ．非奇非偶函数D ．既是奇函数又是偶函数5．已知f (x )＝122-a a(a x -a -x )，且0<a <1，那么，此函数的反函数是( ) A ．奇函数且为减函数 B ．偶函数且为减函数 C ．奇函数且为增函数D ．偶函数且为增函数二、填空题(本大题共5小题，每小题3分，共15分)1．用“五点法”画函数y ＝2-sin x ，x ∈［0，2π］的图象时，五个关键点分别是________．2．函数y ＝1sin 2-x 的定义域是________．3．已知奇函数f (x )，当x >0时，f (x )＝x ＋cos x ，则x <0时，f (x )的解析式为________． 4．已知奇函数y ＝f (x )对一切x ∈R 满足f (x ＋1)＝f (x -1)，当x ∈［-1，0］时，f (x )＝3x＋94，则f (5log31)＝________．5．设函数y ＝f (x )是最小正周期为2的偶函数，它在区间［0，1］上的图象为线段AB ，如图，则在区间［1，2］上，f (x )的解析式为________．三、解答题(本大题共5小题，每小题6分，共30分)1．求函数y ＝x xx sin 1cossin 22+⋅的最大值和最小值．2．把截面直径为40cm 的圆形木料锯成矩形木料，问如何选择矩形的尺寸，才能使得废弃的木料最少？3．若cos 2θ＋2msin θ-2m -2<0恒成立，试求实数m 的取值范围．4．求证：f (x )＝lg x x xx cos sin cos sin -+为奇函数．5．若(x ＋2y )3＋x 3＋2x ＋2y ＝0，求(x ＋y )10的值．参考答案一、选择题(本大题共5小题，每小题3分，共15分)1．B 分析：sin(5x ＋27π)＝-cos5x ．2．D 分析：y ＝xx 22tan 1tan1+-＝cos2x ．3．D分析：y ＝3sin|x |＝⎩⎨⎧<-≥0sin 30sin 3x xx x ． -3≤3sin x ≤3，-3≤-3sin x ≤34．B 分析：∵ f (x )的图象关于x ＝T 对称 ∴ f (T -x )＝f (T ＋x ) ① 又f (x )的周期为2T∴ f (T ＋x )＝f (T ＋x -2T )＝f (x -T )②由①、②有f (T -x )＝f (x -T ) 令x -T ＝t ，则f (-t )＝f (t )对一切t ∈R 都成立∴ f (x )是偶函数．5．C 分析：∵ f (-x )＝122-a a(a -x -a x )＝-f (x )∴ f (x )为奇函数∵ g (x )＝a x 和ϕ(x )＝-(a 1)x 都是减函数，122-a a<0∴ f (x )＝122-a a［g (x )＋ϕ(x )］是增函数．二、填空题(本大题共5小题，每小题3分，共15分)1．(0，2)，(2π，1)，(π，2)，(23π，3)，(2π，2)2．{x |6π＋2k π≤x ≤65π＋2k π，k ∈Z }分析：2sin x -1≥0 sin x ≥21由图象或单位圆可得6π＋2k π≤x ≤65π＋2k π，k ∈Z 3．x -cos x 分析：x <0，则-x >0 ∴ f (-x )＝-x ＋cos(-x )＝-x ＋cos x 又f (-x )＝-f (x )∴ -f (x )＝-x ＋cos x ∴ f (x )＝x -cos x (x <0)4．-1 分析：令t ＝x -1，即x ＝t ＋1 ∴ f (t )＝f (t ＋2)∴ f (x )是周期为2的函数∵ 5log31＝-log 35∵ 1<log 35<2 ∴ -1<log 35-2<0f (5log31)＝-f (log 35)1)9495()943(2log53-=+-=+-=- 5．x 分析：线段AB 的方程为 f (x )＝-x ＋2(0≤x ≤1)当1≤x ≤2时 0≤-x ＋2≤1 则有f (-x ＋2)＝-(-x ＋2)＋2＝x ．三、解答题(本大题共5小题，每小题6分，共30分)1．解：y ＝xx x xxx sin 1)sin1(sin 2sin 1cossin 222+-=+⋅21)21(s i n 2)1)(s i n s i n 1(s i n 2s i n 1)s i n 1)(sin 1(sin 22+--=-≠-=+-+=x x x x x x x x∵ -1<sin x ≤1∴ -4<y ≤21∴ 当sin x ＝21时，即x ＝2k π＋6π或x ＝2k π＋65π，k ∈Z 时，y 有最大值21． ∵ sin x ≠-1∴ y 无最小值．2．解：如图，BD ＝40 cm ，设∠DBC ＝θ，矩形面积为S ，则S ＝40cos θ·40sin θ＝1600sin θcos θ＝800sin2θ 当sin2θ＝1时，即2θ＝90°，θ＝45°时 S 有最大值800 cm 2 ∴ 当矩形为正方形且边长为202cm 时，废弃的木料最少． 3．解：设sin θ＝t ，t ∈［-1，1］，要使cos 2θ＋2m sin θ-2m -2<0恒成立． 也就是t 2-2mt ＋2m ＋1>0，t ∈［-1，1］恒成立．设f (t )＝t 2-2mt ＋2m ＋1，对称轴方程为t ＝m ．(1)当t <-1时，只要f (-1)>0．即1＋2m ＋2m ＋1>0 m >-21这与m <-1矛盾，舍去 (2)当-1≤m ≤1时只要f (m )>0，即m 2-2m 2＋2m ＋1>0 m 2-2m -1<01-2<m <1＋2．∴ 1-2<m ≤1．(3)当m >1时，只要f (1)>0，即1-2m ＋2m ＋1>0．即2>0． ∴ m >1时，f (t )>0恒成立 综上(1)、(2)、(3)有m >1-2．4．证明：x x xx cos sin cos sin -+>01t a n 1t a n -+xx >0 (tan x ＋1)(tan x -1)>0 tan x >1或tan x <-1k π＋4π<x <k π＋2π，k ∈Z 或k π＋2π<x <k π＋43π，k ∈Z函数的定义域为{x |k π＋4π<x <k π＋2π或k π＋2π<x <k π＋43π，k ∈Z }，关于原点对称．)(c o ss i n c o s s i n lg)cos sin cos sin lg(cos sin cos sin lgcos sin sin cos lg )cos()sin()cos()sin(lg)(1x f x x x x xx x x xx x x x x x x x x x x x f -=-+-=-+=+-=---=----+-=--又∴ f (x )为奇函数．5．解：∵ (x ＋2y )3＋x 3＋2x ＋2y ＝0∴ (x ＋2y )3＋(x ＋2y )＝-(x 3＋x )①构造函数f(t)＝t3＋t(t∈R)f(-t)＝(-t)3＋(-t)＝-(t3＋t)＝-f(t)∴f(t)是奇函数∵g(t)＝t3，h(t)＝t为R上的增函数∴f(t)＝g(t)＋h(t)＝t3＋t为R上的增函数．由①得f(x＋2y)＝-f(x)＝f(-x)∴x＋2y＝-x∴x＋y＝0∴(x＋y)10＝0。

6．1正弦函数和余弦函数的图像与性质（一）上海曙光中学陶慰树一．教学内容分析本章节内容是在学生学习了三角比及有关三角恒等变形公式后，从函数的角度和层面来研究相关三角问题。

对于函数的研究，学生已经具备了一定的知识基础和对简单的具体函数的研究经验，结合三角函数的特殊性，教材改变了研究函数由性质到图像的研究策略，而是先得出三角函数的图像，再由图像归纳性质这一途径。

为此通过函数图像作图的一般方法---描点法（五点发）及正余弦函数在单位圆中正弦线和余弦线所具备的特征构造正弦函数和余弦函数的图像，学生容易接受，而对于通过函数的图像的平移或对称得出余弦函数和相关其他三角函数的图像可能比较困难，需要在教学时加以指导和突破。

正弦函数和余弦函数的图像在三角函数的研究中是一个基础和前提，为后面得出正弦函数和余弦函数的性质、进一步加深对函数图像的研究将起着至关重要的作用。

二．教学目标设计1、能结合单位圆中的正弦线、余弦线理解正弦函数及余弦函数中函数值的变化规律；2、通过五点法能正确作出正弦函数的图像，并能归纳正弦函数图像的特征；3、通过函数图像的变换，能作出余弦函数及相关函数图像；4、在渗透数形结合的数学思想过程中，培养学生类比和转化的思维习惯。

三．教学重点难点正弦函数和余弦函数的图像的形成和应用。

四．教学用具准备多媒体设备五．教学流程设计六．教学过程设计一．复习引入1．复习：学生口述函数的定义。

2．引入：结合我们刚学过的三角比，就以正弦（或余弦）为例，对每一个给定的角x 和正弦值x sin （或x cos ）之间是否也存在一种函数关系？若存在，请对这种函数关系下一个定义，若不存在请说明理由。

3．讨论：对自变量x 的取值类型和范围进行讨论，并给出相应的正弦函数和余弦函数的记号。

复习引入正弦函数、余弦函数的概念正弦函数和余弦函数的图像 转化 转化单位圆中的正弦线和余弦线 五点作图法巩固与深化、应用课堂总结以往我们在研究函数时，先探究函数所具备的性质，再作出函数的图像，今天我们先探究正弦函数和余弦函数的图像，再得出函数的性质。

第11课时　正弦函数、余弦函数的性质(1)——周期性、奇偶性 课时目标1.掌握周期函数概念，会求三角函数周期．2．能判断三角函数的奇偶性． 识记强化1．周期性：(1)对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f (x ＋T )＝f (x )，则函数y ＝f (x )叫做周期函数，非零常数T 叫做这个函数的周期．对于一个周期函数f (x )，如果它所有的周期中存在一个最小的正数，那么这个最小正数就叫做f (x )的最小正周期．(2)y ＝sin x ，y ＝cos x 都是周期函数，2k π(k ∈Z ，k ≠0)都是它们的周期，最小正周期是2π.2．y ＝A sin(w x ＋φ)，x ∈R 及y ＝A cos(ωx ＋φ)，x ∈R (其中A 、ω、φ为常数且A ≠0，ω>0)的周期为T ＝.2πω3．y ＝sin x ，x ∈R 是奇函数，y ＝cos x ，x ∈R 是偶函数；sin(－x )＝－sin x ，cos(－x )＝cos x .4．反映在图象上，正弦曲线关于原点对称，余弦曲线关于y 轴对称． 课时作业一、选择题1．下列说法中正确的是( )A ．当x ＝时，sin≠sin x ，所以不是f (x )＝sin x 的周期π2(x ＋π6)π6B ．当x ＝时，sin＝sin x ，所以是f (x )＝sin x 的一个周期5π12(x ＋π6)π6C ．因为sin(π－x )＝sin x ，所以π是y ＝sin x 的一个周期D ．因为cos ＝sin x ，所以是y ＝cos x 的一个周期(π2－x )π2答案：A解析：T 是f (x )的周期，对应f (x )的定义域内任意x 都有f (x ＋T )＝f (x )成立．2．函数y ＝－5cos(3x ＋1)的最小正周期为( )A. B ．3ππ3C. D.2π33π2答案：C解析：该函数的最小正周期T ＝＝.2πω2π33．函数y ＝cos的最小正周期是( )(π4－x 3)A ．πB ．6πC ．4πD ．8π答案：B解析：最小正周期公式T ＝＝＝6π.2π|ω|2π|－13|4．下列函数中，最小正周期为π的是( )A ．y ＝sin xB ．y ＝cos xC ．y ＝sinD ．y ＝cos2xx 2答案：D解析：A 项，y ＝sin x 的最小正周期为2π，故A 项不符合题意；B 项，y ＝cos x 的最小正周期为2π，故B 项不符合题意；C 项，y ＝sin 的最小正周期为T ＝＝4π，故C 项不x 22πω符合题意；D 项，y ＝cos2x 的最小正周期为T ＝＝π，故D 项符合题意．故选D.2πω5．函数f (x )＝x sin ( )(π2－x )A ．是奇函数B ．是非奇非偶函数C ．是偶函数D ．既是奇函数又是偶函数答案：A解析：由题，得函数f (x )的定义域为R ，关于原点对称．又f (x )＝x sin ＝x cos x ，∴f (－x )＝(－x )cos(－x )＝－x cos x ＝－f (x )，∴函数f (x )为奇函数．(π2－x )6．已知函数f (x )＝的定义域为R ，则( )cos (sin x )A ．f (x )是奇函数B ．f (x )是偶函数C ．f (x )既是奇函数又是偶函数D ．f (x )既不是奇函数又不是偶函数答案：B解析：∵函数f (x )＝的定义域为R ，关于原点对称，且f (－x )cos (sin x )＝＝＝＝f (x )，∴f (x )＝为偶函数．cos[sin (－x )]cos (－sin x )cos (sin x )cos (sin x )二、填空题7．若f (x )是奇函数，当x ＞0时，f (x )＝x 2－sin x ，则当x ＜0时，f (x )＝________.答案：－x 2－sin x解析：利用奇函数的定义求解．当x ＜0时，－x ＞0，因f (x )为奇函数，所以f (x )＝－f (－x )＝－[(－x )2－sin(－x )]＝－x 2－sin x .8．函数f (x )是以2为周期的函数，且f (2)＝3，则f (6)＝________.答案：3解析：∵函数f (x )是以2为周期的函数，且f (2)＝3，∴f (6)＝f (2×2＋2)＝f (2)＝3.9．已知函数f (x )＝ax ＋b sin x ＋1，若f (20 15)＝7，则f (－2 015)＝________.答案：－5解析：由f (2 015)＝2 015a ＋b sin2 015＋1＝7，得2 015a ＋b sin2 015＝6，∴f (－2 015)＝－2 015a －b sin2 015＋1＝－(2 015a ＋b sin2 015)＋1＝－6＋1＝－5.三、解答题10．已知函数f (x )＝log |sin x |.12(1)求其定义域和值域；(2)判断奇偶性；(3)判断周期性，若是周期函数，求其周期．解：(1)|sin x |>0⇒sin x ≠0，∴x ≠k π(k ∈Z )．∴定义域为{x |x ≠k π，k ∈Z }∵0<|sin x |≤1，∴log |sin x |≥0，12∴函数的值域是{y |y ≥0}．(2)定义域关于原点对称∵f (－x )＝log |sin(－x )|12＝log |sin x |＝f (x )，12∴函数f (x )是偶函数．(3)∵|sin x |在定义域{x |x ≠k π，k ∈Z }内是周期函数，且最小正周期是π，∴函数f (x )＝log |sin x |是周期函数，最小正周期为π.1211．设f (x )＝log 3.1－2sin x1＋2sin x (1)求函数f (x )的定义域；(2)判断函数f (x )的奇偶性．解：(1)∵>0，1－2sin x1＋2sin x ∴－<sin x <，1212∴k π－<x <k π＋，k ∈Z ，π6π6∴该函数的定义域为.{xk π－π6<x <k π＋π6，k ∈Z }(2)由(1)知定义域关于原点对称，又f (－x )＝log 31＋2sin x 1－2sin x＝log 3－1(1－2sin x1＋2sin x )＝－log 31－2sin x1＋2sin x＝－f (x )，∴该函数为奇函数． 能力提升12．函数f (x )满足f (x ＋2)＝－，则f (x )的最小正周期是________．1f (x )答案：4解析：f (x ＋4)＝－＝f (x )所以函数f (x )的最小正周期是4.1f (x ＋2)13．求函数f (x )＝|sin x |＋|cos x |的最小正周期．解：设f (x )的最小正周期为T ，则有f (x ＋T )＝f (x )，对x ∈R 恒成立．即|sin(x ＋T )|＋|cos(x ＋T )|＝|sin x |＋|cos x |.令x ＝0，得|sin T |＋|cos T |＝1.两边平方，得|sin T |·|cos T |＝0.∴角T 的终边在坐标轴上．∴T ＝(k ∈N ＋)．k π2又f＝|sin |＋|cos |(x ＋π2)(x ＋π2)(x ＋π2)＝|cos x |＋|－sin x |＝|cos x |＋|sin x |＝f (x )，∴f (x )＝|sin x |＋|cos x |的最小正周期为.π2。

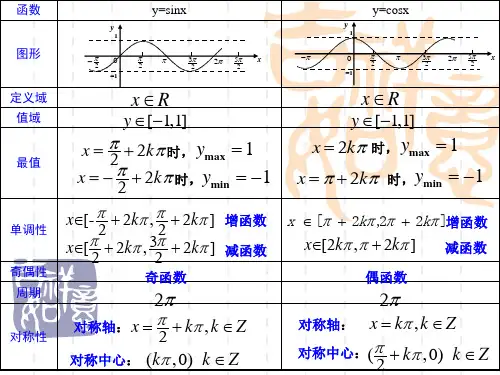
讲解新课：正弦、余弦函数的图象（1）函数y=sinx 的图象：叫做正弦曲线第一步：在直角坐标系的x 轴上任取一点1O ，以1O 为圆心作单位圆，从这个圆与x 轴的交点A 起把圆分成n(这里n=12)等份.把x 轴上从0到2π这一段分成n(这里n=12)等份.（预备：取自变量x 值—弧度制下角与实数的对应）.第二步：在单位圆中画出对应于角6,0π，3π，2π,…，2π的正弦线正弦线（等价于“列表” ）.把角x 的正弦线向右平行移动，使得正弦线的起点与x 轴上相应的点x 重合，则正弦线的终点就是正弦函数图象上的点（等价于“描点” ）.第三步：连线.用光滑曲线把正弦线的终点连结起来，就得到正弦函数y=sinx ，x ∈[0，2π]的图象．根据终边相同的同名三角函数值相等，把上述图象沿着x 轴向右和向左连续地平行移动，每次移动的距离为2π，就得到y=sinx ，x ∈R 的图象.把角x ()x R ∈的正弦线平行移动，使得正弦线的起点与x 轴上相应的点x 重合，则正弦线的终点的轨迹就是正弦函数y=sinx 的图象.（2）余弦函数y=cosx 的图象：叫做余弦曲线 根据诱导公式,可以把正弦函数y=sinx 的图象向左平移2π单位即得余弦函数y=cosx 的图象.（3）用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的五个点关键是哪几个？(0,1) (2π,0) (π,-1) (23π,0) (2π,1) 讲解范例：例1 作下列函数的简图(1)y=1+sinx ，x ∈[0，2π]， （2）y=-COSx探究 如何利用y=sinx ，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到 （1）y ＝1＋sinx ,ｘ∈〔0，２π〕的图象； （2）y=sin(x- π/3)的图象？y=cosxy=sinxπ2π3π4π5π6π-π-2π-3π-4π-5π-6π-6π-5π-4π-3π-2π-π6π5π4π3π2ππ-11y x-11o xy小结：函数值加减，图像上下移动；自变量加减，图像左右移动。