统计学作业第六章方差分析
- 格式:docx
- 大小:2.34 MB
- 文档页数:16
第六章方差分析(五)[测量实验设计的方差分析一、重复测量的方差分析(一)重复测量实验设计的相关含义⑴重复测量实验设计的定义又叫:被试内设计、受试者内设计、单组实验设计、相关样本设计。
是每个被试或每组被试必须接受自变量的所有情况的处理(每个被试接受所有的实验处理水平或处理水平的结合)。
由于被试的行为是重复测量的,所以被试内实验设计也称重复测量实验设计。
(2)重复测量设计的基本原理每个被试者参与所有的实验处理,然后比较相同被试者在不同处理下的行为变化。
这种实验设计下的同一被试者既为实验组提供数据,也为控制组提供数据。
因此,被试者内设计无需另找控制组的被试者。
被试内设计不但节省了被试人数,而且不同组的被试个体差异也得到了最好的控制,被试内设计比被试间设计更有力,能更好的考察实验组和控制组之间的差异,这个优点使得许多研究者更倾向于使用被试内设计。
和被试间设计相反,被试内设计不会受到来自被试个体差异的困扰但却必需面对实验处理之间相互污染的问题。
可以采用平衡技术来控制这些差异。
(3)使用重复测量设计的主要目的重复测量实验设计的目的是所有被试自已做控制,使被试的各方面特点在该因素所有水平上保持恒定,克服被试间设计中存在的被试不同质的问题,以最大限度地控制由被试的个体差异带来的变异。
如果实验者主要想研究一个被试者对实验处理所引起的行为上的变化,一般可以考虑采用被试者内设计。
(二)重复测量实验设计的方差分析的条件重复测量实验设计方差分析是一般方差分析的深化,也具有正态性、变异的可加性和方差齐性等先决条件,还要求各重复测量数据组成的协方差矩阵满足球形性假设。
博克斯指出,若球状性假设得不到满足,则方差分析的F值是有偏的,会增加犯I类错误的可能。
(三)重复测量实验设计的方差分析的过程①建立检验假设;②计算离差平方和与均方;③进行F检验;④列出方差分析表。
二、单因素重复测量的方差分析(一)重复测量实验设计的基本方法实验中每个被试接受所有的处理水平。

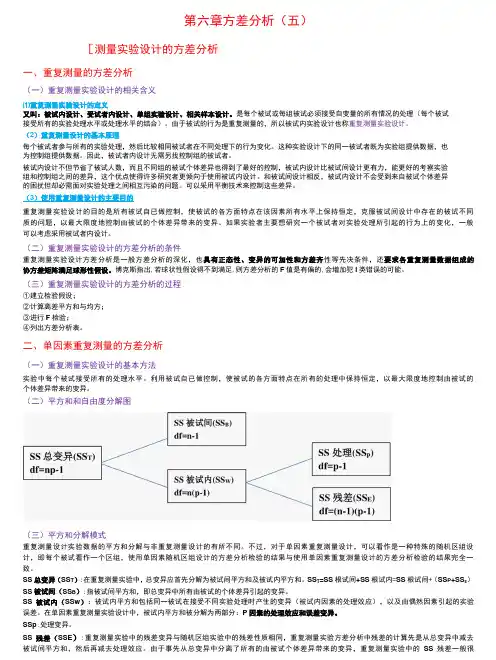
(1)平方和的计算
C = T2/nk (T为总和,n为处理数,k为重复数) 总平方和SS T = ∑x2–C
处理间平方和SS t= ∑ Ti2– C
处理内平方和SSe =SST - SSt
(2)自由度的计算
dfT = nk-1 总自由度dfT
dft = k-1 处理间自由度(dft)
dfe = dfT - dft = k(n-1) 处理内自由度(dfe)
(3) 方差的计算
处理间方差st2 = SSt/ dft
处理内方差se2 = Sse/dfe
(4) 显著性F检验
F = st2 /se2
F < F0.05 P >0.05 接受Ho 处理间差异不显著 F > F0.05 P <0.05 否定Ho 处理间差异显著 F > F0.01 P <0.01 否定Ho 处理间差异极显著
多重比较
最小显著差数法(LSD 法,实质是成组t 检验。
)
在F 检验显著的前提下,先计算出显著水平为α的最小显著差数 LSD α,然后将任意两个处理平均数的差数的绝对值与其比较。
若 |X1-X2| >LSD α 时,则 X1 与 X2在α水平上差异显著;反之,则在α水平上差异不显著。
组内观察次数不等 ()()()1022--∑∑∑=k n n n i i i n 02022 21n s s n s s e x x e x ==-或。

第五章 假设检验 第六章 方差分析1、某厂生产一种产品,原月产量服从)14,75(N 。
设备更新后,为了考察产量是否提高,抽查了6个月的产量,其平均产量为78。
问在显著水平5%条件下,设备是否值得更新?2、某工厂对所生产的产品进行质量检验,规定:次品率不得超过0.01,方可出厂。
现从一批产品中随机抽查80件,发现次品2件。
试问在0.05的显著水平下,这批产品是否可以出厂?3、已知某种电子元件的使用寿命服从标准差为100小时的正态分布,要求平均寿命不得低于1000小时。
现在从一批这种电子元件中随机抽取25件,测得平均寿命为950小时。
试在0.02 的显著性水平下,检验这批元件是否合格.4、在正常生产情况下,某厂生产的无缝钢管的内径服从均值为54mm 、 标准差为0.9mm 的正态分布。
某日从当天生产的产品中随机抽取10根,测得内径分别为:53.8,54.0,55.1,54.2,52.1,54.2,55.0,55.8,55.4,55.5(单位:mm )。
试检验该日产品生产是否正常(α=5%)。
5、某专家认为A 地男孩入学率明显高于女孩,小学男女学生比例至少是6:4。
从A 地小学中随机抽取400个学生的调查结果是:男生258人,女生142人.问当α=5%时,调查结果是否支持该专家的观点?6、某饮料厂生产一种新型饮料,其颜色有四种分别为:橘黃色、粉色、绿色、和无色透明。
随机从5家商场收集了前一期其销售量,数据如下表:数据计算结果如下:组间平方和为76.8445,组内平方和为39.084。
问饮料的颜色是否对产品的销售量产生显著的影响?{66.8)3,16(05.0=F ,24.3)16,3(05.0=F ,29.5)16,3(01.0=F ,69.26)3,16(01.0=F }。


第六章方差分析第一节方差分析概述一.方差分析的定义[用途]定义:用途方差分析也称为变异数分析,是在教育与心理研究中最常用的变量分析方法,其主要功能在于分析测量或实验数据中不同来源的变异对总变异的贡献大小,从而确定测量或实验中因素对反应变量是否存在显著影响。
即用于置信度不变情况下的多组平均数之间的差异检验。
它既可以比较两个以上的样本平均数的差异检验,也可以应用于一个因素多种水平以及多个因素有多种水平的数据分析。
二.方差分析的作用方差分析主要应用于两种以上实验处理的数据分析,同时匕徽两个以上的样本平均数,推断多组资料的总体均数是否相同,也即检验多组数据之间的均数差异是否有统计意义。
在这个意义,也可以将其理解为平均数差异显著性检验的扩展。
当我们用多个t检验来完成这一过程时,相当于从t分布中随机抽取多个t值,这样落在临界范围之外的可能大大增加,从而增加了I型错误的概率,我们可以把方差分析看作t检验的增强版。
方差分析一次检验多组平均数的差异,降低了多次进行两组平均数检验所带来的误差。
在进行方差分析时,设定的假设是综合虚无假设,即假设样本所归属的所有总体的平均数都相等。
如果检验的结果是存在显著性差异,只能说明多组平均数之间存在显著性差异,但是无法确定究竟哪些组之间存在显著性差异,此时需要运用事后检验的方法来确定。
三.方差分析的相关概念一(一)数据的变异(1)变异:统计中的变异是普遍存在的7一般意义上的变异是指标志(包括品质标志和数量标志)在总体单位之间的不同表现。
可变标志的属性或数值表现在总体各单位之间存在的差异,统计上称之为变异,这是广义上的变异,即包括了品质标志和数量标志,有时仅指品质标志和在总体单位之间的不同表现。
注:随机性,即变异性。
(2)组间变异[组间差异]:组间变异表示处理间变异,主要指由于接受不同的实验处理(实验处理效应)而造成的各组之间的变异,可以用两个平均数之间的离差来表示,可将组间离差平方和记为SS AO组间差异可用组间方差来表征,用符号MS B表示。





一、单选题1、方差分析的主要目的是()。
A.研究类别自变量对数值因变量的影响是否显著B.比较各总体的方差是否相等C.判断各总体是否存在有限方差D.分析各样本数据之间是否有显著差异正确答案:A2、在方差分析中,一组内每个数据减去该组均值后所得结果的平方和叫做()A.组间离差平方和B.组内离差平方和C.以上都不是D.总离差平方和正确答案:C3、在单因素方差分析中,若原假设是H0: α1=α2=⋯=αr=0,则备择假设是()A. α1>α2>⋯>αrB. α1<α2<⋯<αrC.不全为0D. α1≠α2≠⋯≠αr正确答案:C4、下面选项中,不属于方差分析所包含的假定前提是()。
A.等方差假定B.独立性假定C.非负性假定D.正态性假定正确答案:C5、只考虑主效应的双因素方差分析是指用于检验的两个因素()A. 对因变量的影响是有交互作用的B.对自变量的影响是独立的C.对因变量的影响是独立的D. 对自变量的影响是有交互作用的正确答案:C6、下列不属于检验正态分布的方法是()A.Shapiro-Wilk统计检验法B.饼图C.K-S统计检验法D. 正态概率图正确答案:B7、在单因素方差分析中,用于检验的F统计量的计算公式是()A.[(n-r)SSA]/[(r-1)SSE]B.SSA/SSEC. SSA/SSTD.[(n-1)SSE]/[(r-1)SSA]正确答案:A8、在只考虑主效应的双因素方差分析中,因素A有r个水平,因素B有s个水平,因素A和B每个水平组合只有一个观测值,观测值共rs个,下面结论正确的是()A.随机误差的均方差为SSE/(rs-1)B. 因素A检验统计量[SSA/(r-1)]/[SSE/(rs-r-s+1)]C. SSA+SSB=SSTD.因素A的均方差为SSA/r正确答案:B9、在考虑交互效应的双因素方差分析中,因素A有r个水平,因素B有s个水平,因素A、B每个水平组合都有m个观测值,下面结论正确的是()A.因素A检验统计量[SSA/(r-1)]/[SSE/(rs-r-s+1)]B.SSA+SSB+SSE≤SSTC.SSAB≤SSED.随机误差的均方差为SSE/(rsm-rs+1)正确答案:B10、只考虑主效应的双因素方差分析中,因素A、B的水平数分别是3和4,因素A和B每个水平组合只有一个观测值,则随机误差的自由度等于()A. 3B.6C.12D.11正确答案:B二、多选题1、对于方差分析法,叙述正确的有()A.是用于多个总体的方差是否相等的检验B.是用于多个总体是否相互独立的检验C.是区分观测值变化主要受因素水平还是随机性影响的检验D.是用于多个总体的均值是否相等的检验正确答案:C、D2、应用方差分析的前提条件是()A.各个总体相互独立B.各个总体具有相同的方差C.各个总体均值不等D.各个总体服从正态分布正确答案:A、B、D3、对于方差分析,下面哪些说法是对的?()A.双因素方差分析一定存在交互效应B.组内均方差一定小于组间均方差C.组内均方差消除了观测值多少对误差平方和的影响D.综合比较了随机因素和系统因素的影响正确答案:C、D4、为研究教学方法和本科生年级对教学效果的影响,将教学方法分为三个水平,本科生年级分为四个水平,对这种方差分析叙述正确的是()A.双因素方差分析B. 没有交互效应C.三因素方差分析D.未知方差齐性正确答案:A、D5、在只考虑A、B主效应的双因素方差分析中,已知SSA=13004.55,自由度为3;SSE=2872.7,自由度为12;SST=17888.95,自由度为19,则下列结论中正确的有:()A.统计量FB的值等于2.1008B.因素B的自由度为4C.统计量FA的值等于8.6193D.SSB=2011.7正确答案:A、B、D三、判断题1、在双因素方差分析中,总离差平方和自由度等于因素A的自由度、因素B的自由度、交互作用的自由度、随机误差的自由度相加减去4。

统计学作业第六章方差分析
习题6.4 为研究氟对种子发芽的影响,分别用0μg/g(对照)、10μg/g、50μg/g、100μg/g、4种不同浓度的氟化钠溶液处理种子(浸种),每一种浓度处理的种子用培养皿进行发芽实验(每盆50粒,每处理重复三次)。
观察它们的发芽情况,测得芽长(cm)资料如下表。
试作方差分析,并用LSD法、SSR法和q法分别进行多重比较。
解:1、假设H0:不同处理浓度对种子发芽情况没有显著性差异。
对H1:不同处理浓度对种子发芽情况有显著性差异。
2、取显著水平α=0.05
3、用SPSS软件进行方差检验计算如下:
(1)打开SPSS软件,输入数据,如图:
(2)在主菜单栏中选择“分析”选项的“比较均值”,在下拉菜单中选择“单因素ANOVA”,如图:
(3)将左边方框里的“芽长”放到右边的“因变量列表”方框中,“处理浓度”放到右边的“因子”中。
如图:
(4)点击“对比”,打开对话框,选中“多项式”。
在“度”中选
择“线性”,点击“继续”如图:
(5)点击“选项”,在“统计量”中选中“描述性”和“方差同质性检验”,点击“继续”。
再点击“继续”即得到结果。
如图:
从检验结果可知sig显著性概率0.224>0.05,说明方差具有齐次性。
(6)经过方差同质性检验,再进行两两比较,前面步骤同上,然后点击“两两比较”,在假定方差齐次性中选中“LSD”、“S-N-K”、“Duncan”,点击“继续”,然后点击“确定”,即得到结果。
如图:
4、结果分析:
(1)根据方差分析表得到的sig.显著概率0.001<0.05,所以否定H0,接受H1,即不同处理浓度对种子发芽情况有显著性差异。
(2)LSD法多重比较表明:
处理浓度0μg/g与50μg/g、100μg/g之间存在显著性差异;
处理浓度10μg/g与50μg/g、100μg/g之间存在显著性差异;
处理浓度50μg/g与0μg/g、10μg/g之间存在显著性差异;
处理浓度100μg/g与0μg/g、10μg/g之间存在显著性差异;
(3)SSR法多重比较表明:
处理浓度0μg/g与50μg/g、100μg/g之间存在显著性差异;
处理浓度10μg/g与50μg/g、100μg/g之间存在显著性差异;
处理浓度50μg/g与0μg/g、10μg/g之间存在显著性差异;
处理浓度100μg/g与0μg/g、10μg/g之间存在显著性差异;习题6.6 选取4个品种的家兔,每一品种用兔7只,测定其不同室温下血糖值,以每100mg血中含葡萄糖的mg数表示,问各种家兔血糖值间有无差异?室温对家兔的血糖值有无影响?试验资料见下表。
解:1、假设H0:各种家兔血糖值间无显著差异;室温对家兔的血糖值无显著差异;对H1:各种家兔血糖值间有显著差异;室温对家兔的血糖值有显著差异;
2、取显著水平为α=0.05
3、用SPSS软件进行方差检验计算如下:
(1)打开SPSS软件,输入数据,如图:
(2)在主菜单栏中选择“分析”选项的“一般线性模型”,在下拉菜单中选择“单变量”,如图:
(3)将左边方框里的“血糖值”放到右边的“因变量”方框中,“室温”“品种”放到右边的“固定因子”中。
如图:
(4)单击模型,选中“设定”,在“类型”中选择“主效应”,
然后将左边方框里的“室温”和“品种”放到右边方框中,点击“继续”。
然后点击“确定”,即可得到检验结果。
如图:
4、结果分析
由SPSS“单变量”检验结果可知:
(1)不同室温对家兔血糖值的偏差均方为1755.036,F值为
19.119,显著概率是0.000<0.05,所以否定H0,接受假设H1,
即不同室温对家兔血糖值有显著性差异。
(2)不同品种对家兔血糖值的偏差均方为919.464,F值为
10.016,显著概率是0.000<0.05,所以否定H0,接受假设H1,
即不同品种对家兔血糖值有显著性差异。
习题6.8药物处理大豆种子试验中,使用了大、中、小粒三种类型种子,分别用五种浓度、两种处理时间进行试验处理,播种后45d对每种处理各取两个样本,每个样本取10株测定其干物重(g),求其平均数,结果如下表。
试进行方差分析。
解:1、假设H0:不同处理时间对种子干重没有显著性差异;
不同种子类型对种子干重没有显著性差异;
不同处理浓度对种子干重没有显著性差异;
不同处理时间与不同种子类型共同对种子干重没有显著性差异;
不同种子类型与不同处理浓度共同对种子干重没有显著性差异;
不同处理时间与不同浓度共同对种子干重没有显著性差异;
不同处理时间、不同种子类型与不同浓度共同对种子干重没有显著性差异。
则对H1:不同处理时间对种子干重有显著性差异;
不同种子类型对种子干重有显著性差异;
不同处理浓度对种子干重有显著性差异;
不同处理时间与不同种子类型共同对种子干重有显著性差异;
不同种子类型与不同浓度共同对种子干重有显著性差异;
不同处理时间与不同浓度共同对种子干重有显著性差异;
不同处理时间、不同种子类型与不同浓度共同对种子干重有显著性差异。
2、取显著水平为α=0.05
3、用SPSS软件进行方差检验计算如下:
(1)打开SPSS软件,输入数据,如图:
(2)在主菜单栏中选择“分析”选项的“一般线性模型”,在下拉菜单中选择“单变量”,如图:
(3)将左边方框里的“干重”放到右边的“因变量”方框中,“A”“B”“C”放到右边的“固定因子”中。
如图:
(4)单击模型,选中“全因子”,点击“继续”。
然后点击“确定”,
即可得到检验结果。
如图:
4、结果分析
由SPSS“单变量”检验结果可知:
(1)不同处理时间对种子干重的偏差均方为1189.04,F值为2239.95,显著概率是0.000<0.05,所以否定H0,接受假设H1,即不同处理时间对种子干重有显著性差异。
(2)不同处理浓度对种子干重的偏差均方为228.881,F值为431.173,显著概率是0.000<0.05,所以否定H0,接受假设H1,即不同处理浓度对种子干重有显著性差异。
(3)不同种子类型对种子干重的偏差均方为10.186,F值为19.188,显著概率是0.000<0.05,所以否定H0,接受假设H1,即不同种子类型对种子干重有显著性差异。
(4)不同处理时间、浓度对种子干重的偏差均方为100.805,F值为189.899,显著概率是0.000<0.05,所以否定H0,接受假设H1,即不同处理时间、浓度共同对种子干重有显著性差异。
(5)不同处理时间、种子类型对种子干重的偏差均方为0.707,F值为1.332,显著概率是0.279>0.05,所以接受假设H0,即不同处理时间、种子类型共同对种子干重没有显著性差异。
(6)不同处理浓度、种子类型对种子干重的偏差均方为5.987,F值为11.279,显著概率是0.000<0.05,所以否定H0,接受假设H1,即不同处理浓度、种子类型共同对种子干重有显著性差异。
(7)不同处理时间、处理浓度、种子类型对种子干重的偏差均方为
3.720,F值为7.008,显著概率是0.000<0.05,所以否定H0,接
受假设H1,即不同处理时间、处理浓度、种子类型共同对种子干重有显著性差异。