统计学课件第10章方差分析

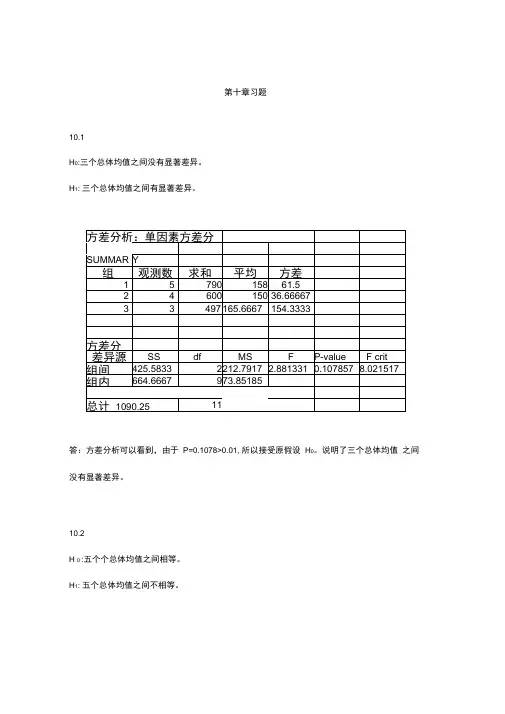
第十章习题10.1H0:三个总体均值之间没有显著差异。

H1: 三个总体均值之间有显著差异。

答：方差分析可以看到，由于P=0.1078>0.01, 所以接受原假设H0。

说明了三个总体均值之间没有显著差异。

10.2H 0 :五个个总体均值之间相等。

H1: 五个总体均值之间不相等。

P=1.02E-05<0.01, H0值之间不相等。

10.3H 0 :四台机器的装填量相等。

H1: 四台机器的装填量不相等答：方差分析可以看到，由于P=0.00068<0.01, 所以拒接原假设H0。

说明了四台机器装填量不相同。

10.4H 0 :不同层次管理者的满意度没有差异。

H1: 不同层次管理者的满意度有差异P=0.000849<0.05, H0理者的满意度有差异。

10.5H0：3 个企业生产的电池平均寿命之间没有显著差异。

H1: 3 个企业生产的电池平均寿命之间有显著差异单因素方差分析多重比较因变量: VAR00002*. 0.05答：方差分析可以看到，由于P=0.00031<0.01, 所以拒接原假设H0。

说明了不同 3 个企业生产的电池平均寿命之间有显著差异。

通过SPSS分析（1,2,3代表A,B,C公司），通过显著性对比可知道A和B以及B和C 公司有差异。

10.6H0：不同培训方式对产品组装的时间没有显著影响。

答：方差分析可以看到，由于P=0.00196<0.05, 所以拒接原假设H0。

说明了不同培训方式对产品组装的时间没有显著影响。

10.8H 0:u 1=u 2=u 3=u 4=u 5 H 1:u i (i=1,2,3,4,5) 不全相等 H 0:u 1=u 2=u 31i对于行因素， P=0.000236<0.01, 所以拒绝原假设。

说明不同供应商生产的轮胎对磨损 程度有显著影响。

对于列因素， p=2.39E-06<0.01 ，所以拒绝原假设，说明不同车速对磨损程度有显著 影响。

统计学方差分析方差分析（Analysis of Variance，缩写为ANOVA）是一种常用的统计学方法，广泛应用于数据分析中。

它的主要目的是用于比较多个样本群体之间的均值是否存在显著差异。

通过方差分析，可以确定因素对于不同组之间的差异程度有无显著影响。

方差分析的基本原理是将数据进行分解，并据此计算各部分之间的均方差（mean square），然后通过比较这些均方差的比值，得出各部分对总体的贡献程度，并进行显著性检验。

在方差分析中，数据通常被分为几个不同的组别，每个组别称为一个因素（factor）。

每个因素可以有不同的水平（level），例如性别因素可以有男和女两个水平。

而一个水平下的所有观测值构成一个处理（treatment）或条件（condition）。

方差分析的基本模型是一种线性模型，假设因变量与自变量之间存在线性关系。

对于单因素方差分析，它的模型可以表示为：Y=μ+α+ε其中，Y表示因变量，μ表示总体的平均值，α表示组别之间的差异，ε表示组内误差。

方差分析的目标是判断组别之间的差异（α）与组内误差（ε）的比值是否显著。

方差分析的核心思想是通过计算均方差，评估不同因素水平之间的差异是否显著。

均方差是方差与其自由度的比值，用于度量数据的离散程度。

通过计算组间均方差（MSTr）和组内均方差（MSE），我们可以得出F值，进而进行显著性检验。

F值是组间均方差与组内均方差的比值F = (MSTr / dfTr) / (MSE / dfE)其中，dfTr表示组间自由度，dfE表示组内自由度。

在统计学中，F值与显著性水平相关。

当F值大于显著性水平对应的临界值时，我们可以拒绝原假设，认为组别之间存在显著差异。

否则，我们不能拒绝原假设，即组别之间的差异不显著。

方差分析不仅可以应用于单因素情况，还可以扩展到多因素情况。

多因素方差分析可以用于研究多个自变量对因变量的影响，并评估这些自变量之间是否存在交互作用。

统计学方差分析方差分析（ANOVA）是统计学中一种用于比较多个样本平均值之间差异的方法。

它能够确定因素（或者称之为自变量）对因变量的影响是否显著。

在进行方差分析时，常常使用F检验来判断不同组之间的平均值是否存在显著差异。

方差分析常被用于实验设计和自然观察研究中，特别是在多个因素同时影响因变量的情况下。

方差分析基于总体的假设，即总体的均值相等。

方差分析的目的是确定是否存在一个或多个因素对于因变量的影响。

这些因素可以是分类因素（例如不同的治疗组）或者连续因素（例如不同的剂量水平）。

方差分析通过计算组内变异和组间变异之间的比率来判断这种影响是否显著。

方差分析的基本原理是将组内变异（即观测值之间的差异）与组间变异（即组均值之间的差异）进行比较。

如果组间变异大于组内变异，那么可以推断存在一个或多个因素对于因变量的影响。

通过计算F统计量（组间均方与组内均方之比），可以判断这种影响是否显著。

方差分析有几个基本假设需要满足。

首先，观测值必须是互相独立的。

其次，观测值必须是正态分布的。

最后，方差必须是均匀的，也就是方差齐性假设。

方差分析可以分为单因素方差分析和多因素方差分析。

单因素方差分析适用于只有一个因素对因变量的影响进行研究的情况。

多因素方差分析适用于有多个因素同时对因变量进行影响的情况。

在多因素方差分析中，可以考虑因素之间的交互作用。

方差分析还可以通过进行事后多重比较来进一步研究组之间的差异。

常用的事后比较方法包括LSD（最小显著差异）方法、Tukey HSD（Tukey honestly significant difference）方法和Bonferroni校正方法等。

方差分析在实际应用中具有广泛的应用。

例如，在医学研究中，可以使用方差分析来比较不同治疗组的效果；在工程设计中，可以使用方差分析来确定不同因素对产品质量的影响；在社会科学研究中，可以使用方差分析来研究不同教育程度对工资的影响等等。

方差分析是统计学中重要的一种方法，能够帮助我们了解不同因素对因变量的影响程度。

统计学中的方差分析统计学是研究人类活动中涉及到随机事件和不确定性因素的科学。

方差分析（Analysis of Variance, ANOVA）是一种统计学方法，可用于比较两个或多个组之间的差异。

本文将介绍方差分析的基本概念和原理。

一、方差分析的基本概念方差分析是指基于数据的方差计算和分析，以确定比较两组或更多组数据差异的方法。

在方差分析中，被比较的组称为因素，因素又可分为单因素和多因素。

单因素方差分析包括一组数据，而多因素方差分析包括两个及以上的组数据。

方差分析的目的是确定不同组的平均值（即均数）的变异程度。

当平均数之间的差异大于各组内部个体数据的方差时，方差分析可以用来检测这种变异，而不是寻找单一的差异。

方差分析通过比较组之间的方差和误差方差来确定组之间的显著性差异性。

二、方差分析的原理方差分析的原理是基于样本和总体的假设。

以单因素方差分析为例，假设总体是由不同平均数的正态分布组成，且方差相等（即方差齐性）。

然后，从每组中随机地取样本，计算每组的均数和样本方差。

接下来，计算每组的平均数之间的方差（即组间方差）和每组内部样本方差之间的平均数（即组内方差）。

根据方差分析的原理，如果组间方差显著大于组内方差，则说明组间的差异显著，即这些组之间存在显著差异。

否则，如果组间方差与组内方差相等或组内方差超过组间方差，则说明差异不显著。

三、方差分析的步骤通常包括以下步骤：1、获取数据：数据必须充分、均匀，且符合正态分布。

2、检验方差齐性：检验各组数据的方差是否相等。

3、建立假设：建立总体假设和样本假设。

4、计算统计量：计算f值。

5、确定P值：确定P值以确定显著性水平。

6、作出结论：根据显著性水平的大小，对假设的接受或拒绝进行结论。

四、方差分析的应用方差分析应用广泛。

在医学统计学中，方差分析被用于研究不同治疗方案对患者疗效的影响。

在经济学中，方差分析用于分析不同市场条件下商品价格的波动和供求曲线变化的因素。

在生态学中，方差分析可用于分析各种生境因素对植物和动物物种多样性的影响。

统计学中的方差分析方差分解方差分析（analysis of variance，简称ANOVA）是一种常用的统计方法，它用于比较两个或多个组之间的差异。

在方差分析中，方差分解是一项重要的计算过程，用于将总方差分解成不同来源的方差成分，从而了解各因素对总体差异的影响程度。

1. 概述方差分析方差分解是对方差分析结果进行深入分析的一种方法。

方差分析通过比较组间变异与组内变异来评估不同组之间的差异是否显著。

而方差分解则将总体方差分解为几个基本的成分，以揭示不同因素对差异的贡献。

2. 方差分析方差分解的步骤2.1 总体方差计算首先，我们需要计算总体方差。

总体方差是整个数据集的方差，表示整体的差异程度。

2.2 组间方差计算接下来，计算组间方差。

组间方差反映了不同组之间的差异程度。

2.3 组内方差计算然后，计算组内方差。

组内方差表示同一组内部的差异程度。

2.4 方差分解通过将总体方差分解成组间方差和组内方差，我们可以计算各成分对总差异的贡献。

3. 方差分解的应用方差分解是统计学中广泛应用的一种分析方法，它在众多领域中都有重要的应用价值。

3.1 实验设计在实验设计中，方差分解可以帮助我们分析不同因素对实验结果的影响程度，从而优化实验设计。

3.2 质量控制在质量控制领域，方差分解可以帮助企业分析产品质量的差异来源，以制定相应的质量改进策略。

3.3 教育研究在教育研究中，方差分解可以用于评估不同因素对学生成绩的影响，帮助改进教学方法和教育政策。

4. 总结方差分析方差分解是统计学中一个重要的工具，它可以帮助我们理解不同因素对差异的贡献，为实验设计、质量控制和教育研究等领域提供决策支持。

总之，方差分析方差分解是统计学中的一项重要技术，通过将总方差分解成不同来源的方差成分，我们可以深入分析各因素对总体差异的影响程度。

方差分解在实验设计、质量控制和教育研究等领域都有广泛的应用，为这些领域提供了可靠的数据分析基础。

通过学习和应用方差分析方差分解的方法，我们可以更好地理解和解释数据，为决策提供科学支持。